Apex hydrogen bonds in dendron assemblies modulate close-packed mesocrystal structures†
Taesuk
Jun
a,
Hyunjun
Park
b,
Seungbae
Jeon
a,
Hyungju
Ahn
 c,
Woo-Dong
Jang
c,
Woo-Dong
Jang
 *b,
Byeongdu
Lee
*b,
Byeongdu
Lee
 *d and
Du Yeol
Ryu
*d and
Du Yeol
Ryu
 *a
*a
aDepartment of Chemical and Biomolecular Engineering, Yonsei University, 50 Yonsei-ro, Seodaemun-gu, Seoul 03722, Korea. E-mail: dyryu@yonsei.ac.kr
bDepartment of Chemistry, Yonsei University, 50 Yonsei-ro, Seodaemun-gu, Seoul 03722, Korea. E-mail: wdjang@yonsei.ac.kr
cIndustry Technology Convergence Centre, Pohang Accelerator, Laboratory, 80 Jigok-ro, Nam-gu, Pohang 37673, Korea
dAdvanced Photon Source, Argonne National Laboratory, Argonne, IL 60439, USA. E-mail: blee@anl.gov
First published on 2nd November 2022
Abstract
The close-packed mesocrystal structures from soft-matter assemblies have recently received attention due to their structural similarity to atomic crystals, displaying various sphere-packing Frank–Kasper (FK) and quasicrystal structures. Herein, diverse mesocrystal structures are explored in second-generation dendrons (G2-X) designed with identical wedges, in which the terminal functionalities X = CONH2 and CH2NH2 represent two levels of the strong and weak hydrogen-bonding apexes, respectively. The cohesive interactions at the core apex, referred to as the core interactions, are effectively modulated by forming heterogeneous hydrogen bonds between these two functional units. For the dendron assemblies compositionally close to each pure component of G2-CONH2 and G2-CH2NH2, their own FK A15 and C14 phases dominate other phases, respectively. We show the existence of the wide-range FK σ including the dodecagonal quasicrystal (DDQC) phases from the dendron mixtures between G2-CONH2 and G2-CH2NH2, providing an experimental phase sequence of A15–σ–DDQC–C14 as the core interactions are alleviated. Intriguingly, the temperature dependence of particle sizes shows that the high plateau values of particle sizes are maintained equivalently until each threshold temperature (Tth), followed by a prompt decrease above the Tth. A decrease in Tth by alleviating the core interactions and its composition dependence suggest that the more size-dispersed particles, the more susceptibility to chain exchange with increasing temperature. Our results on the formation of supramolecular dendron assemblies provide a guide to understand the core-interaction-dependent mesocrystal structures toward the fundamental principle underlying the temperature dependence of their particle sizes.
Introduction
Most of the metallic elements usually pack together into simple high-symmetry structures, such as body-centred cubic (BCC), face-centred cubic, and hexagonal close-packed phases,1–3 except for a few complex structures of manganese and uranium.4–6 In contrast, the soft-matter spheres obtained from single-component molecular assemblies have recently emerged as synthetic building units prone to transform into complex close-packed mesocrystal structures, where the spherical particles with different sizes and shapes pack into low-symmetry structures.7–9 These point-like particle assemblies are analogous to those of metal alloys in terms of three-dimensional (3D) packing characteristics such as the coordination number (CN), particle size and shape dispersity.10,11 The low-symmetry phases observed in soft-matter assemblies include Frank–Kasper (FK) structures12–15 as well as 10- and 12-fold quasiperiodic lattices.16–19 To date, these sophisticated mesocrystal structures have been identified in the molecular self-assemblies of dendritic molecules,12,20–22 surfactants,9,15 block copolymers,14,23 amphiphiles,24,25 and other soft matters.26–28 Some of these unconventional structures have been found to possess unique properties applicable for photonic and electronic devices.29,30In order to infer the assembling principle of molecules into thermodynamically stable structures, it is essential to understand the formation of complex phases and their packing mechanism. Thermotropic and lyotropic liquid crystals (LCs) are found beneficial for addressing such challenges because their modular features can afford to provoke the packing diversity arising from the delicate thermodynamic balance in such systems.31 In particular, a dendron assembly is a simple and versatile platform that has provided a rich series of 2D columnar and 3D sphere-packing structures,32,33 in which the cohesive interactions at the core apex, referred to as the core interactions, are the attractive force acting radially towards the body and peripheral chains.21,25,34–36 Their supramolecular assemblies associated with unique architectures have enabled earlier access to well-defined mesocrystal structures such as the FK and quasicrystal phases.12,20,22,37
The pioneering studies by Percec, Ungar, and co-workers well demonstrated the FK A15 and σ phases and the dodecagonal quasicrystal (DDQC) phase was demonstrated by adjusting the structural combination and generation number of dendrons.12,20–22,34,38 By presenting the radial distribution of volume functions (dV/dr) for the sphere-packing structures, they suggested that the dendritic wedges determine the geometry of particle assemblies.12,13,39 In this concept of topologically close-packed structures, the body–periphery composition in dendron architectures influences the mesoscale packing structures of dendritic assemblies.35,40–42 Furthermore, it has been believed that the cohesive interactions from the apex functional units also play an important role in guiding specific packing structures. Our previous study highlighted that the discrete increase in the core interactions in single-component dendron assemblies resulted in a remarkable increase in the dendron's interfacial tension (γo) between alkyl chains (corona) and benzyl ether bodies (core).43 The thermotropic and lyotropic approaches to form apex-dependent second-generation (G2) dendrons led to the observation of columnar and various mesocrystal structures. This finding triggered an interesting question as to how delicate control of the core interactions can affect diverse supramolecular assemblies, transitions, and the temperature dependence of particle sizes.
To answer this question, we explored core-interaction-dependent mesocrystal structures with two types of G2 dendrons, G2-CONH2 and G2-CH2NH2, which represent two levels of the strong and weak hydrogen-bonding apexes, respectively. The core interactions were effectively modulated by forming heterogeneous hydrogen bonds between these two apex units. In the dendron assemblies compositionally close to each pure component of G2-CONH2 and G2-CH2NH2, their own FK A15 and C14 phases dominated other phases, respectively. However, the FK σ phase including the DDQC phase widely existed over the composition of the dendron mixtures, providing an experimental phase sequence of A15–σ–DDQC–C14 by alleviating the core interactions. From the temperature dependence of particle sizes, we generalized that the high plateau values of particle sizes are maintained equivalently until each threshold temperature (Tth), followed by a prompt decrease above the Tth. Our concept of a master curve for the Tth pointed out the size dispersity effect induced by the core-interaction-dependent mesocrystal structures.
Experimental
Synthesis and chemical characterisation
All reagent-grade chemicals were purchased from Sigma-Aldrich, TCI, Alfa Aesar, Duksan, or Fluka. The commercial products dichloromethane (CH2Cl2), n-hexane, tetrahydrofuran (THF), and methanol (CH3OH) were freshly distilled before each use, and all other chemicals were used as received without further purification. To characterise the molecular structures, 1H and 13C NMR spectra were measured using a DPX 400 (Bruker) at room temperature in deuterated CH2Cl2 (CD2Cl2) and chloroform solutions, respectively. Matrix-assisted laser desorption ionisation time-of-flight mass spectrometry (MALDI-TOF-MS) was performed using an LRF20 (Bruker) using dithranol (1,8,9-trihydroxyanthracene) as a matrix. Detailed information on the synthetic processes has been described in the previous study.43 The bulk densities of the dendrons were evaluated using a solution mixture of water and ethanol once the sample species were constantly suspended in the solution for 30 min. The thermal properties of all samples were characterised using a PerkinElmer Diamond differential scanning calorimetry (DSC) instrument with loading amounts of approximately 10 mg under a nitrogen flow. The temperature and heat flow scales were calibrated using indium as the standard material.Small-angle X-ray scattering (SAXS) measurements
SAXS experiments were performed at the 4C and 9A beamlines of the Pohang Accelerator Laboratory, Korea, or the 12-ID-B beamline of Advanced Photon Source, USA. The operating conditions for the 4C and 9A beamlines were set at a wavelength of λ = 0.633 Å, a sample-to-detector distance (SDD) of 1 m, and an exposure time of 1–15 s; these were similarly set at the 12-ID-B beamline with λ = 0.954 Å, SDD = 2 m, and an exposure time of 1–10 s. The scattered intensities were collected using 2D detectors (Rayonix SX165 and Pilatus2M) at the target temperatures. The system temperature was selected as the mean value during heating at a rate of 1.0 °C min−1 under a nitrogen flow.Electron density (ED) map reconstructions
The SAXS intensity profiles of all dendron assemblies were recorded to obtain the ED maps of each characteristic sphere-packing phase. Using MATLAB, the structure-factor intensities and positions for each peak over q = 0.1–5.0 nm−1 were assigned according to each space-group symmetry and lattice parameter,44,45 and then recorded as the input values for SUPERFLIP.46 Random phases were initially generated through a charge-flipping algorithm of SUPERFLIP, and the densities at each pixel in a unit cell were examined. If the calculated density is below zero (indicating an unphysical result), it is multiplied by −1 to make it positive. A discrete Fourier transform of the resulting density maps was employed to regenerate new structural factors, which were again subjected to other iterations. The converged results were averaged and visualised using MATLAB software (in 90% contour levels) to construct Voronoi cells for the experimental polyhedra.Results and discussion
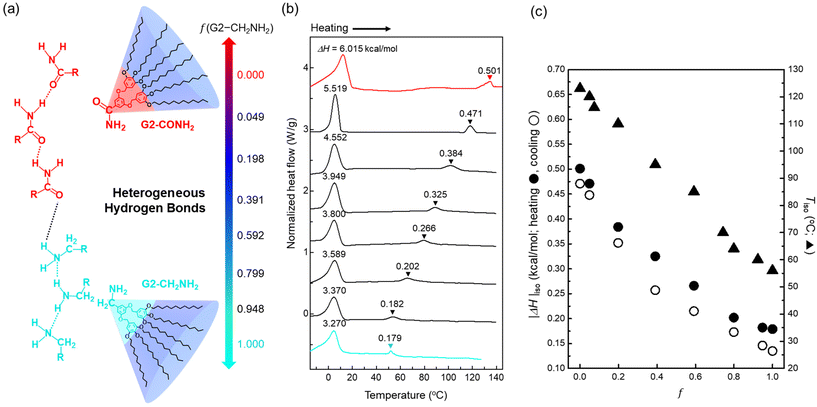
Fig. 1a illustrates the chemical structures of (3,4,5-3,5)12G2-X dendrons with two different terminal units, X = CONH2 and CH2NH2, at the same body and peripheral chains, where the two functionalities represent the strong and weak hydrogen-bonding apexes, respectively.43 If the G2 dendron analogues possessing identical wedges are miscible, a heterogeneous hydrogen bond can be formed between these two apex units. As an easy way of controlling the supramolecular sphere-packing structures, this chemical compatibility is essentially required for modulating the core interactions that attract the wedges.The dendron mixtures between G2-CONH2 and G2-CH2NH2 were prepared by a solvent casting method from a co-solvent of chloroform and subsequently dried under vacuum before thermal treatments. DSC measurements were conducted at heating/cooling rates of ±10 °C min−1 between −30 and 150 °C to trace the phase behaviours of the dendron assemblies (Fig. 1b and Fig. S1†). The large endotherms and exotherms at lower temperatures upon heating and cooling, respectively, imply that the peripheral alkyl chains melt below room temperature, and the second endotherms (or exotherms upon cooling) at higher temperatures represent each clearing temperature of LC phases into an isotropic state (Tiso).
As the mass fraction (f) of G2-CH2NH2 increases, the magnitude of the enthalpy change (|ΔH|iso) at isotropisation and the Tiso decrease (Fig. 1c). Above all, there are no indications of macrophase separation that would generate two separate transitions in the immiscible binary mixtures. In this framework of dendron assemblies arising from the heterogeneous hydrogen bonds between two apex units attached to identical wedges, |ΔH|iso can be an indicator of the dendron's overall interfacial tension (γo) that signifies the core interactions. Thus, we speculate that the consistent decreases in |ΔH|iso and Tiso upon compositionally increasing f are attributed to weakening of the core interactions in the dendron assemblies. Even the values of |ΔH| at lower temperatures are found to show the same decreasing trend as |ΔH|iso, indicating that the alkyl chain melting is also affected by a gradual reduction of the core interactions.
The SAXS intensity profiles of all dendron assemblies were recorded for structural analysis at the target temperatures, at which a constant interval of 5 min was applied to all samples during a stepwise heating process because of the relatively rapid kinetics in forming the mesocrystal structures. The scattering vector q = (4π/λ) sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, where 2
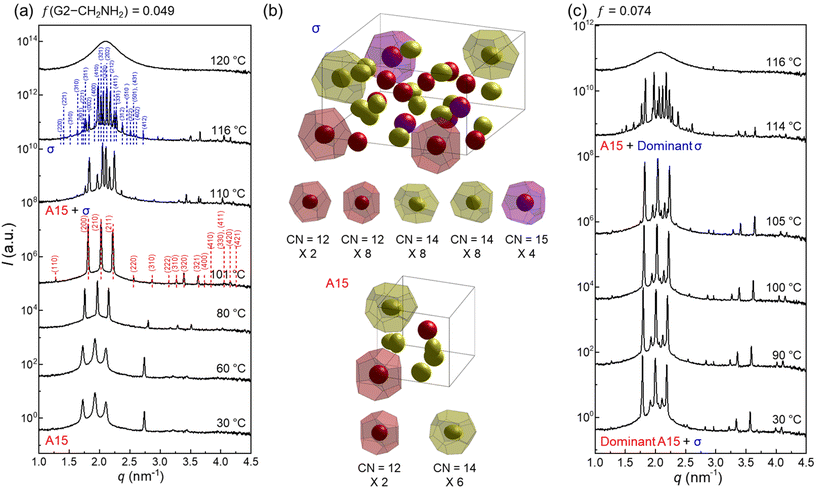
θ, where 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and λ are the scattering angle and wavelength of the X-ray beam, respectively. To erase the previous thermal histories, the sample aggregates were first heated to 130 °C and cooled to room temperature at a rate of −10 °C min−1. All samples were then annealed at 30 °C under vacuum, which is still higher than the crystallisation temperatures (5–12 °C) of the peripheral alkyl chains. Note that pure G2-CONH2 exhibited hexagonal columnar (Colh), A15, and BCC phases with increasing temperature.43 At a small fraction of f = 0.049 (Fig. 2a), the SAXS profile measured at 30 °C shows a pattern corresponding to a cubic A15 phase, which becomes increasingly distinctive up to 101 °C, representing that a small amount of G2-CH2NH2 is sufficient to modify the packing structures manifested in pure G2-CONH2. This cubic structure first reorganises to a tetragonal σ phase in a narrow temperature window of 110 to 116 °C, and then to an isotropic phase above 120 °C. The A15–σ transition is accessed by a small alleviation of the core interactions; this type of transition was reported in a G3 dendron with a terminal COOH apex.12
θ and λ are the scattering angle and wavelength of the X-ray beam, respectively. To erase the previous thermal histories, the sample aggregates were first heated to 130 °C and cooled to room temperature at a rate of −10 °C min−1. All samples were then annealed at 30 °C under vacuum, which is still higher than the crystallisation temperatures (5–12 °C) of the peripheral alkyl chains. Note that pure G2-CONH2 exhibited hexagonal columnar (Colh), A15, and BCC phases with increasing temperature.43 At a small fraction of f = 0.049 (Fig. 2a), the SAXS profile measured at 30 °C shows a pattern corresponding to a cubic A15 phase, which becomes increasingly distinctive up to 101 °C, representing that a small amount of G2-CH2NH2 is sufficient to modify the packing structures manifested in pure G2-CONH2. This cubic structure first reorganises to a tetragonal σ phase in a narrow temperature window of 110 to 116 °C, and then to an isotropic phase above 120 °C. The A15–σ transition is accessed by a small alleviation of the core interactions; this type of transition was reported in a G3 dendron with a terminal COOH apex.12
Electron density (ED) maps were reconstructed from the X-ray scattering data using a SUPERFLIP software program.44–46 The dendron cores are displayed at 90% contour levels (isosurfaces) and colour-coded with a sequence of red-yellow-magenta-cyan-blue according to each particle type for clarity, displaying that the larger the particles (with higher CN) are, the more rounded are the cores. An A15 phase has two polyhedra with CN = 14 and 12, whereas a σ phase has five different types of polyhedra with CN = 15, 14, 14, 12, and 12 (Fig. 2b); these are analyzed with the number of Voronoi cells, surface area, volume, and isoperimetric quotient (IQ), as listed in Table S1.† At f = 0.074 (Fig. 2c), the A15 and σ phases coexist at temperatures lower than 116 °C. However, the σ phase continues to grow at the expense of the A15 phase as the temperature increases, as observed similarly at f = 0.103 (Fig. S2†). In principle, this phenomenon indicates that an increase in temperature in the system is consistent with a reduction of the hydrogen-bonding strength at the core apexes to produce more diverse particle species.
When increasing f to 0.198 (Fig. 3a), the A15 phase completely disappears and only the σ phase appears during the heating process before it becomes an isotropic phase at 110 °C. The σ phase window extends to f = 0.592 (Fig. S3†), although the characteristic intensities of the σ phase diminish with increasing f. At f = 0.698 (Fig. 3b), interestingly, the DDQC phase appears at 30 °C and retains the same structure up to 50 °C, which has three different types of polyhedra with CN = 15, 14, and 12 (Fig. 3f). It further transforms into the σ phase at 70 °C. The weak intensity of the σ phase is presumably attributable to smaller grain sizes prior to becoming an isotropic phase. The same trend continues up to f = 0.743 (Fig. S4†), although the DDQC–σ transition and isotropisation occur at slightly lower temperatures than those of f = 0.698. This type of DDQC–σ transition was also often observed in G3 dendrons with a terminal CH2OH apex,22 oligomeric G1 dendrons,47 and ABn dendron-like giant molecules.48
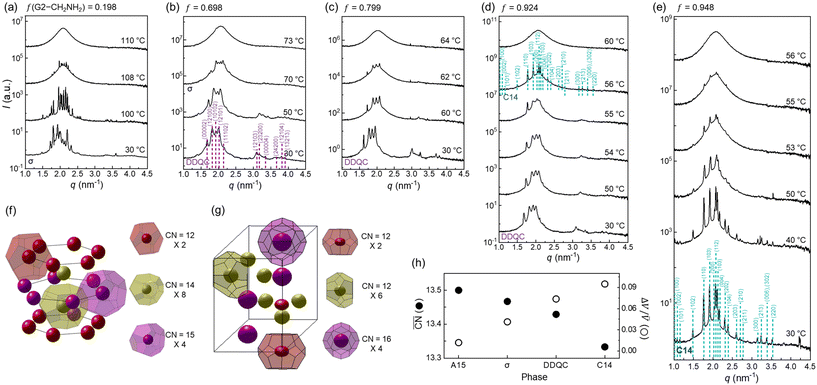 | ||
Fig. 3 SAXS intensity profiles of dendron assemblies with (a) f = 0.198 (only σ phase), (b) f = 0.698 (DDQC–σ transition), (c) f = 0.799 (only DDQC phase), (d) f = 0.924 (DDQC–C14 transition), and (e) f = 0.948 (only C14 phase). ED maps of (f) DDQC and (g) C14 phases obtained from dendron assemblies with f = 0.799 (c) and f = 0.948 (e) at 30 °C, respectively. For the ED map of the DDQC phase, Voronoi cells were retrieved from its ideal fractional coordinates and the unit cell size determined from the X-ray data (Fig. S7†). (h) 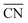 and ΔV/ and ΔV/![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) for the sphere-packing structures. Our experimental phase sequence of A15–σ–DDQC–C14 with increasing f follows an increase in ΔV/ for the sphere-packing structures. Our experimental phase sequence of A15–σ–DDQC–C14 with increasing f follows an increase in ΔV/![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) and a decrease in and a decrease in 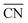 as the core interactions are alleviated. as the core interactions are alleviated. | ||
The slow-cooling (−1 °C min−1) phase from an isotropic state was not the DDQC but the σ phase within the experimental time scale of 1 day. However, the DDQC phase at f = 0.698 was fully recovered when the sample was reannealed at 30 °C for a long period of 2 months, as shown by the 2D diffraction pattern and intensity profile of the DDQC phase (Fig. S5†). This evidence supports that the DDQC phase obtained from our dendron assemblies is an equilibrium state requiring long-time annealing, and not a metastable state. For f = 0.799 (Fig. 3c), only the DDQC phase forms at 30 °C and becomes an isotropic phase at 64 °C, similar to that observed up to f = 0.897 (Fig. S6†).
When the f approaches 0.924 (Fig. 3d), the DDQC phase formed at 30 °C undergoes a transition to the hexagonal C14 phase at 56 °C, which has three different types of polyhedra with CN = 16, 12, and 12 (Fig. 3g), before becoming an isotropic phase at 60 °C. Notably, this unique DDQC–C14 transition is elicited by further alleviating the core interactions, which has never been reported to date. However, the dendron assembly at f = 0.948 (Fig. 3e) begins with a C14 phase at 30 °C and retains the same structure up to 55 °C prior to becoming an isotropic phase; this Tiso is slightly higher than that (50 °C) measured in pure G2-CH2NH2. In addition, the advent of the C14 phase only above f = 0.924 indicates that the delicate tuning of the core interactions from the dendron mixtures meets the demanding conditions for the rare C14 phase and its transition. It should be pointed out that the Tiso follows a decreasing tendency from 120 to 60 °C with increasing f because of the gradual reduction of the hydrogen-bonding strength at the core apex. Furthermore, all the LC transitions such as A15–σ, DDQC–σ, and DDQC–C14 were reproducible upon heating when the isotropic samples were annealed at 30 °C for a short period of 10 min.
Based on the four experimental phases of A15, σ, DDQC, and C14 (Table S1†) obtained at the specified temperatures, the dendron assemblies are treated as Voronoi cells composed of polyhedra. The average particle volume is set to 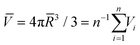 , where
, where ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) and Vi are the average spherical sizes of the polyhedra and the ith polyhedron volume of n particles, respectively. We analyzed the average coordination number (
and Vi are the average spherical sizes of the polyhedra and the ith polyhedron volume of n particles, respectively. We analyzed the average coordination number (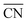 ) and particle size dispersity (ΔV/
) and particle size dispersity (ΔV/![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) ) depending on the sphere-packing structures (Fig. 3h). In principle, the more coordinated with the others, the less size-dispersed the sphere-packing particles are, and vice versa.49 Our experimental phase sequence of A15–σ–DDQC–C14 with increasing f follows an increase in ΔV/
) depending on the sphere-packing structures (Fig. 3h). In principle, the more coordinated with the others, the less size-dispersed the sphere-packing particles are, and vice versa.49 Our experimental phase sequence of A15–σ–DDQC–C14 with increasing f follows an increase in ΔV/![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) and a decrease in
and a decrease in 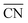 as the core interactions are alleviated. This suggests that the weak hydrogen-bonding dendrons are prone to generate larger and smaller particles, whereas the strong hydrogen-bond dendrons favour more uniform-sized particles rather than larger and smaller ones, which is consistent with a theoretical consideration from the previous study.43
as the core interactions are alleviated. This suggests that the weak hydrogen-bonding dendrons are prone to generate larger and smaller particles, whereas the strong hydrogen-bond dendrons favour more uniform-sized particles rather than larger and smaller ones, which is consistent with a theoretical consideration from the previous study.43
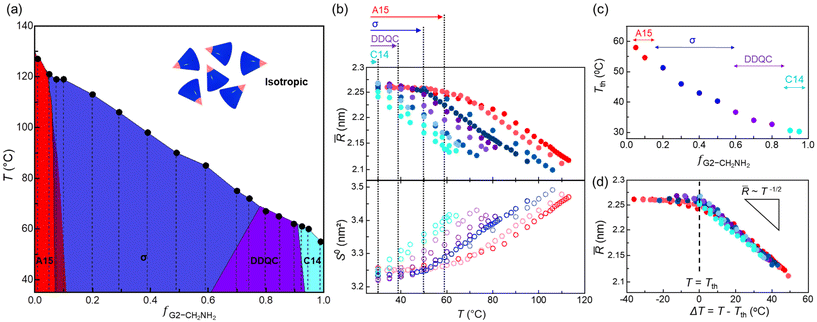
Fig. 4a shows the overall phase diagram of temperature versus f, and the red, blue, purple, and cyan phase regions represent the A15, σ, DDQC, and C14 phases, respectively. It displays the composition-dependent phases of A15–σ–DDQC–C14 along with a linear decrease in Tiso. The σ and DDQC phases occupy 87.5% with respect to the entire range of f, representing that they accommodate a moderate and broad range of hydrogen-bonding strengths at the core apex. For more details, we examined the temperature dependence of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) and the interfacial area per chain (S0 = 4π
and the interfacial area per chain (S0 = 4π![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2/Nagg), where Nagg denotes the aggregation number of average particles by
2/Nagg), where Nagg denotes the aggregation number of average particles by ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) agg = 4π
agg = 4π![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 3NAρ/3M. Here, NA, ρ, and M are the Avogadro's number, density, and the molecular weight of each dendron depending on f, respectively. Since the Nagg is proportional to the average particle volume
3NAρ/3M. Here, NA, ρ, and M are the Avogadro's number, density, and the molecular weight of each dendron depending on f, respectively. Since the Nagg is proportional to the average particle volume ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 3, S0 is in turn inversely proportional to
3, S0 is in turn inversely proportional to ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) .
.
Fig. 4b shows the ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) and S0 curves as a function of temperature. The symbols coloured in red, blue, purple, and cyan with increasing f denote the A15, σ, DDQC, and C14 phases, respectively. At lower temperatures, all the values remain relatively constant in each range of 2.24 <
and S0 curves as a function of temperature. The symbols coloured in red, blue, purple, and cyan with increasing f denote the A15, σ, DDQC, and C14 phases, respectively. At lower temperatures, all the values remain relatively constant in each range of 2.24 < ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) < 2.27 nm and 3.22 < S0 < 3.26 nm2. From the A15 to DDQC phases (the red to purple colours indicated at the top of Fig. 4b), the plateau
< 2.27 nm and 3.22 < S0 < 3.26 nm2. From the A15 to DDQC phases (the red to purple colours indicated at the top of Fig. 4b), the plateau ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) and S0 values were maintained equivalently until each threshold temperature (Tth), which is the maximum temperature for maintaining a consistent
and S0 values were maintained equivalently until each threshold temperature (Tth), which is the maximum temperature for maintaining a consistent ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) . When temperatures further increase above the Tth, the
. When temperatures further increase above the Tth, the ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) promptly decreases (S0 increases) with the same slopes. Unlike the plateau
promptly decreases (S0 increases) with the same slopes. Unlike the plateau ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) for the lower-f dendron assemblies close to the A15 phase, the
for the lower-f dendron assemblies close to the A15 phase, the ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) for the higher-f dendron assemblies close to the C14 phase immediately decreases (the S0 increases) as soon as the temperature increases.
for the higher-f dendron assemblies close to the C14 phase immediately decreases (the S0 increases) as soon as the temperature increases.
A decrease in the Tth by alleviating the core interactions and its composition dependence (Fig. 4c) suggest that the more size-dispersed particles, along with the phase sequence of A15–σ–DDQC–C14, the more susceptibility to chain exchange with increasing temperature. Considering ΔT = T − Tth, we constructed a master curve for ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) (Fig. 4d) as a function of temperature, where all the
(Fig. 4d) as a function of temperature, where all the ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) curves were shifted and superimposed along the temperature axis onto a designated f = 0.950 with no Tth. Above each Tth of the sphere-packing structures, the
curves were shifted and superimposed along the temperature axis onto a designated f = 0.950 with no Tth. Above each Tth of the sphere-packing structures, the ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) values follow a scaling relationship of
values follow a scaling relationship of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) ∼T−1/2, indicating that the average particle sizes decrease with increasing temperature and the core–corona interfaces per chain become broader. As a consequence, our results on the temperature dependence of particle sizes establish an opportunity to associate the core-interaction-dependent phases with their particle size dispersities.
∼T−1/2, indicating that the average particle sizes decrease with increasing temperature and the core–corona interfaces per chain become broader. As a consequence, our results on the temperature dependence of particle sizes establish an opportunity to associate the core-interaction-dependent phases with their particle size dispersities.
As another aspect of the particle analysis, one can adopt the average radial distribution functions of volume (dV/dr) to explain dendritic particles as a function of radial distance (r) from the centre.12,13,39 The dV/dr function with increasing temperature requires a higher dV/dr peak due to the lateral thermal expansion of peripheral chains and a shorter dV/dr tail due to the longitudinal contraction of the chains. This effect may bring about the less size-dispersed phase at higher temperatures towards uniform-sized structures such as a BCC phase; this concept can be applied to the DDQC–σ transition measured in our study. However, the A15–σ and DDQC–C14 transitions, as observed in our study, indicate that the particle size dispersity increases with increasing temperature; this is against the general explanation from the dV/dr for temperature-dependent particles.
Conclusion
We have demonstrated that the core-interaction-dependent phases could be readily achieved by two homologous dendrons of G2-CONH2 and G2-CH2NH2 possessing different apexes but identical wedges. As the amount of weak hydrogen-bonding G2-CH2NH2 increases, the |ΔH|iso and Tiso of the dendron assemblies gradually decrease, indicating that the heterogeneous hydrogen bonds between the two apex units successfully tune the core interactions. In the dendron assemblies compositionally close to each pure component of G2-CONH2 and G2-CH2NH2, their own FK A15 and C14 phases dominate other phases, respectively. We show the existence of the wide-range FK σ phase, including the DDQC phase from the dendron mixtures, providing an experimental phase sequence of A15–σ–DDQC–C14 by alleviating the core interactions. Particularly, the DDQC–C14 transition elicited at f = 0.924 has never been accessed in soft-matter assemblies to date. This phase sequence also corresponds to the increase in the particle size dispersity (or volume asymmetry).The temperature dependence of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) (and S0) reveals that all the
(and S0) reveals that all the ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) curves are shifted and superimposed along the temperature axis onto a master curve for
curves are shifted and superimposed along the temperature axis onto a master curve for ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) with temperature, of which the Tth for maintaining a consistent
with temperature, of which the Tth for maintaining a consistent ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) decreases as the core interactions are alleviated. The stronger hydrogen-bonding dendrons with higher Tth favour more uniform-sized sphere-packing structures, whereas for the weaker hydrogen-bonding dendrons with lower or no Tth, the size-dispersed particles are more susceptible to chain exchange with increasing temperature, following the same phase sequence of A15–σ–DDQC–C14. Our thermotropic approach for supramolecular dendron assemblies offers valuable insight into the size dispersity effect induced by the core-interaction-dependent mesocrystal structures. Moreover, our systematic concept based on controlling the hydrogen-bonding or cohesive interaction can be a simple strategy applicable for exploring the formation of a predictable, unidentified structure in supramolecular assemblies.
decreases as the core interactions are alleviated. The stronger hydrogen-bonding dendrons with higher Tth favour more uniform-sized sphere-packing structures, whereas for the weaker hydrogen-bonding dendrons with lower or no Tth, the size-dispersed particles are more susceptible to chain exchange with increasing temperature, following the same phase sequence of A15–σ–DDQC–C14. Our thermotropic approach for supramolecular dendron assemblies offers valuable insight into the size dispersity effect induced by the core-interaction-dependent mesocrystal structures. Moreover, our systematic concept based on controlling the hydrogen-bonding or cohesive interaction can be a simple strategy applicable for exploring the formation of a predictable, unidentified structure in supramolecular assemblies.
Author contributions
T. J. performed SAXS measurements and analyzed the properties of each Voronoi cell obtained from the reconstructed ED maps (under the instructions of D. Y. R. and B. L.). H. P. synthesised and characterised the dendron samples using NMR spectroscopy and MALDI-TOF mass spectrometry (under the instructions of W.-D. J.). S. J. assisted and reviewed the experimental results. H. A. assisted with the SAXS measurements and provided advice for data analysis. D. Y. R., W.-D. J., and B. L. discussed the results and wrote the manuscript. D. Y. R. and B. L. co-directed all aspects of the project.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We acknowledge the NRF grants (2020R1A2C3004520, 2021R1A2C2006588, and 2022R1A4A1020543) funded by the Ministry of Science, ICT & Future Planning (MSIP), Korea. SAXS measurements were performed at Pohang Accelerator Laboratory (Korea) (4C and 9A beamlines) and Advanced Photon Source in the Argonne National Laboratory (USA) (12-ID-B beamline). The use of the APS is supported by the U.S. Department of Energy, Office of Basic Energy Sciences, under contract no. DE-AC0206CH11357.References
- H. L. Skriver, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 1909–1923 CrossRef CAS PubMed.
- P. Söderlind, O. Eriksson, B. Johansson, J. M. Wills and A. M. Boring, Nature, 1995, 374, 524–525 CrossRef.
- G. Grimvall, B. Magyari-Köpe, V. Ozoliņš and K. A. Persson, Rev. Mod. Phys., 2012, 84, 945–986 CrossRef CAS.
- D. Hobbs, J. Hafner and D. Spišák, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 014407 CrossRef.
- J. Hafner and D. Hobbs, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 014408 CrossRef.
- A. C. Lawson, C. E. Olsen, J. W. Richardson Jr., M. H. Mueller and G. H. Lander, Acta Crystallogr., Sect. B: Struct. Sci., 1988, 44, 89–96 CrossRef.
- S. Lee, C. Leighton and F. S. Bates, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17723–17731 CrossRef CAS PubMed.
- K. Yue, M. Huang, R. L. Marson, J. He, J. Huang, Z. Zhou, J. Wang, C. Liu, X. Yan, K. Wu, Z. Guo, H. Liu, W. Zhang, P. Ni, C. Wesdemiotis, W.-B. Zhang, S. C. Glotzer and S. Z. D. Cheng, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 14195–14200 CrossRef CAS PubMed.
- G. C. Shearman, A. I. I. Tyler, N. J. Brooks, R. H. Templer, O. Ces, R. V. Law and J. M. Seddon, Liq. Cryst., 2010, 37, 679–694 CrossRef CAS.
- N. Mott and H. Jones, Nature, 1937, 139, 348–349 CrossRef.
- S. L. Altmann, Band theory of metals: the elements, Elsevier, 1970 Search PubMed.
- G. Ungar, Y. Liu, X. Zeng, V. Percec and W.-D. Cho, Science, 2003, 299, 1208–1211 CrossRef CAS PubMed.
- G. Ungar and X. Zeng, Soft Matter, 2005, 1, 95–106 RSC.
- S. Lee, M. J. Bluemle and F. S. Bates, Science, 2010, 330, 349–353 CrossRef CAS PubMed.
- S. A. Kim, K. J. Jeong, A. Yethiraj and M. K. Mahanthappa, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 4072–4077 CrossRef CAS PubMed.
- G. Ungar, V. Percec, X. B. Zeng and P. Leowanawat, Isr. J. Chem., 2011, 51, 1206–1215 CrossRef CAS.
- T. M. Gillard, S. Lee and F. S. Bates, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5167–5172 CrossRef CAS PubMed.
- A. Jayaraman, C. M. Baez-Cotto, T. J. Mann and M. K. Mahanthappa, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2101598118 CrossRef CAS PubMed.
- Y. Liu, T. Liu, X.-Y. Yan, Q.-Y. Guo, H. Lei, Z. Huang, R. Zhang, Y. Wang, J. Wang, F. Liu, F.-G. Bian, E. W. Meijer, T. Aida, M. Huang and S. Z. D. Cheng, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2115304119 CrossRef CAS PubMed.
- V. S. K. Balagurusamy, G. Ungar, V. Percec and G. Johansson, J. Am. Chem. Soc., 1997, 119, 1539–1555 CrossRef CAS.
- V. Percec, C. H. Ahn, G. Ungar, D. J. P. Yeardley, M. Möller and S. S. Sheiko, Nature, 1998, 391, 161–164 CrossRef CAS.
- X. Zeng, G. Ungar, Y. Liu, V. Percec, A. E. Dulcey and J. K. Hobbs, Nature, 2004, 428, 157–160 CrossRef CAS PubMed.
- K. Kim, M. W. Schulze, A. Arora, R. M. Lewis, M. A. Hillmyer, K. D. Dorfman and F. S. Bates, Science, 2017, 356, 520–523 CrossRef CAS PubMed.
- Z. Su, C.-H. Hsu, Z. Gong, X. Feng, J. Huang, R. Zhang, Y. Wang, J. Mao, C. Wesdemiotis, T. Li, S. Seifert, W. Zhang, T. Aida, M. Huang and S. Z. D. Cheng, Nat. Chem., 2019, 11, 899–905 CrossRef CAS PubMed.
- Y. Liu, T. Liu, X.-Y. Yan, Q.-Y. Guo, J. Wang, R. Zhang, S. Zhang, Z. Su, J. Huang, G.-X. Liu, W. Zhang, W. Zhang, T. Aida, K. Yue, M. Huang and S. Z. D. Cheng, Giant, 2020, 4, 100031 CrossRef.
- M. Huang, C.-H. Hsu, J. Wang, S. Mei, X. Dong, Y. Li, M. Li, H. Liu, W. Zhang, T. Aida, W.-B. Zhang, K. Yue and S. Z. D. Cheng, Science, 2015, 348, 424–428 CrossRef CAS PubMed.
- X. Y. Feng, G. X. Liu, D. Guo, K. N. Lang, R. M. Zhang, J. H. Huang, Z. B. Su, Y. W. Li, M. J. Huang, T. Li and S. Z. D. Cheng, ACS Macro Lett., 2019, 8, 875–881 CrossRef CAS PubMed.
- K. K. Lachmayr, C. M. Wentz and L. R. Sita, Angew. Chem., Int. Ed., 2020, 59, 1521–1526 CrossRef CAS PubMed.
- J. M. Dubois, Useful quasicrystals, World Scientific, 2003 Search PubMed.
- W. Man, M. Megens, P. J. Steinhardt and P. M. Chaikin, Nature, 2005, 436, 993–996 CrossRef CAS PubMed.
- C. Tschierske, J. Mater. Chem., 2001, 11, 2647–2671 RSC.
- B. M. Rosen, C. J. Wilson, D. A. Wilson, M. Peterca, M. R. Imam and V. Percec, Chem. Rev., 2009, 109, 6275–6540 CrossRef CAS PubMed.
- E. Apartsin and A.-M. Caminade, Chem. – Eur. J., 2021, 27, 17976–17998 CrossRef CAS PubMed.
- S. D. Hudson, H.-T. Jung, V. Percec, W.-D. Cho, G. Johansson, G. Ungar and V. S. K. Balagurusamy, Science, 1997, 278, 449–452 CrossRef CAS.
- B. M. Rosen, M. Peterca, C. Huang, X. Zeng, G. Ungar and V. Percec, Angew. Chem., Int. Ed., 2010, 49, 7002–7005 CrossRef CAS PubMed.
- N. Huang, Q. Xiao, M. Peterca, X. Zeng and V. Percec, Mol. Phys., 2021, 119, e1902586 CrossRef.
- X. B. Liu, R. M. Zhang, Y. Shao, L. G. Xu, G. R. He, J. H. Huang, Z. H. Guo, W. B. Zhang, W. Tang and K. Yue, ACS Macro Lett., 2021, 10, 844–850 CrossRef CAS PubMed.
- V. Percec, M. N. Holerca, S. Uchida, D. J. P. Yeardley and G. Ungar, Biomacromolecules, 2001, 2, 729–740 CrossRef CAS PubMed.
- X. Yao, L. Cseh, X. Zeng, M. Xue, Y. Liu and G. Ungar, Nanoscale Horiz., 2017, 2, 43–49 RSC.
- V. Percec, W.-D. Cho, G. Ungar and D. J. P. Yeardley, Angew. Chem., Int. Ed., 2000, 39, 1597–1602 CrossRef CAS PubMed.
- V. Percec, M. N. Holerca, S. Nummelin, J. J. Morrison, M. Glodde, J. Smidrkal, M. Peterca, B. M. Rosen, S. Uchida, V. S. Balagurusamy, M. J. Sienkowska and P. A. Heiney, Chem. – Eur. J., 2006, 12, 6216–6241 CrossRef CAS PubMed.
- X. Y. Yan, Q. Y. Guo, Z. W. Lin, X. Y. Liu, J. Yuan, J. Wang, H. M. Wang, Y. C. Liu, Z. B. Su, T. Liu, J. H. Huang, R. M. Zhang, Y. C. Wang, M. J. Huang, W. Zhang and S. Z. D. Cheng, Angew. Chem., Int. Ed., 2021, 60, 2024–2029 CrossRef CAS PubMed.
- T. Jun, H. Park, S. Jeon, S. Jo, H. Ahn, W.-D. Jang, B. Lee and D. Y. Ryu, J. Am. Chem. Soc., 2021, 143, 17548–17556 CrossRef CAS PubMed.
- T. Li, A. J. Senesi and B. Lee, Chem. Rev., 2016, 116, 11128–11180 CrossRef CAS PubMed.
- B. Lee, I. Park, H. Park, C.-T. Lo, T. Chang and R. E. Winans, J. Appl. Crystallogr., 2007, 40, 496–504 CrossRef CAS.
- L. Palatinus and G. Chapuis, J. Appl. Crystallogr., 2007, 40, 786–790 CrossRef CAS.
- M. N. Holerca, D. Sahoo, B. E. Partridge, M. Peterca, X. Zeng, G. Ungar and V. Percec, J. Am. Chem. Soc., 2018, 140, 16941–16947 CrossRef CAS PubMed.
- J. H. Huang, Z. B. Su, M. J. Huang, R. C. Zhang, J. Wang, X. Y. Feng, R. Zhang, R. M. Zhang, W. P. Shan, X. Y. Yan, Q. Y. Guo, T. Liu, Y. C. Liu, Y. P. Cui, X. P. Li, A. C. Shi and S. Z. D. Cheng, Angew. Chem., Int. Ed., 2020, 59, 18563–18571 CrossRef CAS PubMed.
- D. He, N. N. Ekere and L. Cai, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 7098–7104 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr05458b |
| This journal is © The Royal Society of Chemistry 2022 |