An effective and recyclable decolorization method for polysaccharides from Isaria cicadae Miquel by magnetic chitosan microspheres

Abstract

The purpose of this research was to develop an efficient and non-destructive method for decolorizing of polysaccharides extracted from Isaria cicadae Miquel by magnetic chitosan microspheres (MCM). The optimum decolorization parameters were achieved by response surface methodology as follows: the MCM amount was 8.0%, the adsorption temperature was 48 °C, the adsorption time was 82 min and the pH was 7. Under these optimal conditions, the D_r%, R_r%, and K_c were 90.31 ± 0.12%, 95.40 ± 0.11% and 19.66 ± 0.49, respectively. MCM adsorption of pigment molecules was a spontaneous and endothermic process that could be fitted with the pseudo-second-order equation and the Freundlich equation. Besides, the adsorption mechanism could be controlled by multiple-diffusion steps, including film diffusion and intra-particle diffusion. Furthermore, MCM is a recyclable material. Adsorption with MCM is a promising method to remove pigment molecules of polysaccharide, it may replace the traditional decolorization method.

---

1. Introduction

Polysaccharide is one of the substances that maintain life activities,¹ existing in animals, plants, algae and fungi.² Nowadays, much research has proved that entomogenous fungi (such as Cordyceps sinensis) are rich in polysaccharides, and their bioactivities are closely related to polysaccharides.^3,4 Isaria cicadae Miquel (I. cicadae) is an entomogenous fungi, and has a long history of application in functional food and medicine in traditional Chinese medicine. It has been reported that I. cicadae possesses a variety of pharmacological activities, such as antitumor, antioxidation, and immunomodulatory activity.⁵ In addition, in previous studies, we found that I. cicadae is rich in polysaccharides.⁶ However, in the extraction process, we found that Isaria cicadae Miquel polysaccharides (ICMP) contains a lot of pigments. These pigments contaminate the ion exchange column and cause a lot of waste.⁷ At the same time, the in-depth research and further application of ICMP are also restricted due to the influence of pigments on its biological activity. Therefore, it is very important to decolorize before separating and purifying polysaccharides.

Several typical and traditional decolorization methods are wildly used in the field of polysaccharides, such as activated carbon adsorption and hydrogen peroxide oxidation.^8,9 Unfortunately, low selectivity of activated carbon leads to high loss rate of polysaccharide.⁷ The separation of activated carbon by filtration or centrifugation is very tedious and may also result in the loss of polysaccharide. The structure and some functional groups of polysaccharide will be destroyed under the oxidation of hydrogen peroxide. Besides, the strong oxidizing properties of H₂O₂ will lead to the complete loss of the antioxidant capacity of polysaccharide.¹⁰ Although macroporous resin has a good decolorization effect, there are many types and the screening process is complicated. Therefore, an efficient and non-destructive decolorization method needs to be developed urgently.

Magnetic chitosan microsphere (MCM), a kind of high polymer material, has good adsorption properties for dyes, proteins and metal ions due to lots of primary amino and hydroxyl groups.¹¹ Furthermore, MCM has the characteristics of metal ion adsorption and magnetic material for easy magnetic separation and recovery,¹² which overcome the disadvantage of traditional decolorization methods. In our previous study, MCM was synthesized and applied to deproteinization of polysaccharide. Meanwhile, MCM was characterized by scanning electron microscopy and other techniques.¹³ We found that MCM is a magnetic microsphere with smooth surface and diameter of 2–6 μm. It mainly contains C, O and Fe, and has good deproteinization effect.¹³ MCM is non-toxic, biocompatible, hydrophilic and biodegradable. It has been used in the treatment of environmental pollutants, biotechnology, biomedicine and other fields. However, to the best of our knowledge, there is no report about the MCM used in decolorization of polysaccharide.

In this research, a new method of removing pigments by MCM in the field of polysaccharide decolorization was developed. Firstly, parameters influencing decolorization efficiency were optimized by response surface method. Then we studied the adsorption kinetics and adsorption thermodynamics models. Finally, under the optimal condition, the desorption and regeneration capacity were measured. In addition, the polysaccharide before and after decolorization were characterized.

2. Experimental

2.1 Materials and reagents

The I. cicadae was purchased from Qingping Herbal Medicine market (Guangzhou, China). Chitosan (degree of deacetylation was 95%, viscosity was 100–200 mPa s) and Fe₃O₄ (average particle diameter: 20 nm) was obtained from Aladdin Chemical Co., Ltd. (Shanghai, China). Ethanol absolute, acetic acid, petroleum ether, paraffin liquid, Span 80, Tween 80, n-butanol and sodium hydroxide (NaOH) were obtained from Zhiyuan Chemical Reagents Co., Ltd. (Tianjin, China). Glutaric dialdehyde was obtained from Kermel Chemical Reagents Co., Ltd. (Tianjin, China). Hydrochloric acid was obtained from Guangzhou Chemical Reagent Factory (Guangzhou, China). Deionized water was prepared by Aquaplore Water Purification system (Aquaplore, DE, USA). The reagents used in the experiment were analytical grade unless otherwise specified.

2.2 Preparation of ICMP and MCM

The ICMP was extracted by water and precipitated by ethanol according to the reported method,⁶ and the protein was removed using the Sevag reagent.¹⁴ MCM was prepared by the microemulsion process which our previously reported.¹³ In brief, chitosan was dissolved in 3% acetic acid, and then Fe₃O₄ was added under high-speed stirring, and mix well as the aqueous phase. The aqueous phase was mixed with the oil phase, and then the crosslinking agent was added. The pH value was adjusted to 9, and the MCM was obtained after washing and drying.

2.3 Analytical methodology

2.3.1 Determination of decolorization ratio. Briefly, all sample solutions, including both before and after treatment by MCM with static adsorption, were adjusted to neutral with 5% HCl or 5% NaOH. Then above solutions were diluted to appropriate multiple with distilled water. After that, the absorbances of solutions were determined using ultraviolet spectrophotometer (TU1810 UV spectrophotometer, PUXI General Instruments Co., Ltd, China) at 420 nm. The decolorization rate was calculated as follows:¹⁵

D_r (%) = (A_D0 − A_D1)/A_D0 × 100% (1)

where A_D0 is the absorbance value at 420 nm before decolorization and A_D1 is the absorbance value at 420 nm after decolorization, D_r% is decolorization ratio.

2.3.2 Determination of recovery ratio. After adjusting pH and diluting as process described in Section 2.3.1, the content of polysaccharide was determined by the method of phenol-sulfuric acid.¹⁶ The recovery rate of polysaccharide was calculated as follows:¹⁰

R_r (%) = A_R1/A_R0 × 100% (2)

where A_R0 is the concentration of ICMP before decolorization and A_R1 is the concentration of ICMP after decolorization, R_r% is recovery ratio.

2.3.3 Calculation of selectivity coefficient. The decolorizing agent will cause a certain degree of polysaccharide loss during the decolorization process. In order to take into account D_r% and R_r%, the selectivity coefficient (K_c) is introduced to comprehensively evaluate the effect of the decolorization agent. The K_c was calculated by reported formula with a few modifications,¹⁷ which was expressed as follow:

K_c = D_r (%)/(100 − R_r (%)) (3)

where D_r% and R_r% are decolorization ratio and recovery ratio of ICMP respectively. K_c represent selectivity coefficient.

2.4 Adsorption experiment

2.4.1 Signal factor design. The effects of adsorption conditions including amount of MCM, temperature, time and pH were explored by single-factor method. Briefly, the crude polysaccharide was dissolved in distilled water to prepare stock solution (3 mg mL⁻¹). 10 mL of the above solution was statically adsorbed under different MCM design amount (2.0, 4.0, 6.0, 8.0 and 10.0%, g mL⁻¹), adsorption temperature (30, 40, 50, 60 and 70 °C), time (20, 40, 60, 80 and 100 min) and pH (5.0, 6.0, 7.0, 8.0 and 9.0). Each experiment was carried out in triplicate. Decolorization ratio and recovery ratio of polysaccharide were determined as methods described in Section 2.3.

2.4.2 Optimization of decolorization conditions. According to the result of single factor test, the Box–Behnken design with four factors and three levels was adopted. Amount of MCM (A), adsorption temperature (B), adsorption time (C) and pH (D) were selected as independent variables and the selectivity coefficient (K_c) was chosen as dependent variable. The levels of each independent variable were represented with the codes −1, 0, and +1, a total of 29 experimental runs was carried out in a certain order as shown Tables 1 and 2. The experimental data was analyzed by Design-Expert software (version 8.0.6, Stat-Ease Inc., Minneapolis, MN, USA).

Table 1 Level code for each independent variable

Factors	Unit	Symbols	Level of factors
			−1	0	1
Amount of MCM	%	A	6.0	8.0	10.0
Adsorption temperature	°C	B	40.0	50.0	60.0
Adsorption time	min	C	60.0	80.0	100.0
pH	—	D	6.0	7.0	8.0

---

Table 2 Design and results of response surface methodology

No.	A	B	C	D	Kc
1	−1	−1	0	0	16.1931
2	0	−1	1	0	17.8333
3	0	1	1	0	13.9689
4	0	1	−1	0	14.4795
5	−1	0	−1	0	14.2447
6	1	0	0	1	7.31365
7	1	0	−1	0	13.113
8	0	0	0	0	19.2376
9	0	−1	−1	0	14.2202
10	0	0	−1	−1	13.2757
11	0	−1	0	−1	12.136
12	−1	0	0	−1	10.2699
13	−1	1	0	0	10.5673
14	0	0	0	0	19.7802
15	0	0	0	0	20.053
16	0	0	0	0	19.597
17	0	1	0	−1	12.5896
18	0	0	1	1	9.68682
19	0	0	1	−1	12.4086
20	0	0	0	0	19.4093
21	1	0	1	0	15.9765
22	0	1	0	1	8.6802
23	1	−1	0	0	12.1425
24	−1	0	1	0	13.5912
25	0	0	−1	1	9.9243
26	1	0	0	−1	13.9154
27	−1	0	0	1	10.1126
28	1	1	0	0	15.1809
29	0	−1	0	1	11.5109

---

2.5 Adsorption studies

2.5.1 Adsorption kinetic studies. The studies on adsorption kinetics were carried out by mixing 0.8 g MCM with 10 mL crude polysaccharide solution (3 mg mL⁻¹). pH of the solutions was adjusted to 7 with 5% HCl or 5% NaOH. Then the mixture was incubated in static state at 20, 30 and 40 °C for 180 min. After adsorption for designed interval (10 min), samples were collected and the adsorption capacity of pigment were determined using ultraviolet spectrophotometer at 420 nm as described in Section 2.3. All experiments were carried out three times.

2.5.2 Adsorption thermodynamic study. To carry out adsorption thermodynamics experiments, different amount of MCM (1, 1.5, 2, 2.5, 3 g) was added to fixed volume solutions containing of polysaccharide (30 mL, 10 mg mL⁻¹). Then the mixed liquid was incubated in static state for 150 min at different temperatures (20, 30, 40 °C). Then the adsorption capacity of pigment was measured using ultraviolet spectrophotometer at 420 nm as Section 2.3. All experiments were carried out three times.

2.6 Desorption and regeneration experiments

After the process of static adsorption under optimum conditions was finished, the MCM were separated from ICMP solution with magnet and immersed in 0.5 M NaOH solution for repeated washing until the solution was colorless. Next, repeatedly wash the MCM with distilled water until the solution is neutral. Afterwards, MCM were activated by soaked in 0.2% glutaraldehyde solution for 30 min. Activated MCM were used to desorption and regeneration assay. The cycles of desorption and regeneration were carried out for 6 times. Pigment adsorption rate of polysaccharide were determined as described in Section 2.3.

2.7 Comparison of characterization of samples before and after decolorization with MCM

The ICMP sample solution was characterized by UV-vis spectroscopy and FT-IR (Nicolet iS50, Thermo Fisher, USA) as reported methods.¹⁸ In order to obtain concentration of total carbohydrates, Vis spectra in the 400–600 nm was determined after sulfuric acid phenol coloration. In addition, the ICMP sample solutions before and after decolored by MCM were photographed by a Canon SX70 HS digital camera.

2.8 Statistical analysis

All data were expressed as means ± standard deviation (SD) and statistical analyses were conducted by SPSS (Statistical Product and Service Solutions, Version 18.0, SPSS Inc., Chicago, IL, USA). Statistical difference was existed if P < 0.05.

3. Results and discussion

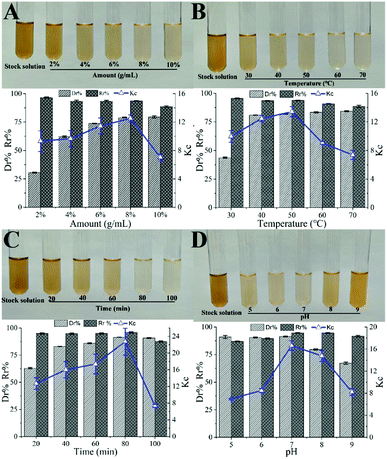
3.1 Single factor effect on decolorization efficiency

3.1.1 Effect of MCM amount on decolorization efficiency. The amount of adsorbent is an important factor which influences adsorption efficiency. Therefore, the effects of amount of MCM (2.0, 4.0, 6.0, 8.0 and 10.0%) on decolorization efficiency were explored when temperature, time and pH were fixed at 40 °C, 40 min and 7.0, respectively. As shown in Fig. 1A, the value of D_r% increased with amount of MCM ranging from 2.0% to 8.0%. When the amount of MCM increased over 8.0%, the value of D_r% remained unchanged. However, the value of R_r% continued to decrease with increasing amount of MCM. The value of K_c reached the maximum level when the amount of MCM was 8.0%. So, the amount of 8.0% was selected for the following experiments.

Fig. 1 Effects of different amount of MCM (A), adsorption temperature (B), adsorption time (C) and pH value (D) on the efficiency of decolorization (n = 3).

3.1.2 Effect of temperature on decolorization efficiency. To study the effect of temperature on decolorization efficiency of MCM, the temperature was set at 30, 40, 50, 60, and 70 °C, while the other three factors were as follows: the amount of MCM was 8.0%, adsorption time was 40 min and the value of pH was 7. As shown in Fig. 1B, the value of D_r% increased rapidly when temperature ranged from 30 °C to 40 °C. When adsorption temperature was more than 40 °C, the value of D_r% increased slowly. However, when the temperature continuously increased, a significant decrease in the value of R_r% was observed. The value of K_c increased significantly with the increasing temperature until 50 °C and a maximum value of K_c was observed at this point. The adsorption capacity of pigment molecule increased with the increasing temperature can be explained by theory of thermal motion. With the increase of temperature, molecule would be more active, which may improve the probability of pigment molecules reaching the surface of MCM, lead to continued increase of decolorization ratio. However, the adsorption capacity of polysaccharide also increased owing to the same reason. Besides that, the retention ratio of polysaccharide could be partly attributed to the degradation of it at high temperature. Accordingly, 50 °C of adsorption temperature was selected for the next experiments.

3.1.3 Effect of time on decolorization efficiency. The effect of adsorption time on decolorization efficiency of MCM was evaluated in the present assay, the amount of MCM, adsorption temperature and value of pH were set at 8.0%, 50 °C and 7.0, respectively. The adsorption time was set at 20, 40, 60, 80, and 100 min sequentially. As shown in Fig. 1C, the value of D_r% increased significantly during the previous stage of static adsorption, before reaching its maximum at the adsorption time of 80 min. However, the value of R_r% decreased when adsorption time varied from 20 to 100 min. The value of K_c increased with the elevation of adsorption time at first, before reaching the maximum at a time of 80 min. But a higher adsorption time (>80 min) could lead to a lower value of K_c, which due to the excessive prolongation of adsorption time could also conduct a massive loss of polysaccharide. Based on these results, adsorption time of 80 min was selected for the next experiments.

3.1.4 Effect of pH on decolorization efficiency. The surface charge of MCM and pigment molecule can be affected by value of pH, thus altering the combination of pigment molecule with active sites of MCM. In present study, pH value of 5.0, 6.0, 7.0, 8.0 and 9.0 were set while amount of MCM, adsorption temperature and adsorption time were fixed at 8%, 50 °C and 80 min, respectively. As shown in Fig. 1D, the value of D_r% continued to decrease with the increasing pH value from 5.0 to 9.0. The value of R_r% increased when pH value ranged from 5.0 to 8.0 and then decreased when the pH value exceeded 8.0. The value of K_c rapidly increased with an increase of pH value from 5.0 to 7.0. Then a tendency of decrease was observed when the pH value was more than 7.0. Thus, the pH value of 7.0 was selected to be the optimal condition in further study.

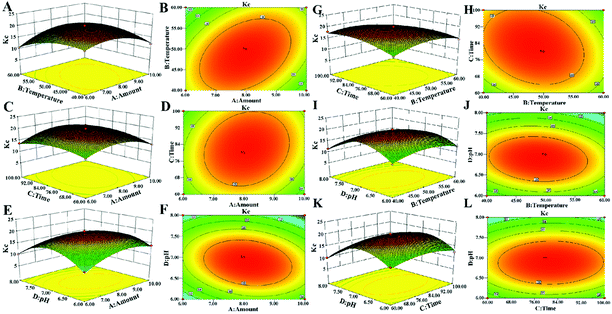
3.2 Optimization of decolorization conditions

3.2.1 Experimental design and ANOVA. The value of K_c at each point, based on the experimental design, are shown in Table 2. After estimating the experimental date through multiple regression analysis, the relationship between responses and independent variables can be constructed as follows:

Y = 19.62 + 0.22A − 0.71B + 0.35C − 1.45D + 2.17AB + 0.88AC − 1.61AD − 1.03BC − 0.82BD + 0.16CD − 3.37A² − 2.51B² − 2.11C² − 5.97D²

where Y is the value of K_c, A, B, C, D are the amount of MCM, adsorption temperature, adsorption time, and pH value, respectively. The equation is in terms of coded factors.

The results of ANOVA study, which used to evaluate the significance of the regression equation in model are shown in Table 3. The F-value of model was 79.55 (P < 0.01) which can be confirmed that the model is highly significant. The “Lack of Fit P-value” of 0.1005 (P > 0.05) indicated that the lack of fit is not significant relative to the pure error. The value of Pred R-squared (0.9333) is in reasonable agreement with the value of Adj R-squared (0.9752). In this case, the results also shown that B, C, D, AB, AC, AD, BC, BD, A², B², C², D² are significant model terms (P < 0.05).

Table 3 Analysis of variance for fitted quadratic polynomial model^a

Source	SS	DF	MS	F-value	P-value	Significance
a R^2 = 0.9876, Radj^2 = 0.9752, “**” was very significant (P < 0.01), “*” was significant (P < 0.05), SS denotes sum of squares; DF denotes degree of freedom; MS denotes mean square.
Model	346.29	14	24.74	79.55	<0.0001	**
A	0.59	1	0.59	1.90	0.1896
B	6.12	1	6.12	19.68	0.0006	**
C	1.48	1	1.48	4.75	0.0470	*
D	25.13	1	25.13	80.83	<0.0001	**
AB	18.77	1	18.77	60.36	<0.0001	**
AC	3.09	1	3.09	9.94	0.0070	**
AD	10.38	1	10.38	33.39	<0.0001	**
BC	4.25	1	4.25	13.67	0.0024	**
BD	2.70	1	2.70	8.67	0.0107	*
CD	0.099	1	0.099	0.32	0.5813
A^2	73.63	1	73.63	236.78	<0.0001	**
B^2	40.83	1	40.83	131.31	<0.0001	**
C^2	28.78	1	28.78	92.55	<0.0001	**
D^2	231.08	1	231.08	743.17	<0.0001	**
Residual	4.35	14	0.31
Lack of fit	3.95	10	0.39	3.91	0.1005
Pure error	0.40	4	0.10
Cor. total	350.65	28

---

3.2.2 Interaction analysis. Contour plots and response surface plots can be used to explain the interaction between independent variables, and can intuitively reflect the interaction between variables.¹⁹ The steeper the slope of response surface plots is, the more significant the interaction effect of the two factors on the response value is. On the contrary, the slope of response surface plots is gentle, which indicates that the interaction effect on the response value is not significant. In addition, the shape and density of contour plots lines also reflect the strength of the interaction effect of the two factors. If the contour plots lines are dense and oval, the interaction effect on the response value is significant; if the contour plots lines are sparse and round, the interaction effect on the response value is not significant.

It can be seen from Fig. 2, that the opening of each response surface is downward, and there is a highest point, indicating that the response surface plots have a slope. When other factors remain unchanged, as a certain factor increases, the response value increases. When the response value reaches the extreme value, the factor increases but the response value gradually decreases, indicating that there is an interaction between the factors. As shown in Fig. 2, when other factors are fixed, the contour plots are oval, but the density of contour plots lines are not the same, showing that there is an interaction between factors, but the strengths of interaction are different.

Fig. 2 Response surface plots for the mutual effects and contour plots of amount of MCM and temperature (A and B), amount of MCM and time (C and D), amount of MCM and pH (E and F), temperature and time (G and H), temperature and pH (I and J), pH and time (K and L) on the values of K_c.

3.2.3 Validation of the model. According to the experimental results of response surface method, the optimum theoretical conditions were obtained as follows: amount of MCM (A) of 8.07%, adsorption temperature (B) of 48.67 °C, adsorption time (C) of 82.36 min and the pH value (D) of 6.88. Under the optimal conditions, the predicted K_c value was 19.7707. Taking actual operation into consideration, the optimal parameters were adjusted as follows: amount of MCM (A) was 8.0%, adsorption temperature (B) was 48 °C, adsorption time (C) was 82 min and the value of pH (D) was 7. Under above conditions, the value of K_c for MCM was 19.66 ± 0.49 (D_r% was 90.31 ± 0.12% and R_r% was 95.40 ± 0.11%, respectively, triplicated experiments were performed), which showed little difference with the predicted value (P > 0.05).

3.3 Adsorption kinetics study

The study of adsorption kinetics can help us understand the dynamic interaction between pigments and adsorbents.²⁰ In this study, the pseudo-first-order, pseudo-second-order kinetic models,^21,22 Elovich kinetic model and intra-particle diffusion kinetic model have been employed to study the mechanism of adsorption process of MCM for pigment molecule.²³

The pseudo-first-order kinetics model equation could be expressed as follows:

ln(q_e − q_t) = ln q_e − k₁t (4)

The pseudo-second order kinetics model is generally written as follows:

t/q_t = 1/(k₂q_e²) + t/q_e (5)

where q_e (g⁻¹) is the adsorption capacity at equilibrium. q_t (g⁻¹) is the adsorption capacity at different time. k₁ and k₂ are the rate constant of the pseudo-first-order and pseudo-second-order kinetics model, respectively.

The Evolich kinetic model is widely used in the study of adsorption kinetics of solid/liquid systems. Its general form is as follows:

q_t = (1/β) × ln(αβ) + (1/β) × ln(t) (6)

where q_t (g⁻¹) is the adsorption capacity at different time. α, β both are the Elovich constants, which represent the initial adsorption rate and desorption constant, respectively.

The intra-particle diffusion model is often reported to reveal the adsorption reaction mechanism, and its expression is as follows:

q_t = K_idt^1/2 + C (7)

where q_t (g⁻¹) is the adsorption capacity at different time. K_id and C is the intra-particle diffusion constant.

Here the dimensionless concentration of pigment in the ICMP solution was defined as A/A₀. Therefore, the adsorption capacity of the adsorbent to the pigment in the ICMP solution was calculated as [((A₀ − A)/A₀)/m].²⁴

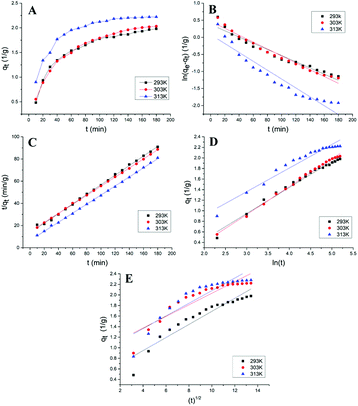
The change process of ICMP adsorption capacity q_t on MCM with time (t) at different temperatures were shown in Fig. 3A. It can be seen from the figure that the adsorption capacity of MCM for ICMP increases with time at three temperatures, and the adsorption speed is faster in the first 40 minutes, then increases slowly, and finally tends to equilibrium. In addition, temperature has a certain effect on the adsorption capacity of MCM. With the increase of temperature within a certain range, the adsorption rate and adsorption capacity of MCM also increase. These results were coincided with the results of the adsorption temperature experiments.

Fig. 3 Adsorption kinetics curves (A), linear plots of the pseudo-first-order kinetic model (B), the pseudo-second-order kinetic model (C), the Evolich kinetic model (D) and the intra-particle diffusion model (E) at different temperature.

Kinetic plots for the pseudo-first-order, the pseudo-second-order reactions, the Elovich kinetic model and intra-particle diffusion kinetic model of the adsorption of ICMP onto MCM at different temperature are shown in Fig. 3. Values of these model constants are given in Table 4.

Table 4 Corresponding parameters of adsorption kinetic models at different temperature

T (K)	qe, exp (g^−1)	Pseudo-first-order			Pseudo-second-order			Elovich			Intra-particle diffusion
		qe, cal (g^−1)	k1	R^2	qe, cal (g^−1)	k2	R^2	α	β	R^2	Kid	C	R^2
293	2.297	1.453	0.0091	0.9501	2.313	0.0138	0.9983	0.1672	2.025	0.9859	0.1239	0.4509	0.9035
303	2.335	1.085	0.0145	0.9358	2.446	0.0254	0.9995	0.4707	2.242	0.9545	0.1097	0.9347	0.8405
313	2.368	1.140	0.0162	0.9324	2.532	0.0228	0.9988	0.3835	2.046	0.9432	0.1194	0.8865	0.8200

---

It can be seen from the Table 4, that the pseudo-first-order model and pseudo-second-order model have good adaptability for describing the adsorption process of ICMP pigment on MCM. But compared with the pseudo-first-order model, the pseudo-second-order model has a better fitting degree and can more accurately describe the adsorption process of ICMP pigment on MCM. In addition, the q_e value in the pseudo-second-order model is closer to the experimental value. All these results indicated that the adsorption kinetic data was better fitted by the pseudo-second-order model. The linear plot of ln(q_e − q_t) versus t (Fig. 3B) and t/q_t versus t (Fig. 3C) also confirmed the above results.

According to the Table 4, the Elovich model equation fitting has a high correlation (Fig. 3D). Since the Elovich equation is a description of the heterogeneous diffusion process comprehensively controlled by the reaction rate and the diffusion factor, it suggests that the adsorption of the ICMP pigment by MCM is a heterogeneous diffusion process. It is not a simple reaction, but a process controlled by reaction rate and diffusion.

The adsorption rate is determined by the adsorption mechanism and the rate-limiting step. It is generally believed that the adsorption process of the adsorbent to the substrate mainly includes the following three steps: ① liquid-film diffusion; ② intra-particle diffusion; ③ adsorption reaction. In general, the reaction speed of the third step is very fast, so liquid film diffusion or (and) intra-particle diffusion is the control step of the entire adsorption reaction.²⁵ According to the experimental data of kinetics, the q_t − t_1/2 graph can be drawn. If the graph shows straight line and passes through the origin, it means that the adsorption process is only controlled by the intra-particle diffusion. If the graph gives a multi-linear characteristic or does not pass the origin, it suggests that the intra-particle diffusion is not the only rate-limiting step of the reaction.²⁶ As seen from Fig. 3E, the plot does not pass through the origin, which indicates that the intra-particle diffusion is not the only rate limiting step of reaction. Moreover, according to the scatter diagram, the plot can be roughly divided into two parts, indicating that the adsorption mechanism of ICMP on MCM may be controlled by multiple-diffusion steps, including film diffusion and intra-particle diffusion.²⁵ The R² of intra-particle diffusion is relatively small, which also proves this point (Table 4).

3.4 Adsorption isotherm analysis

In this study, the Langmuir, Freundlich and Temkin equations have been employed to study the adsorption isotherm of MCM for ICMP pigment. The Langmuir model is an isotherm model widely used to describe the performance of adsorbents. It is assumed that the binding sites have the same adsorption energy for each molecule, and there is no interaction between the adsorbed molecules. The monolayer adsorption occurs on the adsorbent with uniform surface structure.²⁷ The linear form of Langmuir isotherm is represented as the following equation:

C_e/q_e = C_e/q_max + 1/(K_Lq_max) (8)

where q_e (g⁻¹) is the adsorption capacity at equilibrium; C_e is the equilibrium concentration of pigment in ICMP solution; q_max (g⁻¹) is the theoretical saturation adsorption capacity of the monolayer; K_L is the adsorption equilibrium constant.

In contrast to the Langmuir model, the Freundlich adsorption isotherm is used to describe a kind of adsorption process on heterogeneous surfaces.²⁵ The Freundlich model is expressed as follows:

ln q_e = ln K_f + ln C_e/n (9)

where q_e (g⁻¹) is the adsorption capacity at equilibrium; C_e is the equilibrium concentration of pigment in ICMP solution; K_f and n are the Freundlich constants which related to adsorption capacity and adsorption intensity, respectively.

The Temkin isotherm model assumed that the heat of adsorption decreases linearly with surface coverage of adsorbent as a result of adsorbent or adsorbate interactions.²⁸ It has generally been applied in the following form:

q_e = RT/b_T × (ln A) + RT/b_T × (ln C_e) (10)

where q_e (g⁻¹) is the adsorption capacity at equilibrium; C_e is the equilibrium concentration of pigment in ICMP solution; b_T (J mol⁻¹) and A are the Temkin constants which related to the heat of adsorption and adsorption equilibrium, respectively; T (K) is the kelvin temperature; R is the gas constant, 8.314 J (mol⁻¹ K⁻¹).

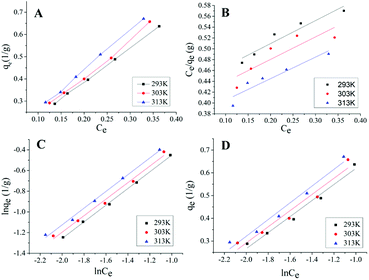
As shown in Fig. 4A, the adsorption isotherms at different temperatures were similar, with the increases of temperatures, q_e gradually increased. Isotherm plots for the Langmuir model, the Freundlich model and the Temkin model of the adsorption of ICMP onto MCM at different temperature are shown in Fig. 4B–D, values of these model constants are given in Table 5.

Fig. 4 Line of isothermal adsorption at different temperatures (A), linear plots of the Langmuir (B), Freundlich (C) and Temkin (D) models at different temperature.

Table 5 Parameters for Langmuir, Freundlich and Temkin modelling at different temperatures

T (K)	Langmuir			Freundlich			Temkin
	qmax (g^−1)	KL	R^2	Kf	n	R^2	A	bT (J mol^−1)	R^2
293	2.360	1.003	0.9322	1.425	1.241	0.9985	15.735	6906.73	0.9781
303	2.411	0.958	0.7669	1.494	1.252	0.9905	16.798	7090.18	0.9539
313	2.517	1.087	0.8920	1.635	1.237	0.9962	17.713	7081.04	0.9745

---

From the data in Table 5, it can be found that in the Langmuir equation constants, the value of q_max increase with the increase of temperature, indicating that the pigment in ICMP is more likely to be adsorbed on MCM at higher temperatures. However, the R² value of Langmuir fitting equation is small, which indicates that the adaptation of ICMP pigment onto MCM do not fit well with Langmuir model. In the Freundlich isotherm, n represent the type of adsorption isotherm as follows: favorable (0 < 1/n < 1), irreversible (1/n = 0), or unfavorable (1/n > 1).²⁶ From Table 5, we found that, all the values of n are higher than 1, which indicated that pigment in ICMP were adsorbed favorably by the MCM during this study. The value of K_f is related to adsorption capacity of MCM and the value of K_f (Table 5) increases with the increase of temperature, indicating that the adsorption process is endothermic in nature. According to the intercept and slope of Fig. 4D, the Temkin constants A and b_T can be obtained (Table 5). The value of A increases with the increase of temperature, indicating that the strength of the interaction between ICMP and MCM also increases. b_T is related to the heat of adsorption, and it also tends to increase as the temperature rises.

Based on these results, both Freundlich and Temkin models could be used to fit the equilibrium data. However, the R² value of Freundlich model is higher than that of Temkin model (Table 5). This implies that the Freundlich model may be more suitable to predict the adsorption ability of MCM on the pigment in ICMP.

3.5 Thermodynamic analysis of adsorption

Gibbs free energy (ΔG), enthalpy change (ΔH) and entropy change (ΔS) are important parameters of adsorption thermodynamics. Their values can be calculated from the following equations:

The value of ΔH can be calculated using the Clausius–Clapeyron equation:²⁹

dln(C_e)/dT = −ΔH/RT² (11)

After integral calculated it may be linearized as:³⁰

ln C_e = ΔH/RT + C (12)

where C is the constant, the values of ΔH can be calculated by the slope and intercept of ln C_e versus 1/T curve (figure not shown).

Because the Freundlich model is more suitable for this adsorption process, the ΔG and ΔS value can be calculated by equation below as shown by:³⁰

ΔG = −nRT (13)

ΔS = (ΔH − ΔG)/T (14)

where R is the gas constant 8.314 J (mol⁻¹ K⁻¹), T (K) is the kelvin temperature, n is the characteristic constant from Freundlich model.³⁰

The parameters of thermodynamic are shown in Table 6. At different temperatures, all ΔG values are negative, which suggests that the adsorption of pigment in ICMP on MCM is a spontaneous process. In addition, the value of ΔG decreased with the increase of temperature, indicating that higher temperature is conducive to the adsorption, which is consistent with the results of adsorption equilibrium study. The absolute value of ΔG is less than 20 kJ mol⁻¹, indicating the involvement of physical adsorption.²⁵ Because ΔH > 0, but less than 30 kJ mol⁻¹, we believe that the adsorption process is an endothermic process, and physical adsorption is the main one.³¹ Table 6 shows that the values of entropy change (ΔS) were both positive, which indicates an increase in the randomness at the solid/liquid interface during the adsorption process.²⁷

Table 6 Thermodynamic parameters for ICMP pigment adsorption onto the MCM

qe (g^−1)	ΔH (kJ mol^−1)	ΔG (kJ mol^−1)			ΔS (J (mol^−1 K^−1)
		293 K	303 K	313 K	293 K	303 K	313 K
0.1	6.070	−3.023	−3.154	−3.219	31.033	30.441	29.676
0.2	6.168				31.368	30.765	29.990
0.4	6.266				31.702	31.088	30.302
0.6	6.323				31.897	31.277	30.485
0.8	6.364				32.036	31.411	30.615

---

3.6 The material recycling

The desorption and regeneration capacity of the adsorbent is an important criterion for evaluating the quality of the adsorbent. To evaluate the desorption and regeneration property of MCM, adsorption desorption experiments were carried out six times. The D_r% values of the six times adsorption desorption experiments were 90.35%, 90.11%, 89.23%, 87.87%, 85.75% and 83.52%, respectively. After six times adsorption desorption experiments, the value of D_r% decreased from 90.35% to 83.52%. It shows that MCM has good desorption and regeneration ability, and has the potential of development and utilization.

3.7 Comparison of characterization of samples before and after decolorization with MCM

In order to validate the decolorization efficiency of MCM, the ICMP solutions before and after treatment by MCM under the above optimal conditions were characterized by digital photography, UV-vis Spectroscopy, Vis Spectroscopy after sulfuric acid phenol coloration and IR Spectroscopy. As shown in Fig. 5A, the pigment absorption peak in the region of 200–800 nm disappeared after MCM treatment, indicating that most of the pigments were removed by the MCM. Meanwhile, the photograph of ICMP solutions before and after adsorption also demonstrated that most of the pigments had been absorbed by MCM. The absorbance at 490 nm of polysaccharide solution after color development by phenol-sulphate acid method represents the concentration of polysaccharide.¹⁶ As shown in Fig. 5B, there is no significant difference in the absorbance at 490 nm of the ICMP solution before and after decolorization, indicating that the loss of polysaccharide during the adsorption process is very small. The characterizations of IR Spectroscopy (Fig. 5D) before and after decolorization demonstrated the characteristic groups of ICMP were adequately retained after MCM treatment. The above results show that MCM has good decolorization performance and has little effect on ICMP.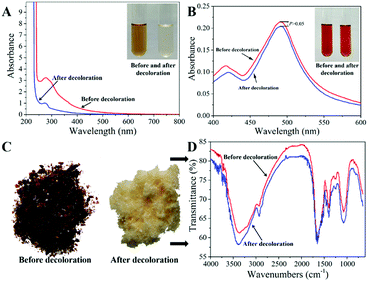

Fig. 5 The UV-vis spectrogram (A), Vis spectrogram after sulfuric acid phenol coloration (B), IR spectrogram (C and D) of ICMP solutions before and after decolorization by MCM.

3.8 Comparison of different decolorization methods

In order to verify the decolorization effect of MCM, different decolorization methods were compared (ESI†). As shown in Table 7, MCM presented higher K_c value than that of hydrogen peroxide and activated carbon. The adsorption process of MCM was spontaneous and endothermic. In addition, the adsorption process of MCM is mainly physical adsorption, which has little damage to the structure of polysaccharide. Besides, MCM is a kind of magnetic material, easy to magnetic separation and recovery, and can reduce the waste of polysaccharide in the separation process. Therefore, MCM displayed higher D_r% and R_r% values. The D_r% of activated carbon is low, indicating that its decolorization effect is not good, but because it belongs to physical adsorption, it has no effect on the structure of polysaccharide, its R_r% value is higher than that of hydrogen peroxide. But the separation process of activated carbon is complicated, resulting in some polysaccharide is lost, so its R_r% is lower than MCM. The decolorization process of hydrogen peroxide is chemical decolorization, and the effect is obvious. Its D_r% value is higher than that of activated carbon, which is equivalent to MCM, but because it destroys the structure of polysaccharide, its R_r% value is lower.

Table 7 Comparison of different decolorization methods^a

Methods	Dr (%)	Rr (%)	Kc
a Data were presented as mean ± SD (n = 3). Superscript “**” represent very significant (P < 0.01) compared with present method.
Activated carbon adsorption	80.72 ± 0.64^**	90.14 ± 0.10^**	8.19 ± 0.02^**
Hydrogen peroxide oxidation	90.82 ± 0.50	86.59 ± 0.04^**	6.77 ± 0.03^**
Present method	90.31 ± 0.12	95.40 ± 0.11	19.66 ± 0.49

---

3.9 Discussion

In this study, the emulsion cross-linking method was used to prepare MCM, and its structure is a shell–core structure. The outer shell of the microsphere is chitosan and the core is Fe₃O₄.¹³ The external chitosan has hydrophilic, large specific surface area and more adsorption sites, so MCM has good decolorization effect and high D_r% value.^11,32 The internal Fe₃O₄ makes MCM have magnetic properties, easy to separate from the solution, reducing the loss of polysaccharide. In addition, the results show that the decolorization process of ICMP by MCM is mainly physical adsorption, and has little effect on the structure of polysaccharide, so MCM has high R_r% value. The higher values of D_r% and R_r% proved that MCM was an excellent decolorizing agent under the optimal decolorization conditions.

In the study of adsorption mechanism, we found that the decolorization process of ICMP by MCM conformed to pseudo-second order equation and belonged to heterogeneous diffusion process, which was controlled by reaction rate, membrane diffusion and intra-particle diffusion. Freundlich model may be more suitable for predicting the adsorption capacity of MCM to pigments in ICMP. The results of thermodynamic experiments prove that the decolorization process of ICMP by MCM is remarked by physical adsorption, which is an endothermic reaction that occurs spontaneously. Within a certain range, the increase in temperature is conducive to the progress of adsorption; the adsorption reaction is an entropy-driven process, during the adsorption process the randomness of the solid/liquid interface increases.

In addition, we examined the zeta potential value of the polysaccharide solution before and after decolorization (ESI†). It was found that the zeta potential value increased after decolorization, indicating that the pigment in the polysaccharide solution was negatively charged. Due to the presence of protonated amino groups (–NH³⁺) on the surface of chitosan, it has excellent adsorption performance for negatively charged pigments, so the selective adsorption of MCM may be determined by surface charge.

4. Conclusion

In this study, MCM was proved to have a good decolorization effect on ICMP. The experimental results showed that the optimal decolorization conditions were operated at 48 °C for 82 min (pH = 7) and MCM dosage of 8% (g ml⁻¹). Under these conditions, values of D_r%, R_r% and K_c were 90.31 ± 0.12%, 95.40 ± 0.11% and 19.66 ± 0.49, respectively. From the results of adsorption kinetics experiments, the adsorption process of MCM fitted better with the pseudo-second order equation. Elovich equation shows that the adsorption of the ICMP pigment by MCM is a heterogeneous diffusion process. In addition, the adsorption mechanism of ICMP on MCM may be controlled by multiple-diffusion steps, including film diffusion and intra-particle diffusion. From the adsorption isotherms studies, the adsorption isotherms were better fitted by the Freundlich equation. Moreover, the adsorption process of MCM was spontaneous and endothermic. In addition, the adsorption process of MCM is mainly physical adsorption, which has little damage to the structure of polysaccharide. Most significantly, MCM has good desorption and regeneration ability, and the decolorization effect is better than traditional decolorization methods. In summary, MCM adsorption is a promising decolorization method of polysaccharide which can be used in the field of food industry and pharmaceuticals.

Author contributions

Bingbing Yu: investigation, writing – original draft; Yao Chen: investigation, writing – original draft; Lijun Zhu: investigation, writing – original draft; Mengmeng Ban: validation; Li Yang: investigation; Yeda Zeng: investigation; Shijie Li: resources; Chunzhi Tang: review & editing; Dnayan Zhang: investigation, writing-review & editing; Xiaoqing Chen: investigation, writing-review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Opening Funding of Guangdong Provincial Key Laboratory of New Drug Development and Research of Chinese Medicine (grant numbers: 2017B030314096-02).

References

1. Y. F. Wang, Y. Q. Tian, J. J. Shao, X. Shu, J. X. Jia, X. J. Ren and Y. Guan, Int. J. Biol. Macromol., 2018, 108, 300–306.
2. Q. Li, Y. M. Niu, P. F. Xing and C. M. Wang, Chin. Med., 2018, 13(1), 7.
3. Y. B. Wang, P. F. He, L. He, Q. R. Huang, J. W. Cheng, W. Q. Li, Y. Liu and C. Y. Wei, Carbohydr. Polym., 2019, 216, 270–281.
4. Y. Chen, T. Wang, X. Zhang, F. M. Zhang and R. J. Linhardt, Carbohydr. Polym., 2021, 254(1), 117462.
5. Q. Wang, C. L. Wang, F. G. He and H. Y. Zhang, J. Chin. Oncol., 2013, 19, 227–230.
6. Z. C. Xu, X. T. Yan, Z. Y. Song, W. Li, W. B. Zhao, H. H. Ma, J. L. Du, S. J. Li and D. Y. Zhang, Int. J. Biol. Macromol., 2018, 117, 610–616.
7. Y. Y. Shi, T. T. Liu, Y. Han, X. F. Zhu, X. J. Zhao, X. J. Ma, D. Y. Jiang and Q. H. Zhang, Food Chem., 2017, 217, 461–468.
8. A. Simaratanamongkol and P. Thiravetyan, J. Food Eng., 2010, 96(1), 14–17.
9. P. Baldrian, V. Merhautova, J. Gabriel, F. Nerud, P. Stopka, M. Hruby and M. J. Benes, Appl. Catal., B, 2006, 66, 258–264.
10. J. Liu, J. G. Luo, Y. Sun, H. Ye, Z. X. Lu and X. X. Zeng, Bioresour. Technol., 2010, 101(15), 6077–6083.
11. C. Zhang, S. Y. Liu, S. X. Li, Y. Tao, P. P. Wang, X. Y. Ma and L. Z. Chen, Colloids Surf., A, 2019, 581, 123813.
12. C. Z. Fan, K. Li, Y. He, Y. L. Wang, X. F. Qian and J. P. Jia, Sci. Total Environ., 2018, 627, 1396–1403.
13. Z. Y. Song, Y. D. Hu, L. K. Qi, T. T. Xu, Y. S. Yang, Z. C. Xu, X. P. Lai, X. L. Wang, D. Y. Zhang and S. J. Li, Carbohydr. Polym., 2018, 195, 558–565.
14. M. G. Sevag, D. B. Lackman and J. Smolens, J. Biol. Chem., 1938, 124(1), 42–49.
15. L. Liang, G. M. Liu, G. Y. Yu, Y. Song and Q. H. Li, Food Chem., 2018, 277, 744–752.
16. M. Dubois, K. A. Gilles, J. K. Hamilton, P. A. Rebers and F. Smith, Anal. Chem., 1956, 28(3), 350–356.
17. Q. P. Xiong, S. Huang, J. H. Chen, B. L. Wang, L. He, L. Zhang, S. J. Li, J. Z. Wang, J. G. Wu, X. P. Lai and D. Y. Zhang, J. Cleaner Prod., 2017, 142, 3409–3418.
18. D. Y. Zhang, S. J. Li, Q. P. Xiong, C. X. Jiang and X. P. Lai, Carbohydr. Polym., 2013, 95(1), 114–122.
19. C. Chen, L. J. You, A. M. Abbasi, X. Fu and R. H. Liu, Carbohydr. Polym., 2015, 130, 122–132.
20. Q. S. Wang, T. J. Ying, M. M. Jahangir and T. J. Jiang, J. Food Eng., 2012, 111(2), 386–393.
21. Y. S. Ho and G. Mckay, Process Saf. Environ. Prot., 1998, 76(4), 332–340.
22. Y. S. Ho and G. Mckay, Water Res., 2000, 34(3), 735–742.
23. K. D. Belaid, S. Kacha, M. Kameche and Z. Derriche, J. Environ. Chem. Eng., 2013, 1(3), 496–503.
24. A. Serpen, B. Atac and V. Goekmen, J. Food Eng., 2007, 82(3), 342–350.
25. Z. P. Gao, Z. F. Yu, T. L. Yue and S. Y. Quek, J. Food Eng., 2013, 116(1), 195–201.
26. S. Vasiliu, I. Bunia, S. Racovita and V. Neagu, Carbohydr. Polym., 2011, 85(2), 376–387.
27. Y. Y. Xu, Q. F. Dang, C. S. Liu, J. Q. Yan, B. Fan, J. P. Cai and J. J. Li, Colloids Surf., A, 2015, 482, 353–364.
28. T. L. Yue, C. X. Guo, Y. H. Yuan, Z. L. Wang, Y. Luo and L. Wang, J. Food Sci., 2013, 78(10-11-12), T1629–T1635.
29. T. S. Anirudhan and P. G. Radhakrishnan, Appl. Surf. Sci., 2009, 255(9), 4983–4991.
30. J. H. Huang, R. J. Deng and K. L. Huang, Chem. Eng. J., 2011, 171(3), 951–957.
31. F. Q. Liu, J. L. Chen, C. Long, A. M. Li, G. D. Gao and Q. X. Zhang, Chin. J. Polym. Sci., 2004, 22(3), 219–224.
32. X. J. Hu, J. S. Wang, Y. G. Liu, X. Li, G. M. Zeng, Z. L. Bao, X. X. Zeng, A. W. Chen and F. Long, J. Hazard. Mater., 2011, 185(1), 306–314.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra07758a

‡ These authors contributed equally to this paper.

---