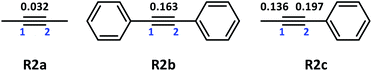Open Access Article
Open Access ArticleTheoretical investigation on the effect of the ligand on bis-silylation of C(sp)–C(sp) by Ni complexes†
Li Hui *ab,
He Yuhana and
Wang Jiaqia
*ab,
He Yuhana and
Wang Jiaqia
aCollege of Chemistry and Chemical Engineering, North Minzu University, Yinchuan, China. E-mail: lihui@nun.edu.cn
bKey Laboratory of Chemical Engineering and Technology, North Minzu University, State Ethnic Affairs Commission, Yinchuan, China
First published on 5th January 2022
Abstract
Density functional theory is used to study the bis-silylation of alkyne catalysed by a transition metal nickel–organic complex. The active catalyst, organic ligand, reaction mechanism, and rate-determining step were discussed with regard to dynamics and thermodynamics. COD or SIPr (COD = cyclooctadiene, SIPr = 1,3-bis(2,6-diisopropyl-phenyl)-4,5-dihydroimidazol-2-ylidene) coordination with Ni will greatly reduce the energy barrier of the Si–Si insertion step, that is, ΔΔG reaches 15.5 kcal mol−1. Furthermore, the structure of alkynes will change the energy barrier of the alkyne insertion step.
Introduction
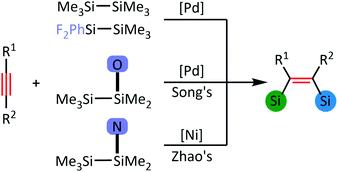
Organosilicon compounds are widely used in organic synthetic chemistry,1 materials science,2 and pharmaceutical chemistry.3 It is important to develop a rapid and efficient method for preparing silane compounds. Transition metal-catalysed bis-silylation of alkynes with disilanes, particularly chain disilanes, has received considerable interest amongst researchers.4–6 1, 2-Bisilicyl alkenes have wide and important application potential in the field of organic synthesis.7–10 The two silicon pieces based on alkenes show different activities in the subsequent transformation of products, and organic molecules with various structures can be synthesised through stepwise regional and chemically selective transformation. The transition metal-catalysed bis-silylation of the alkyne is an effective method of synthesising disubstituted alkenes.11,12 However, this method has the following limitations: the use of symmetrical ethyl silane to introduce two identical silyl groups, which can hardly distinguish the two silyl groups effectively in subsequent transformation. Transition metal complexes of platinum group metals with low valence are used as catalysts. Therefore, developing asymmetric bis-silylation catalysed by earth-abundant metal is important.In 1994, Ozawa and co-workers13 reported the bis-silylation of acetylene using Me3SiSiF2Ph as silane reagent in the presence of a palladium catalyst to construct bis-silylated olefin. In 2015, Spencer14 reported intermolecular bis-silylation (hexamethyldisilane) catalysed by a palladium complex to construct cis-bis-silylation alkenes. In 2018, Song15 used asymmetric disilane reagents for the region- and stereo-selective bis-silylation of alkynes. One Si-atom was connected to an amide group that could coordinate with transition metal Pd to achieve asymmetric di-silicification of terminal alkynes. In 2021, Zhao16 adjusted the amide group with weak coordination ability to quinoline group 8-(2-substituted 1,1,2,2-tetramethyldisilanyl) quinoline (TMDQ). The strong coordination of TMDQ was used to form complexes with nickel to achieve Si–Si activation, and then the bis-silicification between TMDQ and various unsaturated bonds was further obtained. In addition, using quinoline as directing group, the two adjacent silicon groups in the product can be distinguished efficiently in the subsequent chemical transformation, thereby generating bis-silicon alkene products. Although many production methods can be used to construct vinylsilane, the synthesis of tetra-substituted vinylsilane remains challenging for researchers.17–23
Based on the above-mentioned experimental research results, the author focussed on the following contents. Introducing the directing group in silane, which can be coordinated with metal centre Ni, can improve the catalytic activity of Ni. In addition, the structure of alkynes may affect the coordination capacity and selectivity of products. The regio-selective synthesis of di-silane has always been concerned by several researchers, and many difficulties are identified during synthesis. Theoretical calculation work can provide theoretical support with guiding significance for experimental work.
Results and discussion
Ligands and coordination capacity of catalysts
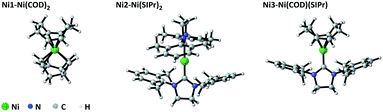
As shown in Scheme 1, Zhao and co-author16 have reported bis-silylation of internal alkynes enabled by Ni(0) catalysis. As shown in Fig. 1, Ni1, Ni2 and Ni3 are used as COD/COD, SIPr/SIPr and COD/SIPr ligands, respectively (COD = cyclooctadiene, SIPr = 1,3-bis(2,6-diisopropyl-phenyl)-4,5-dihydroimidazol-2-ylidene). In the case of Ni1, the multiplicity of Ni1a is 1, and the multiplicity of Ni1b is 3. In the reaction system,16 10 mol% Ni(COD)2 and 12 mol% SIPr were added to the reaction system, and the yield reached 98%, following the addition of SIPr compared with ICy and PPh3.With regards to the phenomenon, we think that the starting point of the catalytic cycle for the reaction may not be Ni1. Therefore, the ligands and multiplicity are discussed below. In the case of ligand exchange between the neutral ligand SIPr and COD, SIPr coordinated with Ni and generated Ni2, and either SIPr or COD both coordinated with Ni simultaneously and then generated Ni3. In addition, the electron configuration outside the nucleus of Ni is 3d84s2, and the eight electronic configurations in the d orbital may result in the multiplicity of Ni(COD)2 being 1 or 3. Meanwhile, the SIPr system shows singlet and triplet states. Furthermore, the Ni1, Ni2 and Ni3 intermediates show singlet and triplet states. Then, we label the singlet 1Ni1 state as Ni1a, the triplet 3Ni1 state as Ni1b, and the other intermediates.
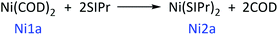 | (1) |
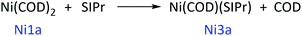 | (2) |
| ΔG = GNi2a/GNi3a + nGCOD − GNi1a − nGSIPr | (3) |
The calculated results show that the Gibbs free energy of triplet Ni1b is 26.9 kcal mol−1 higher than that of singlet Ni1a (Ni1a as the relative zero point) after correction for solvation effect. The singlet states of Ni2a and Ni3a are stable in thermodynamics (relative energy comparable to Ni2a/Ni2b and Ni3a/Ni3b in ESI†). Then, delta Gibbs free energy for reaction (1) and reaction (2) was calculated. In reaction (1), two neutral COD ligands are dissociated and coordinated with two neutral SIPr ligands. In reaction (2), one neutral molecular COD is dissociated and coordinated with one neutral molecular SIPr. The Gibbs free energy calculation formula is based on eqn (3). The delta Gibbs free energy of reaction (1) is −14.6 kcal mol−1, whereas that of reaction (2) is −1.3 kcal mol−1. Therefore, Ni(SIPr)2 is the most stable structure. However, whether or not Ni(SIPr)2 is an active catalyst remains unknown.
Next, the coordination capacity of Ni-atom with COD and/or SIPr in Ni1a, Ni2a and Ni3a catalysts was studied. The sum of natural adaptive orbital (NAdO) eigenvalues24 of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond is 1.87382 in COD. The NAdO eigenvalue is an orbital closely related to bond order density, which can exhibit the source of delocalisation index with regards to an orbital picture. In addition, the delocalisation index is visualised and important in understanding the nature and interatomic interaction. The sum of NAdO eigenvalues of the C–N bond is 1.44774 in SIPr. By contrast, the sum of NAdO eigenvalues of the C
C bond is 1.87382 in COD. The NAdO eigenvalue is an orbital closely related to bond order density, which can exhibit the source of delocalisation index with regards to an orbital picture. In addition, the delocalisation index is visualised and important in understanding the nature and interatomic interaction. The sum of NAdO eigenvalues of the C–N bond is 1.44774 in SIPr. By contrast, the sum of NAdO eigenvalues of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond reduces to 1.33252 after the C
C bond reduces to 1.33252 after the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond as η2 ligand coordinated with Ni-atom in the Ni1a complex. The sum of NAdO eigenvalues of the C–N bond decreases to 1.30377 after nitrene coordination with Ni-atom in the Ni2a complex. The sum of NAdO eigenvalues of the C
C double bond as η2 ligand coordinated with Ni-atom in the Ni1a complex. The sum of NAdO eigenvalues of the C–N bond decreases to 1.30377 after nitrene coordination with Ni-atom in the Ni2a complex. The sum of NAdO eigenvalues of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond decreases to 1.35341, and the sum of the NAdO eigenvalues of the C–N bond decreases to 1.28442. The sum of NAdO eigenvalues of the C–Ni bond in Ni1a is 0.64763/0.66437/0.66454/0.64781/0.64778/0.66453/0.66472/0.64799, and the average value is 0.65617. The sum of NAdO eigenvalues of N–Ni bonds in Ni2a is 1.20931/1.20918, and the mean value is 1.20925. The sum of NAdO eigenvalues of N–Ni bonds in Ni3a is 1.22928, and that of C–Ni is 0.69151/0.68551/0.68543/0.69140. The average value is 0.68846.
C double bond decreases to 1.35341, and the sum of the NAdO eigenvalues of the C–N bond decreases to 1.28442. The sum of NAdO eigenvalues of the C–Ni bond in Ni1a is 0.64763/0.66437/0.66454/0.64781/0.64778/0.66453/0.66472/0.64799, and the average value is 0.65617. The sum of NAdO eigenvalues of N–Ni bonds in Ni2a is 1.20931/1.20918, and the mean value is 1.20925. The sum of NAdO eigenvalues of N–Ni bonds in Ni3a is 1.22928, and that of C–Ni is 0.69151/0.68551/0.68543/0.69140. The average value is 0.68846.
Based on the NAdO value of ligands and complexes, the NAdO eigenvalues of COD and SIPr decreased because of the coordination with Ni-atoms. The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond in COD as η2 ligands and N-atoms in SIPr were delocalised because of coordination. In addition, the coordination capacity of the C
C double bond in COD as η2 ligands and N-atoms in SIPr were delocalised because of coordination. In addition, the coordination capacity of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond in COD is significantly stronger than that of nitrene in SIPr. Combined with the reaction mechanism and free energy surface, we hypothesise that the coordination capacity of COD is stronger than SIPr, and COD as a strong ligand ‘locks up’ the coordination site between Ni-atom and the substrate.
C bond in COD is significantly stronger than that of nitrene in SIPr. Combined with the reaction mechanism and free energy surface, we hypothesise that the coordination capacity of COD is stronger than SIPr, and COD as a strong ligand ‘locks up’ the coordination site between Ni-atom and the substrate.
Reaction mechanism
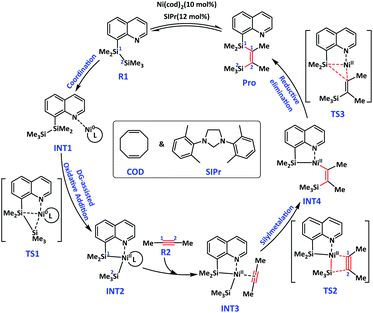
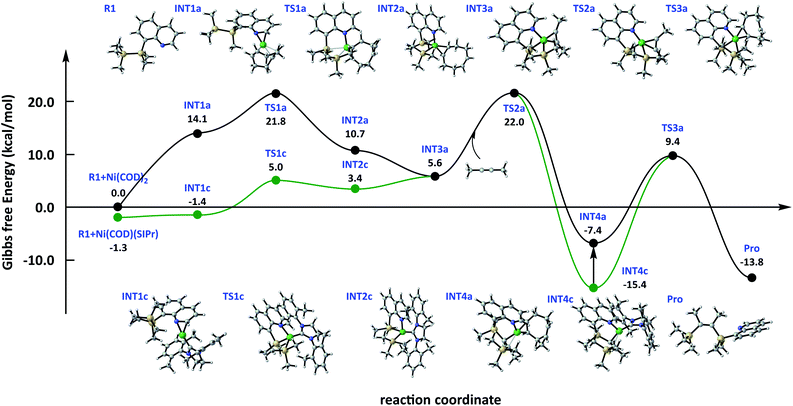
Theoretical calculation of quinoline and dimethylacetylene was used as a model reaction to conduct a reaction mechanism study under optimal reaction conditions. R1 generation Pro catalysed by Ni(COD)2 and SIPr is shown in Fig. 2. The reaction consists of three steps, oxidation addition/Si–Si bond broken, alkyne insertion/C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C activation, and reductive elimination. The metal centre Ni of the catalyst underwent Ni0–NiII–Ni0 during the catalytic cycle. The N-atom coordination with Ni in TMDQ effectively controlled the catalytic activity of catalyst centre Ni-atom.
C activation, and reductive elimination. The metal centre Ni of the catalyst underwent Ni0–NiII–Ni0 during the catalytic cycle. The N-atom coordination with Ni in TMDQ effectively controlled the catalytic activity of catalyst centre Ni-atom.
As shown in Fig. 2, intermediate INT1a was formed by coordination of Ni-atom in catalyst and N-atom in reagent R1. Then, the Si–Si bond oxidative addition was catalysed by the Ni-complex, which underwent ternary ring transition state TS1 by breaking the Si1–Si2 bond and generating the Si1–Ni–Si2 bond. In the Si–Si oxidative step, the Si1 atom attacked the Ni atom, and then a three-membered ring was formed. The distance of Si1–Ni from 4.54 Å in INT1a decreased to 2.65 Å in TS1a and then further decreased to 2.23 Å in INT2a. Meanwhile, the distance of Si2–Ni from 6.77 Å in INT1a decreased to 2.62 Å in TS1a and then further decreased to 2.28 Å in INT2a. We hypothesise that the N-atom coordination with Ni in TMDQ controlled the catalytic activity of catalyst centre Ni-atom. The bond length of Ni–N is 1.94, 1.97 and 2.05 Å in INT1a, TS1a and INT2a, respectively. Evidently, the generation of the Si1–Ni–Si2 bond weakens the chemical bond strength of the Ni–N bond. The bond length of Si1–Si2 is 2.38, 2.43 and 2.80 Å in INT1a, TS1a and INT2a, respectively.
The transition metal centre Ni0 is oxidised to NiII form the cyclometallation intermediate INT2. The intermediate INT3 is formed after alkyne(R2) coordination with Ni in INT2, which occurs during the alkyne insertion reaction. The C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C in R2 as η3 ligand coordinated with Ni-atom in INT2a, followed by dissociation of COD, and then generation INT3a. In INT3a, the bond length of Ni–C1, Ni–C2 and C1–C2 is 1.92, 1.89 and 1.28 Å, respectively. Compared with the coordination of C
C in R2 as η3 ligand coordinated with Ni-atom in INT2a, followed by dissociation of COD, and then generation INT3a. In INT3a, the bond length of Ni–C1, Ni–C2 and C1–C2 is 1.92, 1.89 and 1.28 Å, respectively. Compared with the coordination of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C in COD with Ni in INT2a, C
C in COD with Ni in INT2a, C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C coordination with Ni in INT3a is markedly enhanced. After C
C coordination with Ni in INT3a is markedly enhanced. After C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C in R2 coordinated with Ni, the bond length increased from 1.21 Å to 1.28 Å. The intermolecular silylmetalation reaction via Ni–C1–C2–Si2 quaternary ring transition state TS2 forms the intermediate INT4. The bond length of C1–C2 is 1.28, 1.32 and 1.41 Å in INT3a, TS2a and INT4a, respectively. In addition, the bond length of Ni–N is 2.03, 1.97, 2.05 and 2.09 Å in INT3a, TS2a, INT4a and INT4c, respectively. Therefore, the N-atom modulated the coordination activity of Ni-atom, and SIPr had a stronger coordination capacity than COD, thereby leading to a longer bond length in Ni–N(8-Qu). Then, Then, COD or coordination with Ni-atom could ensure coordinative saturation in INT4a/INT4c. Reductive elimination of INT4a is accompanied by Si1–Ni–C1 three-membered ring transition state of TS3, generating the bis-silylation product Pro. Meanwhile, the Ni0 catalyst is regenerated.
C in R2 coordinated with Ni, the bond length increased from 1.21 Å to 1.28 Å. The intermolecular silylmetalation reaction via Ni–C1–C2–Si2 quaternary ring transition state TS2 forms the intermediate INT4. The bond length of C1–C2 is 1.28, 1.32 and 1.41 Å in INT3a, TS2a and INT4a, respectively. In addition, the bond length of Ni–N is 2.03, 1.97, 2.05 and 2.09 Å in INT3a, TS2a, INT4a and INT4c, respectively. Therefore, the N-atom modulated the coordination activity of Ni-atom, and SIPr had a stronger coordination capacity than COD, thereby leading to a longer bond length in Ni–N(8-Qu). Then, Then, COD or coordination with Ni-atom could ensure coordinative saturation in INT4a/INT4c. Reductive elimination of INT4a is accompanied by Si1–Ni–C1 three-membered ring transition state of TS3, generating the bis-silylation product Pro. Meanwhile, the Ni0 catalyst is regenerated.
The free energy surface (Fig. 3) serves (Ni1a + R1) as the relative zero point. All the energies were corrected by using a continuum solvation model based on density (SMD)25 in toluene (the free energy surface in a vacuum is shown in Fig. SI†). As shown in Fig. 3, the energy span of the oxidation addition step is 6.3 kcal mol−1 using Ni3a as catalyst, whereas the energy barrier is 21.8 kcal mol−1 using Ni1a as the catalyst. The calculation results are in consistent with our prediction about active catalysts either from thermodynamics or kinetics. Next, the same mechanism in alkyne insertion steps is observed, and the energy barrier is 16.4 kcal mol−1. Considering that SIPr has a stronger coordination capacity than COD, INT4c is 8.0 kcal mol−1 lower than INT4a. Therefore, COD coordination with Ni is the suitable path, whose energy barrier is 16.8 and 24.8 kcal mol−1 from INT4a and INT4c to Pro in the reductive elimination step, respectively. Therefore, using Ni3a as the catalyst is more advantageous than Ni1a, and the rate-determining step is a reductive elimination step.
 | ||
| Fig. 3 Free energy surface of bis-silylation of the C(sp)–C(sp) bond catalysed by the Ni complex was corrected by SMD solvation model in toluene. | ||
Disparity of alkyne structure during alkyne insertion
Theoretical calculations were performed for the three representative alkynes, namely, R2a, R2b and R2c, to investigate the influence of the alkyne structure on alkyne silylmetalation during alkyne insertion. As shown in Fig. 4, the alkynes R2a and R2b have a symmetric structure, and R2c has asymmetric substitution. These three alkyne structures are selected to explore the influence of aliphatic substituent methyl and aromatic substituent phenyl connected to the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C triple bond and to study the interaction between Me/Ph and the C
C triple bond and to study the interaction between Me/Ph and the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C triple bond. We hypothesise that the reaction energy barrier and selectivity might affect the alkyne insertion reaction.
C triple bond. We hypothesise that the reaction energy barrier and selectivity might affect the alkyne insertion reaction.
Firstly, the Mulliken charge was calculated for sp-C in R2a, R2b and R2c, and the values are 0.032, 0.163 and 0.136/0.197, respectively. In addition, the nucleophilicity of phenyl is stronger than that of methyl. The π electron conjugation between phenyl and C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C has evident delocalisation characteristics. Meanwhile, the Mulliken charge of C1-atom connected to –Me in R2c is 0.136, and that of C2-atom connected to –Ph is 0.197. The charge is redistributed because of the substitution of Me and Ph in C1
C has evident delocalisation characteristics. Meanwhile, the Mulliken charge of C1-atom connected to –Me in R2c is 0.136, and that of C2-atom connected to –Ph is 0.197. The charge is redistributed because of the substitution of Me and Ph in C1![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C2. The locally delocalised frontier molecular orbital indicating π–π conjugation of C
C2. The locally delocalised frontier molecular orbital indicating π–π conjugation of C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C and phenyl and the electron cloud are biased towards phenyl in R2c. Based on the characteristics of electron-delocalised conjugation, the conjugation of C1
C and phenyl and the electron cloud are biased towards phenyl in R2c. Based on the characteristics of electron-delocalised conjugation, the conjugation of C1![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C2 and –Ph might affect the selectivity of alkyne insertion.
C2 and –Ph might affect the selectivity of alkyne insertion.
The coordination of Ni-atom with N-atom in the N heterocyclic segment in R1 will directly affect the catalytic activity and will determine whether the sites for the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C triple bond coordination with Ni-atom are adequate. Then, hole–electron analysis was used to investigate electron excitation characteristics in substrates. The contribution of the substituent group for HOMO in R2a, R2b and R2c is shown in Fig. 5. The exciton binding energy (coulomb attraction energy) is 8.98 eV in R2a; the orbital delocalisation index (ODI) of methyl is 29.72% for HOMO, and the fragment contribution and ODI of the fragment are 12.131% and 35.31%, respectively. Therefore, the C
C triple bond coordination with Ni-atom are adequate. Then, hole–electron analysis was used to investigate electron excitation characteristics in substrates. The contribution of the substituent group for HOMO in R2a, R2b and R2c is shown in Fig. 5. The exciton binding energy (coulomb attraction energy) is 8.98 eV in R2a; the orbital delocalisation index (ODI) of methyl is 29.72% for HOMO, and the fragment contribution and ODI of the fragment are 12.131% and 35.31%, respectively. Therefore, the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C triple bond forms a distinct π bond in HOMO, and the methyl group is in a relatively independent state. The exciton binding energy is 6.35 eV in R2b; the ODI of phenyl is 24.83% for HOMO, and the fragment contribution and ODI of the fragment are 92.96% and 28.34%, respectively. Therefore, a delocalised π–π bond formatted between C
C triple bond forms a distinct π bond in HOMO, and the methyl group is in a relatively independent state. The exciton binding energy is 6.35 eV in R2b; the ODI of phenyl is 24.83% for HOMO, and the fragment contribution and ODI of the fragment are 92.96% and 28.34%, respectively. Therefore, a delocalised π–π bond formatted between C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C and phenyl contributed greatly to HOMO. The exciton binding energy is 6.60 eV in R2c; the ODI of methyl/phenyl is 24.88%/24.88% for HOMO; the fragment contribution is 0.17%/93.12%, and the ODI of the fragment is 51.20%/28.28%.
C and phenyl contributed greatly to HOMO. The exciton binding energy is 6.60 eV in R2c; the ODI of methyl/phenyl is 24.88%/24.88% for HOMO; the fragment contribution is 0.17%/93.12%, and the ODI of the fragment is 51.20%/28.28%.
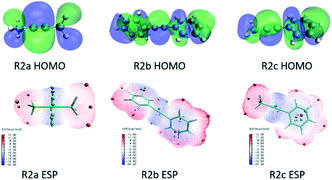 | ||
| Fig. 5 Contribution of the substituent group for HOMO in R2a, R2b and R2c, and restrained electrostatic potential (RESP) surface in R2a, R2b and R2c. | ||
The restrained electrostatic potential (RESP)26 charge was used to study R2a, R2b and R2c reactants. Fitting the electrostatic potential charge near and outside the van der Waals surface of the molecule calculated on the basis of the wave function reproduces an atomic charge, which is graphically displayed as RESP. In R2a, the minimum electrostatic potential point (blue area) is concentrated nearby the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C triple bond, and the minimum value is −19.47 kcal mol−1. In the R2b reactant, the minimum value of the C
C triple bond, and the minimum value is −19.47 kcal mol−1. In the R2b reactant, the minimum value of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C fragment is −15.81 kcal mol−1. In the R2c reactant, the minimum value of C
C fragment is −15.81 kcal mol−1. In the R2c reactant, the minimum value of C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C is −19.32 kcal mol−1. The C
C is −19.32 kcal mol−1. The C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C triple bond must coordinate with metal Ni in the following step. The calculation results indicated that R2b had the lowest RESP charge compared with the other two substrates, in which the conjugation of phenyl led to weakness coordination, making it conducive to subsequent alkyne insertion.
C triple bond must coordinate with metal Ni in the following step. The calculation results indicated that R2b had the lowest RESP charge compared with the other two substrates, in which the conjugation of phenyl led to weakness coordination, making it conducive to subsequent alkyne insertion.
We conducted transition state search and activation energy calculation for alkyne insertion to elucidate the effect of the alkyne structure on the reaction energy barrier and the influence of asymmetric alkyne on selectivity. As shown in Fig. 6, INT3c and INT3d are intermediates coordinated by methyl-phenyl-acetylene (R2c) and Ni-atom, and INT3e is an intermediate coordinated by dibenzenyl (R2b) and Ni-atom. The free energy surface of INT3 to TS2 serves (Ni1a + R1) as the relative zero point. The binding energy of complexes increases significantly (ΔG increases) after phenyl appears in alkynes, indicating that the stagnation point of INT3c, INT3d and INT3e has a lower Gibbs free energy than INT3a. In addition, the coordination direction of C1–C2 is flipped in R2c, and the delta relative energy of INT3c and INT3d is 1.3 kcal mol−1. Moreover, INT3d has lower relative energy because of the presence of π–π conjugation between 8-Qu in R1 and phenyl in R2c (Fig. 6). The energy barrier of intermediates INT3c/INT3d to TS2c/TS2d is 15.1 and 16.4 kcal mol−1, respectively. Furthermore, the bond length of Ni–Si from 2.29/2.28 Å increased to 2.41/2.38 Å compared with INT3a → TS2a (2.28 Å to 2.38 Å) and INT3e → TS2e (2.29 Å to 2.42 Å). Therefore, the bond length in the substrate and the structure in the transition state are due to the coordination capacity, which leads to the difference in energy barrier. In addition, phenyl-substituted alkynes have the lowest reaction energy barrier during alkyne insertion.
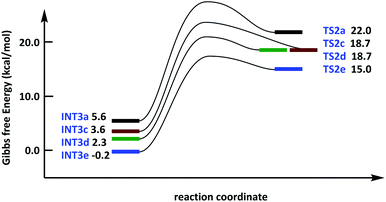 | ||
| Fig. 6 Free energy surface of bis-silylation of the C(sp)–C(sp) bond catalysed by the Ni complex was corrected by SMD solvation model in toluene. | ||
Conclusions
Density functional theory calculation results of TMDQ and alkyne show that the reaction consists of three steps, oxidation addition, alkyne insertion and reductive elimination. The metal centre Ni of the catalyst underwent Ni0–NiII–Ni0 during the catalytic cycle. In addition, the N-atom coordination with Ni in TMDQ effectively controlled the catalytic activity of the catalyst centre Ni-atom. The alkyne insertion step is closely related to the coordination intensity between the catalyst Ni and C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C triple bond. Phenyl-substituted alkynes have the lowest reaction energy barrier during alkyne insertion. Moreover, the coordination capacity of the C
C triple bond. Phenyl-substituted alkynes have the lowest reaction energy barrier during alkyne insertion. Moreover, the coordination capacity of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond in COD is significantly stronger than that of nitrene in SIPr, and COD as a strong ligand ‘locks up’ the coordination site between Ni-atom and the substrate.
C bond in COD is significantly stronger than that of nitrene in SIPr, and COD as a strong ligand ‘locks up’ the coordination site between Ni-atom and the substrate.
Computational details
All the optimised structures and frequency analysis were calculated at the B3LYP/BSI level using hybrid DFT27 implemented in Gaussian 09.28 BSI denotes the SDD29 basis set for Ni and the 6-31G(d)30 basis set for the other atoms (H, C, N and Si). The transition states were further confirmed by vibrational analysis and characterised by using only imaginary frequencies. Intrinsic reaction coordinate calculations were performed to confirm the INTs along the reaction pathway. Optimised structures and frequency analysis calculations were conducted using the SMD to evaluate the effects of the solvent on the potential energy surface. The ωB97X-D/BSII level31,32 was used to calculate solvation single-point energies and provide accurate energy information, in which BSII denotes the SDD basis set for Ni and the 6-311 + G(d, p)33 basis set for the other atoms (H, C, N and Si). The hybrid density functional B3LYP and ωB97X-D method is reliable, which has been used in previous studies.34–36 Moreover, SDD is suitable for the Ni-atom. The energies discussed in this paper are Gibbs free energies (kcal mol−1) in the solution. The importance of orbital wavefunction in the plane was drawn by Multiwfn.37Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by Science and Technology Research Project of Ningxia Institution Foundation (No. NGY2018-145), Natural Science Foundation of Ningxia Province (2019AAC03140, 2018AAC03251), the National Natural Science Foundation of China (21963001), and Ningxia low-grade resource high value utilization and environmental chemical integration technology innovation team project, China.Notes and references
- K. Matsuoka, N. Komami, M. Kojima, T. Mita, K. Suzuki, S. Maeda, T. Yoshino and S. Matsunaga, J. Am. Chem. Soc., 2021, 143, 103 CrossRef CAS PubMed.
- A. P. Amrute, B. Zibrowius and F. Schüth, Chem. Mater., 2020, 32, 4699 CrossRef CAS.
- S. Guariento, M. Biagetti and P. Ronchi, Future Med. Chem., 2021, 13, 595 CrossRef CAS PubMed.
- W. Gao and S. Ding, Synthesis, 2020, 52, 3549 CrossRef CAS.
- T. Fuchigami and S. Inagi, Curr. Opin. Electrochem., 2020, 24, 24 CrossRef CAS.
- F. Ye, Z. Xu and L. W. Xu, Acc. Chem. Res., 2020, 54, 452 CrossRef PubMed.
- R. Waterman, P. G. Hayes and T. D. Tilley, Acc. Chem. Res., 2007, 40, 712 CrossRef CAS PubMed.
- F. M. Mück, J. A. Baus, R. Bertermann, C. Burschka and R. Tacke, Organometallics, 2016, 35, 2583 CrossRef.
- Y. Wang, H. P. Hickox, Y. Xie, P. Wei, H. F. Schaefer III and G. H. Robinson, J. Am. Chem. Soc., 2017, 139, 16109 CrossRef CAS PubMed.
- C. Xu, Z. Ye, L. Xiang, S. Yang, Q. Peng, X. Leng and Y. Chen, Angew. Chem., Int. Ed., 2021, 60, 3189 CrossRef CAS PubMed.
- N. Lassauque, P. Gualco, S. Mallet-Ladeira, K. Miqueu, A. Amgoune and D. Bourissou, J. Am. Chem. Soc., 2013, 135, 13827 CrossRef CAS PubMed.
- J. Li, Y. Li, I. Purushothaman, S. De, B. Li, H. P. Zhu, P. Parameswaran, Q. S. Ye and W. P. Liu, Organometallics, 2015, 34, 4209 CrossRef CAS.
- F. Ozawa, M. Sugawara and T. Hayashi, Organometallics, 1994, 13, 3237 CrossRef CAS.
- M. B. Ansell, D. E. Roberts, F. G. N. Cloke, O. Navarro and J. Spencer, Angew. Chem., Int. Ed., 2015, 54, 5578 CrossRef CAS PubMed.
- P. Xiao, Y. Cao, Y. Gui, L. Gao and Z. Song, Angew. Chem., Int. Ed., 2018, 130, 4859 CrossRef.
- Y. Zhang, X. C. Wang, C. W. Ju and D. Zhao, Nat. Commun., 2021, 12, 1 CrossRef PubMed.
- T. A. Blumenkopf and L. E. Overman, Chem. Rev., 1986, 86, 857 CrossRef CAS.
- D. S. W. Lim and E. A. Anderson, Synthesis, 2012, 44, 983 CrossRef CAS.
- M. Zhang, Y. Zhang, X. Jie, H. Zhao, G. Li and W. Su, Org. Chem. Front., 2014, 1, 843 RSC.
- R. Shintani, H. Kurata and K. Nozaki, J. Org. Chem., 2016, 81, 3065 CrossRef CAS.
- T. Iwamoto, T. Nishikori, N. Nakagawa, H. Takaya and M. Nakamura, Angew. Chem., Int. Ed., 2017, 129, 13483 CrossRef.
- T. He, L. C. Liu, L. Guo, T. He, L. C. Liu and L. Guo, Angew. Chem., Int. Ed., 2018, 130, 11034 CrossRef.
- M. F. Wisthoff, S. B. Pawley, A. P. Cinderella and D. A. Watson, J. Am. Chem. Soc., 2020, 142, 12051 CrossRef CAS PubMed.
- J. L. Casals-Sainz, A. Fernández-Alarcón, E. Francisco, A. Costales and A. M. Pendás, J. Phys. Chem. A, 2019, 124, 339 CrossRef PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378 CrossRef CAS PubMed.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269 CrossRef CAS.
- J. A. Pople, P. M. W. Gill and B. G. Johnson, Chem. Phys. Lett., 1992, 199, 557 CrossRef CAS.
- J. E. Peralta Jr, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Wallingford CT, 2013 Search PubMed.
- T. H. Dunning Jr and P. J. Hay, Modern Theoretical Chemistry, ed. H. F. Schaefer III, vol. 3, Plenum, New York, 1976, pp. 1–28 Search PubMed.
- G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081 CrossRef CAS.
- R. G. Parr and W. Yang Density Functional Theory of Atoms and Molecules, Oxford University Press, Oxford, U.K. 1989 Search PubMed.
- T. Ziegler, Chem. Rev., 1991, 91, 651 CrossRef CAS.
- L. A. Curtiss, M. P. McGrath, J. P. Blaudeau, N. E. Davis, R. C. Binning Jr and L. Radom, J. Chem. Phys., 1995, 103, 6104 CrossRef CAS.
- H. Li, X. Ma, B. Zhang and M. Lei, Organometallics, 2016, 35, 3301 CrossRef CAS.
- H. Li, X. Ma and M. Lei, Dalton Trans., 2016, 45, 8506 RSC.
- H. Li, W. Tang and Z. Ma, Dalton Trans., 2021, 50, 10291 RSC.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra08153e |
| This journal is © The Royal Society of Chemistry 2022 |