Open Access Article
Open Access ArticleStructural, optical, electric and dielectric characterization of a NaCu0.2Fe0.3Mn0.5O2 compound
Ichrak Ben Slimaa,
Karim Karoui a,
Abdelfattah Mahmoud
a,
Abdelfattah Mahmoud b,
Frédéric Boschinib and
Abdallah Ben Rhaiem
b,
Frédéric Boschinib and
Abdallah Ben Rhaiem *a
*a
aLaboratory LaSCOM, University of Sfax, BP1171, 3000, Sfax, Tunisia. E-mail: abdallahrhaiem@yahoo.fr
bGREENMAT, CESAM, Institute of Chemistry B6, University of Liège, 4000, Liège, Belgium
First published on 10th January 2022
Abstract
The compound NaCu0.2Fe0.3Mn0.5O2 was synthesized using a solid-state method and it crystallized in a hexagonal system with a R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group in an O3-type phase. The optical properties were measured using UV-Vis absorption spectrometry to determine the absorption coefficient α and the optical band gap Eg. The optical band gap energy of this sample is 2.45 eV, which indicates that it has semiconductor characteristics. Furthermore, the electrical and dielectric properties of the material were investigated using complex impedance spectroscopy between 10−1 Hz and 106 Hz at various temperatures (333–453 K). The permittivity results prove that there are two types of polarization, dipolar polarization and space charge polarization. The Nyquist diagrams show the contribution of the effects of the grain, grain boundary, and electrode properties. The frequency dependence of the conductivity was interpreted in terms of Jonscher's law. The DC conductivity follows both the Mott and Arrhenius laws at low and high temperature, respectively. The temperature dependence of the power law exponent(s) suggests that the overlapping large polaron tunneling (OLPT) model is the dominant transport process in this material. The optimum hopping length of the polaron (4 Å) is large compared with the interatomic spacing (2.384 Å for Na–O and 2.011 Å for Cu, Fe, Mn–O).
m space group in an O3-type phase. The optical properties were measured using UV-Vis absorption spectrometry to determine the absorption coefficient α and the optical band gap Eg. The optical band gap energy of this sample is 2.45 eV, which indicates that it has semiconductor characteristics. Furthermore, the electrical and dielectric properties of the material were investigated using complex impedance spectroscopy between 10−1 Hz and 106 Hz at various temperatures (333–453 K). The permittivity results prove that there are two types of polarization, dipolar polarization and space charge polarization. The Nyquist diagrams show the contribution of the effects of the grain, grain boundary, and electrode properties. The frequency dependence of the conductivity was interpreted in terms of Jonscher's law. The DC conductivity follows both the Mott and Arrhenius laws at low and high temperature, respectively. The temperature dependence of the power law exponent(s) suggests that the overlapping large polaron tunneling (OLPT) model is the dominant transport process in this material. The optimum hopping length of the polaron (4 Å) is large compared with the interatomic spacing (2.384 Å for Na–O and 2.011 Å for Cu, Fe, Mn–O).
1. Introduction
The NaxMO2 ternary oxides, where M is a 3d transition metal (Co, Cr, Fe, Mn, V, and their combinations), are used as positive electrodes for sodium ion batteries because of their simple structure, easy of synthesis, environmental friendliness, high exploitation potential and feasibility of commercial production.1 Furthermore, those oxides have not only important electrochemical properties but also exhibit various interesting physical properties.However, these electrode compounds are characterized by a layered framework structure in which the sodium ion layers (Na+) are intercalated between two MO2 sheets. The arrangement of these sheets determines the type of structure of the sample, and the MO2 sheets are formed either by MO6 octahedrons in the ‘O’ structure, where Na+ occupy an octahedral site, or by MO4 polyhedrons in the ‘P’ structure, where Na+ occupy a prismatic site.2 This type of structure influences the electrical properties of these compounds, in particular the electrical conductivity because the charge carrier, Na+, is free to move. In addition, to the band gap between the valence band and the conduction band, which indicates the semiconductor comportment, the 3d transition metals, are characterized by the overlap between the narrow 3d bands.3
In this study, there was interest in the combination between Cu, Fe and Mn due to their abundant resources, inexpensive price and because they are harmless to the environment.4–6 Furthermore, the compound O3-Na0.9[Cu0.22Fe0.30Mn0.48]O2 shows interesting electrochemistry results such as: an energy density equal to 210 W h kg−1, a 90% round-trip energy efficiency and good cycling stability.7
These results encouraged the investigation and study of the NaCu0.2Fe0.3Mn0.5O2 compound. Firstly, a structural study using X-ray diffraction (XRD) at room temperature is reported. Then, the band gap and Urbach energies obtained from the absorbance spectra of UV-visible (UV-Vis) spectroscopy, at ambient temperature were investigated. Finally, the complex impedance spectroscopy measurements were performed, in the temperature and frequency ranges of 333–453 K and 10−1 to 106 Hz, respectively, which were used to determine the electric and dielectric properties.
2. Materials and methods
The NaCu0.2Fe0.3Mn0.5O2 compound was synthesized using a solid-state reaction. The precursors, of Na2CO3 (99%), CuO (99%), Fe2O3 (99%) and Mn2O3 (99%) were obtained from Sigma-Aldrich, and were mixed in proportional ratios. The obtained powder was burned at 500 °C for 16 h, and then, the sample was ground, pressed into pellets and transferred to an oven at 850 °C for 24 h.To determine the purity of the sample, powder XRD was performed using a Bruker D8 Discover with Twin/Twin optics, at room temperature, with Cu Kα radiation (λ = 1.5406 Å, 10° ≤ 2θ ≤ 80°). To precisely determine the optical properties of the prepared sample, a Shimadzu UV-3101 PC scanning spectrophotometer was used at room temperature, with a wavelength range of 200–800 nm, with a sample pellet of 0.5 mm of diameter. Finally, the electrical property measurements were obtained using complex impedance spectroscopy with a Solartron SI 1260 impedance/gain phase analyzer in the temperature and frequency ranges of 333–453 K and 10−1 to 106 Hz, respectively, with a sample pellet with a thickness of 1 mm and a diameter of 8 mm.
3. Results and discussion
3.1. Structural properties
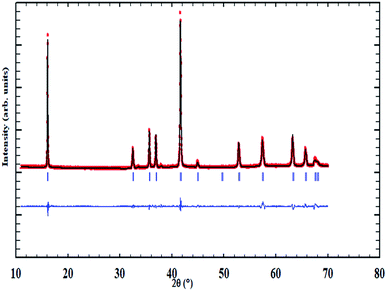
The XRD pattern associated with the NaCu0.2Fe0.3Mn0.5O2 compound is shown in Fig. 1. The results of the structural refinement by Rietveld method proved that this sample crystallized in a hexagonal system with a R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group and the cell unit: a = 2.9389(1) Å, c = 16.5208(11) Å, α = β = 90° and γ = 120°. Yet, the refinement factors, which were the fit criteria, such as reliability factor χ2, fit factors Rp and Rwp, which are shown in Table 1, show small values indicating the perfect conformity between the experimental and theoretical spectra and suggesting the purity of the sample. In addition, these results are in good agreement with those found by Mu et al.7
m space group and the cell unit: a = 2.9389(1) Å, c = 16.5208(11) Å, α = β = 90° and γ = 120°. Yet, the refinement factors, which were the fit criteria, such as reliability factor χ2, fit factors Rp and Rwp, which are shown in Table 1, show small values indicating the perfect conformity between the experimental and theoretical spectra and suggesting the purity of the sample. In addition, these results are in good agreement with those found by Mu et al.7
| χ2 | Rp | Rwp | Rexp | Bragg R-factor | RF-factor |
|---|---|---|---|---|---|
| 4.71 | 14.5 | 11.8 | 5.42 | 2.728 | 3.523 |
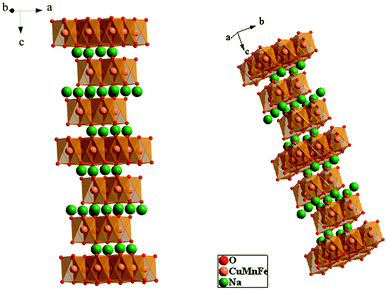
Fig. 2 shows the crystalline structure of the prepared sample. It is marked by an alternate arrangement of NaO2 sheets with those of CuFeMnO2. Here, both of the sodium ions and transition metals are linked to six oxygen atoms which build the NaO6 and MO6 octahedra. Thus, the structure is an O3 type where ‘O’ means that the Na ion occupies an octahedral site and ‘3’ indicates the number of sheets of transition metals in a repeated unit of stacking. The NaCu0.2Fe0.3Mn0.5O2 sample has a cell volume of 123.75(1) Å3 and the interatomic distances are 2.384 Å and 2.011 Å for Na–O and CuFeMn–O, respectively. The atomic coordinates are reported in Table 2.
| Atom | Wyckoff | x (Å) | y (Å) | z (Å) |
|---|---|---|---|---|
| Na | 3b | 0 | 0 | 0.500 |
| Cu | 3a | 0 | 0 | 0 |
| Fe | 3a | 0 | 0 | 0 |
| Mn | 3a | 0 | 0 | 0 |
| O | 6c | 0 | 0 | 0.268 |
3.2. Optical properties
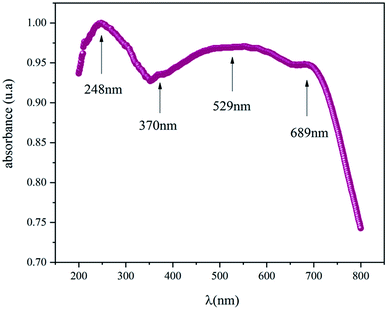
The optical properties were obtained from the UV-Vis absorbance spectra measured at room and are displayed in Fig. 3. This spectrum is characterized by a high absorbance in both the ultra-violet and the visible region which means the NaCu0.2Fe0.3Mn0.5O2 compound is a suitable candidate for applications in optoelectronics and photovoltaics.8,9 The presence of four absorbance peaks at 248 nm, 370 nm, 529 nm and 689 nm are noted. The peak which showed the maximum absorbance was in the UV region at 248 nm and indicated the charges transferring from the valence band to the conduction band.10 The peaks at 370 nm, 529 nm and 689 nm were associated with the absorption of Mn, Fe and Cu, respectively,.11–13For the determination of the optical gap energy the model proposed by Tauc was used.14 In the region of high absorption, Eg is related to the absorption coefficient α by the following relationship:
| αhν = B(hν − Eg)r | (1) |
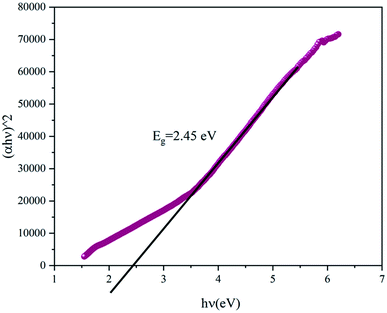
Fig. 4 presents the Tauc plot of (αhν)2 versus hν. The value of the gap energy can be determined from the intersection of the extrapolation of the linear part of (αhν)2 with the energy axis. The gap energy of the NaCu0.2Fe0.3Mn0.5O2 compound was equal to 2.45 eV which indicated the semiconductor character of this compound. Indeed, the band gap of this sample is smaller than the band gap of LiCoO2, which is widely used as an electrode in lithium-ion batteries, which is 2.7 eV.15
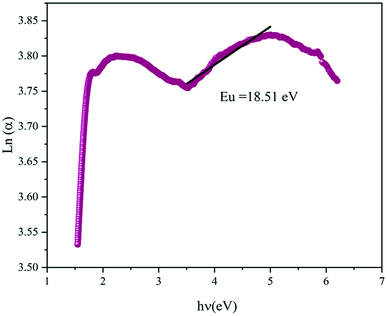
The variation of Ln(α) versus (hν) is plotted in Fig. 5 and it was used to determine the Urbach energy, which describes the disorder of a material, using:16
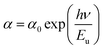 | (2) |
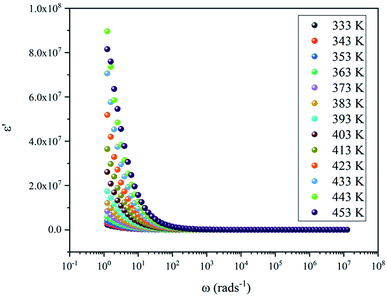
3.3. Dielectric properties
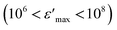 , compared to that of Na2CoSiO4
, compared to that of Na2CoSiO4 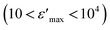 which was used as battery electrode,18 implies that this compound could be a candidate for use in energetic devices. Indeed, materials with a large dielectric constant can be used as a dielectric gate or an active channel in field-effect transistor (FET) devices.19
which was used as battery electrode,18 implies that this compound could be a candidate for use in energetic devices. Indeed, materials with a large dielectric constant can be used as a dielectric gate or an active channel in field-effect transistor (FET) devices.19
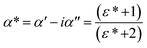 | (3) |
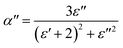 | (4) |
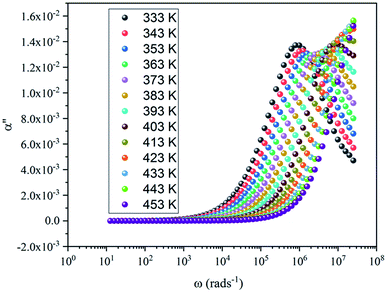
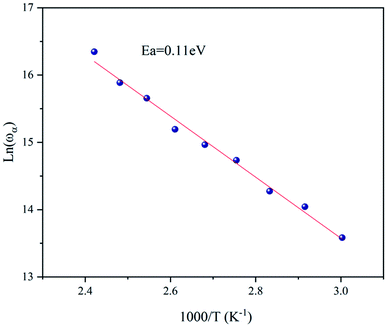
Fig. 7 shows the imaginary part of the complex polarizability as a function of frequency at different temperatures. This is characterized by relaxation peaks, defined by a maximum frequency ωαm, which shifted towards high frequency with the increase of temperature (see Fig. 8). This variation follows the Arrhenius behavior:
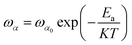 | (5) |
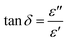 | (6) |
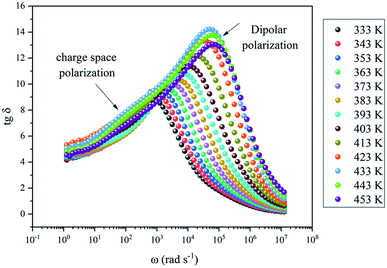
Fig. 9 shows that the relatively low value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, is about 0–15. It should be noted that, materials with a low energy loss are necessary for battery applications, which means that the NaCu0.2Fe0.3Mn0.5O2 compound is a good candidate for such applications. This also shows two relaxation peaks in a low and a high frequency region, respectively. These peaks were indexed for space charge and dipolar polarization, respectively. With the increase of temperature, the dielectric loss shifts to a higher frequency which indicated that the polarization was thermally activated.
δ, is about 0–15. It should be noted that, materials with a low energy loss are necessary for battery applications, which means that the NaCu0.2Fe0.3Mn0.5O2 compound is a good candidate for such applications. This also shows two relaxation peaks in a low and a high frequency region, respectively. These peaks were indexed for space charge and dipolar polarization, respectively. With the increase of temperature, the dielectric loss shifts to a higher frequency which indicated that the polarization was thermally activated.
3.4. Electric properties
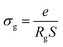 | (7) |
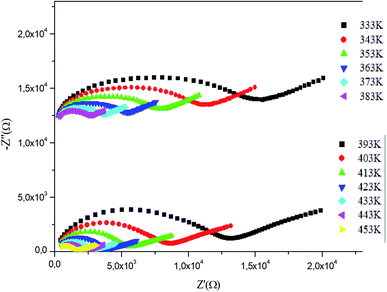
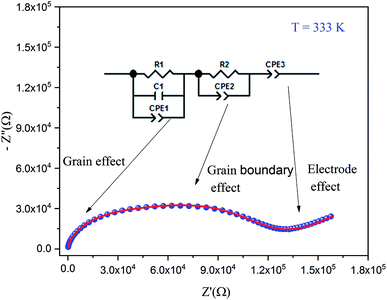
By increasing in temperature, the resistivity, decreased, which involved the increase of the conductivity of the grain. This means that the conductivity was thermally activated and confirmed the semiconductor behavior of the sample. To understand the variation of the grain conductivity better, Fig. 12 shows Ln(σg) a function of temperature. It is characterized by the presence of two domains: high and low temperature.
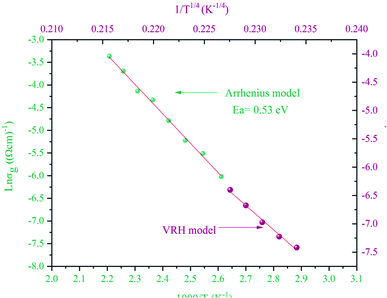
At a high temperature of 383–453 K, all of the charge carriers were thermally active, so, the variation of the grain conductivity followed the Arrhenius law:21
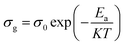 | (8) |
By comparing the activation energies found from the grain conductivity and the complex polarizability, which were 0.53 eV and 0.11 eV, respectively, it was shown that they were not the same, which means that the conduction process cannot occur by a hopping process.
At low temperatures of 333–373 K, a small number of the charge carriers were thermally active and their movement was not the same, so, the variation of grain conductivity followed variable range hopping (VRH) known as the Mott [T]−1/4 law:22
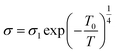 | (9) |
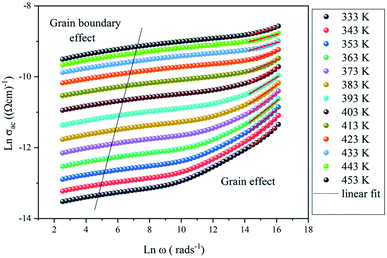 | ||
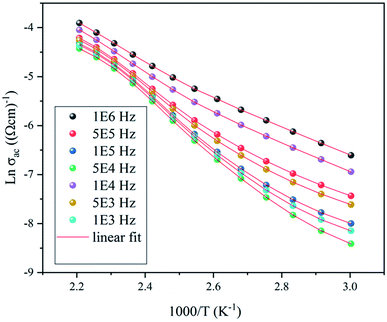
| Fig. 13 The variation of Ln(σac) versus Ln(ω) at different temperatures for the NaCu0.2Fe0.3Mn0.5O2 compound. | ||
The variation of AC conductivity at high frequencies is marked by the presence of a plateau (σ0) and a dispersion domain. This evolution follows the Jonscher power law:23
| σac(ω) = σ0 + Aωs(T) | (10) |
The slope obtained by the fit of the linear part at high frequency of Ln(σac) = f(Ln(ω)) allowed the determination of the ‘S’ exponent which shows the degree of interaction of the mobile ion and its environment. The variation of ‘S’ as a function of the temperature makes it possible to specify the conduction mechanism in the sample (Fig. 14).
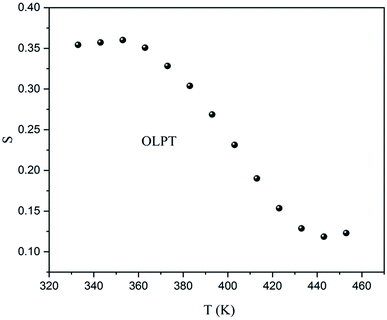
As previously indicated, at low temperatures, the sample was not totally thermally activated, and as a result, the variation as a function of the temperature of ‘S’ did not give an adequate conduction model. Although, for T > 360 K the exponent ‘S’ decreased when the temperature increased, to give a minimum above 443 K, and then began to increase which meant that the conduction mechanism was overlapping the OLPT.24
As the frequency dependence of conductivity is important for investigating the mechanism of conduction, the temperature dependence of conductivity is also important to determine the evolution of the OLPT model. Fig. 15 shows the variation of AC conductivity as function of the inverse of the temperature at different frequencies. The good agreement between the experimental data and the theoretical calculation fit proved that the OLPT model described the behavior of the NaCu0.2Fe0.3Mn0.5O2 sample well, enabling an estimation of the parameters according to the equation:25,26
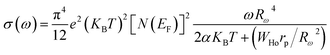 | (11) |
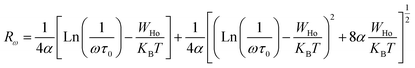 | (12) |
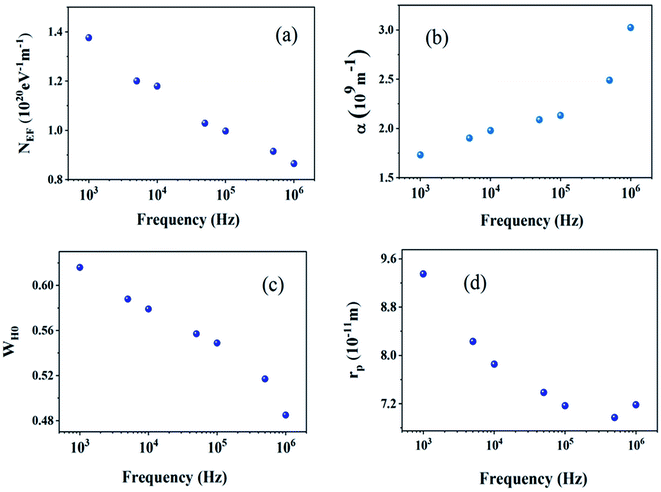
Table 3 regroups the parameters of the theoretical adjustment of the OLPT model and Fig. 16 displays the variation function of frequency. It was noticed that the density of states decreased with increasing frequency as deduced by Mott law,27 and also there was a decrease of the polaron radius, and the hopping energy as a function of the frequency was remarkable although this was expected because the decrease in frequency stimulated the mobility of the free charge carriers. It was also noted that the extracted values of Rω varied over a range of 4 Å, and also with the interatomic spacing (2.384 Å for Na–O and 2.011 Å for Cu, Fe, Mn–O). This finding suggests that the conduction process of these samples, was ensured because of the large polaron. In this case, the spatial extent of the polaron was large when compared with the interatomic distance.28
| Frequency (103 Hz) | NEF (1019 eV−1 m−1) | α (109 m−1) | WH0 (eV) | rp (Å) |
|---|---|---|---|---|
| 1000 | 8.6461 | 3.025 | 0.485 | 0.718 |
| 500 | 9.1461 | 2.490 | 0.517 | 0.697 |
| 100 | 9.9728 | 2.132 | 0.549 | 0.716 |
| 50 | 10.293 | 2.089 | 0.557 | 0.738 |
| 10 | 11.794 | 1.978 | 0.579 | 0.785 |
| 5 | 12.004 | 1.901 | 0.588 | 0.823 |
| 1 | 13.756 | 1.732 | 0.616 | 0.935 |
In comparison with other similar compounds such as LiCoO2, which is the most preferred positive electrode material, an improvement of conduction in NaCu0.2Fe0.3Mn0.5O2 was noticed. Indeed, the conductivity of NaCu0.2Fe0.3Mn0.5O2, which is 6 × 10−4 Ω−1 cm−1, was greater than that of LiCoO2, which is 2.29 × 10−4 Ω−1 cm−1 at room temperature.29 Therefore, NaCu0.2Fe0.3Mn0.5O2 is a good candidate for Na ion battery applications.
4. Conclusions
The NaCu0.2Fe0.3Mn0.5O2 sample was synthesized via a solid-state method. The XRD results prove that this compound crystallizes in a hexagonal system with the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. In addition, optical evaluation indicates that its energy gap is 2.5 eV, which verifies its semiconductor behavior. A dielectric study of this sample was carried out and the polarization phenomena exhibited were due to space charge polarization at low frequency and dipolar polarization at high frequency. The high dielectric constant of NaCu0.2Fe0.3Mn0.5O2
m space group. In addition, optical evaluation indicates that its energy gap is 2.5 eV, which verifies its semiconductor behavior. A dielectric study of this sample was carried out and the polarization phenomena exhibited were due to space charge polarization at low frequency and dipolar polarization at high frequency. The high dielectric constant of NaCu0.2Fe0.3Mn0.5O2 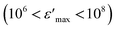 shows that this material could be a candidate for use in energetic devices. Indeed, materials with a large dielectric constant can be used as dielectric gates or active channels in FET devices. Then, analysis of the complex impedance measurements proves the presence of grain, grain boundary, and electrode effects using Nyquist diagrams. The choice for the adequate equivalent circuit allows for the evaluation of the grain conductivity and shows that the evolution follows the VRH model at a low temperature and the Arrhenius law at a high temperature, with an activation energy of 0.53 eV. The variation of AC conductivity was used to investigate the conduction mechanism, which is the overlapping large polaron tunneling model. In this model the value of the jump distance Rω is bigger than the interatomic distance and it was seen that the parameters NEF, WH0, and rp decrease with an increase in frequency. The electrical performance of this material shows that it may be a good candidate for Na-ion battery applications.
shows that this material could be a candidate for use in energetic devices. Indeed, materials with a large dielectric constant can be used as dielectric gates or active channels in FET devices. Then, analysis of the complex impedance measurements proves the presence of grain, grain boundary, and electrode effects using Nyquist diagrams. The choice for the adequate equivalent circuit allows for the evaluation of the grain conductivity and shows that the evolution follows the VRH model at a low temperature and the Arrhenius law at a high temperature, with an activation energy of 0.53 eV. The variation of AC conductivity was used to investigate the conduction mechanism, which is the overlapping large polaron tunneling model. In this model the value of the jump distance Rω is bigger than the interatomic distance and it was seen that the parameters NEF, WH0, and rp decrease with an increase in frequency. The electrical performance of this material shows that it may be a good candidate for Na-ion battery applications.
Conflicts of interest
There are no conflicts to declare.References
- Q. Liu, Z. Hu, M. Chen, C. Zou, H. Jin, S. Wang, S. L. Chou and S. X. Dou, Small, 2019, 15, 1805381 CrossRef PubMed.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636 CrossRef CAS PubMed.
- Y. Xiao, Y. Liu, N. Frederick and F. C. Zhang, Solid State Ionics, 2017, 307, 26 CrossRef CAS.
- S. Guo, H. Yu, Z. Jian, P. Liu, Y. Zhu, X. Guo, M. Chen, M. Ishida and H. Zhou, ChemSusChem, 2014, 7, 2115 CrossRef CAS PubMed.
- Y. Huang, Y. Zheng, X. Li, F. Adams, W. Luo, Y. Huang and L. Hu, ACS Energy Lett., 2018, 3, 1604 CrossRef CAS.
- S. Y. Xu, X. Y. Wu, Y. M. Li, Y.-S. Hu and L. Q. Chen, Chin. Phys. B, 2014, 23, 118202 CrossRef.
- L. Mu, S. Xu, Y. Li, Y.-S. Hu, H. Li, L. Chen and X. Huang, Adv. Mater., 2015, 27, 6928 CrossRef CAS PubMed.
- V. Priyanka, A. S. VijaiAnand, K. Mahesh and S. Karpagam, IOP Conf. Ser.: Mater. Sci. Eng., 2017, 263, 022016 Search PubMed.
- R. Kalthoum, M. Ben Bechir and A. Ben Rhaiem, Physica E Low Dimens. Syst. Nanostruct., 2020, 124, 114235 CrossRef CAS.
- A. Jellibi, I. Chaabane and K. Guidara, Physica E Low Dimens. Syst. Nanostruct., 2016, 79, 167 CrossRef CAS.
- L. He, Y. Lu, F. Wang, W. Jing, Y. Chen and Y. Liu, Sens. Actuators,B, 2018, 254, 468 CrossRef CAS.
- A. K. Tangra and G. S. Lotey, Curr. Appl. Phys., 2021, 27, 103 CrossRef.
- Y. Xiong, L. Su, X. He, Z. Duan, Z. Zhang, Z. Chen, W. Xie, D. Zhu and Y. Luo, Sens. Actuators, B, 2017, 253, 384 CrossRef CAS.
- K. Trabelsi, K. Karoui, F. Jomni and A. Ben Rhaiem, J. Alloys Compd., 2021, 867, 159099 CrossRef CAS.
- T. Balakrishnan, N. Sankarasubramanian, A. Kavitha and A. Kathalingam, Mater. Res. Innovations, 2019, 23, 216 CrossRef CAS.
- A. Barhoumi, G. Leroy, B. Duponchel, J. Gest, L. Yang, N. Waldhoff and S. Guermazi, Superlattice. Microst., 2015, 82, 483 CrossRef CAS.
- S. Abdul Moyez and S. Roy, J. Nanoparticle Res., 2017, 20, 5 CrossRef.
- K. Trabelsi, K. Karoui, A. Mahmoud, J. Bodart, F. Boschini, A. Ben Rhaiem and J. RSC, Advances, 2020, 10, 27456 CAS.
- E. J. Juarez-Perez, R. S. Sanchez, L. Badia, G. Garcia-Belmonte, Y. S. Kang, I. M. Sero and J. Bisquert, J. Phys. Chem. Lett., 2014, 5, 2390 CrossRef CAS PubMed.
- B. K. P. Scaife, Proc. Phys. Soc., 1963, 81, 124 CrossRef CAS.
- A. Ajmi, M. Chemingui, A. Mahmoud, F. Boschini and A. Ben Rhaiem, Ionics, 2019, 25, 1091 CrossRef CAS.
- N. F. Mott, J. Non-Cryst. Solids, 1972, 8, 1 CrossRef.
- A. K. Jonscher, Nature, 1977, 267, 673 CrossRef CAS.
- S. R. Elliott, Phil. Mag. B, 1978, 36, 129 Search PubMed.
- M. Tana, Y. Köseoglu, F. Alana and E. Sentürk, J. Alloys Compd., 2011, 509, 9399 CrossRef.
- W. Ben Nasr, H. Kcaou and A. Ben Rhaiem, Physica E Low Dimens. Syst. Nanostruct., 2018, 102, 110 CrossRef CAS.
- N. F. Mott and E. A. Davis, Electronic processes in non-crystalline materials, Clarendon Press, Oxford, 2nd edn, 1979 Search PubMed.
- S. R. Elliott, Adv. Phys., 1987, 36, 135 CrossRef CAS.
- B. Nageswara Rao, M. Venkateswarlu and N. Satyanarayana, Ionics, 2014, 20, 175 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |