Open Access Article
Open Access ArticleA method to estimate the size of single-chain nanoparticles under severe crowding conditions
Isabel Asenjo-Sanza,
Ester Verde-Sestoa and
José A. Pomposo *abc
*abc
aCentro de Física de Materiales (CSIC, UPV/EHU) – Materials Physics Center MPC, Pº Manuel de Lardizabal 5, 20018 Donostia, Spain. E-mail: josetxo.pomposo@ehu.eus
bDepartamento de Polímeros y Materiales Avanzados: Física, Química y Tecnología, University of the Basque Country (UPV/EHU), PO Box 1072, 20800 Donostia, Spain
cIKERBASQUE – Basque Foundation for Science, Plaza de Euskadi 5, 48009 Bilbao, Spain
First published on 10th January 2022
Abstract
Single-chain nanoparticles (SCNPs) result from the folding of isolated polymer chains via intramolecular interactions. Currently, there is no theory able to rationalize the astonishing conformational behaviour of SCNPs under severe crowding conditions (e.g., highly concentrated solutions, all-polymer nanocomposites) and, specifically, the significant size reduction observed in highly crowded solutions of covalent-bonded SCNPs and all-polymer nanocomposites containing SCNPs. Herein, we propose a valuable method to estimate the size of SCNPs under crowding. The method – which is based on combining MD simulations results with scaling concepts – is also useful for ring polymers and nanostructured Janus-shaped SCNPs.
1. Introduction
The effect of macromolecular crowding on polymer conformations is modulated by chain topology.1 In good solvent at high dilution a linear macromolecule composed of N segments adopts a self-avoiding conformation2 with chain size R ∼ N3/5 (R, radius of gyration). However, under crowding conditions in a highly concentrated solution and in the melt the macromolecule adopts an ideal, random-walk configuration2 such as: R ∼ N1/2. On the contrary, in a melt of unknotted and unconcatenated ring polymers the strong effect of topology induces significantly more compaction to give fractal, crumpled globule conformations3 such as: R ∼ N1/3 at sufficiently large N. The crumpled globule is characterized by a fractal space-filling-like structure, with a wide range of scales which are self-similar and almost unknotted.1It is worthy of mention that the collapse process of a linear chain into a self-similar, fractal globule on changing from good to bad solvent conditions was first treated by de Gennes,4 and later by Grosberg, Nechaev, and Shakhnovich.5 Interestingly, the fractal, crumple globule behaviour of ring polymers under crowding was applied as a tentative model to explain the packing of chromatin fibbers into segregated “territories” in the cell nucleus.6 Moreover, the effect of macromolecular crowding on polymer conformations is of significant interest in the case of other complex topologies (e.g., dendrimers7) for both academic and practical applications (i.e., dendrimers as processing aids in industrial extrusion processes).
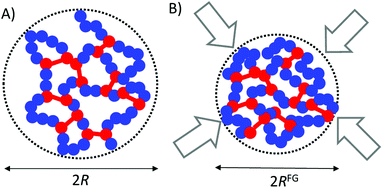
Recently, a nontrivial polymer topology comprising discrete macromolecules folded individually via intra-chain interactions, i.e., so-called single-chain nanoparticles (SCNPs), has become an important research topic.8–12 A SCNP can be considered as an ultra-fine nanogel composed of only one cross-linked polymer chain (Fig. 1A). In a SCNP, the own folding process induces the formation of locally compact domains and, at the end, it gives a notable degree of global chain compaction.13 Remarkably, the local domains of SCNPs can be used to immobilize e.g. catalysts, sensing probes or drug molecules paving the way to a variety of potential applications.12 In this sense, the folding of a synthetic polymer chain to a SCNP resembles the folding of certain biomacromolecules to its native, functional state. Nevertheless, SCNPs produced from precursors in good solvent conditions often display a conformation far from the globular one displayed e.g. by compact 3D-structured proteins. In fact, the morphology of these SCNPs is more akin to that typically shown by intrinsically disordered proteins (IDPs).13 For details about the relationship between the phase behaviour and size of IDPs we refer the interested reader to ref. 8 and 9.
A combination of theory, simulations and experimental techniques has been very successful to understand the structure of SCNPs in different scenarios.10 From the theoretical side, the elastic SCNPs model (ESM) – introduced a few years ago by our team – provides a connection between the SCNP size, number of segments and fraction of reactive groups in the precursor polymer in terms of a parameter related to the elasticity of the unimolecular network (see ref. 14 for details). When combined with scaling concepts, the ESM allows one to estimate the size of locally compact domains in SCNPs,11 the translocation of SCNPs through nanopores and nanoslits,15 as well as the size of brushes composed of SCNPs under different solvent conditions.16 This model has been also adopted to estimate the size of tadpole-shaped SCNPs in good solvent at high dilution.17
However, the ESM is not able to reproduce the astonishing conformational behaviour of SCNPs under severe crowding conditions (e.g., highly concentrated solutions, all-polymer nanocomposites) and, specifically, the significant size reduction observed in highly crowded solutions of covalent-bonded SCNPs and all-polymer nanocomposites containing SCNPs (see Fig. 1B).19 The full agreement between molecular dynamics (MD) simulations (R ∼ N0.37) and small-angle neutron scattering (SANS) experiments (R ∼ N0.37) suggests that SCNPs adopt a “crumpled globule” conformation in highly crowded environments.18 Since some of the potential applications of SCNPs rely on the actual size of these soft nano-objects in bulk conditions, a predictive tool providing the size of SCNPs under crowding at bulk density would be very valuable to establish reliable structure–properties relationships.10 Moreover, as SCNPs are simple models of IDPs the knowledge generated would be of potential interest to construct models of unstructured polypeptides under crowding. Also, it could be useful for modelling dynamic networks (e.g., vitrimers)20 made from SCNPs.
2. Method
We propose herein a method to estimate the size of SCNPs under strong crowding conditions by combining coarse-grained MD simulations results with simple scaling concepts.21 In this section, we first introduce the method and most relevant concepts. In next section, we will compare predictions for several systems based on SCNPs to experimental data, and we will extend our predictions to melts of ring polymers and nanostructured Janus-shaped SCNPs.Along the work, in the case of computer simulations size dimensions are scaled to the bead size that is taken as 1 nm. In the case of experimental systems, R – the radius of gyration – and d – the domain size – are always given in nm.
Coarse-grained MD simulations of SCNPs in terms of the bead spring model provided accurate data of the size reduction experienced by a solution of SCNPs upon increasing concentration up to the bulk concentration.18 Simulations were performed at constant temperature via a Langevin thermostat. Chemical details were not accounted for, although the simulations were able to capture appropriately the effect of chain connectivity and excluded volume. Consequently, the results obtained came from the topology of the SCNPs (see Fig. 1) and not from their chemical composition or changes in temperature. Due to severe computational costs, only SCNPs with N = 200 beads were simulated with very good accuracy from very diluted conditions up to bulk concentration (i.e., ϕbulk ≡ 1).
From simple scaling arguments2,21 we can write:
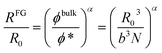 | (1) |
| ϕ* = b3N/R03 | (2) |
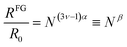 | (3) |
| RFG = R0Neffβ (SCNPs under crowding) | (4) |
| R(ϕ) = R0 (ϕ ≤ ϕ*) | (5a) |
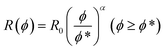 | (5b) |
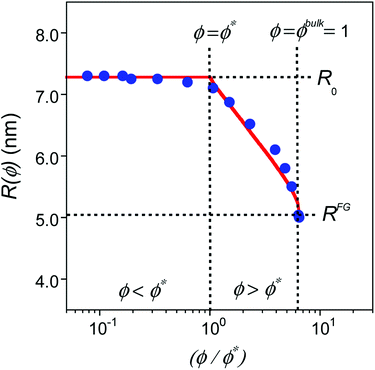 | ||
| Fig. 2 Comparison of MD simulations results18 (blue solid circles) to predictions from eqn (5) (red traces) for SCNPs in solution as a function (ϕ/ϕ*) where ϕ is the volume fraction of SCNPs in the system and ϕ* is the overlap volume fraction (eqn (2)). ϕ* is the concentration at which SCNPs start to touch one to another. The maximum concentration corresponds to ϕ = ϕbulk = 1; i.e. (ϕbulk/ϕ*) = R03/b3N (see text for details). | ||
Concerning Neff for real SCNPs, we adopt a mapping of R0 (actual size of the real SCNP at high dilution) to the SCNP size from the simulations16 such as:
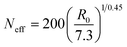 | (6) |
Hence, based on available R0 data, Neff can be obtained from eqn (6), and we can estimate RFG by means of eqn (4) with β = −0.068 to be compared with the available RFG data of different SCNPs of varying size under severe crowding conditions.
3. Results and discussion
3.1. Crumpled globule single-chain nanoparticles
We first compare predictions from eqn (4) to reported data from the literature about crumpled globule SCNPs (see Table 1). Data available result from complementary large-scale MD simulations at both coarse-grained and full atomistic level as well as experimental data of near-athermal all-polymer nanocomposites containing SCNPs.Crumpled globule conformations of SCNPs were found by Jia et al.22 in all-polymer nanocomposites composed of poly(styrene) (PS) chains and PS-SCNPs from large-scale MD simulations at both coarse-grained and full atomistic level. Without crowding effects, PS-SCNPs showed R0 = 2.5 nm whereas in the all-polymer nanocomposites the simulations revealed RFG = 2.1 nm. From eqn (4) and Neff = 19 (eqn (6)) we estimate a value of RFG = 2.07 nm (Table 1) which is in very good agreement with the reported value of RFG.
PS-SCNPs in blends with deuterated PS chains were investigated by Mackay et al.23 via small angle neutron scattering (SANS) experiments. PS-SCNPs of R0 = 4.8 nm were found to exhibit a size reduction to RFG = 2.7 nm when blended with linear deuterated PS of 63 kDa in molar mass at 50 wt%. From eqn (4) and Neff = 79 (eqn (6)) we obtain RFG = 3.57 nm (Table 1) which is slightly larger than the reported value of RFG – obtained by assuming that the SCNPs were hard spheres.23
Additionally, as reported by our group,18 poly(methyl methacrylate) (PMMA)-SCNPs synthesized from a precursor of 92 kDa in molar mass displayed R0 = 6.8 nm in good solvent at high dilution, whereas in blends with linear deuterated poly(ethylene oxide) (PEO) of 96 kDa they showed RFG = 5.8 nm, as determined from SANS experiments. From eqn (4) and Neff = 171 (eqn (6)) we obtain RFG = 4.80 nm (Table 1) which is in good agreement with the experimental RFG value.
Fig. 3 (blue symbols) provides a comparison of the size of SCNPs under crowding as calculated from eqn (4) to reported literature values. Further experimental and simulations data will be very useful to establish the general validity of eqn (4) at larger values of N and for SCNPs of different chemical composition.
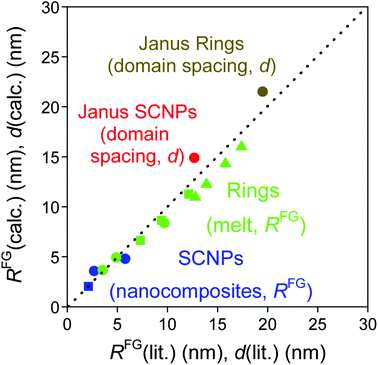 | ||
| Fig. 3 Size (RFG) of SCNPs under severe crowding conditions as calculated from eqn (4) (blue symbols), ring polymers in the melt as estimated from eqn (7) and (8) (green symbols), and domain spacing (d) of nanostructured Janus-shaped SCNPs and Janus ring polymers as derived from eqn (9) (red and brown symbols) in comparison to literature values3,16,20–25,27 (see text for details). | ||
3.2. Crumpled globule ring polymers
Next, we explore the predictive capability of eqn (4) to provide useful values of the crumpled globule size of unknotted and unconcatenated ring polymers in the melt, as revealed by the extensive coarse-grained MD simulations of Halverson et al.3 for large rings with N ≫ Ne, where Ne is the is the entanglement length for linear polymers in a melt. By combining eqn (3) and (6), we arrive at the following simple expression:| RFG = 0.673N0.382 (rings in bulk as SCNPs, N ≫ Ne) | (7) |
A comparison of predictions from eqn (7) for ring polymers with N = 400, 800 and 1600 to values of RFG obtained through MD simulations is given in Fig. 3. Eqn (7) provides values of RFG (6.64, 8.65 and 11.27 nm) that are systematically lower (see Fig. 3, green solid squares) than the RFG data from MD simulations (7.3, 9.4 and 12.1 nm).3 A similar conclusion is reached when predictions from eqn (7) are compared to Monte Carlo simulations reported by Suzuki et al.24 for ring polymers with N = 1536, 2048, 3072 and 4096 (see Fig. 3, green solid triangles). The small deviations observed in Fig. 3 can be actually attributed to the different topologies of SCNPs and ring polymers. Obviously, the topological difference is more notorious upon increasing the ring polymer size.
For the case of real ring polymers in the melt, it is convenient to express eqn (7) in terms of N/Ne such as:
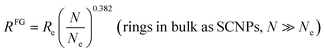 | (8) |
For ring PS in bulk with N/Ne = 20 (Ne = 173, λ = 0.7 nm)26 we estimate RFG = 8.35 nm from eqn (8) which compares favourably to RFG = 9.7 ± 0.6 nm obtained by SANS measurements of highly-pure ring PS samples by Iwamoto et al.26
For ring PEO in bulk with N/Ne = 44 and 20 (Ne = 45, λ = 0.6 nm)25 we obtain RFG ≈ 4.93 and 3.65 nm from eqn (8) in good agreement with the SANS values of highly-pure ring PEO samples reported by Kruteva et al. (RFG = 4.90 ± 0.14 nm and 3.54 ± 0.07 nm).25
3.3. Crumpled globule Janus-shaped single-chain nanoparticles
Very recently, Janus-shaped SCNPs have been proposed by Watanabe et al.27 as valuable nanomaterials for potential applications in ultrahigh resolution block copolymer lithography. Functionalized block copolymers composed of mutually immiscible PS and poly(glycolic acid) (PGA) blocks (PS-b-PGA) were subjected to one-shot intra-block cross-linking by these authors giving to compartmentalized Janus-shaped SCNPs with excellent self-assembling behaviour as determined by small-angle X-ray scattering (SAXS) measurements. Interestingly, the microphase-separated structure of Janus-shaped SCNPs in the bulk state was found to be up to 47% smaller (domain spacing d = 12.7 nm) than that of the precursor block copolymer (d0 = 24.0 nm).27We hypothesize here that the astonishing conformational behaviour of SCNPs under severe crowding conditions could contribute, to some extent, to this behaviour. Based on the size of the Janus-shaped SCNPs at high dilution determined by Watanabe et al.27 (R0 = 2.2 nm) we estimate RFG = 1.83 nm from eqn (4) as the size of these Janus-shaped SCNPs in the bulk state (a reduction of 27% when compared to the estimated size of the precursor block copolymer in the bulk state).
We can obtain an estimation of the expected d/d0 ratio from the ratio of the apparent molar mass 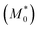 of the precursor block copolymer to the apparent molar mass (M*) of the Janus-shaped SCNPs according to:
of the precursor block copolymer to the apparent molar mass (M*) of the Janus-shaped SCNPs according to:
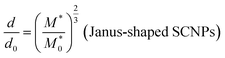 | (9) |
Eqn (9) is obtained from the well-known dependence of the domain spacing (d) on molecular weight (M) such as:28 d ∼ M2/3. From the reported data by Watanabe et al.27 – as determined by size exclusion chromatography – (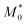 = 23.8 kDa and M* = 11.7 kDa) we obtain d/d0 ≈ 0.62 from eqn (9) and hence d = 14.9 nm, which is a value close to the experimental value (see Fig. 3).
= 23.8 kDa and M* = 11.7 kDa) we obtain d/d0 ≈ 0.62 from eqn (9) and hence d = 14.9 nm, which is a value close to the experimental value (see Fig. 3).
In addition, the predicted domain spacing of nanostructured Janus-shaped ring polymers (cyclic PS-block-PEO copolymers)29 is included in Fig. 3 for comparison. The estimated value from eqn (9), d = 21.5 nm, based on the values: 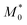 = 18.35 kDa, M* = 13.90 kDa and d0 = 25.9 nm reported by Poelma et al.,29 is also near to the SAXS experimental result, d = 19.5 nm.
= 18.35 kDa, M* = 13.90 kDa and d0 = 25.9 nm reported by Poelma et al.,29 is also near to the SAXS experimental result, d = 19.5 nm.
4. Conclusions
In summary, we disclose in this work a useful method to predict the size of SCNPs under severe crowding conditions, RFG. A simple expression (eqn (4)) is provided that relates RFG with the size of a SCNP in good solvent at high dilution, R0, and two parameters which are estimated in a self-consistent way from available MD simulations data: a general scaling exponent (β = −0.068) and the effective number of monomers in the chain, Neff, – connected with R0 via eqn (6). The method is also useful to estimate – as a first level approach – the size of large ring polymers in the melt (N ≫ Ne) as well as the size of Janus-shaped SCNPs in the bulk state. To conclude, this work can be considered as a first step towards the establishment of clear structure–properties relationships for SCNPs under severe crowding conditions. Additionally, it would be of potential interest to elaborate minimal models of both intrinsically disordered proteins (IDPs) under crowding and vitrimers composed of SCNPs.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support by MCIN/AEI/10.13039/501100011033 and “ERDF – A way of making Europe” (PGC2018-094548-B-I00), Eusko Jaurlaritza – Basque Government (IT-1175-19), and Gipuzkoako Foru Aldundia, Programa Red Gipuzkoana de Ciencia, Tecnología e Innovación (2021-CIEN-000010-01) is gratefully acknowledged.References
- Topology and Condensed Matter Physics, ed. S. M. Bhattacharjee, M. Mj and A. Bandyopadhyay, Springer Nature, Singapore, 2017 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, Inc., New York, 2003 Search PubMed.
- J. D. Halverson, W. B. Lee, G. S. Grest, A. Y. Grosberg and K. Kremer, J. Chem. Phys., 2011, 134, 204904 CrossRef PubMed.
- P.-G. de Gennes, J. Phys., Lett., 1985, 46, L-639 CrossRef.
- A. Y. Grosberg, S. K. Nechaev and E. I. Shakhnovich, J. Phys., 1988, 49, 2095 CrossRef CAS.
- A. Grosberg, Y. Rabin, S. Havlin and A. Neer, Europhys. Lett., 1993, 23, 373 CrossRef CAS.
- M. Wengenmayr, R. Dockhorn and J.-U. Sommer, Macromolecules, 2019, 52, 2616 CrossRef CAS.
- X. Zeng, A. S. Holehouse, A. Chilkoti, T. Mittag and R. V. Pappu, Biophys. J., 2020, 119, 402 CrossRef CAS PubMed.
- H.-Y. Chou and A. Aksimentiev, J. Phys. Chem. Lett., 2020, 11, 4923 CrossRef CAS PubMed.
- Single-Chain Polymer Nanoparticles: Synthesis, Characterization, Simulations and Applications, ed. J. A. Pomposo, Wiley-VCH, Weinheim, 2017 Search PubMed.
- J. A. Pomposo, A. J. Moreno, A. Arbe and J. Colmenero, ACS Omega, 2018, 3, 8648 CrossRef CAS PubMed.
- E. Verde-Sesto, A. Arbe, A. J. Moreno, D. Cangialosi, A. Alegría, J. Colmenero and J. A. Pomposo, Mater. Horiz., 2020, 7, 2292 RSC.
- J. A. Pomposo, I. Perez-Baena, F. Lo Verso, A. J. Moreno, A. Arbe and J. Colmenero, ACS Macro Lett., 2014, 3, 767 CrossRef CAS.
- J. De-La-Cuesta, E. Gonzalez, A. J. Moreno, A. Arbe, J. Colmenero and J. A. Pomposo, Macromolecules, 2017, 50, 6323 CrossRef CAS.
- J. A. Pomposo, J. Rubio-Cervilla, E. Gonzalez, A. J. Moreno, A. Arbe and J. Colmenero, Polymer, 2018, 148, 61 CrossRef CAS.
- I. Asenjo-Sanz, A. J. Moreno, A. Arbe, J. Colmenero and J. A. Pomposo, Polymer, 2019, 169, 207 CrossRef CAS.
- I. Asenjo-Sanz, E. Verde-Sesto and J. A. Pomposo, Phys. Chem. Chem. Phys., 2019, 21, 10884 RSC.
- A. J. Moreno, F. Lo Verso, A. Arbe, J. A. Pomposo and J. Colmenero, J. Phys. Chem. Lett., 2016, 7, 838 CrossRef CAS PubMed.
- M. González-Burgos, A. Arbe, A. J. Moreno, J. A. Pomposo, A. Radulescu and J. Colmenero, Macromolecules, 2018, 51, 1573 CrossRef.
- W. Denissen, G. Rivero, R. Nicolaÿ, L. Leibler, J. M. Winne and F. E. Du Prez, Adv. Funct. Mater., 2015, 25, 2451 CrossRef CAS.
- P.-G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, London, 1979 Search PubMed.
- X.-M. Jia, R. Shi, G.-S. Jiao, T. Chen, H.-J. Qian and Z.-Y. Lu, Macromol. Chem. Phys., 2017, 218, 1700029 CrossRef.
- M. E. Mackay, T. T. Dao, A. Tuteja, D. L. Ho, B. Van Horn, H.-C. Kim and C. J. Hawker, Nat. Mater., 2003, 2, 762 CrossRef CAS PubMed.
- J. Suzuki, A. Takano and Y. Matsushita, J. Chem. Phys., 2009, 131, 144902 CrossRef PubMed.
- M. Kruteva, J. Allgaier, M. Monkenbusch, L. Porcar and D. Richter, ACS Macro Lett., 2020, 9, 507 CrossRef CAS.
- T. Iwamoto, Y. Doi, K. Kinoshita, Y. Ohta, A. Takano, Y. Takahashi, M. Nagao and Y. Matsushita, Macromolecules, 2018, 51, 1539 CrossRef CAS.
- K. Watanabe, N. Kaizawa, B. J. Ree, T. Yamamoto, K. Tajima, T. Isono and T. Satoh, Angew. Chem., Int. Ed., 2021, 60, 18122 CrossRef CAS PubMed.
- G. R. Strobl, The Physics of Polymers, Springer, Berlin, 1997 Search PubMed.
- J. E. Poelma, K. Ono, D. Miyajima, T. Aida, K. Satoh and C. J. Hawker, ACS Nano, 2012, 6, 10845 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2022 |