Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enhanced thermoelectric performance in Sb–Br codoped Bi2Se3 with complex electronic structure and chemical bond softening†
Ju Zhang ,
Shiqi Zhong and
San-Huang Ke*
,
Shiqi Zhong and
San-Huang Ke*
MOE Key Laboratory of Microstructured Materials, School of Physics Science and Engineering, Tongji University, 1239 Siping Road, Shanghai 200092, China. E-mail: shke@tongji.edu.cn
First published on 11th January 2022
Abstract
Prior experimental work showed that Bi2Se3, as a sister compound of the best room-temperature thermoelectric material Bi2Te3, has remarkably improved thermoelectric performance by Sb–Br codoping. But the relationship between its crystalline structure and thermoelectric properties is still unclear to date. Here, we use first-principles calculations to explore the possible reasons for such improvement. The electronic structures of Bi2−xSbx(Se1−yBry)3 (x = 0, 1, 2; y = 0, 0.08) are systematically investigated. Significant effects of 8% Br codoping in BiSbSe3 are found. First, the Br atom acts as an electron donor, thus greatly increasing the carrier concentration. Second, similar to the effect of Sb doping, Br codoping further improves greatly the degeneracy of the conduction band edge, which leads to a remarkably increased density-of-states effective mass without deterioration of the carrier mobility, and simultaneously preserves a large Seebeck coefficient of ∼−254 μV K−1 at 800 K. In addition, the Br codoping softens the chemical bonds, which enhances anharmonic scattering and further reduces the lattice thermal conductivity. We predict that the maximum zT of BiSb(Se0.92Br0.08)3 at 800 K can reach 0.96 with the carrier concentration of 9.22 × 1019 cm−3. This study rationalizes a potential strategy to improve the thermoelectric performance of Bi2Se3-based thermoelectric materials.
Introduction
With about two-thirds of the world's produced energy being lost as waste heat,1 thermoelectric (TE) materials which can directly convert exhaust heat into usable electricity have been investigated widely as clean and sustainable energy materials.2 The TE performance depends on the dimensionless figure of merit zT = S2σT/κ, where S, σ, κ, and T are the Seebeck coefficient, electrical conductivity, total thermal conductivity (including the lattice contribution κL and carrier contribution κe), and absolute temperature, respectively.3–5 An excellent TE material requires a high value of zT simultaneously with a high power factor (PF = S2σ) and a low κ.6,7 Because of the strong coupling between S, σ, and κe, it is very difficult to enhance zT by optimizing only one of these parameters.8 To date, decoupling of these electronic parameters by band engineering approaches through increasing the number of effective energy valley and minimizing κL (the only independent parameter) have proved to be effective strategies for enhancing zT.9It is well known that the electrical transport properties of a material are dominated by the details of its band structure and scattering mechanism. The optimized electrical transport properties of a thermoelectric material depend on the weighted mobility,10 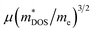 , here μ,
, here μ, 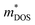 and me are the mobility of carriers, density-of-states (DOS) effective mass and electron mass, respectively. The DOS effective mass is given as11
and me are the mobility of carriers, density-of-states (DOS) effective mass and electron mass, respectively. The DOS effective mass is given as11 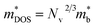 , where Nv is the band degeneracy and
, where Nv is the band degeneracy and  is the band effective mass. Actually, for the charge carriers predominantly scattered by acoustic phonons, the mobility is expected that
is the band effective mass. Actually, for the charge carriers predominantly scattered by acoustic phonons, the mobility is expected that 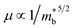 .12 Consequently, increasing the
.12 Consequently, increasing the 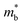 should be detrimental to the thermoelectric performance. In contrast, the convergence of many charge carrying valleys has virtually no detrimental effects. Therefore, multiple degenerate valleys are generally desired, thanks to the separate pockets of Fermi surface with the same energy, which have the effect of producing large
should be detrimental to the thermoelectric performance. In contrast, the convergence of many charge carrying valleys has virtually no detrimental effects. Therefore, multiple degenerate valleys are generally desired, thanks to the separate pockets of Fermi surface with the same energy, which have the effect of producing large 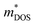 without explicitly increasing
without explicitly increasing 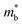 . Besides, materials with soft chemical bonds and anharmonic lattice dynamics would suppress the lattice thermal conductivity.1,13,14 However, the combination of all these features has been identified12,15 with a large challenge in achieving high-performance thermoelectrics through an avenue simultaneously possessing large band degeneracy and strong anharmonic lattice dynamics, which are highly inter-dependent. As the best commercialized thermoelectric material found so far, Bi2Te3 has excellent σ, S, and large zT (for both n-type and p-type), and therefore have been widely applied for TE power generation and electronic cooling around room temperature.16 However, Te is a scarce element in the crust of the earth and its cost would rise sharply along with large-scale applications. Therefore, Te-free TE materials have attracted great attention.
. Besides, materials with soft chemical bonds and anharmonic lattice dynamics would suppress the lattice thermal conductivity.1,13,14 However, the combination of all these features has been identified12,15 with a large challenge in achieving high-performance thermoelectrics through an avenue simultaneously possessing large band degeneracy and strong anharmonic lattice dynamics, which are highly inter-dependent. As the best commercialized thermoelectric material found so far, Bi2Te3 has excellent σ, S, and large zT (for both n-type and p-type), and therefore have been widely applied for TE power generation and electronic cooling around room temperature.16 However, Te is a scarce element in the crust of the earth and its cost would rise sharply along with large-scale applications. Therefore, Te-free TE materials have attracted great attention.
As an important low-cost thermoelectric material, Bi2Se3, a sister compound of Bi2Te3, has also been receiving attention due to the constituent of abundant elements. Specifically, it possesses the same layered structure and the weak inter-layer van der Waals bonding, which makes it easier to be separated into plates.17 Smaller plates with more interfaces mean lower κL theoretically, which is very favorable to thermoelectric applications. However, Bi2Se3 has drawn little attention owing to its relatively poor TE performance with zT being ∼0.4.18 Many efforts have been focused on optimizing the TE merit value of Bi2Se3 in recent years. Liu et al. demonstrated that the key limitations for the zT of Bi2Se3 are its poor electrical transport properties and high κ.18,19 With the intrinsically small band gap (Eg) ∼ 0.3 eV and low carrier concentration (n), Bi2Se3 displays bipolar effect.20 The excitation of minor carriers attenuates the S, while the κe is enhanced at the same time, suggesting a small PF and a high κe.21 Shakouri et al. proposed that enlarging the band gap would be an effective method to avoid bipolar conduction.57 Increasing n directly is another adequate means to minify the effects of minority carriers. In addition, the single valley of conduction band minimum (CBM) (Nv = 1) will lead to a low DOS and also a small power factor for n-type Bi2Se3.22 In the meantime, suppression of phonon transport is also critical to largely enhance the zT of Bi2Se3. Recently, Zhao et al. successfully introduced Sb–Br into the intrinsic semiconductor Bi2Se3 and obtained a maximum zT of 1.4 for n-type BiSb(Se0.94Br0.06)3 at 800 K. That is analogous to the most n-type Te-free TE materials, indicating that Sb–Br codoping is an effective approach in improving TE properties of Bi2Se3 alloy compounds. They found that Sb doping reduced κ on account of strong anharmonicity and soft bonds.23 But the electrical transport properties of BiSbSe3 is still poor because of the extremely low n and the imbalance between the effective mass and n. Then, via heavy Br-doping in BiSbSe3, Liu et al. acquired a high n and further optimized TE properties. Although there is a computational work about the electronic structure of BiSbSe3 alloy22 and a parameterized model theoretical analysis about the effects of Br doping,23 the detailed physical reasons in atomic level for Br codoping to further significantly improve TE properties have not been investigated yet. Particularly, the relationship between the crystalline atomic structure and the TE performance for Bi2−xSbx(Se1−yBry)3 (x = 0, 1, 2; y = 0, 0.08) is still unclear so far.
In this work, we report a systematic first-principles study on the TE properties of the Bi2−xSbx(Se1−yBry)3 (x = 0, 1, 2; y = 0, 0.08) alloy. The calculations are based on the density functional theory (DFT) for the atomic and electronic structures and based on the Boltzmann transport theory for the electron and phonon transport processes. It has been shown in literature that DFT is one of the most common and successful theoretical tools for probing TE materials, such as Cu12Sb4S13.56 x = 0, 1 in the Bi2−xSbxSe3 system is identified to be the transition boundary of the rhombohedral structure and orthorhombic structure. The strong hybridization between Sb and Se atoms in the complex crystal structure of orthorhombic BiSbSe3 with alloying 50% Sb on Bi sites makes it have a lower κL. In addition, the increase of structural symmetry is helpful to obtain a large energy valley degeneracy (Nv), and a large σ can be achieved by increasing conductive channels. The Nv and chemical bond softening can be further improved significantly by codoping 8% Br at Se sites. The improved Nv will enhance the 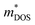 without reducing the μ. The further softened phonons are beneficial to enhancing anharmonic scattering and further decrease the κL. The Br codoping also moves the Fermi level (EF) into the conduction band (CB), resulting in a significant increase of n and σ. Interestingly, the increase of n does not reduce largely S because of the increased
without reducing the μ. The further softened phonons are beneficial to enhancing anharmonic scattering and further decrease the κL. The Br codoping also moves the Fermi level (EF) into the conduction band (CB), resulting in a significant increase of n and σ. Interestingly, the increase of n does not reduce largely S because of the increased  . Eventually, a peak zT value of ∼0.96 at 800 K can be realized in n-type alloy compounds BiSb(Se0.92Br0.08)3 with the carrier concentration of 9.22 × 1019 cm−3.
. Eventually, a peak zT value of ∼0.96 at 800 K can be realized in n-type alloy compounds BiSb(Se0.92Br0.08)3 with the carrier concentration of 9.22 × 1019 cm−3.
Results and discussion
Crystal structure and electronic structure
Bi2Se3 compound has a rhombohedral crystal structure with space group D53d(R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) no. 166 (Fig. 1(a)). In order to generate a reliable atomic structure for this compound, we first optimized its crystal structure with PBE functional as implemented in VASP in the total energy method. Its lattice constants a, b and c are found to be 4.19, 4.19 and 30.8 Å, respectively, which are in good agreement with the experimental values 4.14, 4.14 and 28.63 Å,27 proving the reliability of our theoretical modeling. The distinct layered structure consists of a regular octahedron structure with Bi atom as the center and Se atom as the vertex. On the other hand, Sb2Se3 exhibits an orthorhombic structure composed of a tetragonal conical pentahedron with Sb as the bottom center and Se as the vertex, as shown in Fig. 1(b). According to the previous results of Zhao et al.,23 the substitution of Sb for 50% Bi atoms in Bi2Se3 will induce a phase transition from the rhombohedral structure to the orthorhombic structure. Therefore, we utilize Bi atoms to replace the two nonequivalent sites of Sb1 atom in Sb2Se3, and adopt a structure with the lower energy to simulate the BiSbSe3. It displays a significant chain-like structure of orthorhombic phase by forming an octahedral structure with Bi atom as the center and Se atom as the vertex, and a triangular pyramidal tetrahedron with Sb and three Se atoms as the vertex is also formed (Fig. 1(c)).
m) no. 166 (Fig. 1(a)). In order to generate a reliable atomic structure for this compound, we first optimized its crystal structure with PBE functional as implemented in VASP in the total energy method. Its lattice constants a, b and c are found to be 4.19, 4.19 and 30.8 Å, respectively, which are in good agreement with the experimental values 4.14, 4.14 and 28.63 Å,27 proving the reliability of our theoretical modeling. The distinct layered structure consists of a regular octahedron structure with Bi atom as the center and Se atom as the vertex. On the other hand, Sb2Se3 exhibits an orthorhombic structure composed of a tetragonal conical pentahedron with Sb as the bottom center and Se as the vertex, as shown in Fig. 1(b). According to the previous results of Zhao et al.,23 the substitution of Sb for 50% Bi atoms in Bi2Se3 will induce a phase transition from the rhombohedral structure to the orthorhombic structure. Therefore, we utilize Bi atoms to replace the two nonequivalent sites of Sb1 atom in Sb2Se3, and adopt a structure with the lower energy to simulate the BiSbSe3. It displays a significant chain-like structure of orthorhombic phase by forming an octahedral structure with Bi atom as the center and Se atom as the vertex, and a triangular pyramidal tetrahedron with Sb and three Se atoms as the vertex is also formed (Fig. 1(c)).
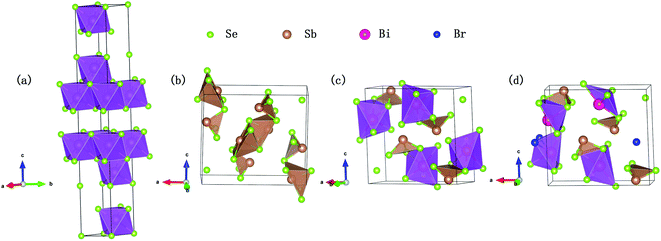 | ||
| Fig. 1 Crystal structure of Bi2Se3 (a), Sb2Se3 (b), BiSbSe3 (c), and BiSb(Se0.92Br0.08)3 (d), with Bi, Sb, Se, and Br atoms shown as red, brown, green, and blue spheres, respectively. | ||
This complex crystal structure of BiSbSe3 is favorable to reducing the κL because of the structural phase transition and the formation of the chain-like structure. Since the structural rhombohedral–orthorhombic phase transition is related to the breakage of part of the cation–anion bonds, half of the octahedral coordination cations are converted to five coordination, as reported previously by Yang et al.22 Finally, we consider the possible substitution of single Br atom for Se. There are three nonequivalent sites of Se atom in BiSbSe3, therefore, three possible structures can be formed. It is found by calculation that the total energies per cell of the three structures are −78.373, −78.285 and −78.308 eV, respectively. Furthermore, we calculate the energy band structures and thermoelectric transport properties for the three structures, respectively. The results are compared in Fig. S1 and S2,† which show that the results are qualitatively similar. Herein, we take the lowest energy structure with Se3 replaced by Br atom to model the BiSb(Se0.92Br0.08)3.
As shown in Fig. 1(d), this structure also possesses a stable orthorhombic structure (space group Pnma) but is more complex: not only an octahedral structure with Bi atom as the center and Se atom as the apex, and a triangular pyramidal tetrahedron with one Sb and three Se atoms as the apex are formed, but also formed is an octahedral structure with Bi as the center and both Se and Br atoms as the vertices. This more complex structure may be helpful to further suppressing the lattice thermal conductivity.
The conduction band and valence band model can be used to analyze how the carrier concentration and the band gap affect the TE properties. The calculated electronic band structures of Bi2−xSbx(Se1−yBry)3 (x = 0, 1, 2; y = 0, 0.08) are shown in Fig. 2. It is worth mentioning that the band structures of Bi2−xSbx(Se1−yBry)3 (x = 1, 2; y = 0, 0.08) are given by the TB-mBJ functional, while those of Bi2Se3 (band gap ∼ 0.17 eV) is given by the PBE-GGA functional so that we can have a direct comparison with a previous PBE-GGA result (∼0.16 eV), as shown in Table 1.
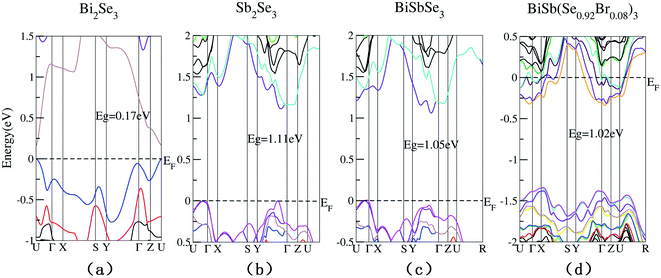 | ||
| Fig. 2 Calculated electronic band structures of Bi2Se3 (a), Sb2Se3 (b), BiSbSe3 (c), and BiSb(Se0.92Br0.08)3 (d). | ||
| Compounds | Experimental value | Previously calculated value | Our calculated value | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | Eg | a | b | c | Eg | a | b | c | Eg | |
| a Result from ref. 27.b Result from ref. 28.c Result from ref. 29.d Result from ref. 23. | ||||||||||||
| Bi2Se3 | 4.14a | 4.14a | 28.63a | 0.25a | 4.17a | 4.17a | 30.29a | 0.16a | 4.19 | 4.19 | 30.80 | 0.17 |
| Sb2Se3 | 11.77b | 3.96b | 11.62b | 1.17b | 11.53b | 3.96b | 11.22b | 0.75b | 12.82 | 4.03 | 11.53 | 1.11 |
| BiSbSe3 | 11.70c | 3.91c | 11.62c | 0.88c | 12.59c | 4.10c | 11.65c | 0.63c | 12.63 | 4.10 | 11.62 | 1.05 |
| BiSb(Se0.92Br0.08)3 | 10.52d | 5.26d | 10.17d | — | 11.84d | 4.07d | 11.67d | — | 12.36 | 4.16 | 11.65 | 1.02 |
One can see in Table 1 that the previous PBE-GGA result of the Eg of Sb2Se3 (∼0.7 eV) is largely underestimated with respect to the experimental value (∼1.17 eV), while our TB-mBJ result (∼1.11 eV) is in good agreement. In order to ensure the accuracy of the calculated results, we use TB-mBJ to calculate the band structures of Bi2−xSbx(Se1−yBry)3 (x = 1, 2; y = 0, 0.08). The SOC are considered in our calculations due to the heavy element. As can be seen in Table 1 and Fig. 2, the Bi2−xSbx(Se1−yBry)3 (x = 1, 2; y = 0, 0.08) have much larger band gaps than Bi2Se3, which can largely suppress the intrinsic excitation and the bipolar effect to prevent them from reaching a higher zT value. In addition, the 8% Br codoping further makes the Fermi level (EF) shifted to deeper conduction states, indicating that the Br codoping increases significantly the majority carrier concentration.
As is well known, a large Nv is beneficial to a large DOS effective mass  without deterioration of the carrier mobility μ.4,39 Nv is the effective total number of independent carrier pockets or valleys in the Brillouin zone, including both symmetry and orbital degeneracies. For Bi2Se3, it can be seen that alloying 50% Sb on Bi sites increases the valley number of effective energy from the degeneracy 2 to 10. As one can see in Fig. 2(c), the energy difference between the CBM and the fourth valence valley is less than ∼0.14 eV, which is smaller than the 0.15 eV between the first and the second valence bands of PbTe.40 Such small energy difference can be easily crossed at elevated temperatures, making it possible to improve the electrical transport properties. Furthermore, 8% Br subsequent codoping at Se12 position exhibits remarkably distinct electronic structures, which further significantly increases the effective Nv, accompanied by pushing the EF deep into the band structure, which significantly enlarges the n. A high Nv number generally results in a larger
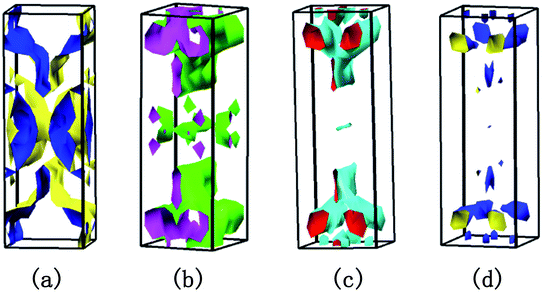
without deterioration of the carrier mobility μ.4,39 Nv is the effective total number of independent carrier pockets or valleys in the Brillouin zone, including both symmetry and orbital degeneracies. For Bi2Se3, it can be seen that alloying 50% Sb on Bi sites increases the valley number of effective energy from the degeneracy 2 to 10. As one can see in Fig. 2(c), the energy difference between the CBM and the fourth valence valley is less than ∼0.14 eV, which is smaller than the 0.15 eV between the first and the second valence bands of PbTe.40 Such small energy difference can be easily crossed at elevated temperatures, making it possible to improve the electrical transport properties. Furthermore, 8% Br subsequent codoping at Se12 position exhibits remarkably distinct electronic structures, which further significantly increases the effective Nv, accompanied by pushing the EF deep into the band structure, which significantly enlarges the n. A high Nv number generally results in a larger 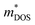 for the conduction band and eventually maintains a high S for n-type samples in spite of the increased n. Interestingly, the conduction bands of BiSb(Se0.92Br0.08)3 are much more complex than those of BiSbSe3: the activated multiple conduction-band minima lie close together in energy, forming complex multiband valence states. Another illustration of the complex band structure is shown in the Fermi surface, which has multiple types of valleys coming from the four conduction bands of EF crossing, all within a small energy window (see Fig. 3(a)–(d)). Such a good band feature may be associated with excellent thermoelectric properties, as found in other thermoelectric materials.39,41
for the conduction band and eventually maintains a high S for n-type samples in spite of the increased n. Interestingly, the conduction bands of BiSb(Se0.92Br0.08)3 are much more complex than those of BiSbSe3: the activated multiple conduction-band minima lie close together in energy, forming complex multiband valence states. Another illustration of the complex band structure is shown in the Fermi surface, which has multiple types of valleys coming from the four conduction bands of EF crossing, all within a small energy window (see Fig. 3(a)–(d)). Such a good band feature may be associated with excellent thermoelectric properties, as found in other thermoelectric materials.39,41
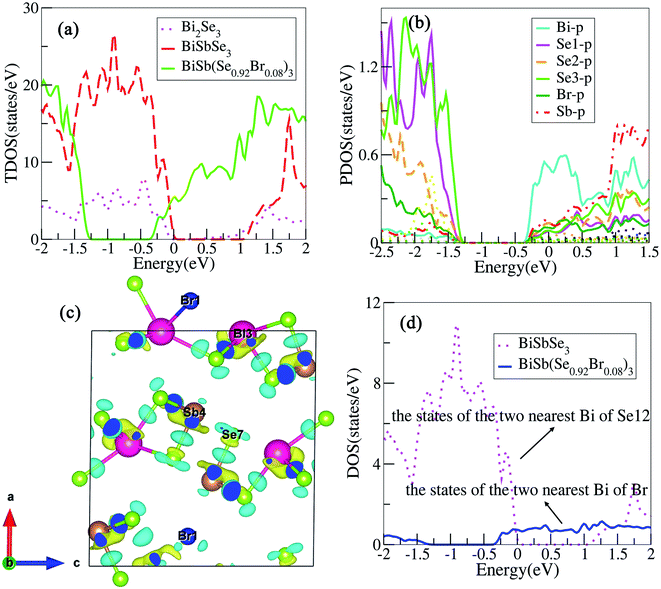
To clearly understand the states near the EF, we calculate the total density of states (TDOS) for Bi2Se3, BiSbSe3, and BiSb(Se0.92Br0.08)3 respectively, as shown in Fig. 4(a). It should be noted that TDOS near the Fermi level of doped Bi2Se3 is larger than that of pristine Bi2Se3. 50% Sb doping on Bi sites of Bi2Se3 slightly increased the TDOS near the EF. This is mainly originated from the substitution of Sb for Bi, which increases Nv. Furthermore, 8% Br codoping at Se12 site in BiSbSe3 tremendously increases the TDOS in the vicinity of the EF, which will enhance σ significantly. These results manifest that Sb and Br dual doped Bi2Se3 can be expected to have enhanced electrical transport and thermoelectric properties. To analyze the reasons for the enhanced TDOS by Br substitution, we calculate the partial density of states (PDOS) of BiSb(Se0.92Br0.08)3. As can be seen in Fig. 4(b), the bottom of CB edge is mainly contributed by the hybridized p orbitals from Bi, Se, Br, and Sb atoms (see the next section for more details). Thus, the Br atom replacement on the Se12 site can effectively adjust the band structure near the CB edge, and strongly enhances the thermoelectric performance.
Bonding properties
To visualize the electronic environments and bonding conditions, charge density difference (CDD) is calculated for BiSb(Se0.92Br0.08)3 compound. Fig. 4(c) reveals that the negative electron density is mainly around atoms Bi and Sb, meaning overall Bi and Sb atoms donate their valence electrons to the [Se0.92Br0.08]32−. The electronegativity on the Pauling scale for Bi, Sb, Se and Br are 2.02, 2.05, 2.55, and 2.96, respectively. The electropositive elements Bi and Sb dedicate all of their valence electrons to the more electronegative elements Se and Br, ultimately, BiSb(Se0.92Br0.08)3 can be described as (BiSb)3+(Se0.92Br0.08)32−. It coincides with the above analysis that, in BiSb(Se0.92Br0.08)3, Bi and Sb atoms tend to lose electrons, while Se and Br atoms tend to gain electrons owing to their larger electronegativity. These also manifest that Br–Bi has a stronger interaction than Se–Bi. In fact, the stronger hybridization between Br and Bi atoms will conduce to increasing the DOS near the CB edge, as indicated in Fig. 4(d). The electrons between the Bi and Br atoms mainly localizes around Br, while a certain number of electrons appear around the center position between Bi and Se, and Sb and Se atoms, indicating Bi and Br atoms incline to form an ionic bond, while there is a distinct covalent bond characteristics between Bi and Se, and Sb and Se atoms. The ionicity of the bonding in a material usually is characterized by the electronegativity difference (Δχ). The larger Δχ (≈0.9 between Br and Bi atoms), the more likely there will be interaction between carriers and the optical vibrations of the lattice atoms,42 thus suppressing the κL. For instance, observations by Ioffe et al. showed a decrease of κ with an increase of the ionicity of the bonds between atoms.42 Spitzer reported a correlation between increasing coordination number (CN) in a crystal structure and decreasing κL (by relating the κL to the strength of the chemical bonds in a material).42 In our case, the bond lengths between atoms after Br codoping become longer, namely, Se12–Bi bond lengths (2.81, 3.12 Å) in the BiSbSe3 are shorter than the corresponding Br–Bi bond lengths (3.05, 3.23 Å) in BiSb(Se0.92Br0.08)3. This implies that the Br–Bi bond could be relatively weaker according to the bonding descriptor contact developed by Deringer et al.28 The weaker chemical bond among Br and Bi atoms will be also a factor leading to the low κL (see the next section), as also recognized recently in α-MgAgSb.43 In addition, the big “mushroom” CDD shape around Bi/Sb is a clear indicator of the existence of lone-pair electrons, which is alike to the case of CuSbS2.44 According to the valence shell electron pair repulsion (VSEPR) theory,45 the lone-pair electrons almost occupy one bonding site. Hence, the unsymmetrical and disorderly coordinated environment of bonds in BiSb(Se0.92Br0.08)3 indicates the possibility of strong anharmonicity by significantly enhancing heat carrying phonon scatterings. This will also result in ultralow κL.Low lattice thermal conductivities
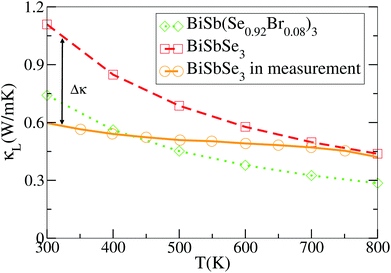
To achieve a high thermoelectric figure of merit, a low lattice thermal conductivity is essential. Therefore, insights into the origin of the extremely low thermal conductivity is meaningful for exploiting high performance thermoelectric materials. Previous work predicted that BiSbSe3 could possess a low κL.23 Nevertheless, the prediction was based on a strong dependence of the elastic properties on volume, and the resulting large Grüneisen parameter (γ, an indicator of anharmonicity) suggests a strong anharmonicity. In this work, we precisely calculate the κL as a function of temperature for BiSbSe3 and BiSb(Se0.92Br0.08)3 using the full linearized ShengBTE code combined with DFT, which is well known for quantitative predictive power.46 The results are presented in Fig. 5.As mentioned previously, the substitution of Sb for 50% Bi in Bi2Se3 decreases the κL partly due to the structural phase transition from rhombohedral to orthorhombic, and partly due to the formation of the more complex chain-like structure with respect to the layered structure, which induces enhanced intrinsic phonon scatterings. In Fig. 5 our ab initio results are compared with the experimental κL values of polycrystalline samples cited from ref. 23. It is worth mentioning that the calculated values are averaged over the three principal axes for the purpose of better vision and comparison with the experimental measurements on polycrystalline samples. It can be seen that the predicted values of BiSbSe3 are below 1.2 W m−1 K−1 at 300 K, which is pretty low in thermoelectric materials.47,48 However, the experimental values are even much lower at low temperatures though the agreement between theory and experiment is improved at high temperatures. The large discrepancy in κL at low temperatures may not be entirely attributed to grain boundary scattering, since this effect is usually small in materials with intrinsically low κL, where heat carrying phonons have smaller mean free paths than the size of the grains.49,50 It has to be noted that the theoretical calculation does not take into account the phonon scattering due to dynamic disorder, an omission that may be responsible for the overestimation of κL.
Here a possible mechanism is that the underlying atomic disorder plays an appreciable role in reducing κL at relatively low temperatures. While at high temperatures atoms occupy higher-symmetry positions,51 and intrinsic phonon–phonon scattering then dominates, as described by Eivari et al.55 For example, the previously mentioned lone-pair electrons may provide an origination of thus disorder which can act as a phonon-blocking mechanism that may help facilitate an ultralow κL. Moreover, we find that 8% Br codoping is also effective to further reduce κL as shown in Fig. 5. BiSb(Se0.92Br0.08)3 shows a lower κL than that of BiSbSe3 at the entire temperature. For instance, their κL are 0.29 and 0.44 W m−1 K−1 at 800 K, respectively. Clearly, the chemical bond softening between Br and Bi atoms is considerably higher than that between Se12 and Bi. As we know, the strong anharmonicity usually not only relies directly on the unsymmetrical and chemical bonds between the atoms in the crystal but also is often associated with atoms and their near neighbors (large coordination numbers). The calculated κL of BiSb(Se0.92Br0.08)3 is found to be in good agreement with an available experimental value 0.22 W m−1 K−1 at 800 K.23
Promising electrical transport properties
To shed light on the influences of Sb–Br codoping, herein the electrical transport properties of BiSbSe3 and BiSb(Se0.92Br0.08)3 are calculated as functions of carrier concentration (n) at 300 K, 600 K, and 800 K within the framework of the semiclassical Boltzmann transport theory.52 While it is possible to calculate σ/τ as a function of n and T, but it is not possible to calculate σ itself without the scattering rate τ−1. Here, the strategy previously used by Ong et al.53 is adopted with available experimental data23 to estimate the relaxation time τ = C0T−1n−1/3 with τ in s, T in K, and n in cm−3. The specific details are that we used 800 °C data from Liu and coworkers,23 who made measurements on the material. They report a thermopower S = −202.462 μV K−1 at this temperature. By comparing with the calculated S(T, n), we obtain a value n = 1.77 × 1020 cm−3 for this sample. The reported experimental σ is 172.899 S cm−1, which combined with the calculated σ/τ yields τ = 2.345 × 10−15 s for this particular sample at 800 °C. As mentioned, we then calculate σ as σ/τ × τ. Ultimately, the results for BiSbSe3 and BiSb(Se0.92Br0.08)3 are plotted in Fig. 6.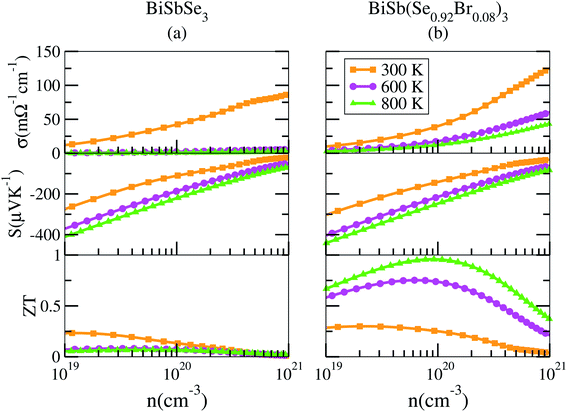 | ||
| Fig. 6 Calculated transport properties of n-type BiSbSe3 (a), and BiSb(Se0.92Br0.08)3 (b), respectively. | ||
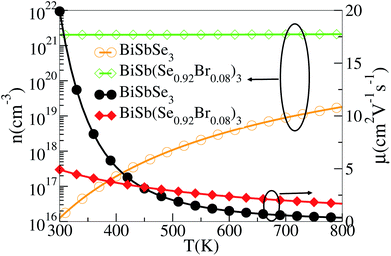
Based on the estimated τ, we can calculate the κe using the BoltzTraP2 code. Unfortunately, with the significant increase of n, the κe augments from ∼0.05 W m−1 K−1 of BiSbSe3 at 300 K, to ∼0.34 W m−1 K−1 of BiSb(Se0.92Br0.08)3 at 800 K. However, as discussed previously, Br codoping notably reduces the κL from ∼1.11 W m−1 K−1 at 300 K to ∼0.29 W m−1 K−1 at 800 K. Therefore, a favorable κ (∼0.63 W m−1 K−1) could still be obtained for BiSb(Se0.092Br0.08)3 at 800 K. Then, by combining the calculated κL, κe, S, and σ of BiSbSe3 and BiSb(Se0.92Br0.08)3, we determine their zTs at different temperatures and carrier concentrations. Fascinatingly, compared with 50% Sb doped BiSbSe3 (maximum zT ∼ 0.23 with the optimal n of 1.163 × 1019 cm−3 at 800 K, see Fig. 6(a)), further 8% Br codoping enhances σ, hence strikingly improves the zT (maximum ∼ 0.96 with the optimal n of 9.224 × 1019 cm−3 at 800 K, see Fig. 6(b)). BiSb(Se0.92Br0.08)3 exhibits a still high S that may originate from the increase of 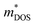 owing to the increase of Nv through Br codoping. On the other hand, the remarkably enhanced σ shown in Fig. 6(b) may originate from the increases of n and/or μ.
owing to the increase of Nv through Br codoping. On the other hand, the remarkably enhanced σ shown in Fig. 6(b) may originate from the increases of n and/or μ.
To show this more clearly, we calculate n and μ as functions of temperature for BiSbSe3 and BiSb(Se0.92Br0.08)3, as depicted in Fig. 7. μ is obtained from the calculated σ and n by using the expression μ = σ/ne. One can see that, 8% Br codoping dramatically enlarges n, and in the meantime, μ is still promoted at medium high temperatures. The significant increase of n in BiSb(Se0.92Br0.08)3 is essentially due to the one more electron of Br atom with respect to Se. Thus, Br atom acts as an electron donor though it has a large electronegativity. Consequently, the EF shifts deeper in the CB and the differential conductivity turns into more symmetric regarding the Fermi level.54 Our Bader charge analyses show consistently that each nearest neighbor Bi atom of Br averagely obtains more 0.44 electrons from the Br atom than that from Se. In addition, the hybridization of the electronic states then provides a large DOS around the Fermi level, as already shown in Fig. 4(d). A direct result is the remarkably enhanced σ. However, the dramatically increased n in the Sb–Br codoping system does not significantly reduce the S: it is −261.93 μV K−1 for BiSbSe3 at 300 K and −254.12 μV K−1 for BiSb(Se0.92Br0.08)3 at 800 K. Based on the aforementioned data and analyses, this explicit increase is most likely due to the Nv augment, which is the key parameter for making a compromise between n and S. Normally, the optimum n for most good TE materials is in the range of 1019 to 1021 cm−3. Optimization of the carrier concentration is still one of the most effective approaches for improving TE performance. Especially, in the case of some TE materials with intrinsically low thermal conductivity, a high zT can be obtained solely through doping.
Methods
First-principles calculations
The atomic structures of Bi2−xSbx(Se1−yBry)3 (x = 0, 1, 2; y = 0, 0.08) are optimized utilizing the plane-wave projector augmented wave (PAW) method24 as implemented in the Vienna ab initio simulation package (VASP)25 based on DFT. The Perdew–Burke–Ernzerhof parametrization of the generalized gradient approximation (PBE-GGA) is used for the exchange–correlation potential. The wave function is expanded using plane waves with a kinetic energy cutoff of 400 eV. A (5 × 15 × 5) Monkhorst–Pack26 k-point mesh is used for the Brillouin zone (BZ) sampling. The spin–orbit coupling (SOC) is considered in all the calculations due to the heavy element. The geometry optimization is performed for every Br doping configuration by relaxing both atomic positions and lattice constants. The energy convergence criterion is chosen to be 10−7 eV. The Hellmann–Feynman forces on each ion are less than 0.001 eV Å−1. The residual stress is set to be less than 0.1 GPa. Here, we discuss only the configuration with the lowest total energy. The calculated lattice constants are listed in Table 1. These values agree well with previous results reported in literature.23,27–29The electronic structures of Bi2−xSbx(Se1−yBry)3 (x = 0, 1, 2; y = 0, 0.08) are then calculated using the linearized augmented plane wave (LAPW) method,30 as implemented in the WIEN2k code.31 The muffin-tin radii (RMT) are set to 2.5, 2.46, 2.46, and 2.5 a.u. for Bi, Sb, Se, and Br, respectively. The cutoff parameter RMT × Kmax = 9 (Kmax is the magnitude of the largest k vector) is used. The self-consistent DFT calculations are performed with a (5 × 15 × 5) k-point mesh in the irreducible BZ, and the total energy is converged to within 0.0001 Ry. Since the local or semilocal exchange–correlation approximation underestimates band gaps as the presence of artificial self-interaction and the absence of the derivative discontinuity in the exchange–correlation functional,32 band gaps with better accuracy are calculated using the Tran–Blaha modified Becke–Johnson (TB-mBJ) functional.33 The calculated electronic structures with the TB-mBJ functional are further used to obtain electrical transport properties. The transport calculations are carried out using the semiclassical Boltzmann theory, as implemented in the BoltzTraP code34 within the constant scattering time approximation, by taking 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 k points in the irreducible BZ.
000 k points in the irreducible BZ.
The lattice thermal conductivity can be determined by using an iterative self-consistent method for solving the phonon Boltzmann transport equation as implemented in the ShengBTE code.35,36 The harmonic lattice dynamics and the second-order interatomic force constants (IFCs) are determined by the density functional perturbation theory (DFPT)37 implemented in VASP with a supercell of 1 × 3 × 1 and the PHONOPY code38 interfaced to VASP. The third-order anharmonic IFCs are extracted from the DFT calculations by applying the finite displacement method with a supercell of 1 × 3 × 1 and a truncation for next–nearest–neighbor interactions up to the tenth order. As for the k-point sampling of the BZ, our test calculations adopting a 1 × 3 × 1 and a 3 × 3 × 3 k-point mesh show that the thermal conductivities are converged very well. In this work, a 3 × 3 × 3 mesh is used for all the supercell calculations.
Summary and conclusion
In this work, we performed comprehensive investigations of both the thermal and electrical transport properties of BiSbSe3 and BiSb(Se0.92Br0.08)3 by using first-principles calculations combined with the Boltzmann transport theory. The results demonstrate that the dual doping of Sb–Br in Bi2Se3 leads to both low κL and promising electrical transport properties. First, the chemical bond softening between Br and Bi atoms and lone-pair electrons act as a phonon-blocking mechanism which greatly suppresses κL with strong anharmonicity. Second, the one more electron of Br atom with respect to Se makes the Br atom acts as an electron donor, which dramatically increases the carrier concentration n in BiSb(Se0.92Br0.08)3. As a result, the DOS near the EF is significantly increased and more conduction bands participate in the electron transport, leading to a remarkably enhanced σ. Third, the 8% Br subsequent codoping exhibits remarkably distinct electronic structures and transport properties, which further significantly increases the effective Nv. This multiple degeneracy of conduction band edges is a distinctive feature of BiSb(Se0.92Br0.08)3, enabling an extraordinary high PF by giving rise to a large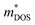 and thus preserving a large S in spite of the dramatically increased n. Combined with the low κ and excellent electrical transport properties, the n-type BiSb(Se0.92Br0.08)3 presents an outstanding thermoelectric performance, especially around 800 K: the maximum zT can reach 0.96 with the optimal n of 9.224 × 1019 cm−3. This work shows theoretically the possibility for crystalline materials to achieve a high thermoelectric performance without introducing defects and/or nanostructures, and provides a possible guidance and inspiration for seeking new promising Te-free thermoelectric materials.
and thus preserving a large S in spite of the dramatically increased n. Combined with the low κ and excellent electrical transport properties, the n-type BiSb(Se0.92Br0.08)3 presents an outstanding thermoelectric performance, especially around 800 K: the maximum zT can reach 0.96 with the optimal n of 9.224 × 1019 cm−3. This work shows theoretically the possibility for crystalline materials to achieve a high thermoelectric performance without introducing defects and/or nanostructures, and provides a possible guidance and inspiration for seeking new promising Te-free thermoelectric materials.
Data availability
The data that support the findings of this study are available from corresponding author upon reasonable request.Author contributions
S.-H. Ke conceived the idea. J. Zhang conducted the simulation and analysis. S. Zhong provided advices on this work. All authors participated in the writing and correction of the manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work was supported by the Natural Science Foundation of Shanghai under Grant No. 19ZR1459100 and by the National Natural Science Foundation of China under Grant No. 11374226.References
- L. D. Zhao, S. H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Ultralow Thermal Conductivity and High Thermoelectric Figure of Merit in SnSe Crystals, Nature, 2014, 508, 373 CrossRef CAS PubMed.
- Y. Wu, F. Liu, Q. Zhang, T. Zhu, K. Xia and X. Zhao, Enhancing the Average Thermoelectric Figure of Merit of Elemental Te by Suppressing Grain Boundary Scattering, J. Mater. Chem. A, 2020, 8, 8455 RSC.
- X. Zhang, C. Liu, Y. Tao, Y. Li, Y. Guo, Y. Chen, X. C. Zeng and J. Wang, High ZT 2D Thermoelectrics by Design: Strong Interlayer Vibration and Complete Band-Extrema Alignment, Adv. Funct. Mater., 2020, 30, 2001200 CrossRef CAS.
- Y. Xiao, D. Wang, Y. Zhang, C. Chen, S. Zhang, K. Wang, G. Wang, S. J. Pennycook, G. J. Snyder and H. Wu, et al., Band Sharpening and Band Alignment Enable High Quality Factor to Enhance Thermoelectric Performance in n-Type PbS, J. Am. Chem. Soc., 2020, 142, 4051 CrossRef CAS PubMed.
- Z. Wei, C. Wang, J. Y. Zhang, J. Yang and J. Luo, Precise Regulation of Carrier Concentration in Thermoelectric BiSbTe Alloys via Magnetic Doping, ACS Appl. Mater. Interfaces, 2020, 12, 20653–20663 CrossRef CAS PubMed.
- L. Xi, S. Pan, X. Li, Y. Xu, J. Ni, X. Sun, J. Yang, J. Luo, J. Xi and W. Zhu, et al., Discovery of High-Performance Thermoelectric Chalcogenides through Reliable High-Throughput Material Screening, J. Am. Chem. Soc., 2018, 140, 10785 CrossRef CAS PubMed.
- S. Wang, L. Su, Y. Qiu, Y. Xiao and L. D. Zhao, Enhanced Thermoelectric Performance in Cl-doped BiSbSe3 with Optimal Carrier Concentration and Effective Mass, Am. J. Mater. Sci. Technol., 2020, 70, 67 CrossRef.
- Z. Z. Luo, S. Cai, S. Hao, T. P. Bailey, I. Spanopoulos, Y. Luo, J. Xu, C. Uher, C. Wolverton and V. P. Dravid, et al., Inducing Strong Valence Band Convergence to Enhance Thermoelectric Performance in PbSe with Two Chemically Independent Knobs, Angew. Chem., Int. Ed., 2020, 132, 2 CrossRef.
- S. Q. Lin, W. Li, Z. L. Bu, B. Shan and Y. Z. Pei, Thermoelectric p-Type Ag9GaTe6 with an Intrinsically Low Lattice Thermal Conductivity, ACS Appl. Energy Mater., 2020, 3, 1892 CrossRef CAS.
- H. J. Goldsmid, Thermoelectric Refrigeration, Electr. Eng., 2013, 79, 380 Search PubMed.
- F. J. Disalvo, Thermoelectric Cooling and Power Generation, Science, 1999, 285, 703 CrossRef CAS PubMed.
- P. Yanzhong, S. Xiaoya, A. LaLonde, W. Heng and C. Lidong, et al., Convergence of Electronic Bands for High Performance Bulk Thermoelectrics, Nature, 2011, 473, 66 CrossRef PubMed.
- W. Qiu, L. Xi, P. Wei, X. Ke and W. Zhang, Part-Crystalline Part-Liquid State and Rattling-Like Thermal Damping in Materials with Chemical-Bond Hierarchy, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15031 CrossRef CAS PubMed.
- S. Wang, J. Yang, L. Wu, P. Wei, J. Yang, W. Zhang and Y. Grin, Anisotropic Multicenter Bonding and High Thermoelectric Performance in Electron-Poor CdSb, Chem. Mater., 2015, 27, 1071 CrossRef CAS.
- K. Peng, X. Lu, H. Zhan, S. Hui, X. Tang, G. Wang, J. Dai, C. Uher, G. Wang and X. Zhou, Broad Temperature Plateau for High ZTs in Heavily Doped p-Type SnSe Single Crystals, Energy Environ. Sci., 2016, 9, 454 RSC.
- L. Hu, H. Wu, T. Zhu, C. Fu, J. He, P. Ying and X. Zhao, Tuning Multiscale Microstructures to Enhance Thermoelectric Performance of n-Type Bismuth-Telluride-Based Solid Solutions, Adv. Energy Mater., 2015, 5, 1500411 CrossRef.
- Y. X. Yang, Y. H. Wu, Q. Zhang, G. S. Cao and X. B. Zhao, Enhanced Thermoelectric Performance of Bi2Se3/TiO2 Composite, Rare Met., 2020, 8, 887–894 CrossRef.
- W. Liu, K. Lukas, K. Mcenaney, S. Lee, Q. Zhang, C. Opeil, G. Chen and Z. Ren, Studies on the Bi2Te3-Bi2Se3-Bi2S3 System for Mid-Temperature Thermoelectric Energy Conversion, Energy Environ. Sci., 2013, 6, 552 RSC.
- W. Zhang, R. Yu, H. Zhang, X. Dai and Z. Fang, First-Principles Studies of the Three-Dimensional Strong Topological Insulators Bi2Te3, Bi2Se3 and Sb2Te3, New J. Phys., 2010, 12, 065013 CrossRef.
- Y. Min, J. W. Roh, H. Yang, M. Park, I. K. Sang, S. Hwang, M. L. Sang, K. H. Lee and U. Jeong, Surfactant-Free Scalable Synthesis of Bi2Te3 and Bi2Se3 Nanoflakes and Enhanced Thermoelectric Properties of Their Nanocomposites, Adv. Mater., 2012, 25, 1425 CrossRef PubMed.
- Y. Pei, H. Wang and G. J. Snyder, Band Engineering of Thermoelectric Materials, Adv. Mater., 2012, 24, 6125 CrossRef CAS PubMed.
- S. Wang, Y. Sun, J. Yang, B. Duan, L. Wu, W. Zhang and J. Yang, High Thermoelectric Performance in Te-free (Bi,Sb)2Se3 via Structural Transition Induced Band Convergence and Chemical Bond Softening, Energy Environ. Sci., 2016, 9, 3436 RSC.
- X. Liu, D. Wang, H. Wu, J. Wang, Y. Zhang, G. Wang, S. J. Pennycook and L. D. Zhao, Intrinsically Low Thermal Conductivity in BiSbSe3: A Promising Thermoelectric Material with Multiple Conduction Bands, Adv. Funct. Mater., 2018, 29, 1806558 CrossRef.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and J. Furthmuller, Efficiency of Ab Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- B. T. Wang and P. Zhang, Phonon Spectrum and Bonding Properties of Bi2Se3: Role of Strong Spin-Orbit Interaction, Appl. Phys. Lett., 2012, 100, 146401 Search PubMed.
- V. L. Deringer, R. P. Stoffel, M. Wuttig and R. Dronskowski, Vibrational Properties and Bonding Nature of Sb2Se3 and Their Implications for Chalcogenide Materials, Chem. Sci., 2015, 6, 5255 RSC.
- Z. Zhang, R. Zhang, N. Qi, Y. Wu and Z. Chen, Microscopic Origin of the Extremely Low Thermal Conductivity and Outstanding Thermoelectric Performance of BiSbX3 (X = S, Se) Revealed by First-Principles Study, Phys. Chem. Chem. Phys., 2020, 22, 15559 RSC.
- E. SjöStedt, L. NordströM and D. J. Singh, An Alternative Way of Linearizing the Augmented Plane-Wave Method, Solid State Commun., 2000, 114, 15 CrossRef.
- R. Nityananda, P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Resonance, 2017, 22, 809 CrossRef.
- L. J. Sham and M. Schlüter, Density-Functional Theory of the Energy Gap, Phys. Rev. Lett., 1983, 51, 1888 CrossRef.
- F. Tran and P. Blaha, Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential, Phys. Rev. Lett., 2009, 102, 226401 CrossRef PubMed.
- A. F. May, E. S. Toberer, A. Saramat and G. J. Snyder, Characterization and Analysis of Thermoelectric Transport in n-Type Ba8Ga16−xGe30+x, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 125205 CrossRef.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, ShengBTE: A Solver of the Boltzmann Transport Equation for Phonons, Comput. Phys. Commun., 2014, 185, 1747 CrossRef CAS.
- W. Li, N. Mingo, L. Lindsay, D. A. Broido, D. A. Stewart and N. A. Katcho, Thermal Conductivity of Diamond Nanowires from First Principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 195436 CrossRef.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Phonons and Related Crystal Properties from Density-Functional Perturbation Theory, Rev. Mod. Phys., 2001, 73, 515 CrossRef CAS.
- A. Togo, F. Oba and I. Tanaka, First-Principles Calculations of the Ferroelastic Transition Between Rutile-Type and CaCl2-type SiO2 at High Pressures, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- Z. Feng, X. Zhang, Y. Wang, J. Zhang, T. Jia, B. Cao and Y. Zhang, Thermoelectric Optimization of AgBiSe2 by Defect Engineering for Room-Temperature Applications, Phys. Rev. B, 2019, 99, 155203 CrossRef CAS.
- L. D. Zhao, G. Tan, S. Hao, J. He, Y. Pei, H. Chi, H. Wang, S. Gong, H. Xu and V. P. Dravid, Ultrahigh Power Factor and Thermoelectric Performance in Hole-Doped Single-Crystal SnSe, Science, 2015, 351, 141 CrossRef PubMed.
- J. Zhang, X. Zhang and Y. Wang, Hf/Sb Co-Doping Induced a High Thermoelectric Performance of ZrNiSn: First-principles Calculation, Sci. Rep., 2017, 7, 14590 CrossRef PubMed.
- W. G. Zeier, A. Zevalkink, Z. M. Gibbs, G. Hautier, M. G. Kanatzidis and G. J. Snyder, Thinking Like a Chemist: Intuition in Thermoelectric Materials, Angew. Chem., Int. Ed., 2016, 55, 6826 CrossRef CAS PubMed.
- P. Ying, X. Li, Y. Wang, J. Yang, C. Fu, W. Zhang, X. Zhao and T. Zhu, Hierarchical Chemical Bonds Contributing to the Intrinsically Low Thermal Conductivity in alpha-MgAgSb Thermoelectric Materials, Adv. Funct. Mater., 2017, 27, 1604145 CrossRef.
- Z. Feng, T. Jia, J. Zhang, Y. Wang and Y. Zhang, Dual Effects of Lone-Pair Electrons and Rattling Atoms in CuBiS2 on Its Ultralow Thermal Conductivity, Phys. Rev. B, 2017, 96, 235205 CrossRef.
- R. J. Gillespie and R. S. Nyholm, Inorganic Stereochemistry, Q. Rev., Chem. Soc., 1957, 11, 339 RSC.
- T. Jia, J. Carrete, Z. Feng, S. Guo, Y. Zhang and G. K. H. Madsen, Localized Dimers Drive Strong Anharmonicity and Low Lattice Thermal Conductivity in ZnSe2, Phys. Rev. B, 2020, 102, 125204 CrossRef CAS.
- K. Xia, Y. Liu, S. Anand, G. J. Snyder, J. Xin, J. Yu, X. Zhao, X. B. Zhao and T. Zhu, Enhanced Thermoelectric Performance in 18-Electron Nb0.8CoSb Half-Heusler Compound with Intrinsic Nb Vacancies, Adv. Funct. Mater., 2018, 28, 1705845 CrossRef.
- Z. Ma, J. Wei, P. Song, M. Zhang, L. Yang, J. Ma, W. Liu, F. Yang and X. Wang, Review of Experimental Approaches for Improving zT of Thermoelectric Materials, Mater. Sci. Semicond. Process., 2021, 121, 105303 CrossRef CAS.
- L. D. Zhao, C. Chang, G. Tan and M. G. Kanatzidis, SnSe: a Remarkable New Thermoelectric Material, Energy Environ. Sci., 2016, 9, 3044 RSC.
- J. M. Hodges, Y. Xia, C. D. Malliakas, G. C. B. Alexander, M. K. Y. Chan and M. G. Kanatzidis, Two-Dimensional CsAg5Te3−xSx Semiconductors: Multi-anion Chalcogenides with Dynamic Disorder and Ultralow Thermal Conductivity, Chem. Mater., 2018, 30, 7245–7254 CrossRef CAS.
- M. T. Dove, Theory of Displacive Phase Transitions in Minerals, Am. Mineral., 1997, 82, 213 CAS.
- G. K. H. Madsen, J. Carrete and M. J. Verstraete, BoltzTraP2, a Program for Interpolating Band Structures and Calculating Semi-Classical Transport Coefficients, Comput. Phys. Commun., 2017, 231, 140 CrossRef.
- K. P. Ong, D. J. Singh and P. Wu, Analysis of the Thermoelectric Properties of n-type ZnO, Phys. Rev. B, 2011, 83, 115110 CrossRef.
- T. Zhu, Y. Liu, C. Fu, J. P. Heremans, J. G. Snyder and X. Zhao, Compromise and Synergy in High-Efficiency Thermoelectric Materials, Adv. Mater., 2017, 29, 1605884 CrossRef PubMed.
- H. A. Eivari, Z. Sohbatzadeh, P. Mele and M. H. N. Assadi, Low thermal conductivity: fundamentals and theoretical aspects in thermoelectric applications, Mater. Today Energy, 2021, 21, 100744 CrossRef.
- J. J. G. Moreno, J. Cao, M. Fronzi and M. H. N. Assadi, A review of recent progress in thermoelectric materials through computational methods, Mater. Renew. Sustain. Energy, 2020, 9, 16 CrossRef.
- A. Shakouri, Recent Developments in Semiconductor Thermoelectric Physics and Materials, Annu. Rev. Mater. Res., 2011, 41, 399–431 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra08726f |
| This journal is © The Royal Society of Chemistry 2022 |