Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational investigation of a covalent triazine framework (CTF-0) as an efficient electrochemical sensor†
Sehrish Sarfaraz‡
a,
Muhammad Yar‡a,
Muhammad Ans b,
Mazhar Amjad Gilanic,
Ralf Ludwig
b,
Mazhar Amjad Gilanic,
Ralf Ludwig de,
Muhammad Ali Hashmi
de,
Muhammad Ali Hashmi f,
Masroor Hussaing,
Shabbir Muhammad
f,
Masroor Hussaing,
Shabbir Muhammad h and
Khurshid Ayub
h and
Khurshid Ayub *a
*a
aDepartment of Chemistry, COMSATS University, Abbottabad Campus, KPK, Pakistan 22060. E-mail: khurshid@cuiatd.edu.pk; Tel: +92-992-383591
bDepartment of Chemistry, University of Agriculture Faisalabad, 38000, Faisalabad, Pakistan
cDepartment of Chemistry, COMSATS University Islamabad, Lahore Campus, 54600, Pakistan
dUniversität Rostock, Institut für Chemie, Abteilung für Physikalische Chemie, Dr.-Lorenz-Weg 1, 18059 Rostock, Germany
eLeibniz-Institut für Katalyse an der Universität Rostock, Albert-Einstein-Strasse 29a, 18059 Rostock, Germany
fDepartment of Chemistry, Division of Science & Technology, University of Education, 54770 Lahore, Pakistan
gDepartment of Data Science, Ghulam Ishaq Khan Institute of Engineering Sciences and Technology, Topi, KPK, Pakistan
hDepartment of Chemistry, College of Science, King Khalid University, P. O. Box 9004, Abha, 61413, Saudi Arabia
First published on 31st January 2022
Abstract
In the current study, a covalent triazine framework (CTF-0) was evaluated as an electrochemical sensor against industrial pollutants i.e., O3, NO, SO2, SO3, and CO2. The deep understanding of analytes@CTF-0 complexation was acquired by interaction energy, NCI, QTAIM, SAPT0, EDD, NBO and FMO analyses. The outcome of interaction energy analyses clearly indicates that all the analytes are physiosorbed onto the CTF-0 surface. NCI and QTAIM analysis were employed to understand the nature of the non-covalent interactions. Furthermore, SAPT0 analysis revealed that dispersion has the highest contribution towards total SAPT0 energy. In NBO analysis, the highest charge transfer is obtained in the case of SO3@CTF-0 (−0.167 e−) whereas the lowest charge transfer is observed in CO2@CTF-0. The results of NBO charge transfer are also verified through EDD analysis. FMO analysis revealed that the highest reduction in the HOMO–LUMO energy gap is observed in the case of O3 (5.03 eV) adsorption onto the CTF-0 surface, which indicates the sensitivity of CTF-0 for O3 analytes. We strongly believe that these results might be productive for experimentalists to tailor a highly sensitive electrochemical sensor using covalent triazine-based frameworks (CTFs).
1. Introduction
Over the past few years, detection of harmful gases and their appropriate monitoring has gained much attention because these gases are extensively released during numerous industrial and domestic activities.1 Therefore, the development of efficient, reliable, and low-cost gas sensors has gained great interest, stretching from industrial to medicinal applications. Seriously harmful gases that are toxic to human health are nitric oxide (NO), carbon dioxide (CO2), ozone (O3), sulphur dioxide (SO2), etc.2 CO2 emission generally occurs as a result of combustion of fossil fuels, and it actively participates in global warming.3–5 Moreover, SO2 and SO3 are the major contributors to air pollution, mainly released during oil and coal burning.6,7 On the other hand, emission of ozone (O3) targets respiratory tissues and ocular mucosa, thus it has been investigated as the most threatening air pollutant.8–10 Hence, the development of highly sensitive, facile, and low-cost gas sensors is of great interest.Well-organized nano porous materials have gained remarkable attention because of their abundance, exceptional sensing properties and potential applications.11 Several nano-porous frameworks have been constructed over the decade such as covalent organic frameworks (COFs), zeolites, and metal–organic frameworks (MOFs). In the past few years, COFs became the center of attention for researchers, due to their highly porous surface, structural properties, physical and chemical durability as well as exhibiting strong covalent bonding.12–14 Covalent triazine-based frameworks (CTFs) are considered as a novel promising class of organic porous crystalline materials, first prepared by Thomas et al. in 2008. CTFs can be synthesized by trimerization reaction of aromatic nitrile in molten ZnCl2 under ionothermal conditions. CTF is a promising class of organic crystalline materials in which their building units are linked through strong covalent bonding to generate 2D and 3D porous structures. Principle modular design of CTFs greatly benefits them to achieve chemical stability, controlled porosity, and valuable adsorption properties.15–17
CTFs have various unique properties, for example, the presence of aromatic linkage (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) in triazine unit endow CTFs with higher chemical stability, heteroatom effect (HAE) and rich nitrogen contents add value for their applications in practical world.18 CTFs have numerous active sites and large π–π stacking, which make them exceptionally potential candidate to acquire some promising characteristics as imparted by graphitic carbon nitride or N-doped graphene surfaces.19 These exceptional characteristics enable CTFs for a number of applications including photocatalysis,20 solar cells,25–28 energy storage,29 degradation of organic pollutants,30 heterogeneous catalysis,31 and electrochemical sensors.31–35
N) in triazine unit endow CTFs with higher chemical stability, heteroatom effect (HAE) and rich nitrogen contents add value for their applications in practical world.18 CTFs have numerous active sites and large π–π stacking, which make them exceptionally potential candidate to acquire some promising characteristics as imparted by graphitic carbon nitride or N-doped graphene surfaces.19 These exceptional characteristics enable CTFs for a number of applications including photocatalysis,20 solar cells,25–28 energy storage,29 degradation of organic pollutants,30 heterogeneous catalysis,31 and electrochemical sensors.31–35
In electrochemical sensors, the use of CTFs has attained growing interest in recent years. Novel electrochemical platform for sensing and biosensing based on CTF was reported by Xu et al.36 Zhang et al. reported electrochemical senor based on CTF for the detection of lead ions (Pb2+), which displayed a strong response against Pb2+ even when the concentration is in nM.37 These key applications of CTF suggested that the conjugated triazine rings can play a same role in sensing as played by N-doped graphene and other related materials.38
These findings motivated us to explore the wider applications of CTF based electrochemical sensor for the determination of greenhouse and industrial gases. CTF-0 surface was selected due to its large π–π stacking, higher thermal stability and high nitrogen content.39,40 The 2D CTF-0 surface provides electron rich porous cavity due to higher nitrogen content which helps in adsorption of analytes.41 DFT calculations are performed to evaluate the adsorption studies of industrial gases on the surface of CTF-0. Therefore, we have designed a theoretical study for the detection of five different analytes such as O3, NO, SO2, SO3, and CO2 on CTF-0. The adsorption behavior of selected analytes, selectivity and sensitivity of CTF-0 surface is investigated through simple optimization and geometry analysis, HOMO–LUMO gap, and charge transfer through natural bond orbital (NBO) analysis. The nature of interactions between analytes and surface are determined by symmetry adapted perturbation theory (SAPT0), non-covalent interaction (NCI), electron density differences (EDD), and quantum theory of atom in molecule (QTAIM) analysis.
2. Computational methodology
Gaussian 09 software42 is used for the geometry optimization of complexes (analytes@CTF-0) at M05-2X/6-31G++(d,p) level of theory without symmetry constraints. Optimized geometries were visualized by using GaussView 5.0 package. Various orientations of analytes@CTF-0 were computed to get the most stable geometry. The lowest energy configuration is the most stable one and therefore considered for subsequent calculations. Other properties such as frontier molecular orbital (FMO), band gap, natural bond orbital (NBO) and interaction energies were also evaluated at the same level of theory. The interaction energies for each analyte@CTF-0 complex were calculated by following formula given:| ΔE = Ecomplex − (Eanalyte + ECTF-0) | (1) |
Ecomplex, Eanalyte and ECTF-0 denote the energies of complex, analyte, and surface, respectively.43
Electronic properties were explored via Frontier Molecular Orbital (FMO) analysis and density of states (DOS) analysis. The electronic properties are important to understand the characteristics of sensors such as selectivity, sensitivity, conductivity, and resistivity.44 Higher conductivity is associated with decreased HOMO–LUMO gaps while enhanced HOMO–LUMO gap reflect higher resistivity.45 DOS analysis was performed to get insight into sensor mechanism by evaluating the number of available energy states for electron in a given energy level.46 DOS spectra are generated by GaussSum software.47 Electronic properties are further elaborated through natural bond analysis (NBO) to evaluate the transfer of charge between analytes and surface (CTF-0).48
NCI analysis is mainly employed to distinguish between steric repulsion, electrostatic forces and van der Waals interactions. Non-covalent interactions are important to estimate the adsorption behavior of analyte on surface; therefore, it is essential to evaluate them precisely.49 The NCI analysis show the relationship between electron density (ρ) and reduced density gradient (RDG) by the following equation:50
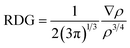 | (2) |
3D plot was used for visual analysis of attractive and repulsive interactions. The scheme of NCI isosurfaces gives insight into the type of interactions present i.e., red color indicates the presence of steric repulsion whereas blue and green parts represent the strong and weak interactions, respectively.51,52 The 2D NCI graphs can be obtained by plotting RDG (a. u.) versus the product of the sign of second eigenvalue and the density (sign(λ2)ρ (a. u.)). The colored maps in the 2D NCI graph correspond to the same colors of isosurfaces enclosed in 3D plot.53 For NCI plots, Multiwfn 3.7 (ref. 54) and VMD55 software were employed.
SAPT0 analysis was employed to evaluate total interaction energies of complexes (analytes@CTF-0). Four main descriptors are used in the components of SAPT0 analysis and are normally given as: electrostatic (ΔEelstat), exchange (ΔEexch), dispersion (ΔEdisp), and induction (ΔEind).56 The equation for ΔEint in SAPT0 analysis is given below:
| ΔEint = ΔEexch + ΔEelstat + ΔEind + ΔEdisp | (3) |
PSI4 software was employed to carry out SAPT0 analysis.57
Non-covalent interactions were further examined via QTAIM analysis. The nature of interactions in QTAIM analysis is evaluated by following parameters: Laplacian of electron density (∇2ρ), electron charge density (ρ), potential energy density V(r), Lagrangian kinetic energy H(r), energy density (H(r)), and Eint. QTAIM analysis is helpful for calculating non-covalent interactions between the fragments from bond critical points.58 Electron Density Difference (EDD) analysis is used to explore the electron-transfer behavior of analytes during adsorption and to examine the type of nonbonding interactions between analytes and surface.
3. Results and discussions
3.1 Geometric optimization
CTFs are special organic materials with covalent bonding between organic building blocks, which give the 2D and 3D porous structure.34 CTFs have gained special attentions due to the availability of numerous active sites, rich nitrogen content, and π linkage among benzene and triazine ring.30,59 These characteristics make CTFs a potential candidate for various applications such as photocatalysis,60 electrochemical sensors,61–63 and degradation of organic pollutants.64,65 CTFs are mainly synthesized by trimerization reaction of carbonitriles to produce triazine rings.66 The structure of CTF-0 consists of alternative triazine and benzene rings (see Fig. 1). The optimized geometry of CTF-0 reveals that there are three types of bonds based upon bond length and connectivity; C–N bonds with bond length of 1.34 Å while other two bonds are C–C (1.39 Å and 1.47 Å).67 Electron rich nitrogen atoms, present in CTF-0 can strongly interact with electron deficient sites of analytes, and hence, resulted in perturbation of electronic structure which provide basis for sensing applications of CTF.68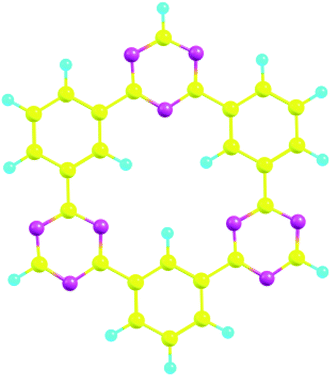 | ||
| Fig. 1 CTF-0 optimized geometry at M05-2X/6-31G++(d,p) level of theory, magenta color for N-atom, yellow denotes C-atom, and turquoise blue for H-atoms. | ||
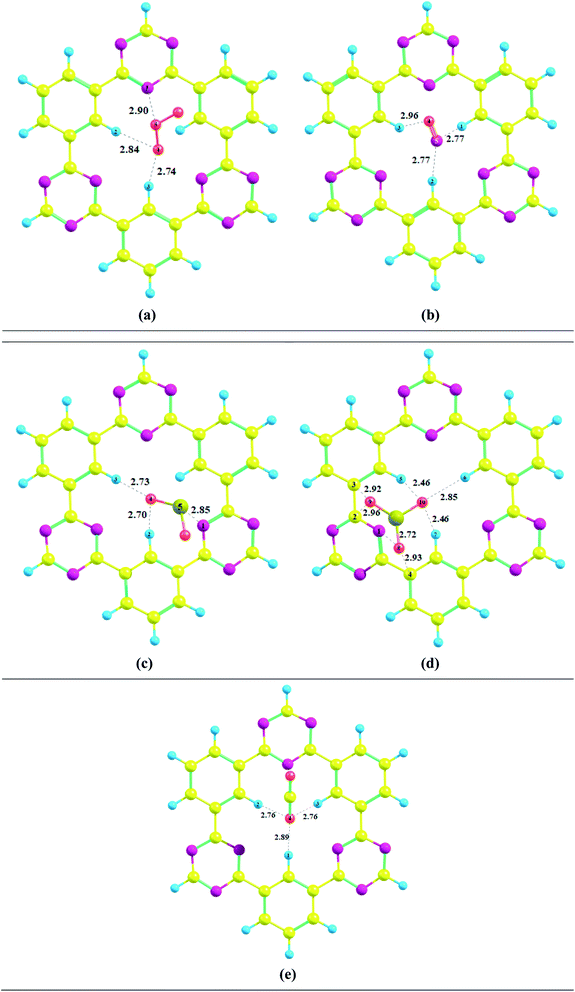
Several possible orientations were considered for each analyte on the surface of CTF-0 to get the most stable configuration of analyte@CTF-0 complexes (Fig. S1†). The most stable geometries for each analyte@CTF-0 complex was considered for further analysis and are shown in Fig. 2. In the current study, we have selected five different analytes and checked the sensitivity and selectivity of CTF-0 surface against these analytes. For the sake of convenience, we named the complexes as O3@CTF-0, NO@CTF-0, SO2@CTF-0, SO3@CTF-0, and CO2@CTF-0 for ozone, nitric oxide, sulfur dioxide, sulfur trioxide, and carbon dioxide adsorbed on the surface of CTF-0, respectively.
Interaction energy results reveals that the most stable geometry is observed for SO3@CTF-0 among the selected complexes because of higher number of possible interactions between SO3 and atoms of CTF-0 surface, and smallest interaction distance (see Table 1). The interaction energy (Eint) trend of studied complexes is SO3 −0.56 eV (−13.00 kcal mol−1) > SO2 −0.30 eV (−7.05 kcal mol−1) > O3 −0.23 eV (−5.44 kcal mol−1) > CO2 −0.22 eV (−5.03 kcal mol−1) > NO −0.16 eV (−3.65 kcal mol−1). For physical adsorption, interaction energies must be less than 1 eV and it has been extensively reported in literature. Thus, species with interaction energy <1 eV are considered to be physiosorbed.69–71 Small interaction energy (eV) values expresses that all the studied analytes are physiosorbed on the surface (CTF-0).
| Analytes@CTF-0 | |||
|---|---|---|---|
| Analyte | Intermolecular bond | Bond length | Eint |
| O3 | O5–N1 | 2.90 | −5.44 |
| O4–H2 | 2.84 | ||
| O4–H3 | 2.74 | ||
| NO | O4–H3 | 2.96 | −3.65 |
| N5–H1 | 2.77 | ||
| N5–H2 | 2.77 | ||
| SO2 | S5–N1 | 2.85 | −7.05 |
| O4–H2 | 2.70 | ||
| O4–H3 | 2.73 | ||
| SO3 | O10–H5 | 2.46 | −13.00 |
| O10–H6 | 2.85 | ||
| O10–H7 | 2.46 | ||
| O9–H2 | 2.96 | ||
| O9–H3 | 2.92 | ||
| O8–N1 | 2.72 | ||
| O8–H4 | 2.93 | ||
| CO2 | O4–H1 | 2.89 | −5.03 |
| O4–H2 | 2.76 | ||
| O4–H3 | 2.76 | ||
For O3@CTF-0 complex, the least interaction distance of 2.76 Å is observed for O4–H3 bond. The corresponding interaction energy for O3@CTF-0 complex is −5.44 kcal mole−1. For NO@CTF-0 complex, the least interaction distance of 2.77 Å is obtained for N5–H1 and N5–H2 bonds. The optimized geometry of NO@CTF-0 complex presents the parallel orientation of NO analyte over the CTF-0 surface (Fig. 2). In SO2 analyte, one O-atom is oriented towards CTF-0 surface while other O-atom is oriented away from the surface. The most stable conformation of SO2@CTF-0 complex shows three strong interactions, (O4–H2) with an interaction distance of 2.70 Å followed by (O4–H3) and (S5–N1) with interaction distances of 2.73 and 2.85 Å, respectively. The highest number of interactions observed in case of SO3@CTF-0 complex with the least interaction distance of 2.46 Å for (O10–H5). While highest interaction distance is 2.96 Å for O9–H2 bond. Order of interacting distance is also justified from the interaction energies trend, e.g., the lowest interaction distance 2.46 Å is observed for SO3@CTF-0 complex with the interaction energy of −13.00 kcal mol−1. In SO3@CTF-0 complex, highest interaction energy might be due to the presence of strong hydrogen bonding between O-atoms of SO3 analyte and H-atoms of surface. Three electron rich oxygen atoms present in SO3 are responsible for the highest interaction energy and lowest interaction distance. On the other hand, the least interaction energy is obtained for NO that is −3.65 kcal mol−1 (see Table 1).
The interaction energies with other functionals such as B3LYP-D3 and M06-2X are also calculated and the obtained results are compared with the results of M05-2X (see Table 2). The same trend of interaction energies is observed with different functionals. For example, the highest interaction energies are observed for SO3@CTF-0 complex and the lowest interaction energies are seen for NO@CTF-0 complex.
| Eint for studied analytes@CTF-O complexes | |||
|---|---|---|---|
| Analytes@CTF-0 | M05-2X | M06-2X | B3LYP-D3 |
| O3@CTF-0 | −5.44 | −6.29 | −6.40 |
| NO@CTF-0 | −3.65 | −3.89 | −3.82 |
| SO2@CTF-0 | −7.05 | −8.48 | −9.90 |
| SO3@CTF-0 | −13.00 | −14.99 | −16.70 |
| CO2@CTF-0 | −5.03 | −4.96 | −5.84 |
3.2 Non-covalent interactions (NCI) analysis
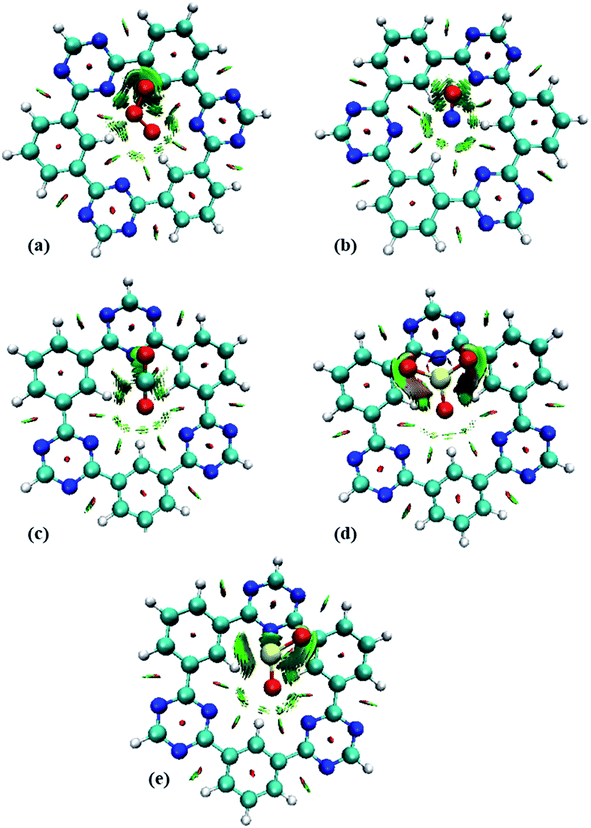
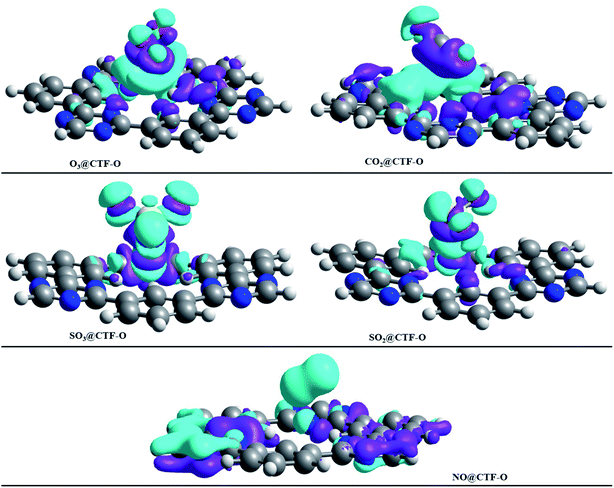
To get insight into the type of non-covalent interactions between analytes and CTF-0 in real space, NCI analysis was carried out on the most stable conformations of analyte@CTF-0 complexes. The 3D isosurfaces and 2D-NCI graphs for studied complexes (analytes@CTF-0) are presented to identify the nature of attractive and repulsive forces between analytes and surface. In 3D isosurfaces, the nature of non-covalent interactions was examined on the basis of three colors (Fig. 3). Green color presents weak forces mainly London dispersion interactions and blue color indicates strong interaction such as hydrogen bonding.72 Whereas red color shows the steric repulsion present between interacting species.73 The isovalue of 0.5 a.u. is used to examine the 3D isosurfaces. The thickness of isosurfaces is directly related with the strength of nonbonding interactions i.e., the thicker patches indicate strong interactions, whereas stippled patches show weak interactions.The 3D and 2D NCI plots of analytes@CTF-0 complexes are shown in Fig. 3 and 4, respectively. The appearance of green spikes in 2D-NCI plots of studied complexes indicate the presence of non-covalent weak interactions between analytes and CTF-0 on X-axis (λ2)ρ 0.00 to −0.015 a.u. are present at the center of benzene and triazine ring of CTF-0, which is the clear indication of steric repulsion presence in the nuclei rings. Furthermore, larger green isosurfaces are observed in case of SO3@CTF-0 and SO2@CTF-0 complexes in 3D plots, which show that these complexes are more stable as compared to the rest of the complexes.
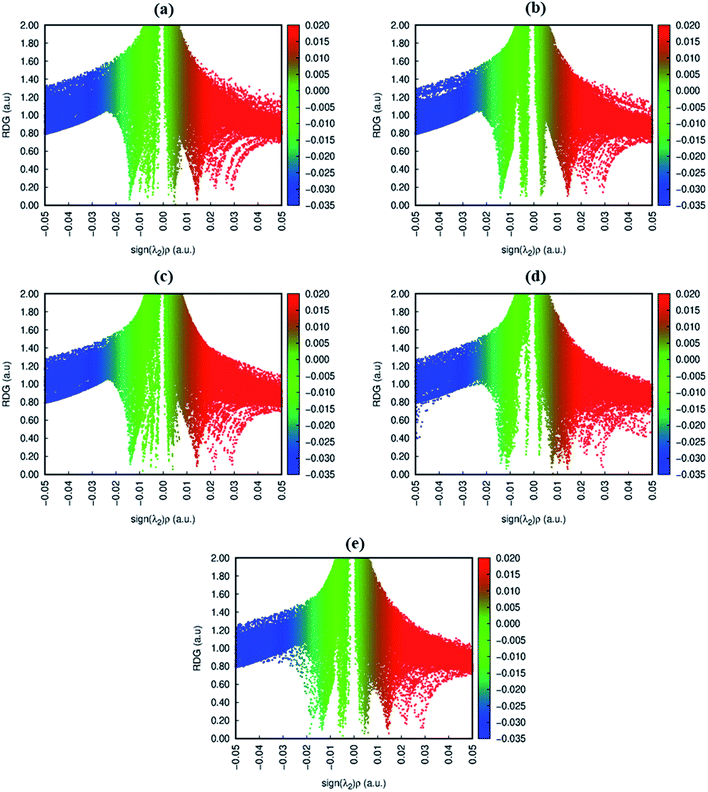 | ||
| Fig. 4 RDG 2D spectra of studied complexes: (a) O3@CTF-0, (b) NO@CTF-0, (c) CO2@CTF-0, (d) SO3@CTF-0 and (e) SO2@CTF-0 complex. | ||
3.3 QTAIM analysis
Bader's quantum theory of atoms in molecules (QTAIM) is mainly used to examine the non-covalent interactions in various molecular systems. QTAIM analysis is the best tool for analyzing intermolecular nonbonding interactions i.e., ionic interactions, van der Waals forces, and hydrogen bonding. The parameters used to investigate the non-covalent interactions via QTAIM analysis at a bond critical point (BCP) of studies complexes are electron density (ρ(r)), kinetic energy density (G(r)), potential energy density (V(r)), total energy density (H(r)), Laplacian of electron density (∇2ρ(r))74 and interaction energy (Eint) of an individual bond. The nature of the nonbonding interactions is characterized through Laplacian of charge density (∇2ρ(r)), whereas the strength of bond at bond critical point (BCP) is evaluated via electron density (ρ). The nature of bonding can be estimated through individual bond interaction energies, calculated by the Espinosa approach.
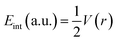 | (4) |
Interaction energy (Eint) values in the range of 3–10 kcal mol−1 indicate the presence of hydrogen bonding.75
If charge concentrations in Laplacian of electron density (∇2ρ(r)) is less than zero i.e., (∇2ρ(r) < 0) it indicates chemical bonding. On the other hand, if charge concentration is greater than zero i.e., (∇2ρ(r) > 0), it shows weak intermolecular interactions. Change in potential and kinetic energy values resulted in the net rise of molecular energy, and these changes that occur in the bonding regions are calculated by Bader equation given below:
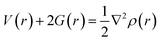 | (5) |
The above equation combines P.E. density V(r) and K.E. density G(r) with Laplacian of electron density (∇2ρ(r)). Moreover, energy density H(r) can be calculated by the formula given below:
| G(r) + V(r) = H(r) | (6) |
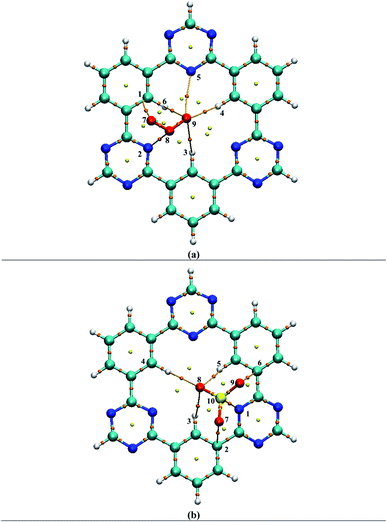
For weak interactions, the energy density H(r) must either be zero or less than zero i.e., H(r) < 0. While the energy density H(r) greater than zero indicates the appearance of covalent bonding in the region.76,77 Furthermore, interatomic interactions can be estimated through the −V(r)/G(r) ratio. If the ratio is less than one i.e., −V(r)/G(r) < 1, it shows the presence of weak interactions, while the ratio −V(r)/G(r) > 2 indicates covalent bonding. Results of topological parameters obtained via QTAIM analysis of analytes@CTF-0 are shown in Table 3. The BCPs between analytes and surface (CTF-0) are presented through colored map and are given in Fig. 5.
| Analytes@CTF-0 | CTF-0—analyte | ρ (a.u.) | ∇2ρ (a.u.) | G(r) (a.u.) | V(r) (a.u.) | H(r) (a.u.) | −V/G | Eint (kcal mol−1) |
|---|---|---|---|---|---|---|---|---|
| O3@CTF-0 | H5–O10 | 0.004 | 0.017 | 0.003 | −0.0026 | 0.0008 | 0.87 | −0.82 |
| H3–O10 | 0.004 | 0.017 | 0.003 | −0.0026 | 0.0008 | 0.87 | −0.82 | |
| N6–O10 | 0.011 | 0.034 | 0.008 | −0.0071 | 0.0070 | 0.88 | −2.19 | |
| H7–O10 | 0.007 | 0.028 | 0.006 | −0.0049 | 0.0011 | 0.82 | −1.53 | |
| C1–O8 | 0.006 | 0.021 | 0.004 | −0.0039 | 0.0006 | 0.97 | −1.22 | |
| N2–O9 | 0.010 | 0.033 | 0.007 | −0.0070 | 0.0060 | 1.00 | −2.19 | |
| NO@CTF-0 | N5–N7 | 0.003 | 0.011 | 0.002 | −0.0020 | 0.0005 | 1.00 | −0.63 |
| H6–N7 | 0.005 | 0.018 | 0.004 | −0.0027 | 0.0009 | 0.67 | −0.85 | |
| N1–N7 | 0.003 | 0.011 | 0.002 | −0.0018 | 0.0005 | 0.90 | −0.56 | |
| H2–N7 | 0.005 | 0.018 | 0.004 | −0.0027 | 0.0009 | 0.67 | −0.85 | |
| H4–N7 | 0.005 | 0.020 | 0.004 | −0.0031 | 0.0009 | 0.77 | −0.97 | |
| N3–O8 | 0.004 | 0.017 | 0.004 | −0.0031 | 0.0005 | 0.77 | −0.97 | |
| SO2@CTF-0 | H6–O8 | 0.006 | 0.025 | 0.005 | −0.0039 | 0.0011 | 0.78 | −1.22 |
| N5–O8 | 0.003 | 0.014 | 0.003 | −0.0024 | 0.0005 | 0.80 | −0.75 | |
| H4–O8 | 0.004 | 0.018 | 0.004 | −0.0029 | 0.0009 | 0.72 | −0.91 | |
| N3–O8 | 0.002 | 0.010 | 0.002 | −0.0014 | 0.0006 | 0.70 | −0.44 | |
| C7–O10 | 0.004 | 0.016 | 0.003 | −0.0027 | 0.0007 | 0.90 | −0.85 | |
| C2–S9 | 0.005 | 0.021 | 0.004 | −0.0030 | 0.0012 | 0.75 | −0.94 | |
| N1–S9 | 0.019 | 0.054 | 0.012 | −0.0112 | 0.0011 | 0.93 | −3.51 | |
| SO3@CTF-0 | H4–O8 | 0.003 | 0.014 | 0.003 | −0.0020 | 0.0008 | 0.67 | −0.63 |
| H5–O8 | 0.010 | 0.039 | 0.009 | −0.0074 | 0.0011 | 0.82 | −2.32 | |
| H3–O8 | 0.010 | 0.039 | 0.009 | −0.0074 | 0.0011 | 0.82 | −2.32 | |
| N1–S10 | 0.018 | 0.052 | 0.004 | −0.0102 | 0.0011 | 0.72 | −3.20 | |
| C2–O7 | 0.011 | 0.039 | 0.009 | −0.0080 | 0.0009 | 0.89 | −2.51 | |
| C6–O9 | 0.011 | 0.039 | 0.009 | −0.0080 | 0.0009 | 0.89 | −2.51 | |
| CO2@CTF-0 | H2–O5 | 0.005 | 0.020 | 0.004 | −0.0031 | 0.0010 | 0.77 | −0.97 |
| H3–O5 | 0.003 | 0.014 | 0.003 | −0.0018 | 0.0008 | 0.60 | −0.56 | |
| H4–O5 | 0.005 | 0.020 | 0.004 | −0.0031 | 0.0010 | 0.77 | −0.97 | |
| N1–O6 | 0.008 | 0.032 | 0.007 | −0.0056 | 0.0012 | 0.80 | −1.76 |
Different BCPs for all complexes are observed which indicate the presence of different types of interactions between analytes and surface. The stable geometry of O3@CTF-0 complex reveals six BCPs, which consist of three H–O, two N–O and one C–O bond interactions (see Table 3). The electronic density ρ(r) values for O3@CTF-0 complex are found in the range of (0.004 to 0.011 a.u.) and Laplacian of electron density ∇2ρ(r) values are 0.017 to 0.034 a.u. The highest values of ρ (0.011 a.u.) and ∇2ρ (0.034 a.u.) indicate the presence of strong non-covalent interaction between N6 of CTF-0 and O10 atom of O3 analyte. In case of NO@CTF-0 complex, six BCPs are observed out of which three are present in H–N bond (see Fig. S2†). The ρ(r) values are observed in the range of 0.003 to 0.005 a.u. While ∇2ρ(r) values for the observed BCPs are in the range of 0.011 to 0.020 a.u. and H(r) values are 0.0005 to 0.0009 a.u. These values indicate medium non-covalent interaction between NO and CTF-0. Seven BCPs are observed in stable geometry of SO2@CTF-0 complex. The results indicate that SO2 get stabilized on CTF-0 surface via two H–O, two N–O, one C–O, one C–S and one N–S types of interactions. The remaining topological parameters such as G(r), V(r), H(r), and −V(r)/G(r) values also show the existence of non-covalent interactions.
In case of SO3@CTF-0 complex, six BCPs obtained and SO3 is stabilized on CTF-0 surface with three H–O, two C–O, and one N–S bonds (Fig. 5). The strongest interaction is observed for N1–S10 bond in SO3@CTF-0 complex (see Table 3). For CO2@CTF-0 complex, four BCPs are found with three H–O and one N–O bonds. The strongest interaction is observed for N–O bond. Topological values for ∇2ρ, ρ, H(r), and −V(r)/G(r) are 0.032 (a.u.), 0.008 (a.u.), 0.0012 (a.u.), and 0.80 (a.u.), respectively. Individual bond interaction energy (Eint) confirms the absence of hydrogen bonding (strong interactions) in all complexes. The Eint values lie in the range of −0.44 kcal mol−1 to −3.20 kcal mol−1 in all analyte@CTF-0 complexes. In QTAIM analysis, all the topological parameters reveal that analyte@CTF-0 complexes are stabilized through non-covalent interactions.
3.4 SAPT0 analysis
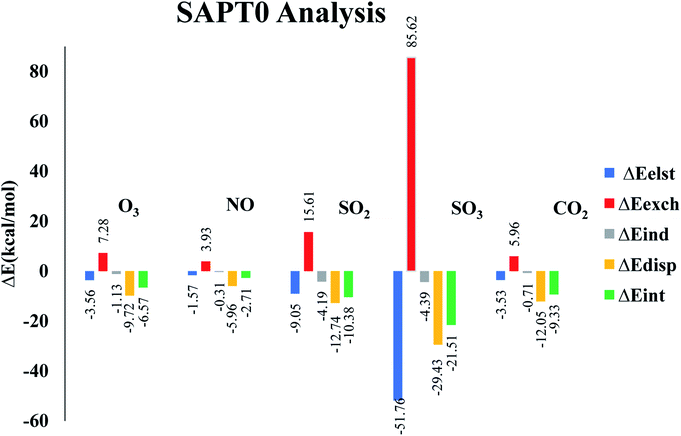
Symmetry adapted perturbation theory (SAPT0) analysis is carried out to fully quantify and understand the nature of interactions between analytes and CTF-0 surface. SAPT0 analysis consists of four interaction energy contributors i.e., induction (ΔEind), exchange (ΔEexch), electrostatic (ΔEelst), and dispersion (ΔEdisp). SAPT0 analysis is a very useful tool for understanding the physical nature of non-covalent bonding. The exchange energy (Eexch) part is responsible for repulsive forces between two interacting components i.e., analyte and surface, while Eest, Eind, and Edis play role in attractive forces. The Edis component attributed towards weak London dispersion forces. The Eelst is crucial in stabilizing complexes, while Eexch component is responsible for destabilizing the complexes.78 Sum of all four components Eind, Eexch, Eelst, and Edis give ESAPT0 (total SAPT0 interaction energy) as presented in eqn (3).79Interaction energy values for SAPT0 analysis of studied analytes@CTF-0 are reported in Table 4. Exchange part (ΔEexch) of SAPT0 analysis is +ive which shows the existence of repulsive force between the filled orbitals of two interacting components. The results also indicate that majority components of energy in SAPT0 analysis are −ive which presents attractive forces between interacting components i.e., analytes and CTF-0 (see Table 4). Trend of ESAPT0 for analytes@CTF-0 complexes show an acceptable agreement with the interaction energy results. ESAPT0 energy values reveals that the highest stabilization energy is obtained for SO3@CTF-0 complex whereas the least value is obtained for O3@CTF-0, consistent with Eint results (see Table 1).
| Analytes@CTF-0 | ΔEelst | % | ΔEexch | ΔEind | % | ΔEdis | % | ΔESAPT0 |
|---|---|---|---|---|---|---|---|---|
| O3@CTF-0 | −3.56 | 24.71 | 7.28 | −1.13 | 7.84 | −9.72 | 67.45 | −6.57 |
| NO@CTF-0 | −1.57 | 20.02 | 3.93 | −0.31 | 3.95 | −5.96 | 76.02 | −2.71 |
| SO2@CTF-0 | −9.05 | 34.83 | 15.61 | −4.19 | 16.12 | −12.74 | 49.04 | −10.38 |
| SO3@CTF-0 | −51.76 | 60.48 | 85.62 | −4.39 | 5.13 | −29.43 | 34.39 | −21.51 |
| CO2@CTF-0 | −3.53 | 21.67 | 5.96 | −0.71 | 4.35 | −12.05 | 73.97 | −9.33 |
The highest contribution of Eexch is observed for SO3@CTF-0 complex (85.62 kcal mol−1) followed by NO@CTF-0, SO2@CTF-0, O3@CTF-0 and CO2@CTF-0 complexes with 3.93, 15.61, 7.28 and 5.96 kcal mol−1, respectively (see Fig. 6). The other SAPT0 energy components for O3@CTF-0 are −3.56 kcal mol−1 (Eelst), −1.13 kcal mol−1 (Eind) and −9.72 kcal mol−1 (Edisp). Results clearly show that major stabilizing factor is the dispersion component (67.45%), while electrostatic and induction components contribute 24.71% 7.84%, respectively. Similar energy trend of SAPT0 components is observed for NO@CTF-0 complex. For SO2@CTF-0 complex, the contribution of Eelst, Eind and Edisp are −9.05 kcal mol−1, −4.19 kcal mol−1 and −12.74 kcal mol−1, respectively. Edisp is a dominant factor for SO2@CTF-0 complex with 49.04% contribution. The trend of SAPT0 energy components of SO2@CTF-0 complex is quite comparable with O3@CTF-0 i.e., Edisp > Eelest > Eind. In case of SO3@CTF-0 complex, Eelest is a dominant component with 60.48% (−51.76 kcal mol−1) contribution, whereas Edisp and Eind are less dominant with 34.39% and 5.13% contribution towards the total SAPT0, respectively. CO2@CTF-0 complex again follows the trend: Edisp > Eelest > Eind with highest contribution of Edisp (73.97%), while Eelest and Eind are less significant with 21.67% and 4.35% contribution, respectively.
Overall order of contribution of SAPT0 components towards total ESAPT0 is Edisp > Eelest > Eind. These SAPT0 component values indicate that the major stabilizing factor is Edisp. The energy trend obtained via SAPT0 analysis show an appreciable agreement with NCI and Eint analysis.
4. Electronic properties
4.1 Natural bond orbital (NBO) and electron density differences (EDD) analysis
EDD analysis was employed to study the isosurfaces of studied analytes@CTF-0 complexes (see Fig. 7) and their NBO charges are presented in Table 5. The charge accumulation in isosurface of analytes@CTF-0 complexes is presented by cyan blue regions, whereas the purple regions show charge depletion or electron deficiency during adsorption process of analytes on the surface (CTF-0). On complexation, the NBO charge values observed on analytes are: 0.007 e− (O3), 0.009 e− (NO), −0.026 e− (SO2), −0.167 e− (SO3), and 0.002 e− (CO2). The NBO values show that in case of SO2 and SO3, charge is transferred from surface (CTF-0) to analytes, whereas in case of O3, NO and CO2, the charge is being transferred from analyte to surface. The highest charge transfer in NBO analysis is observed for SO3@CTF-0 complex, which might be due to the appearance of strong H-bond between O-atom of SO3 and H-atom of CTF-0. Whereas the least charge transfer is observed in case of CO2@CTF-0 complex.| Complexes | LUMO (a.u.) | eV | HOMO (a.u.) | eV | HOMO LUMO band gap | NBO (e−) |
|---|---|---|---|---|---|---|
| O3@CTF-0 | −0.126 | −3.42 | −0.310 | −8.45 | 5.03 | 0.007 |
| NO@CTF-0 | −0.062 | −1.70 | −0.291 | −7.91 | 6.21 | 0.009 |
| SO2@CTF-0 | −0.078 | −2.12 | −0.310 | −8.45 | 6.33 | −0.026 |
| SO3@CTF-0 | −0.081 | −2.20 | −0.313 | −8.51 | 6.32 | −0.167 |
| CO2@CTF-0 | −0.063 | −1.71 | −0.311 | −8.46 | 6.75 | 0.002 |
| CTF-0 | −0.052 | −1.42 | −0.303 | −8.26 | 6.84 |
NBO charges also justify EDD analysis for studied analytes@CTF-0 complexes. In all analytes@CTF-0 complexes, the appearance of green isosurfaces reveal that appreciable charge exchange occurs between analytes and CTF-0 surface.
4.2 Frontier molecular orbital (FMO) and density of states (DOS) analysis
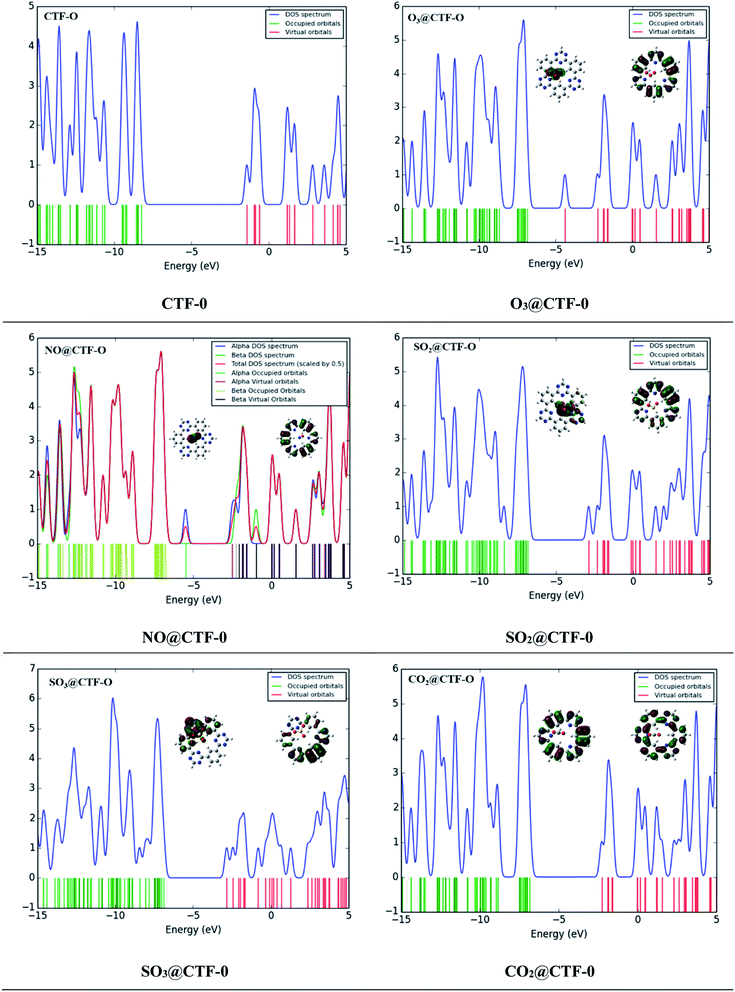
The sensing ability of an electrochemical sensor is solely relying on the behavior of its electronic properties on complexation. Frontier molecular orbitals (FMO) analysis is carried out to disclose the sensing ability of CTF-0 surface towards toxic pollutants. Thus, electronic properties are crucial in understanding sensor's selectivity, sensitivity, and conductivity of surfaces (in our case CTF-0) towards toxic pollutants.44 Higher conductivity is resulted from decreased HOMO–LUMO gaps whereas higher resistivity resulted from increased energy gap. The HOMO–LUMO energies and band gap (EH–L) energies (eV) for bare CTF-0 and complexes (analytes@CTF-0) are given in Table 5.For bare CTF-0 surface, HOMO–LUMO energy gap (EH–L) is 6.84 eV whereas HOMO–LUMO energy values observed are −8.26 eV and −1.42 eV, respectively. On adsorption of analytes, the reduction in HOMO–LUMO energy gap of studied analytes@CTF-0 are 5.03 eV (O3@CTF-0), 6.21 eV (NO@CTF-0), 6.33 eV (SO2@CTF-0), 6.32 eV (SO3@CTF-0), and 6.75 eV (CO2@CTF-0) complexes. Reduction in HOMO–LUMO energy gap (EH–L) of complex results in enhanced sensing ability of surface. Significant decrease in EH–L gap (5.03 eV) has been observed for O3@CTF-0 complex. This decrease in EH–L gap results in better adsorption of O3 analyte on surface, thus making it highly sensitive towards CTF-0. In FMO analysis, HOMO density is mostly localized on analytes, whereas LUMO is observed on CTF-0 surface (see Fig. 8). Electronic excitations result in electron density transfer from analytes to CTF-0 surface, therefore, causes considerable decrease in EH–L gaps in case of O3@CTF-0 (5.03 eV) complex followed by SO3@CTF-0 and SO2@CTF-0 complexes.
Change in conduction properties is the most valuable tool to examine the adsorption behavior of toxic pollutants in gas sensors. A strong correlation exists between the macroscopic property with microscopic property (e.g., conductivity) with density of states (DOS).80–82 DOS analysis of studied analytes@CTF-0 complexes and bare CTF-0 is carried out comparatively to confirm interaction of analytes with CTF-0 surface upon complexation (see Fig. 8). DOS spectrum of O3@CTF-0 reveals the shifting of LUMO from −1.4 eV to −3.42 eV orbital upon complexation. Similarly, in case of other studied complexes, LUMOs are shifted to −1.70, −2.12, −2.20 and −1.71 eV in NO@CTF-0, SO2@CTF-0, SO3@CTF-0 and CO2@CTF-0 complexes, respectively. While EHOMO is originally observed at −8.26 eV, while on complexation these are shifted to −8.45, −7.91, −8.45, −8.51 and −8.46 eV in O3@CTF-0, NO@CTF-0, SO2@CTF-0, SO3@CTF-0 and CO2@CTF-0 complexes, respectively. This shifting of HOMO–LUMO upon complexation reduces the HOMO–LUMO energy gaps (EH–L), consequently accredit to higher conductivity and sensitivity.
5. Recovery response of sensor
Recovery time of a sensor is an important parameter in determination of its superiority over other electrochemical sensors. Higher recovery time will result in surface poisoning, whereas sensor with very small recovery time does not get appreciable time for interaction. Therefore, an ideal sensor should have suitable recovery response time for adsorption of analyte. Recovery times of CTF-0 were measured at three different temperatures i.e., 298 K, 350 K and 400 K. Theoretically, we have measured recovery time of CTF-0 sensor via thermal effect by employing equation from “transition state theory”,83,80 which can be written as:
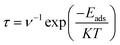 | (7) |
In eqn (7), τ denotes recovery time, Eads is for interaction energy, T is for temperature, K denotes Boltzmann constant and ν is showing attempt frequency. The value of attempt frequency (ν) has already been reported and is 1012 s−1.81,82 K is constant and its value is 1.99 × 10−3 kcal mol−1. Greater Eads value in negative will prolong the recovery time exponentially (from eqn (7)). The recovery time for studied analytes are calculated at three different temperatures on CTF-0 surface. At room temperature, 9.72 × 10−9 s of recovery time is observed for the O3 analyte desorption from CTF-0 surface. It is observed that by rising temperature the recovery time further decreases, for example at 350 K and 400 K, the recovery times observed are 2.48 × 10−9 s and 9.35 × 10−10 s, respectively. Whereas for the desorption of NO, SO2, SO3, and CO2 analytes from CTF-0 at room temperature, the values for recovery time are 4.74 × 10−10 s, 1.47 × 10−7 s, 3.39 × 10−3 s, and 4.87 × 10−9 s, respectively. Already reported optimal accumulation times for C2N surface were 7.8 × 10−4 s and 6.1 × 10−5 s at 350 K and 400 K, respectively.74 Similarly, in literature, optimal recovery time of 200 s is observed for CNTs-GO surface indicating that the surface had the ability to accumulate the analytes effectively.83 The small recovery time values reveal the potential of CTF-0 surface as a fascinating candidate for sensing applications. Additionally, it has been revealed that for all studied analytes rise in temperature result in decline of recovery time (see Table S1†) because the process of desorption gets facilitated by increase in temperature.
6. Conclusions
Herein, we explored 2-D surface CTF-0 as an electrochemical sensor against industrial energy analysis clearly indicates that all the analytes are physiosorbed onto the CTF-0 surface. To get further insight into non-covalent interactions, we performed NCI, SAPT0, and QTAIM analysis. In NCI analysis, the appearance of isosurfaces confirms the existence of intermolecular attractive forces between analytes and CTF-0 surface. Furthermore, SAPT0 analysis unveiled that dispersion interactions are dominant, and overall order of contribution of SAPT0 components towards total ESAPT0 is Edisp > Eelest > Eind. QTAIM analysis further confirms the physisorption of analytes on CTF-0 surface through number of BCPs. The dispersion interactions revealed through the values of ρ, ∇2ρ and H(r) are in accordance with SAPT0 results. Significant modifications in the electronic properties are observed through FMO analysis for all complexes. The highest decrease in HOMO–LUMO energy gap is observed for O3@CTF-0 as compared to bare CTF-0 surface, which indicates the sensitivity of CTF-0 for O3 analyte. Moreover, the ability of CTF-0 to detect industrial pollutants is further explored using NBO charge transfer, EDD and DOS analysis. These properties represented that conductivity is improved with band gap reduction upon complexation. These findings propose the CTF-0 as an efficient electrochemical sensor for the detection of industrial pollutants.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author from King Khalid University extend his appreciation to Deanship of Scientific Research at King Khalid University for funding the work through Research Project (RGP.2/156/42). R. L. is grateful to the Deutsche Forschungsgemeinschaft (DFG) for financing the project LU 506/12-2 (grant No. 6471990).References
- R. B. Onyancha, et al., A systematic review on the detection and monitoring of toxic gases using carbon nanotube-based biosensors, Sens. Bio-Sens. Res., 2021, 34, 100463 CrossRef.
- A. Mir and A. Khachane, Sensing harmful gases in industries using IoT and WSN, in 2018 Fourth International Conference on Computing Communication Control and Automation (ICCUBEA), IEEE, 2018 Search PubMed.
- Q. Sun, et al., In2O3 as a promising catalyst for CO2 utilization: A case study with reverse water gas shift over In2O3, Greenhouse Gases: Sci. Technol., 2014, 4(1), 140–144 CrossRef CAS.
- N. Promthong, et al., Transition metal-doped graphene nanoflakes for CO and CO 2 storage and sensing applications: a DFT study, Struct. Chem., 2020, 31(6), 2237–2247 CrossRef CAS.
- J. Sun, et al., A colorimetric and fluorescent chemosensor for the highly sensitive detection of CO2 gas: experiment and DFT calculation, Sens. Actuators, B, 2016, 233, 76–82 CrossRef CAS.
- A. S. Rad and K. Ayub, O3 and SO2 sensing concept on extended surface of B12N12 nanocages modified by Nickel decoration: a comprehensive DFT study, Solid State Sci., 2017, 69, 22–30 CrossRef CAS.
- A. S. Rad, et al., Study on the adsorption properties of O3, SO2, and SO3 on B-doped graphene using DFT calculations, J. Solid State Chem., 2016, 237, 204–210 CrossRef CAS.
- A. Abbasi, The adsorption of sulfur dioxide and ozone molecules on boron nitride nanotubes: A DFT study, J. Water Environ. Nanotechnol., 2019, 4(2), 147–156 CAS.
- P. K. Rao and S. P. Gejji, Molecular insights for the HFO-1345fz + X (X= Cl, O3 or NO3) reaction and fate of alkoxy radicals initiated by Cl: DFT investigations, J. Fluorine Chem., 2017, 204, 65–75 CrossRef CAS.
- V. Oison, et al., Experimental and ab initio study of the O3 detection at the CuO (111) surface, Surf. Sci., 2014, 622, 44–50 CrossRef CAS.
- I. Stassen, et al., An updated roadmap for the integration of metal–organic frameworks with electronic devices and chemical sensors, Chem. Soc. Rev., 2017, 46(11), 3185–3241 RSC.
- O. Yildirim and B. Derkus, Triazine-based 2D covalent organic frameworks improve the electrochemical performance of enzymatic biosensors, J. Mater. Sci., 2020, 55(7), 3034–3044 CrossRef CAS.
- S. Chen, et al., Electrochemical Sensors Based on Covalent Organic Frameworks: A Critical Review, Front. Chem., 2020, 8, 1082 Search PubMed.
- F. Y. Yi, et al., Chemical sensors based on metal–organic frameworks, ChemPlusChem, 2016, 81(8), 675–690 CrossRef CAS PubMed.
- E. Troschke, et al., Mechanistic Insights into the Role of Covalent Triazine Frameworks as Cathodes in Lithium–Sulfur Batteries, Batteries Supercaps, 2020, 3(10), 1069–1079 CrossRef CAS.
- F. Niu, et al., Covalent triazine-based frameworks for NH3 gas sensing at room temperature, Sens. Actuators, B, 2020, 321, 128513 CrossRef CAS.
- D.-Y. Wang, et al., A fluorescent covalent triazine framework consisting of donor–acceptor structure for selective and sensitive sensing of Fe3+, Eur. Polym. J., 2021, 147, 110297 CrossRef CAS.
- Y. Tang, et al., A new sensing material design based on chemically passivated phosphorene/porous two-dimensional polymer: Highly sensitive and selective detection of NO2, Sens. Actuators, B, 2021, 329, 129233 CrossRef CAS.
- X. Liu, et al., Recent advances in covalent organic frameworks (COFs) as a smart sensing material, Chem. Soc. Rev., 2019, 48(20), 5266–5302 RSC.
- L. Chen, et al., Applications of covalent organic frameworks in analytical chemistry, TrAC, Trends Anal. Chem., 2019, 113, 182–193 CrossRef CAS.
- M. Y. Mehboob, et al., Designing of benzodithiophene core-based small molecular acceptors for efficient non-fullerene organic solar cells, Spectrochim. Acta, Part A, 2021, 244, 118873 CrossRef CAS PubMed.
- M. Y. Mehboob, et al., Designing N-phenylaniline-triazol configured donor materials with promising optoelectronic properties for high-efficiency solar cells, Comput. Theor. Chem., 2020, 1186, 112908 CrossRef CAS.
- M. Y. Mehboob, et al., Quantum chemical design of near-infrared sensitive fused ring electron acceptors containing selenophene as π-bridge for high-performance organic solar cells, J. Phys. Org. Chem., 2021, e4204 CAS.
- M. Y. Mehboob, et al., Designing N-phenylaniline-triazol configured donor materials with promising optoelectronic properties for high-efficiency solar cells, Comput. Theor. Chem., 2020, 1186, 112908 CrossRef CAS.
- C. Krishnaraj, et al., Covalent triazine frameworks–a sustainable perspective, Green Chem., 2020, 22(4), 1038–1071 RSC.
- H. Zhang, et al., DFT calculations of the synergistic effect of λ-MnO2/graphene composites for electrochemical adsorption of lithium ions, Phys. Chem. Chem. Phys., 2019, 21(15), 8133–8140 RSC.
- J. J. Jarju, et al., Covalent Organic Framework Composites: Synthesis and Analytical Applications, Molecules, 2020, 25(22), 5404 CrossRef CAS PubMed.
- Y. Tang, et al., Phosphorus-doped molybdenum carbide/MXene hybrid architectures for upgraded hydrogen evolution reaction performance over a wide pH range, Chem. Eng. J., 2021, 423, 130183 CrossRef CAS.
- M. Liu, et al., Covalent triazine frameworks: synthesis and applications, J. Mater. Chem. A, 2019, 7(10), 5153–5172 RSC.
- P. Katekomol, et al., Covalent triazine frameworks prepared from 1,3,5-tricyanobenzene, Chem. Mater., 2013, 25(9), 1542–1548 CrossRef CAS.
- E. Troschke, et al., Salt templated synthesis of hierarchical covalent triazine frameworks, Microporous Mesoporous Mater., 2017, 239, 190–194 CrossRef CAS.
- M. Xu, et al., Ratiometric electrochemical sensing and biosensing based on multiple redox-active state COFDHTA-TTA, Sens. Actuators, B, 2019, 281, 1009–1015 CrossRef CAS.
- T. Zhang, et al., Covalent organic framework as a novel electrochemical platform for highly sensitive and stable detection of lead, Talanta, 2018, 188, 578–583 CrossRef CAS PubMed.
- K. Yang, et al., Triazine-based two-dimensional organic polymer for selective NO2 sensing with excellent performance, ACS Appl. Mater. Interfaces, 2019, 12(3), 3919–3927 CrossRef PubMed.
- Y. Tang, et al., A thiadiazole-based covalent triazine framework nanosheet for highly selective and sensitive primary aromatic amine detection among various amines, J. Mater. Chem. A, 2020, 8(32), 16542–16550 RSC.
- B. Ball, et al., Computational investigation on the electronic structure and functionalities of a thiophene-based covalent triazine framework, ACS Omega, 2019, 4(2), 3556–3564 CrossRef CAS PubMed.
- A. A. Khan, R. Ahmad and I. Ahmad, Density functional theory study of emerging pollutants removal from water by covalent triazine based framework, J. Mol. Liq., 2020, 309, 113008 CrossRef CAS.
- M. Frisch, F. Clemente, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino and G. Zhe, Gaussian 09, Revision A. 01, 2009 Search PubMed.
- S. U. D. Shamim, et al., Theoretical investigation of emodin conjugated doped B12N12 nanocage by means of DFT, QTAIM and PCM analysis, Phys. E, 2022, 136, 115027 CrossRef.
- M. Yar and K. Ayub, Expanding the horizons of covalent organic frameworks to electrochemical sensors; A case study of CTF-FUM, Microporous Mesoporous Mater., 2020, 300, 110146 CrossRef CAS.
- S. Hussain, et al., Zinc-doped boron phosphide nanocluster as efficient sensor for SO2, J. Chem., 2020, 2020, 1–12 Search PubMed.
- A. Tenderholt, K. Langner and N. O'Boyle, A library for package-independent computational chemistry algorithms, J. Comput. Chem., 2008, 839–845 Search PubMed.
- N. M. O'boyle, A. L. Tenderholt and K. M. Langner, Cclib: a library for package-independent computational chemistry algorithms, J. Comput. Chem., 2008, 29(5), 839–845 CrossRef PubMed.
- M. T. Baei, et al., Al12N12 nanocage as a potential sensor for phosgene detection, Can. J. Chem., 2014, 92(7), 605–610 CrossRef CAS.
- N. S. Venkataramanan, A. Suvitha and Y. Kawazoe, Intermolecular interaction in nucleobases and dimethyl sulfoxide/water molecules: A DFT, NBO, AIM and NCI analysis, J. Mol. Graphics Modell., 2017, 78, 48–60 CrossRef CAS PubMed.
- S. Pan, et al., Selectivity in gas adsorption by molecular cucurbit [6] uril, J. Phys. Chem. C, 2016, 120(26), 13911–13921 CrossRef CAS.
- E. R. Johnson, et al., Revealing noncovalent interactions, J. Am. Chem. Soc., 2010, 132(18), 6498–6506 CrossRef CAS PubMed.
- G. G. Mironov, et al., Revealing equilibrium and rate constants of weak and fast noncovalent interactions, Anal. Chem., 2011, 83(6), 2364–2370 CrossRef CAS PubMed.
- R. Laplaza, et al., NCIPLOT and the analysis of noncovalent interactions using the reduced density gradient, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11(2), e1497 CAS.
- T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33(5), 580–592 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, VMD: visual molecular dynamics, J. Mol. Graphics, 1996, 14(1), 33–38 CrossRef CAS PubMed.
- M. Jabłoński and M. Palusiak, Nature of a Hydride–Halogen Bond. A SAPT-, QTAIM-, and NBO-Based Study, J. Phys. Chem. A, 2012, 116(9), 2322–2332 CrossRef PubMed.
- J. M. Turney, et al., Psi4: an open-source ab initio electronic structure program, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(4), 556–565 CAS.
- A. Mella and D. Cortés-Arriagada, Computational quest of adsorbents based on doped graphene nanosheets for phosgene uptake, and analysis of the co-adsorption phenomena, Synth. Met., 2019, 252, 142–150 CrossRef CAS.
- L. Yang, et al., A novel covalent triazine framework developed for efficient determination of 1-naphthol in water, Environ. Sci. Pollut. Res., 2021, 1–10 Search PubMed.
- Y. Lee, et al., Multifunctional and recyclable TiO2 hybrid sponges for efficient sorption, detection, and photocatalytic decomposition of organic pollutants, J. Ind. Eng. Chem., 2019, 73, 328–335 CrossRef CAS.
- Y. Sun, et al., A selective molecularly imprinted electrochemical sensor with GO@COF signal amplification for the simultaneous determination of sulfadiazine and acetaminophen, Sens. Actuators, B, 2019, 300, 126993 CrossRef CAS.
- T. A. Saleh, G. Fadillah and O. A. Saputra, Nanoparticles as components of electrochemical sensing platforms for the detection of petroleum pollutants: A review, TrAC, Trends Anal. Chem., 2019, 118, 194–206 CrossRef CAS.
- G. Hernandez-Vargas, et al., Electrochemical biosensors: A solution to pollution detection with reference to environmental contaminants, Biosensors, 2018, 8(2), 29 CrossRef PubMed.
- A. V. Bavykina, et al., Facile method for the preparation of covalent triazine framework coated monoliths as catalyst support: Applications in c1 catalysis, ACS Appl. Mater. Interfaces, 2017, 9(31), 26060–26065 CrossRef CAS PubMed.
- Y. Zhang and S. Jin, Recent advancements in the synthesis of covalent triazine frameworks for energy and environmental applications, Polymers, 2019, 11(1), 31 CrossRef PubMed.
- N. Mokhtari, et al., Imine-based covalent triazine framework: Synthesis, characterization, and evaluation its adsorption, Mater. Lett., 2020, 263, 127221 CrossRef CAS.
- M. J. Bojdys, et al., Rational extension of the family of layered, covalent, triazine-based frameworks with regular porosity, Adv. Mater., 2010, 22(19), 2202–2205 CrossRef CAS PubMed.
- Y. Wang, et al., Two-dimensional covalent triazine framework membrane for helium separation and hydrogen purification, ACS Appl. Mater. Interfaces, 2016, 8(13), 8694–8701 CrossRef CAS PubMed.
- J. S. Lim and G. Kim, First-principles modeling of water permeation through periodically porous graphene derivatives, J. Colloid Interface Sci., 2019, 538, 367–376 CrossRef CAS PubMed.
- G. Wang, et al., Newly designed covalent triazine framework based on novel N-heteroaromatic building blocks for efficient CO2 and H2 capture and storage, ACS Appl. Mater. Interfaces, 2017, 10(1), 1244–1249 CrossRef PubMed.
- P. Sruthy, V. Nagarajan and R. Chandiramouli, Interaction studies of kidney biomarker volatiles on black phosphorene nanoring: a first-principles investigation, J. Mol. Graphics Modell., 2020, 97, 107566 CrossRef CAS PubMed.
- D. Wei, et al., Adsorption properties of hydrated Cr3+ ions on Schiff-base covalent organic frameworks: A DFT study, Chem.–Asian J., 2020, 15(7), 1140–1146 CrossRef CAS PubMed.
- H. Ullah, et al., DFT study of polyaniline NH3, CO2, and CO gas sensors: comparison with recent experimental data, J. Phys. Chem. C, 2013, 117(45), 23701–23711 CrossRef CAS.
- M. Yar, et al. , Carbon nitride 2-D surface as a highly selective electrochemical sensor for V-series nerve agents, J. Mol. Liq., 2020, 311, 113357 CrossRef CAS.
- E. Espinosa, E. Molins and C. Lecomte, Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities, Chem. Phys. Lett., 1998, 285(3–4), 170–173 CrossRef CAS.
- D. Cremer and E. Kraka, Chemical bonds without bonding electron density—does the difference electron-density analysis suffice for a description of the chemical bond?, Angew. Chem., Int. Ed. Engl., 1984, 23(8), 627–628 CrossRef.
- K. Yuan, et al., Phthalazinone structure-based covalent triazine frameworks and their gas adsorption and separation properties, RSC Adv., 2016, 6(15), 12009–12020 RSC.
- E. Pastorczak and C. Corminboeuf, Perspective: Found in translation: Quantum chemical tools for grasping non-covalent interactions, J. Chem. Phys., 2017, 146(12), 120901 CrossRef PubMed.
- A. Varadwaj, H. M. Marques and P. R. Varadwaj, Is the fluorine in molecules dispersive? Is molecular electrostatic potential a valid property to explore fluorine-centered non-covalent interactions?, Molecules, 2019, 24(3), 379 CrossRef PubMed.
- Y. Gui, et al., The sensing mechanism of N-doped SWCNTs toward SF6 decomposition products: A first-principle study, Appl. Surf. Sci., 2018, 440, 846–852 CrossRef CAS.
- Y. Zhu, et al., Rapid exfoliation of layered covalent triazine-based frameworks into N-doped quantum dots for the selective detection of Hg2+ ions, J. Mater. Chem. A, 2017, 5(19), 9272–9278 RSC.
- K. KASORNMALA, V. AMORNKITBAMRUNG and P. SREPUSHARAWOOT, Effects of Organic Linkers on Energy Gaps of Covalent Based Triazine Frameworks, Walailak J. Sci. Technol., 2018, 15(11), 811–817 CrossRef.
- M. Samadizadeh, A. A. Peyghan and S. F. Rastegar, Sensing behavior of BN nanosheet toward nitrous oxide: a DFT study, Chin. Chem. Lett., 2015, 26(8), 1042–1045 CrossRef CAS.
- M. Rakib Hossain, et al., First-principles study of the adsorption of chlormethine anticancer drug on C24, B12N12 and B12C6N6 nanocages, Comput. Theor. Chem., 2021, 1197, 113156 CrossRef CAS.
- S. Peng, et al., Ab initio study of CNT NO2 gas sensor, Chem. Phys. Lett., 2004, 387(4–6), 271–276 CrossRef CAS.
- L. Bai and Z. Zhou, Computational study of B-or N-doped single-walled carbon nanotubes as NH3 and NO2 sensors, Carbon, 2007, 45(10), 2105–2110 CrossRef CAS.
- K. Deng, et al., A comparative study of different Fe3O4-functionalized carbon-based nanomaterials for the development of electrochemical sensors for bisphenol A, Anal. Methods, 2017, 9(37), 5509–5517 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra08738j |
| ‡ Sehrish Sarfaraz and Muhmmad Yar have equal contribution for first authorship. |
| This journal is © The Royal Society of Chemistry 2022 |