Open Access Article
Open Access ArticleLanthanide induced variability in localised CoII geometries of four triangular L3Co3IILnIII complexes†
Tyson N. Dais a,
Rina Takanob,
Takayuki Ishida
a,
Rina Takanob,
Takayuki Ishida b and
Paul G. Plieger
b and
Paul G. Plieger *a
*a
aSchool of Natural Sciences, Massey University, Private Bag 11 222, Palmerston North, New Zealand. E-mail: p.g.plieger@massey.ac.nz
bDepartment of Engineering Science, Graduate School of Informatics and Engineering, The University of Electro-Communication, 1-5-1 Chofugaoka, Chofu, Tokyo 182-8585, Japan
First published on 10th February 2022
Abstract
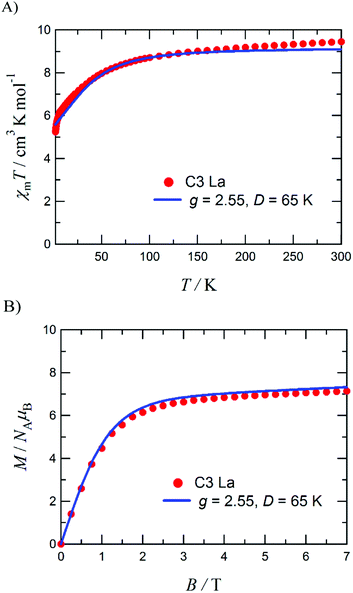
Four tetranuclear heterobimetallic triangle complexes [L3Co3Dy(NO3)2(H2O)(MeOH)5](NO3) (C1), [L3Co3Gd(NO3)3(MeOH)4] (C2), [L3Co3La(NO3)2(H2O)6](NO3)(H2O) (C3), and [L3Co3TbCl(NO3)2(H2O)0.5(MeOH)3.5] (C4), where H2L = 1,4-bisformylnaphthalene-2,3-diol, have been synthesised and structurally characterised. Each complex crystallises with a complete molecule in the asymmetric unit (Z′ = 1) and displays near perfect octahedrality in two out of three CoII centres. The third CoII ion assumes a different coordination geometry in each complex: six-coordinate octahedral in C1, six-coordinate with a distortion towards trigonal prismatic in C2, five-coordinate trigonal bipyramidal in C3, and five-coordinate square pyramidal in C4; which has been attributed to increasing lanthanide cation size, coupled with a non-macrocyclic coordination environment. Continuous Shape Measurement (CShM) calculations and octahedral distortion parameter calculations were performed, using the SHAPE and OctaDist software packages, respectively, in order to aid in the assessment of each metal centre's local coordination geometry. The preliminary magnetic investigation of C3 found χmT = 9.4 cm3 K mol−1 at 300 K and M = 7.1 μB at 1.8 K, which are approximately two thirds the maximum theoretical values for three CoII ions and indicates the presence of a relatively large zero-field splitting parameter (D/kB = 65 K) operative in each CoII ion rather than exchange coupling between the CoII centres.
Introduction
Metal ions have a rich history in aiding otherwise untenable chemical transformations and play a pertinent role in the self-assembly process of many molecular clusters. Of particular importance, is the use of metals to template the formation of macrocycles and interlocked molecules in a controlled and predictable manner.1–8 While mononuclear and homometallic polynuclear complexes are among the most common, there is a great interest in heterometallic complexes with predictable nuclearities and topologies. Heterometallic polynuclear complexes have been explored in many fields of science from antibacterial agents9–11 and molecular machines,12–15 to heterogenous catalysts,16–19 molecular magnets,20–25 and spintronic devices.26–30A hexa-phenolate macrocycle, templated with an all-in-plane tetranuclear Zn3LaO6 3d/4f core, was first reported by Nabeshima.31 This metal cation templated route provided a vast improvement in yield over their previous metal-free attempts to perform 3 + 3 Schiff base condensations of 1,4-diformylbenzene-2,3-diol with various diamine linkers.32 This same method involving templated macrocyclisation was later extended to include various combinations of trivalent lanthanide ions with ZnII,33–40 CuII,41–46 NiII,47 or CoII centres.48 Families of triangular macrocyclic complexes containing ZnII, CuII, and NiII with a variety of LnIII have been investigated by Brooker et al. for their magnetic properties.33,34,41–47 More recently, Mashima and Nozaki et al. have prepared macrocyclic complexes with a CoII3LnIIIO6 core for the catalysis of copolymerisation of CO2 and cyclohexene oxide.
While some of the complexes discussed in these reports have been structurally characterised, many have not. In particular, the aldehyde containing intermediate complexes which self-assemble prior to condensation/macrocyclisation have only been successfully isolated, with full structural characterisation reported, for three older examples (Refcodes: HICLIP31 and XUVVIV/XUVVOB47) and four recently reported Ni3Ln examples (WARKIN, WARKEJ, WARKOT, and WARKUZ).49
MacLachlan et al.50 established a method to obtain heptanuclear ZnII clusters from the reaction of a pre-formed macrocyclic hexa-phenolate ligand with seven equivalents of Zn(OAc)2·2H2O, which was later shown to be capable of forming the Zn3LaO6 type complex by Nabeshima et al.51 Nabeshima further showed that the 3 + 3 condensation reaction can be carried out in the presence of two equivalents of zinc per equivalent dialdehyde, yielding a hexanuclear complex contained within the expected macrocycle.31
While following our interest in exploring the magneto–structural correlations of non-macrocyclic dialdehyde ligated TM3Ln type complexes, four CoII3Ln complexes have been synthesised with notably different CoII coordination geometries. We now report the self-assembly and structural characterisation of four non-macrocyclic triangle complexes containing CoII3LnIIIO6 cores, each of which features two octahedrally coordinated CoII centres and a third CoII featuring a variation in geometry. Preliminary magnetic measurements have been carried out on the LaIII containing complex, C3, and are briefly discussed.
Results and discussion
The four L3Co3Ln complexes reported here were prepared from a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture of methanolic solution of cobaltous nitrate, a lanthanide salt, and the relatively simple ligand, 1,4-bisformylnaphthalene-2,3-diol (H2L). Addition of the cobalt solution caused rapid dissolution of the ligand suspension regardless of order, the same effect was not observed when the lanthanide solution was added prior to the cobalt solution. The reaction mixture required stirring overnight as the reaction proceeded through a (non-product) precipitation stage which redissolved upon further stirring. The lanthanide salts utilised were Dy(NO3)3·6H2O (C1), Gd(NO3)3·6H2O (C2), La(OAc)3·6H2O (C3), and TbCl3·6H2O (C4). While these complexes initially appeared to be stable in air, the crystallinity of some samples was observed to be fragile to desolvation.
3 mixture of methanolic solution of cobaltous nitrate, a lanthanide salt, and the relatively simple ligand, 1,4-bisformylnaphthalene-2,3-diol (H2L). Addition of the cobalt solution caused rapid dissolution of the ligand suspension regardless of order, the same effect was not observed when the lanthanide solution was added prior to the cobalt solution. The reaction mixture required stirring overnight as the reaction proceeded through a (non-product) precipitation stage which redissolved upon further stirring. The lanthanide salts utilised were Dy(NO3)3·6H2O (C1), Gd(NO3)3·6H2O (C2), La(OAc)3·6H2O (C3), and TbCl3·6H2O (C4). While these complexes initially appeared to be stable in air, the crystallinity of some samples was observed to be fragile to desolvation.
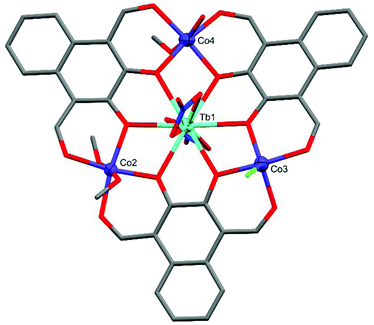
Each lanthanide is bound equatorially in an O6 environment by three catecholate (equivalent to six phenolate) groups in an approximately planar arrangement, selected distances and angles can be found in Table 1. The prearrangement of the three ligand molecules around the lanthanide centre brings the aldehyde groups into proximity akin to the imine nitrogens of a salen moiety (Fig. 1). The two adjacent aldehyde and phenolate groups form an O4 environment to bind to the equatorial sites of the cobalt centres while the remaining axial coordination sites of each metal are bound by a mixture of solvent molecules or anions. Complexes C1–C3 all crystallised in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , while complex C4 crystallised in the monoclinic space group C2/c. Only C1 and C2 contain three 6-coordinate CoII centres, with C3 and C4 each containing one heavily distorted 5-coordinate CoII centre. Of the four structurally characterised CoII3Ln type complexes reported by Mashima and Nozaki et al.48 all but one CoII centre has near perfect octahedral geometry. A single CoII ion in the Co3Ce complex features a near square-pyramidal geometry. In order to assess the local coordination geometry of each CoII centre, Continuous Shape Measurement (CShM) calculations52,53 were employed alongside octahedral distortion calculations (〈D〉, Δ, ζ, and Σ) using the OctaDist software package,54 the values of these parameters can be found in Table 2.
, while complex C4 crystallised in the monoclinic space group C2/c. Only C1 and C2 contain three 6-coordinate CoII centres, with C3 and C4 each containing one heavily distorted 5-coordinate CoII centre. Of the four structurally characterised CoII3Ln type complexes reported by Mashima and Nozaki et al.48 all but one CoII centre has near perfect octahedral geometry. A single CoII ion in the Co3Ce complex features a near square-pyramidal geometry. In order to assess the local coordination geometry of each CoII centre, Continuous Shape Measurement (CShM) calculations52,53 were employed alongside octahedral distortion calculations (〈D〉, Δ, ζ, and Σ) using the OctaDist software package,54 the values of these parameters can be found in Table 2.
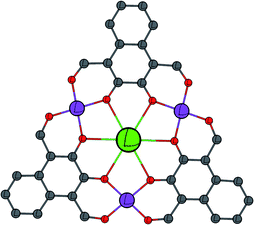 | ||
| Fig. 1 Schematic showing the general metal–ligand connectivity of the complexes reported in this work. C = grey, O = red, CoII = purple, and LnIII = green. | ||
| Distance/Å | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
a Omethanol (C1) and Owater (C3).b Anion is μ1-NO3 (C1), μ2-NO3 (C2), μ1-Cl (C4).c The Co2 cap in C4 has been modelled as a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 disordered methanol/water cap.d The O4 plane corresponds to the least-squares plane of the four ligand-based (equatorial) donors in the idealised octahedral binding environment. 1 disordered methanol/water cap.d The O4 plane corresponds to the least-squares plane of the four ligand-based (equatorial) donors in the idealised octahedral binding environment. |
||||
| LnIII–Ophenol | 2.393(8)–2.460(8) | 2.410(5)–2.552(6) | 2.567(9)–2.657(8) | 2.439(5)–2.546(5) |
| LnIII–Onitrate | 2.450(8)–2.459(7) | 2.455(6)–2.498(5) | 2.625(8)–2.801(9) | 2.438(6)–2.494(5) |
| LnIII–Osolventa | 2.339(7) | — | 2.576(9) | — |
| CoII–Ophenol | 1.980(8)–2.036(9) | 1.989(5)–2.011(5) | 1.984(8)–2.046(8) | 1.984(5)–2.045(5) |
| CoII–Oformyl | 1.996(9)–2.044(10) | 1.990(8)–2.046(5) | 1.982(9)–2.044(9) | 1.988(5)–2.025(4) |
| CoII–Owater | 2.148(9) | — | 1.922(13)–2.177(8) | 2.195c |
| CoII–Omethanol | 2.133(8)–2.191(8) | 2.108(6)–2.178(6) | — | 2.133(6)–2.200(20)c |
| CoII–Anionb | 2.166(8) | 2.130(5)–2.206(6) | — | 2.292(2) |
| Av. CoII–CoII | 6.248(4) | 6.365(2) | 6.392(3) | 6.353(2) |
| Av. CoII–LnIII | 3.610(3) | 3.676(2) | 3.706(2) | 3.671(1) |
| Min. LnIII–LnIII | 10.221(2) | 10.625(2) | 9.598(1) | 10.540(1) |
| LnIII–Co3 plane | 0.139(2) | 0.091(1) | 0.333(1) | 0.143(1) |
| Co4–O4 planed | 0.015(5) | 0.648(3) | 0.609(5) | 0.581(3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Angle/° | ||||
| CoII–O–LnIII | 106.2(4)–109.3(4) | 106.2(2)–111.0(2) | 104.1(3)–108.5(3) | 107.0(2)–109.2(2) |
Molecular structures
Crystal structure and refinement details for C1–C4 can be found in Table S1 of the ESI.†The crystal structure of C1 (Fig. 2) shows the complex takes a non-planar arrangement and is the only complex reported here to contain three near perfect six-coordinate octahedral CoII centres with CShM(OC-6)/Σ values of 1.586/66.70 (Co2), 1.634/68.80 (Co3), and 0.733/38.29 (Co4).
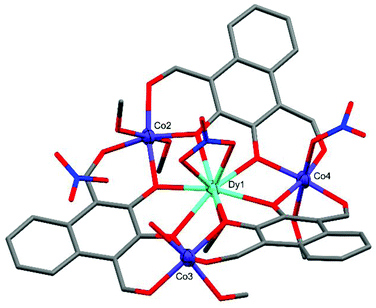 | ||
| Fig. 2 X-ray crystal structure of C1. Thermal ellipsoids of metal atoms shown at 70% probability. H atoms have been omitted for clarity. C = grey, O = red, N = blue. | ||
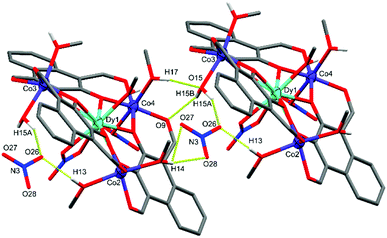
The DyIII centre of C1 occupies a nine-coordinate environment where the three non-equatorial donors are an axially coordinated methanol and an axially coordinated μ2-NO3 group, binding opposite sides of the Co3 plane. The Co2 and Co3 cobalt centres of C1 are axially capped with solvent type molecules, whereas Co4 features an axially coordinated μ1-NO3 group as well as a methanol cap. In order to achieve charge neutrality, the total metal charge of +9 (Dy3+ and 3 × Co2+) is partially balanced by 3 × L2− and the two coordinated NO3− groups, with the final negative charge originating from a non-coordinated NO3− anion, giving an overall formula of [L3Co3Dy(NO3)2(H2O)(MeOH)5](NO3). C1 features extensive intermolecular and intra-complex hydrogen bonding (Fig. 3). The non-coordinated nitrate group forms strong hydrogen bonds from its O26 oxygen to a methanol cap of Co2 (O26⋯H13 = 1.989(10) Å) and the water cap of Co3 (O26⋯H15A = 1.904(10) Å). A symmetry generated complex provides two further hydrogen bonds, stemming from the H14* proton of a methanol cap of Co2* (O27⋯H14* = 2.496(9) Å, and O28⋯H14* = 2.100(8) Å). There are also two strong hydrogen bonds formed between the two units complex by the methanol cap of Co4* with the water cap of Co3 (O15⋯H17* = 2.008(7) Å), and the proton of the Co3 water cap acting as a hydrogen bond donor to the aldehyde binding Co4* in the symmetry generated molecule (O9*⋯H15B = 2.078(8) Å).
| OC-6a | 〈D〉 | Δ | ζ | Σ | |
|---|---|---|---|---|---|
| a Values near or below one indicate minimal distortion from the ideal geometry.b C2–Co4 is distorted towards D3h trigonal prismatic.c The octahedral distortion parameters calculated by OctaDist are defined as: 〈D〉, the average M–L bond length; Δ, the average of the deviations of M–L bond lengths from 〈D〉; ζ, the sum of the deviation of bond lengths from 〈D〉; and Σ, the sum of deviations of the 12 cis angles from 90°. | |||||
| C1–Co2 | 1.586 | 2.0693 | 0.3499 | 0.00091 | 66.701 |
| C1–Co3 | 1.634 | 2.0690 | 0.2849 | 0.00061 | 68.799 |
| C1–Co4 | 0.733 | 2.0589 | 0.4800 | 0.00174 | 38.287 |
| C2–Co2 | 1.263 | 2.0529 | 0.3597 | 0.00106 | 59.272 |
| C2–Co3 | 0.301 | 2.0522 | 0.3569 | 0.00095 | 29.476 |
| C2–Co4b | 4.914 | 2.0612 | 0.4273 | 0.00154 | 115.791 |
| C3–Co2 | 0.355 | 2.0683 | 0.3929 | 0.00114 | 28.613 |
| C3–Co3 | 0.605 | 2.0553 | 0.2738 | 0.00073 | 43.621 |
| C4–Co2 | 0.738 | 2.0545 | 0.3429 | 0.00089 | 43.664 |
| C4–Co4 | 0.947 | 2.0595 | 0.4181 | 0.00137 | 56.121 |
Complex C2 crystallised in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with the formula [L3Co3Gd(MeOH)4(NO3)3] (Fig. 4). C2 is significantly more planar than C1 and features two near perfectly octahedral cobalt centres (Co2 and Co3) each axially coordinated by two methanol molecules with CShM(OC-6)/Σ values of 1.263/59.27 (Co2) and 0.301/29.48 (Co3). The remaining cobalt centre, Co4, is also six-coordinate but is capped by a μ2-NO3 group leading to a heavily distorted octahedral geometry tending towards D3h trigonal prismatic with CShM(OC-6, TPR-6)/Σ values of 4.914, 9.173/115.79. At the heart of C2 is a ten-coordinate GdIII ion, capped either side of the Co3 plane by a μ2-NO3 group, with a pseudo-hexagonal bipyramidal coordination geometry.
with the formula [L3Co3Gd(MeOH)4(NO3)3] (Fig. 4). C2 is significantly more planar than C1 and features two near perfectly octahedral cobalt centres (Co2 and Co3) each axially coordinated by two methanol molecules with CShM(OC-6)/Σ values of 1.263/59.27 (Co2) and 0.301/29.48 (Co3). The remaining cobalt centre, Co4, is also six-coordinate but is capped by a μ2-NO3 group leading to a heavily distorted octahedral geometry tending towards D3h trigonal prismatic with CShM(OC-6, TPR-6)/Σ values of 4.914, 9.173/115.79. At the heart of C2 is a ten-coordinate GdIII ion, capped either side of the Co3 plane by a μ2-NO3 group, with a pseudo-hexagonal bipyramidal coordination geometry.
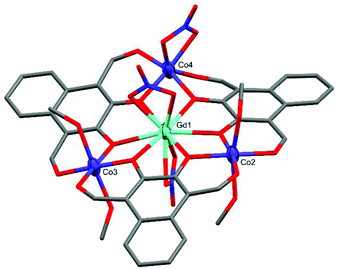 | ||
| Fig. 4 X-ray crystal structure of C2. Thermal ellipsoids of metal atoms shown at 70% probability. H atoms have been omitted for clarity. C = grey, O = red, N = blue. | ||
Similar to C1 and C2, complex C3 (Fig. 5) also crystallised in P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , with the formula [L3Co3La(NO3)2(H2O)6](NO3)(H2O)·[1.5 Et2O], but only has two six-coordinate cobalt centres (Co2 and Co3). Both Co2 and Co3 are axially coordinated by water molecules forming near perfect octahedral coordination geometries with CShM(OC-6)/Σ values of 0.355/28.61 (Co2) and 0.605/43.62 (Co3). In contrast, Co4 has only a single axially coordinated water molecule resulting in a five-coordinate distorted D3h trigonal bipyramidal coordination geometry with a CShM(TBPY-5) value of 1.678.
, with the formula [L3Co3La(NO3)2(H2O)6](NO3)(H2O)·[1.5 Et2O], but only has two six-coordinate cobalt centres (Co2 and Co3). Both Co2 and Co3 are axially coordinated by water molecules forming near perfect octahedral coordination geometries with CShM(OC-6)/Σ values of 0.355/28.61 (Co2) and 0.605/43.62 (Co3). In contrast, Co4 has only a single axially coordinated water molecule resulting in a five-coordinate distorted D3h trigonal bipyramidal coordination geometry with a CShM(TBPY-5) value of 1.678.
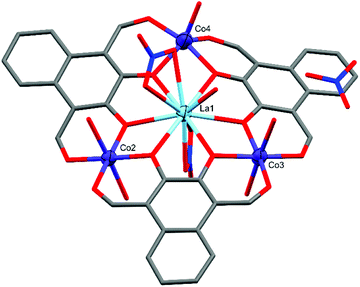 | ||
| Fig. 5 X-ray crystal structure of C3. Thermal ellipsoids of metal atoms shown at 70% probability. H atoms and disordered species have been omitted for clarity. C = grey, O = red, N = blue. | ||
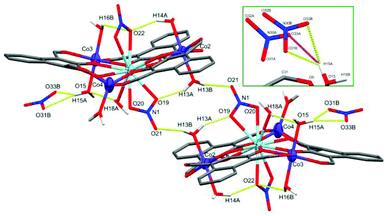
The LaIII ion in the centre of C3 is coordinated by two μ2-NO3 groups and a water molecule, resulting in an 11-coordinate centre with the approximate C5v symmetry of a capped pentagonal antiprism with a CShM(JCPAPR-11) value of 4.655. The final negative charge required to balance the +9 charge of the metal centres, as in C1, is present as a non-coordinated nitrate. This non-coordinated nitrate species is crystallographically disordered over two spatially similar sites with freely refined occupancies of 0.47(2) (site A) and 0.53(2) (site B) (Fig. 6, inset). A water cap of Co3 forms strong hydrogen bonds to three of the four possible oxygen atoms belonging to the disordered nitrate (setting the cut-off distance to 2.50 Å). The inset of Fig. 6 shows both non-coordinated nitrate sites and the hydrogen bonds they form with H15A: O31B⋯H15A = 1.848(9) Å, O33B⋯H15A = 2.281(9) Å, and O33A⋯H15A = 2.154(9) Å, with an O31A⋯H15A distance of 2.905(8) Å.
A second unit complex is generated by inversion symmetry (Fig. 6) which forms a symmetric set of hydrogen bonds between the N1 nitrate cap of La1 and O13 water cap of Co2 in each unit complex, resulting in an intramolecular hydrogen bond (O19⋯H13A = 1.936 Å) and an intermolecular hydrogen bond (O21*⋯H13B = 1.951 Å). The crystal structure of C3 was also found to contain diethyl ether molecules across at least 4 sites in the asymmetric unit. These lattice solvents were heavily disordered and unstable even to isotropic refinement, thus have been modelled within a solvent mask using the Olex2 implementation of BYPASS, containing 64 electrons in 192 Å3 per asymmetric unit which fits well with 1.5 diethyl ether molecules (63 electrons). These solvate species were not observed in the microanalytical data, but are consistent with the observation of the crystalline sample rapidly crumbling upon sitting in air.
The crystal structure of C4 (Fig. 7) revealed a relatively non-planar system featuring one five-coordinate and two six-coordinate cobalt centres. Although the preparation of C3 reported here also utilised a non-nitrate lanthanide salt (La(OAc)3·6H2O), C4 exclusively features a mixture of nitrate and non-nitrate (chloride) anions. Both Co2 and Co3 are octahedral, with CShM(OC-6)/Σ values of 0.738/43.66 (Co2) and 0.947/56.12 (Co4), with Co4 being axially coordinated by two methanol molecules. Co2 has an axially coordinated methanol on one side of the plane, however the other cap is present as a crystallographically disordered 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol/water species. Co3 is unambiguously capped by a single chloride anion originating from the TbCl3·H2O salt with an overall formula of [L3Co3TbCl(NO3)2(H2O)0.5(MeOH)3.5]·[2.5H2O]. This five-coordinate cobalt centre sits in an approximately C4v square pyramidal coordination geometry with a CShM(SPY-5) value of 1.734.
1 methanol/water species. Co3 is unambiguously capped by a single chloride anion originating from the TbCl3·H2O salt with an overall formula of [L3Co3TbCl(NO3)2(H2O)0.5(MeOH)3.5]·[2.5H2O]. This five-coordinate cobalt centre sits in an approximately C4v square pyramidal coordination geometry with a CShM(SPY-5) value of 1.734.
The crystal lattice was found to contain two solvent accessible voids equivalent to 14 electrons in 68 Å3 and 8 electrons in 24 Å3 when modelled within a solvent mask using Olex2, which corresponds to approximately 1.5 water molecules and 1 water molecule, respectively, per asymmetric unit and is consistent with the microanalytical data for C4 – see experimental details.
Based on the general formulation L3Co3Ln(anion)3 + solvents, cobalt is expected to be in the +2 oxidation state (+3 from LnIII, −2 from L, and −1 from each anion, giving an overall charge of −6 to be balanced by three cobalt centres). The same result is evidenced by further examining the average equatorial Co–O bond lengths in Table 1, which are consistent with the longer bonds expected for CoII. Further, the bond valency55,56 of each cobalt centre has been assessed in PLATON57,58 and all sit in the range of 2.18–2.36.
The structural differences between the four complexes are quite striking and in the first instance may be attributed to the differing sizes of the central lanthanide cation. For instance, the structure of C1, with a small DyIII ion at its centre, is dictated by the cobalt centres, each one adopting an ideal octahedral geometry. The differences between the larger lanthanide cations in complexes C2–C4 is more subtle, with no clear or obvious reason for the different cobalt geometries, other than they are now unable to form idealised octahedral geometries.
π–π stacking interactions were analysed in Olex2 (ref. 59) with aromatic centroid–centroid distances listed in Table 3 as well as the cross-sectional molecular area, calculated in the Co3–L3 plane using the inbuilt ChemCraft utility.
| Complex | π–π stacking (Å) | Molecular area (Å3) |
|---|---|---|
| C1 | 3.763–3.824 | 206.5 |
| C2 | 3.731–3.740 | 208.9 |
| C3 | 3.586–3.955 | 213.1 |
| C4 | 3.551–3.791 | 212.1 |
Complex C3, containing the largest trivalent lanthanide ion (LaIII), has the largest calculated molecular area as well as the longest range π–π stacking interaction (as determined by Olex2). It also features the longest average CoII–LnIII and CoII–CoII distances, however it interestingly also has the shortest LnIII–LnIII distance (Table 3). The same trend in ionic radii vs. cross-sectional molecular area is not followed for the other three complexes. Complex C4 contains TbIII which is smaller than GdIII (C2) but larger than DyIII (C1), however C4 has the second largest calculated molecular area which may be attributed to the way in which the chloride cap of Co3 in C4 influences the planarity and shape of the complex and hence the crystal packing.
The crystal packing diagrams of C1 and C2 viewed along the crystallographic a-axis (Fig. 8) show that these complexes pack similar to a two-dimensional layered system along the ab-plane with clear inter-layer separations along the c-axis. Although C3 has the same metric symmetry and space group as C1 and C2, the geometry of the unit cell is considerably different. Where C1 and C2 have similar lengths in a and b and both α and β angles are near 90°, C3 has similar lengths in b and c with the corresponding α and γ angles being near 90°. The shorter length of c in C3 relative to the other two triclinic structures results in a greater proportion of a third molecule, whose centre of mass sits outside of the unit cell, occupying the space to ensure Z = 2.
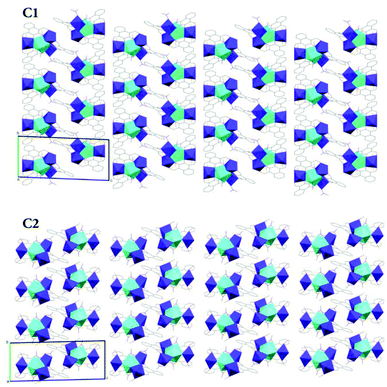 | ||
| Fig. 8 Simplified X-ray crystal structure packing diagrams of C1 and C2 viewed along the crystallographic a-axis. | ||
Magnetic measurement
The DC magnetic susceptibility and magnetisation measurements have been performed to examine the potential Co–Co interactions and/or zero-field splitting effects present within this complex. As complexes C1–C4 each feature a CoII centre with different coordination geometries, this initial study of C3 is not necessarily representative of the other three complexes.Fig. 9A shows the χmT product reaching 9.4 cm3 K mol−1 at 300 K, which clarified the presence of three SCoII = 3/2 spins with g = 2.59. The experimental magnetisation (Fig. 9B) at 7 T was 7.1 μB, which corresponds to ca. 60% of the theoretical limit (11.7 μB). If antiferromagnetic interactions were dominant, the experimentally measured magnetisation would be approximately one third of the theoretical value and the χmT product at 1.8 K would approach one third of the value at 300 K. Hence the measured value of 7.1 μB indicates antiferromagnetic interactions are relatively small for this system. Part of the gradual decrease in the χmT(T) profile is likely to originate from the single-ion nature of the spatially separated CoII centres. To evaluate the zero-field splitting (ZFS) of the CoII ions, simulations were performed using MAGPACK60,61 to better comprehend the magnetic properties of C3.
An approximation based on a three-fold symmetry is applied to the magnetic analysis, to avoid overparameterization. Optimization of the ZFS D value for each cobalt(II) ion with neglecting any E value gave D/kB = 65 K with gavg = 2.55. Calculated χmT(T) and M(H) profiles reproduced the experimental results well (the solid lines superposed in Fig. 9). This D value is relatively large, but possible in comparison with the literature values.62–65 The large D value seems to be related to the five-coordinate cobalt(II) ion (Co4, Fig. 5). On the other hand, the exchange coupling model using a spin-Hamiltonian based on an antiferromagnetic triangle, H = −2J(S1S2 + S2S3 + S3S1), cannot reproduce the experimental M–H data (Fig. S2b, ESI†).
Conclusions
Four new non-macrocyclic heterometallic triangular CoII3LnIII clusters have been prepared by the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3:3 reaction of Dy(NO3)3·6H2O, Gd(NO3)3·6H2O, La(OAc)3·6H2O, or TbCl3·6H2O with Co(NO3)2·6H2O and H2L in methanol. Single-crystal X-ray diffraction quality crystals were obtained by the vapour diffusion of diethyl ether into concentrated methanolic solutions of C1–C4, allowing complete and unambiguous structural characterisation. The coordination geometry of each metal centre was examined by continuous shape measurements (CShM) using the SHAPE software package as well as OctaDist to calculate a series of octahedral distortion parameters. While C1 was found to contain three near-perfectly octahedral CoII centres, the remaining three complexes each contained one non-octahedral CoII ion. This non-octahedral site was found to be strongly distorted towards trigonal prismatic in C2, with five coordinate centres observed for C3, trigonal bipyramidal, and C4, square pyramidal. The magnetic study of C3 clarified a ground-state spin projection of STot = 3/2 where antiferromagnetic contributions to the Co–Co interactions are weak. Throughout the literature, magnetic characterisation for the macrocyclic analogues of this type of complexes have been limited to NiII, CuII, and ZnII with d8, d9, and d10 electron configurations, respectively. While the CoII based systems reported here do not crystallise with the same regularity (in terms of local coordination geometries) as previously published families of macrocyclic analogues, their potentially unique magnetic properties make for an interesting avenue of research, particularly with the inclusion of high spin d7 metal centres.
3:3 reaction of Dy(NO3)3·6H2O, Gd(NO3)3·6H2O, La(OAc)3·6H2O, or TbCl3·6H2O with Co(NO3)2·6H2O and H2L in methanol. Single-crystal X-ray diffraction quality crystals were obtained by the vapour diffusion of diethyl ether into concentrated methanolic solutions of C1–C4, allowing complete and unambiguous structural characterisation. The coordination geometry of each metal centre was examined by continuous shape measurements (CShM) using the SHAPE software package as well as OctaDist to calculate a series of octahedral distortion parameters. While C1 was found to contain three near-perfectly octahedral CoII centres, the remaining three complexes each contained one non-octahedral CoII ion. This non-octahedral site was found to be strongly distorted towards trigonal prismatic in C2, with five coordinate centres observed for C3, trigonal bipyramidal, and C4, square pyramidal. The magnetic study of C3 clarified a ground-state spin projection of STot = 3/2 where antiferromagnetic contributions to the Co–Co interactions are weak. Throughout the literature, magnetic characterisation for the macrocyclic analogues of this type of complexes have been limited to NiII, CuII, and ZnII with d8, d9, and d10 electron configurations, respectively. While the CoII based systems reported here do not crystallise with the same regularity (in terms of local coordination geometries) as previously published families of macrocyclic analogues, their potentially unique magnetic properties make for an interesting avenue of research, particularly with the inclusion of high spin d7 metal centres.
Author contributions
T. N. D., conceptualisation, investigation, data curation, formal analysis, visualisation, writing – original draft, writing – review & editing. R. T., magnetic measurements, analysis, simulation, and manuscript preparation of the magnetic data interpretation. T. I., supervision, investigation, data curation, formal analysis, writing – review & editing. P. G. P, supervision, project administration, writing – review & editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
T. N. D. and P. G. P. would like to thank Massey University for the award of a Massey University Doctoral Scholarship for Māori to T. N. D., T. I. is grateful to the support from JSPS KAKENHI (JP20K21170 and JP17H06371).Notes and references
- C. O. Dietrich-Buchecker, J. P. Sauvage and J. M. Kern, J. Am. Chem. Soc., 1984, 106, 3043–3045 CrossRef CAS.
- C. Dietrich-Buchecker and J.-P. Sauvage, Tetrahedron, 1990, 46, 503–512 CrossRef CAS.
- C. Dietrich-Buchecker, G. Rapenne and J.-P. Sauvage, Coord. Chem. Rev., 1999, 185–186, 167–176 CrossRef CAS.
- J. D. Crowley, S. M. Goldup, A.-L. Lee, D. A. Leigh and R. T. McBurney, Chem. Soc. Rev., 2009, 38, 1530–1541 RSC.
- S. M. Goldup, D. A. Leigh, T. Long, P. R. McGonigal, M. D. Symes and J. Wu, J. Am. Chem. Soc., 2009, 131, 15924–15929 CrossRef CAS PubMed.
- J.-F. Ayme, J. Lux, J.-P. Sauvage and A. Sour, Chem. –Eur. J., 2012, 18, 5565–5573 CrossRef CAS PubMed.
- M. Denis and S. M. Goldup, Nat. Rev. Chem., 2017, 1, 1–17 CrossRef.
- S. Yang, A. Miyachi, T. Matsuno, H. Muto, H. Sasakawa, K. Ikemoto and H. Isobe, J. Am. Chem. Soc., 2021, 143, 15017–15021 CrossRef CAS PubMed.
- N. K. Kaushik, A. Mishra, A. Ali, J. S. Adhikari, A. K. Verma and R. Gupta, J. Biol. Inorg Chem., 2012, 17, 1217–1230 CrossRef CAS PubMed.
- G.-Y. Wu, X. Shi, H. Phan, H. Qu, Y.-X. Hu, G.-Q. Yin, X.-L. Zhao, X. Li, L. Xu, Q. Yu and H.-B. Yang, Nat. Commun., 2020, 11, 3178 CrossRef CAS PubMed.
- J. Ren, X. Wei, R. Xu, Z. Chen, J. Wang, M. Wang, T. Sun, M. Wang and Y. Tang, J. Mol. Struct., 2021, 1229, 129783 CrossRef CAS.
- C.-F. Lee, D. A. Leigh, R. G. Pritchard, D. Schultz, S. J. Teat, G. A. Timco and R. E. P. Winpenny, Nature, 2009, 458, 314–318 CrossRef CAS PubMed.
- X. Chen, S. Yeganeh, L. Qin, S. Li, C. Xue, A. B. Braunschweig, G. C. Schatz, M. A. Ratner and C. A. Mirkin, Nano Lett., 2009, 9, 3974–3979 CrossRef CAS PubMed.
- C. Schouwey, M. Papmeyer, R. Scopelliti and K. Severin, Dalton Trans., 2015, 44, 2252–2258 RSC.
- H. Li, Z.-J. Yao, D. Liu and G.-X. Jin, Coord. Chem. Rev., 2015, 293–294, 139–157 CrossRef CAS.
- P. Buchwalter, J. Rosé and P. Braunstein, Chem. Rev., 2015, 115, 28–126 CrossRef CAS PubMed.
- D. Bansal, S. Pandey, G. Hundal and R. Gupta, New J. Chem., 2015, 39, 9772–9781 RSC.
- J.-J. Du, X. Zhang, X.-P. Zhou and D. Li, Inorg. Chem. Front., 2018, 5, 2772–2776 RSC.
- X.-R. Wu, S.-Y. Yao, L.-Q. Wei, L.-P. Li and B.-H. Ye, Inorg. Chim. Acta, 2018, 482, 605–611 CrossRef CAS.
- V. Chandrasekhar, P. Bag, W. Kroener, K. Gieb and P. Müller, Inorg. Chem., 2013, 52, 13078–13086 CrossRef CAS PubMed.
- J.-L. Liu, J.-Y. Wu, Y.-C. Chen, V. Mereacre, A. K. Powell, L. Ungur, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, Angew. Chem., Int. Ed., 2014, 53, 12966–12970 CrossRef CAS PubMed.
- Y. Ida, S. Ghosh, A. Ghosh, H. Nojiri and T. Ishida, Inorg. Chem., 2015, 54, 9543–9555 CrossRef CAS PubMed.
- S. Zhang, H. Li, E. Duan, Z. Han, L. Li, J. Tang, W. Shi and P. Cheng, Inorg. Chem., 2016, 55, 1202–1207 CrossRef CAS PubMed.
- L. R. Piquer and E. Carolina Sañudo, Dalton Trans., 2015, 44, 8771–8780 RSC.
- H.-L. Wang, Z.-H. Zhu, J.-M. Peng and H.-H. Zou, J. Clust. Sci. DOI:10.1007/s10876-021-02084-7.
- J. M. Clemente-Juan, E. Coronado and A. Gaita-Ariño, Chem. Soc. Rev., 2012, 41, 7464–7478 RSC.
- D. Dong, Philos. Mag., 2015, 95, 2948–2954 CrossRef CAS.
- E. Macaluso, M. Rubín, D. Aguilà, A. Chiesa, L. A. Barrios, J. I. Martínez, P. J. Alonso, O. Roubeau, F. Luis, G. Aromí and S. Carretta, Chem. Sci., 2020, 11, 10337–10343 RSC.
- S. V. Rao, J. M. Ashtree and A. Soncini, Phys. B, 2020, 592, 412237 CrossRef CAS.
- D. Asthana, S. J. Lockyer, S. Nawaz, R. J. Woolfson, G. A. Timco, C. A. Muryn, I. J. Vitorica-Yrezabal, D. Collison, N. A. Burton and R. E. P. Winpenny, Dalton Trans., 2021, 50, 4390–4395 RSC.
- S. Akine, S. Sunaga, T. Taniguchi, H. Miyazaki and T. Nabeshima, Inorg. Chem., 2007, 46, 2959–2961 CrossRef CAS PubMed.
- S. Akine, T. Taniguchi and T. Nabeshima, Tetrahedron Lett., 2001, 42, 8861–8864 CrossRef CAS.
- H. L. C. Feltham, Y. Lan, F. Kloewer, L. Ungur, L. F. Chibotaru, A. K. Powell and S. Brooker, Chem. –Eur. J., 2011, 17, 4362–4365 CrossRef CAS PubMed , S4362/1-S4362/9..
- H. L. C. Feltham, F. Kloewer, S. A. Cameron, D. S. Larsen, Y. Lan, M. Tropiano, S. Faulkner, A. K. Powell and S. Brooker, Dalton Trans., 2011, 40, 11425–11432 RSC.
- S. Akine, S. Sunaga and T. Nabeshima, Chem. –Eur. J., 2011, 17, 6853–6861 CrossRef CAS PubMed.
- A. Yamashita, A. Watanabe, S. Akine, T. Nabeshima, M. Nakano, T. Yamamura and T. Kajiwara, Angew. Chem., 2011, 50, 4016–4019 CrossRef CAS PubMed , S4016/1-S4016/5..
- H. Nagae, R. Aoki, S. Akutagawa, J. Kleemann, R. Tagawa, T. Schindler, G. Choi, T. P. Spaniol, H. Tsurugi, J. Okuda and K. Mashima, Angew. Chem., Int. Ed., 2018, 57, 2492–2496 CrossRef CAS PubMed.
- M. Yamamura, M. Sasaki, M. Kyotani, H. Orita and T. Nabeshima, Chem. –Eur. J., 2010, 16, 10638–10643 CrossRef CAS PubMed.
- M. Yamamura, M. Iida, K. Kanazawa, M. Sasaki and T. Nabeshima, Bull. Chem. Soc. Jpn., 2014, 87, 334–340 CrossRef CAS.
- W. A. Rabanal-León, J. A. Murillo-López and R. Arratia-Pérez, Phys. Chem. Chem. Phys., 2016, 18, 33218–33225 RSC.
- H. L. C. Feltham, R. Clerac, A. K. Powell and S. Brooker, Inorg. Chem., 2011, 50, 4232–4234 CrossRef CAS PubMed.
- H. L. C. Feltham, R. Clerac, L. Ungur, V. Vieru, L. F. Chibotaru, A. K. Powell and S. Brooker, Inorg. Chem., 2012, 51, 10603–10612 CrossRef CAS PubMed.
- H. L. C. Feltham, R. Clerac, L. Ungur, L. F. Chibotaru, A. K. Powell and S. Brooker, Inorg. Chem., 2013, 52, 3236–3240 CrossRef CAS PubMed.
- S. Dhers, H. L. C. Feltham, R. Clerac and S. Brooker, Inorg. Chem., 2013, 52, 13685–13691 CrossRef CAS PubMed.
- S. Dhers, H. L. C. Feltham, M. Rouzieres, R. Clerac and S. Brooker, Dalton Trans., 2016, 45, 18089–18093 RSC.
- S. Dhers, H. L. C. Feltham, M. Rouzieres, R. Clerac and S. Brooker, Inorg. Chem., 2019, 58, 5543–5554 CrossRef CAS PubMed.
- H. L. C. Feltham, S. Dhers, M. Rouzieres, R. Clerac, A. K. Powell and S. Brooker, Inorg. Chem. Front., 2015, 2, 982–990 RSC.
- H. Asaba, T. Iwasaki, M. Hatazawa, J. Deng, H. Nagae, K. Mashima and K. Nozaki, Inorg. Chem., 2020, 59, 7928–7933 CrossRef CAS PubMed.
- T. N. Dais, R. Takano, T. Ishida and P. G. Plieger, Dalton Trans., 2022, 51, 1446–1453 RSC.
- A. J. Gallant, J. H. Chong and M. J. MacLachlan, Inorg. Chem., 2006, 45, 5248–5250 CrossRef CAS PubMed.
- T. Nabeshima, H. Miyazaki, A. Iwasaki, S. Akine, T. Saiki, C. Ikeda and S. Sato, Chem. Lett., 2006, 35, 1070–1071 CrossRef CAS.
- D. Casanova, J. Cirera, M. Llunell, P. Alemany, D. Avnir and S. Alvarez, J. Am. Chem. Soc., 2004, 126, 1755–1763 CrossRef CAS PubMed.
- M. Pinsky and D. Avnir, Inorg. Chem., 1998, 37, 5575–5582 CrossRef CAS PubMed.
- R. Ketkaew, Y. Tantirungrotechai, P. Harding, G. Chastanet, P. Guionneau, M. Marchivie and D. J. Harding, Dalton Trans., 2021, 50, 1086–1096 RSC.
- N. E. Brese and M. O'Keeffe, Acta Crystallogr. B, 1991, 47, 192–197 CrossRef.
- I. D. Brown, Chem. Rev., 2009, 109, 6858–6919 CrossRef CAS PubMed.
- A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7–13 CrossRef CAS.
- A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155 CrossRef CAS PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- J. Borrás-Almenar, J. Clemente-Juan, E. Coronado and B. Tsukerblat, Inorg. Chem., 1999, 38, 6081–6088 CrossRef PubMed.
- J. Borrás-Almenar, J. M. Clemente-Juan, E. Coronado and B. S. Tsukerblat, J. Comput. Chem., 2001, 22, 985–991 CrossRef.
- T. Yamane, K. Sugisaki, H. Matsuoka, K. Sato, K. Toyota, D. Shiomi and T. Takui, Dalton Trans., 2018, 47, 16429–16444 RSC.
- G. Novitchi, S. Jiang, S. Shova, F. Rida, I. Hlavička, M. Orlita, W. Wernsdorfer, R. Hamze, C. Martins, N. Suaud, N. Guihéry, A.-L. Barra and C. Train, Inorg. Chem., 2017, 56, 14809–14822 CrossRef CAS PubMed.
- B. Papánková, R. Boča, Ľ. Dlháň, I. Nemec, J. Titiš, I. Svoboda and H. Fuess, Inorg. Chim. Acta, 2010, 363, 147–156 CrossRef.
- J. Zhou, J. Song, A. Yuan, Z. Wang, L. Chen and Z.-W. Ouyang, Inorg. Chim. Acta, 2018, 479, 113–119 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2105529–2105532. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1ra08797e |
| This journal is © The Royal Society of Chemistry 2022 |