Open Access Article
Open Access ArticleFirst-principal investigations of electronic, structural, elastic and optical properties of the fluoroperovskite TlLF3 (L = Ca, Cd) compounds for optoelectronic applications
Mohammad Sohaila,
Mudasser Husaina,
Nasir Rahmana,
Khaled Althubeiti b,
Merfat Algethamic,
Abid Ali Khand,
Anwar Iqbald,
Asad Ullahe,
Aurangzeb Khanfg and
Rajwali Khan
b,
Merfat Algethamic,
Abid Ali Khand,
Anwar Iqbald,
Asad Ullahe,
Aurangzeb Khanfg and
Rajwali Khan *ah
*ah
aDepartment of Physics, University of Lakki Marwat, 28420, Khyber Pakhtunkhwa, Pakistan. E-mail: rajwalipak@zju.edu.cn; msohail@ulm.edu.pk; nasir@ulm.edu.pk
bDepartment of Chemistry, College of Science, Taif University, P.O. Box 11099, Taif 21944, Saudi Arabia
cDepartment of Physics, College of Science, Taif University, P.O. Box 11099, Taif 21944, Saudi Arabia
dDepartment of Chemical Sciences, University of Lakki Marwat, 28420, Khyber Pukhtunkhwa, Pakistan
eDepartment of Mathematical Sciences, University of Lakki Marwat, Lakki Marwat, 28420, Khyber Pukhtunkhwa, Pakistan
fDepartment of Physics, Abdul Wali Khan University, Mardan, 23200, Pakistan. E-mail: akhan@awkum.edu.pk
gUniversity of Lakki Marwat, Lakki Marwat, 28420 Khyber Pukhtunkhwa, Pakistan
hCollege of Physics and Optoelectronic Engineering, Shenzhen University, 518000, China
First published on 2nd March 2022
Abstract
In this research work, the Tl-based fluoroperovskite compounds TlLF3 (L = Ca, Cd) were investigated computationally using density functional theory (DFT) to comprehend their structural, elastic, optical, and electronic properties. Computation of the tolerance factor and Birch–Murnaghan curve indicated that the compounds are cubic and structurally stable. The structurally optimized lattice constants and the optimum volume corresponding to the optimum energy were measured. Elastic properties were predicted using the IRelast package, and the results showed that the compounds of interest are mechanically stable, ductile, and anisotropic in nature. The electronic properties (band structures and density of states) show that TlCaF3 and TlCdF3 possess a wide direct bandgap from (X–X) symmetry points of 5.7 eV and 5.6 eV, respectively. The contributions of different elemental states to the valence and conduction bands are evaluated from the total and partial density of states (TDOS & PDOS). Analysis of the optical properties showed that these compounds possess a high refractive index, absorption coefficient, and reflectivity at high energy ranges. The values of the direct bandgap indicated that these compounds are expected to be semiconducting in nature, and their use is primarily considered to be in the semiconductor industries and optoelectronic devices. These compounds are new and have been investigated for the first time using the computational approach, which provides comprehensive insight into their different properties; based on the results, they are recommended as industrial candidates.
1. Introduction
Fluoroperovskites are well-known compounds with the typical chemical formula ABF3, where A and B are cations (positive ions), and fluorine (F) is an anion (negative charge). Fluoroperovskite materials are an intriguing family, having a crystal structure that is mechanically stable while exhibiting excellent optoelectronic properties ranging from semiconducting (1–4 eV) to insulating (above 4 eV) nature. Fluoroperovskites have garnered substantial attention in current years because of their industrial significance to lenses for optical lithography, radiation dosimeters, scintillation materials, and the semiconductor processing industry.1–4 Due to their wide range of applications, fluoroperovskite compounds have been extensively investigated experimentally and computationally by a variety of authors, as detailed in ref. 5. Some investigations of fluoroperovskites under high pressure have been reported. It has been found that the materials are indirect bandgap insulators and have a stable equilibrium lattice constant, elastic constants, and bulk modulus.6–8The energy band gap of fluoropyrocytes is often large, so these compounds are technologically important.9–11 KMgF3 and BaLiF3 are utilized in optical lithography steppers as vacuum-ultraviolet materials for lenses11–13 and when doped with lanthanide ions Ce and Er, KMgF3 also shows promise as a material for radiation dosimeters and scintillation.14
Study of the compound SrCl2 has found it to be an insulator with an indirect bandgap of 5.18 eV. The bandgap initially increases and then decreases as a function of pressure. The structural and electronic properties and elastic constants of cubic SrCl2 also show its cubic structure.15 Total energy and elastic constants, as well as the theoretical Young's modulus, shear modulus, Poisson's ratio, sound velocities, and Debye temperature, were calculated and examined. The bulk and shear moduli ratios reveal that Ti3AlN is ductile in nature, with its ductility expected to be greater than that of Ti3Al, but Ti3AlC is brittle.16 A theoretical investigation of the Ag-based fluoroperovskites AgMgF3 and AgZnF3 was described by Murtaza et al.17 The expected wide absorption energy range of the proposed materials makes them appropriate for various applications in modern devices. The optoelectronic characteristics of Sn-based fluoroperovskites were investigated; these compounds were discovered to be electronic insulators, and their Auger-Free luminescence was predicted (AFL).18 The optoelectronic, structural, and magnetic properties of TlMnX3 (X = Cl, and F) were described by F. Hamioud, and his colleagues projected optical-spectrum-based uses for optics technology in ref. 19 and 20. Thallium-based compounds are being developed for radiation detection, and several investigations have shown their usefulness in this application .21,22 Because these compounds contain a thallium atom, their effective atomic number is higher, which improves detection efficiency; because of their single growth requirement, the simple cubic structure of the compounds makes them a technologically promising candidate.
In this work, TlLF3 (L = Ca, Cd) compounds are studied in depth utilizing the Tran and Blaha modified Becke–Johnson (TB-mBJ) technique, which provides insight into their structural, elastic, electrical, and optical properties. Using the computer simulation tool wien2k, we have discovered that TlCdF3 is electrically insulating with high transparency over a wide range of energies, making it a good candidate for optical applications. To the best of our knowledge, there are no reports in the literature of research into Tl-based fluoroperovskites despite the interest in fluoroperovskite compounds for diverse applications.
There are four main components to this study. Section 2 covers the calculation methods, Section 3 covers the results and discussion, and Section 4 covers the conclusions of the study.
2. Methodology
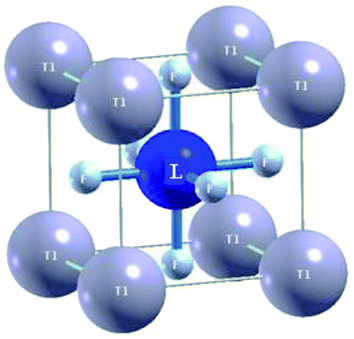
The ternary fluoroperovskite TlLF3 (L = Ca, Cd) compounds are characterized as cubic-structure-type perovskites with the space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (#221). One molecule makes up the unit cell, and Tl and L (L = Ca, Cd) are located at Wyckoff coordinates of (0, 0, 0) and (0.5, 0.5, 0.5), respectively, while the three fluorine atoms in the molecule are located at (0.5, 0, 0.5), (0, 0.5, 0.5) and (0.5, 0.5, 0), as depicted (Fig. 1).
m (#221). One molecule makes up the unit cell, and Tl and L (L = Ca, Cd) are located at Wyckoff coordinates of (0, 0, 0) and (0.5, 0.5, 0.5), respectively, while the three fluorine atoms in the molecule are located at (0.5, 0, 0.5), (0, 0.5, 0.5) and (0.5, 0.5, 0), as depicted (Fig. 1).
The typical structure of DFT was used for simulation studies to investigate their structural, elastic, electrical, and optical properties. In order to use the full potential linearized augmented plane wave (FP-LAPW) approach to its maximum extent, the WIEN2K code was used.23 The energy versus volume curve was fitted using Murnaghan's equation of state to determine structural properties.24 To ensure that there was no charge leakage from either the total or the core energy, a suitable radius of muffin tin (RMT) value was selected during the investigation. The RMT values were 2.50, 2.01, and 2.12 for Tl, Ca, and Cd, respectively, while they were 2.01 and 1.88 for the F in TlCaF3 and TlCdF3, respectively. There are 1000 K-points and 12 Gmax in the muffin tins; hence, the wave function was stretched in harmonics up to lmax = 10 in the muffin tin spheres. The energy difference between the core and valence bands is 6 Ry.
3. Results and discussion
3.1 Electronic properties
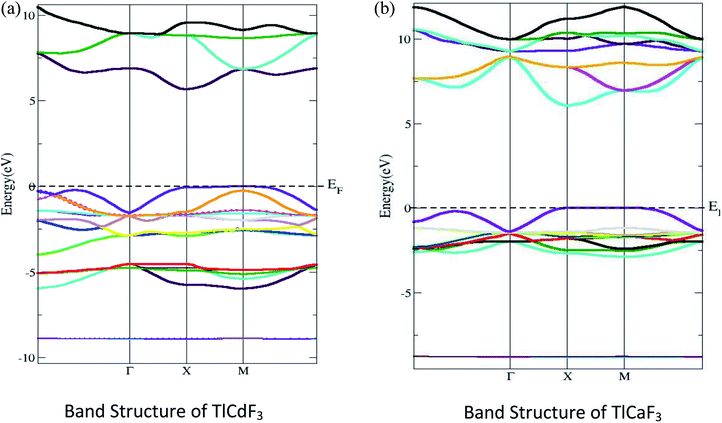
The electronic properties of the compounds under investigation are shown with their energy, band structures and DOS. Fig. 2 shows that the computed band structure for TlLF3 (L = Ca, Cd) at the equilibrium geometry falls in the first Brillouin zone, as well as the symmetry directions in that zone. There is no such thing as a zero; ideally, energy should be at or near the maximum point of the valence band. The bandgaps for the compounds TlCdF3 and TlCaF3 were calculated to be 5.7 and 5.6 eV using the TB-mBJ potential method. In the band structure, the conduction band minima of TlCdF3 occur at the X-symmetry point and the maximum of the valence band Fig. 2(a), showing the direct (X–X) band nature by being at the X symmetry point, and is shown in Fig. 2(b). The conduction band minimum and a maximum of TlCaF3 are both found at the exact X-axis symmetry location of the Brillion zone point, which shows the direct bandgap nature. The band gap is not direct according to previous research; however, its nature is in agreement with TlCdF3, and the band gap properties of the proposed compound TlCaF3 are of interest. The calculated band structure of TlLF3 (L = Ca, Cd) along the symmetry directions of the equilibrium geometry in the first Brillouin zone are given in Fig. 2. The zero energy is set to correspond to the top of the valence bands. Using TB-mBJ, the values predicted for the bandgaps of TlCdF3 and TlCaF3 are 5.7 eV and 5.6 eV, respectively, as shown in Table 1. The direct bandgap nature of TlCaF3 is demonstrated in Fig. 2(a), in which both the CB minima and VB maxima are positioned at the same symmetry point, X, within the Brillion zone. The band structure of TlCaF3 is depicted in Fig. 2(b), which shows that the CB minima and VC maxima lie at the M-symmetry point, indicating a direct band gap nature. The direct band gap nature is consistent with prior research on TlCdF3.20| Compound | EM–Mg | EX–Xg | EГ–Гg | ER–Гg | EГ–Xg |
|---|---|---|---|---|---|
| TlCdF3 | 5.24 | 5.7 | 6.94 | 5.82 | 6.69 |
| TlCaF3 | 5.21 | 5.6 | 3.46 | 6.19 | 3.23 |
3.2 The DOS (density of states)
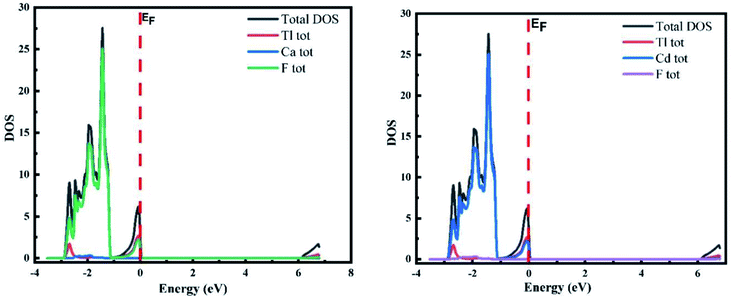
The TDOS and PDOS (total and partial density of states) for both materials under investigation are presented in Fig. 3, which displays the contributions of the electronic states to the VB and CB bands. The Fermi level is shown as the vertical dotted line labelled EF. The portion to the left of the Fermi level represents the VB, while the CB region is to the right. A deeper understanding is obtained from the different states of the constituent materials. The plot of the DOS for TlCaF3 demonstrates that the VB is dominated by the F-p state with a slight contribution from the Tl-s state. In CB, the Tl-s state plays the key role. For TlCdF3, the VB is dominated by the F-p and Cd-d states, while the states of Cd dominate the CB.3.3 Structural and elastic properties
The elastic constants Cij, which are fundamental and indispensable, can be used to characterize elastic properties. The elastic constants are significant characteristics in determining the reaction when macroscopic stress is applied. The elastic constants can be used to describe how a material endures stress deformation and subsequently reinstates and reverts to its original form when the stress has passed.25 The elastic constants can provide a valuable description of structural stability and bonding character within the atomic spheres in addition to the isotropic or anisotropic character. C11, C44, and C12 are three discrete and self-governing elastic constants for cubic systems. To determine Cij, the unit cell is slanted with a suitable strain tensor to obtain an energy–strain relationship. In the present work, the IRelast-package developed by Jamal Murtaza,26 which is used and run within the WIEN2k code, was applied. Fig. 1 shows the ideal cubic crystal structures of the Tl-based fluoroperovskites in this work. Fitting the Birch–Murnaghan equation yields the equilibrium lattice constants.27 Table 2 contains these values. The calculated lattice constant (4.3306 Å) for TlCdF3 agrees reasonably well with the experimentally determined value (4.325 Å) in ref. 28.| Compounds | a0 (lattice constant in Å) | B (bulk modulus in GPa) | B′ (derivative of bulk modulus in GPa) | V0 (ground state volume in a.u.3) | E0 (ground state energy in Ry) |
|---|---|---|---|---|---|
| TlCdF3 | 4.33 | 79.64 | 3.41 | 548.13 | −52333.15 |
| TlCaF3 | 4.37 | 63.74 | 3.48 | 563.83 | −42509.21 |
When forces are applied to a crystal, its response is computed by its elastic constant, which reveals a lot about its mechanical properties. The elastic properties of cubic symmetries crystal, such as rigidity and stability, are calculated using C11, C12, and C44 (three self-governing elastic constants).
Table 3 displays the calculated values of the elastic constants Cij. The elastic constants found in ref. 29 for TlCdF3 were compared with the present results. There is a good match between our computed values of C11, C12 and C44 for TlCdF3 (114.34 GPa, 32.57 GPa, and 15.08 GPa) and the reported values (103.6 GPa, 39.6 GPa, and 18.08 GPa), while those for TlCaF3 C11, C12 and C44 were 220.81 GPa, 40.32 and 30.28 GPa in ref. 30.
| Compounds | C11 | C12 | C44 | B | G | E | A | v | B/G |
|---|---|---|---|---|---|---|---|---|---|
| TlCdF3 | 114.34 | 32.57 | 15.08 | 172.03 | 22.78 | 72.631 | 0.369 | 0.43 | 7.549 |
| TlCaF3 | 220.81 | 40.32 | 30.28 | 172.03 | −346.54 | 5053.076 | −0.016 | −4.39 | −0.96 |
The elastic constants for TlCdF3 were also compared with the values obtained through DFT20 using the generalized gradient approximation of Wu and Cohen (GGA-WC) for C11, C12, and C44 (124.7 GPa, 39.59 GPa, and 11.53 GPa). In the case of TlCdF3, the evaluation indicates that the TB-mBJ method delivers complete additional precise elastic properties closer to the experimental results than the GGA-WC approach.
Using established relationships, the (B) bulk modulus may be determined from the elastic constant (ECs). All the ECs are positive and meet the requirements. For elastic stability, C11 > 0; C44 > 0; (C11–C12) > 0; (C11 + 2C12) > 0; C12 > B > C11.31 Table 3 lists the resulting Young's modulus (E), anisotropy factor (A), Poisson ratio (v), and Pugh index ratio (B/G) values.30 The G (shear modulus) signifies resistance to plastic deformation, whereas the bulk modulus B represents resistance to fracture. The B/G ratio determines whether a material is brittle or ductile.32 If B/G is less than 1.75, the material is brittle, and if it is greater than 1.75, it has a ductile character. According to B/G (Pugh's criteria), both the materials are ductile. The Poisson ratio v33 determines the brittleness of the material; if v is greater than 0.26, the material is ductile; else, it is brittle. Table 3 lists the values. “A” is the elastic anisotropy factor, which is equal to one for an anisotropic material, with any number other than one indicating anisotropy. The degree of elastic anisotropy in the crystal is determined by the amount of deviation from 1. The value of A differs from one for all our compounds, indicating that they all have anisotropy. Young's modulus (E) is the best indicator of the stiffness of a material. When it is high for a given substance, the material becomes stiffer; both compounds are stiff.
The Poisson ratio, which indicates the bonding power, provides more data related to the uniqueness of the bonding power than some other elastic attributes. The Poisson ratio (v) for covalent materials is very small (0.1), but the usual value for ionic materials is 0.25. Table 3 shows that the value for all compounds is more than 0.25, indicating that the nature of the bonding in all our materials is ionic.
3.4 Optical properties
All optical property calculations were carried out using the TB-mBJ potential approach. The optical properties of solids can be investigated by characterizing their electronic complex dielectric function, i.e., ε(ω). Intra-band and inter-band transitions play a significant role in this complicated function. Inter-band contributions are significant for metals34 and can be divided into two types: direct transitions and indirect transitions. We disregard indirect inter-band transitions owing to their modest contribution to ε(ω) and their phonon-scattering character. The dielectric function ε(ω) for anisotropic materials is essentially a complicated kind of symmetrically second-order tensor that perfectly captures the linear response of the electronic system when an external electric field is applied. The complex dielectric function defined by Ehrenreich and Cohen's equation can be used to describe the optical characteristics of the compound.24| ε(ω) = ε1(ω) + iε2(ω) | (1) |
Here, ε1(ω) and the ε2(ω) give the real and imaginary parts, respectively. One can calculate the real part, which can be derived from the imaginary part of the dielectric function and is dependent on ω′2–ω2, which gives the integral denominator; additionally, ω′ has a direct relationship with Eg. The derivation of the real part ε1(ω) can be made by implementing the Kramers–Kronig expression:
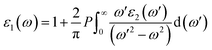 | (2) |
From the real part, the imaginary part can be taken out using the Kramers–Kroning relationship:
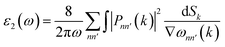 | (3) |
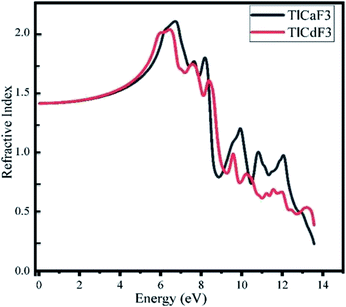
For optical response, the photon energy range is 0–30 eV. The dispersive actions are shown from the real part of the surface of the material, and the absorption of light is shown from the imaginary part of the material.35 The optical transitions and absorption of light within the energy bands are found from the imaginary part. Other optical parameters, comprising the refractive index, absorption coefficient, extinction coefficient, optical conductivity, and reflectivity, can be computed from the dielectric functions.36
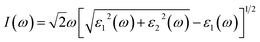 | (4) |
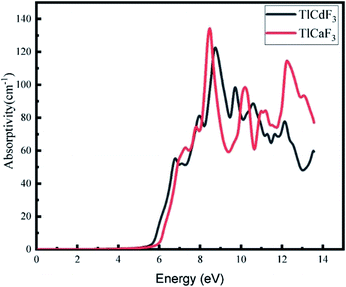
The calculated absorption coefficients of TlCdF3 and TlCaF3 are plotted in Fig. 5. The absorption part of the TlCdF3 spectrum starts at 5.8 eV, and the maximum value for the compound occurs at 8.4 eV, as can be seen in Fig. 5. The absorption part of the TlCaF3 spectrum starts at 5.6 eV, and the maximum absorption appears at 8.5 eV. The energy range of the incident photons for the ultraviolet region is 3 to 124 eV. The absorption coefficient values increase rapidly and reach their maximum when the energy of the radiation reaches a high level; that is, the absorption of the compounds begin, and it becomes high. The very sharp cut-off response, which occurs primarily in the high-energy region, indicates and confirms that these materials can be employed as possible materials for optoelectronic devices working in the UV range.
 | (5) |
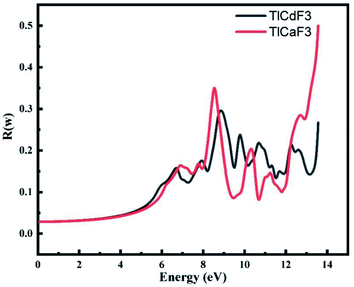
Fig. 6 demonstrates that low optical reflectivity is observed in the low-energy region up to 4 eV before the high energy region. High peaks at 13.8 eV occur for both compounds. Fig. 6 shows the static reflectivity R(ω), which is dependent on the frequency of the radiation or rays, for our two perovskite compounds TlCdF3 and TlCaF3, which both have scores of 0.04, respectively. The maximum reflectivity R(ω) scores for TlCdF3 and TlCaF3 are 0.5, 0.3, respectively, indicating that these materials have a low energy area. This is another important aspect to discuss, because it relates to the optical component. The low score of this term, particularly in the visible and infrared regions, indicates that these compounds have transparency in these regions, which is favorable because scientists use them as anti-reflecting coatings.
4. Conclusions
In the current work, the structural, optical, elastic, and electrical characteristics of TlLF3 (L = Ca, Cd) fluoroperovskites were studied using the TB-mBJ potential approximation. The lattice constants at equilibrium were discovered to be between 4.15 Å and 4.94 Å. The inelastic properties, ECs, anisotropy factors, bulk moduli, Poisson's ratios, Young's moduli, and Pugh's ratios all indicate elastic characteristics. The Pugh (B/G) ratio reveals that the investigated compounds are ductile. The obtained Poisson ratio values further support their ductile nature. TlCaF3 has direct bandgap behavior at the X-symmetry point, whereas TlCdF3 has an indirect band nature, according to our predictions. The predicted findings were compared to existing experimental and theoretical data and found to be consistent. The investigated compounds are exciting materials for scintillation detectors. They have simple cubic structures, large effective Z (atomic number) values due to the presence of the element thallium, and bandgaps within the range for insulator materials.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have influenced the work reported in this paper.Acknowledgements
The authors thanks Taif University Researchers Supporting Project number (TURSP-2020/241), Taif University, Taif, Saudi Arabia.References
- T. Nishimatsu, et al., Band structures of perovskite-like fluorides for vacuum-ultraviolet-transparent lens materials, Jpn. J. Appl. Phys., 2002, 41(4A), L365 CrossRef CAS.
- M. Husain, et al., Insight into the physical properties of the inter-metallic titanium-based binary compounds, Eur. Phys. J. Plus, 2021, 136(6), 1–10 Search PubMed.
- N. Rahman, et al., First principle study of structural, electronic, optical and mechanical properties of cubic fluoro-perovskites:(CdXF3, X= Y, Bi), Eur. Phys. J. Plus, 2021, 136(3), 1–11 Search PubMed.
- V. Kanchana, G. Vaitheeswaran, A. Svane and A. Delin, First-principles study of elastic properties of {CeO}2, {ThO}2and {PoO}2, J. Phys.: Condens. Matter, 2006, 18(42), 9615–9624, DOI:10.1088/0953-8984/18/42/008.
- S. Körbel, M. A. L. Marques and S. Botti, Stability and electronic properties of new inorganic perovskites from high-throughput ab initio calculations, J. Mater. Chem. C, 2016, 4(15), 3157–3167 RSC.
- G. Vaitheeswaran, et al., High-pressure structural study of fluoro-perovskite CsCdF 3 up to 60 GPa: A combined experimental and theoretical study, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(7), 75105 CrossRef.
- G. Vaitheeswaran, V. Kanchana, X. Zhang, Y. Ma, A. Svane and N. E. Christensen, Calculated high-pressure structural properties, lattice dynamics and quasi-particle band structures of perovskite fluorides KZnF3, CsCaF3 and BaLiF3, J. Phys.: Condens. Matter, 2016, 28(31), 315403 CrossRef CAS PubMed.
- R. M. Dubrovin, et al., Incipient geometric lattice instability of cubic fluoroperovskites, Phys. Rev. B, 2021, 104(14), 144304 CrossRef CAS.
- N. Chouit, S. A. Korba, M. Slimani, H. Meradji, S. Ghemid and R. Khenata, First-principles study of the structural, electronic and thermal properties of CaLiF3, Phys. Scr., 2013, 88(3), 35702 CrossRef CAS.
- T. Seddik, R. Khenata, O. Merabiha, A. Bouhemadou, S. Bin-Omran and D. Rached, Elastic, electronic and thermodynamic properties of fluoro-perovskite KZnF 3 via first-principles calculations, Appl. Phys. A: Mater. Sci. Process., 2012, 106(3), 645–653 CrossRef CAS.
- M. Harmel, et al., Ab initio study of the mechanical, thermal and optoelectronic properties of the cubic CsBaF3, Acta Phys. Pol., 2015, 128, 34–42 CrossRef CAS.
- G. Vaitheeswaran, et al., High-pressure structural, elastic, and electronic properties of the scintillator host material K Mg F 3, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(1), 14107 CrossRef.
- S. A. Korba, H. Meradji, S. Ghemid and B. Bouhafs, First principles calculations of structural, electronic and optical properties of BaLiF3, Comput. Mater. Sci., 2009, 44(4), 1265–1271 CrossRef CAS.
- C. Furetta, F. Santopietro, C. Sanipoli and G. Kitis, Thermoluminescent (TL) properties of the perovskite KMgF3 activated by Ce and Er impurities, Appl. Radiat. Isot., 2001, 55(4), 533–542 CrossRef CAS PubMed.
- V. Kanchana, G. Vaitheeswaran and A. Svane, Calculated structural, elastic and electronic properties of SrCl2, J. Alloys Compd., 2008, 455(1), 480–484, DOI:10.1016/j.jallcom.2007.01.163.
- V. Kanchana, Mechanical properties of Ti 3 {AlX} (X = C, N): Ab initio study, Europhys. Lett., 2009, 87(2), 26006, DOI:10.1209/0295-5075/87/26006.
- G. Murtaza, et al., First principle study of cubic perovskites: AgTF3 (T= Mg, Zn), Phys. B, 2011, 406(24), 4584–4589 CrossRef CAS.
- I. Khan, N. Shehzad, I. Ahmad, Z. Ali and S. Jalali-Asadabadi, First-principle studies of the optoelectronic properties of ASnF3 (A= Na, K, Rb and Cs), Int. J. Mod. Phys. B, 2017, 31(21), 1750148 CrossRef CAS.
- F. Hamioud, G. S. AlGhamdi, S. Al-Omari and A. A. Mubarak, Ab initio investigation of the structural, electronic, magnetic and optical properties of the perovskite TlMnX3 (X= F, Cl) compounds, Int. J. Mod. Phys. B, 2016, 30(7), 1650031 CrossRef CAS.
- A. Cheriet, B. Lagoun, M. Halit, M. Zaabat, C. Abdelhakim and L. Hamza, First-principles study of structural, electronic, optical and elastic properties of cadmium based Fluoro-Perovskite MCdF3 (M= Rb, Tl), Solid State Phenom., 2019, 297, 173–186 Search PubMed.
- H. J. Kim, G. Rooh, H. Park and S. Kim, Luminescence and scintillation properties of the new Ce-doped Tl2LiGdCl6 single crystals, J. Lumin., 2015, 164, 86–89 CrossRef CAS.
- A. Khan, G. Rooh, H. J. Kim and S. Kim, Ce3+-activated Tl2GdCl5: novel halide scintillator for X-ray and γ-ray detection, J. Alloys Compd., 2018, 741, 878–882 CrossRef CAS.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, Wien2k, An Augment. Pl. wave+ local orbitals Progr. Calc. Cryst. Prop., 2001, vol. 60 Search PubMed.
- C. Ambrosch-Draxl and J. O. Sofo, Linear optical properties of solids within the full-potential linearized augmented planewave method, Comput. Phys. Commun., 2006, 175(1), 1–14 CrossRef CAS.
- A. H. Reshak and M. Jamal, DFT calculation for elastic constants of orthorhombic structure within WIEN2K code: A new package (ortho-elastic), J. Alloys Compd., 2012, 543, 147–151 CrossRef CAS.
- M. Jamal, M. Bilal, I. Ahmad and S. Jalali-Asadabadi, IRelast package, J. Alloys Compd., 2018, 735, 569–579 CrossRef CAS.
- F. D. Murnaghan, The compressibility of media under extreme pressures, Proc. Natl. Acad. Sci. U. S. A., 1944, 30(9), 244 CrossRef CAS PubMed.
- M. Rousseau, J. Y. Gesland, J. Julliard, J. Nouet, J. Zarembowitch and A. Zarembowitch, Crystallographic, elastic, and Raman scattering investigations of structural phase transitions in RbCd F 3 and TlCd F 3, Phys. Rev. B: Solid State, 1975, 12(4), 1579 CrossRef CAS.
- M. Irfan, et al., Electronic structure and optical properties of TaNO: An ab initio study, J. Mol. Graph. Model., 2019, 92, 296–302 CrossRef CAS PubMed.
- J. Berger, G. Hauret and M. Rousseau, Brillouin scattering investigation of the structural phase transition of TlCdF3 and RbCaF3, Solid State Commun., 1978, 25(8), 569–571 CrossRef CAS.
- G. Grimvall, Thermophysical properties of materials, Elsevier, 1999 Search PubMed.
- C. Duan, et al., Electronic properties of NaCdF3: A first-principles prediction, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69(3), 33102 CrossRef.
- B. Bakri, Z. Driss, S. Berri and R. Khenata, First-principles investigation for some physical properties of some fluoroperovskites compounds ABF 3 (A= K, Na; B= Mg, Zn), Indian J. Phys., 2017, 91(12), 1513–1523 CrossRef CAS.
- S. Azam and S. A. Khan, A first principles study of electronic and optical properties of the polar quaternary chalcogenides β-A2Hg3Ge2S8 (A= K and Rb), Mater. Sci. Semicond. Process., 2015, 34, 250–259 CrossRef CAS.
- M. Makhdoom, et al., First-Principles Description of the Different Phases in the Li 2 NH Compound: Electronic Structure and Optical Properties, J. Korean Phys. Soc., 2019, 74(12), 1140–1145 CrossRef CAS.
- S. Azam, et al., DFT study of the electronic and optical properties of ternary chalcogenides AlX2Te4, Mater. Res. Express, 2019, 6(11), 116314 CrossRef.
- M. Dressel and G. Grüner, Electrodynamics of solids: optical properties of electrons in matter, American Association of Physics Teachers, 2002 Search PubMed.
| This journal is © The Royal Society of Chemistry 2022 |