DOI:
10.1039/D2RA00530A
(Paper)
RSC Adv., 2022,
12, 12344-12354
Unusual semiconductor–metal–semiconductor transitions in magnetite Fe3O4 nanoparticles†
Received
25th January 2022
, Accepted 19th April 2022
First published on 25th April 2022
Abstract
Magnetite (Fe3O4) nanoparticles were successfully prepared by a co-precipitation method. Rietveld refinement on the X-ray diffraction pattern confirmed the development of a single-phase cubic spinel structure with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. However, 57Fe Mössbauer spectroscopy suggested the presence of Fe3+ and Fe2.5+ (mixed Fe3+ and Fe2+) ions at the tetrahedral and octahedral sites of the inverse spinel structure, respectively. Impedance spectroscopy measurements showed a discontinues variation in the temperature dependence of the sample's resistive behavior, indicating the appearance of semiconductor–metal–semiconductor like transitions between the temperature range of 293 and 373 K. A similar dual transition was also observed from the dielectric and conductivity measurements around the same temperature regions. The observed unusual transition is explained in term of the competitive effects among the hopping of localized/delocalized and short-range/long-range charge carriers present in the sample. Moreover, the prepared sample exhibits colossal dielectric permittivity (∼106), reduced tangent loss (∼0.2) and moderate conductivity (>10−6 S cm−1) values, making Fe3O4 nanoparticles a potential candidate for electromagnetic absorbing materials.
m. However, 57Fe Mössbauer spectroscopy suggested the presence of Fe3+ and Fe2.5+ (mixed Fe3+ and Fe2+) ions at the tetrahedral and octahedral sites of the inverse spinel structure, respectively. Impedance spectroscopy measurements showed a discontinues variation in the temperature dependence of the sample's resistive behavior, indicating the appearance of semiconductor–metal–semiconductor like transitions between the temperature range of 293 and 373 K. A similar dual transition was also observed from the dielectric and conductivity measurements around the same temperature regions. The observed unusual transition is explained in term of the competitive effects among the hopping of localized/delocalized and short-range/long-range charge carriers present in the sample. Moreover, the prepared sample exhibits colossal dielectric permittivity (∼106), reduced tangent loss (∼0.2) and moderate conductivity (>10−6 S cm−1) values, making Fe3O4 nanoparticles a potential candidate for electromagnetic absorbing materials.
1. Introduction
Magnetite (Fe3O4) is a well-known ferrimagnetic material having an inverse spinel cubic structure with a space group of Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. In the inverse spinel structure, 1/3 of the Fe ions are located in the tetrahedral (A) sites as Fe3+ while the rest are located in octahedral (B) sites as Fe2.5+ in a closely packed array of oxygen atoms.1 Th ferrimagnetic nature is caused by the ferromagnetic sub-lattices (A- and B-sites) and their mutual antiferromagnetic interaction. Fe3O4 has the highest value of magnetization, i.e., M = 4.2 μB below the Curie temperature (Tc = 850 K) and electrically is a good semiconducting material at room temperature and above.1,2 However, on decreasing the temperature, the semiconducting behavior of Fe3O4 changed into metallic character along with a decrease in the conductivity by two orders of magnitude due to a structural phase transition from cubic to monoclinic and charge-orbital ordering.3 This unusual transition usually occurs at Tv ≈ 120 K and is termed a Verwey transition; however, this Verwey transition temperature (Tv) is found to be quite sensitive to the stoichiometry of the constituents in Fe3O4.4 Although, the Verwey transition has a low operating temperature for most of the practical applications, it plays a vital role in the importance of iron based materials (ferrites) due to their promising applications in spintronics and nano-electronic switching devices.5
m. In the inverse spinel structure, 1/3 of the Fe ions are located in the tetrahedral (A) sites as Fe3+ while the rest are located in octahedral (B) sites as Fe2.5+ in a closely packed array of oxygen atoms.1 Th ferrimagnetic nature is caused by the ferromagnetic sub-lattices (A- and B-sites) and their mutual antiferromagnetic interaction. Fe3O4 has the highest value of magnetization, i.e., M = 4.2 μB below the Curie temperature (Tc = 850 K) and electrically is a good semiconducting material at room temperature and above.1,2 However, on decreasing the temperature, the semiconducting behavior of Fe3O4 changed into metallic character along with a decrease in the conductivity by two orders of magnitude due to a structural phase transition from cubic to monoclinic and charge-orbital ordering.3 This unusual transition usually occurs at Tv ≈ 120 K and is termed a Verwey transition; however, this Verwey transition temperature (Tv) is found to be quite sensitive to the stoichiometry of the constituents in Fe3O4.4 Although, the Verwey transition has a low operating temperature for most of the practical applications, it plays a vital role in the importance of iron based materials (ferrites) due to their promising applications in spintronics and nano-electronic switching devices.5
In the last decade, efforts have been made to alter such unusual semiconductor to metal like conductivity transition in Fe3O4 derived compounds (MFe2O4; where M is transition metal ions) at higher temperature without changing the crystal symmetry for the novel microwave switching applications in communication and sensing. The fundamental requirements for such applications are the creation of soft ferrimagnetic characteristics at room temperature, high electrical conductivity, reduced eddy current loss, and chemical stability.6 Several studies have been published on the magnetic and electrical properties of different Fe3O4 derived compounds such as CoFe2O4,7 MnFe2O4,8 Co1.25Fe1.75O4,9 Ni1−xZnxFe2O4,10 Mg0.5Co0.5Fe2O4,11 and Ni0.4Cu0.2Zn0.4Fe2−xDyxO4 spinel ferrite nanoparticles.12 From these studies, we found that the magnetic exchange interactions and charge carriers hopping mechanism in these ferrites are considerably influenced by the cation distribution, surface spin structure, interparticle interactions, magnetocrystalline anisotropy and surface morphology. However, to understand the mechanism of semiconductor to metal transition (SMT) at higher temperature in the spinel ferrites, different concepts have been presented. Rahman et al. explained the presence of SMT at ∼330 K in CoFe2O4 nanoparticles by suggesting the dominance of direct cation–cation interaction (i.e., Fe3+–Fe2+) compared to cation–anion–cation interactions (i.e., Fe3+–O–Fe3+ and Co2+–O–Co2+) at the B-sites.13 Bastianello et al. observed a semiconducting behavior in the cobalt ferrite nanoparticles up to 400 °C due to hole hopping among the Co2+ and Co3+, while a SMT arises at higher temperature because of additional electron hopping among the Fe2+ and Fe3+ at the B-sites.14 Younas et al. also found a similar type of SMT in NiFe2O4 nanoparticles at around 358 K.15 According to them, the existence of SMT is attributed to a competitive effect among the thermally stimulated localized and delocalized charge carriers, which could be further influenced by the magnetic spins order in doubly (eg) and triply (t2g) degenerate electronic states at the B-sites. Later, Bhowmik et al. reported a dual transition in Ni1.5Fe1.5O4 ferrite, where they found a semiconductor to metal transition (SMT) at around 373 K; however, on further increase in temperature, system returned back from metallic to semiconductor transition (MST) at around 413 K.16 They revealed that hopping of localized and long-range charge carriers governs the semiconducting behavior at low and high temperatures, respectively. While, the occurrence of metal-like behavior in the middle temperature region could be attributed to the hidden charge conduction phase which could be manifested depending on the coupling among the ferromagnetic spin order and electronic states along with the reconfiguration of charge carrier's conduction mechanism in the system. Similarly, Özdemir et al. confirmed a semiconductor–metal–semiconductor transition in pure CuFe2O4 and CuO/CuFe2O4 nanocomposites by impedance spectroscopy.17 According to them, a metallic conduction is formed as a result of the delocalization of localized states and the formation of conducting channels. Moreover, the addition of CuO nanoparticles decreased the temperature at which metallic conductivity could be observed, which might be due to the composites' reduced cation and anion content. So far, none of the above-mentioned report obtained such unusual semiconductor–metal–semiconductor transition in other spinel ferrites. Moreover, the effects of cation distribution on the conduction mechanism along with the existence of metal like behavior between the two semiconductor states still need attention. Thus, in the present study, it was proposed to investigate the conductivity and dielectric properties of the nanostructured Fe3O4 at higher temperatures (i.e., well above the Verwey transition temperature) for the probable occurrence of such type of transitions in the inverse spinel system.
In this work, Fe3O4 nanoparticles were synthesized by a co-precipitation method and then investigated for their structural and magnetic properties along with the impedance spectroscopy measurements as a function of frequency (0.5–107 Hz) and temperature (293–373 K). Our impedance results confirmed the presence of semiconductor–metal–semiconductor transition in the prepared sample and also exhibited a colossal dielectric permittivity, reduced tangent loss and dissimilar conduction mechanism governed at high and low temperatures which make this material applicable for different technological applications.
2. Experimental
Magnetite (Fe3O4) nanoparticles were synthesized via co-precipitation method. The stoichiometric amounts of iron sulfate heptahydrate [FeSO4·7H2O; Sigma-Aldrich; ≥99%] and iron chloride hexahydrate [FeCl3·6H2O; Sigma-Aldrich; ≥98%] were separately dissolved in the beakers containing 50 ml of deionized water using magnetic stirrer on the hot plate. Then, both solutions were mixed together in a beaker placed on a hot plate at 75 °C for 1 h. After an hour of stirring, ammonia (NH3) was added dropwise in the mixed solution until brownish solution turned into blackish. The sample was kept on the hot plate for further 1 h under same temperature and stirring conditions. Afterward, the beaker was moved from the hot plate and allowed to cool down to room temperature. The sample was then washed multiple times with deionized water and once with ethanol, and placed in a vacuum oven for 24 h at 70 °C for drying. Lastly, the dried powder was ground and compacted in the form of pellet by applying a pressure of 5 ton per cm2 using hydraulic press and then sintered at 200 °C for 5 h.
Structural characterization was performed using X-ray diffractometer (ARL EQUINOX 3000) with CuKα X-ray source (λ = 1.54 Å). The experimental XRD data was fitted with Rietveld refinement using FullProf software. The morphology of the prepared Fe3O4 nanoparticles was analyzed by high-resolution transmission electron microscopy (HRTEM) and selected area electron diffraction (SAED) using a JEOL JEM-2100F. Elemental analysis was conducted using scanning electron microscopy (VEGA3, TESCAN) equipped with an EDX detector (Oxford Instruments). At room temperature, the 57Fe Mössbauer spectrum of the ground powder was collected at room temperature using 57Co in Rh-matrix source in the transmission geometry. The Mössbauer data were fitted by assuming that all peaks were Lorentzian in shape. Magnetic measurements were made using a Quantum Design Inc. vibrating sample magnetometer (PPMS-VSM). To measure electrical/dielectric properties, the pelletized sample was connected on a probe with copper wires and silver paint. The probe was then connected to dielectric analyzer (Novocontrol Alpha N-Analyzer), which was connected to a computer through fully automated software WINDETA, which calculated different electrical parameters while varying the temperature via a resistive filament mounted inside the probe.
3. Results and discussion
3.1. Structural analysis
X-ray diffraction (XRD) pattern of the pelletized Fe3O4 sample is shown in Fig. 1. All of the obtained diffraction peaks are well-matched with the JCPDS card no. 19-0629, confirming the formation of pure and single-phase spinel structure with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.18 The XRD data was further analyzed by Rietveld refinement using the FullProf software. It can be seen from the figure that the experimentally obtained XRD patterns almost coincide with the calculated XRD patterns with an adequate value of goodness of fit (χ2 = 0.978), showing the best fit to the experimental data. Here, the black colored circle represents the experimental data, the red colored line denotes the calculated intensities, the black vertical lines indicate the allowed Bragg's position, and the blue colored baseline indicates the difference among the calculated and experimental intensities. The estimated values of lattice constant and crystallite size are found to be 8.340 Å and 12 nm, respectively. However, the obtained value of lattice constant is smaller than its bulk counterpart which is attributed to the high surface energy and surface tension, resulting in an overall shrinkage of the lattice.10 Moreover, to illustrate the crystal structure of the spinel Fe3O4, the crystallographic information file was used by employing the VESTA software. A representative 3-D view of Fe3O4 sample is shown in the inset of figure. Here, the solid circles (red colored) indicate oxygen atoms, whereas the tetrahedral and octahedral cation sites are represented in yellow and blue colored regions, respectively. Fe atom is located in the middle of four and six oxygen atoms forming the corners of a regular tetrahedron and octahedron in the unit cell.
m.18 The XRD data was further analyzed by Rietveld refinement using the FullProf software. It can be seen from the figure that the experimentally obtained XRD patterns almost coincide with the calculated XRD patterns with an adequate value of goodness of fit (χ2 = 0.978), showing the best fit to the experimental data. Here, the black colored circle represents the experimental data, the red colored line denotes the calculated intensities, the black vertical lines indicate the allowed Bragg's position, and the blue colored baseline indicates the difference among the calculated and experimental intensities. The estimated values of lattice constant and crystallite size are found to be 8.340 Å and 12 nm, respectively. However, the obtained value of lattice constant is smaller than its bulk counterpart which is attributed to the high surface energy and surface tension, resulting in an overall shrinkage of the lattice.10 Moreover, to illustrate the crystal structure of the spinel Fe3O4, the crystallographic information file was used by employing the VESTA software. A representative 3-D view of Fe3O4 sample is shown in the inset of figure. Here, the solid circles (red colored) indicate oxygen atoms, whereas the tetrahedral and octahedral cation sites are represented in yellow and blue colored regions, respectively. Fe atom is located in the middle of four and six oxygen atoms forming the corners of a regular tetrahedron and octahedron in the unit cell.
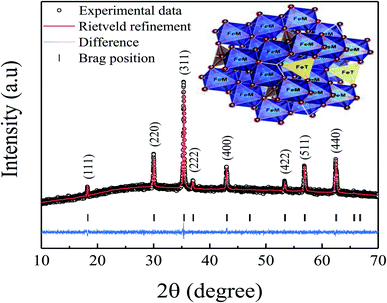 |
| | Fig. 1 X-ray diffraction pattern (experimental and Rietveld refinement) of the prepared Fe3O4 sample. Inset shows a representative 3-D view of spinel Fe3O4 sample. | |
Fig. 2(a) shows the transmission electron microscopy (TEM) image for the prepared Fe3O4 sample which confirmed the development of spherical nanoparticles. While, the inset of Fig. 2(a) displays the particle size distribution which were estimated from the TEM image using ImageJ software. The estimated value of particle size was found to be 11 nm, which is in good agreement with the XRD result. Fig. 2(b) shows the pattern of selected area electron diffraction (SAED) for the prepared nanoparticles which confirms the development of cubic phase, in accordance with the XRD pattern, by showing the bright spots over the concentric rings. Fig. 2(c) shows a HR-TEM image of the prepared nanoparticles which indicates an interplanar spacing of 0.284 nm corresponding to the (220) plane of Fe3O4,19 as confirmed by the line profile. Moreover, the energy dispersive X-ray spectroscopy (EDX) was employed to investigate the elemental composition of the prepared nanoparticles and the elemental mapping, as shown in Fig. 2(d). Here, the EDX spectrum and elemental mapping confirm the existence of Fe and O in the prepared nanoparticles without presence of any impurity. Table 1 shows the elemental compositions present in the prepared nanoparticles that agree with the experimental values, and the crystal structure exhibited a homogeneous chemical composition.
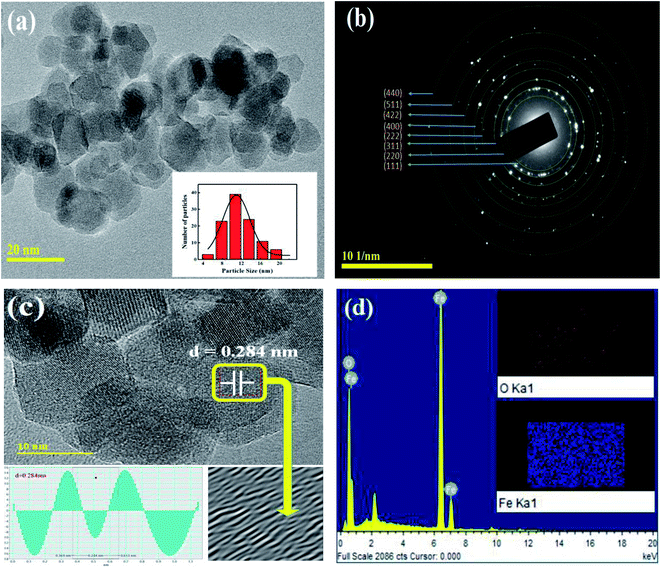 |
| | Fig. 2 (a) TEM micrograph, (b) SAED pattern, (c) HR-TEM image showing the respective plane, and (d) EDX spectrum for the prepared nanoparticles. Insets of (a) and (d) show the particle size distribution and elemental mapping analysis, respectively. | |
Table 1 EDX analysis showing elemental composition for the prepared Fe3O4 nanoparticles
| Element |
Weight% |
Atomic% |
| O K |
24.46 |
53.06 |
| Fe K |
75.54 |
46.94 |
| Totals |
100.00 |
|
3.2. Mössbauer spectroscopy
Mössbauer spectroscopy technique is commonly utilized to investigate the electronic, magnetic, and nuclear structure of iron-containing compounds. Fig. 3 shows the 57Fe Mössbauer spectra at room temperature for the prepared Fe3O4 sample. The hyperfine parameters are tabulated in Table 2. Here, the obtained spectrum was fitted with four well-resolved sextets and a doublet. The sextet with lower isomer shift (IS) is attributed to the tetrahedral (A) site, which contains only Fe3+ ions while the other three sextets are believed to be due to the octahedral (B) site, which corresponds to the random distribution of both Fe3+ and Fe2+ ions. The comparatively larger IS corresponding to the Fe ions are attributed to an effective mean charge of +2.5 at the B-site. This usually happens due to fast charge transfer transition between the Fe3+–Fe2+ centers at the same crystallographic site, which causes delocalization of spin electrons by super-exchange mechanism.20 Furthermore, in nanoparticles the surface layers are more active and have a strong effect on the cationic distribution. Due to these hopping and surface effects, the structural formula for Fe3O4 can be written as [Fe3+]A[Fe2−x2.5+Fex3+]BO42− instead of [Fe3+]A[Fe3+Fe2+]BO42−.21 Moreover, the emergence of a sextet verifies the magnetic behavior of the sample at room temperature while the doublet is assumed to be related to the nanoparticle's super-paramagnetic nature.
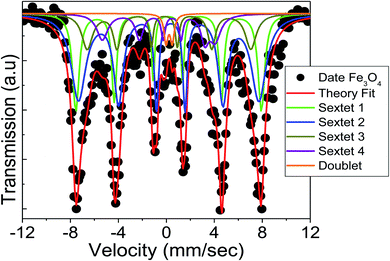 |
| | Fig. 3 Mössbauer spectrum of the prepared Fe3O4 nanoparticles measured at room temperature. | |
Table 2 Mössbauer parameters for the prepared Fe3O4 nanoparticles
| Heff (kOe) |
QS (mm s−1) |
IS (mm s−1) |
Width |
Area (%) |
Sites |
| 479.63 |
0.068 |
0.26 |
0.66 |
32.15 |
A-site Fe3+ (sextet-1) |
| 466.46 |
−0.18 |
0.68 |
1.47 |
45 |
B-site Fe2+ (sextet-2) |
| 423.07 |
0.38 |
0.13 |
1.07 |
11.69 |
B-site Fe3+ (sextet-3) |
| 291.66 |
−1.11 |
0.13 |
1.11 |
9.03 |
Surface Fe3+ (sextet-4) |
| — |
0.52 |
0.33 |
0.40 |
2.13 |
Superparamagnetic (doublet) |
Quadrupole splitting (QS) is another critical Mössbauer parameter for defining the asymmetry of the charge distribution surrounding Fe ions. The strength of the quadrupole interaction is determined by the electric field gradient (EFG) generated by the nucleus's s-electron density. The EFG at the B-site could be a result of the nearest neighbours' deformed octahedral geometry, which results in a non-spherical charge distribution.21 While, the negative QS values may be attributed to the Fe ion's oblate charge distribution.22 It can be observed from Table 2 that the sign of QS changes from Fe3+ to Fe2.5+ in the octahedral B-site, which confirms a charge re-distribution by the surface modification of Fe3O4.
The cation distribution among the A- and B-sites may be determined using the area and intensity of the 2nd and 5th peaks in the normalized Mössbauer data, which are listed in Table 2. It can be observed that the tetrahedral A-site consists of about 32% of trivalent Fe ions and the B-site consists of a mixture of about 11% of trivalent and 45% of divalent Fe ions, while, some 9% of Fe3+ ions reside on the surface. For stoichiometric magnetite, the area ratio of A-site to the B-site remains 0.5. However, in this study, we found that the area ratio of A-site to B-site comes out to be 0.567, which is slightly higher than a perfect stoichiometry. This usually happens due to the strong contribution of the surface layers, which has been observed from the Mössbauer data analysis. Hence, the stoichiometry of the Fe3O4 sample can be written based on Mössbauer data as follows:
| [Fe3+]A[Fe2.912.5+Fe0.093+]BO4 |
3.3. Magnetic properties
Fig. 4(a) shows temperature-dependent magnetic measurements of the prepared Fe3O4 nanoparticles in zero-field (ZFC) and field-cooled (FC) modes using produced nanoparticles and a magnetic field of 50 Oe. The ZFC curve exhibits a broad peak with a maximum at TB = 122 K, corresponding to the average blocking temperature (TB) of nanoparticles. Above TB, the thermal stimulation energy overcomes the anisotropy energy barrier, causing the spins of the nanoparticles to oscillate between their two easy axis directions.23 However, the overlapping of ZFC and FC curves above TB specifies the presence of certain particle size distribution and/or interparticle interactions in the prepared nanoparticles (see Fig. 2(a)).23 Fig. 4(b) shows the hysteresis loop (M–H) of the prepared nanoparticles which was measured by applying a magnetic field of ±20 kOe at room temperature. Here, a symmetric unsaturated hysteresis loop with a small coercive field (Hc) of 18 Oe is observed which shows a superparamagnetic behavior of the prepared Fe3O4 nanoparticles. Moreover, the maximum value of room temperature magnetization (M20kOe) for the prepared nanoparticles is 32 emu g−1 which is obviously lower than that of the bulk Fe3O4 (90 emu g−1) and other reported values for Fe3O4 nanoparticles.24,25 Here, the smaller value of Ms for the prepared nanoparticles can be justified by the smaller particle size effect because a non-collinear spin arrangement occurs effectively at/near the surface, resulting reduced magnetic moment of prepared Fe3O4 nanoparticles.25
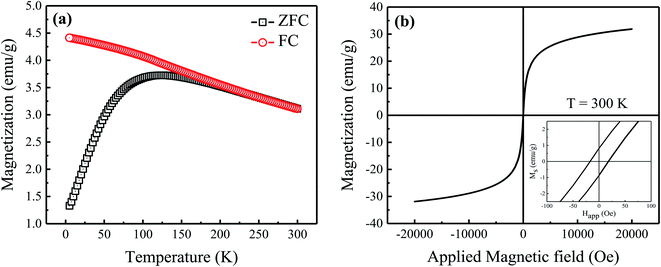 |
| | Fig. 4 (a) Zero-field cooled (ZFC) and field cooled (FC) magnetization measurements, and (b) magnetic hysteresis loop measured at room temperature for the prepared sample. Inset of (b) shows enlarged view of hysteresis loop at low field. | |
3.4. Impedance spectroscopy
The electrical properties of the prepared Fe3O4 nanoparticles were analyzed using a complex impedance spectroscopy. This technique is especially useful in characterizing the electrical properties of electro-ceramic materials like dielectric relaxation and conduction mechanism. Fig. 5(a and b) displays the complex impedance plane plots of the prepared nanoparticles measured at different temperatures (293–373 K). Arrows in the impedance plane plot represents the increasing direction of frequency. Two semicircular arcs are clearly observed for the temperature range from 293 K to 333 K (see Fig. 5(a)); however, above 333 K, a single semicircular arc is only visible (see Fig. 5(b)). Here, the presence of different semicircular arcs represents different electro-active regions arise from the contribution of grains (Gs), grain boundaries (GBs) and/or electrode effect (Es) having dissimilar relaxation times.15 The intercept of these semicircular arcs at x-axis provides the total resistance of the sample. It can be seen from the figure that the diameter of the semicircular arcs reduces with increasing temperature and displays its minima around 313 K. With further increase in temperature, the diameter of the semicircular arcs begins to increase and shows its maxima around 343 K (see Fig. 5(a)). However, beyond 343 K, the diameter of semicircular arc begins to decrease again with increasing temperature (see Fig. 5(b)). Here, the temperatures at which the diameter of the semicircular arcs is minimum and maximum are labeled as semiconductor to metal (SMT) and metal to semiconductor (MST) like transition temperatures, respectively. To obtain a better understanding of these relaxation processes, we have fitted our experimental data with different equivalent circuit models involving a series and parallel combinations of resistance (R), capacitance (C), and constant phase element (Q) using ZView software. Generally, the constant phase element (CPE) is a deviation from the actual capacitative behavior indicating the presence of more than one relaxation phenomena with same relaxation time. The capacitance of CPE is calculated using the relation:| |
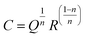 | (1) |
where n represents the dispersion parameter and the value of n is 1 for ideal capacitor and 0 for ideal resistor.15 Fig. 5(c and d) shows the fitting of experimental data recorded at 303 K using the equivalent circuits as shown in the insets of these figures along with their corresponding residuals. Here, the residual is an average deviation of the fitted curve from the measured data points. From these fitting procedures, a clear deviation in the fitting and measured data points is observed along with the poor residuals using the proposed circuit (R1–CPE1)(R2–CPE2)(R3–CPE3), as shown in Fig. 5(c). Since, the series combination of RC circuits with CPE is typically a representation of grains (Gs), grain boundaries (GBs), and electrode effect, which is not suitable here due to the poor quality of fit (see inset of Fig. 5(c)). However, the other combination of (R1–C1–CPE1)(R2–CPE2), as shown in Fig. 5(d), is found to be a good representation of the typical bulk impedance response with different ionic/electronic hopping conductors.26 Therefore, based on the obtained minimum residual value and good fit, we have fitted the obtained complex plane plots at different temperatures (293–373 K) using an equivalent circuit model of (R1–C1–CPE1)(R2–CPE2), as shown in Fig. 5(d). The estimated values of the fitting parameters for each temperature are listed in Table 3. Based on the obtained values of R and C, the semicircular arc at high frequency region is associated with the bulk counterpart of merged Gs-GBs with both capacitance C1 and CPE1 lying within the geometrical values of Gs (10−11 to 10−13 F cm−1).27 The possible reason for the merged Gs-GBs might be due to smaller particle size where Gs have high resistance despite the presence of multiple GBs around them. While the semicircular arcs in the impedance plane plots at low frequencies show the sample-electrode effect with capacitance values comparable to those of the electrode effect (10−6 to 10−7 F cm−1).27 Therefore, the second semicircular arc appearing in the impedance plot at lower frequency might be due to electrode effect (Es); however, this low-frequency semicircular arc disappears above 333 K (see Fig. 5(b)). Beyond 333 K, we have fitted the obtained data using a parallel combination of R1–C1–CPE1 equivalent circuit model. We found that these single semicircular arcs have parameters comparable to the geometrical capacitance for Gs; therefore, these single semicircular arcs are attributed to the contribution of Gs.
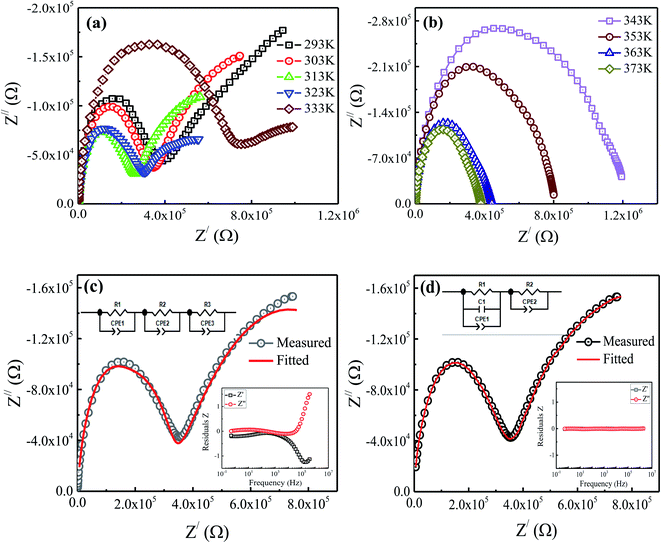 |
| | Fig. 5 (a and b) Impedance plane plots (Z′ vs. Z′′) of prepared sample measured at different temperatures, and (c, d) the fitting of experimental data recorded at 303 K using the equivalent circuits as shown in the insets of these figures along with their corresponding residuals. | |
Table 3 Fitted parameters of Cole–Cole plots (R1, R2, RT, C1, C and C2) and Jonscher's power law (σdc, A, n) for the prepared Fe3O4 nanoparticles
| T (K) |
Equivalent electrical circuit model |
Power law |
| R1 (Ω) |
C1 (F) |
C (F) |
R2 (Ω) |
C2 (F) |
RT (Ω) |
σdc |
A |
n |
| 293 |
4.34 × 105 |
3.25 × 10−12 |
4.67 × 10−12 |
9.02 × 105 |
2.94 × 10−7 |
1.32 × 106 |
1.67 × 10−6 |
7.77 × 10−10 |
0.777 |
| 303 |
3.41 × 105 |
3.20 × 10−12 |
5.20 × 10−12 |
8.32 × 105 |
3.71 × 10−7 |
1.16 × 106 |
1.97 × 10−6 |
8.33 × 10−10 |
0.770 |
| 313 |
2.53 × 105 |
3.18 × 10−12 |
5.25 × 10−12 |
5.97 × 105 |
4.09 × 10−7 |
8.50 × 105 |
2.61 × 10−6 |
1.51 × 10−9 |
0.728 |
| 323 |
2.94 × 105 |
3.14 × 10−12 |
7.88 × 10−12 |
3.98 × 105 |
2.28 × 10−7 |
6.92 × 105 |
2.40 × 10−6 |
2.35 × 10−9 |
0.695 |
| 333 |
7.31 × 105 |
2.79 × 10−12 |
1.16 × 10−11 |
3.22 × 105 |
2.85 × 10−7 |
1.05 × 106 |
1.53 × 10−6 |
1.16 × 10−9 |
0.737 |
| 343 |
1.22 × 106 |
2.55 × 10−12 |
1.14 × 10−11 |
— |
— |
1.22 × 106 |
1.18 × 10−6 |
4.96 × 10−10 |
0.789 |
| 353 |
8.16 × 105 |
2.45 × 10−12 |
5.84 × 10−12 |
— |
— |
8.16 × 105 |
1.90 × 10−6 |
3.44 × 10−10 |
0.813 |
| 363 |
4.44 × 105 |
2.40 × 10−12 |
3.51 × 10−12 |
— |
— |
4.44 × 105 |
3.31 × 10−6 |
3.52 × 10−10 |
0.809 |
| 373 |
3.79 × 105 |
2.28 × 10−12 |
2.65 × 10−12 |
— |
— |
3.79 × 105 |
3.86 × 10−6 |
2.34 × 10−10 |
0.836 |
Fig. 6 shows the variations in the resistance of grains (Gs) and electrode effect (Es) with temperature for the prepared nanoparticles. The inset of figure displays the variation in the total resistance (RT = R1 + R2) with temperature. Here, the initial decreasing trend in the value of resistance with increasing temperature shows the semiconducting behavior. Above 313 K, an increasing trend in the Gs resistance is visible up to 343 K, which exhibits a metal-like behavior. However, the Es and RT resistance still show decreasing trends which might be due to increase in the mobility and decrease in the density of the hopping carriers with temperature. An increasing trend in the value of total resistance (RT) is observed at 323 K as shown in the inset of figure. However, beyond 343 K, the values of Gs and RT begin to decrease again with temperature, representing the recurrence of semiconducting behavior. Generally, the coexistence of exchange and superexchange interactions is responsible for showing insulating, semiconducting, and metallic behavior in the metal oxides at different frequencies and temperatures. Moreover, below the Curie temperature, the presence of cations of the same elements with distinct valence states result in the metallic nature.15 In the present study, the coexistence of Fe3+ and Fe2+ are found to exist in the prepared nanoparticles, as inferred from the Mössbauer measurements. The electrostatic interaction among these different ionic states of metal ions (i.e., cation–anion–cation) causes a formation of relatively less stable doubly degenerate eg electrons and more stable triply degenerate t2g electrons.28 Therefore, to understand the observed semiconductor to metal (SMT) and metal to semiconductor (MST) like transitions at different temperatures, it is necessary to consider the energy of eg electrons as well as the potential for oxygen vacancies. For this, let Ek be the energy of the carriers participating in hopping (i.e., eg electrons), n be the number density of eg electrons, and ϕ be the potential of the oxygen vacancy. Mathematically,
| |
n = no![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) expeϕ/kBTe expeϕ/kBTe
| (2) |
where
no,
e,
kB and
Te are the number density of electrons at
ϕ = 0, charge on a single electron, Boltzmann constant and temperature of e
g electrons.
29 Here it is assumed that below 313 K, the carrier energy is smaller than the applied potential energy (
i.e.,
Ek <
eϕ) due to the presence of some electronic trap center and disorientation of surface/core spins. Thus, the hopping probability of e
g electrons between Fe
3+–O–Fe
3+ network at the B-site increases with increasing temperature up to 313 K, which in turn reduces the resistance of the sample and displays the semiconducting behavior. Above 313 K, the efficient conducting channels begin to appear with further increase in temperature, causing the delocalization of charges and alignment of surface/core spins which satisfies the condition
Ek >
eϕ. These conducting channels in the form of Fe
3+–Fe
2+ network facilitate the electron hopping thereby increasing the mobility of charge carriers and we observe a metal-like behavior up to 343 K. However, above 343 K, the hopping probability of e
g electrons increases again due to increase in the conductivity caused by the un-trapped delocalized charges, which represent the recurrence of semiconducting behavior.
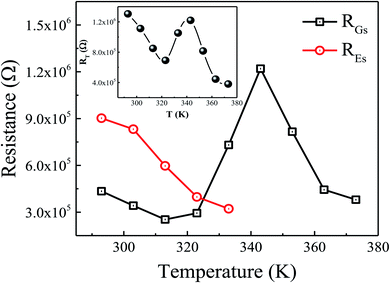 |
| | Fig. 6 Variation in the resistance of grains (RGs) and electrode (REs) with temperature. Inset shows the variation of total resistance (RT) with temperature. | |
To better understand into whether the relaxation process is dominated by short-range or long-range charge carrier movement, Fig. 7(a–c) compares the normalized plots of the imaginary part of modulus (M′′) and impedance (Z′′) as a function of frequency for various representative temperatures. It can be seen from the figure that, within the available frequency window, only one peak is visible in both components of normalized M′′ and Z′′ at higher frequency region. At 303 K (low-temperature semiconducting regime), a distinct mismatch between the two peaks is observed, indicating that charge carriers are localized and that the relaxation process is governed by short-range mobility of charge carriers.30 With the increase in temperature, the observed mismatch between the two peaks decreases at 323 K (intermediate-temperature metal-like regime) which suggests that the conduction process become less localized and translated to long-range mobility of charge carriers (see Fig. 7(b)). However, with increasing temperature, the mismatch between the M′′ and Z′′ becomes nearly same at 363 K (high-temperature semiconducting regime) as shown in Fig. 7(c), indicating the relaxation process is dominated by the long-range movement of charge carriers.30 Hence, the increase of temperature promotes the long-range hopping movement of the charge carriers activated by the lattice oscillations.
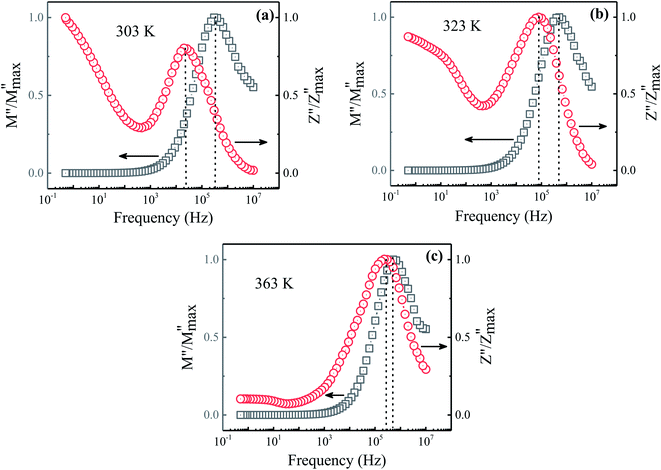 |
| | Fig. 7 Comparison of the imaginary parts of the impedance (Z′) and modulus (M′′) as a function of frequency for the prepared sample at (a) 303 K, (b) 323 K, and (c) 363 K. | |
3.5. AC conductivity
Fig. 8(a) displays the temperature and frequency dependent behavior of AC conductivity (σac) for the prepared Fe3O4 nanoparticles. Here, the frequency-dependent behavior shows a typical trend where the conductivity values are weakly frequency-dependent at low frequency regions and strongly frequency-dependent at high frequency regions, which is in accordance with the Jonscher's power law:| | |
σac(w,T) = σdc(T) + A(T)ωn(T)
| (3) |
where w, σdc, A and n are the angular frequency (w = 2πf), dc conductivity (frequency-independent conductivity), strength of polarizability and slope of the frequency-dependent region (0.0 ≤ n ≤ 1.0), respectively.31 We have fitted the measured data using eqn (3) and found an agreement among the experimental and fitted data within the frequency region (i.e., 102 to 107 Hz). The obtained fitted parameters at different temperatures are tabulated in Table 3. The temperature-dependent dc conductivity (σdc) behavior in Fig. 8(b) shows three thermal activated conductivity regions. The σdc curves transform from semiconductor behavior (region-I: increase of σdc) to metal-like behavior (region-II: decrease of σdc) at T = 313 K with increasing temperature. Afterward, with the further increase in temperature, the metal-like behavior is transformed into second semiconductor behavior (region-III: increase of σdc) above T = 343 K. Here, the observed metal-like behavior in the prepared sample is not considered as a real metallic behavior because of the fact that the σac behavior of the prepared sample follows the Jonscher's power law.9 Thus, the observed metal-like behavior (region-II) at intermediate temperature range (313–343 K) might be due to the presence of trapped conducting charge carriers, which can be evident from the correlation among the disordered surface spins and electronic trap centers at the B-sites. Moreover, in the semiconducting regions (i.e., region-I & III), the linear trends of σdc obey Arrhenius equation as follows:| |
σdc = σo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/kBT) exp(−Ea/kBT)
| (4) |
where σo is the pre-exponential factor, Ea is the activation energy, KB is the Boltzmann's constant and T is the absolute temperature.32 The activation energies (Ea) are found to be 0.262 eV and 1.019 eV in region-I and region-III, respectively. Here, the obtained values of Ea suggest the dominance of hopping of electrons and hole hopping process along with polaron conduction at the low- and high-temperature regimes, respectively.17 Hence, the activation energies estimated for the prepared sample predict both hopping and polaronic conduction mechanisms among the localized sites. Moreover, the inset of Fig. 8(b) displays the variation of slope exponent (n) with temperature. It can be seen that the value of n decreases with increasing temperature up to 323 K and then it begins to increase. Here, the minimum value of n is obtained in the intermediate temperature region (region-II) which might be associated to the charge carrier's delocalized character in comparison to charge localization at low (region-I) and high (region-III) temperatures. However, the observed variation in n(T) reveals that charge conduction in the prepared sample is governed by the overlapping large polaron tunneling (OLPT) mechanism.33
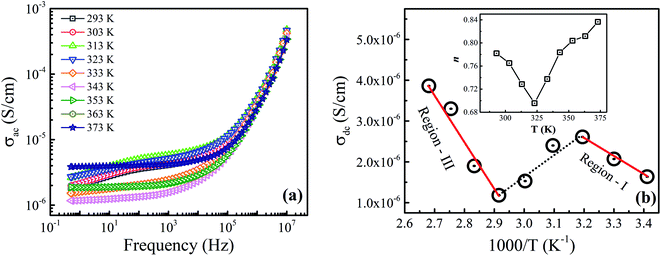 |
| | Fig. 8 (a) Variation of frequency-dependent ac conductivity measured at different temperatures, and (b) the Arrhenius plots of the dc conductivity for the prepared sample. Solid lines show the linear fit to the experimental data. Inset of (b) shows the variation of slope parameter n with temperature. | |
3.6. Dielectric properties
Fig. 9(a) shows the behavior of real part of dielectric permittivity (ε′) measured at different temperatures. The graph shows the typical permittivity vs. frequency pattern where dielectric permittivity values are higher at low frequency region and decreases as frequency increases at all temperatures and displays a constant behavior at higher frequencies. Dispersion in dielectric values could be understood using Maxwell–Wagner polarization model in accordance with Koop's theory.34,35 It is proposed that ferrites are composed of conducting Gs, separated by resistive GBs. At low frequencies, charges transport via Gs to GBs and creating a local lattice distortion by asymmetric charge distribution which moves along the applied field.36 Such type of polarization is known as space charge polarization. But, as frequency increases, this slowly moving lattice distortion (space charge polarization) cannot follow the higher applied field and lag behind, resulting in the decrease of dielectric permittivity values with the increase in frequency. Moreover, the value of dielectric permittivity initially increases as temperature rises to 313 K due to thermally activated dipoles, increasing the electron exchange interaction which results in the increase of dielectric permittivity. Here, the obtained value of dielectric permittivity at room temperature is found to be comparatively higher than the reported ones.37–40 The reason for such a high dielectric permittivity is that the prepared sample has electrical inhomogeneity caused by the Gs and GBs effect. Above 313 K, a decrease in the value of dielectric permittivity is observed due to the delocalization of conducting channels. However, above 343 K, the value of dielectric permittivity begins to increase again due to the oxygen ion hopping at relatively higher temperatures, supporting our earlier MST discussion.
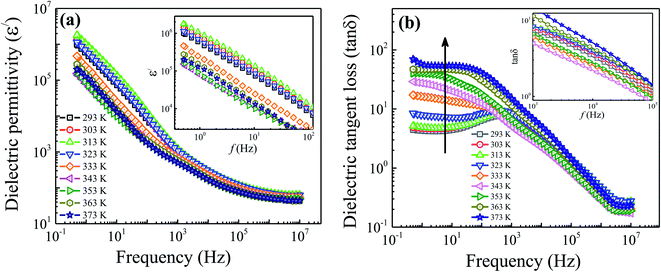 |
| | Fig. 9 Variation of the (a) real part of dielectric permittivity and (b) dielectric tangent loss with frequency measured at different temperatures. Insets of each part show the enlarged view of dielectric permittivity and dielectric tangent loss at low and high frequency regimes, respectively. | |
Fig. 9(b) shows the variation of dielectric tangent loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) vs. frequency for the prepared Fe3O4 nanoparticles measured at different temperatures. It can be seen that, for all temperatures, the value of tangent loss decreases with increasing frequency followed by a peak behavior appearing in the frequency range of 102 to 103 Hz. This peak behavior usually appears when hopping frequency matches the frequency of external applied field.41 Moreover, it can be seen from the figure that the tan
δ) vs. frequency for the prepared Fe3O4 nanoparticles measured at different temperatures. It can be seen that, for all temperatures, the value of tangent loss decreases with increasing frequency followed by a peak behavior appearing in the frequency range of 102 to 103 Hz. This peak behavior usually appears when hopping frequency matches the frequency of external applied field.41 Moreover, it can be seen from the figure that the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ plot exhibit two distinct features. At low frequency region (0.5–103 Hz), the tan
δ plot exhibit two distinct features. At low frequency region (0.5–103 Hz), the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values increase linearly with temperature as indicated by arrow-head. The electrode effect is predominant in our sample at low frequency up to 343 K and then vanished at higher temperatures, as discussed in the impedance section. Therefore, an increasing value of tan
δ values increase linearly with temperature as indicated by arrow-head. The electrode effect is predominant in our sample at low frequency up to 343 K and then vanished at higher temperatures, as discussed in the impedance section. Therefore, an increasing value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ in the low frequency region might be due to the fact that energy is consumed in overcoming the electrode effect. However, the increasing trend of tan
δ in the low frequency region might be due to the fact that energy is consumed in overcoming the electrode effect. However, the increasing trend of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values above 343 K is explained by a drift of surface-spins and appearance of increased conductive channels. While, at high frequency region (103–107 Hz), one can see from the inset of figure that the value of tan
δ values above 343 K is explained by a drift of surface-spins and appearance of increased conductive channels. While, at high frequency region (103–107 Hz), one can see from the inset of figure that the value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ initially increases as temperature rises up to 313 K. This observed increase in tan
δ initially increases as temperature rises up to 313 K. This observed increase in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is accredited to the increase in thermally activated charge carriers showing the semiconducting behavior, as discussed earlier. However, above 313 K (i.e., SMT temperature), the tan
δ is accredited to the increase in thermally activated charge carriers showing the semiconducting behavior, as discussed earlier. However, above 313 K (i.e., SMT temperature), the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ value is found to decrease due to the delocalization of charge carriers. Since, the movement or flipping of delocalized conductive channels with AC-field is easier; therefore, less energy is dissipated which results in the decrease of tan
δ value is found to decrease due to the delocalization of charge carriers. Since, the movement or flipping of delocalized conductive channels with AC-field is easier; therefore, less energy is dissipated which results in the decrease of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values till 343 K. Afterwards, the value of tan
δ values till 343 K. Afterwards, the value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ begins to increase again with temperature which is explained by the increased conductivity values at high temperatures. Here, the obtained values of tan
δ begins to increase again with temperature which is explained by the increased conductivity values at high temperatures. Here, the obtained values of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ for the prepared sample are <0.18 at high frequencies (107 Hz) and found to be comparatively small in comparison to the literature values.37,38 Hence, the reduced value of tan
δ for the prepared sample are <0.18 at high frequencies (107 Hz) and found to be comparatively small in comparison to the literature values.37,38 Hence, the reduced value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ for the prepared sample along with a high dielectric permittivity making these sample interesting for the electromagnetic absorbing material.
δ for the prepared sample along with a high dielectric permittivity making these sample interesting for the electromagnetic absorbing material.
4. Conclusions
In summary, the existence of novel semiconductor–metal-semiconductor (SMST) type of transition has been investigated using impedance spectroscopy technique and we observed a semiconductor–metal transition at 313 K and a metal–semiconductor transition at 343 K in the Fe3O4 nanoparticles. Here, the dominating cause for the existence of SMST is described by the coexistence of exchange and superexchange mechanisms and conductivity on the basis of doubly degenerate eg levels and relatively more stable triply degenerate t2g levels. Moreover, we found that both short-range and long-range movements of charge carriers governs the conduction process in the sample. While the presence of metal-like behavior at intermediate temperature could be a result of the semiconductor state transitioning from short-range to long-range conduction at low and high temperatures, respectively. The prepared sample also exhibits a colossal dielectric permittivity at room temperature compared to the values reported for other spinel ferrite systems. The origin of such high dielectric permittivity lies in the sample's electrical inhomogeneity caused by the Gs and GBs effect. Hence, from this work, it can be concluded that the colossal dielectric permittivity, reduced tangent loss, high conductivity and moderate magnetization values make Fe3O4 nanoparticles as a potential candidate for electromagnetic absorbing material. However, to understand whether the SMST transition found in Fe3O4 nanoparticles is an intrinsic/reversible properties of the system, more experiments are in progress.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Authors appreciate the financial support provided by the Higher Education Commission (HEC), Pakistan, via research grant no. TDF-044/2017.
References
- H. Y. Huang, Z. Y. Chen, R.-P. Wang, F. M. F. de Groot, W. B. Wu, J. Okamoto, A. Chainani, A. Singh, Z.-Y. Li, J.-S. Zhou, H.-T. Jeng, G. Y. Guo, J.-G. Park, L. H. Tjeng, C. T. Chen and D. J. Huang, Jahn-Teller distortion driven magnetic polarons in magnetite, Nat. Commun., 2017, 8(1), 15929 CrossRef CAS PubMed.
- J. Smit and H. P. J. Wijn, Ferrites: Physical Properties of Ferrimagnetic Oxides in Relation to their Technical Applications, Eindhoven Philips Technical Library, 1959 Search PubMed.
- E. J. W. Verwey, Electronic Conduction of Magnetite (Fe3O4) and its Transition Point at Low Temperatures, Nature, 1939, 144, 327–328 CrossRef CAS.
- H. Liu and C. Di Valentin, Band Gap in Magnetite above Verwey Temperature Induced by Symmetry Breaking, J. Phys. Chem. C, 2017, 121(46), 25736–25742 CrossRef CAS PubMed.
- A. Mitra, J. Mohapatra, S. S. Meena, C. V. Tomy and M. Aslam, Verwey Transition in Ultrasmall-Sized Octahedral Fe3O4 Nanoparticles, J. Phys. Chem. C, 2014, 118(33), 19356–19362 CrossRef CAS.
- T. Dippong, E. A. Levei and O. Cadar, Recent Advances in Synthesis and Applications of MFe2O4 (M = Co, Cu, Mn, Ni, Zn) Nanoparticles, Nanomaterials, 2021, 11, 1560 CrossRef CAS PubMed.
- R. Zhang, L. Sun, Z. Wang, W. Hao, E. Cao and Y. Zhang, Dielectric and magnetic properties of CoFe2O4 prepared by sol-gel auto-combustion method, Mater. Res. Bull., 2018, 98, 133–138 CrossRef CAS.
- R. S. Yadav, I. Kuřitka, J. Vilcakova, T. Jamatia, M. Machovsky, D. Skoda, P. Urbánek, M. Masař, M. Urbánek, L. Kalina and J. Havlica, Impact of sonochemical synthesis condition on the structural and physical properties of MnFe2O4 spinel ferrite nanoparticles, Ultrason. Sonochem., 2020, 61, 104839 CrossRef PubMed.
- R. N. Bhowmik and A. K. Sinha, Improvement of room temperature electric polarization and ferrimagnetic properties of Co1.25Fe1.75O4 ferrite by heat treatment, J. Magn. Magn. Mater., 2017, 421, 120–131 CrossRef CAS.
- M. Atif and M. Nadeem, Sol–gel synthesis of nanocrystalline Zn1-xNixFe2O4 ceramics and its structural, magnetic and dielectric properties, J. Sol-Gel Sci. Technol., 2014, 72, 615–626 CrossRef CAS.
- T. Dabbebi, S. Hcini, B. Alzahrani, H. Rahmouni, E. Dhahri, H. Al Robei and M. L. Bouazizi, Structural and dielectric behaviors for Mg0.5Co0.5Fe2O4 spinel ferrite synthesized by sol–gel route, J. Mater. Sci.: Mater. Electron., 2021, 33, 490–504 CrossRef.
- M. A. Almessiere, Y. Slimani, H. Güngüneş, A. D. Korkmaz, S. V. Trukhanov, S. Guner, F. Alahmari, A. V. Trukhanov and A. Baykal, Correlation between chemical composition, electrical, magnetic and microwave properties in Dy-substituted Ni-Cu-Zn ferrites, Mater. Sci. Eng. B, 2021, 270 CrossRef CAS.
- A. u. Rahman, M. A. Rafiq, S. Karim, K. Maaz, M. Siddique and M. M. Hasan, Semiconductor to metallic transition and polaron conduction in nanostructured cobalt ferrite, J. Phys. D: Appl. Phys., 2011, 44, 165404 CrossRef.
- M. Bastianello, S. Gross and M. T. Elm, Thermal stability, electrochemical and structural characterization of hydrothermally synthesised cobalt ferrite (CoFe2O4), RSC Adv., 2019, 9, 33282–33289 RSC.
- M. Younas, M. Nadeem, M. Atif and R. Grossinger, Metal-semiconductor transition in NiFe2O4 nanoparticles due to reverse cationic distribution by impedance spectroscopy, J. Appl. Phys., 2011, 109, 093704 CrossRef.
- R. N. Bhowmik and K. S. A. Kumar, Role of pH value during material synthesis and grain–grain boundary contribution on the observed semiconductor to metal like conductivity
transition in Ni1.5Fe1.5O4 spinel ferrite, Mater. Chem. Phys., 2016, 177, 417–428 CrossRef CAS.
- Z. G. Özdemir, M. Kılıç, Y. Karabul, B. S. Mısırlıoğlu, Ö. Çakır and N. D. Kahya, A transition in the electrical conduction mechanism of CuO/CuFe2O4 nanocomposites, J. Electroceram., 2020, 44, 1–15 CrossRef.
- H. He, Y. Zhong, X. Liang, W. Tan, J. Zhu and C. Y. Wang, Natural magnetite: an efficient catalyst for the degradation of organic contaminant, Sci. Rep., 2015, 5, 10139 CrossRef CAS PubMed.
- A. Rajan, M. Sharma and N. K. Sahu, Assessing magnetic and inductive thermal properties of various surfactants functionalised Fe3O4 nanoparticles for hyperthermia, Sci. Rep., 2020, 10, 15045 CrossRef PubMed.
- T. Douglas, D. P. E. Dickson, S. Betteridge, J. Charnock, C. D. Garner and S. Mannt, Synthesis and Structure of an Iron(III) Sulfide-Ferritin Bioinorganic Nanocomposite, Science, 1995, 269, 54 CrossRef CAS PubMed.
- P. Gütlich, E. Bill and A. Trautwein, Mössbauer Spectroscopy and Transition Metal Chemistry: Fundamentals and Applications, Springer Berlin Heidelberg, 2010 Search PubMed.
- Y. Tian, B. B. Yu, X. Li and K. Li, Facile solvothermal synthesis of monodisperse Fe3O4 nanocrystals with precise size control of one nanometre as potential MRI contrast agents, J. Mater. Chem., 2011, 21, 2476–2481 RSC.
- M. Atif, Synthesis and temperature dependent magnetic properties of nanocrystalline Ni0.5Zn0.5Fe2O4 ferrites, Mater. Res. Express, 2019, 6, 076104 CrossRef CAS.
- K. Tao, H. Dou and K. Sun, Interfacial coprecipitation to prepare magnetite nanoparticles: concentration and temperature dependence, Colloids Surf., A, 2008, 320(1–3), 115–122 CrossRef CAS.
- Y. Wei, B. Han, X. Hu, Y. Lin, X. Wang and X. Deng, Synthesis of Fe3O4 Nanoparticles and their Magnetic Properties, Procedia Eng., 2012, 27, 632–637 CrossRef CAS.
- M. A. Hernandez and A. R. West, Dipolar relaxation and impedance of an yttria-stabilised zirconia ceramic electrolyte, J. Mater. Chem. A, 2016, 4(4), 1298–1305 RSC.
- J. T. S. Irvine, D. C. Sinclair and A. R. West, Electroceramics: Characterization by Impedance Spectroscopy, Adv. Mater., 1990, 2, 132 CrossRef CAS.
- K. S. Aneeshkumar and R. N. Bhowmik, Semiconductor to metallic type transition in Ni1.5Fe1.5O4 ferrite, AIP Conf. Proc., 2016, 1731, 110015 CrossRef.
- I. Bunget and M. Popescu, Physics of Solid Dielectrics, Editura Stiinsificâ Si Enciclopedicã, Bucharest, 1978 Search PubMed.
- R. Gerhardt, Impedance and dielectric spectroscopy revisited: distinguishing localized relaxation from long-range conductivity, J. Phys. Chem. Solids, 1994, 55, 1491 CrossRef CAS.
- A. K. Jonscher, Dielectric relaxations in solids, Chelsea Dielectrics, London, 1983 Search PubMed.
- E. Barsoukov and J. R. Macdonald, Impedance Spectroscopy Theory, Experiments and Applications, Wiley, New York, 2005 Search PubMed.
- A. Arunkumar, D. Vanidha, K. Oudayakumar, S. Rajagopan and R. Kannan, Metallic magnetism and change of conductivity in the nano to bulk transition of cobalt ferrite, J. Appl. Phys., 2013, 114, 183905 CrossRef.
- K. W. Wagner, The distribution of relaxation times in typical dielectrics, Ann. Phys., 1993, 40, 817–819 Search PubMed.
- C. G. Koops, On the dispersion of resistivity and dielectric constant of some semiconductors at audio frequencies, Phys. Rev., 1951, 83, 121 CrossRef CAS.
- M. Atif, T. Rafique, A. U. Rehman, H. Wahab, W. Khalid, Z. Ali and M. Nadeem, Effect of cation distribution on the structural and dielectric properties of Ni0.5-xCoxZn0.5Fe2O4 (0.0 ≤ x ≤ 0.5) ferrites, J. Mater. Sci.: Mater. Electron., 2020, 31, 10970–10980 CrossRef CAS.
- A. Radoń, D. Łukowiec, M. Kremzer, J. Mikuła and P. Włodarczyk, Electrical conduction mechanism and dielectric properties of spherical shaped Fe3O4 nanoparticles synthesized by co-precipitation method, Materials, 2018, 11, 735 CrossRef PubMed.
- Zulfiqar, S. Afzal, R. Khan, T. Zeb, M. ur Rahman, Burhanullah, S. Ali, G. Khan, Z. ur Rahman and A. Hussain, Structural, optical, dielectric and magnetic properties of PVP coated magnetite (Fe3O4) nanoparticles, J. Mater. Sci.: Mater. Electron., 2018, 29, 20040–20050 CrossRef CAS.
- N. Kumari, V. Kumar and S. K. Singh, Synthesis, Structural and dielectric properties of Cr3+ substituted Fe3O4 nano-particles, Ceram. Int., 2014, 40, 12199–12205 CrossRef CAS.
- A. A. Azab and E. M. El-Menyawy, Effect of cobalt dopant on the structural, magnetic and dielectric properties of Fe3O4 nanoparticles prepared by co-precipitation method, J. Electron. Mater., 2019, 48, 3229–3238 CrossRef CAS.
- M. Atif, M. Nadeem, R. Grossinger and R. Sato Turtelli, J. Alloys Compd., 2011, 509, 5720–5724 CrossRef CAS.
Footnote |
| † Dedicated to M. Younas (1982–2021) for his contributions to the field of dielectric materials. |
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
M. Atif
a,
M. Atif *a,
M. Younas
*a,
M. Younas b,
T. Rafiquea,
H. Wahabb,
A. Ul-Hamidc,
N. Iqbal
b,
T. Rafiquea,
H. Wahabb,
A. Ul-Hamidc,
N. Iqbal d,
Z. Alia,
W. Khalida and
M. Nadeemb
d,
Z. Alia,
W. Khalida and
M. Nadeemb
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. However, 57Fe Mössbauer spectroscopy suggested the presence of Fe3+ and Fe2.5+ (mixed Fe3+ and Fe2+) ions at the tetrahedral and octahedral sites of the inverse spinel structure, respectively. Impedance spectroscopy measurements showed a discontinues variation in the temperature dependence of the sample's resistive behavior, indicating the appearance of semiconductor–metal–semiconductor like transitions between the temperature range of 293 and 373 K. A similar dual transition was also observed from the dielectric and conductivity measurements around the same temperature regions. The observed unusual transition is explained in term of the competitive effects among the hopping of localized/delocalized and short-range/long-range charge carriers present in the sample. Moreover, the prepared sample exhibits colossal dielectric permittivity (∼106), reduced tangent loss (∼0.2) and moderate conductivity (>10−6 S cm−1) values, making Fe3O4 nanoparticles a potential candidate for electromagnetic absorbing materials.
m. However, 57Fe Mössbauer spectroscopy suggested the presence of Fe3+ and Fe2.5+ (mixed Fe3+ and Fe2+) ions at the tetrahedral and octahedral sites of the inverse spinel structure, respectively. Impedance spectroscopy measurements showed a discontinues variation in the temperature dependence of the sample's resistive behavior, indicating the appearance of semiconductor–metal–semiconductor like transitions between the temperature range of 293 and 373 K. A similar dual transition was also observed from the dielectric and conductivity measurements around the same temperature regions. The observed unusual transition is explained in term of the competitive effects among the hopping of localized/delocalized and short-range/long-range charge carriers present in the sample. Moreover, the prepared sample exhibits colossal dielectric permittivity (∼106), reduced tangent loss (∼0.2) and moderate conductivity (>10−6 S cm−1) values, making Fe3O4 nanoparticles a potential candidate for electromagnetic absorbing materials.![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. In the inverse spinel structure, 1/3 of the Fe ions are located in the tetrahedral (A) sites as Fe3+ while the rest are located in octahedral (B) sites as Fe2.5+ in a closely packed array of oxygen atoms.1 Th ferrimagnetic nature is caused by the ferromagnetic sub-lattices (A- and B-sites) and their mutual antiferromagnetic interaction. Fe3O4 has the highest value of magnetization, i.e., M = 4.2 μB below the Curie temperature (Tc = 850 K) and electrically is a good semiconducting material at room temperature and above.1,2 However, on decreasing the temperature, the semiconducting behavior of Fe3O4 changed into metallic character along with a decrease in the conductivity by two orders of magnitude due to a structural phase transition from cubic to monoclinic and charge-orbital ordering.3 This unusual transition usually occurs at Tv ≈ 120 K and is termed a Verwey transition; however, this Verwey transition temperature (Tv) is found to be quite sensitive to the stoichiometry of the constituents in Fe3O4.4 Although, the Verwey transition has a low operating temperature for most of the practical applications, it plays a vital role in the importance of iron based materials (ferrites) due to their promising applications in spintronics and nano-electronic switching devices.5
m. In the inverse spinel structure, 1/3 of the Fe ions are located in the tetrahedral (A) sites as Fe3+ while the rest are located in octahedral (B) sites as Fe2.5+ in a closely packed array of oxygen atoms.1 Th ferrimagnetic nature is caused by the ferromagnetic sub-lattices (A- and B-sites) and their mutual antiferromagnetic interaction. Fe3O4 has the highest value of magnetization, i.e., M = 4.2 μB below the Curie temperature (Tc = 850 K) and electrically is a good semiconducting material at room temperature and above.1,2 However, on decreasing the temperature, the semiconducting behavior of Fe3O4 changed into metallic character along with a decrease in the conductivity by two orders of magnitude due to a structural phase transition from cubic to monoclinic and charge-orbital ordering.3 This unusual transition usually occurs at Tv ≈ 120 K and is termed a Verwey transition; however, this Verwey transition temperature (Tv) is found to be quite sensitive to the stoichiometry of the constituents in Fe3O4.4 Although, the Verwey transition has a low operating temperature for most of the practical applications, it plays a vital role in the importance of iron based materials (ferrites) due to their promising applications in spintronics and nano-electronic switching devices.5
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.18 The XRD data was further analyzed by Rietveld refinement using the FullProf software. It can be seen from the figure that the experimentally obtained XRD patterns almost coincide with the calculated XRD patterns with an adequate value of goodness of fit (χ2 = 0.978), showing the best fit to the experimental data. Here, the black colored circle represents the experimental data, the red colored line denotes the calculated intensities, the black vertical lines indicate the allowed Bragg's position, and the blue colored baseline indicates the difference among the calculated and experimental intensities. The estimated values of lattice constant and crystallite size are found to be 8.340 Å and 12 nm, respectively. However, the obtained value of lattice constant is smaller than its bulk counterpart which is attributed to the high surface energy and surface tension, resulting in an overall shrinkage of the lattice.10 Moreover, to illustrate the crystal structure of the spinel Fe3O4, the crystallographic information file was used by employing the VESTA software. A representative 3-D view of Fe3O4 sample is shown in the inset of figure. Here, the solid circles (red colored) indicate oxygen atoms, whereas the tetrahedral and octahedral cation sites are represented in yellow and blue colored regions, respectively. Fe atom is located in the middle of four and six oxygen atoms forming the corners of a regular tetrahedron and octahedron in the unit cell.
m.18 The XRD data was further analyzed by Rietveld refinement using the FullProf software. It can be seen from the figure that the experimentally obtained XRD patterns almost coincide with the calculated XRD patterns with an adequate value of goodness of fit (χ2 = 0.978), showing the best fit to the experimental data. Here, the black colored circle represents the experimental data, the red colored line denotes the calculated intensities, the black vertical lines indicate the allowed Bragg's position, and the blue colored baseline indicates the difference among the calculated and experimental intensities. The estimated values of lattice constant and crystallite size are found to be 8.340 Å and 12 nm, respectively. However, the obtained value of lattice constant is smaller than its bulk counterpart which is attributed to the high surface energy and surface tension, resulting in an overall shrinkage of the lattice.10 Moreover, to illustrate the crystal structure of the spinel Fe3O4, the crystallographic information file was used by employing the VESTA software. A representative 3-D view of Fe3O4 sample is shown in the inset of figure. Here, the solid circles (red colored) indicate oxygen atoms, whereas the tetrahedral and octahedral cation sites are represented in yellow and blue colored regions, respectively. Fe atom is located in the middle of four and six oxygen atoms forming the corners of a regular tetrahedron and octahedron in the unit cell.

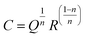
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) expeϕ/kBTe
expeϕ/kBTe


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/kBT)
exp(−Ea/kBT)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) vs. frequency for the prepared Fe3O4 nanoparticles measured at different temperatures. It can be seen that, for all temperatures, the value of tangent loss decreases with increasing frequency followed by a peak behavior appearing in the frequency range of 102 to 103 Hz. This peak behavior usually appears when hopping frequency matches the frequency of external applied field.41 Moreover, it can be seen from the figure that the tan
δ) vs. frequency for the prepared Fe3O4 nanoparticles measured at different temperatures. It can be seen that, for all temperatures, the value of tangent loss decreases with increasing frequency followed by a peak behavior appearing in the frequency range of 102 to 103 Hz. This peak behavior usually appears when hopping frequency matches the frequency of external applied field.41 Moreover, it can be seen from the figure that the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ plot exhibit two distinct features. At low frequency region (0.5–103 Hz), the tan
δ plot exhibit two distinct features. At low frequency region (0.5–103 Hz), the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values increase linearly with temperature as indicated by arrow-head. The electrode effect is predominant in our sample at low frequency up to 343 K and then vanished at higher temperatures, as discussed in the impedance section. Therefore, an increasing value of tan
δ values increase linearly with temperature as indicated by arrow-head. The electrode effect is predominant in our sample at low frequency up to 343 K and then vanished at higher temperatures, as discussed in the impedance section. Therefore, an increasing value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ in the low frequency region might be due to the fact that energy is consumed in overcoming the electrode effect. However, the increasing trend of tan
δ in the low frequency region might be due to the fact that energy is consumed in overcoming the electrode effect. However, the increasing trend of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values above 343 K is explained by a drift of surface-spins and appearance of increased conductive channels. While, at high frequency region (103–107 Hz), one can see from the inset of figure that the value of tan
δ values above 343 K is explained by a drift of surface-spins and appearance of increased conductive channels. While, at high frequency region (103–107 Hz), one can see from the inset of figure that the value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ initially increases as temperature rises up to 313 K. This observed increase in tan
δ initially increases as temperature rises up to 313 K. This observed increase in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is accredited to the increase in thermally activated charge carriers showing the semiconducting behavior, as discussed earlier. However, above 313 K (i.e., SMT temperature), the tan
δ is accredited to the increase in thermally activated charge carriers showing the semiconducting behavior, as discussed earlier. However, above 313 K (i.e., SMT temperature), the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ value is found to decrease due to the delocalization of charge carriers. Since, the movement or flipping of delocalized conductive channels with AC-field is easier; therefore, less energy is dissipated which results in the decrease of tan
δ value is found to decrease due to the delocalization of charge carriers. Since, the movement or flipping of delocalized conductive channels with AC-field is easier; therefore, less energy is dissipated which results in the decrease of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values till 343 K. Afterwards, the value of tan
δ values till 343 K. Afterwards, the value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ begins to increase again with temperature which is explained by the increased conductivity values at high temperatures. Here, the obtained values of tan
δ begins to increase again with temperature which is explained by the increased conductivity values at high temperatures. Here, the obtained values of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ for the prepared sample are <0.18 at high frequencies (107 Hz) and found to be comparatively small in comparison to the literature values.37,38 Hence, the reduced value of tan
δ for the prepared sample are <0.18 at high frequencies (107 Hz) and found to be comparatively small in comparison to the literature values.37,38 Hence, the reduced value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ for the prepared sample along with a high dielectric permittivity making these sample interesting for the electromagnetic absorbing material.
δ for the prepared sample along with a high dielectric permittivity making these sample interesting for the electromagnetic absorbing material.





