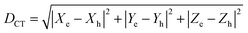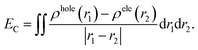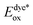Open Access Article
Open Access ArticleUV-selective organic absorbers for the cosensitization of greenhouse-integrated dye-sensitized solar cells: synthesis and computational study†
Rua B. Alnomana,
Eman Nabil *b,
Shazia Parveen
*b,
Shazia Parveen a,
Mohamed Hagar
a,
Mohamed Hagar ab and
Mohamed Zakaria*b
ab and
Mohamed Zakaria*b
aDepartment of Chemistry, Faculty of Science, Taibah University, Yanbu, 46423, Saudi Arabia
bDepartment of Chemistry, Faculty of Science, Alexandria University, Alexandria 21321, Egypt. E-mail: mohamed.zakaria@alexu.edu.eg; eman.nabil@alexu.edu.eg
First published on 12th April 2022
Abstract
Molecular cosensitization is favorable for manipulating solar radiation through the judicious choice of cosensitizers having complementary absorption spectra. For greenhouse-integrated dye-sensitized solar cells (DSCs), the manipulation of solar radiation is crucial in order to maximize the flow of photosynthetically active radiation (PAR) for the effectual photosynthetic activity of plants; meanwhile, non-PAR is utilized in agrivoltaics for generating electricity. In this study, we report the synthesis of novel four UV-selective absorbers, based on the diimide scaffold, functionalized with carboxylate and pyridyl anchoring groups, for adequate adsorption onto the TiO2 electrode in DSC. The UV/Vis absorption spectra of the DMF solution-based free dyes were measured experimentally. Basic photophysical and energetics requirements for operating greenhouse-integrated DSCs were examined at the molecular level via (time-dependent) density functional theory-based calculations. The computational results revealed the outperformance of the biphenyldiimide-structured DI-CA1 dye, especially for maximum charge transferred to its anchor, lower thermodynamic barrier for dissociating the photogenerated exciton, largest Stokes' shift, strong electronic coupling with TiO2 nanoparticles, and higher degree of charge separation at the DI-CA1/TiO2 interface. PDOS showed deeper existence for the LUMO level in the CB of TiO2, which expedites the electron injection process. The chemical and optical compatibility of DI-CA1 were then investigated as a potential cosensitizer of a reference BTD–DTP1, a green light-absorbing dye. Considerable overlap between the fluorescence spectrum of DI-CA1 and absorption spectrum of the reference BTD–DTP1 advocated the opportunity of excitation energy transfer via the radiative trivial reabsorption mechanism, which confirms the cosensitization functionality. Energy decomposition analysis and reduced density gradient maps estimated the chemical compatibility owing to weak dispersion interactions as the dominant stabilizing attractive force. This noncovalent functionalization retains the chemical compatibility without distorting the π–π conjugation and the associated physicochemical properties of the individual dye molecules. Along with the expanded consumption of non-photosynthetically active solar radiation, an improved power conversion efficiency of greenhouse-integrated DSC is accordingly expected.
1. Introduction
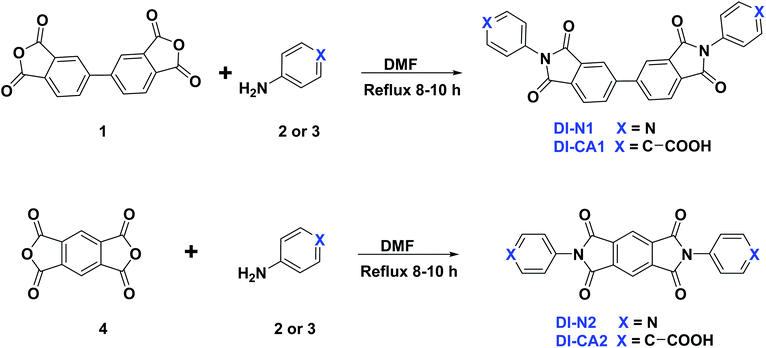
A sustainable socioeconomic development requires renewable energy (RE) at an affordable rate with low environmental impacts and low greenhouse gas (GHG) emissions to mitigate climate change. In the field of solar energy, dye-sensitized solar cells (DSCs) is an attractive third-generation eco-friendly solar energy technology with low cost of fabrication, tunability, short energy payback time, and remarkable performance in diffuse or ambient sunlight conditions without suffering from the angular dependence of incident light.1 Moreover, DSCs represent the only truly transparent type of building-integrated (BI) and automotive-integrated (AI) photovoltaic (PV) devices, besides being one of the most promising candidates of portable energy supply.2,3 DSCs are also advantageous for agrivoltaics, which integrates PVs into agricultural settings, such as greenhouses, aiming at harvesting solar energy without hampering plant growth and crop productivity.4,5 The first DSC device was reported by O'Regan and Grätzel who achieved a photoactive bandgap-engineered semiconducting oxide (TiO2) via sensitization with the organometallic dye adsorbed on semiconductor nanoparticles.6 Similar to doping semiconductor, the objective of the sensitization approach is to provide the excitation energy, though not essentially the bandgap, which is comparable to the energy of photons in a definite part of the solar emission spectrum. However, in a sensitized semiconductor, the bandgap is defined primarily by the nature of the photosensitizer with distinct dynamics of the photogenerated electron, wherein the photosensitizing dye is the accountable component for capturing light energy and generating photoexcited electron, which is subsequently injected into the conduction band (CB) of the semiconductor.7 In a working DSC device, the redox mediator (I−/I3− or Co3+/Co2+) serves to close this electric circuit by transferring the electron to the oxidized dye and restoring it to its neutral charge, making a new photoexcitation cycle possible. One of the emerging strategies to tailor the absorption coverage of the solar emission spectrum and to improve the power conversion efficiency (PCE) of DSC is the cosensitization of the semiconducting electrode with two or more dyes having complementary absorption spectra.8 The cosensitization technique usually aims at affording panchromatic optical absorption emulating that of the solar spectrum. This is achievable by the coadsorption of opaque cosensitizers having optical profiles that cover the entire visible and near-infrared (NIR) regions of the solar spectrum.9 Contrastively, cosensitization can be employed in colored see-through DSC, which is fabricated with cosensitizers having little absorption in the high human-eye-sensitivity region (500–600 nm).2 Fully transparent and colorless DSCs devices can also be attained with cosensitizers selectively absorbing in the ultraviolet (UV) and NIR regions of the solar spectrum, through which only the nonvisible part of the solar spectrum is converted into electricity.10,11 Overall, the cosensitization technique is favorable for manipulating solar radiation through the optimum choice of cosensitizers. In the context of greenhouse-integrated DSC agrivoltaics, the manipulation of solar radiation is extremely crucial to maximize the flow of photosynthetically active radiation (PAR) into the interior space of the greenhouse, i.e., blue light (425–475 nm) and red light (625–750 nm), to be captured by chlorophyll a and b pigments, as well as phytochromes in plants, so as to drive photosynthesis. In the meanwhile, the unused radiation (non-PAR) is to be utilized by the integrated DSC for electricity production. The non-PAR is the light that falls outside these wavelengths including infrared (IR) and UV radiation, as well as the green light in the visible region.12 Dessì et al. recently reported the fabrication of greenhouse-integrated DSC systems utilizing three organic dyes, which are intensely absorb only the green light of the visible spectrum, whilst maintaining good transmittance in the red and blue regions as the two photosynthetically active regions.13 One of these dyes is the BTD–DTP1 dye, which is based on the benzothiadiazole (BTD)–dithienopyrrole (DTP) scaffold. It provided an energy conversion efficiency up to 8.18% and 8.77% in THF and chlorobenzene solvents, respectively. The measured maximum light absorption (λmax) was found to be centered in the green region of the spectrum at 532 nm, and the reported incident-photon-to-current-efficiency (IPCE) reached 80% at ca. 500 nm in THF solvent. On the other hand, diimides, a subclass of rylenes dyes, have tunable electronic properties as well as chemical, thermal, and photochemical stability with near-unity fluorescence quantum yields.14,15 In this context, we report the synthesis and spectroscopic properties of four new symmetrical UV-selective organic dyes based on diimides (DI-CA and DI-N) incorporating carboxyl and pyridyl anchoring groups. Computational quantum chemical investigation was subsequently performed to explore the potential application of the synthesized diimides as photosensitizers in DSCs and as promising cosensitizers of the green-selective BTD–DTP1 organic dye, as reported by Dessì et al.13 Evidently, an entirely organic mix of UV-selective diimides and green-selective BTD–DTP1 dyes would represent a good scenario from a purely environmentally sustainable perspective. In addition, it provides a rational approach to enhance the overall efficiency, and in the meantime, retain good transmittance in the photosynthetically active regions for greenhouse-integrated DSC applications.2. Methodology
2.1. Experimental methods and materials
All commercial chemicals and analytical reagents were purchased from Sigma-Aldrich and used as received (purity 99%). The progress of the reactions was monitored using thin layer chromatography (TLC) on silica gel 60 F254 E-Merck (layer thickness 0.2 mm) plates with a hexane–ethyl acetate (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 v/v) mobile phase, wherein the spots were visualized under a UV lamp at λ = 254 nm. Melting points were recorded on a Melt-Temp apparatus and were uncorrected. Infrared (IR) spectra were recorded in a KBr matrix using a Unicam SP 1025 spectrophotometer within the range of 400–4000 cm−1. The 1H NMR (400 MHz) and 13C NMR (100 MHz) spectra were recorded using a Bruker NMR spectrometer with TMS (0.00) as an internal standard to calibrate the chemical shifts (δ) reported in ppm. The UV-Vis absorption spectra of the solution-based free dyes were measured in N,N-dimethylformamide (DMF) using a ThermoScientific Evolution 201/220 UV-Visible Spectrophotometer. The uncertainty in the UV/vis measurement is 2 nm.
9 v/v) mobile phase, wherein the spots were visualized under a UV lamp at λ = 254 nm. Melting points were recorded on a Melt-Temp apparatus and were uncorrected. Infrared (IR) spectra were recorded in a KBr matrix using a Unicam SP 1025 spectrophotometer within the range of 400–4000 cm−1. The 1H NMR (400 MHz) and 13C NMR (100 MHz) spectra were recorded using a Bruker NMR spectrometer with TMS (0.00) as an internal standard to calibrate the chemical shifts (δ) reported in ppm. The UV-Vis absorption spectra of the solution-based free dyes were measured in N,N-dimethylformamide (DMF) using a ThermoScientific Evolution 201/220 UV-Visible Spectrophotometer. The uncertainty in the UV/vis measurement is 2 nm.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 v/v) was used to monitor the four reactions, and after completion, the reaction mixtures were allowed to cool. The formed precipitates were subsequently collected by filtration, washed with ethanol, and recrystallized from DMF to afford the targeted products.
9 v/v) was used to monitor the four reactions, and after completion, the reaction mixtures were allowed to cool. The formed precipitates were subsequently collected by filtration, washed with ethanol, and recrystallized from DMF to afford the targeted products.
Characterization of 2,2′-di(pyridin-4-yl)-[5,5′-biisoindoline]-1,1′,3,3′-tetraone, DI-N1. This compound was obtained in 81% yield; mp: 298, IR (ν, cm−1): 1776 and 1727 (asymmetric and symmetric C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); 1589 (C
O); 1589 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N). 1H NMR (400 MHz, DMSO-d6): δppm 8.95 (s, 2H), 8.12 (d, J = 4 Hz, 4H), 7.99 (br, 4H). 13C NMR (100 MHz, DMSO-d6): δppm 171.73 (C
N). 1H NMR (400 MHz, DMSO-d6): δppm 8.95 (s, 2H), 8.12 (d, J = 4 Hz, 4H), 7.99 (br, 4H). 13C NMR (100 MHz, DMSO-d6): δppm 171.73 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 163.08, 160.56, 158.83, 150.99, 147.82, 137.04, 127.21, 126.14, 113.86.
O), 163.08, 160.56, 158.83, 150.99, 147.82, 137.04, 127.21, 126.14, 113.86.
4,4′-(1,1′,3,3′-Tetraoxo-[5,5′-biisoindoline]-2,2′-diyl)dibenzoic acid, DI-CA1. This compound was obtained in 83.6% yield; mp: >300, IR (ν, cm−1): 1778 and 1730 (asymmetric and symmetric C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); 1610 (C
O); 1610 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N); 3500–2500 broad band (OH). 1H NMR (400 MHz, DMSO-d6): δppm 13.17 (br, 2H, 2 COOH, D2O exchangeable), 8.50 (s, 2H), 8.44 (d, J = 4 Hz, 2H), 8.15 (d, J = 4 Hz, 2H), 8.13 (d, J = 4 Hz, 4H), 7.66 (d, J = 2 Hz, 4H). 13C NMR (100 MHz, DMSO-d6): δppm 167.23 (COOH), 166.80 (C
N); 3500–2500 broad band (OH). 1H NMR (400 MHz, DMSO-d6): δppm 13.17 (br, 2H, 2 COOH, D2O exchangeable), 8.50 (s, 2H), 8.44 (d, J = 4 Hz, 2H), 8.15 (d, J = 4 Hz, 2H), 8.13 (d, J = 4 Hz, 4H), 7.66 (d, J = 2 Hz, 4H). 13C NMR (100 MHz, DMSO-d6): δppm 167.23 (COOH), 166.80 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 146.25, 136.13, 134.39, 133.17, 131.91, 130.53, 130.37, 127.52, 124.82, 122.98.
O), 146.25, 136.13, 134.39, 133.17, 131.91, 130.53, 130.37, 127.52, 124.82, 122.98.
2,6-Di(pyridin-4-yl)pyrrolo[3,4-f]isoindole-1,3,5,7(2H,6H)-tetraone, DI-N2. This compound was obtained in 84% yield; mp: >300, IR (ν, cm−1): 1725 and 1657 (asymmetric and symmetric C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); 1587 (C
O); 1587 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N). 1H NMR (400 MHz, DMSO-d6): δppm 8.45 (s, 2H), 8.15 (d, J = 4 Hz, 4H), 7.69 (d, J = 4 Hz, 4H). 13C NMR (100 MHz, DMSO-d6): δppm 167.74 (C
N). 1H NMR (400 MHz, DMSO-d6): δppm 8.45 (s, 2H), 8.15 (d, J = 4 Hz, 4H), 7.69 (d, J = 4 Hz, 4H). 13C NMR (100 MHz, DMSO-d6): δppm 167.74 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 160.15, 140.17, 138.06, 136.20, 109.25.
O), 160.15, 140.17, 138.06, 136.20, 109.25.
4,4′-(1,3,5,7-Tetraoxo-5,7-dihydropyrrolo[3,4-f]isoindole-2,6(1H,3H)-diyl)dibenzoic acid, DI-CA2. This compound was obtained in 87.4% yield; mp: >300, IR (ν, cm−1): 1762 and 1722 (asymmetric and symmetric C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); 1609 (C
O); 1609 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N); 3500–2500 broad band (OH). 1H NMR (400 MHz, DMSO-d6): δppm 13.20 (br, 2H, 2COOH, D2O exchangeable), 8.77 (s, 2H), 8.34 (d, 4H), 7.66 (d, 4H). 13C NMR (100 MHz, DMSO-d6): δppm 167.80 (COOH), 165.62 (C
N); 3500–2500 broad band (OH). 1H NMR (400 MHz, DMSO-d6): δppm 13.20 (br, 2H, 2COOH, D2O exchangeable), 8.77 (s, 2H), 8.34 (d, 4H), 7.66 (d, 4H). 13C NMR (100 MHz, DMSO-d6): δppm 167.80 (COOH), 165.62 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 137.58, 130.44, 127.47, 124.17, 121.36, 118.58.
O), 137.58, 130.44, 127.47, 124.17, 121.36, 118.58.
2.2. Computational methodology
With the purpose of exploring the potential application of the synthesized diimide dyes as sensitizers in DSCs and cosensitizers of a green light absorbing the BTD–DTP1 reference dye, the isolated diimide (DI) dyes, adsorbed DI@(TiO2)38 simulated complexes, and (DI/BTD–DTP1) heterodimers were systematically investigated by means of density functional theory (DFT) and time-dependent density functional theory (TD-DFT) quantum chemical calculations.
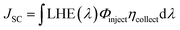 | (1) |
LHE(λ) is the light-harvesting efficiency at a wavelength λ, Φinject is the electron injection quantum yield, and ηcollect is the charge collection efficiency, which is governable by the architecture of the DSC-device only. However, the LHE and Φinject are considerably influenced by the structural and quantum phenomenon of the dye. LHE(λ), at a maximum absorption wavelength, could be calculated from Beer–Lambert's law, if the absorbance A is measured experimentally, according to the following equation.37
| LHE(λ) = 1 − 10−A | (2) |
The electron injection quantum yield Φinject is relevant to the free energy change of the electron injection; Φinject ∝ f(−ΔGinj). The electron injection driving force (ΔGinj) of the photogenerated electrons from the dyes' excited states into the conduction band (CB) of the nanocrystalline TiO2 substrate, is calculated by the following equation.38,39
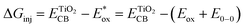 | (3) |
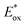 and Eox are the oxidational potential of the dye at the excited state and the ground state, respectively.
and Eox are the oxidational potential of the dye at the excited state and the ground state, respectively. 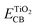 is the reduction potential of the CB of TiO2. In the present study, the experimental value of −4.00 eV (ref. 40) (vs. vacuum) is considered. E0–0 is the electronic vertical transition energy at λmax, which must be smaller than the energy of the incident photon (hν ≥ E0–0) so that the photoexcitation of the dye is achievable.
is the reduction potential of the CB of TiO2. In the present study, the experimental value of −4.00 eV (ref. 40) (vs. vacuum) is considered. E0–0 is the electronic vertical transition energy at λmax, which must be smaller than the energy of the incident photon (hν ≥ E0–0) so that the photoexcitation of the dye is achievable.
The injection of the photoexcited electron into the CB of TiO2 takes place over a time scale of ca. 100 fs, then it is transported through the TiO2 porous film by diffusion. This step is kinetically opposed by injected electron recombination with the oxidized dye or the electrolyte, the main unwanted competing loss pathways reducing the JSC and VOC. The free energy driving force of such a recombination reaction can be estimated using the following equation.41,42
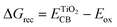 | (4) |
After the completion of the injection process, the dye would be regenerated if its photogenerated hole is neutralized through the oxidation of the I− ions to the I3− ions in the electrolyte. The free energy driving force (ΔGreg) of this dye regeneration step can be evaluated by comparing the oxidation potential of the dye in its ground state to the oxidation potential of the electrolyte (E(I−/I3−) = −4.8 eV)43 according to the following equation.41,44
| ΔGreg = E(I−/I3−) − Eox | (5) |
In the present study, eqn (2)–(5) are employed for assessing the DSC-device photovoltaic (PV) performance based on the sensitization of the synthesized diimide dyes.
3. Results and discussion
3.1. Synthesis and characterization
The synthetic route adopted for the synthesis of diimide compounds is described in Scheme 1, wherein, the condensation of 3,3′,4,4′-biphenyltetracarboxylic anhydride (1) or pyromellitic dianhydride (4) with 4-aminopyridine (2) or 4-aminobenzoic acid (3) in refluxing DMF afforded the four diimides DI-N and DI-CA in 81–87% yield. The structures of the resultant compounds DI-N and DI-CA were deduced based on their IR and NMR spectral data. The IR spectra of all the diimides were employed to confirm the success of the condensation reaction, in which the appearance of the diagnostic two absorption bands with the vibrational frequencies in the ranges of 1762–1778 and 1722–1730 cm−1 is respectively the asymmetric and symmetric stretching modes for the two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O of the imide group. These C
O of the imide group. These C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching frequencies are lower than those known for the anhydride at 1851 and 1787 cm−1. This can be explained by the different contributions of the lone pairs of X in resonance (O
O stretching frequencies are lower than those known for the anhydride at 1851 and 1787 cm−1. This can be explained by the different contributions of the lone pairs of X in resonance (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–X–C
C–X–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, X = O or N) as well as a variance in the electronegativity of X. The investigation of the 1H NMR and 13C NMR spectra displayed extra aromatic protons and carbons, respectively, confirming the success of the condensation reaction. In particular, the 13C NMR spectra of DI-N1 and DI-N2 showed two signals for the carbonyl carbon directly attached to the nitrogen atom of the pyridyl group with an explicit downfield shift at δc 171.73 and 167.74 ppm, respectively. Also, the 13C NMR spectra of DI-CA1 and DI-CA2 exhibited two signals distinguishing the carbons of the COOH groups to resonate at δc 167.23 and 167.80 ppm, respectively. Therefore, the incorporated carboxyl and pyridyl anchoring groups in the DI-CA and DI-N diimide products were confirmed. Other carbon signals for the synthesized diimides were found resonating at their appropriate positions.
O, X = O or N) as well as a variance in the electronegativity of X. The investigation of the 1H NMR and 13C NMR spectra displayed extra aromatic protons and carbons, respectively, confirming the success of the condensation reaction. In particular, the 13C NMR spectra of DI-N1 and DI-N2 showed two signals for the carbonyl carbon directly attached to the nitrogen atom of the pyridyl group with an explicit downfield shift at δc 171.73 and 167.74 ppm, respectively. Also, the 13C NMR spectra of DI-CA1 and DI-CA2 exhibited two signals distinguishing the carbons of the COOH groups to resonate at δc 167.23 and 167.80 ppm, respectively. Therefore, the incorporated carboxyl and pyridyl anchoring groups in the DI-CA and DI-N diimide products were confirmed. Other carbon signals for the synthesized diimides were found resonating at their appropriate positions.
3.2. Molecular structures of the isolated sensitizers
The molecular structure and structural attributes, such as the torsion angle between different fragments of the sensitizer, has a direct impact on the optical properties and electronic transitions under full illumination. Fig. 2 presents the 2D chemical structures of the synthesized diimide dyes and the positions of torsion angles, where their calculated values are listed in Table 1. The optimized 3D molecular structures (calculated at the B3LYP/6-31+g(d)/SMD(DMF) level of theory) are displayed in Fig. S1.† The diimide (DI) dyes are structured based on the donor–acceptor–donor (D–A–D) architecture. The electron-acceptor core in DI-N1 and DI-CA1 is biphenyldiimide (BPDI), whilst DI-N2 and DI-CA2 employed pyrrolo[3,4-f]isoindole-1,3,5,7(2H,6H)-tetraone (PITO) as electron acceptors. Each was attached to benzoic acid or pyridine electron-donor. The dyes are grouped into two sets of molecules pursuant to the anchoring group, namely, DI-CA and DI-N, with carboxylate and pyridyl groups as anchors for adsorption onto TiO2 substrates, respectively.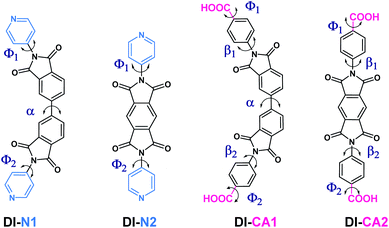 | ||
| Fig. 2 The 2D chemical structures of the synthesized diimide dyes with annotated critical torsion angles marked for each dye. | ||
| Dye | Φ1 | Φ2 | α | β1 | β2 |
|---|---|---|---|---|---|
| DI-N1 | 55 | 56 | 37 | NA | NA |
| DI-N2 | 59 | 59 | NA | NA | NA |
| DI-CA1 | 19 | 20 | 39 | 62 | 61 |
| DI-CA2 | 25 | 25 | NA | 64 | 63 |
DFT calculations showed that all the molecules belong to the C1 point group symmetry, i.e., lacking the inversion center and having no symmetry operations except identity E. The torsion angle α in the biphenyl ring is ca. 37° and 39° in DI-N1 and DI-CA1, respectively. Therefore, these compounds could form atropisomers that are a particular class of enantiomers resulting from hindered rotation about a single bond. The torsion angle β between BPDI and benzene in DI-CA1 is ca. 62°. Due to the fusion of pyridine and the BPDI moiety, the torsion angle Φ in DI-N1 is slightly reduced to ca. 56°, suggesting enhanced electron delocalization. Similarly, the planarity of DI-N2 is slightly enhanced by ca. 5° due to the fusion of PITO and pyridine compared to benzene in DI-CA2. This could be attributed to the presence of the N heteroatom that contracts the electron density of pyridine, reducing its repulsion relative to that of benzene. The deviation from planarity in the investigated molecules could be beneficial for preventing the π-stacking aggregation of the dyes on the surface of the TiO2 electrode. Such an intermolecular π–π interaction is the main reason for the self-quenching of the excited dyes, reducing the photovoltaic performance of the DSC. Considering the critical torsion angle Φ between the anchoring carboxyl group and the benzene ring in DI-CA1 and DI-CA2, it can be seen that the planarity between the anchoring group and the molecular plane in the former is relatively improved by ca. 5°. A relative enhancement of charge flow and electron injection into the CB of TiO2 is estimated for DI-CA1 accordingly.
3.3. Electronic structures of the isolated sensitizers
The intrinsic electronic structure of the sensitizer, such as energetics and spatial localization of the calculated Kohn–Sham orbitals, determines the driving forces for electron injection and dye regeneration processes as well as the excitation characteristics of the dyes. Basically, the prerequisite of high quantum yield of electron injection from the excited dye molecules to the CB of the semiconductor is that the lowest unoccupied molecular orbital (LUMO) of the sensitizer should be higher than the CB (−4.00 eV) of TiO2 with at least 0.2 eV.45 Concurrently, to guarantee the regeneration of the oxidized dye molecules, the highest occupied molecular orbital (HOMO) of the dye should lie beneath the redox potential (−4.8 eV) of the iodine/triiodide (I−/I3−) redox couple in the electrolyte. The energetics and spatial distributions of frontier molecular orbitals (FMOs), calculated at the B3LYP/6-31+g(d)/SMD(DMF) level of theory, are displayed in Fig. 3 for the new synthesized diimide sensitizers. As can be shown, all dyes comply with the basic energy level alignment requirements of an operating DSC. The calculated LUMO energy levels of the studied dyes range from −3.31 to −2.79 eV, which are ca. 0.69 to 1.21 higher than the CB minima of TiO2 for DI-N2 and DI-CA1, respectively. Therefore, photoinduced electron injection efficiency in all the dyes is thermodynamically favored. In particular, the LUMO level of the dye DI-CA1 is shifted relatively upward (−2.79), suggesting an easier injection process with greater driving force, when compared to other diimide dyes. Generally, a larger energy difference between the conduction band minima of TiO2 and the ELUMO of the dye is regulating the electron injection efficiency or short circuit current density. The HOMO energy levels ranging from −7.47 to −6.86 eV is significantly lower than the electrode potential of the redox couple, implying that the regeneration process of these dyes is expected to be thermodynamically feasible. Excluding DI-N2, the electron density distributions in both HOMO and LUMO reveals that conjugation is extended between the dye fragments. In particular, a more extended π-system can be observed in DI-CA2, which could rationalize the broadening of its absorption profile and enhanced molar extinction coefficient. For DI-N2, a clear disconnection of π-conjugation can be seen between the PITO core and pyridine rings. A common pattern of localizing the LUMOs on the internal acceptor cores is detected in all dyes. Photoinduced electron transfer in n-type semiconductor, such as TiO2, proceeds through one of the two pathways, namely, direct and indirect injection.46 In the direct injection pathway, the direct excitation of the photoinduced electron from the HOMO of the dye to the CB takes place, whereas the indirect pathway involves the injection of the excited electron from the LUMO of the dye to the CB of the semiconductor. It is worth mentioning that both direct and indirect mechanisms are active for electron injection from some squaraine (SQ) dyes to TiO2,47 where these SQ dyes are known to have the same architecture (D–A–D) as that of the diimides in the present study. Herein, though the indirect pathway is energetically allowed, the spatial distribution of FMOs advocates the direct electron transfer pathway for all the systems under study, especially for DI-N2 and DI-CA2. Therefore, the electron injection pathway could not be identified by FMO analysis only, and NTOs and hole–electron should be further investigated.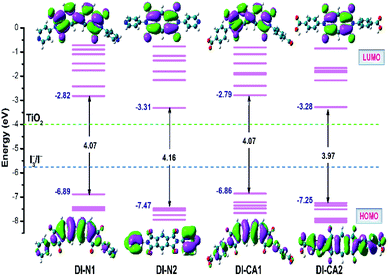 | ||
| Fig. 3 Orbital energy diagram and contour plots of HOMO and LUMO along with the energies of I−/I3− redox potential and CB of TiO2. | ||
3.4. Photoabsorption spectra of the isolated sensitizers
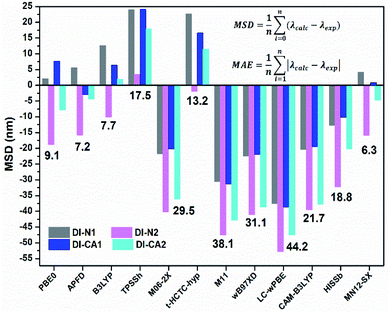
In greenhouse-integrated DSC, the key advantage of applying cosensitization is to manipulate the solar radiation by selecting complementary absorption spectra such that the transmittance of photosynthetically active radiation is maximized, while the non-photosynthetically active radiation is only utilized in generating electricity. Consequently, the UV-Vis absorption spectra of the newly synthesized diimide dyes are thoroughly investigated, experimentally and theoretically. Fig. 4(a) depicts the experimental UV-Vis absorption spectra of solution-based free diimide dyes as measured in DMF. The corresponding measurements of λmax are tabulated in Table 2 along with the optical data obtained from TD-MN12-SX/6-31+G(d)/SMD(DMF) calculations. As stated above, FMOs analysis cannot be considered for analyzing the character of electronic states owing to the simultaneous non-negligible contributions of multiple MO pair, as can be seen in Table 2. This difficulty can be eliminated by calculating natural transition orbitals (NTOs), which separately performs unitary transformation for occupied and virtual MOs to find a compact orbital representation for the electronic transition density matrix so that only one or very few number of orbital pairs have dominant contributions. Therefore, assigning the dominant configurations of the electronic states will depend on NTOs analysis as well as hole–electron distribution maps, as visualized in Fig. 4(b) and 5, respectively.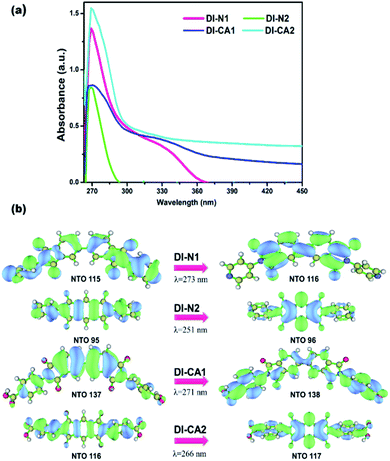 | ||
| Fig. 4 (a) Experimental UV-Vis spectra of the synthesized DI dyes, measured in DMF solvent. (b) The dominant natural transition orbital (NTO) pairs at the corresponding calculated λmax. | ||
| Dye | State | Exp λmax | Abs | λmax | E (eV) | f | τe (ns) | Major MOs contributions | Dominant configuration |
|---|---|---|---|---|---|---|---|---|---|
| DI-N1 | S12 | 269 | 1.37 | 273 | 4.54 | 0.60 | 0.94 | H → L + 3 (28%); H - 8 → L (28%) | π–π* (LE) + ICT (HLCT) |
| DI-N2 | S15 | 265 | 0.86 | 251 | 4.94 | 1.24 | 1.50 | H - 2 → L + 1 (88%) | π–π* (LE) |
| DI-CA1 | S12 | 271 | 0.89 | 271 | 4.57 | 0.39 | 1.51 | H → L + 2 (57%); H – 5 → L (23%) | π–π* (LE) + ICT (HLCT) |
| DI-CA2 | S11 | 270 | 1.53 | 266 | 4.66 | 1.25 | 0.87 | H - 8 → L + 1 (87%) | π–π* (LE) |
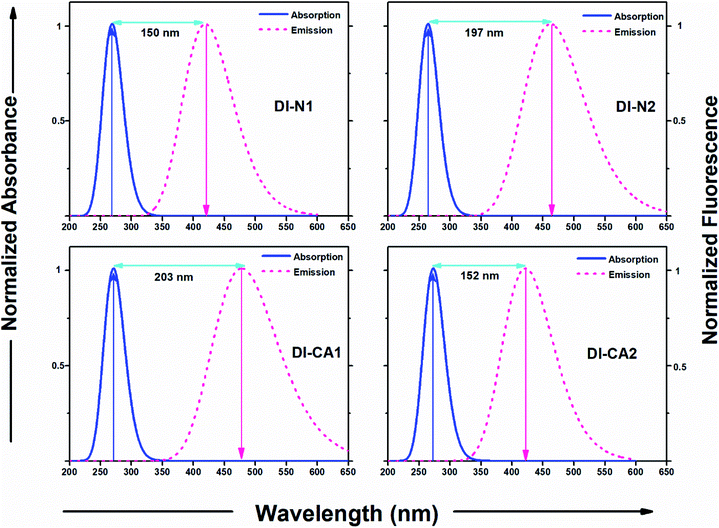
The experimental UV-Vis spectra show that, excluding DI-N2, all dyes exhibit an absorption band covering the mid-UV (267–300 nm) of the solar spectrum with shoulder peaks in the near-UV region of 315–360 nm. Concerning DI-N2, the absorption peak is centered at 265 nm with relative hypsochromic shift consistently with its largest energy gap (4.16 eV, Fig. 3) and the previously observed disconnected π-conjugation between the donor and acceptor; thus, this state could be assigned as π → π* local excitation. Similarly, the main absorption peak λmax was measured at 270 nm (calculated at 266 nm) for DI-CA2 bearing the same PITO electron-accepting core. This state is corresponding to transition from the occupied NTO 116 → virtual NTO 117, reflecting electron delocalization along the entire molecular backbone, characterized by π → π* local excitation. For DI-N1, the band peak with maximum absorption at 269 nm (calculated at 273 nm) could be characterized by hybridized intramolecular charge transfer (ICT) and local π–π* excitation (HLCT). Typically, local excitation occurs in the BPDI core, whereas ICT involves electron donation from pyridine rings, indicating that upon photoexcitation, charge accumulation is inwardly directed away from the anchoring group. Consistent with FMOs analysis, these findings of NTOs reveal clues to the direct injection pathway for DI-N1, DI-N2, and DI-CA2 systems depending on the localization of the photoexcited electron density. In contrast, there is a clear accumulation of photoinduced charge in DI-CA1 that is directed toward the anchoring carboxylate group (virtual NTO 138, Fig. 4). This pattern of charge accumulation has a pronounced effect on charge injection into the CB of the semiconductor and advocates that the DI-CA2@TiO2 system would follow the indirect mechanisms of electron injection. Photoinduced electron injection from the excited dye to the CB of the semiconductor takes place within 100 fs. As a consequence, the dye remains in the cationic form until regeneration by a redox mediator occurs, with a timescale of 100 ns to 1 μs.48 Therefore, the long-term stability of the dye and the durability of the DSC devices is related to the photostability of the cationic state and a longer excited state lifetime. Here, the lifetime of the excited state (τe, ns) was estimated using the formula τe = 1.499/(f × E2), in which E is the excitation energy of different electronic states (cm−1) and f is the oscillator strength of the electronic state. Considering the relative limitation of the MN12-SX functional in reproducing the optical data of DI-N2, with a discrepancy of ca. 14 nm (0.26 eV, Fig. 1), which is reflected in the overestimation of the DI-N2 oscillator strength, and a different trend pattern than the experimentally measured absorbance intensities (Table 2). Thus, τe was calculated considering the corrected values of the oscillator strength according to the relative values of the measured absorbance. Also, the experimentally-measured vibrational energies were considered, namely, 37.175, 37.736, 36.901, and 37.037 × 103 cm−1. The calculated excited state lifetimes of all the dyes were found within the range from 0.87 ns to 1.51 ns (Table 2) with the following trend: DI-CA1 > DI-N2 > DI-N1 > DI-CA2. The longest lifetime for DI-CA1 is expected to definitely enhance the electron injection into the CB of TiO2, as well as stability after injection. Altogether, the investigated optoelectronic properties of the synthesized UV-absorbing diimide dyes suggest the obtainability of complementary absorption of non-photosynthetically active radiation when combined with the green light-absorbing BTD–DTP1 reference dye. In particular, the DI-CA1 dye, which also exhibited greater photostability of its excited state, improved charge separation and injection after coupling with TiO2.
3.5. Intramolecular charge transfer pathway
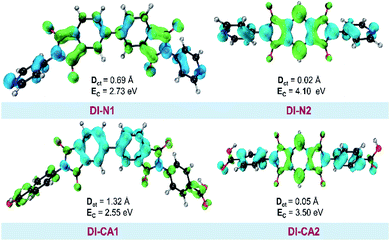
The photoinduced charge separation at the sensitizer/TiO2 interface is governed by two major factors, namely, electronic coupling between the molecular adsorbate (sensitizer) and the semiconductor (TiO2) surface addition to the extent of outward-directed ICT in the sensitizer. The former will be investigated later for the adsorbed dyes onto TiO2. Here, the hole–electron analysis19 module of the Multiwfn code is employed to reveal properties of the intramolecular charge transfer characteristics. Generally, polarizability represents the deformation feasibility of a molecular system to the applied electric field of the incident light and thus is usually associated with an efficient internal charge transfer character (CT). The calculated values of dipole moment (μ) and average isotropic polarizability 〈α〉 were found to be in line with the estimated CT features in the studied dyes. The trend of dipole moment (μ) is DI-CA1 (11.25 D) > DI-N1 (6.94 D) > DI-CA2 (5.63 D) > DI-N2 (zero), while the values of polarizability 〈α〉 are as follows: DI-CA1 (581.24 au) > DI-N1 (512.71 au) > DI-CA2 (457.39 au) > DI-N2 (387.93 au). Accordingly, the most efficient CT characteristics can be predictable for DI-CA1, while no CT features is estimated for DI-N2. For photoinduced electronic transitions, the hole–electron theory can provide a definitive picture about the distribution of the hole and the electron in density form rather than in wavefunction form, which are defined as where the excited electron leaves and arrives, respectively. Typically, the theory defined the density distribution of the electron and hole as ρele(r) = ρele(loc)(r) + ρele(cross)(r) and ρhole(r) = ρhole(loc)(r) + ρhole(cross)(r), respectively. In which, “loc” and “cross” signify the contribution of local term and cross term to the hole and electron distribution, respectively. Fig. 5 depicts real space representation of hole and electron distributions along with calculated charge transfer distance (DCT) and exciton binding energy (EC). The charge transfer distance is defined asin which X, Y, and Z stand for the three-dimensional coordinates of the centroids; hence, DCT is usually utilized for estimating the extent of spatial distance between the hole and electron centroids in X, Y, and Z directions. For instance, Xe signifies the electron density at X orientation, where the detailed expression is as follows:
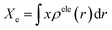 with the electron density distribution of ρele(r) and x being the X component of position vector r. The exciton binding energy is defined in the context of hole–electron analysis as the Coulomb attraction between the hole and the electron, which estimates the energy required to dissociate the photoinduced exciton, and is expressed as follows.
with the electron density distribution of ρele(r) and x being the X component of position vector r. The exciton binding energy is defined in the context of hole–electron analysis as the Coulomb attraction between the hole and the electron, which estimates the energy required to dissociate the photoinduced exciton, and is expressed as follows.It is shown in Fig. 5 that hole–electron analysis supports the NTOs and FMOs analyses, in which photoexcited electron accumulation is clearly observed on the central BPDI unit in the DI-N1 and PITO unit in DI-N2 and DI-CA2. Only DI-CA1 shows promising outward-directed intramolecular charge transfer, such that the central BPDI unit is dominated with the hole distribution, i.e., the regions offer electrons while the localization of the photoinduced electron density is exhibited on the anchoring group. Indeed, this pattern of hole–electron distribution is advantageous for interfacial electron injection that will be further investigated for the adsorbed DI-CA1@TiO2 system. Quantitatively, according to the interfragment charge transfer (IFCT) method, about 80% of the hole population is delocalized over the central BPDI moiety; meanwhile, 60% of excited electrons are localized on benzoic acid. Typically, benzoic acid of the DI-CA1 dye donates ca. 0.13 |e−| to the BPDI core and in the meantime accepts ca. 0.32 |e−| from it; therefore, benzoic acid in total gains ca. 0.19 electrons, with ca. 0.13 |e−| increased electron population of the –COOH anchor upon photoexcitation at 271 nm. Considering the charge transfer distance (DCT, Å), it is clear that maximal DCT was obtained by DI-CA1, where the sequence of dyes considering DCT is DI-CA1 (1.32 Å) > DI-N1 (0.69 Å) > DI-CA2 (0.05 Å) > DI-N2 (0.02 Å). Nevertheless, we emphasize that, even in the DI-CA1 case, DCT remains smaller than the C–C bond length (ca. 1.54 Å). The optimum EC match to the maximal DCT is achieved by DI-CA1, where the predicted trend of EC is as follows: DI-CA1 (2.55 eV) < DI-N1 (2.73 eV) < DI-CA2 (3.50 eV) < DI-N2 (4.10 eV). Since the propitious separation of the photoinduced exciton requires a smaller value of EC for the efficient promotion of exciton dissociation. Consequently, the exciton in the dye DI-CA1 is easier to separate, which facilitates the electron injection addition process to the created directionality of the photoinduced electron transfer.
3.6. Photoemission spectra of the isolated sensitizers
Diimide-based derivatives are known to manifest intrinsic photoluminescence properties and fluorescence detection capability with near unity fluorescence quantum yield.14,49 In the present work, the emission spectra of the synthesized diimides dyes were simulated at the TD-MN12SX/6-31+G(d) level of theory by applying SMD, the solvation model based on the density of DMF solvent. The radiative lifetime was estimated through the Einstein transition model50 τflu = c3/(2 × (Eflu)2 × f), in which c stands for the velocity of light in au, Eflu is the emission energy in cm−1, and f is the oscillator strength for the S0 ← S1 transition, based on optimized excited state structures. The simulated emission spectra and related computed fluorescence properties of the diimide dyes are depicted in Fig. 6 and Table 3, respectively. The figure also represents a comparison with the experimental absorption maxima along with the calculated Stokes' shifts of the fluorescent states. As shown in Table 3, the radiative lifetime (τflu) increases showing the trend of DI-N1 < DI-CA1 < DI-CA2 < DI-N2. However, for PITO-based dyes DI-CA2 and DI-N2, despite their relatively prolonged lifetime (1.2 and 2.7 ns), the negligible values of oscillator strength (ca. 0.002 and 0.001) predicts that no emission exists. Concerning DI-N1 and DI-CA1, the nanosecond scale of the radiative fluorescence lifetime is in reasonable agreement with the 100 fs timescale of electron injection from the excited dye to the CB of the semiconductor and suggests suppressing the extent of charge recombination. The simulated emission spectra of the biphenyldiimide-based dyes showed S1 emission bands in the range from 419 to 474 nm, with calculated Stokes' shift of ca. 150 nm (Δν = 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 308 cm−1) and 203 nm (Δν = 15
308 cm−1) and 203 nm (Δν = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 804 cm−1) for DI-N1 and DI-CA1, respectively. Stokes' shift is a measure of self-absorption of the emitted light as self-quenching occurs frequently in fluorophores with small Stokes' shifts.51 Conformational transformations of molecules taking place exclusively upon excitation is one of the common photochemical mechanisms that causes such a high (10
804 cm−1) for DI-N1 and DI-CA1, respectively. Stokes' shift is a measure of self-absorption of the emitted light as self-quenching occurs frequently in fluorophores with small Stokes' shifts.51 Conformational transformations of molecules taking place exclusively upon excitation is one of the common photochemical mechanisms that causes such a high (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–15
000–15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) Stokes' shift of fluorescence. The excited state optimized geometries of the synthesized diimide dyes are displayed in Fig. S2.† Comparing the structural features of the ground and excited states, for DI-N1, an enhanced planarity of the fluorescent molecular structure can be clearly observed with significantly decreasing torsion angles Φ1 and Φ2 by ca. 11° and 31°, respectively. A great reduction (ca. 19°) of torsion angle α connecting the biphenyl ring enforces the resonance effect upon excitation to dominate over the steric hindrance, which manifests the non-planar geometry of the ground state. This achieved better electron delocalization of the excited state is reflected in a changed biphenyl C–C bond character with bond length and bond order of 1.4 Å and 1.5, respectively. Also, a more planar arrangement with respect to the core biphenyl diimide framework can be observed in DI-CA1. The geometrical relaxation of the molecule taking place in its excited state is detected with the depletion of all torsion angles by ca. 2–31°, except for the Φ2 angle, between the –COOH group and the benzene ring, which is increased by ca. 8° with respect to the ground state. The deflattening of the planar benzoic fragment, upon excitation, could be attributed to the formation of the twisted intramolecular charger transfer (TICT) state. Yet, the flattening of the initially (ground state) nonplanar biphenyl system can be regarded as the main origin of enlarging the Stokes' shift in all the studied diimides.
000 cm−1) Stokes' shift of fluorescence. The excited state optimized geometries of the synthesized diimide dyes are displayed in Fig. S2.† Comparing the structural features of the ground and excited states, for DI-N1, an enhanced planarity of the fluorescent molecular structure can be clearly observed with significantly decreasing torsion angles Φ1 and Φ2 by ca. 11° and 31°, respectively. A great reduction (ca. 19°) of torsion angle α connecting the biphenyl ring enforces the resonance effect upon excitation to dominate over the steric hindrance, which manifests the non-planar geometry of the ground state. This achieved better electron delocalization of the excited state is reflected in a changed biphenyl C–C bond character with bond length and bond order of 1.4 Å and 1.5, respectively. Also, a more planar arrangement with respect to the core biphenyl diimide framework can be observed in DI-CA1. The geometrical relaxation of the molecule taking place in its excited state is detected with the depletion of all torsion angles by ca. 2–31°, except for the Φ2 angle, between the –COOH group and the benzene ring, which is increased by ca. 8° with respect to the ground state. The deflattening of the planar benzoic fragment, upon excitation, could be attributed to the formation of the twisted intramolecular charger transfer (TICT) state. Yet, the flattening of the initially (ground state) nonplanar biphenyl system can be regarded as the main origin of enlarging the Stokes' shift in all the studied diimides.
| Dye | Eflu (eV) | λmax (nm) | f (au) | τflu (ns) |
|---|---|---|---|---|
| DI-N1 | 2.96 | 419 | 0.790 | 0.003 |
| DI-N2 | 2.68 | 462 | 0.001 | 2.748 |
| DI-CA1 | 2.59 | 474 | 0.106 | 0.027 |
| DI-CA2 | 2.94 | 422 | 0.002 | 1.204 |
These molecular structure perturbations occurring during the excitation of DI-CA1 guarantee a large amount of torsional work, which is then translated into the observed largest (>15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) Stokes' shift. Indeed, biphenyls and biaryls are the most typical example of compounds showing a substantial increase in the Stokes' shifts of fluorescence as a consequence of photoinduced geometrical relaxation.52
000 cm−1) Stokes' shift. Indeed, biphenyls and biaryls are the most typical example of compounds showing a substantial increase in the Stokes' shifts of fluorescence as a consequence of photoinduced geometrical relaxation.52
Concerning the possibility of excitation energy transfer between the synthesized diimide UV-dyes and BTD–DTP1 green light-absorbing cosensitizer, through the analysis of both UV-Vis absorption and emission spectra for DI-CA1 and BTD–DTP1, a considerable overlap between the fluorescence spectrum of DI-CA1 (474 nm, Table 3) and the absorption spectrum of BTD–DTP1 (532 nm)13 can be clearly observed. In particular, the molar extinction coefficient of BTD–DTP1 is quite high (ca. 3 × 104 M−1 cm−1) in the spectral overlap area at 474 nm. Accordingly, the emitted photons from DI-CA1 are expected to be captured by the BTD–DTP1 cosensitizer via the radiative trivial reabsorption mechanism of the excitation energy transfer process, which endorses the cosensitization functionality.
3.7. Predicted photovoltaic performance
In order to estimate the relative electrochemical performance of the synthesized diimide dyes, some critical factors affecting the overall power conversion efficiency (PCE) of the DSC device were calculated according to eqn (2)–(5), namely, light-harvesting efficiency (LHE), the oxidation potential of the dye in the excited state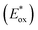 addition to the free energy diving forces for electron injection (ΔGinj), oxidized dye regeneration (ΔGreg), and recombination (ΔGrec) reactions. The results are listed in Table 4. The measured absorbance of the diimide dyes (Fig. 4(a)) shows the trend DI-CA2 (1.53 au) > DI-N1 (1.37 au) > DI-CA1 (0.89 au) > DI-N2 (0.86 au). Therefore, calculated LHE displays the same trend of DI-CA2 (0.97) > DI-N1 (0.96) > DI-CA1 (0.87) > DI-N2 (0.86). The highest absorbance of the light harvesting ability of DI-CA2 signifies an electric-dipole-allowed transition, which is consistent with the delocalization of electron density along the molecular backbone (Fig. 3 and 4(a)) since the large hole–electron overlap is a precondition for large transition dipole moment.53 Considering the critical energy parameters, the relative thermodynamical feasibility (ΔGinj) of electron injection follows the trend DI-CA1 (−1.71 eV) > DI-N1 (−1.65 eV) > DI-N2 (−1.47 eV) > DI-CA2 (−1.41 eV), implying that DI-CA1 has the greatest energetic driving force for the injection process as it is characterized by the highest gradient to the CB edge of TiO2. However, the sequence of dyes considering ΔGreg is DI-N2 (−2.67 eV) > DI-CA2 (−2.45 eV) > DI-N1 (−2.09 eV) > DI-CA1 (−2.06 eV). Hence, DI-N2 predictably has the greatest affinity to be regenerated by electron donation from iodide. This can be attributed to the largest HOMO energy level down-shift (−7.47 eV, Fig. 3) in DI-N2. Generally, the negative values of ΔGinj and ΔGreg indicate the thermodynamical spontaneity (exoergic) of electron injection and dye regeneration, respectively, with higher stability expected for dye regeneration dynamics. Also, all the studied diimide dyes are estimated to display electron injection quantum yield (Φinject) approaching 1, as it was proven that Φinject tends to approach 1 when ΔGinj is greater than 0.20 eV.44 On the other hand, the positive calculated values of ΔGrec, varying from 2.86 to 3.47 eV, estimate the absence of thermodynamical spontaneity of the undesirable electrolyte–oxide interaction and electron loss to the electrolyte, which is beneficial for operating DSC devices.
addition to the free energy diving forces for electron injection (ΔGinj), oxidized dye regeneration (ΔGreg), and recombination (ΔGrec) reactions. The results are listed in Table 4. The measured absorbance of the diimide dyes (Fig. 4(a)) shows the trend DI-CA2 (1.53 au) > DI-N1 (1.37 au) > DI-CA1 (0.89 au) > DI-N2 (0.86 au). Therefore, calculated LHE displays the same trend of DI-CA2 (0.97) > DI-N1 (0.96) > DI-CA1 (0.87) > DI-N2 (0.86). The highest absorbance of the light harvesting ability of DI-CA2 signifies an electric-dipole-allowed transition, which is consistent with the delocalization of electron density along the molecular backbone (Fig. 3 and 4(a)) since the large hole–electron overlap is a precondition for large transition dipole moment.53 Considering the critical energy parameters, the relative thermodynamical feasibility (ΔGinj) of electron injection follows the trend DI-CA1 (−1.71 eV) > DI-N1 (−1.65 eV) > DI-N2 (−1.47 eV) > DI-CA2 (−1.41 eV), implying that DI-CA1 has the greatest energetic driving force for the injection process as it is characterized by the highest gradient to the CB edge of TiO2. However, the sequence of dyes considering ΔGreg is DI-N2 (−2.67 eV) > DI-CA2 (−2.45 eV) > DI-N1 (−2.09 eV) > DI-CA1 (−2.06 eV). Hence, DI-N2 predictably has the greatest affinity to be regenerated by electron donation from iodide. This can be attributed to the largest HOMO energy level down-shift (−7.47 eV, Fig. 3) in DI-N2. Generally, the negative values of ΔGinj and ΔGreg indicate the thermodynamical spontaneity (exoergic) of electron injection and dye regeneration, respectively, with higher stability expected for dye regeneration dynamics. Also, all the studied diimide dyes are estimated to display electron injection quantum yield (Φinject) approaching 1, as it was proven that Φinject tends to approach 1 when ΔGinj is greater than 0.20 eV.44 On the other hand, the positive calculated values of ΔGrec, varying from 2.86 to 3.47 eV, estimate the absence of thermodynamical spontaneity of the undesirable electrolyte–oxide interaction and electron loss to the electrolyte, which is beneficial for operating DSC devices.
3.8. Sensitizers adsorbed on (TiO2)38 nanocluster
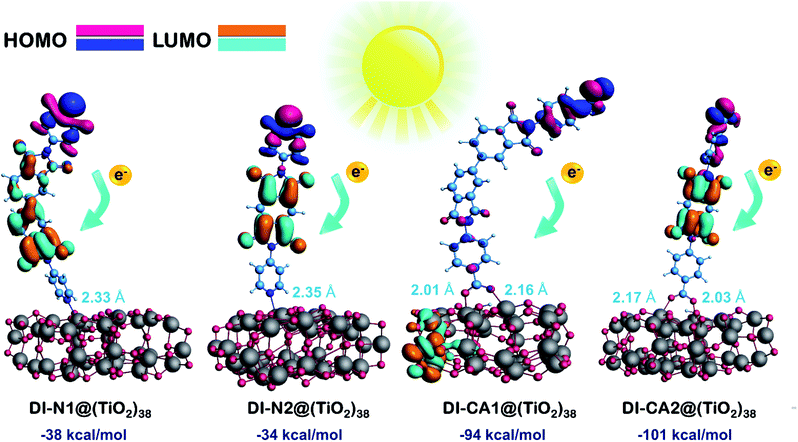
Here, the electronic coupling of the synthesized dyes adsorbed on the TiO2 nanoparticles is simulated for a deeper understanding of the electron injection process at the dye-semiconductor interface. The interaction between the dye and TiO2 can alter the surface state energetic activity and trigger electron injection, which is crucial for judging the dye performance. The ground state optimized geometries for the diimides' adsorption structures DI@(TiO2)38, which were obtained by the ADF at PBE/TZP(DZP) level by full relaxation of all the atomic positions, are presented in Fig. S3.† The spatial distribution of FMOs of the adsorption structures are displayed in Fig. 7 along with the calculated adsorption energies and critical geometrical parameters of the equilibrium interface geometries. The adsorption energy (Eads, kcal mol−1) was calculated according to the equation Eads = E(dye@TiO2) − (Edye + ETiO2), where Edye, ETiO2, and E(dye@TiO2) refers to the energy of the isolated DI dye, bare (TiO2)38 nanocluster, and DI@(TiO2)38 systems, respectively. For pursuing more accurate energetics, these energy values were calculated by single-point calculations of dye@(TiO2)38 systems at the B3LYP/6-31G(d) level of theory using the Gaussian 09 software based on the optimized adsorption structures obtained by the ADF software. It can be seen that the adsorption energies are obtained with negative values, implying that the adsorption process is stable and spontaneous for all DI dyes. Expectedly, the presence of the carboxylate anchoring group enhanced the adsorption stability of the dyes DI-CA1 (Eads of −94 kcal mol−1) and DI-CA2 (−101 kcal mol−1) on the metal oxide surface when compared to the pyridyl–TiO2 interactions in dyes DI-N1 (−38 kcal mol−1) and DI-N2 (−34 kcal mol−1) bearing the same BPDI and PITO cores, respectively. These findings are in line with the fact that the high stability of the dye is usually associated with a lower value of pKa for the anchor group with the usual observation that higher affinities to the metal oxide surface are exerted by stronger acidic binding groups.54 The interacting distances of the Ti–O bonds in DI-CA dyes range from 2.01 to 2.17 Å, while that of the Ti–N bonds in DI-N dyes are ca. 2.33 and 2.35 Å. This is consistent with the relatively improved adsorption stability of the carboxylate-anchored dyes and advocates the formation of stable complexes of tightly-adsorbed DI-CA dyes onto the TiO2 surface. For DI-CA dyes, the bond lengths of the O–H bonds formed by carboxyl dissociation are 1.019 and 1.013 Å, whereas the bond angles of the C–O–C bonds in the carboxyl group are 125.4° and 125.6° in DI-CA1 and DI-CA2, respectively. Moreover, the optimized geometric features reveal that the dyes stay vertically above the TiO2 cluster surface, with a maximum inclination of ca. 23° detected in the DI-N1 dye.Adsorption is usually associated with deteriorating planarity of the adsorbed dyes and increased torsion angles, as a consequence of the steric hindrance induced by the adsorption.55 Surprisingly, all the simulated optimized geometries of the DI dyes adsorbed on the surface of TiO2 revealed similar features, i.e., all torsional angles, excluding angle α, were significantly reduced due to adsorption, when compared to that of isolated dyes (Table 1). On the other hand, the torsion angle α in the biphenyl ring is slightly increased by ca. 5° and 3° in DI-N1 and DI-CA1, respectively. Alternatively, adsorption significantly decreased the torsion angles β between benzene and the molecular core by ca. 20–25°, where the values of β1 and β2 lie in the ranges of 20–24° and 22–25° for DI-CA1 and DI-CA2, respectively. Similarly, for DI-N1 and DI-N2, torsion angles Φ1 and Φ2 lie in the ranges of 27–36° and 28–37°, thus enhancing their planarity by ca. 19° and 29°, respectively. Considering the torsion angle Φ1 between the carboxylate anchoring group and benzene ring in DI-CA1 and DI-CA2, a significant improvement (ca. 14° and 19°) in the planarity is also observed as a result of depletion of the Φ1 angle to 5° and 6°, respectively, upon dye adsorption. The enhanced planarity of the adsorbed dyes could be attributed to the increase in the negative charge of the imide N atom that hinders its participation in resonance with the carbonyl group, thus enforcing the carbonyl groups for relatively improved planarity.
Excluding adsorbed DI-CA1 on the (TiO2)38 cluster, the spatial distribution of FMOs of all the studied systems shows a comparable pattern, namely, the localization of HOMO and LUMO electron densities respectively on the terminal donor moieties and the central acceptor units of the dyes. In contrast, a different pattern is observed in the DI-CA1@(TiO2)38 system with the partial delocalization of HOMO to the donor position close to the TiO2 surface besides, being localized on the terminal donor moiety, while for the electron density distribution of LUMO, it is clearly distinguishable residing on the TiO2 nanocluster. Such a relocation of the FMOs electron density not only empowers the charge transfer at the DI-CA1/TiO2 interface but also constructs a high degree of charge separation and stability of the photogenerated electron–hole pair. This is in accordance with the predicted (Fig. 4) lowest barrier for exciton dissociation in the DI-CA1 dye.
Next, the nature of intramolecular interactions in the four DI@(TiO2)38 complexes was characterized by analyzing the bonding energy decomposition as obtained by the ADF code. In which the bond energy is computed as an energy difference between the molecule (complex) and its constituent atoms that are approximated as spherically symmetrical and spin-restricted. As listed in Table 5, the computed bonding energy values (ΔEb in Hartree, Ha) ranked in decreasing order are −48.21 (DI-CA1) > −46.21 (DI-N1) > −45.71 (DI-CA2) > −43.70 (DI-N2). For DI-CA1@(TiO2)38, the bonding energy consists of a Pauli repulsion (ΔEPauli) of 135.40 Ha, an attractive electrostatic interaction of (ΔVelstat) −41.38 Ha, and an orbital interaction (ΔEoi) of −142.23 Ha. Despite this largest value of the destabilizing repulsive ΔEPauli when compared to other complexes, the strongest bonding energy in CA1@(TiO2)38 complex can be regarded as the highest electrostatic attractions and orbital interactions. The sequence of dye complexes considering ΔEoi is DI-CA1 (−142.23 Ha) > DI-N1 (−133.48 Ha) > DI-CA2 (−131.11 Ha) > DI-N2 (−122.31 Ha). Since orbital interaction accounts for polarization and charge transfer (CT) effects, we could argue that the most efficient CT features would be exhibited in the CA1@(TiO2)38 complex.
| Complex | ΔEb | ΔEPauli | ΔVelstat | ΔEoi |
|---|---|---|---|---|
| DI-N1@(TiO2)38 | −46.21 | 126.74 | −39.47 | −133.48 |
| DI-N2@(TiO2)38 | −43.70 | 115.89 | −37.27 | −122.31 |
| DI-CA1@(TiO2)38 | −48.21 | 135.40 | −41.38 | −142.23 |
| DI-CA2@(TiO2)38 | −45.71 | 124.60 | −39.20 | −131.11 |
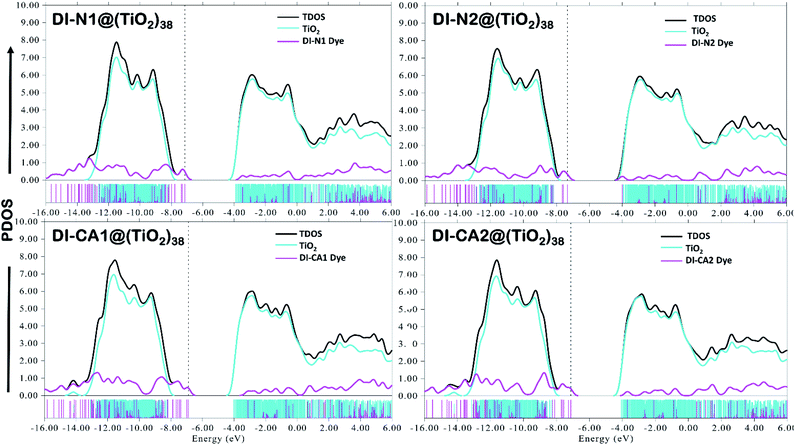
A deeper insight into the bonding interaction of the adsorbed complexes, can be also obtained by plotting the computed PDOS profile of dye@(TiO2)38. PDOS plots for the different studied interfaces are displayed in Fig. 8. It clearly shows that dye-sensitization has introduced intermediate states in the bandgap of the semiconductor, resulting in the reduction of the original bandgap. Especially, upon adsorption of the dye DI-CA1 onto the TiO2 surface, there are greater localized states that appear clearly within the bandgap and have projection solely over the atoms of the dye. Typically, these states (magenta discrete lines) are corresponding to occupied MOs between −6.89 (HOMO) to −8.23 eV (HOMO−9) and are 100% contributed by DI-CA1 dye. Lesser sharp occupied molecular energy levels, namely HOMO to HOMO−6, HOMO to HOMO−4 and HOMO to HOMO−2 are introduced in the bandgap of TiO2 upon adsorption of DI-CA2, DI-N1 and DI-N2, respectively. Accordingly, the estimated trend of reduced bandgap is as following: DI-CA1 (2.87 eV) < DI-CA2 (3.05 eV) < DI-N1 (3.25 eV) < DI-N2 (3.35 eV). Moreover, the energy of the LUMO level of the free DI-CA1 dye molecule goes deeper in the CB of the semiconductor, corresponding to the energy of the LUMO+40 level of the DI-CA1@(TiO2)38 system. The LUMO of the adsorbed DI-N2@(TiO2)38 system is 100% contributed by the dye fragment, whereas the LUMO levels of the free DI-N1 and DI-CA2 dyes correspond to the energy of the LUMO+14 and LUMO+12 levels of the dye-semiconductor systems. This confirms the stronger electronic coupling between the DI-CA1 dye and TiO2, which is favorable for overcoming thermodynamic and kinetic barriers in interfacial exciton dissociation. It is supported by the narrower bandgap, allowing for an extended absorption region; besides, the inner LUMO of the dye expedites the electron injection process and regulates short circuit current density.
As is known, the UV-selective organic DI-CA1 dye (271–345 nm) can be chosen for the cosensitization of the green-selective BTD–DTP1 (532 nm) in greenhouse-integrated dye-sensitized solar cells. The maximized utilization of non-photosynthetically-active radiation (non-PAR) is anticipated without minimizing the flow of PAR used for plant photosynthesis.
3.9. Electronic structure of the proposed cosensitizers
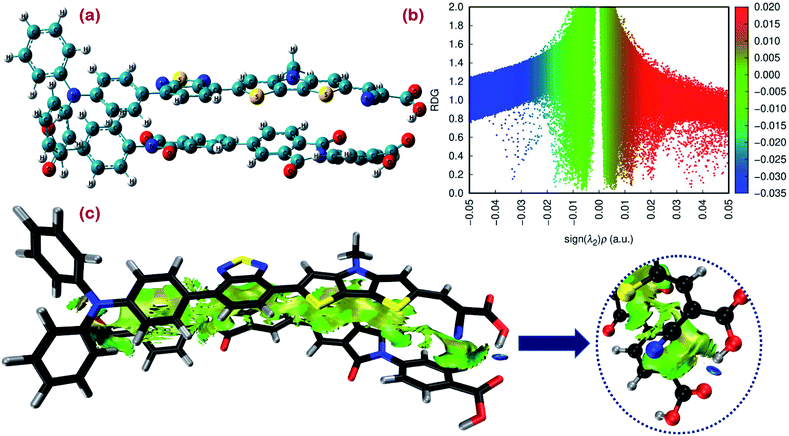
Among the fundamental optochemical requirements that need to be fulfilled for the optimal combinations of cosensitizing dyes are the complementarity of optical profiles and chemical compatibility between the cosensitizers. So far, the first factor has been deeply investigated and validated for the proposed cosensitizers DI-CA1/BTD–DTP1. Here, the chemical or electronic compatibility of the heterodimer DI-CA1/BTD–DTP1 is examined based on the aforementioned electronic structure calculations. The obtained ground state optimized geometry of the dimer, calculated at the B3LYP-D3(BJ)/6-31G(d) level, is depicted in Fig. 9(a). Again, it can be observed that the planarity of the biphenyl diimide core is boosted with a significant depletion of the α torsion angle by ca. 18°, confirming the flexibility of the biphenyl system. The interlayer distance is ca. 3.5 Å of the superimposed DI-CA1/BTD–DTP1 structure. The planarity is preserved along the BTD–DTP–anchor conjugated backbone, with exactly the same wider angle of ca. 34 between the benzothiadiazole (BTD) unit and the donor triphenylamine in free BTD–DTP1 dye, as reported by Dessì et al.13 This implies that cosensitization with DI-CA1 is not disturbing the molecular structure of BTD–DTP1 or deteriorating its extended π-conjugation along the BTD–DTP scaffold; thus, its spectral response is expected to be attained. Quantitatively assessing the stability of the dimer DI-CA1/BTD–DTP1 can be achieved by calculating the total interaction energy ΔEtot and simple energy decomposition analysis (EDA). Total interaction energy was calculated by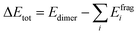 , corresponding to the energy variation of forming a dimer when combining the wavefunctions of its fragments.
, corresponding to the energy variation of forming a dimer when combining the wavefunctions of its fragments.
In simple EDA, the total interaction energy is decomposed as ΔEtot = ΔEorb + ΔEsteric + ΔEdisp. The dispersion weak intermolecular attractive interaction (Edisp) can be estimated as ΔEdisp = EDFT−D3tot − EDFTtot, in which the D3 Grimme's correction accounts for the dispersion correlation that is missing in the DFT energy. The steric energy, ΔEsteric = ΔEels + ΔEXC + ΔEPauli, is the sum of the electrostatic energy, the exchange–correlation energy, and the Pauli repulsion, respectively. Eels is the electrostatic interaction between the fragment charge distributions, which is normally attractive (negative), provided the fragments are not too close. Eorb is the orbital interaction term due to mixing occupied and virtual MOs. For the studied dimer, a total interaction energy between DI-CA1 and BTD–DTP1 is ca. −60 kcal mol−1, implying the overall stability of the dimer. It was found that the orbital interaction energy (ΔEorb) and the dispersion energy (ΔEdisp) of ca. −28.944 kcal mol−1 and −58.704 kcal mol−1, respectively, stabilized the formation of the dimer. However, the steric energy destabilized the dimer by ca. 27.611 kcal mol−1. Therefore, the total interaction energy of −38.07 kcal mol−1 indicates that the formation of the dimer DI-CA1/BTD–DTP1 is maintained by the dispersion and orbital intermolecular attractive interactions. Fig. 9(b) presents a scatter map with the Y-axis and X-axis corresponding respectively to the reduced density gradient (RDG) and sign (λ2)ρ. The latter quantity is the electron density ρ(r) multiplied by the sign of the second largest eigenvalue λ2 (λ1 ≤ λ2 ≤ λ3) of the electron density Hessian matrix at each point of the isosurface. Each point in the scatter map corresponds to a grid point in the 3D space. Electron density ρ(r) defines the strength of interactions, whereas the sign of λ2 distinguishes the bonded (λ2 < 0) from the nonbonded (λ2 > 0) interactions. Accordingly, high ρ(r) regions signify strong interactions, either stabilizing attractive (λ2 < 0) such as dipole–dipole and H-bonding (blue dots), or destabilizing repulsion (λ2 > 0) like steric effect in rings and cages (red dots). Weak intermolecular reactions such as dispersion or vdW interactions are denoted at a low-gradient low ρ(r) regions (green dots). The RDG isosurface map is displayed in Fig. 9(c) for simultaneously visualizing the nature and physical origin of these calculated noncovalent interactions, in which the intramolecular interactions are screened out so that the isosurfaces in the intermolecular area can be distinguished clearly. The isosurface of both intra(inter)molecular interactions is displayed in Fig. S4.† The gradient isosurface with RDG = 0.5 a.u. is colored on the same blue-green-red scale according to the values of sign(λ2)ρ(r) function. In Fig. 9(b), low-gradient (RDG < 0.4 au) spike (few blue dots) with negative λ2 and relatively higher density (sign(λ2)ρ(r) of ca. −0.035 au) is attributed to the H-bonding in the studied dimer but not very strong. Also, low-gradient spike (red dots) with high density at the positive part (sign(λ2)ρ(r) of ca. +0.022 au) advocates the existence of destabilizing steric repulsion. However, the lack of red RDG isosurface in the extended area between the two dyes in Fig. 9(c) indicates that these steric effects are exhibited within benzene, thiophene, and pyrrole rings (Fig. S4†). Fig. 9(b) also shows that the low-gradient spike is near zero at the low-density (0 ≤ ρ(r) ≤ 0.01). This can be realized as extended elliptical green or light brown slab in the interaction area along the molecular backbones of the two monomers in Fig. 9(c), which shows that the electron density in this region is low and pinpoints the dispersion intermolecular attraction. Consequently, this weak dispersion attractive interaction, stabilizing the dimer formation, agrees with the calculated stabilizing ΔEdisp of −58.704 kcal mol−1. Overall, according to the calculated low destabilizing repulsion with respect to the high stabilizing orbital and the dispersion attractive interactions of the studied dimer, we could argue that the DI-CA1 and BTD–DTP1 cosensitizers obtained electronic compatibility and are applicable for cosensitization in DSCs.
4. Conclusions
In this work, we report the synthesis of four new symmetrical UV-absorbing diimides organic dyes for potential cosensitization process in greenhouse-integrated dye-sensitized solar cells (DSCs). The compounds with donor–acceptor–donor (D–A–D) architecture are based on biphenyldiimide (BPDI) or pyrrolo[3,4-f]isoindole-1,3,5,7(2H,6H)-tetraone (PITO) as electron-acceptors, each functionalized with a carboxylate or pyridyl group for adsorption onto the TiO2 semiconductor. The UV/Vis absorption spectra of DMF solution-based free dyes were measured experimentally. Quantum chemical calculations were subsequently employed to investigate the potential application of the synthesized diimides as sensitizers in DSCs and cosensitizers of a green light absorbing BTD–DTP1 reference dye, which is benzothiadiazole (BTD)–dithienopyrrole (DTP) scaffold structured. Electronically and energetically, all dyes were found to fulfill the basic energy level alignment requirements of an operating DSC. Also, a promising photovoltaic performance, with thermodynamical spontaneity of electron injection and dye regeneration processes, is predicted, adding to the estimated stability of adsorption onto TiO2 nanoparticles. Nevertheless, the biphenyldiimide-structured DI-CA1 UV-dye produced superior results and outperforms others in the series. In particular, DI-CA1 exhibited the most advantageous structural attributes as an individual dye with boosted planarity between the anchoring group and the molecular plane; the greatest thermodynamical driving force for electron injection; a clear localization of virtual natural transition orbitals on the anchoring carboxylate group; the largest dipole moment and isotropic polarizability, besides the longest lifetime and photostability of the excited state. Moreover, intramolecular charge transfer characteristics are relatively improved in DI-CA1 with the largest spatial distance between the hole and electron centroids, the lowest energy required to dissociate the photoinduced exciton and the largest photogenerated electron population on its anchoring group. The simulated S1 emission band of DI-CA1 showed the largest calculated Stokes' shift of ca. 203 nm (Δν = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 804 cm−1). The considerable overlap between the fluorescence spectrum of DI-CA1 (474 nm) and the absorption spectrum of reference BTD–DTP1 (532 nm) cosensitizer suggests the opportunity of excitation energy transfer between the proposed cosensitizers via the radiative trivial reabsorption mechanism, which endorses the cosensitization functionality. The simulated DI-CA1@(TiO2)38 system advocates the formation of a stable adsorption structure of tightly-adsorbed DI-CA dye onto the TiO2 nanoparticles, exhibiting the highest orbital interactions. The spatial distribution of FMOs electron density enables a high degree of charge separation at the DI-CA1/TiO2 interface. PDOS showed minimum bandgap with greater localized states within the bandgap. Also, PDOS displayed a deeper existence of the LUMO level of the DI-CA1 dye in the CB of TiO2, which expedites electron injection process, with the highest gradient at the CB edge of TiO2. These findings approve the stronger electronic coupling between the DI-CA1 molecule and the TiO2 nanoparticles that is promising for overcoming thermodynamic and kinetic barriers in interfacial photogenerated exciton dissociation with a constructive relatively enhanced degree of charge separation. The electronic compatibility of the proposed cosensitizer DI-CA1/BTD–DTP1 was then estimated according to the calculated total interaction energy with a high stabilizing orbital and dispersion attractive intermolecular interactions besides a low destabilizing steric repulsion. The reduced density gradient isosurface designated these steric effects within rings, while the dispersion interactions were clearly displayed in the contact extended area. This was reflected in the geometrical relaxation of the biphenyl diimide core in the DI-CA1 monomer and the maintained planarity along the BTD–DTP–anchor conjugated backbone. Unlike covalent functionalization that could distort π–π conjugation and the associated physicochemical properties, this noncovalent functionalization maintains the atomic and electronic structures of individual dyes. In short, the UV absorbing organic DI-CA1 dye (271–345 nm) can be recommended for the cosensitization of the green light-absorbing organic BTD–DTP1 photosensitizer (532 nm) in greenhouse-integrated dye-sensitized solar cells. Accordingly, an estimated improved utilization of non-photosynthetically active radiation for electricity production was obtained, whilst maintaining good transmittance in the photosynthetically active regions of the solar spectrum to be captured by plants for photosynthesis. Indeed, an entirely organic combination of UV-selective diimides and green-selective BTD–DTP1 dye represents a good scenario from a purely environmentally sustainable perspective.
804 cm−1). The considerable overlap between the fluorescence spectrum of DI-CA1 (474 nm) and the absorption spectrum of reference BTD–DTP1 (532 nm) cosensitizer suggests the opportunity of excitation energy transfer between the proposed cosensitizers via the radiative trivial reabsorption mechanism, which endorses the cosensitization functionality. The simulated DI-CA1@(TiO2)38 system advocates the formation of a stable adsorption structure of tightly-adsorbed DI-CA dye onto the TiO2 nanoparticles, exhibiting the highest orbital interactions. The spatial distribution of FMOs electron density enables a high degree of charge separation at the DI-CA1/TiO2 interface. PDOS showed minimum bandgap with greater localized states within the bandgap. Also, PDOS displayed a deeper existence of the LUMO level of the DI-CA1 dye in the CB of TiO2, which expedites electron injection process, with the highest gradient at the CB edge of TiO2. These findings approve the stronger electronic coupling between the DI-CA1 molecule and the TiO2 nanoparticles that is promising for overcoming thermodynamic and kinetic barriers in interfacial photogenerated exciton dissociation with a constructive relatively enhanced degree of charge separation. The electronic compatibility of the proposed cosensitizer DI-CA1/BTD–DTP1 was then estimated according to the calculated total interaction energy with a high stabilizing orbital and dispersion attractive intermolecular interactions besides a low destabilizing steric repulsion. The reduced density gradient isosurface designated these steric effects within rings, while the dispersion interactions were clearly displayed in the contact extended area. This was reflected in the geometrical relaxation of the biphenyl diimide core in the DI-CA1 monomer and the maintained planarity along the BTD–DTP–anchor conjugated backbone. Unlike covalent functionalization that could distort π–π conjugation and the associated physicochemical properties, this noncovalent functionalization maintains the atomic and electronic structures of individual dyes. In short, the UV absorbing organic DI-CA1 dye (271–345 nm) can be recommended for the cosensitization of the green light-absorbing organic BTD–DTP1 photosensitizer (532 nm) in greenhouse-integrated dye-sensitized solar cells. Accordingly, an estimated improved utilization of non-photosynthetically active radiation for electricity production was obtained, whilst maintaining good transmittance in the photosynthetically active regions of the solar spectrum to be captured by plants for photosynthesis. Indeed, an entirely organic combination of UV-selective diimides and green-selective BTD–DTP1 dye represents a good scenario from a purely environmentally sustainable perspective.
Author contributions
R. B. A. and S. P. project administration. M. H. supervision, M. H. and M. Z. experimental investigation. E. N. conceptualization. E. N., R. B. A. and S. P. data curation. M. Z. formal analysis. E. N. computational methodology and analysis. M. Z. and E. N. writing – original draft. M. Z, E. N. and R. B. A. writing – review & editing. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work, the project number (442/47). Also, the authors would like to extend their appreciation to Taibah University for its supervision support.References
- L. Tian, Y. Wang, Y. Zhang, X. Li, W. Wu and B. Liu, ACS Appl. Energy Mater., 2021, 4, 242–248 CrossRef CAS.
- K. Zhang, C. Qin, X. Yang, A. Islam, S. Zhang, H. Chen and L. Han, Adv. Energy Mater., 2014, 4, 1301966 CrossRef.
- W. Naim, V. Novelli, I. Nikolinakos, N. Barbero, I. Dzeba, F. Grifoni, Y. Ren, T. Alnasser, A. Velardo, R. Borrelli, S. Haacke, S. M. Zakeeruddin, M. Graetzel, C. Barolo and F. Sauvage, JACS Au, 2021, 1, 409–426 CrossRef CAS PubMed.
- L. Lu, M. E. Ya’acob, M. S. Anuar, G. Chen, M. H. Othman, A. Noor Iskandar and N. Roslan, Energy Rep., 2020, 6, 238–253 CrossRef.
- G. K. Ntinas, K. Kadoglidou, N. Tsivelika, K. Krommydas, A. Kalivas, P. Ralli and M. Irakli, Horticulturae, 2019, 5, 42 CrossRef.
- B. O'regan and M. Grätzel, Nature, 1991, 353, 737–740 CrossRef.
- N. Mariotti, M. Bonomo, L. Fagiolari, N. Barbero, C. Gerbaldi, F. Bella and C. Barolo, Green Chem., 2020, 22, 7157–7167 RSC.
- J. M. Cole, G. Pepe, O. K. Al Bahri and C. B. Cooper, Chem. Rev., 2019, 119, 7279–7327 CrossRef CAS PubMed.
- K. Kakiage, Y. Aoyama, T. Yano, K. Oya, J. Fujisawa and M. Hanaya, Chem. Commun., 2015, 51, 15894–15897 RSC.
- L. Zuo, X. Shi, W. Fu and A. K. Y. Jen, Adv. Mater., 2019, 31, 1901683 CrossRef PubMed.
- R. B. Alnoman, E. Nabil, S. Parveen, M. Hagar, M. Zakaria and A. A. Hasanein, Molecules, 2021, 26, 7336 CrossRef CAS.
- N. Roslan, M. Ya'acob, M. Radzi, Y. Hashimoto, D. Jamaludin and G. Chen, Renewable Sustainable Energy Rev., 2018, 92, 171–186 CrossRef.
- A. Dessì, D. A. Chalkias, S. Bilancia, A. Sinicropi, M. Calamante, A. Mordini, A. Karavioti, E. Stathatos, L. Zani and G. Reginato, Sustainable Energy Fuels, 2021, 5, 1171–1183 RSC.
- Z. Wang, X. Zhu, S. Zhang, L. Xu, Z. Zhao and G. He, Adv. Opt. Mater., 2021, 9, 2001764 CrossRef CAS.
- S. Maniam, H. F. Higginbotham, T. D. Bell and S. J. Langford, Chem.–Eur. J., 2019, 25, 7044–7057 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, D. J. Fox, Gaussian 09, Gaussian Inc., Wallingford CT, 2013 Search PubMed.
- R. Peverati and D. G. Truhlar, Phys. Chem. Chem. Phys., 2012, 14, 16187–16191 RSC.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777 CrossRef CAS.
- Z. Liu, T. Lu and Q. Chen, Carbon, 2020, 165, 461–467 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- W. Li, J. Wang, J. Chen, F.-Q. Bai and H.-X. Zhang, Spectrochim. Acta, Part A, 2014, 118, 1144–1151 CrossRef CAS.
- W. Li, F.-Q. Bai, J. Chen, J. Wang and H.-X. Zhang, J. Power Sources, 2015, 275, 207–216 CrossRef CAS.
- F. Nunzi, S. Agrawal, A. Selloni and F. De Angelis, J. Chem. Theory Comput., 2015, 11, 635–645 CrossRef CAS.
- M. J. Lundqvist, M. Nilsing, P. Persson and S. Lunell, Int. J. Quantum Chem., 2006, 106, 3214–3234 CrossRef CAS.
- G. Te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- R. Rüger, M. Franchini, T. Trnka, A. Yakovlev, E. van Lenthe, P. Philipsen, T. van Vuren, B. Klumpers and T. Soini, S. AMS 2020, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com Search PubMed.
- M. Pastore and F. D. Angelis, J. Phys. Chem. Lett., 2012, 3, 2146–2153 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- E. Van Lenthe, A. Ehlers and E.-J. Baerends, J. Chem. Phys., 1999, 110, 8943–8953 CrossRef CAS.
- T. Lu, Molclus Program, Version 1.9, 2019, available online: http://www.keinsci.com/research/molclus.html, accessed on 6 December 2019 Search PubMed.
- J. J. P. Stewart, MOPAC2016, Stewart Computational Chemistry, Colorado Springs, CO, USA, 2016 Search PubMed.
- J. J. P. Stewart, J. Mol. Model., 2013, 19, 1–32 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS.
- J. K. Roy, S. Kar and J. Leszczynski, ACS Sustainable Chem. Eng., 2020, 8, 13328–13341 CrossRef CAS.
- P. N. Samanta, D. Majumdar, S. Roszak and J. Leszczynski, J. Phys. Chem. C, 2020, 124, 2817–2836 CrossRef CAS.
- J. K. Roy, S. Kar and J. Leszczynski, ACS Sustainable Chem. Eng., 2020, 8, 13328–13341 CrossRef CAS.
- S.-Q. Zhou, Q.-Y. Xia, L.-X. Kong, K. Ayyanar and X.-H. Ju, ACS Omega, 2020, 5, 23491–23496 CrossRef CAS PubMed.
- W. Zhang, L. Wang, L. Mao, J. Jiang, H. Ren, P. Heng, H. Ågren and J. Zhang, J. Phys. Chem. C, 2020, 124, 3980–3987 CrossRef CAS.
- R. Kesavan, F. Attia, R. Su, P. Anees, A. El-Shafei and A. V. Adhikari, J. Phys. Chem. C, 2019, 123, 24383–24395 CrossRef CAS.
- A. Majid, M. Sana, S. U. D. Khan and N. Ahmad, Int. J. Quantum Chem., 2020, 120, e26253 CrossRef CAS.
- Y. Gao, W. Guan, L.-K. Yan and Z.-M. Su, J. Mater. Chem. C, 2020, 8, 219–227 RSC.
- J. K. Roy, S. Kar and J. Leszczynski, Sci. Rep., 2018, 8, 1–12 CAS.
- H. Liu, L. Liu, Y. Fu, E. Liu and B. Xue, J. Chem. Inf. Model., 2019, 59, 2248–2256 CrossRef CAS PubMed.
- T. Manzoor and A. H. Pandith, J. Comput. Chem., 2019, 40, 2444–2452 CrossRef CAS PubMed.
- H.-H. G. Tsai, C.-J. Tan and W.-H. Tseng, J. Phys. Chem. C, 2015, 119, 4431–4443 CrossRef CAS.
- K. Chaitanya, X.-H. Ju and B. M. Heron, RSC Adv., 2014, 4, 26621–26634 RSC.
- H.-J. Ben, X.-K. Ren, B. Song, X. Li, Y. Feng, W. Jiang, E.-Q. Chen, Z. Wang and S. Jiang, J. Mater. Chem. C, 2017, 5, 2566–2576 RSC.
- B. Xu, Y. Li, P. Song, F. Ma and Y. Yang, J. Phys. Chem. C, 2021, 125, 13109–13122 CrossRef CAS.
- P. Horváth, P. Sebej, T. Solomek and P. Klán, J. Org. Chem., 2015, 80, 1299–1311 CrossRef PubMed.
- M. Baumgarten, L. Gherghel, J. Friedrich, M. Jurczok and W. Rettig, J. Phys. Chem. A, 2000, 104, 1130–1140 CrossRef CAS.
- Z. Liu and T. Lu, J. Phys. Chem. C, 2020, 124, 7353–7360 CrossRef CAS.
- Y. Farré, F. Maschietto, J. Föhlinger, M. Wykes, A. Planchat, Y. Pellegrin, E. Blart, I. Ciofini, L. Hammarström and F. Odobel, ChemSusChem, 2020, 13, 1844–1855 CrossRef PubMed.
- E. Nabil, A. A. Hasanein, R. B. Alnoman and M. Zakaria, J. Chem. Inf. Model., 2021, 61, 5098–5116 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Exchange–correlation functionals assessment, additional figures concerning optimized geometries of studied UV-dyes addition to 13C and 1H NMR spectra of compounds. See https://doi.org/10.1039/d2ra01099b |
| This journal is © The Royal Society of Chemistry 2022 |