 Open Access Article
Open Access ArticlePotential energy barrier for proton transfer in compressed benzoic acid†
Dominik Kurzydłowski *
*
Faculty of Mathematics and Natural Sciences, Cardinal Stefan Wyszyński University in Warsaw, 01-038 Warsaw, Poland. E-mail: d.kurzydlowski@uksw.edu.pl
First published on 12th April 2022
Abstract
Benzoic acid (BA) is a model system for studying proton transfer (PT) reactions. The properties of solid BA subject to high pressure (exceeding 1 kbar = 0.1 GPa) are of particular interest due to the possibility of compression-tuning of the PT barrier. Here we present simulations aimed at evaluating the value of this barrier in solid BA in the 1 atm – 15 GPa pressure range. We find that pressure-induced shortening of O⋯O contacts within the BA dimers leads to a decrease in the PT barrier, and subsequent symmetrization of the hydrogen bond. However, this effect is obtained only after taking into account zero-point energy (ZPE) differences between BA tautomers and the transition state. The obtained results shed light on previous experiments on compressed benzoic acid, and indicate that a common scaling behavior with respect to the O⋯O distance might be applicable for hydrogen-bond symmetrization in both organic and inorganic systems.
Introduction
Proton transfer reactions lie at the heart of many chemical transformations, such as acid–base reactions, catalytic processes or hydrogen transport in the Earth's mantle.1–3 Studying proton dynamics not only gives insight into these transformations, but also leads to a deeper understanding of the quantum effects that are strongly manifested during the PT process.4–9 Benzoic acid, with its centrosymmetric dimers bound by strong hydrogen bonds, is considered a model system for studying proton transfer processes.10,11 This molecule was studied with a multitude of experimental techniques, including X-ray and neutron scattering,12–15 optical spectroscopy,16–20 and nuclear magnetic resonance (NMR),21–25 as well as ab initio modelling.26–36High pressure (exceeding 0.1 GPa = 1 kbar) can greatly alter proton dynamics in solids.37 Hence, experiments were conducted for solid benzoic acid at pressures reaching 18 GPa.38–43 However, the challenging nature of these experiments led to ambiguity in the interpretation of the obtained data. In particular, some studies gave conflicting values of phase transition pressures,40,42 while others reported no phase change in compressed BA.41,43 Furthermore, structural data obtained by Kang and co-workers suggested that the O⋯O distance within the BA dimers remains constant upon compression to 18 GPa,43 while single-crystal X-ray measurements conducted by Cai and Katrusiak indicated drastic reduction of this contact with pressure.41 It was also suggested that at 17 GPa symmetrization of hydrogen bonds occurs in solid BA,43 but this conclusions was mostly based on Density Functional Theory (DFT) calculations utilizing the local-density approximation (LDA) which is an inadequate method for modelling hydrogen-bonded systems. At the same time theoretical studies on benzoic acid at high pressures are scarce.44,45
With the aim of elucidating the problems mentioned above we present a computational study on how high pressure influences the properties of solid benzoic acid. We model the changes in geometry of BA crystals upon compression up to 15 GPa with the use of the recently proposed SCAN functional,46 which was shown to correctly reproduce the properties of liquid water, an archetypical hydrogen-bonded system.47 We also asses the potential energy surface (PES) barrier towards the concerted double proton transfer within the benzoic acid dimers taking into account the differences in the ZPE energies between the initial and transition state. The obtained data sheds light on the experimental results and lead to a better understanding of the proton-transfer process in compressed solids.
Computational tools
DFT calculations utilizing periodic boundary conditions were conducted in VASP 6.2.1 (ref. 48 and 49) for the ambient pressure structure of benzoic acid of P21/c symmetry containing four molecules (two dimers) in the unit cell.15 A plane waves basis set with a 800 eV cut-off was used for the description of valence electrons, while the 1s electrons of C and O were modelled with a projector-augmented-wave potential. Full geometry optimization (only symmetry constraints were applied) of the lattice vectors and fractional atomic coordinates of crystals containing BA tautomers was performed with the use of the regularized version of the SCAN functional (r2SCAN).50 The convergence criterion for the electronic minimization was 10−8 eV per cell. Sampling of the Brillouin zone was done through a Monkhorst–Pack mesh with a 2π × 0.05 Å−1 spacing. For an optimization at a given pressure its value was added to the diagonals of the stress tensor and the p·V term was added to the calculated electronic energy yielding the enthalpy of the system (not corrected for zero-point energy motion, ZPE).The ZPE correction was evaluated from Γ-point vibrational frequencies obtained from the optimized structures with the use of r2SCAN and the finite-displacement method (0.005 Å displacement), as implemented in VASP. These vibrations include both intermolecular modes (translations and librations of BA molecules), as well as intramolecular modes, including O–H stretching modes. For obtaining proton-transfer barriers single-point energy calculations on the r2SCAN-optimized structures were done with the use of the hybrid HSE06 functional.51 These calculations utilized the same computational parameters as used in the r2SCAN calculations.
Results
At ambient and high pressure benzoic acid crystallizes in the P21/c space group with two equivalent dimers present in the unit cell.15 The two tautomeric forms of these centrosymmetric dimers (A and B) are shown in Fig. 1. They can convert to each other through a transfer of two protons. Due to crystal packing effects A and B tautomers are not energetically equivalent and at ambient conditions crystals containing the A form have an energy lower by 0.2–0.8 kJ mol−1 (throughout the text the energies are referenced to one dimer), as determined by various experimental techniques.25 This is one of the smallest energy difference between tautomeric forms of solidcarboxylic acid dimers – e.g. nearly 8 kJ mol−1 is found for ibuprofen.52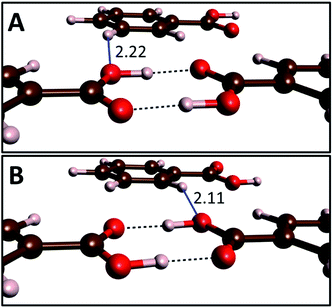 | ||
| Fig. 1 Arrangement of molecules in the A (top) and B (bottom) tautomers of benzoic acid dimers. The length at 10 GPa of the interdimer O⋯H contacts formed by the hydroxyl oxygen atom (blue lines) are given in Å. Visualization performed with the VESTA software.53 | ||
It can be expected that the enthalpy difference between crystals containing A and B tautomers, hereinafter referred to as asymmetry enthalpy, will increase upon compression. To verify this hypothesis geometry optimization, utilizing the r2SCAN functional, was performed in the 1 atm – 15 GPa pressure range for solids containing in their unit cells solely A or B dimers, and subsequently the enthalpy of the two crystals was compared. In agreement with experiment we find that at ambient conditions the energy of the A tautomer is lower by 0.6 kJ mol−1 (0.4 kJ mol−1 after including ZPE differences between the tautomers) than that of the B form. As can be seen in Fig. 2(a) compression up to 10 GPa increases the enthalpy difference between the two tautomers to 2.6 kJ mol−1 (1.6 kJ mol−1 after including the ZPE correction). Above this pressure the ZPE-corrected asymmetry enthalpy starts to decrease due to the increased differences in the zero-point energy between the two tautomers. The lower ZPE of the B form stems from a more elongated O–H bond (1.04 Å and 1.05 Å for A and B, respectively at 10 GPa), and consequently lower O–H stretching frequencies (2309/2173 cm−1 for Ag modes for A/B). The lengthening of the O–H bond in B as compared to A can be linked with the destabilizing effect of the interdimer O⋯H–C contact of the hydroxyl atom which is shorter in this form (see Fig. 1).
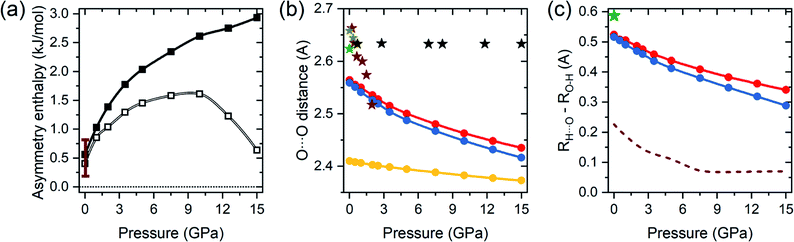 | ||
| Fig. 2 (a) Value of the asymmetry enthalpy as a function of pressure (solid squares) obtained with the r2SCAN functional. Empty squares denote ZPE-corrected values, vertical bars denote the range of experimental values determined at 1 atm. (b) Calculated pressure evolution of the O⋯O distances within the hydrogen bond (dots) for A (red), B (blue), and the MEP transition state (yellow) structures of BA. Stars denote experimental values from ref. 15 (green), ref. 39 (dark yellow), ref. 41 (maroon), and ref. 43 (black). (c) Calculated difference between the length of the O⋯H contact and the O–H bond (dots) for A (red) and B (blue) forms of benzoic acid dimers. Green star denotes the experimental value for A at 1 atm and 6 K.15 Dashed line denotes values obtained from previous LDA calculations.43 | ||
The calculations not only correctly reproduce the enthalpy difference between A and B tautomers, but also yield geometry parameters in good agreement with experiment. As shown in Table S1 in the ESI,† differences in lattice parameters and bond lengths do not exceed 2.2% when comparing with both ambient pressure,15 and high pressure data,39,41 with the exception of the X-ray data of ref. 43 for which much larger discrepancies are found. However, the structural parameters reported in that study yield unphysically constant O⋯O distances at high pressure, as shown by black stars in Fig. 2(b), hinting at a possible error in the experimental structure determination. We note that inclusion of dispersion corrections, in the form of the D3 correction,54,55 does not lead to better agreement with experimental values.
Upon compression the O⋯O contact is predicted to shorten in both forms of BA, as seen in Fig. 2(b), although this decrease is less abrupt than in the experimental data. Shorter O⋯O distance lead to strengthening of the hydrogen bond, and consequently the decrease in the difference between the O–H bond and H⋯O distance – see Fig. 2(c). Nevertheless, even at 15 GPa the system is far from hydrogen-bond symmetrization, in contrast to the results of previous LDA calculations.43
Pressure-induced strengthening of the hydrogen bond should lead to the decrease of the barrier for the double proton transfer within the benzoic acid dimers. In order to evaluate this effect a structure being a linear combination of A and B forms was constructed at each pressure point. The coefficients of this combination, both close to 0.5, where fine-tuned in such a way that the transferring protons in the resulting structure were position half-way between the O atoms. This structure was be used as a proxy for the transition state along the linear path (LP) trajectory for the concerted double proton transfer. This trajectory is characterized by minimal displacement of heavy atoms, in particular the O⋯O distance remains nearly unchanged during PT.
The barrier along LP is larger than along the minimum energy path (MEP). However, it is postulated that the proton transfer trajectory follows a path of minimum action with a barrier height lying in between that of LP and MEP.56 Therefore, the LP barrier can be treated as the upper bound, while the MEP barrier as a lower bound for the true PT barrier. In order to obtain information on the MEP barrier, a constrained geometry optimization of the LP transition state was performed at each pressure point. In the optimization, done with the use of the r2SCAN functional, the fractional positions of the acidic hydrogen atoms were fixed while positions of other atoms, as well as the lattice parameters, were allowed to vary. Constraining the position of the transferring protons allowed for relaxing the structure without it falling back to one of the tautomers. The structure obtained after this procedure was used as a proxy for the transition state along the MEP. As can be seen in Fig. 2(b), this structure is characterized by O⋯O contacts below 2.41 Å – considerably shorter than those found in the A and B tautomers, and much smaller that O⋯O distances observed so far for carboxylic acid dimers at ambient conditions.57 The predicted shortening of oxygen distance in the MEP transition state of solid BA mirrors the result of DFT calculations performed for isolated dimers,30,32,33 and highlights the fact that concerted proton transfer along the MEP path is connected with considerable movement of heavy atoms. In fact, comparison of the tautomeric structures and the MEP transition state indicated that the shortening of O⋯O contacts is a result of the movement of whole BA molecules.
By constructing the proxies of the LP and MEP transition state structures we are able to estimate the value of the barrier for a concerted transfer of both protons within the BA dimers, which is the dominating mechanism of proton transfer in carboxylic acid dimers.58 The barrier was estimated at each pressure point by subtracting the enthalpy of the A tautomer from the enthalpy of the given transition state (LP or MEP) – in analogy with the methodology used in previous studies on BA dimers.30,32,33 The correct description of PT barriers by DFT methods requires the use of hybrid functionals which incorporate a portion of Hartree–Fock exchange.59,60 However, the large computational cost of these methods precludes its use for geometry optimization and phonon frequency calculations. Therefore the values of the barriers were extracted from enthalpy differences obtained from single-point calculations (no geometry optimization) performed with the use of the hybrid HSE06 functional.51 ZPE corrections were evaluated at the r2SCAN level. We note that the barriers extracted directly from r2SCAN calculations are substantially lower (by about 30%) than those obtained with HSE06.
The PT barriers obtained for solid BA with the methodology described above are presented in Fig. 3 as a function of pressure and the O⋯O distance in the A tautomer. The MEP barrier at 1 atm (4.5 kcal mol−1) is smaller than theoretical values previously reported for isolated dimers of this compound (6.5–7.4 kcal mol−1).6,29,30,32,33 Inspection of Fig. 3(d) reveals that this can be traced back to the shorter O⋯O distance in the r2SCAN-optimized structure, as the MEP barrier decreases upon compression due to the shortening of the O⋯O distance.
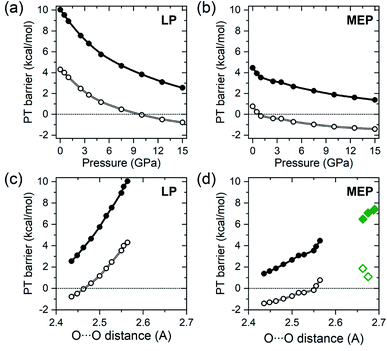 | ||
| Fig. 3 Pressure dependence of the proton transfer barrier (dots), given in kcal mol−1 (=4.184 kJ mol−1), along the LP (a) and MEP (b) trajectories obtained with the HSE06 functional. Open symbols denote ZPE-corrected values. Negative values correspond to the situation when the enthalpy of the LP and MEP transition states is lower than that of the A tautomer. The same quantities as a function of the O⋯O distance in the A tautomer are shown in (c) and (d). Diamonds in (d) denote theoretical values of the MEP barrier for isolated BA dimers obtained with the B3LYP functional,30,32,33 and the MP2 method29 (open diamonds denote ZPE-corrected values). | ||
At ambient pressure the LP barrier (10.1 kcal mol−1) is substantially larger than MEP barrier, but due to a more pronounced dependence on the O⋯O distance it decreases much faster with increasing pressure, as shown in Fig. 3(a). Nevertheless, even at 15 GPa the barriers for both the LP (2.6 kcal mol−1) and MEP (1.5 kcal mol−1) trajectories are still substantially larger than thermal energy at room temperature (0.6 kcal mol−1). However, inclusion of ZPE corrections (calculated with the r2SCAN functional) leads to a substantial lowering of the barriers at all pressures (Fig. 3). This is due to the fact that the high-energy symmetric O–H stretching modes of Ag symmetry have imaginary frequencies in the transition states and therefore do not contribute to the zero-point energy of LP and MEP. The ZPE-corrected value of the MEP barrier is only 0.7 kcal mol−1 at 1 atm, and is predicted to vanish upon compression to 0.8 GPa.
Above this pressure, which corresponds to an O⋯O distance in the A tautomer of 2.55 Å, benzoic acid crystals with a symmetric hydrogen bond have a lower ZPE-corrected enthalpy than either the A or B tautomers, which is reflected by a negative value of the barrier in Fig. 3. For the LP trajectory the ZPE-corrected barrier (4.5 kcal mol−1 at 1 atm) becomes zero at 9.7 GPa which corresponds to an O⋯O distance in A of 2.46 Å. We note that the range of O⋯O distances spanned by the values at which the MEP and LP barriers vanish are close to the 2.5 Å value recently proposed as the borderline for ZPE overcoming the PT barrier height in hydrogen-bonded systems.61 Moreover the distance at which the LP barrier becomes null (2.46 Å) is close to the critical O⋯O distance (2.44 Å) at which hydrogen-bond symmetrization is proposed for a number of inorganic systems.62 This hints that the energetics of the PT process may be similar regardless of the environment surrounding the hydrogen bond, although more studies are needed to confirm this.
The current results indicate that pressure-induced symmetrization of the hydrogen bond should occur in solid BA, but retrieving this effect requires taking into account the quantum nature of the system. Calculations suggest that this process should occur between 0.8 and 9.7 GPa. Taking into account the 2.2% underestimation of the length of O⋯O contacts in both tautomers, leading to the underestimation of PT barriers, the experimental pressure at which the MEP and LP barriers vanish can be estimated as closer to 6 and 20 GPa, respectively. Nonetheless, even at lower pressure the barrier for the PT transition, which as mentioned earlier should lie in between the MEP and LP barriers, should become comparable to thermal energy. As a result, structural data obtained from experiments yielding time-averaged information (e.g. X-ray diffraction) should contain a considerable admixture from the PT transition state, particularly in the case of room-temperature experiments. This, together with the fact that the MEP transition state is predicted to exhibit very short O⋯O contacts, might explain the dramatic decrease of O⋯O distances in the room-temperature measurements.41
Conclusions
Simulations presented in this work show how pressure can be used to tune the barrier of the proton transfer reaction in solid benzoic acid. It is shown for the first time that compression induces a barrierless transfer of proton, and that the vanishing of the barrier is strongly connected with differences in the ZPE energy. This indicates that quantum effects retain their important role in PT processes even at large compression. The obtained results shed light on previous experiments on compressed benzoic acid, in particular the drastic reduction of the O⋯O distance with pressure. The current findings are also of importance for other high-pressure studies on strongly hydrogen bonded systems,62 most notably water.63–65 In particular, it seems that the recently proposed critical O⋯O distance for hydrogen bond symmetrization (ref. 62) might be common also to organic compounds. Benzoic acid is of special interest in this context, as this distance can obtained for this compound at relatively low pressure (p < 20 GPa). Therefore new experimental investigation aimed at establishing the proton dynamics in this compound are required.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author acknowledges the support from the Polish National Science Centre (NCN) within the OPUS (grant number UMO-2016/23/B/ST4/03250). This research was carried out with the support of the Interdisciplinary Centre for Mathematical and Computational Modelling (ICM), University of Warsaw, within allocation no. GA83-26.References
- M. Eigen, Angew Chem. Int. Ed. Engl., 1964, 3, 1–19 CrossRef.
- T. Yoshino, T. Matsuzaki, S. Yamashita and T. Katsura, Nature, 2006, 443, 973–976 CrossRef CAS PubMed.
- R. da Silva Alvim, I. Borges and A. A. Leitão, J. Phys. Chem. C, 2018, 122, 21841–21853 CrossRef CAS.
- M. Benoit and D. Marx, ChemPhysChem, 2005, 6, 1738–1741 CrossRef CAS PubMed.
- D. Luckhaus, Phys. Chem. Chem. Phys., 2010, 12, 8357 RSC.
- L. Wang, S. D. Fried, S. G. Boxer and T. E. Markland, Proc. Natl. Acad. Sci. U.S.A., 2014, 111, 18454–18459 CrossRef CAS PubMed.
- Y. Litman, J. Behler and M. Rossi, Faraday Discuss., 2020, 221, 526–546 RSC.
- C. Qu and J. M. Bowman, Phys. Chem. Chem. Phys., 2019, 21, 3397–3413 RSC.
- F. Camargo Dalmatti Alves Lima, R. da Silva Alvim and C. Rodrigues Miranda, Appl. Surf. Sci., 2020, 529, 147103 CrossRef CAS.
- A. J. Horsewill, Prog. Nucl. Magn. Reson. Spectrosc., 2008, 52, 170–196 CrossRef CAS.
- A. J. Horsewill, J. Phys. Org. Chem., 2010, 23, 580–585 CrossRef CAS.
- R. Feld, M. S. Lehmann, E. W. Muir and J. C. Speakman, Z. Kristallogr., 1981, 157, 215–231 CAS.
- C. C. Wilson, N. Shankland and A. J. Florence, J. Chem. Soc., Faraday Trans., 1996, 92, 5051 RSC.
- M. Plazanet, N. Fukushima, M. R. Johnson, A. J. Horsewill and H. P. Trommsdorff, J. Chem. Phys., 2001, 115, 3241–3248 CrossRef CAS.
- F. Fillaux and A. Cousson, Chem. Phys., 2016, 479, 26–35 CrossRef CAS.
- I. Kalkman, C. Vu, M. Schmitt and W. L. Meerts, ChemPhysChem, 2008, 9, 1788–1797 CrossRef CAS PubMed.
- P. Ottiger and S. Leutwyler, J. Chem. Phys., 2012, 137, 204303 CrossRef PubMed.
- M. Boczar, K. Szczeponek, M. J. Wójcik and C. Paluszkiewicz, J. Mol. Struct., 2004, 700, 39–48 CrossRef CAS.
- F. Fillaux, F. Romain, M.-H. Limage and N. Leygue, Phys. Chem. Chem. Phys., 2006, 8, 4327 RSC.
- B. A. Kolesov, Spectrochim. Acta, Part A, 2015, 142, 320–323 CrossRef CAS PubMed.
- R. I. Jenkinson, A. Ikram, A. J. Horsewill and H. P. Trommsdorff, Chem. Phys., 2003, 294, 95–104 CrossRef CAS.
- Q. Xue, A. J. Horsewill, M. R. Johnson and H. P. Trommsdorff, J. Chem. Phys., 2004, 120, 11107–11119 CrossRef CAS PubMed.
- Y. Masuda, T. Nakano and M. Sugiyama, J. Phys. Chem. A, 2012, 116, 4485–4494 CrossRef CAS PubMed.
- I. Frantsuzov, M. R. Johnson, H. P. Trommsdorff and A. J. Horsewill, J. Phys. Chem. B, 2014, 118, 7777–7784 CrossRef CAS PubMed.
- G. Wu, I. Hung, Z. Gan, V. Terskikh and X. Kong, J. Phys. Chem. A, 2019, 123, 8243–8253 CrossRef CAS PubMed.
- D. Antoniou and S. D. Schwartz, J. Chem. Phys., 1998, 109, 2287–2293 CrossRef CAS.
- M. R. Johnson and H. P. Trommsdorff, Chem. Phys. Lett., 2002, 364, 34–38 CrossRef CAS.
- Z. Smedarchina, W. Siebrand and A. Fernández-Ramos, J. Phys. Chem. A, 2013, 117, 11086–11100 CrossRef CAS PubMed.
- H. Chojnacki, Pol. J. Chem., 2002, 76, 295–300 CAS.
- M. Wójcik, K. Szczeponek and M. Boczar, Int. J. Mol. Sci., 2003, 4, 422–433 CrossRef.
- G. M. Florio, T. S. Zwier, E. M. Myshakin, K. D. Jordan and E. L. Sibert, J. Chem. Phys., 2003, 118, 1735–1746 CrossRef CAS.
- C. S. Tautermann, A. F. Voegele and K. R. Liedl, J. Chem. Phys., 2004, 120, 631–637 CrossRef CAS PubMed.
- Z. Smedarchina, A. Fernández-Ramos and W. Siebrand, J. Chem. Phys., 2005, 122, 134309 CrossRef PubMed.
- D. S. Middlemiss, M. Facchini, C. A. Morrison and C. C. Wilson, CrystEngComm, 2007, 9, 777 RSC.
- M. Takahashi, Y. Kawazoe, Y. Ishikawa and H. Ito, Chem. Phys. Lett., 2009, 479, 211–217 CrossRef CAS.
- R. Li, J. A. Zeitler, D. Tomerini, E. P. J. Parrott, L. F. Gladden and G. M. Day, Phys. Chem. Chem. Phys., 2010, 12, 5329 RSC.
- B. Yu, Y. Wang, L. Wang, X. Tan, Y.-M. Zhang, K. Wang, M. Li, B. Zou and S. X.-A. Zhang, Phys. Chem. Chem. Phys., 2019, 21, 17696–17702 RSC.
- A. J. Horsewill, P. J. McDonald and D. Vijayaraghavan, J. Chem. Phys., 1994, 100, 1889–1894 CrossRef CAS.
- D. F. Brougham, A. J. Horsewill, A. Ikram, R. M. Ibberson, P. J. McDonald and M. Pinter-Krainer, J. Chem. Phys., 1996, 105, 979–982 CrossRef CAS.
- Z. P. Wang, X. D. Tang and Z. J. Ding, J. Phys. Chem. Solids, 2005, 66, 895–901 CrossRef CAS.
- W. Cai and A. Katrusiak, CrystEngComm, 2012, 14, 4420 RSC.
- Y. Tao, Z. A. Dreger and Y. M. Gupta, Vib. Spectrosc., 2014, 73, 138–143 CrossRef CAS.
- L. Kang, K. Wang, X. Li and B. Zou, J. Phys. Chem. C, 2016, 120, 14758–14766 CrossRef CAS.
- P. Cysewski, J. Mol. Model., 2015, 21, 83 CrossRef PubMed.
- L. Chen, J. Qu, Z. Tao, Q. Xie, G. Xie and J. Chen, Int. J. Mod. Phys. C, 2017, 28, 1750125 CrossRef CAS.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- M. Chen, H.-Y. Ko, R. C. Remsing, M. F. Calegari Andrade, B. Santra, Z. Sun, A. Selloni, R. Car, M. L. Klein, J. P. Perdew and X. Wu, Proc. Natl. Acad. Sci. U.S.A., 2017, 114, 10846–10851 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, J. Phys. Chem. Lett., 2020, 11, 8208–8215 CrossRef CAS PubMed.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- A. G. Demkin and B. A. Kolesov, J. Phys. Chem. A, 2019, 123, 5537–5541 CrossRef CAS PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Ehlert, U. Huniar, J. Ning, J. W. Furness, J. Sun, A. D. Kaplan, J. P. Perdew and J. G. Brandenburg, J. Chem. Phys., 2021, 154, 061101 CrossRef CAS PubMed.
- V. A. Benderskii, E. V. Vetoshkin, S. Y. Grebenshchikov, L. von Laue and H. P. Trommsdorff, Chem. Phys., 1997, 219, 119–142 CrossRef CAS.
- M. Ratajczak-Sitarz and A. Katrusiak, J. Mol. Struct., 2011, 995, 29–34 CrossRef CAS.
- S. D. Ivanov, I. M. Grant and D. Marx, J. Chem. Phys., 2015, 143, 124304 CrossRef PubMed.
- V. Barone, L. Orlandini and C. Adamo, Int. J. Quantum Chem., 1995, 56, 697–705 CrossRef CAS.
- L. Wang, M. Ceriotti and T. E. Markland, J. Chem. Phys., 2014, 141, 104502 CrossRef PubMed.
- B. A. Kolesov, Int. J. Mol. Sci., 2021, 22, 5380 CrossRef CAS PubMed.
- T. Meier, F. Trybel, D. Laniel, S. Khandarkhaeva, T. Ishii, A. Aslandukova, N. Dubrovinskaia and L. Dubrovinsky, arXiv 2201.06195, 2022.
- J.-A. Hernandez and R. Caracas, J. Chem. Phys., 2018, 148, 214501 CrossRef PubMed.
- F. Trybel, M. Cosacchi, T. Meier, V. M. Axt and G. Steinle-Neumann, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 102, 184310 CrossRef CAS.
- R. Yamane, K. Komatsu and H. Kagi, Phys. Rev. B, 2021, 104, 214304 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org.10.1039/d2ra01736a |
| This journal is © The Royal Society of Chemistry 2022 |
