Thermoelectric performance enhancement of eco-friendly Cu₂Se through incorporating CB₄

Abstract

We have prepared Cu₂Se + x wt% CB₄ composites with x = 0, 0.1, 0.3, 0.5, and 0.7 by a hydrothermal method and hot-pressing technique. The structural and compositional analysis indicates that pure phase Cu₂Se powders were synthesized and the densified layered bulk samples were obtained. Electrical properties testing showed that the sample with x = 0.5 has the high power factor of 0.886 mW m⁻¹ K⁻² due to its high Seebeck coefficient. Meanwhile, the thermal conductivity was suppressed to 0.6 W m⁻¹ K⁻¹ at 773 K. As a result, the final optimized ZT value of 1.46 at 773 K was achieved. These results suggest that CB₄ could be an alternative inclusion to improve effectively the thermoelectric performance of Cu₂Se.

---

1. Introduction

With the wide demand for environment-friendly energy, thermoelectric (TE) materials have received significant attention during the past two decades.^1–6 TE materials can realize the conversion directly between thermal and electrical energy.^7–9 High-efficiency TE materials require a high dimensionless figure of merit (ZT), ZT = S²σT/κ, where S is the Seebeck coefficient, σ is the electrical conductivity, T is the absolute temperature, and κ is the total thermal conductivity respectively.^10–13 Numerous exploratory efforts tried to optimize these parameters, i.e., enhance the power factor (PF = S²σ) and reduce the thermal conductivity simultaneously, to achieve high TE performance.^14,15 However, these parameters are strongly coupled together, making it challenging to improve the ZTs.^16,17

Chalcogenide TE materials have attracted widespread interests and have been intensively studied because of their intrinsically low lattice thermal conductivity (κ_L).^18–21 Very recently, Chung and co-workers reported²² the ultralow κ_L of 0.07 W m⁻¹ K⁻¹ obtained in polycrystal SnSe and thereby got a high ZT of 3.1, which breaks thermoelectric performance limits.²³ Cu-based chalcogenide also received much attention for environmental-friendly TE application and Cu₂Se is one of the strongest candidates.^24,25 To improve the TE performance of Cu₂Se, numerous strategies have been developed, such as nano-engineering,^26,27 solid solution alloying,^28,29 element doping,^30–32 and introducing highly dispersed nanoparticles.^33–36 Among them, adding nanoparticles to Cu₂Se matrix has been demonstrated to be an effective and prevailing approach to improve TE performance. The nanoparticles in composites, such as TiO₂,³⁷ graphene,³⁸ nano-boron,³⁹ carbon dots^40,41 and CNTs,⁴² can effectively scatter intermediate frequency phonons and hence suppress κ_L.

In this work, we try to introduce boron carbide (CB₄) as a second phase in the Cu₂Se matrix because nano-CB₄ has good thermal stability, high temperature electrical conductivity and relatively large Seebeck coefficient.⁴³ For preparing Cu₂Se samples with different contents of CB₄, the hydrothermal method and hot-pressing technique are employed. The results show that CB₄ inclusions do reduce κ significantly and meanwhile enhance PF slightly over a wide range of temperature. As a result, the highest ZT reaches 1.46 at 773 K, which is much higher than the value of undoped sample.

2. Experimental section

Cu₂Se nanopowders were prepared by hydrothermal method and CB₄ nanopowders were added during the hydrothermal process. We first mixed 20 mmol copper chloride dehydrate (CuCl₂·2H₂O, 99.9%), 10 mmol selenium dioxide (SeO₂, 99.9%) and a recommended amount of CB₄ (99%) into about 60 milliliters deionized water, and then magnetic stirred continuously for 12 h. The amount of CB₄ is determined by the mass ratio of Cu₂Se and CB₄. In this work, we consider five Cu₂Se + x wt% CB₄ (x = 0, 0.1, 0.3, 0.5, 0.7) samples, which are named as S0, S1, S3, S5 and S7 respectively for the convenience of description. After the components were completely dissolved, we added 20 milliliters hydrazine hydrate (N₂H₄·H₂O) into the mixture solution. The solution was then loaded into a Teflon-lined stainless steel autoclave and sealed. The autoclave was heated at 453 K for 24 h and cooled down to room temperature naturally. The product was collected by centrifuging and washed by deionized water and anhydrous ethanol for several times. We finally dried the product in vacuum at 333 K for at least 12 h. For getting the final samples, the synthesized powders were sintered into pallets with a diameter of 20 mm by hot-pressing method at 973 K and under a pressure of 40 MPa in the vacuum for 30 minutes.

The phase compositions of the prepared samples were identified by X-ray diffraction measurements (XRD, PANalytical, Netherlands) with Cu Kα radiation. The fracture surface microstructure was observed by field emission scanning electron microscopy (SEM, TM4000) and Energy-dispersive X-ray spectroscopy (EDS, X-MAX^N20, England). Seebeck coefficients and electrical conductivity simultaneously were measured by using a CTA-3 system (Cryoall, China) from 323 K to 773 K in a helium atmosphere. κ was calculated according to the formula κ = ρDC_p, where ρ is the density of the samples, D is the thermal diffusivity, and C_p is the heat capacity respectively. D was measured using the laser flash method (DFL-1600, Netzsch) on a square piece specimen with 10 mm in side and 1.5 mm in thickness. C_p was measured by differential scanning calorimetry (DSCQ-2000, TA). The density of the samples ρ was obtained from Archimedes' method.

3. Results and discussion

Fig. 1(a) shows the XRD patterns of the synthesized Cu₂Se + x wt% CB₄ (x = 0, 0.1, 0.3, 0.5, 0.7) nanopowders. The main diffraction peaks are all in consistent with the ICDD file No. 00-006-0680, indicating β-phase Cu₂Se is prepared successfully.^40,44–46 No CB₄ phase is to be detected, which might be due to introducing only a small amount into the main β-phase Cu₂Se. Fig. 1(b) shows the XRD patterns of the sintered bulk samples. The results match with the ICDD file No. 00-019-0401 very well, indicating that the as-prepared β-Cu₂Se nanostructures has transferred to pure α-Cu₂Se after sintering.^40,46,47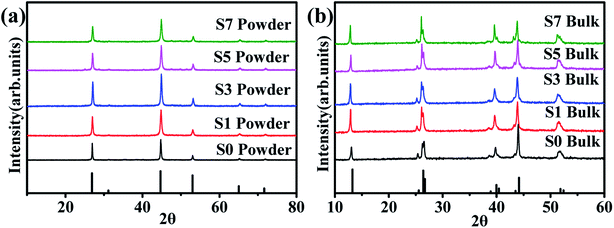

Fig. 1 (a) XRD patterns of the β-Cu₂Se (ICDD file No. 00-006-0680) synthesized nanopowders. (b) XRD patterns of α-Cu₂Se (ICDD file No. 00-019-0401) bulk samples.

The typical morphology of the synthesized Cu₂Se precursor nanopowders is shown in Fig. 2(a). Nanoplates with a lateral size of 100–500 nm, often aggregating together, can be clearly observed. Fig. 2(b–f) display the cross-sectional microstructures of the hot-pressed Cu₂Se + x wt% CB₄ bulk samples. Similar lamellar structure is observed for each sample. Such structure is conducive to reducing the thermal conductivity due to the increased scattering of phonons between layered interfaces.⁴⁸ A few pores on the surface can be spotted which might be due to Se volatilization during the sintering process and hence the corresponding density is slightly lower than the pure Cu₂Se. The samples S0, S1, S3, S5, and S7 have densities of 5.75, 5.65, 5.38, 5.29, 5.20 g cm⁻³ respectively (theoretical density of Cu₂Se is 6.74 g cm⁻³). Fig. 3 shows the surface EDS mapping of the sample S5. These maps suggest that copper, selenium, carbon and boron signals overlap, showing CB₄ is uniformly distributed in the sample.

Fig. 2 SEM images for (a) Cu₂Se nanopowders, the samples of (b) S0, (c) S1, (d) S3, (e) S5 and (f) S7.

Fig. 3 (a) SEM image of the typical morphology of the S5. (b)–(e) The corresponding EDS maps.

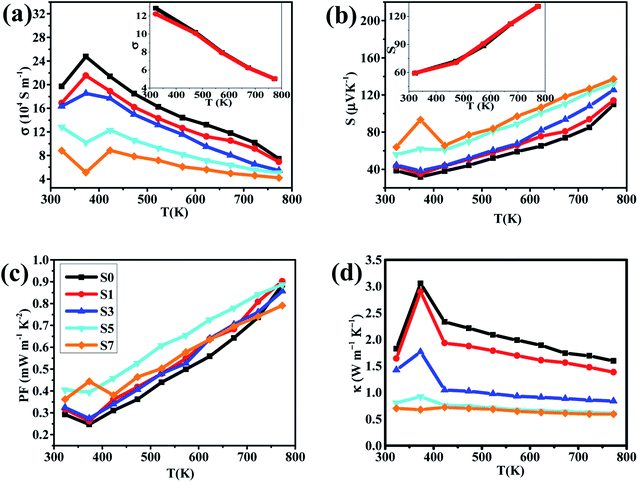
The temperature dependence of the electrical conductivity σ of our samples is shown in Fig. 4(a). Within the temperature range of 400–773 K, the electrical conductivity σ of all samples decreases monotonously with temperature increasing, which shows the typical behaviors of metallic-like characteristic. However, we can clearly find that the electrical conductivity σ varies abnormally around 400 K, which have been proved to be due to the phase transition from α-Cu₂Se to β-Cu₂Se.⁴⁹ In addition, the electrical conductivity σ decreases with the increasing of CB₄ components at each testing temperature. For example, compared to the sample S0, the electrical conductivity σ is about 3 times smaller around 400 K and 2 times smaller at 773 K for the sample S7. This trend in electrical conductivity σ is very different from the report of Cu₂Se/SiC composite,²⁷ but similar to the report of Cu₂S/SiC composite.¹⁷ For clarifying the underlying mechanism of the electrical transport behaviors, the room temperature carrier concentration (n) and carrier mobility (μ) are measured, as shown in Table 1. Clearly, there is a reduction in carrier concentration and an increase in carrier mobility with increasing of the CB₄ composite content. For the superionic conductor Cu₂Se, unstable copper ions show a liquid-like behavior and hence cause the unrepeatable electrical transport properties. The carrier concentration n contains two parts: the majority carrier (n_hole) and the ion carrier (n_ion), and therefore, the electrical conductivity σ = σ_hole + σ_ion. In our work, the introduction of CB₄ might effectively block the migration of copper ions, which causes the reduction in n_ion and hence in the whole carrier concentration n. In addition, the migration restrictions of copper ions can also effectively enhance the stability of Cu₂Se chemical structure, which is confirmed by the cyclic testing shown in Fig. 4. The increase in mobility μ might be due to the grain growth during the process of hot pressing, as can be clearly seen in Fig. 2. Because of the difficulty for measuring the transport of ions, more related discussions do not be present here.

Fig. 4 Temperature dependence of (a) electrical conductivities, (b) Seebeck coefficients, (c) power factors and (d) thermal conductivities for the samples of S0, S1, S3, S5 and S7. Insets of (a) and (b) are the heating (red line) and cooling (black line) curves for electrical conductivity and Seebeck coefficient of sample S5 respectively.

Table 1 Carrier concentration (n), mobility (μ) at room temperature

Sample	nhole + nion (10^19 cm^−3)	μ (cm^2 V^−1 s^−1)
S0	7.9	73.6
S1	6.6	101
S3	5.5	104
S5	5.3	112
S7	3.6	119

---

In our work, the samples S5 and S7 show a quite low electrical conductivity σ. This fact would not be very good for optimizing the thermoelectric properties of Cu₂Se. However, thankfully, the reduction in electrical conductivity σ is often accompanied by enhancement of the Seebeck coefficient. As we can see from Fig. 4(b), the samples S5 and S7 exhibit a larger Seebeck coefficient than the others within the entire testing temperature range and the optimal value reaches 137 μV K⁻¹ at 773 K for the sample S7. Additionally, the positive Seebeck coefficient for all samples suggests the p-type electrical transport in Cu₂Se. The calculated PFs of the samples are shown in Fig. 4(c). Very clearly, PFs curves of the samples S0, S1, S3 and S5 show a valley around 400 K due to the phase transition from β-Cu₂Se to α-Cu₂Se,^50,51 while the sample S7 has the abnormal high PF because of its very high S and low σ. However, we cannot evaluate precisely these parameters around 400 K because they are very sensitive to temperature change during the process of phase transformation. This might be the reason that some previous studies did not show the related data close to 400 K.

As T >400 K, all PFs increase rapidly as temperature increases. However, the sample S7 does not show the superior PF value, which might be due to its very low electrical conductivity. In contrast, the sample S5 has the optimal PF as T >400 K (PF_max = 0.886 mW m⁻¹ K⁻² at 773 K), indicating that a moderate content of CB₄ composites may result in a better electrical performance of Cu₂Se.

Another important parameter to determine the TE properties is the thermal conductivity κ. The thermal conductivity can be divided into two parts: κ = κ_L + κ_carrier, where κ_L comes from heat phonons travelling through the crystal lattice and κ_carrier arises from heat carriers' movement. Generally, at high temperature, κ_L dominates in Cu₂Se matrix.³⁹ The measured thermal conductivity is shown in Fig. 4(d). Clearly, all of the thermal conductivity κ decrease with temperature increasing, which is a reasonable trend because of the increasing in phonon scattering and the reduction in carrier concentration. For a fixed temperature, as CB₄ component increases from 0.0 to 0.7%, the thermal conductivity decreases very rapidly. To take a step further, carrier thermal conductivity (κ_carrier) is calculated by using the Wiedemann–Franz relationship, κ_carrier = LσT, where L is the Lorenz number. When the detailed band structure and scattering mechanism are not known, the Lorenz number can not be viewed as a constant but can be calculated by L = 1.5 + exp [−|S|/116], where L is in unit of 10⁻⁸ W Ω K⁻² and S (Seebeck coefficient) in unit of μV K−¹.⁵² The calculated L and κ_carrier are showed in Fig. 5. However, it seems that the measured total thermal conductivity of S5 and S7 are lower than the calculated values. The similar phenomenon happened to Cu₂Se/SiC system²⁷ and Cu–S system.^17,53 It might be due to the different thermal transport properties between electron/hole carriers and ion carriers. The equation κ_carrier = LσT may not be suitable for Cu₂Se/CB₄ composite. The ion carriers have a non-negligible contribution to total thermal transport, so the modified equation can be taken as κ_carrier = L (σ − σ_ion)T + κ_ion,^27,30,53 where κ_ion is the ionic thermal conductivity, σ_ion is ionic electrical conductivity. However, σ_ion and κ_ion cannot be measured precisely now and hence the carrier thermal conductivity and lattice thermal conductivity are not offered here.

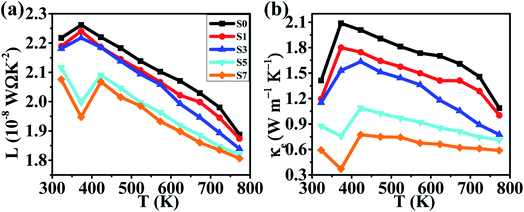Fig. 5 Temperature dependence of (a) the calculated Lorenz number, (b) the calculated thermal conductivities for samples of S0, S1, S3, S5 and S7.

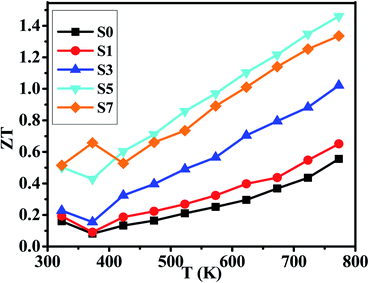
Considering the total thermal conductivity, the samples S5 and S7 remain very low values and very close to each other as T >400 K. The lowest κ value is 0.59 W m⁻¹ K⁻¹ at 773 K for S7 sample. This result indicates that the higher concentration of CB₄ inclusions could not improve further the thermal conductivity. Moreover, as shown in Fig. 4(c), the PF of sample S7 is also smaller than sample S5. Therefore, in this work, the S5 sample would show the optimal thermoelectric performance. This can be confirmed positively by the relationship between ZT values and temperature, as shown in Fig. 6. Sample S5 exhibits the largest ZT than the others as T >400 K and the largest value is of 1.46 at 773 K, which is much larger than that of undoped sample S0 (ZT_max = 0.55 at 773 K). The average ZT value of S5 (ZT_average = 1.034) is also larger than one within the temperature range of 400–773 K. These results suggest that Cu₂Se compositing a certain amount of CB₄ is very promising for TE application.

Fig. 6 Temperature dependence of ZTs for samples of S0, S1, S3, S5 and S7.

4. Conclusions

We have prepared the pure phase Cu₂Se + x wt% CB₄ (x = 0, 0.1, 0.3, 0.5, 0.7) nanopowders by hydrothermal method and have sintered the corresponding bulk samples by hot-pressing technique. With the content of CB₄ increasing, the electrical conductivities of our samples decrease very rapidly, while the Seebeck coefficients steadily increase. The final PFs show that the sample S5 possesses the optimal value within the testing temperature range. The thermal conductivity testing confirms that the CB₄ nano-inclusions can drastically reduce the κ of our samples. The lowest κ value is 0.59 W m⁻¹ K⁻¹ at 773 K for S7 sample. However, the κ of sample S5 is very close to that of sample S7 as T >400 K. Finally, the optimized ZT value of 1.46 at 773 K is achieved for S5 sample, which is about 165% larger than the undoped sample.

Conflicts of interest

The authors have no conflicts to declare.

Acknowledgements

This work is supported the Projection of State Key Laboratory of Environment-friendly Energy Materials, Southwest University of Science and Technology (No. 20FKSY23).

References

1. Z. G. Chen, G. Han, L. Yang, L. N. Chen and J. Zhou, Prog. Nat. Sci.: Mater. Int., 2012, 22, 535.
2. P. Sundarraj, D. Maity, S. S. Roy and R. A. Taylor, RSC Adv., 2014, 87, 46860.
3. M. Li, S. M. K. N. Islam, S. X. Dou and X. L. Wang, J. Alloys Compd., 2018, 769, 59.
4. T. J. Zhu, Y. T. Liu, C. G. Fu, J. P. Heremans, J. G. Snyder and X. B. Zhao, Adv. Mater., 2017, 29, 1605884.
5. J. Zhang, T. Zhu, C. Zhang, Y. G. Yan, G. J. Tan, W. Liu, X. L. Su and X. F. Tang, J. Alloys Compd., 2021, 881, 857916.
6. M. Rull-Bravo, A. Moure, J. F. Fernandez and M. Martin-Gonzalez, RSC Adv., 2015, 24, 41653.
7. J. He and T. M. Tritt, Science, 2017, 357, 1369.
8. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105.
9. L. Yang, Z. G. Chen, M. S. Dargusch and Z. Jin, Adv. Energy Mater., 2017, 8, 170197.
10. H. Zhu, C. Xiao and Y. Xie, Adv. Mater., 2018, 30, 180200.
11. X. L. Su, P. Wei, H. Li, W. Liu, Y. G. Yan, P. Li, C. Q. Su, C. J. Xie, W. Y. Zhao, P. C. Zhai, Q. J. Zhang, X. F. Tang and C. Uher, Adv. Mater., 2017, 29, 160213.
12. W. Suwannasri, R. Chueachot, T. Seetawan and R. Nakhowong, J. Alloys Compd., 2021, 863, 158749.
13. K. Biswas, H. J. Qing, K. Biswas, J. Q. He, I. D. Blum, C. I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414.
14. Fitriani, R. Ovik, B. D. Long, M. C. Barma, M. Riaz, M. F. M. Sabri, S. M. Said and R. Saidur, Renewable Sustainable Energy Rev., 2016, 64, 635.
15. W. D. Liu, X. L. Shi, M. Hong, L. Yang, R. Moshwan, Z. G. Chen and J. Zou, J. Mater. Chem. C, 2018, 6, 13225.
16. J. Shuai, J. Mao, S. W. Song, Q. Y. Zhang, G. Chen and Z. F. Ren, Mater. Today Phys., 2017, 1, 74.
17. Q. Peng, G. Z. Hua and J. Feng, J. Alloys Compd., 2017, 696, 782.
18. W. S. Liu, J. Z. Hu, S. M. Zhang, M. J. Deng, C. G. Han and Y. Liu, Mater. Today Phys., 2017, 1, 50.
19. Z. X. Zhang, K. P. Zhao, T. R. Wei, P. F. Qiu, L. D. Chen and X. Shi, Energy Environ. Sci., 2020, 13, 3307.
20. M. Beekman, D. T. Morelli and G. S. Nolas, Nat. Mater., 2015, 14, 1182.
21. K. P. Zhao, P. F. Qiu, L. D. Chen and X. Shi, Adv. Funct. Mater., 2020, 30, 1903867.
22. C. J. Zhou, Y. K. Lee, Y. Yu, S. Byun, Z. Z. Luo, H. Lee, B. Z. Ge, Y. L. Lee, X. Q. Chen, J. Y. Lee, O. Cojocaru-Miredin, H. Chang, J. Im, S. P. Cho, M. Wuttig, V. P. M. G. Kanatzidis and I. Chung, Nat. Mater., 2021, 20, 1378.
23. I. B. Brummerstedt, Nat. Mater., 2021, 20, 1309.
24. H. L. Liu, X. Shi, F. F. Xu, L. L. Zhang, W. Q. Zhang, L. D. Chen, Q. Li, C. Uher, T. Day and G. J. Snyder, Nat. Mater., 2012, 11, 422.
25. L. Yang, Z. G. Chen, G. Han, M. Hong, Y. C. Zou and J. Zou, Nano Energy, 2015, 16, 367.
26. B. Gahtori, S. Bathula, K. Tyagi, M. Jayasimhadri, A. K. Srivastava, S. Singh, R. C Budhani and A. Dhar, Nano Energy, 2015, 13, 36.
27. J. D. Lei, Z. Ma, D. Zhang, Y. Q. Chen, C. Wang, X. Y. Yang, Z. X. Cheng and Y. X. Wang, J. Mater. Chem. A, 2019, 7, 7006.
28. K. P. Zhao, M. J. Guan, P. F. Qiu, A. B. Blichfeld, E. Eikeland, C. X. Zhu, D. D. Ren, F. F. Xu, B. B. Iversen and L. D. Chen, J. Mater. Chem. A, 2018, 6, 6977.
29. K. P. Zhao, A. B. Blichfeld, E. Eikeland, P. F. Qiu, D. D. Ren, B. B. Iversen, X. Shi and L. D. Chen, J. Mater. Chem. A, 2017, 5, 6367.
30. Z. H. Ge, X. Y. Liu, D. Feng, J. Y. Lin and J. Q. He, Adv. Energy Mater., 2016, 6, 1600607.
31. S. D. Kang, J. H. Pohls, U. Aydemir, P. F. Qiu, C. C. Stoumpos, R. Hanus, M. A. White, X. Shi, L. D. Chen, M. G. Kanatzidis and G. J. Snyder, Mater. Today Phys., 2017, 1, 7.
32. W. H. Gao, Z. H. Liu, W. H. Zhang, N. Sato, Q. S. Guo and T. Mori, Appl. Phys. Lett., 2021, 118, 033901.
33. F. S. Liu, Z. N. Gong, M. J. Huang, W. Q. Ao, Y. Li and J. Q. Li, J. Alloys Compd., 2016, 688, 521.
34. R. M. Lu, A. Olvera, T. P. Bailey, C. Uher and P. F. P. Poudeu, ACS Appl. Mater. Interfaces, 2020, 12, 58018.
35. L. L. Zhao, S. M. K. N. Islam, J. Wang, D. L. Cortie, X. G. Wang, Z. X. Cheng, J. Y. Wang, N. Ye, S. X. Dou, X. Shi, L. D. Chen, G. J. Snyder and X. L. Wang, Nano Energy, 2017, 41, 164.
36. F. S. Liu, Z. N. Gong, M. J. Huang, W. Q. Ao, Y. Li and J. Q. Li, J. Alloys Compd., 2016, 688, 521.
37. F. F. Kong, J. Bai, Y. W. Zhao, Y. Liu, J. Shi, Z. Y. Wang and R. Xiong, Appl. Phys. Lett., 2019, 115, 203901.
38. M. Li, D. L. Cortie, J. X. Liu, D. H. Yu, S. M. K. N. Islam, L. L. Zhao, D. R. G. Mitchell, R. A. Mole, M. B. Cortie, S. X. Dou and X. L. Wang, Nano Energy, 2018, 53, 9931.
39. S. M. K. N. Islam, M. Li, U. Aydemir, X. Shi, L. D. Chen, G. J. Snyder and X. L. Wang, J. Mater. Chem. A, 2018, 6, 18409.
40. Q. J. Hu, Y. Zhang, Y. W. Zhang, X. J. Li and H. Z. Song, J. Alloys Compd., 2020, 813, 152204.
41. C. Y. Oztan, B. Hamawandi, Y. Q. Zhou, S. Ballikaya, M. S. Toprak, R. M. Leblanc, V. Coverstone and E. Celik, J. Alloys Compd., 2021, 864, 857916.
42. R. Nunna, P. F. Qiu, M. Yin, H. Y. Chen, R. Hanus, Q. F. Song, T. S. Zhang, M. Y. Chou, M. T. Agne, J. Q. He, G. J. Snyder, X. Shi and L. D. Chen, Energy Environ. Sci., 2017, 10, 1928.
43. C. Wood and D. Emin, Phys. Rev., 1984, 29, 4582.
44. F. Jia, S. Zhang, X. K. Zhang, X. L. Peng, H. T. Zhang and Y. Xiang, Chem. - Eur. J., 2014, 20, 15941.
45. A. Bhaskar, C. H. Hu, C. L. Chang and C. J. Liu, J. Eur. Ceram. Soc., 2016, 36, 2755.
46. L. Yang, Z. G. Chen, G. Han, M. Hong, Y. C. Zou and Z. Jin, Nano Energy, 2015, 16, 367.
47. F. Gao, S. L. Leng, Z. Zhu, X. J. Li, X. Hu and H. Z. Song, J. Electron. Mater., 2018, 47, 2454.
48. H. Q. Jun, Z. Zheng, Y. W. Zhang, X. J. Li, H. Z. Song and Y. J. Zhang, J. Mater. Chem. A, 2018, 6, 3417.
49. E. Eikeland, A. B. Blichfeld, K. A. Borup, K. P. Zhao, J. Overgaard, X. Shi, L. D. Chen and B. B. Iversen, IUCrJ, 2017, 4, 476.
50. H. L. Liu, X. Yuan, P. Lu, X. Shi, F. F. Xu, Y. He, Y. S. Tang, S. Q. Bai, W. Q. Zhang, L. D. Chen, Y. Lin, L. Shi, H. Lin, X. Y. Gao, X. M. Zhang, H. Chi and C. Uher, Adv. Mater., 2013, 25, 6607.
51. D. R. Brown, T. Day, K. A. Borup, S. Christensen, B. B. Iversen and G. J. Snyder, APL Mater., 2013, 1, 052107.
52. H. S. Kim, Z. M. Gibbs, Y. G. Tang, H. Wang and G. J. Snyder, APL Mater., 2015, 3, 041506.
53. Y. B. Zhu, B. P. Zhang and Y. Liu, Phys. Chem. Chem. Phys., 2017, 9, 27664.

---