Open Access Article
Open Access ArticleConduction band-edge valley splitting in two-dimensional ferroelectric AgBiP2S6 by magnetic doping: towards electron valley-polarized transport†
Dongxue Zhang and
Baozeng Zhou *
*
Tianjin Key Laboratory of Film Electronic & Communicate Devices, School of Integrated Circuit Science and Engineering, Tianjin University of Technology, Tianjin 300384, China. E-mail: baozeng@tju.edu.cn
First published on 6th May 2022
Abstract
Two-dimensional valleytronic systems, using the valley index of carriers to perform logic operations, serves as the basis of the next-generation information technologies. For efficient use of the valley degree of freedom, the major challenge currently is to lift the valley degeneracy to achieve valley splitting. In this work, using first-principles calculations, we propose that valley splitting can be readily achieved in a ferroelectric AgBiP2S6 monolayer by TM doping (TM = V, Cr, Mn, Fe, Co, and Ni), which is highly feasible in experiments. In sharp contrast to most previous reports of valley-related features in the valence band-edge, the pristine AgBiP2S6 monolayer has a direct band-gap located at K/K′ points of the Brillouin zone and harbors strong coupled spin and valley physics around the conduction band-edge, due to inversion symmetry breaking combined with strong spin–orbit coupling. By TM-doping, the local magnetic moment can be introduced into the system, which can destroy the valley degeneration of the conduction band-edge and induce valley splitting. Especially in a V-doped system, accompanied with a large valley splitting (26.8 meV), there is a serious n-type doping in AgBiP2S6. The efficient electron-doping moves the Fermi level just located between the conduction band minimum of the K/K′ valleys, which is suitable for valley-polarized transport. Moreover, the valley-polarized index can be flipped by applying a small magnetic field to rotate the magnetocrystalline direction. The magnitude of valley splitting relies on the strength of orbital hybridization between the TM-d and Bi-p states and can be tuned continually by applying biaxial strain. Under an in-plane electric field, such valley degeneracy breaking would give rise to the long-sought anomalous valley Hall effect, which is crucial to design a valleytronic device.
Introduction
Manipulating different degrees of freedom (DOF) of electrons is at the heart of modern information processing technology. In addition to charge and spin, electrons are endowed with an additional DOF, namely, the valley DOF.1–5 The utilization of valley DOF is analogous to charge for electronics and spin for spintronics, leading to the vision of valley-based information processing and storage, which has now expanded into a well-known field named valleytronics.3,6–10 In crystalline solids, valley refers to the degenerate energy extreme of a conduction band or valence band at special k points, have a large separation in the momentum space that enables valley pseudospin to be very robust against phonon and impurity scatterings.3,11,12 As the first stable two-dimensional (2D) crystal produced by mechanical exfoliation,13 graphene has been demonstrated to have many interesting valleytronic properties. However, in such a nonmagnetic centrosymmetric system, the combination of inversion with time-reversal symmetries ensures Berry curvature and magnetic moments to be zero, thus limiting the constitution of a binary valley index. The valleys can be distinguishable by breaking the inversion symmetry via stacking of graphene on hexagonal boron nitride or an application of out-of-plane electric field to bilayer graphene.14,15 Different from graphene, monolayer transition-metal dichalcogenides (TMDs; MX2, where M = Mo and W, and X = S and Se) with the hexagonal nature inherit broken inversion symmetry because the M and X atoms occupy one of the two inequivalent triangular sublattice. These materials have two valleys at the K and K′, which are related to each other by time-reversal symmetry and no longer being equivalent.16 The electrons and holes residing at the K and K′ valleys possess opposite spin, orbital magnetic moment, and Berry curvature.11,17 The broken inversion symmetry with strong spin–orbit coupling (SOC) introduce valley-contrasting physical properties in TMDs.18In order to distinguish and manipulate the carriers at defined valleys, the K and K′ valley degeneracy should be lifted to introduce the valley splitting, and previous studies have provided various strategies. One is to use an ultrafast circularly polarized laser pump to break the valley degeneracy through the optical Stark effect,6,19 another is to apply a vertical magnetic field by taking advantage of the Zeeman effect.20–22 However, the optical pumping technology may only be used for experimental measurements but not for practical applications because of the restricted lifetime of carriers and the efficiency of external magnetic field is usually too low that a 1 T magnetic field can only give rise to a splitting of 0.1–0.2 meV. Thus, magnetic proximity coupling is proposed and studied intensively, where magnetic substrates, such as EuO,23,24 CoO,25 MnO,12,26 EuS,27,28 Fe3O4,29 and YMnO3,30 contribute to the interfacial magnetic exchange. A giant valley splitting in WS2/EuS heterostructures have been experimentally realized.31 But the bulk substrates intrinsically limit the device applications in nanoscale. A 2D magnetic van der Waals (vdW) heterostructure WSe2/CrI3, which is favored for forming a relatively clean interface to eliminate impurity scattering and can minimize the effect of lattice mismatch, has been both theoretically predicted and experimentally realized, showing sizable valley splitting and optical-controllable valley pseudospin.32,33 Compared with the construction of 2D magnetic heterostructure, internal magnetic moments induced by magnetic dopants should also be able to engineer the valley splitting and is more feasible.34–36 With the innovation of laboratory equipment and methods, transition-metal (TM) doped 2D TMDs have been reported in many experiments, and can avoid the formation of metal clusters.37–41 However, for most 2D TMDs, the valence band undergoes larger spin splitting with SOC which varies from 150 meV in MoS2 to 460 meV in WSe2.42,43 We expect that the holes in a given valley may retain their spin information even at room temperature. Thus, p-type TMDs are promising candidates for valleytronic applications. Although magnetic doping can break valley degeneracy and induce valley splitting, the Fermi level must be tuned to the valence band maximum (VBM) by subsequent gating or hole doping, and then the longitudinal transport will be both spin and valley-polarized.
In view of the above analysis, materials with larger SOC-induced spin splitting at the conduction bands may have more advantages for magnetic doping and practical application. Our previous reports have demonstrated that the broken inversion symmetry with strong SOC in 2D ferroelectric AgBiP2S6 will introduce large spin splitting at the conduction band-edge.44 Here, we performed density functional theory (DFT) and Berry curvature calculations to explore the valley splitting related properties of AgBiP2S6 induced by the TM doping (TM = V, Cr, Mn, Fe, Co, and Ni). In previous report, B-site (In) substitution effect in ferroelectric CuInP2S6 monolayer have been investigated.45 Ferromagnetism and ferroelectricity can coexist in both CuCrP2S6 and CuVP2S6. However, complete substitution may induce large structural distortion or even phase transformation. Thus, A-site (Ag) substitution doping in ferroelectric AgBiP2S6 can destroy the time-reversal symmetry of the system by maintaining the valley behavior related to the heavy element Bi at the conduction bands, which is beneficial to the subsequent investigation of valley splitting. We find that pristine AgBiP2S6 monolayer has a direct band-gap located at K/K′ points of the Brillouin zone and harbors coupled spin and valley physics around the conduction band-edge. By TM-doping, the local magnetic moment can be introduced into the system, which can destroy the valley degeneration of the conduction band-edge and induce valley splitting. Especially in V-doped system, accompany with a large valley splitting (26.8 meV), there is a serious n-type doping in AgBiP2S6. The efficient electron-doping moves the Fermi level just located between the conduction band minimum (CBM) of the K/K′ valleys, which is suitable for valley-polarized transport. Moreover, the valley-polarized index can be flipped by applying a small magnetic field to rotate the magnetocrystalline direction. The magnitude of valley splitting relies on the strength of orbital hybridization between the TM-d and Bi-p states and can be tuned continually by applying biaxial strain. Under an in-plane electric field, such valley degeneracy breaking would give rise to the long-sought anomalous valley Hall effect, which is crucial to design a valleytronic device.
Computational details and models
Density functional theory (DFT) calculations for structural relaxation and electronic structures are performed by using the Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA) for the exchange and correlation function as implemented in the Vienna ab initio simulation package (VASP).46–48 The projector augmented wave (PAW) is used to describe the electron–ion interaction.49,50 The cutoff energy is set to 500 eV for plane-wave expansion after convergence tests. A 2 × 2 AgBiP2S6 supercell with one substituted dopant atom is used. The Γ-centered k-grids of 2 × 2 × 1 and 4 × 4 × 1 are adopted to sample the Brillouin zone for geometry optimization and static electronic calculation, respectively. During the structural relaxation, the energy convergence criterion is 10−5 eV per unit cell, and the forces on all relaxed atoms are less than 0.01 eV Å−1. The vacuum space larger than 20 Å is adopted to eliminate the interaction between adjacent layers. The PBE + U method with Ueff = 3.0 eV for TM atoms is used to take strong correlation effects into account,51 which has been widely used in previous works.35,52 The SOC effect explicitly included in the band structure calculations. For the calculations of Berry curvature and anomalous Hall conductivity, the maximally localized Wannier functions (MLWFs) implemented in the WANNIER90 package are employed.53Results and discussion
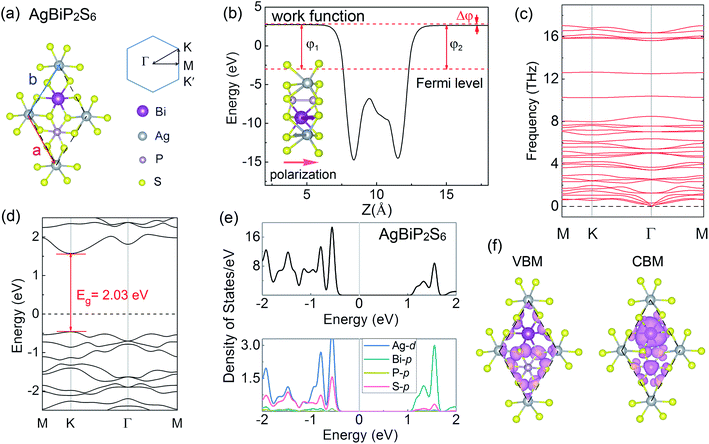
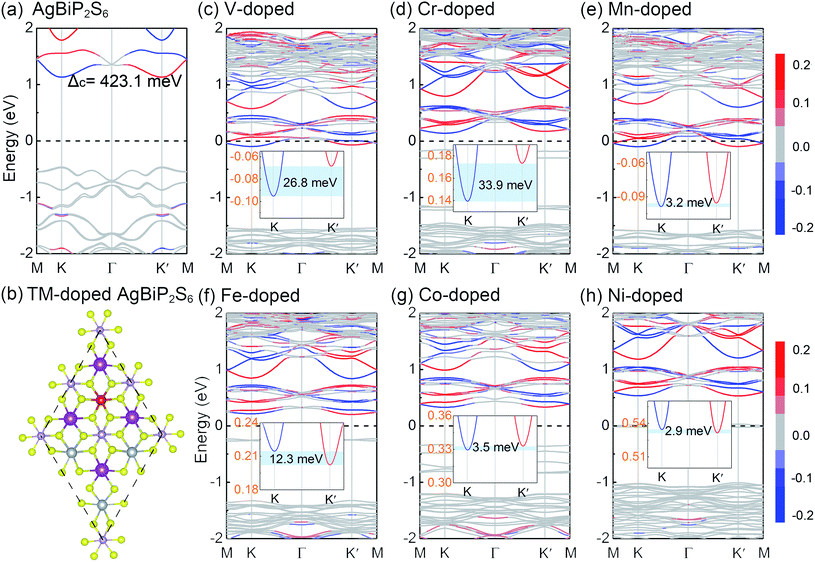
TM thio/selenophosphates is a broad class of vdW layered structures with two sulfur or selenium layers sandwiching a layer of metal ions and P2 pairs and general compositions of M4[P2X6]4−, [M2+]2[P2X6]4−, and M1+M3+[P2X6]4−, where M1+ = Cu, Ag; M3+ = Cr, V, Al, Ga, Bi; and X = S, Se.54,55 Especially, those quaternary compounds exhibit mixed electron-ionic conductivity, promising optical and catalytic properties.56 As shown in Fig. 1(a), AgBiP2S6 is a typical quaternary compounds with a rhombohedral structure and contains a sulfur framework with the octahedral voids filled by Ag, Bi, and P–P triangular patterns. The [P2S6]4− anions are bridged by alternating and ordered arrangement of Ag and Bi metal centers. The inset of Fig. 1(b) shows the side view of the crystal structure. Both Ag+ and Bi3+ ions are distorted from the octahedral environment, constituting a collinear two-sublattice system. They shift to opposite directions and the Ag+ ion off-centering is much greater than that of the Bi3+ ions. Consequently, spontaneous polarization emerges with the polar axis normal to the layer plane.57 The non-centrosymmetric unit cell illustrated by the dashed line belongs to the space group P3. The optimized lattice constant of AgBiP2S6 monolayer is 6.45 Å, while the thickness d is 3.44 Å. The Ag+ and Bi3+ ions shifting opposite away from the center of the layer along the z axis by 0.49 Å and 0.17 Å, respectively. These structure parameters are in good agreement with the previous work.55 The average electric potential energy of AgBiP2S6 is shown in Fig. 1(b), suggesting a potential gradient arising from the broken mirror symmetry in the vertical direction, and the net electric field pointing from Bi to Ag. According to the Helmholtz equation, the energy difference between the two vacuum levels is actually the change of work function (Δφ = 0.11 eV), which is proportional to the dipole moment.58 The phonon dispersion relations of AgBiP2S6 monolayer display no imaginary frequency (see Fig. 1(c)), suggesting that it is dynamically stable.59,60 The band structure of AgBiP2S6 without considering SOC is shown in Fig. 1(d). It can be seen that AgBiP2S6 monolayer is a nonmagnetic semiconductor with a direct band-gap of 2.03 eV, wherein the band edges located at the same high symmetry K point. In a hexagonal system with broken inversion symmetry, the valley DOF will be present when a local minimum in the conduction band or local maximum in the valence band appears at the K/K′ points.16,43 Apart from the VBM and CBM, there are also some valleys appearing in the other conduction and valence bands, and we do not consider them because they lie too far away from the Fermi level to be useful. Fig. 1(e) shows the total density of states (DOS) and the orbital-resolved partial density of states (PDOS) for each atom of AgBiP2S6. The bands near the VBM are mainly contributed by Ag-d and S-p orbitals, while the bands near the CBM arise from Bi-p and S-p orbitals. These phenomena can also be obtained intuitively from the related band decomposed charge density of the VBM and CBM in Fig. 1(f). Since PBE is known to underestimate the band-gap, the hybrid Heyd–Scuseria–Ernzerhof (HSE06) method is used to predict a more reasonable energy band-gap.61 Fig. S1† shows the total DOS and orbital-resolved PDOS calculated by the HSE06 method. It is worth mentioning that the HSE06 functional only enhances the band-gap to 2.45 eV, but have no significant changes in the orbital contributions of the VBM and CBM.Upon considering SOC, as shown in Fig. 2(a), the spin degeneracy for the valleys of AgBiP2S6 monolayer is deformed because of the broken inversion symmetry. And the time-reversal symmetry leads to the opposite ordering of the spin-up and spin-down states at the K and K′ valleys. The SOC-induced spin splitting is 423 meV in conduction band (Δc), whereas the splitting of spin-up and spin-down states near valence band (Δv) is found to be very small (∼30 meV), which is exactly opposite to that of TMDs,43 where large SOC-induced spin splitting is observed at valence band. This phenomenon is attributed to the fact that the valence and conduction band-edges are dominated by different orbitals. The conduction band-edges are mainly contributed by heavy Bi atoms as plotted in the orbital-resolved PDOS and band decomposed charge density, thus the strong SOC of Bi-p orbitals will lift the out-of-plane spin degeneracy of the band-edges at K and K′ by a significant amount. Because of the time-reversal symmetry, the K and K′ valleys of AgBiP2S6 exhibit opposite spin signs but are energetically degenerate. To make use of the valley index as an information carrier, the crucial step is to lift this degeneracy, thereby producing valley splitting. Hence, 3d TM (V, Cr, Mn, Fe, Co, and Ni) with large atomic magnetic moments are selected as the magnetic dopants to break the time-reversal symmetry of AgBiP2S6. For retaining the Bi-p orbital-related large spin splitting at the conduction band-edge, substitution doping of Ag atom is performed in a 2 × 2 supercell. The TM atom replaces one of the four Ag atoms in the supercell with a doping concentration of 25%. It should be mentioned that the electronic structures of the 2 × 2 supercell at the K/K′ points are the same as those of the unit cell. Thus, we do not need to consider the band unfolding technique here.35,52 The binding energy (Eb) is given by the expression
| Eb = Edoped − (Evacancy + ETM) | (1) |
The band structures of all TM-doped systems with considering SOC are shown in Fig. 2(c)–(h).
We can see that all of the TM-doped AgBiP2S6 monolayers maintain the semiconducting nature with different degree of n-type doping, which mainly depends on the valence states of dopants. Moreover, some impurity states appear in the band-gap, but fortunately, the K and K′ valleys at the conduction band-edge are preserved well. Especially for the cases of V, Mn, and Ni-doped AgBiP2S6, the valleys in the conduction bands lie far away from the defect states, making it easy to realize further manipulations and practical applications. Upon considering SOC, the degeneracy of the CBM at K and K′ valleys is lifted for all TM-doped systems, successfully achieving the valley splitting. Herein, valley splitting is quantified by the energy difference between the K and K′ valleys of the CBM as ΔEKK′ = |EK − EK′|. In V and Cr-doped AgBiP2S6, the valley splitting in the conduction bands can reach 26.8 and 33.9 meV, respectively, which are comparable to those of the previously reported systems, like V/Cr-doped MoSSe (10–59 meV),35 V/Mn-doped CrS2 (40–65 meV),62 and N/C-doped Tl2O (23–44 meV).63 Considering that the external magnetic field can also induce valley splitting with a value of 0.1–0.2 meV/T,64 the obtained ΔEKK′ of V and Cr-doped AgBiP2S6 even corresponds to an equivalent magnetic field of about 150–350 T. Such a large external magnetic field, of course, is difficult to be achieved in experiments, strongly suggesting that magnetic doping is a very promising method for realizing the valley splitting. From the PDOS of the doped systems shown in Fig. 3, we can see that V, Mn, and Ni-doped AgBiP2S6, have a clean band-gap, the TM-d orbitals only hybridize with Ag-d and S-p orbitals near the VBM, but in Cr, Fe, and Co-doped systems, the TM-d orbitals will also form impurity state in the band-gap. In any case, the Bi-p orbitals contribution at the CBM is not affected, indicating that the TM-doping destroys the time-reversal symmetry of the system by introducing local magnetic moments, providing an ideal platform for studying the conduction band-edge valley splitting. More surprisingly, with V-doping, the high-valence substitution also moves the Fermi level through the valleys at the CBM by n-type doping, which is conducive to the device application of electron valley-polarized transport. We further discuss the effect of doping concentration on valley splitting. In Fig. S4(a) and (b),† when Ag atoms in the AgBiP2S6 are completely replaced with a doping concentration of 100%, VBiP2S6 monolayer is a semiconductor with an indirect band-gap of about 0.12 eV. The electronic states at the CBM and VBM are mainly contributed from the d orbitals of V and p orbitals of Bi, respectively. The carriers at the CBM are spin polarized and the degeneracy of the CBM at K and K′ valleys is lifted with an energy difference of about 171 meV due to the SOC effect. This intrinsic valley splitting in such a magnetic semiconductor is similar to the previous reports, such as Nb3I8,65 NbSe2,66 and LaBr2.67 In Fig. S4(c) and (d),† with a lower doping concentration of 11% in a 3 × 3 AgBiP2S6 supercell, the valley polarized states at K and K′ points in the unit cell are folded to Γ point. It should be noted that, the coordinate overlap of the K and K′ points in a 3 × 3 supercell does not affect the electronic properties at the two valleys. The two nondegenerate and inequivalent valleys still exist with an energy difference of about 7.2 meV. Also, the electronic bands at the two non-equivalent valleys are mainly contributed by V-d and Bi-p orbitals. These results indicate that the value of valley splitting in AgBiP2S6 is proportional to the doping concentration of magnetic elements.
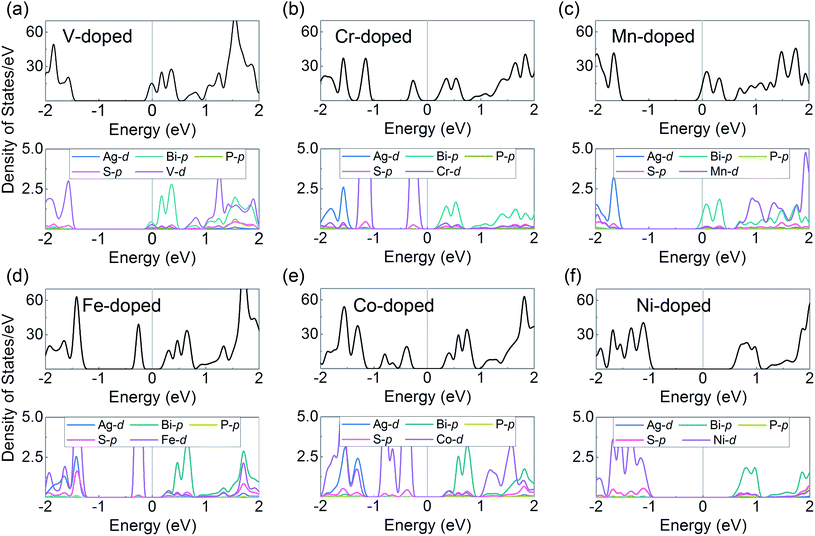 | ||
| Fig. 3 (a)–(f) The total DOS and orbital-resolved PDOS for each atom of TM-doped AgBiP2S6 monolayers by the PBE method with SOC. The Fermi level is set to zero. | ||
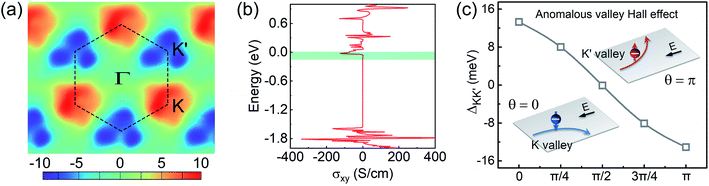
It is known that in systems with broken inversion symmetry, the charge carriers in the K and K′ valleys will acquire a nonzero Berry curvature Ω along the out-of-plane direction. The Berry curvature induced intrinsic transverse velocity shows the physical nature of the anomalous Hall effect. The Berry curvature can be written as68
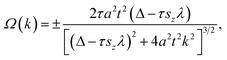 | (2) |
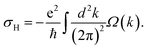 | (3) |
In the absence of a magnetic field, the net effect is a pure valley Hall current with a vanishing charge Hall current. However, an external magnetic field will cause a net charge current because the Hall currents from the two valleys do not completely cancel. Thus, the internal magnetic field induced by introducing magnetic dopants in AgBiP2S6 is expected to cause AHC owing to the broken time-reversal symmetry. In Fig. 4(a), the calculated Berry curvatures for the K and K′ valleys have the same absolute value but opposite signs, which reveals that the valley-contrasting characteristic remains in AgBiP2S6 even strongly hybridized with magnetic dopants. Under an in-plane electric field E, Bloch electrons in this system will acquire an anomalous velocity υ ∼ E × Ω(k). As signs of Berry curvature are opposite, the electrons in the K and K′ valleys will move to opposite edges of V-doped AgBiP2S6. Since the Fermi level is just located between the K and K′ valleys in the conduction band-edges, as shown from the inset of Fig. 4(c), the spin-down electrons from the K valley are accumulated at the downside of the sample under an in-plane electric field. When such a system is magnetized in the opposite direction, the spin-up electrons in the K′ valley will move to the upside of the sample in the presence of an in-plane electric field, realizing the anomalous valley Hall effect. As electrons are only accumulated at one edge of the sample, a more easily measurable charge Hall current as a voltage can be detected, offering a possible avenue to realize data storage using valley splitting. The AHC is also calculated and shown in Fig. 4(b). The valley splitting of the AHC is prominent because it changes from a small finite value to zero when the Fermi level shifts from the CBMK to the CBMK′. When the Fermi level lies between the CBMK to the CBMK′ as denoted by the shaded region, a fully spin- and valley-polarized Hall conductivity will be generated. This provides us with a method to detect the valley pseudospin by electrical measurements and forms the basis for the application of the valleytronic device.
Finally, we focus on engineering the valley splitting in V-doped AgBiP2S6. The external magnetic field, which can modulate the spin orientation, is expected to be an effective approach to control the valley splitting. As shown in Fig. 4(c), valley splitting is strongly correlated with the magnetization direction. When the spin orientation is along the in-plane direction (θ = π/2), the valley splitting of the doped system vanishes. When the spin orientation is reversed (θ = π), the valley splitting is also reversed. Furthermore, since the magnetic dopant induced valley splitting is mediated with the orbital hybridization, we expect that its magnitude can be modulated by changing the hybridization strength. In experiment, one can apply a specific substrate supporting the system to achieve the strain, and then the lattice constant, atomic distance, and orbital hybridization can be adjusted. The biaxial strain is defined as ε = (a − a0)/a0, where a0 and a are the lattice constants of the unstrained and strained systems. The related band structures under various biaxial strain are shown in Fig. 5(a)–(g). Fig. 5(h) shows the variation of the valley splitting as a function of the biaxial strain ε (%). We can see that compressed strain will inhibit the spin splitting in both K and K′ valleys, decreasing the valley splitting. When tensile strain is applied, the SOC-induced spin splitting in K valley is enhanced, but suppressed in K′ valley. Particularly, when ε = +2% (see Fig. 5(b)), valley splitting increases to 63 meV, and its morphology is similar to the recent reported “single-valley state” in 2D antiferromagnetic BiFeO3.69 With further increasing the tensile strain, this phenomenon gradually disappears, suggesting that the V-doped AgBiP2S6 under appropriate tensile strain is an ideal valleytronic material.
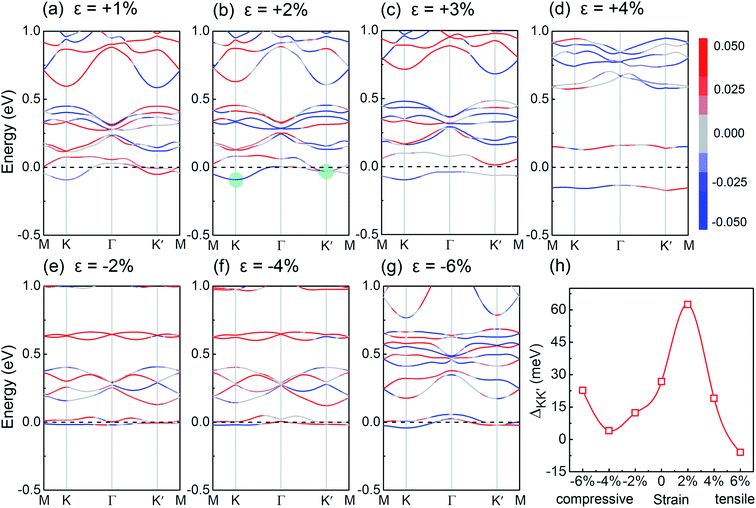 | ||
| Fig. 5 (a)–(g) Calculated band structures with various biaxial strain. (h) Valley splitting as a function of the biaxial strain ε (%). | ||
Conclusions
In conclusion, using first-principles calculations, we demonstrate that valley splitting can be readily achieved in TM-doped 2D ferroelectric AgBiP2S6. In sharp contrast to most previous reports of valley-related features in the valence band-edge, pristine AgBiP2S6 monolayer has a direct band-gap located at K/K′ points of the Brillouin zone and harbors strong coupled spin and valley physics around the conduction band-edge, due to inversion symmetry breaking combined with strong spin–orbit coupling. By TM-doping, the local magnetic moment can be introduced into the system, which can destroy the valley degeneration of the conduction band-edge and induce valley splitting. Especially in V-doped system, accompany with a large valley splitting (26.8 meV), the high-valence substitution also moves the Fermi level through the valleys at the CBM by n-type doping, which is conducive to the device application of electron valley-polarized transport. Moreover, the valley-polarized index can be flipped by applying a small magnetic field to rotate the magnetocrystalline direction. The magnitude of valley splitting relies on the strength of orbital hybridization between the TM-d and Bi-p states and can be tuned continually by applying biaxial strain. Under an in-plane electric field, such valley degeneracy breaking would give rise to the long-sought anomalous valley Hall effect for both spin/valley filter, which is crucial to design a valleytronic device.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was partially supported by the National Natural Science Foundation of China (No. 11704282), Natural Science Foundation of Tianjin City (No. 18JCQNJC72900), Education Commission Research Project of Tianjin City (No. 2017KJ251).References
- S. A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, S. von Molnar, M. L. Roukes, A. Y. Chtchelkanova and D. M. Treger, Science, 2001, 294, 1488–1495 CrossRef CAS PubMed.
- J. R. Schaibley, H. Yu, G. Clark, P. Rivera, J. S. Ross, K. L. Seyler, W. Yao and X. Xu, Nat. Rev. Mater., 2016, 1, 16055 CrossRef CAS.
- A. Rycerz, J. Tworzydło and C. W. J. Beenakker, Nat. Phys., 2007, 3, 172–175 Search PubMed.
- M. Ezawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 161406 CrossRef.
- Z. Zhu, A. Collaudin, B. Fauqué, W. Kang and K. Behnia, Nat. Phys., 2011, 8, 89–94 Search PubMed.
- T. Cao, G. Wang, W. Han, H. Ye, C. Zhu, J. Shi, Q. Niu, P. Tan, E. Wang, B. Liu and J. Feng, Nat. Commun., 2012, 3, 887 Search PubMed.
- H. Yu and W. Yao, Nat. Mater., 2017, 16, 876–877 CrossRef CAS PubMed.
- D. Xiao, G.-B. Liu, W. Feng, X. Xu and W. Yao, Phys. Rev. Lett., 2012, 108, 196802 CrossRef PubMed.
- A. Castellanos-Gomez, M. Poot, G. A. Steele, H. S. van der Zant, N. Agrait and G. Rubio-Bollinger, Adv. Mater., 2012, 24, 772–775 CrossRef CAS PubMed.
- H. Fang, S. Chuang, T. C. Chang, K. Takei, T. Takahashi and A. Javey, Nano Lett., 2012, 12, 3788–3792 CrossRef CAS PubMed.
- X. Xu, W. Yao, D. Xiao and T. F. Heinz, Nat. Phys., 2014, 10, 343–350 Search PubMed.
- L. Xu, M. Yang, L. Shen, J. Zhou, T. Zhu and Y. P. Feng, Phys. Rev. B, 2018, 97, 041405 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- R. V. Gorbachev, J. C. Song, G. L. Yu, A. V. Kretinin, F. Withers, Y. Cao, A. Mishchenko, I. V. Grigorieva, K. S. Novoselov, L. S. Levitov and A. K. Geim, Science, 2014, 346, 448–451 CrossRef CAS PubMed.
- M. Sui, G. Chen, L. Ma, W.-Y. Shan, D. Tian, K. Watanabe, T. Taniguchi, X. Jin, W. Yao, D. Xiao and Y. Zhang, Nat. Phys., 2015, 11, 1027–1031 Search PubMed.
- D. Xiao, W. Yao and Q. Niu, Phys. Rev. Lett., 2007, 99, 236809 CrossRef PubMed.
- K. F. Mak, K. L. McGill, J. Park and P. L. McEuen, Science, 2014, 344, 1489–1492 CrossRef CAS PubMed.
- Y. Ye, J. Xiao, H. Wang, Z. Ye, H. Zhu, M. Zhao, Y. Wang, J. Zhao, X. Yin and X. Zhang, Nat. Nanotechnol., 2016, 11, 598–602 CrossRef CAS PubMed.
- H. Zeng, J. Dai, W. Yao, D. Xiao and X. Cui, Nat. Nanotechnol., 2012, 7, 490–493 CrossRef CAS PubMed.
- G. Aivazian, Z. Gong, A. M. Jones, R.-L. Chu, J. Yan, D. G. Mandrus, C. Zhang, D. Cobden, W. Yao and X. Xu, Nat. Phys., 2015, 11, 148–152 Search PubMed.
- D. MacNeill, C. Heikes, K. F. Mak, Z. Anderson, A. Kormanyos, V. Zolyomi, J. Park and D. C. Ralph, Phys. Rev. Lett., 2015, 114, 037401 CrossRef CAS PubMed.
- Y. Li, J. Ludwig, T. Low, A. Chernikov, X. Cui, G. Arefe, Y. D. Kim, A. M. van der Zande, A. Rigosi, H. M. Hill, S. H. Kim, J. Hone, Z. Li, D. Smirnov and T. F. Heinz, Phys. Rev. Lett., 2014, 113, 266804 CrossRef PubMed.
- J. Qi, X. Li, Q. Niu and J. Feng, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 121403 CrossRef.
- Q. Zhang, S. A. Yang, W. Mi, Y. Cheng and U. Schwingenschlogl, Adv. Mater., 2016, 28, 959–966 CrossRef CAS PubMed.
- G. Yang, J. Li, H. Ma, Y. Yang, C. Li, X. Mao and F. Yin, Phys. Rev. B, 2018, 98, 235419 CrossRef CAS.
- W. Zhou, Z. Yang, A. Li, M. Long and F. Ouyang, Phys. Rev. B, 2020, 101, 045113 CrossRef CAS.
- C. Zhao, T. Norden, P. Zhang, P. Zhao, Y. Cheng, F. Sun, J. P. Parry, P. Taheri, J. Wang, Y. Yang, T. Scrace, K. Kang, S. Yang, G. X. Miao, R. Sabirianov, G. Kioseoglou, W. Huang, A. Petrou and H. Zeng, Nat. Nanotechnol., 2017, 12, 757–762 CrossRef CAS PubMed.
- X. Liang, L. Deng, F. Huang, T. Tang, C. Wang, Y. Zhu, J. Qin, Y. Zhang, B. Peng and L. Bi, Nanoscale, 2017, 9, 9502–9509 RSC.
- Y. Song, Q. Zhang, W. Mi and X. Wang, Phys. Chem. Chem. Phys., 2016, 18, 15039–15045 RSC.
- Y. Song, X. Wang and W. Mi, Adv. Electron. Mater., 2017, 3, 1700245 CrossRef.
- T. Norden, C. Zhao, P. Zhang, R. Sabirianov, A. Petrou and H. Zeng, Nat. Commun., 2019, 10, 4163 CrossRef PubMed.
- K. Zollner, P. E. Faria and J. Fabian, Phys. Rev. B, 2019, 100, 085128 CrossRef CAS.
- K. L. Seyler, D. Zhong, B. Huang, X. Linpeng, N. P. Wilson, T. Taniguchi, K. Watanabe, W. Yao, D. Xiao, M. A. McGuire, K. C. Fu and X. Xu, Nano Lett., 2018, 18, 3823–3828 CrossRef CAS PubMed.
- Y. C. Cheng, Q. Y. Zhang and U. Schwingenschlögl, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 155429 CrossRef.
- R. Peng, Y. Ma, S. Zhang, B. Huang and Y. Dai, J. Phys. Chem. Lett., 2018, 9, 3612–3617 CrossRef CAS PubMed.
- X. W. Zhao, Y. Li, R. D. Liang, G. C. Hu, X. B. Yuan and J. F. Ren, Appl. Surf. Sci., 2020, 504, 144367 CrossRef CAS.
- J. Zhou, J. Lin, H. Sims, C. Jiang, C. Cong, J. A. Brehm, Z. Zhang, L. Niu, Y. Chen, Y. Zhou, Y. Wang, F. Liu, C. Zhu, T. Yu, K. Suenaga, R. Mishra, S. T. Pantelides, Z. G. Zhu, W. Gao, Z. Liu and W. Zhou, Adv. Mater., 2020, 32, 1906536 CrossRef CAS PubMed.
- S. J. Yun, D. L. Duong, D. M. Ha, K. Singh, T. L. Phan, W. Choi, Y. M. Kim and Y. H. Lee, Adv. Sci., 2020, 7, 1903076 CrossRef CAS PubMed.
- Y. T. H. Pham, M. Liu, V. O. Jimenez, Z. Yu, V. Kalappattil, F. Zhang, K. Wang, T. Williams, M. Terrones and M. H. Phan, Adv. Mater., 2020, 32, 2003607 CrossRef CAS PubMed.
- F. Zhang, B. Zheng, A. Sebastian, D. H. Olson, M. Liu, K. Fujisawa, Y. T. H. Pham, V. O. Jimenez, V. Kalappattil, L. Miao, T. Zhang, R. Pendurthi, Y. Lei, A. L. Elias, Y. Wang, N. Alem, P. E. Hopkins, S. Das, V. H. Crespi, M. H. Phan and M. Terrones, Adv. Sci., 2020, 7, 2001174 CrossRef CAS PubMed.
- S. Fu, K. Kang, K. Shayan, A. Yoshimura, S. Dadras, X. Wang, L. Zhang, S. Chen, N. Liu, A. Jindal, X. Li, A. N. Pasupathy, A. N. Vamivakas, V. Meunier, S. Strauf and E. H. Yang, Nat. Commun., 2020, 11, 2034 CrossRef CAS PubMed.
- H. Yuan, M. S. Bahramy, K. Morimoto, S. Wu, K. Nomura, B.-J. Yang, H. Shimotani, R. Suzuki, M. Toh, C. Kloc, X. Xu, R. Arita, N. Nagaosa and Y. Iwasa, Nat. Phys., 2013, 9, 563–569 Search PubMed.
- D. Xiao, G. B. Liu, W. Feng, X. Xu and W. Yao, Phys. Rev. Lett., 2012, 108, 196802 CrossRef PubMed.
- B. Zhou, Nanoscale, 2020, 12, 5533–5542 RSC.
- J. Qi, H. Wang, X. Chen and X. Qian, Appl. Phys. Lett., 2018, 113, 043102 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- M. Fuchs and M. Scheffler, Comput. Phys. Commun., 1999, 119, 67–98 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- T. Zhang, Y. Ma, X. Xu, C. Lei, B. Huang and Y. Dai, J. Phys. Chem. C, 2020, 124, 20598–20604 CrossRef CAS.
- A. A. Mostofi, J. R. Yates, G. Pizzi, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2014, 185, 2309–2310 CrossRef CAS.
- W. Bai, Z. Hu, C. Xiao, J. Guo, Z. Li, Y. Zou, X. Liu, J. Zhao, W. Tong, W. Yan, Z. Qu, B. Ye and Y. Xie, J. Am. Chem. Soc., 2020, 142, 10849–10855 CrossRef CAS PubMed.
- M. A. Gave, D. Bilc, S. D. Mahanti, J. D. Breshears and M. G. Kanatzidis, Inorg. Chem., 2005, 44, 5293–5303 CrossRef CAS PubMed.
- L. Ju, J. Shang, X. Tang and L. Kou, J. Am. Chem. Soc., 2020, 142, 1492–1500 CrossRef CAS PubMed.
- B. Xu, H. Xiang, Y. Xia, K. Jiang, X. Wan, J. He, J. Yin and Z. Liu, Nanoscale, 2017, 9, 8427–8434 RSC.
- Q.-F. Yao, J. Cai, W.-Y. Tong, S.-J. Gong, J.-Q. Wang, X. Wan, C.-G. Duan and J. H. Chu, Phys. Rev. B, 2017, 95, 165401 CrossRef.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- C. Lei, Y. Ma, T. Zhang, X. Xu, B. Huang and Y. Dai, New J. Phys., 2020, 22, 033002 CrossRef CAS.
- X. Xu, Y. Ma, T. Zhang, C. Lei, B. Huang and Y. Dai, J. Phys. Chem. Lett., 2019, 10, 4535–4541 CrossRef CAS PubMed.
- N. Singh and U. Schwingenschlogl, Adv. Mater., 2017, 29, 1600970 CrossRef PubMed.
- R. Peng, Y. Ma, X. Xu, Z. He, B. Huang and Y. Dai, Phys. Rev. B, 2020, 102, 035412 CrossRef CAS.
- Y. Zang, Y. Ma, R. Peng, H. Wang, B. Huang and Y. Dai, Nano Res., 2020, 14, 834–839 CrossRef.
- P. Zhao, Y. Ma, C. Lei, H. Wang, B. Huang and Y. Dai, Appl. Phys. Lett., 2019, 115, 261605 CrossRef.
- T. Cai, S. A. Yang, X. Li, F. Zhang, J. Shi, W. Yao and Q. Niu, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 115140 CrossRef.
- X. Xu, Z. He, Y. Dai, B. Huang and Y. Ma, Phys. Rev. B, 2021, 104, 205430 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Total DOS and orbital-resolved PDOS for each atom of AgBiP2S6 monolayer calculated by the HSE06 method (Fig. S1); calculated binding energies of TM-doped AgBiP2S6 (Fig. S2); spin charge density of TM-doped AgBiP2S6 monolayers (Fig. S3), lattice vectors and fractional coordinates of each atom in TM-doped AgBiP2S6 (Tables S1–S6). See https://doi.org/10.1039/d2ra01697d |
| This journal is © The Royal Society of Chemistry 2022 |