Stretched three-dimensional white graphene with a tremendous lattice thermal conductivity increase rate

Abstract

Despite the increasing interest in the physical properties of the newly synthesized three-dimensional (3D) nano-architectured graphene, there are still few studies on the thermal transport properties of this family of materials. In the present work, heat transport of 3D h-BN and its mechanical response are systematically explored through first principles calculations. It is fascinating to find that the thermal conductivity of the 3D h-BN honeycomb structure could be significantly modulated by mechanical tension. Its lattice thermal conductivity perpendicular to the hole axis increases by 7.2 times at 6% critical strain, compared to only 0.67 times for that of the strained 3D graphene counterpart. The structure's thermal conductivity versus mechanical tension differs quantitatively and qualitatively from the monotonic downward trend of traditional bulk diamond or silicon under tension. This deviation from the classic behavior could be attributed to the modification of the phonon lifetimes, together with the competition between group velocities of low- and high-lying phonons under strain. Finally, the phonon vibrational modes contribution analysis indicates that the BN ribbon atoms contribute mainly at a lower frequency range. Our results provide important insights into potential employment of nano-architectured 3D white graphene for thermal management in relevant industrial applications.

---

1. Introduction

The newly synthesized three dimensional (3D) graphene with a hollow channel network has the characteristics of high mechanical strength, large thermal conductivity and light weight, possessing great potential capacities especially for energy engineering applications.^1–9 Since its experimental synthesis, several research groups have become more and more interested in the thermal transport characteristics of the stable dimerized carbon honeycomb (named as dCHC-n, where n represents the number of zigzag chains inside each ribbon section), carrying out in-depth numerical calculations in their research. First of all, Gu and Wei et al. have calculated the lattice thermal conductivity of dCHC-n structures with different porous channel sizes by using classical molecular dynamics (MD) simulations.^10,11 Later on, the first-principles calculations combined with the phonon Boltzmann transport equation (BTE) were employed to study the lattice thermal transport properties of the dCHC-2 structure, obtaining the lattice thermal conductivity value of ∼150/24 W m⁻¹ K⁻¹ in the direction parallel/perpendicular, respectively, to the hole axis,¹² which is lower than the ones from the previous classical MD simulations.¹⁰ In this framework, recently researchers have also studied the strain influence on the thermal transport performance of dCHC-2 structure based on the first-principles calculations. It was shown that the lattice thermal conductivity increases abnormally with the structure volume expansion.¹² After that, Zhang's simulation results have indicated that the thermal conductivity of the non-dimerized carbon honeycomb CHCs could be greatly reduced by the irregularity of their cell shapes.¹³ Moreover, in Du et al.’s current work, the effects of defects including Stone–Wales (SW) defect and vacancy (SV) one on the mechanical and thermal properties of CHCs were investigated by using MD simulations.¹⁴ It was reported that the Young's modulus of defective CHCs has nearly a constant value that was almost independent with the defect concentration. Besides, a reduction was seen in the thermal conductivity of CHCs containing SW and SV defects.

Three-dimensional (3D) h-BN honeycomb structure (BNHC) (space group: P6̄m2 with No. 187) as a counterpart of 3D graphene, was firstly proposed theoretically using DFT calculations by Wu et al. in 2011.¹⁵ It is a stable 3D hexagonal honeycomb structure composed of two-dimensional (2D) zigzag edge h-BN nanoribbons. Although, the 3D graphene honeycomb structure including its derivatives and the 3D h-BN one were both predicted first theoretically in 2011,¹⁵ the latter has not yet been successfully prepared in experiments so far. In contrast, the 2D h-BN sheet has been already successfully prepared by experiments more than ten years ago.¹⁶ The 2D counterpart has many unique electrical, magnetic and optical properties.¹⁷ Therefore, since the successful experimental preparation of 3D graphene in 2016, and due to the proven structural stability of BNHC,^15,18,19 we expect that the same or similar synthesis technology would be able to be used to prepare 3D h-BN honeycomb structure. Zhang has studied extensively the piezoelectric properties of BNHC,²⁰ while a very recent publication exhibited the mechanically and dynamically stable characteristics of several three-dimensional boron nitride nanoribbons.²¹

Concerning the 3D BN counterpart, it also performs well in many fields and a number of studies have been reported. For example, Dai et al. have reported in 2013 that the microporous BN structure entails large surface area more than 3000 m² g⁻¹ and showed a preference toward organic molecule adsorption (such as ethanol molecules) compared to water molecules.¹⁸ This preferential adsorption can be explored for water cleaning, similar to the porous BN sheet which has been used for water purification and filtration by recent experiments.²² It is expected that porous h-BN honeycomb materials will be widely used in gas packaging, surface chemistry, catalysis, toxic gas filtration and water purification fields, etc. Therefore, there are several theoretical studies on 3D h-BN honeycomb structures, which focus on various physical properties as mechanical, electronic structure, piezoelectricity and magnetism, etc.^3,23

Theoretical investigation on its mechanical properties showed that the Young's modulus in the direction of the hole axis is more than 7 times larger than that in the direction perpendicular to the hole axis, which is mainly caused by the structural anisotropy.¹⁵ About electronic properties, Wu et al. showed that the 3D h-BN honeycomb structure was metal through DFT calculations in 2011.¹⁵ Two years later, Dai et al. successfully predicted two kinds of metallic 3D BN porous structures with all B and N atoms in the structure linked by sp² hybridization through a structure prediction software combined with the first-principles calculations. One of the two kinds is just the zigzag bond linked 3D h-BN honeycomb structure, which we also propose here (space group: P6̄m2 with No. 187).¹⁸ Phonon spectrum and first-principles molecular dynamics at 1000 K (which is much higher than the room temperature 300 K) identified that the structure is stable. Electronic band structure analysis showed that the metallicity is mainly attributed to p-electron contribution along the hole axis. In 2017, Wang et al. studied again by using the same numerical calculation method the physical properties of zigzag bond linked all sp² hybridized 3D h-BN honeycomb structure. It is found that the structure is thermodynamically and dynamically stable, showing the same metallicity, which comes from the contribution of nonlocal B-2p electron, as is consistent with previous work.^15,18,24

In 2017, Zhang et al. have used hybrid finite element-molecular dynamics simulations to study the piezoelectric effect of the recently proposed boron nitride honeycomb (BNHC) structures.²⁰ The results showed that the structure had not only high tensile failure strain, but also excellent and tunable piezoelectric properties. Due to their unique polarization distribution BNHCs possess a tensile piezoelectricity in the armchair direction and a shear piezoelectricity in the zigzag direction. These excellent properties make the 3D h-BN honeycomb structure material to be a good candidate for the future design of novel nano-piezoelectric ultralight devices with high tensile strain resistant properties. In 2012, Wang et al. studied the structural stability, electronic structure and magnetism of a 3D three-winged BN nanoribbon (TBNNRs).¹⁹ TBNNR is a 3D structure composed of three BN nanoribbons combined by a junction, which is the basic component of the three-dimensional h-BN honeycomb structure.

At present, graphene based heat dissipation application in the industrial research and development is very attractive, especially in mobile phone electrical heat dissipation area the technology is becoming more and more mature, but the fundamental understanding of the principle advantages of graphene heat dissipation film over artificial graphite polyimide (PI) heat dissipation film has not been fully studied. Besides, heat dissipation issues are extremely critical in the application process of porous h-BN honeycomb materials. However, until now, there are scarce investigations on lattice thermal transport properties of the 3D h-BN honeycomb structures. On the other hand, in the practical application of materials, which are more or less in the strain state due to the external compression or tension, the geometrical structure and several physical properties such as heat transfer properties will be modified.²⁵ Therefore, the study of strain effect on the materials' properties not only has great basic research significance, but also provides a possible way for the experimental preparation of specific functional materials.²⁶

In this work, we have studied the thermal transport properties of porous h-BN honeycomb materials and their tensile response. We applied mechanical strain on the BNHC to mimic its structural deformations while used in molecular sieves, energy storage and catalysis, etc., and further investigated the strain influence on phonon transport behavior from first-principles lattice dynamics. The obtained results will be useful to render the porous h-BN honeycomb materials' application in several domains as molecular sieve and water purification equipment or efficient evacuation of hot spot in microelectronics.

2. Simulation model and computational method

2.1. Model and geometry optimization

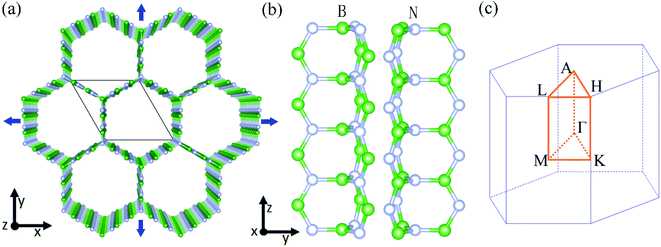
Boron nitride honeycomb (BNHC) structure with all B and N atoms hybridized by sp² is depicted in Fig. 1. This is the difference of BNHC from the 3D graphene, in the later a pair of carbon atoms in the junction is all sp³-hybridized.¹² According to previous studies,^10,13,27,28 the zigzag and armchair d-CHCs have the similar mechanical and thermal transport behaviors. BNHC as a counterpart of 3D graphene has the analogous structure and a similar physical behavior is expected under mechanical tension. Thus, to simplify our analysis without losing generality, in the present study only the BNHC structure with two zigzag BN chains inside the BN ribbon composition part is taken as a representative, since the major objective of this work is to study the tension effects on thermal properties of BNHC.

Fig. 1 (a) Perspective view of boron nitride honeycomb (BNHC) structure with its B and N linkages shown in detail in (b). The B and N atoms are represented by green and gray spheres, respectively. The blue arrows mean that the strain are loaded isotropically in all directions. (c) The first Brillouin zone with high symmetry points and routines noted.

The first-principles calculations (DFT) were used in the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation,^29,30 as utilized in the Vienna ab initio Simulation Package (VASP).³¹ The projected augmented wave (PAW) method^30,32 was employed. For the plane-wave basis set, a kinetic energy cutoff up to 600 eV was considered. We treated the 2s²3p¹ orbitals of B atom and 2s²3p³ orbitals of N atom as valence electrons, respectively. To ensure energy convergence in calculating total energy during structure relaxation, enough Monkhorst–Pack³³ k-points (8 × 8 × 32) were set for the summation in the 1st Brillouin zone (BZ). The simulation box with all atoms inside was thoroughly relaxed. Structure relaxation was done by employing the conjugate-gradient (CG) algorithm³⁴ to guarantee the maximum residual force at each atom less than 10⁻⁵ eV Å⁻¹. For the electron self-consistent loop, the tolerance in total energy was set to be 10⁻⁸ eV. With respect to the strain effect, only tensile strain (isotropic) was considered here to simulate the expansion effect, for example when the structure is used as molecular sieve or in the field of energy storage and catalysis. For isotropic strain, specific strain is loaded simultaneously in xyz-direction as shown in Fig. 1. Besides, we noticed that negative frequencies existed in phonon dispersion of BNHC under isotropic compression, so here in this work only tension effect was concerned.

2.2. Mechanical and thermodynamic stability check

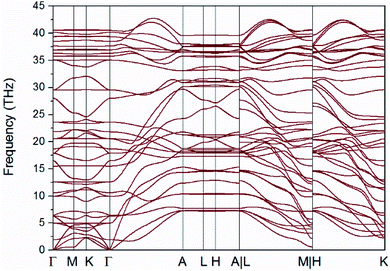
In order to test the mechanical stability of BNHC under tension, we initially verified the phonon dispersion curve by solving the eigenvalues of the dynamic matrix constructed from the harmonic force constants. It was found that there existed no imaginary frequency for the phonon dispersion curve of BNHC under strain until ε = 15%, proving that BNHC structures under strain less than 15% were all mechanically stable. We also tested phonon dispersions for larger strains, finding that imaginary frequencies appeared and the structures were not mechanically stable any more under larger deformations (ε = 16%). The phonon dispersion of the free standing BNHC (ε = 0%) is depicted in Fig. 2, which is in good agreement with previous DFT LDA result.¹⁸ Due to the structure similarity with experimental synthesized 3D graphene, an analogous phonon frequency gap was also observed at around 32 THz in the phonon dispersion curves of BNHC, like that bigger one found at around 37 THz for the 3D graphene from previous DFT results.¹² Besides, BN bonds' weak ionic property makes them not as strong as those covalent ones of C–C, thus generating a smaller phonon frequency range (0–43 THz) for phonon dispersion in BNHC structure, in comparison with that larger range of 0–48 THz for phonon dispersion in 3D graphene.¹²

Fig. 2 Phonon dispersion of unstrained BNHC.

The thermodynamic stability of BNHC structure has also been tested by ab initio molecular dynamics (AIMD) simulation of NVT ensemble at T = 1000 K for 5 ps with timestep of 1 fs. Because a small unit cell may easily lead to pseudo-stability, here we used a relatively large (2 × 2 × 4) supercell (224 atoms included in total). Our AIMD simulation results showed that the structure could be kept stable at T = 1000 K. Energy and temperature evolution with the simulation time are plotted in Fig. 3, indicating clearly that the system has reached its thermal equilibrium state and the system exhibits stability during the whole simulation process. The corresponding structure at the end of AIMD simulation is shown as an inset in Fig. 3. We can see from the inset figure that the configuration experienced slight distortions, but both the BN nanoribbon sections and all linkage parts are still well maintained.

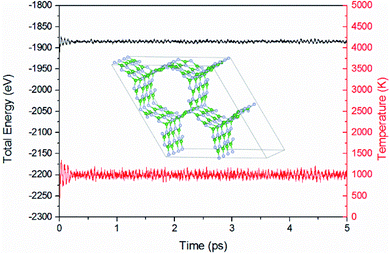Fig. 3 Energy (left axis in black) and temperature (right axis in wine) vs. time during AIMD simulation of the BNHC structure. (Inset) The corresponding structure at the end of simulation (5 ps).

2.3. Thermal conductivity calculation

To further study the heat transport in BNHC structure, it is of great importance to understand the quantum interactions of phonons.^35,36 By only considering phonon–phonon scattering processes, we calculated the intrinsic lattice thermal conductivity by iteratively solving the semi-classical phonon Boltzmann transport equation using the ShengBTE software package,³⁷ which does not need any initial parameters and only based on the atomic structure information. Calculation of the thermal conductivity via iterative solution of the BTE requires anharmonic third-order IFCs along with the harmonic second order IFCs. We used a 2 × 2 × 4 supercell containing 224 atoms for calculating the harmonic and anharmonic IFCs with a Monkhorst–Pack³³ k-point meshes of 1 × 1 × 3 to sample the 1st BZ of BNHC. The second order harmonic IFCs were obtained within the linear response framework by employing density functional perturbation theory (DFPT),³⁸ which calculated the dynamical matrix through the linear response of the electron density. The phonon dispersions were obtained by using the Phonopy code³⁹ with the harmonic IFCs as input. For anharmonic IFCs calculations (3rd order IFC), interactions were taken into account up to the 11th nearest neighbors to achieve convergence. Also, the convergence of k-point grid in BZ for solving BTE has also been tested. Unless specified otherwise, all thermal conductivities were calculated at room temperature (T = 300 K).

As well known, anharmonic IFCs calculations were rather time and computational resource consuming and lattice thermal conductivity always goes down under strain large enough due to bond interaction weakening caused by mass density decrease under tension. Besides, what we are interested in is the abnormal enhancement of thermal transport in BNHC under tension, we only computed in our work the structures' lattice thermal conductivity under strain until ε = 8% which is large enough for us because the maximum κ value has already been obtained at ε = 6%.

3. Results and discussions

3.1. Anisotropic thermal conductivity under strain

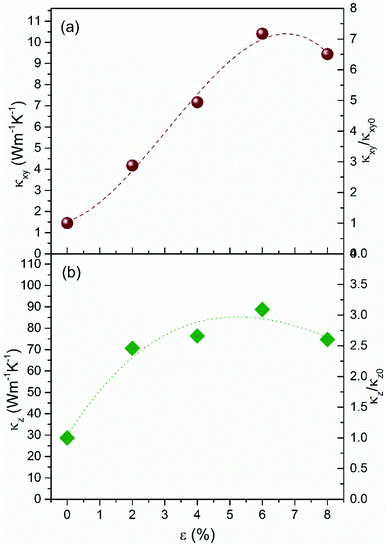
The honeycomb BNHC structure will expand or contract while using as sieving devices. Therefore, the structure deformation is supposed to have a great influence on heat transport which could be simulated by applying mechanical stress. Firstly, an obvious anisotropy exists in thermal transport capability of unstrained BNHC. For example, at zero stress, the value of the lattice thermal conductivity (κ) perpendicular to the honeycomb axis (xy) is 1.5 W m⁻¹ K⁻¹, which is severely less than that of 28.7 W m⁻¹ K⁻¹ along the honeycomb axis (z). From the structure aspect, BNHC consists of three BN nanoribbons connected together at the junction shown in Fig. 1. From an intuitive point of view, thermal energy (phonons) can transport more easily along and inside the ribbon parts until they are heavily scattered when they reach the junction parts. The computed percentage of phonon modes with non-zero group velocities in different directions are 85.7% (xy) and 92.9% (z), respectively, and these values do not change with the applied strains. This anisotropy thermal conductivity factor of 20 is very important and compares to the thermal anisotropy observed in GaAs parallel and perpendicular to the dislocations in the case of high density of edge dislocations.⁴⁰ Anisotropic thermal transport properties should be related to the reported 7 times larger Young's modulus in the hole axis direction than that in the perpendicular direction due to structure anisotropy i.e. the honeycomb channel structure characteristics.¹⁵

Besides, it is observed in Fig. 4 that the κ of BNHC demonstrates surprising modifications when strain loaded. As isotropic strain increases from 0 to 6%, the κ of BNHC is greatly enhanced and reaches a maximum at the strain of 6%. After that, the κ of BNHC decreases as the strain is further enlarged. For instance, the room-temperature κ perpendicular to the honeycomb axis (xy) significantly increases from 1.5 W m⁻¹ K⁻¹ at zero strain to 10.4 W m⁻¹ K⁻¹ at 6% strain i.e. 7.2 times larger in contrast to the value being only 0.67 times larger for the 3D graphene counterpart dCHC-2 under tension, while κ along the honeycomb axis (z) increases from 28.7 W m⁻¹ K⁻¹ at zero strain to 88.8 W m⁻¹ K⁻¹ i.e. 3.1 times larger relative to 0.29 times larger for its 3D graphene counterpart.¹² Additionally, such dramatic tremendous lattice thermal conductivity enhancement rate under tension was also previously found once for the proposed auxetic carbon crystals⁴¹ by DFT calculations in 2007.⁴² From atomic interaction perspective, the B–N bonds have some kind of weak ionic tendency compared to the strong covalent C–C ones in graphene, leading to its much more sensitive tension dependency in thermal transport properties. Such anomalous change of κ in BNHC structure is fundamentally different from that for most semiconductors such as bulk diamond and silicon which exhibit nearly linear relation (thermal conductivity decreases with isotropic tensile strain), as indicated in previous work.^12,43–45

Fig. 4 The strain dependent lattice thermal conductivity of BNHC structure (a) perpendicular to (κ_xy) and (b) along (κ_z) the honeycomb axis (left axis) and the corresponding normalized values (right axis). The spline line is to guide the eye.

3.2. Cumulative thermal conductivity (CTC) under strain

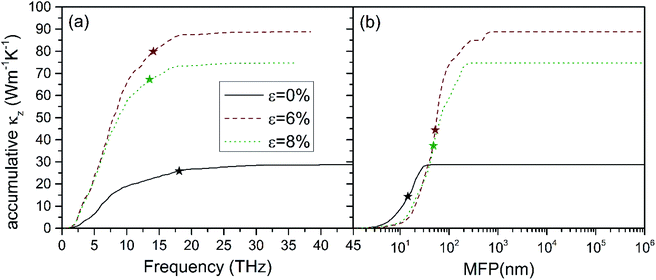
In order to essentially explain the anomalous response of phonon transport in the BNHC under strain, taking the axial direction as an example, we first calculated the accumulated κ_z versus phonon frequencies to identify the frequency range for which phonons mainly contributed to the total κ_z. From Fig. 5(a), it is first observed that the accumulative κ_z curves go up monotonically to 90% of the total κ_z values until phonon frequencies of 18.1, 14.1 and 13.5 THz for 0, 6% and 8% strains, respectively, presenting that low-lying acoustic phonons play still a leading role for contributing to the overall κ_z. Under strain, lower and lower frequency phonons contribute gradually more to the total κ_z, which could ascribe to the larger phonon lifetimes under strain as can be seen from Fig. 6(b).

Fig. 5 The accumulative lattice thermal conductivity in z direction (κ_z) of BNHC versus (a) phonon frequency and (b) phonon mean-free-path (MFP) for some typical strains: 0% in black solid, 6% in wine dashed and 8% in olive dotted lines, respectively. The corresponding solid stars denote the frequencies (MFP), below which the phonons contribute 90% (50%) of the overall thermal conductivities.

Fig. 6 The phonon mode dependent (a) group velocity, (b) phonon relaxation lifetime and (c) Grüneisen parameter γ of BNHC structure under some typical strains: 0% in black up triangles, 6% in wine diamonds and 8% in olive pentagons, respectively. In the inset of (c), we zoom in for phonons frequencies in the range of 0–5 THz.

The cumulative thermal conductivity in z direction κ_z with respect to the phonon mean free path (MFP) is plotted in Fig. 5(b). It is found that the phonons with mean free paths smaller than MFP_50% = 14.4 nm contributes nearly half (50%) of the total thermal conductivity of BNHC under strain of ε = 0%. In other words, in order to improve heat dissipation performance to further increase heat transport, such a characteristic length could provide a valuable reference for the size design of nanostructures. When the strain up to 6% and 8% were loaded to the structure, MFP_50% values increased to as large as 52.4 nm and 48.0 nm, respectively. From the structure aspect, as strain is loaded, the distance between adjacent atoms is enlarged, which means that phonons can transport farther than in the free-standing case.

3.3. Mode analysis of strain modulated thermal conductivity

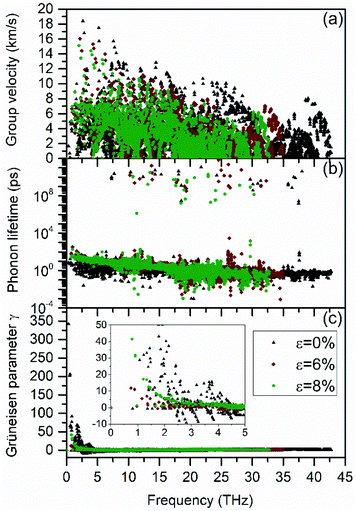
A spectral analysis of the group velocity and phonon lifetimes with and without strain could give more depth in our discussion. Fig. 6(a) shows that the mode group velocity slightly increases with strain from 0 to 6%, then to 8%, for phonons in the frequency range of 0–3 THz studied here. This can be explained from the phonon dispersion curves under strain. When strain is applied, some low-lying flattened acoustic phonon branches become steep and group velocities increase. However, group velocities of those phonon modes in higher frequency range (large than 3 THz) have almost an opposite trend to the low-lying phonons while strains are loaded. Moreover, for the phonon lifetimes, there also exhibits anomalous change with strain increasing from 0 to 6%. In Fig. 6(b), it is observed that the τ is slightly increased from 0 to 6% but then it is reduced in the range from 6% to 8%. On this basis, the abnormal change of phonon lifetime together with the competition between group velocities of low- and high-lying phonons might be the key factors to interpret the particular thermal transport behavior of BNHC under strain. In addition, the Umklapp process of phonon–phonon interaction will lead to thermal resistance. In the Debye–Callaway model of lattice thermal conductivity, the Umklapp phonon–phonon scattering rate is proportional to Grüneisen parameter square.⁴⁶ From the inset of Fig. 6(c), we can see an obvious decline in the amplitude of the Grüneisen parameter as the strain goes up from 0 to 6% and a follow increase for strain from 6% to 8%, indicating that the Umklapp phonon–phonon scattering is first weakened and then strengthened again, especially for phonons in the frequency range of 0–5 THz.

3.4. Root mean squared displacement and phonon anharmonicity

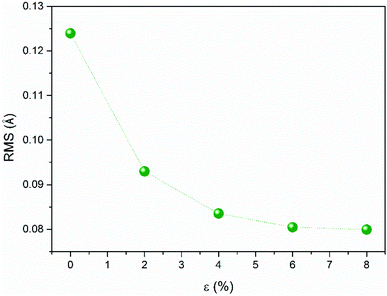
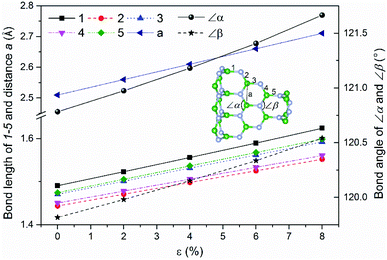
At finite temperatures, atoms in a structure vibrate frequently in some extend. When the vibration distances are small enough, they could be treated as harmonic vibrations. But if the vibrations' amplitude is too large, they will enter anharmonic vibration range. To further explore the physical mechanisms behind the phonon lifetime dependence of the BNHC phonon transport under strain, we analyzed the root mean-square (RMS) displacement that can be used to roughly quantify the phonon anharmonic effect.⁴³ RMS values of the strained BNHC computed are shown in Fig. 7. The trend of RMS as a function of the strain is exactly opposite to that of the thermal conductivity (Fig. 4), suggesting that the anharmonicity trend is indeed consistent with that of the RMS.

Fig. 7 The root mean squared displacement of BNHC as a function of strain.

In order to elucidate the phonon anharmonicity in the strained BNHC in detail, the variation of their typical geometry parameters with strain is plotted in Fig. 8. We found that all bonds, distances and angles increase monotonically with tensile strains. This trend is completely different from that of its graphene counterpart dCHC-2 for which non-monotonic strain dependence of thermal conductivity observed should be related to the shrinkage or elongation of the bond (distance) a at the dimerized C–C linkage line.¹² This means that for BNHC, which does not exhibit dimerization phenomena at linkage junctions there must be some other physical mechanisms behind to explain the abnormal non-monotonic strain dependence of thermal conductivity.¹² Phonon transport capability is dependent on each atom in the structure. All atoms and bonds coupling interaction must mutually contribute to the abnormal response of thermal conductivity of BNHC under strain.

Fig. 8 The typical geometric structure parameters of BNHC bond length and distance between linkage atoms (left axis) and bond angle (right axis) under different strains. The bonds, distance and angles in the structure are labeled in the inset.

3.5. Phonon fat bands and atomic vibration mode contribution analysis

To further explore the physical mechanism of the BNHC thermal conductivity increasing first as strain goes from 0 to 6% and then declining under the larger strains, the phononic k.p theorem usually used to sort the phonon branches through the continuity of their eigenvectors.^47,48 In previous work, this technique was widely used to analyze the atom–phonon correlation.^49–51 The line widths of the fat bands were scaled by the amplitudes of specified vibrations, as shown in Fig. 9. Here, we only consider some representative contribution larger than some criteria and we neglect the smaller and nonsignificant ones. Finally, only the bubbles meeting the standard of partial contribution larger than 5% are displayed. From the structure aspect, BNHC is composed of BN nanoribbons connected at junctions with all ribbon atoms classified into 3 types (B or N junction atoms and BN ribbon atoms) as shown in the inset of Fig. 9. For different types, the average partial contribution of each atom in each phonon mode is superimposed on the total phonon dispersion.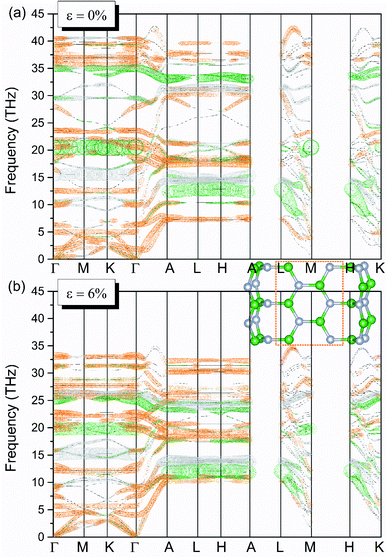

Fig. 9 Phonon fat bands (black dashed line) of BNHC at strains of (a) ε = 0% and (b) ε = 6%. To show clarity and brevity, here, only modes with value of average partial contribution larger than 5% are overlaid by bubbles in different colors corresponding to different partial atoms (B junction atoms in olive, N junction atoms in light gray and BN ribbon part in an orange short dotted rectangle) as indicated in the middle inset. The q-path is taken to be the same as that for phonon dispersion in Fig. 2 but with break points separated by blank regions.

Firstly, we can see from Fig. 9(a) and (b) that, phonon group velocities of transverse acoustic (TA) modes are higher at the strained case than at the free standing one in the directions Γ → M, Γ → K and Γ → A as mode analyzed in Fig. 6(a). Besides, it is obviously that these low-lying acoustic branches under strain in Fig. 9(b) are less intersecting with optical branches compared with the unstrained case in Fig. 9(a), indicating that low frequency phonons of the strained structure are less scattered with higher phonon lifetimes which is in good agreement with mode phonon lifetimes analysis in Fig. 6(b).

Moreover, at zero strain, B or N junction atoms contribute mainly to the middle internal regions of the whole phonon frequency range, as shown in olive and light gray. But the ribbon atoms' contribution is more dispersive and they mainly control the other parts including the lower and higher frequency regions. Combining with the analysis from accumulative thermal conductivity versus phonon frequency shown in Fig. 5(a), it is found that ribbon atoms are the dominate contributors to the overall thermal conductivity, as can be seen from Fig. 9 that BN ribbon part in orange dominates in lower frequency region. Compared to phonon fat-bands of BNHC at zero strain (Fig. 9(a)), that at 6% strain looks more condensed due to red shift of the phonons in the frequency range larger than 20 THz as depicted in Fig. 9(b). In contrast, phonons inside 10–20 THz are almost kept unmoved. Since the main contribution to the total thermal conductivity comes from the low frequency region, this red shift causes more phonons to condense in the low frequency region, resulting in an abnormal increase in the thermal conductivity of BNHC under tension.

4. Summary and conclusions

In summary, we have systematically investigated the thermal transport properties of three dimensional white graphene and its mechanical response by solving the Peierls–Boltzmann transport equation with interatomic force constants procured from the first-principles calculations. In addition, a comparative study was executed on phonon dispersions and phonon vibrational modes analysis. The thermal conductivity of BNHC could be adjusted effectively and easily by tensile strain: for example, the lattice thermal conductivity of BNHC perpendicular to the hole axis (κ_xy) at 6% tensile strain is increased by 7.2 times than that at zero strain, in contrast to only 0.67 times enhancement for that of 3D graphene counterpart dCHC-2 under tension. The thermal conductivity strain dependence behavior in BNHC is also very different from the thermal conductivity of the strained traditional bulk diamond and silicon, in latter ones a monotonically reduction trend with strain was observed. By comparing the key factors affecting thermal conductivity at phonon mode level, we believe that the profound increase of thermal conductivity in BNHC under tensile strain is mainly due to the enhancement of phonon lifetimes and group velocities increase of low-lying phonons in phonon dispersion curves, conquered the decrease of group velocities of high-lying phonons under strain. Through the reduction of root mean square displacement, the dominant physics behind this huge growth is further revealed. Finally, the contribution of phonon vibration mode was analyzed. It showed that BN ribbon atoms contribute the most to the thermal conductivity in the lower frequency range. Our results provide important insights into the response of thermal transport in 3D white graphene upon external tensile strain, mimicking the effect of structural deformation upon sieving process, and offer useful guidelines for the thermal management in relevant industrial applications.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors acknowledge financial support from the National Natural Science Foundation of China with No. 12104111, the Fundamental Research Funds for the Central Universities (3072020CFJ0302, HEUCFG201819 and 3072020CFT303), the research fund of University of Macau, Macau SAR (File no. MYRG2018-00079-IAPME, MYRG2019-00115-IAPME), and the Science and Technology Development Fund, Macau SAR (File no. 081/2017/A2, 0059/2018/A2, 009/2017/AMJ). We are grateful for computational resources support from the High-Performance Computing Center of Collaborative Innovation Center of Advanced Microstructures and the High Performance Computing Center of Nanjing University. Y. Han gratefully acknowledges fruitful discussions with Dr Prof. Jinming Dong (Nanjing University).

References

1. H. Wang, Q. Cao, Q. Peng and S. Liu, Atomistic study of mechanical behaviors of carbon honeycombs, Nanomaterials, 2019, 9(1), 109.
2. L. Xie, H. An, C. He, Q. Qin and Q. Peng, Mechanical properties of vacancy tuned carbon honeycomb, Nanomaterials, 2019, 9(2), 156.
3. L. Xie, T. Wang, C. He, Z. Sun and Q. Peng, Molecular dynamics simulation on mechanical and piezoelectric properties of boron nitride honeycomb structures, Nanomaterials, 2019, 9, 1044.
4. H. Feng, F. Zhang, N. Chen, L. Tan, C. Liu and D. Hu, et al., Enhanced capacitive performance of polyaniline on hydroquinone-functionalized three-dimensional porous graphene substrate for supercapacitors, J. Mater. Sci.: Mater. Electron., 2021, 32(5), 5655–5667.
5. M. Hao, W. Zeng, Y. Q. Li and Z. C. Wang, Three-dimensional graphene and its composite for gas sensors, Rare Met., 2021,(15), 1494–1514.
6. Y. C. Wang, Y. B. Zhu and H. A. Wu, Porous characteristics of three-dimensional disordered graphene networks, Crystals, 2021, 11(2), 127.
7. D. Weng, L. Song, W. Li, J. Yan and Y. Liu, Review on synthesis of three-dimensional graphene skeletons and their absorption performance for oily wastewater, Environ. Sci. Pollut. Res., 2021, 28(1), 1–19.
8. A. Zaka, K. Hayat and V. Mittal, Recent trends in the use of three-dimensional graphene structures for supercapacitors, ACS Appl. Electron. Mater., 2021, 3(2), 574–596.
9. D. Zhi, T. Li, J. Li, H. Ren and F. Meng, A review of three-dimensional graphene-based aerogels: synthesis, structure and application for microwave absorption, Composites, Part B, 2021, 211, 108642.
10. X. Gu, Z. Pang, Y. Wei and R. Yang, On the influence of junction structures on the mechanical and thermal properties of carbon honeycombs, Carbon, 2017, 119, 278–286.
11. Z. Pang, X. Gu, Y. Wei, R. Yang and M. S. Dresselhaus, Bottom-up design of three-dimensional carbon-honeycomb with superb specific strength and high thermal conductivity, Nano Lett., 2016, 17(1), 179–185.
12. Y. Han, J.-Y. Yang and M. Hu, Unusual strain response of thermal transport in dimerized three-dimensional graphene, Nanoscale, 2018, 10(11), 5229–5238.
13. J. Zhang, Effects of cell irregularity on the thermal conductivity of carbon honeycombs, Carbon, 2018, 131, 127–136.
14. Y. Du, J. Zhou, P. Ying and J. Zhang, Effects of cell defects on the mechanical and thermal properties of carbon honeycombs, Comput. Mater. Sci., 2021, 187, 110125.
15. M. Wu, X. Wu, Y. Pei, Y. Wang and X. C. Zeng, Three-dimensional network model of carbon containing only sp²-carbon bonds and boron nitride analogues, Chem. Commun., 2011, 47(15), 4406–4408.
16. D. Pacile, J. C. Meyer, C. O. Girit and A. Zettl, The two-dimensional phase of boron nitride: few-atomic-layer sheets and suspended membranes, Appl. Phys. Lett., 2008, 92(13), 133107.
17. S. Yuan, J. Catherine, L. Sébastien, G. Vincent, S. Philippe and B. Stéphane, et al., How to increase the h-BN crystallinity of microfilms and self-standing nanosheets: a review of the different strategies using the PDCs route, Crystals, 2016, 6(5), 55.
18. J. Dai, X. Wu, J. Yang and X. C. Zeng, Unusual metallic microporous boron nitride networks, J. Phys. Chem. Lett., 2013, 4(20), 3484–3488.
19. Y. Wang, Y. Ding and J. Ni, Stereo boron nitride nanoribbons with junction-dependent electronic structures from first-principles, J. Phys. Chem. C, 2012, 116(10), 5995–6003.
20. J. Zhang, Boron nitride honeycombs with superb and tunable piezopotential properties, Nano Energy, 2017, 41, 460–468.
21. M. Xiong, H. Hasi, Q. Gao, D. Jin, Q. Wu and X. Li, et al., Prediction of three-dimensional stretchable boron nitride nanoribbons, Diamond Relat. Mater., 2022, 121, 108740.
22. W. Lei, D. Portehault, D. Liu, S. Qin and Y. Chen, Porous boron nitride nanosheets for effective water cleaning, Nat. Commun., 2013, 4, 1777.
23. M. Xu, T. Liang, M. Shi and H. Chen, Graphene-like two-dimensional materials, Chem. Rev., 2013, 113(5), 3766–3798.
24. W. Hao, Z. Wei and H. Ping, Novel 3D metallic boron nitride containing only sp² bonds, J. Phys. D: Appl. Phys., 2017, 50(38), 385302.
25. C. Shao, X. Yu, N. Yang, Y. Yue and H. Bao, A review of thermal transport in low-dimensional materials under external perturbation: effect of strain, substrate, and clustering, Nanoscale Microscale Thermophys. Eng., 2017, 21(4), 201–236.
26. T. Wang, Z. Wang, R. V. Salvatierra, E. McHugh and J. M. Tour, Top-down synthesis of graphene nanoribbons using different sources of carbon nanotubes, Carbon, 2020, 158, 615–623.
27. Z. Zhang, A. Kutana, Y. Yang, N. V. Krainyukova, E. S. Penev and B. I. Yakobson, Nanomechanics of carbon honeycomb cellular structures, Carbon, 2017, 113, 26–32.
28. F. Meng, C. Chen, D. Hu and J. Song, Deformation behaviors of three-dimensional graphene honeycombs under out-of-plane compression: Atomistic simulations and predictive modeling, J. Mech. Phys. Solids, 2017, 109(dec.), 241–251.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868.
30. J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B, 1986, 33(12), 8822.
31. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B, 1996, 54(16), 11169–11186.
32. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B, 1994, 50(24), 17953–17979.
33. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B, 1976, 13(12), 5188–5192.
34. X. Gonze, First-principles responses of solids to atomic displacements and homogeneous electric fields: implementation of a conjugate-gradient algorithm, Phys. Rev. B, 1997, 55(16), 10337–10354.
35. H. Yang, Q. Guangzhao, J. Christoph and H. Ming, Strain-modulated electronic and thermal transport properties of two-dimensional O-silica, Nanotechnology, 2016, 27(26), 265706.
36. M. Hu and D. Poulikakos, Si/Ge superlattice nanowires with ultralow thermal conductivity, Nano Lett., 2012, 12(11), 5487–5494.
37. W. Li, J. Carrete, A. Katcho, N. Mingo and N. Sheng, BTE: a solver of the Boltzmann transport equation for phonons, Comput. Phys. Commun., 2014, 185(6), 1747–1758.
38. P. Giannozzi and S. Baroni, Density-functional perturbation theory, in Handbook of Materials Modeling: Methods, ed., S. Yip, Springer Netherlands, Dordrecht, 2005, pp. 195–214.
39. A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5.
40. K. Termentzidis, Thermal conductivity anisotropy in nanostructures and nanostructured materials, J. Phys. D: Appl. Phys., 2018, 51(9), 094003.
41. R. H. Baughman and D. S. Galvao, Crystalline networks with unusual predicted mechanical and thermal properties, Nature, 1993, 365(6448), 735.
42. Y. Han, Y. Zhou, G. Qin, J. Dong, D. S. Galvao and M. Hu, Unprecedented mechanical response of the lattice thermal conductivity of auxetic carbon crystals, Carbon, 2017, 122, 374–380.
43. K. D. Parrish, A. Jain, J. M. Larkin, W. A. Saidi and A. J. McGaughey, Origins of thermal conductivity changes in strained crystals, Phys. Rev. B, 2014, 90(23), 235201.
44. V. Kuryliuk, O. Nepochatyi, P. Chantrenne, D. Lacroix and M. Isaiev, Thermal conductivity of strained silicon: molecular dynamics insight and kinetic theory approach, J. Appl. Phys., 2019, 126(5), 055109.
45. D. Broido, L. Lindsay and A. Ward, Thermal conductivity of diamond under extreme pressure: a first-principles study, Phys. Rev. B, 2012, 86(11), 115203.
46. J. Callaway, Model for lattice thermal conductivity at low temperatures, Phys. Rev., 1959, 113(4), 1046.
47. L. Feng Huang and Z. Zeng, Lattice dynamics and disorder-induced contraction in functionalized graphene, J. Appl. Phys., 2013, 113(8), 083524.
48. L. F. Huang, P. L. Gong and Z. Zeng, Correlation between structure, phonon spectra, thermal expansion, and thermomechanics of single-layer MoS 2, Phys. Rev. B, 2014, 90(4), 045409.
49. L.-F. Huang, P.-L. Gong and Z. Zeng, Phonon properties, thermal expansion, and thermomechanics of silicene and germanene, Phys. Rev. B, 2015, 91(20), 205433.
50. L.-F. Huang and Z. Zeng, Roles of mass, structure, and bond strength in the phonon properties and lattice anharmonicity of single-layer Mo and W dichalcogenides, J. Phys. Chem. C, 2015, 119(32), 18779–18789.
51. M. Verdier, Y. Han, D. Lacroix, P.-O. Chapuis and K. Termentzidis, Radial dependence of thermal transport in silicon nanowires, J. Phys.: Mater., 2018, 2(1), 015002.

---