Open Access Article
Open Access ArticleElucidating the mechanism of nucleation inhibition of pathology crystallization of gout based on the evidence from amorphous form and in solution†
Dan Zhou‡
,
Shiqi Jiao,
Pengfei Zhang‡,
Yige Jin,
Yonglan Pan,
Chunyan Ou,
Xingde Zhang,
Tingming Fu and
Yonghai Liu *
*
School of Pharmacy, Nanjing University of Chinese Medicine, Nanjing 210046, China. E-mail: liuyh@njucm.edu.cn
First published on 12th August 2022
Abstract
The first gout attack in a hyperuricaemic patient may be regarded as a nucleation event which is caused by monosodium urate monohydrate (MSUM) deposition in the synovial fluid. The effect of Tailor-Made Inhibition (TMI) may be effective as drugs for the prevention of aberrant nucleation and crystallization. Therefore, the understanding of the underlying mechanisms in inhibiting the MSUM nucleation by TMI has proven to be of great significance. Yet most of the published studies about nucleation inhibition have tended to focus on simpler molecular models with a hydrogen-bonded acceptor and donor, which may be not suitable for the uric acid molecule with multiple hydrogen-bonded acceptors and donors under physiological conditions. Herein, the mechanisms of nucleation inhibition of MSUM were explored in a simulated biological environment (0.15 M Na+ and pH 7.40) in the presence and absence of TMI. And the evidence of nucleation inhibition by TMI in solution and the amorphous form of MSUM was investigated by HNMR, IR, Raman, PXRD, Dynamic light scattering (DLS), induction time measurements, and density functional theory (DFT) calculations. Results showed that the inhibition comes from a combination of kinetic and thermodynamic effects, with an impact of kinetics as the TMI inhibition effects far exceeded what could be accounted for by changes in usual factors of classical nucleation theory. The data demonstrated that the complex between urate and TMI disturbed the formation of two-dimensional sheets of sodion and purine rings parallel to the (011) plane and further impeded the formation of a three-dimensional structure with aromatic stacking interactions in solution. To our knowledge, the nucleation inhibition of TMI is achieved by suppressing interplanar stacking, which is a mechanism proposed for the first time.
Introduction
Gout, a crystal-induced arthritis connected with hyperuricemia, is a kind of severe joint disease and prevailingly occurs in the big toe, ankles, and knees; it is very commonly caused by the deposition of MSUM in the synovial fluid.1,2 The effect of TMI on the nucleation process has been an area of growing focus,3 since TMI may be effective as drugs for the prevention of aberrant nucleation and crystallization.4,5 Therefore, MSUM mimics, as the candidate drug molecules, may provide a rational strategy for the prophylaxis of acute gout attack and treatment of tophus in the context of hyperuricemic patients. As a result, the fundamental and theoretical understanding of the underlying mechanisms in inhibiting the MSUM nucleation by TMI has proven to be of great significance. Yet most of the published studies about nucleation inhibition,6–8 to the knowledge of the authors, have tended to focus on simpler molecular models with a hydrogen-bonded acceptor and donor, which may be not suitable for uric acid molecules with multiple hydrogen-bonded acceptors and donors under physiological conditions.Recently, we report that the growth of MSUM crystals was strongly modulated by additives or different ions.9 Particularly, xanthine, a TMI of uric acid, could strongly inhibit the growth of MSUM, indicating that MSUM solubility and precipitation may be modulated by local and systemic biological environments.10
In this study, we focused on uncovering inhibition mechanisms of xanthine on MSUM nucleation based on the evidence from amorphous form and in solution, which is determined by induction time measurements and other combined experimental identification (DLS, HNMR, IR, Raman, PXRD, DFT calculations).
Experimental
Measurement of induction time and design of experiments
The induction times of MSUM nucleation from solutions in the absence/presence of xanthine were measured at 15 °C. Each experiment for induction time was carried out in a 100 mL glass jacketed beaker at 15 °C. In each run, a 50 mL MSUM solution was prepared in a properly capped glass bottle at an elevated temperature of 95–97 °C, in a given concentration and additive. This solution was kept agitated at 95–97 °C for 20 min to make sure all solids were totally dissolved. And it was quickly transferred to a 100 mL jacketed beaker controlled at 15 °C, agitating with a magnetic stirrer at 60 rpm. And the solution was recorded by a high definition web camera. The onset of nucleation was surveyed as a very rapid change from a clear to a cloudy solution. The induction time was defined as the period from the moment at which the solution was transferred to the 100 mL beaker to the moment at which the cloud point was identified. The distribution of induction times in this study can be analyzed using eqn (1) to determine the time-independent nucleation rate of the experimental system.| ln(1 − P(t)) = −JV(t − tg) | (1) |
Solubility measurement
The solubility of MSUM in water was measured after 72 hours of crystal cultivation at 15 °C and at pH = 7.4. Supersaturated solutions of different concentrations of MSUM were made by adding a known amount of solute and 100 mL water in a beaker. The beakers were placed in the drying oven at a temperature of 15 °C for 72 hours. And the MSUM crystal appeared after 72 hours of cultivation. The drying oven and suction filter device were utilized to obtain dry crystals. The solubility was obtained by subtracting the mass of the acquired crystal from the mass of solute. Moreover, a certain amount of xanthine were added to the standard MSUM solution, respectively. For the standard MSUM solution, the concentration of MSUM was 8 mM and that of sodium chloride was 150 mM. The obtained crystals of sample were handled in the same way as them to acquire the solubility.Characterization method
The DLS experiments were conducted at 37 °C, which was controlled by a Grant LTD-6 water bath system. The samples were measured on a Malvern Zetasizer Nano ZS90 zeta (USA). 1H NMR were measured on a Bruker AM 600 MHz spectrometer. Fourier transform infrared spectroscopy of sample was employed to be characterized by a Bruker Alpha FTIR-ATR instrument in 4 cm−1 resolution with a 4000–400 cm−1 range. Raman spectroscopy was used to characterize the structure of MSUM and a ReactRaman 0163 instrument scanned the sample from 3200 to 100 cm−1 for three times. The samples of amorphous MSUM were obtained by the same procedure as the nucleation experiments, and the sample collection time was set to the induction time based on the results of the measurement of Induction Time. And the wet sample was instantly characterized by PXRD, IR and Raman in order to avoid any effects of the phase transition. All experiments were run three times.Computational details of DFT
| EBE = Epurine1−+2cation++purine2− − Epurine1− − 2Ecation+ − Epurine2− |
Results and discussion
Solubility
The solubility of MSUM in the presence of 150 mM NaCl, 8 mM urate, and xanthine at 15 °C (experimental conditions) was measured in this study and presented in Fig. S1.† The solubility increases significantly with the increase in the concentration of xanthine, showing that xanthine has a great salting-in effect on MSUM, which appears to be an expected trend and consistent with our previous report.10,13,14Induction time theory and results
Induction time measurements of MSUM in different concentrations of solutions were primarily performed at a temperature of 15 °C in the absence/presence of xanthine. The stochastic nature of MSUM nucleation can be investigated and analyzed from these large data sets via cumulative probability distributions (CPD) of induction times.15 P(t) is the probability to be formed in an experiment after an elapsed time of t.| P(t) = 1 − exp(−JV(t − tg)) | (2) |
Supersaturation in this work is defined in eqn (3).
| S = c/c* | (3) |
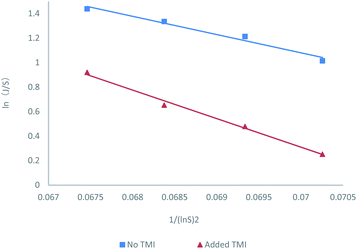
In eqn (3), S is the reported supersaturation, c is the dissolved concentration of MUSM in water including 150 mM NaCl (pH = 7.4) in the absence/presence of xanthine, and c* is the saturation concentration of MUSM in water including 150 mM NaCl (pH = 7.4) in the absence/presence of xanthine. To compensate for shifts in solubility in the presence of xanthine, and an adjusted excess amount of MSUM had to be added to samples that contained xanthine to ensure that every experiment was carried out at a constant supersaturation, thereby ensuring that the measured results could be compared with respect to a common set of baseline conditions. And the effect of adjusting the supersaturation in the presence of xanthine is reflected in Fig. 1 and Table 1. The data demonstrate the expected behavior of monotonically decreasing nucleation rates with reducing supersaturation.
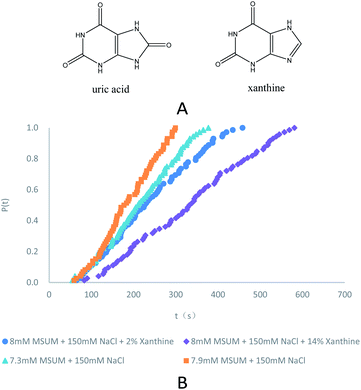 | ||
| Fig. 1 (A) Molecular structure of uric acid and xanthine. (B) Probability distributions of the induction times in the presence of different concentrations of MSUM and different concentrations of xanthine (note: for clarity, the data in the third and fourth rows of the Table 1 are not plotted). | ||
| Samplea | Sb | J (m−3 s−1) | τ (s) | Samplec | S | J (m−3 s−1) | τ (s) |
|---|---|---|---|---|---|---|---|
| a Sample is a solution of different concentrations of urate at pH = 7.4 in the presence of 150 mM NaCl.b S is the supersaturation.c Sample is a solution of different concentrations of xanthine at pH = 7.4 in the presence of 150 mM NaCl and 8 mM urate. | |||||||
| 7.9 mM | 47.0 | 198 | 101 | 2% TMI | 46.8 | 118 | 170 |
| 7.7 mM | 45.8 | 174 | 115 | 6% TMI | 46.1 | 88 | 227 |
| 7.5 mM | 44.6 | 150 | 133 | 10% TMI | 44.3 | 72 | 278 |
| 7.3 mM | 43.5 | 120 | 167 | 14% TMI | 43.4 | 56 | 357 |
The nucleation rate information was shown in Fig. 2. The resulting correlations provided good fits for the nucleation rate data and promoted the estimation of the representative pre-exponential factor (A) and activation energy (B) constants for the two systems with and without TMI. And the values shown in Table 2, indicate an increase in both A and B parameters for the nucleation experiments in the presence of TMI. The calculated increase in B is about approximately 57% with respect to that of the no TMI system, which seems like a reasonable conclusion since the increase in B should theoretically decrease the nucleation rate. However, the change in the pre-exponential parameter A is striking, considering the nearly 20 fold increase in the value of A in the presence of TMI.
The pre-exponential parameter A is defined by Classical nucleation theory15 in eqn (4).
| A = (4π/3v0)1/3(γef/kbT)1/2DCe | (4) |
DLS detection
We recently demonstrated that clusters or “nucleation precursors” existing in MSUM solutions could be dramatically stable with the assistance of additive cations based on the DLS test results.14 Along the same lines, DLS experiments were also used to investigate the nucleation of MSUM in presence of xanthine (Fig. S2†). And the notable is the fact that the average particle size, after the addition of xanthine with a concentration of 1 mM (concentration of control sample is 10 mM MSUM in the absence of xanthine), obviously decreased from 750 nm to 520 nm. This result confirmed the existence of clusters or “nucleation precursors” which could be dramatically stable and smaller with the assistance of additive TMI. This data appears to be reasonable since the nucleation in the system with xanthine needs to surmount a higher energy barrier, given that total Gibbs free energy in the nucleation process is the competitive outcome between bulk energy and interfacial energy.DFT calculations on binding energies of solute–solute and solute-TMI in presence of sodion
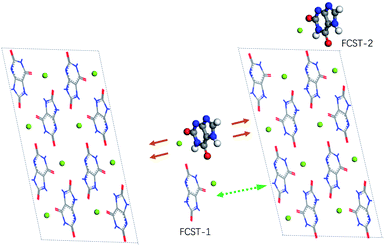
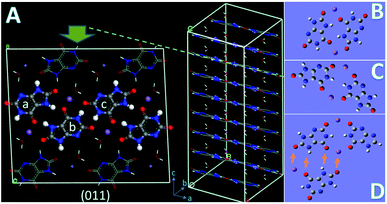
The crystal structure (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ; a = 10.888 Å, b = 9.534 Å, c = 3.567 Å, α = 95.06°, β = 99.47°, γ = 97.17°) of MSUM has been reported from the 1970s. The urate anions interact by virtue of hydrogen bonding and coordinate with the sodium ion through short Na/O electrostatic interactions to form two-dimensional sheets of purine rings parallel to the dominant (011) plane of MSUM (Fig. 3A). Our previous work confirmed that not xanthine but its negative ion could act as an inhibitor at pH = 7.4 to suppress the MUSM crystallization.10 Furthermore, our recent report demonstrated that the nucleation rate of MSUM increased significantly with increasing sodium ion concentration.14 As a result, based on the analysis of the electrostatic potential distribution of urate and xanthine ion (Fig. S3†), a series of structures of dimers in solute–solute and solute-TMI in presence of sodion were optimized and their binding energies were calculated (Fig. S4 and S5†). As shown in Fig. 3, for the most favorable conformation of dimer in the solute–solute system (FCSS) (the ball urate a and b displayed in Fig. 3A and B), on the basis of the negative EBE values (Fig. S4A†), is formed by the interaction of two head-to-tail chain bridges (urate−⋯Na+⋯urate−) and two intermolecular hydrogen-bonding (N–H⋯O). And secondarily favored conformation is formed by the interaction of two head-to-head chain bridges (urate−⋯Na+⋯urate−) (the ball urate b and c displayed in Fig. 3A and C). As a result, by virtue of these two docking modes, urate and sodium ions could bind into a stable planar structure in solution, since a sodium ion can be paired with multiple oxygen atoms at the same time. Very interestingly, these two pairing structures really dominate almost the whole major (011) face of MSUM (The ball urate in a⋯b and b⋯c displayed in Fig. 3A).17 Hence, it could be inferred that those optimum conformations may increase in solution as the major “growth units” with increasing of sodium ion concentration, thus leading to the promotion of nucleation by sodium ions. Meanwhile, the most favorable conformation of dimer in the solute-TMI system (FCST) is formed by the interaction of two head-to-head chain bridges (urate−⋯Na+⋯urate−), showing that the solute may have a higher affinity with TMI than itself by comparing the difference in negative EBE values (Fig. S5A† and 3D). These results may reasonably explain that xanthine could strongly inhibit MSUM nucleation because it could effectively suppress the major growth units of MSUM. Furthermore, as shown in Fig. 3D, it's interesting to note that xanthine can only inhibit the growth of FCST in a specific direction, so FCST could continue to develop into a planar in other directions by binding with foreign urates and Na ions. Therefore, this direction-specific inhibition effect also could effectively explain why the cluster size is reduced.
; a = 10.888 Å, b = 9.534 Å, c = 3.567 Å, α = 95.06°, β = 99.47°, γ = 97.17°) of MSUM has been reported from the 1970s. The urate anions interact by virtue of hydrogen bonding and coordinate with the sodium ion through short Na/O electrostatic interactions to form two-dimensional sheets of purine rings parallel to the dominant (011) plane of MSUM (Fig. 3A). Our previous work confirmed that not xanthine but its negative ion could act as an inhibitor at pH = 7.4 to suppress the MUSM crystallization.10 Furthermore, our recent report demonstrated that the nucleation rate of MSUM increased significantly with increasing sodium ion concentration.14 As a result, based on the analysis of the electrostatic potential distribution of urate and xanthine ion (Fig. S3†), a series of structures of dimers in solute–solute and solute-TMI in presence of sodion were optimized and their binding energies were calculated (Fig. S4 and S5†). As shown in Fig. 3, for the most favorable conformation of dimer in the solute–solute system (FCSS) (the ball urate a and b displayed in Fig. 3A and B), on the basis of the negative EBE values (Fig. S4A†), is formed by the interaction of two head-to-tail chain bridges (urate−⋯Na+⋯urate−) and two intermolecular hydrogen-bonding (N–H⋯O). And secondarily favored conformation is formed by the interaction of two head-to-head chain bridges (urate−⋯Na+⋯urate−) (the ball urate b and c displayed in Fig. 3A and C). As a result, by virtue of these two docking modes, urate and sodium ions could bind into a stable planar structure in solution, since a sodium ion can be paired with multiple oxygen atoms at the same time. Very interestingly, these two pairing structures really dominate almost the whole major (011) face of MSUM (The ball urate in a⋯b and b⋯c displayed in Fig. 3A).17 Hence, it could be inferred that those optimum conformations may increase in solution as the major “growth units” with increasing of sodium ion concentration, thus leading to the promotion of nucleation by sodium ions. Meanwhile, the most favorable conformation of dimer in the solute-TMI system (FCST) is formed by the interaction of two head-to-head chain bridges (urate−⋯Na+⋯urate−), showing that the solute may have a higher affinity with TMI than itself by comparing the difference in negative EBE values (Fig. S5A† and 3D). These results may reasonably explain that xanthine could strongly inhibit MSUM nucleation because it could effectively suppress the major growth units of MSUM. Furthermore, as shown in Fig. 3D, it's interesting to note that xanthine can only inhibit the growth of FCST in a specific direction, so FCST could continue to develop into a planar in other directions by binding with foreign urates and Na ions. Therefore, this direction-specific inhibition effect also could effectively explain why the cluster size is reduced.
HNMR
1H chemical shift is sensitive to subtle changes in the local environment of a molecule, and it is usually used to study molecular association in solution.18 Based on the investigation of FCST structure, urate and xanthine are almost located in the same plane, which leads to xanthine being in the nuclear magnetic de-shielding field of urate. Therefore, on the one hand, the samples in presence of different concentrations of xanthine were investigated by HNMR and the results showed that the chemical shift of H(8) (Fig. S3†) did not change with the concentration of xanthine. On the other hand, pre-mixed samples of different ratios of MSUM to xanthine were investigated by HNMR (Table 3), and remarkable lower-field proton shifts, associated with increasing the mole ratio of MSUM to xanthine, were observed from the chemical shifts of the C-8 protons of xanthine in D2O. Hence, this result is consistent with the structural features of FCST obtained from DFT calculations, showing the presence of a de-shielding effect, resulting from the de-shielding field of the urate, which markedly increased along with the improvement of the mole ratio of MSUM to xanthine in solution.DFT calculations on chemical shifts of HNMR
Quantum-chemical calculations have become highly important tools in the usually difficult assignment of experimental NMR spectra.19,20 The chemical shifts of H(8) of xanthine, xanthine ion, and xanthine in FCST were investigated by DFT calculation method. As shown in Table 4, in an aqueous xanthine (pKa1 = 7.53) solution at pH = 7.4 (note: about 46.8% mol of xanthine ionized at pH = 7.4), the calculated values of HNMR (δ = 7.449) deviated by only about 1% when comparing the detection values (δ = 7.372). And the results of these calculations further demonstrate that FCSTs exist in the solution, and they cannot dominate the entire solution environment but exert a significant inhibitory effect.| Sample | Xanthine | Xanthine ion | FCST | Xanthine solution at pH = 7.4a | FCST and xanthineb |
|---|---|---|---|---|---|
| a A solution consisting of 46.8% xanthine ion and 53.2% un-ionized xanthine molecule (xanthine molecule and xanthine ion content based on calculations of pKa1 values of xanthine at pH = 7.4).b A solution consisting of 46.8% FAST and 53.2% un-ionized xanthine molecule based on the assumption that all urate ions are docked by xanthine ions (xanthine molecule and xanthine ion content based on calculations of pKa1 values of xanthine at pH = 7.4). | |||||
| Chemical shift of H(8) in xanthine | 7.510 | 7.380 | 7.530 | 7.449 | 7.519 |
Detection of the amorphous form of MSUM in presence of TMI by FTIR, Raman spectra, and PXRD
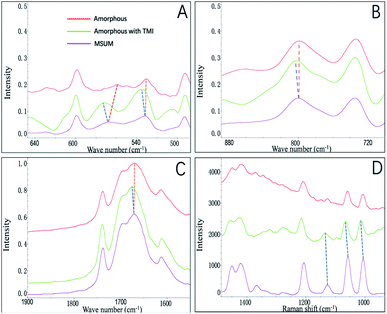
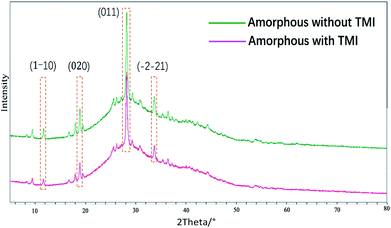
In this study, we focused on the amorphous form that appeared before the formation of crystals of MSUM, since it may be obtained the critical information in nucleation and crystal growth.21 The FTIR and Raman spectra were employed to probe the structures of the crystal form of MSUM and the amorphous form in the absence/presence of TMI, and the results are shown in Fig. 4A–C and D, respectively. And the structural difference of the three can be carefully studied in the three vibrational regions of IR peaks.17,22,23 Firstly, the oxygen−sodium peaks of MSUM is located at 450–600 cm−1. Secondly, the vibration peak at 787 cm−1 of the MSUM represents the –NH− in purine rings. Thirdly, the peaks at 1647 cm−1 corresponds to the –OH vibration of water molecules. Moreover, the corresponding symmetrical vibration Raman peaks of the MSUM can be found at 1011, 1062, and 1208 cm−1. As can be seen in Fig. 4, on the one hand, the structural difference between the MSUM and amorphous form without TMI can be inspected in the three vibrational regions of IR peaks. And those peaks of the amorphous form in absence of TMI at 450−600 cm−1, 787 cm−1, and 1647 cm−1 all display a red shift in comparison to the corresponding peak position of MSUM crystal.17 And on the other hand, those peaks from the samples of amorphous form in presence of TMI all present a blue shift in comparison to the corresponding peak position of MSUM crystal. Meanwhile, the similarly symmetrical vibration Raman peaks of the amorphous phase in presence of TMI all exhibit different degrees of the shift to higher wavenumber in comparison to the corresponding peak position of MSUM crystal and its amorphous phase (Fig. 4D). As a result, these interesting results confirm the following three facts.17,24 Firstly, the amorphous phase in presence of TMI exhibited a weaker ionic bond between sodium and oxygen (blue shift in 450–600 cm−1). Secondly, intermolecular interactions between purine rings on the plane (011) were changed (blue shift in 787 cm−1). Thirdly, the structures of the amorphous phase in presence of TMI had different water contents, and both the hydrogen bonding between water and purine molecules were weakened (blue shift in 1647 cm−1).Recently, the transition process over time from an amorphous structure to a crystalline structure was presented by the time-resolved detection of PXRD.17 The first diffraction peak appears at 28.18° corresponding to the (011) face, and the following developments are the diffraction peaks at 33.70, 18.87, and 11.68°, which correspond to (−2−21), (020) and (1−10) faces. This data showed that an MSUM crystalline structure initially takes place on a dominant two-dimensional (011) face, then spreads out to form a three-dimensional crystal structure by aromatic stacking interactions, as evidenced by the formation of (−2−21), (020) and (1−10) faces. Here PXRD was also used to distinguish the difference in the amorphous phase in the presence/absence of TMI, since the amorphous form as a transition state may provide valuable clues about nucleation and crystallization in presence of additives.25 As shown in Fig. 5, PXRD patterns showed that xanthine did not change the lattice structure of the amorphous phase of MSUM at 6 mM MSUM solution in the presence of 0.3 mM xanthine, and the amorphous form in the absence/or presence of xanthine all show the high intensity of the (011) peak. However, when the ratios of intensity of (1−10)/(011), (020)/(011) and (−2−21)/(011) are calculated, then they decrease from 0.081, 0.199 and 0.186 to 0.056, 0.145 and 0.130, respectively. It is interesting to note that they all decrease by about 30%. Furthermore, the variation of ratio intensity of PXRD has been shown to be an effective evidence to elucidate the subtle changes in the nucleation and crystallization process.25–27 Hence, this result further clarifies that the main inhibitory effect of xanthine is to disturb and suppress the three-dimensional crystallization process.
Understanding the mechanism of nucleation inhibition
Based on the above observations in solutions (DFT calculations, DLS, HNMR, and induction time results) and the reconfirmation of the detection on amorphous form of MSUM in the presence/absence of TMI (FTIR, Raman spectra, and PXRD), the mechanism of nucleation inhibition by xanthine in a solution, could be attributed to the following three aspects. Firstly, it could be accounted for not classical nucleation theory but the non-classical prenucleation phenomena (e.g., ordering and aggregation), which, happening before the formation of the well-structured nuclei in solution, play a great role in affecting the nucleation process.28 Secondly, xanthine could only inhibit the assembly of the FCSS and the growth of FCST in a specific direction in solution, so FCST could continue to develop into a planar in other directions, but its size would be reduced. Thirdly, as shown in Fig. 6, FCST could act as an “imposter” of FCSS to binding the (011) by the aromatic stacking interactions between the urate in the structure of FCST and urate in (011) plane, while xanthine in FCST causes a large binding barrier between the two (011) planes and the reduction in cluster size in solution. This special binding obstacle brings about an amplifying impact of inhibition, leading to a very huge inhibitory effect of a small amount of inhibitor, which could further explain the significant and unreasonable fluctuations of the pre-exponential parameter A. To the best of our knowledge, the nucleation inhibition of TMI is achieved by suppressing interplanar stacking, which is a mechanism to be proposed at the first time.Conclusions
This study, by means of DLS, HNMR, IR, Raman, PXRD, induction time measurements, and DFT calculations in the presence/absence of xanthine, revealed that the inhibition came from a combination of kinetic and thermodynamic effects, with an impact of kinetics as the TMI inhibition effects far exceeded what could be accounted for by changes in solubility and or other usual factors in classical nucleation theory. And these results demonstrated that the complexes between urate and TMI ion disturbed the formation of two-dimensional sheets of sodion and purine rings parallel to the (011) plane and further impeded the formation of three-dimensional structure. To our knowledge, the nucleation inhibition of TMI is achieved by suppressing interplanar stacking, which is a mechanism to be proposed at the first time.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank prof. Xuehai Ju of Nanjing University of Science and Technology for their quantum chemistry calculations. This work supported by the National Natural Science Foundation of China (81873013).Notes and references
- N. Dalbeth, T. R. Merriman and L. K. Stamp, Lancet, 2016, 388, 2039–2052 CrossRef CAS.
- R. Pascal and B. Thomas, Lancet, 2010, 375, 318–328 CrossRef.
- J. Ulrich, Chem. Eng. Technol., 2003, 26, 832–835 CrossRef CAS.
- J. Chung, I. Granja, M. G. Taylor, G. Mpourmpakis, J. R. Asplin and J. D. Rimer, Nature, 2016, 536, 446–450 CrossRef CAS.
- L. Hu, Y. Yang, H. Aloysius, H. Albanyan, M. Yang, J. J. Liang, A. Yu, A. Shtukenberg, L. N. Poloni, V. Kholodovych, J. A. Tischfield, D. S. Goldfarb, M. D. Ward and A. Sahota, J. Med. Chem., 2016, 59, 7293–7298 CrossRef CAS.
- C. A. P. Siepermann, S. Huang and A. S. Myerson, Cryst. Growth Des., 2017, 17, 2646–2653 CrossRef.
- C. A. P. Siepermann and A. S. Myerson, Cryst. Growth Des., 2018, 18, 3584–3595 CrossRef.
- P. L. Kaskiewicz, I. Rosbottom, R. B. Hammond, N. J. Warren, C. Morton, P. J. Dowding, N. George and K. J. Roberts, Cryst. Growth Des., 2021, 21, 1946–1958 CrossRef CAS.
- Y. Liu, R. Cheng, C. Ou, X. Zhang and T. Fu, Cryst. Growth Des., 2020, 20, 2842–2846 CrossRef CAS.
- Y. Liu, J. Jing, C. Ou, X. Zhang, S. Jiang, R. Chen and T. Fu, CrystEngComm, 2019, 21, 3774–3778 RSC.
- S. Jiang and J. H. Horst, Cryst. Growth Des., 2011, 11, 256–261 CrossRef CAS.
- M. J. Frisch, et al.Gaussian 09, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- I. Kippen, J. R. Klinenberg, A. Weinberger and W. R. Wilcox, Ann. Rheum. Dis., 1974, 33, 313–317 CrossRef CAS PubMed.
- A. Da, A. Ren, R. Cheng, X. Zhang, Y. Pan, C. Ou, T. Fu and Y. Liu, Crystengcomm, 2021, 23, 8411–8417 RSC.
- D. Kashchiev and G. M. van Rosmalen, Cryst. Res. Technol., 2003, 38, 555–574 CrossRef CAS.
- I. Souvignet and S. V. Olesik, Anal. Chem., 1998, 70, 2783–2788 CrossRef CAS PubMed.
- M. Li, S. Li, W. Tang and J. Gong, Cryst. Growth Des., 2020, 20, 804–812 CrossRef CAS.
- D. Attwood, R. Waigh, R. Blundell, D. Bloor, A. Thévand, E. Boitard, J. P. Dubès and H. Tachoire, Magn. Reson. Chem., 1994, 32, 468–472 CrossRef CAS.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- D. Flaig, M. Maurer, M. Hanni, K. Braunger, L. Kick, M. Thubauville and C. Ochsenfeld, J. Chem. Theory Comput., 2014, 10, 572–578 CrossRef CAS PubMed.
- I. Weissbuch, M. Lahav and L. Leiserowitz, Cryst. Growth Des., 2003, 3, 125–150 CrossRef CAS.
- B. B. Parekh, S. R. Vasant, K. P. Tank, A. Raut, A. D. Vaidya and M. J. Joshi, Am. J. Infect. Dis., 2009, 5, 232–237 Search PubMed.
- S. Ahmed, M. M. Hasan and Z. A. Mahmood, Pak. J. Pharm. Sci., 2017, 30, 2101–2108 CAS.
- N. N. Mafy, T. Afrin, M. M. Rahman, M. Y. A. Mollah and M. A. B. H. Susan, RSC Adv., 2015, 5, 59263–59272 RSC.
- S. Xu, D. Cao, Y. Liu and Y. Wang, Cryst. Growth Des., 2022, 22, 2001–2022 CrossRef CAS.
- S. Castro-Garcia, A. Castro-Couceiro, M. Senaris-Rodriguez, A. F. Soulette and C. Julien, Solid State Ionics, 2003, 156, 15–26 CrossRef CAS.
- G. G. Amatucci, J. M. Tarascon, D. Larcher and L. C. Klein, Solid State Ionics, 1996, 84, 169–180 CrossRef CAS.
- D. Gebauer, M. Kellermeier, J. D. Gale, L. Bergstro and H. Colfen, Chem. Soc. Rev., 2014, 43, 2348–2371 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra03289a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
: