Open Access Article
Open Access ArticleInvestigation of structural, morphological, and transport properties of a multifunctional Li-ferrite compound
Ibtihel. Soudani a,
Khawla. Ben Brahim
a,
Khawla. Ben Brahim *b,
Abderrazek. Oueslati
*b,
Abderrazek. Oueslati b,
Houda. Slimi
b,
Houda. Slimi a,
Abdelhedi. Aydia and
Kamel. Khirounic
a,
Abdelhedi. Aydia and
Kamel. Khirounic
aLaboratory of Multifunctional Materials and Applications (LaMMA), LR16ES18, Faculty of Sciences of Sfax, University of Sfax, BP 1171, 3000 Sfax, Tunisia
bLaboratory for Spectroscopic and Optical Characterization of Materials (LaSCOM), Faculty of Sciences, University of Sfax, B. P. 1171, 3000 Sfax, Tunisia. E-mail: benbrahimkhawla75@gmail.com
cLaboratory of Physics of Materials and Nanomaterials Applied to the Environment (LaPHYMNE), Faculty of Sciences, University of Gabès Cited Erriadh, 6079 Gabès, Tunisia
First published on 24th June 2022
Abstract
The development of multifunctional materials is an exceptional research area, which is aimed at enhancing the versatility of materials in various applications. In this context, the exceptional properties of ferrite materials have attracted the attention of researchers. For this reason, we synthesized LiMn0.5Fe2O4 sintered at a temperature of 1100 °C. The X-ray powder diffraction analysis reveals the presence of one cubic phase with the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group and confirms the spinel structure formation. Moreover, the elemental analysis by EDX reveals the homogeneous distribution of iron and manganese cations. Scanning electron microscopy shows that the grain size is of the order of 2.48 μm. Impedance spectroscopy was performed in the temperature and frequency ranges from 200 K to 380 K and 40 Hz to 106 Hz, respectively. The Nyquist plots revealed the presence of grains and grain boundary contributions. The semiconductor nature, obtained by the conductivity study, indicates that LiMn0.5Fe2O4 is promising in optoelectronic applications. Dc conductivity is found to be thermally activated with an activation energy of 370 meV, 255 meV, and 199 meV for 200–270 K, 280–330 K, and 340–380 K regions, respectively. From the Jonscher power law, the correlated barrier hopping model (CBH) and non-overlapping small polaron tunneling (NSPT) prevailed in the conduction process. Besides, the temperature coefficient of resistivity (TCR) affirmed that LiMn0.5Fe2O4 is a good candidate for detecting infrared radiations and infrared bolometric applications.
m space group and confirms the spinel structure formation. Moreover, the elemental analysis by EDX reveals the homogeneous distribution of iron and manganese cations. Scanning electron microscopy shows that the grain size is of the order of 2.48 μm. Impedance spectroscopy was performed in the temperature and frequency ranges from 200 K to 380 K and 40 Hz to 106 Hz, respectively. The Nyquist plots revealed the presence of grains and grain boundary contributions. The semiconductor nature, obtained by the conductivity study, indicates that LiMn0.5Fe2O4 is promising in optoelectronic applications. Dc conductivity is found to be thermally activated with an activation energy of 370 meV, 255 meV, and 199 meV for 200–270 K, 280–330 K, and 340–380 K regions, respectively. From the Jonscher power law, the correlated barrier hopping model (CBH) and non-overlapping small polaron tunneling (NSPT) prevailed in the conduction process. Besides, the temperature coefficient of resistivity (TCR) affirmed that LiMn0.5Fe2O4 is a good candidate for detecting infrared radiations and infrared bolometric applications.
1. Introduction
Many efforts have been focused during the last years on the preparation of ferrite materials, which has become the object of numerous experimental studies.1–3 Spinel ferrites generally possess a cubic spinel structure with the formula AFe2O4, where A is usually a divalent metal for satisfying the current manufacturing demands. This structure presents the ideal stoichiometry of spinel ferrite, which fulfills the conditions of the cation/anion ratio of 3/4. However, the existing spinel materials that are far from this stoichiometry are the most known spinel ferrites, such as maghemite (g-Fe2O3).4 This implies the presence of nonstoichiometric spinels depending on the overall cation/anion ratio. When the cation-to-anion ratio is lower than 3/4, hypostoichiometry is observed. Spinels show hyperstoichiometry when the ratio is higher than 3/4.Significant findings and achievements have been attained for ferrite substances, especially lithium ferrites, which comprise an exciting class of materials having a nonstoichiometric spinel structure. For instance, Li–Co,5 Li–Zn,6,7 Li–Ti,8 Li–Mg,9 and Li–Ni (ref. 10 and 11) generally show excellent physicochemical properties. It is observed that there is a significant change in the properties of lithium ferrites by substitution of different metal cations. This fact motivated G. Aravind et al. to synthesize nickel-substituted lithium ferrites.12 Ni-doped Li0.5Fe2.5O4 show superparamagnetic behavior that makes it a good candidate for biomedical applications. Also, the magnetic investigation of Li0.06Fe2.94O4 reveals that it may be suitable for magnetic hyperthermia (MHT) treatments in cancer applications.13
This category of materials belongs to soft materials that can be extensively used in computer memory chips, transformer cores rod antennas, microwave devices, medical diagnostics, magnetic resonance imaging, magnetic caloric refrigeration, and radiofrequency coil fabrication.14–18 Besides, these substances have drawn a great deal of interest in modern technological applications in the telecommunication field, electronics engineering, electric vehicles, and memory storage devices.19,20 It can be a good inductive component in an enormous diversity of electrical instruments, for instance impedance matching networks,6 filters,21 voltage-controlled rectifiers,5 and low noise amplifiers.22
The distinguishable properties such as environmental benignity,23 low eddy current values,24 high electrical resistivity,24 availability at low cost,25 lightweight, and superior high-temperature performance can give it a considerable stature in future multifunctional application. Therewith, its efficacity can be improved by tuning the electrical resistivity and eddy current. This may explain the increasing scientific curiosity toward Li-ferrite materials.
Several synthetic approaches have been developed to prepare the nanoparticles of this eminent category of ferrites including sol–gel,26 hydrothermal,27 micro-emulsion technique,5 auto-combustion,28 and the solid-state reaction route (ceramic).29 A majority of these synthesis methods are economically impracticable for large-scale production. However, the solid-state reaction has proven its effectiveness for several years due to its simplicity, high crystallinity, homogeneity of the product, and its low cost compared with other synthesis methods.
To date, the reports on Li–Mn-based ferrites are limited, despite it being suitable for the fabrication of cathode materials for Li-rechargeable batteries,30 and it is used in the improvement of memory cores that merge low-temperature sensitivity with fast switching.31
In this context, we report a further study on LiMn0.5Fe2O4 prepared by the solid-state reaction technique. This compound is a hyper stoichiometric spinel material with a cation/oxygen ratio higher than 3/4. After discussing its structure and morphological analysis, the electrical properties are investigated to thoroughly explain the transport phenomena by combining conductivity and impedance studies. The main objective of this work is not only to show an excellent material but also a large range of applications in the future.
2. Experimental details
2.1 Materials synthesis
In general, before the preparation of the material, a series of synthesis optimization were done separately for obtaining a sample sufficiently homogenous and well crystallized with expected and reasonable final properties. All reagents obtained from Sigma-Aldrich Li2CO3, MnO, and Fe2O3 were of analytical purity grade (99.9%, Sigma-Aldrich) and used without further purification. They were used for synthesizing LiMn0.5Fe2O4. In the first stage, these precursors were carefully weighted in stoichiometric amounts. In the next step, the mixed powder was ground neatly in an agate mortar for 2 hours to reduce the size of the grain, and hereafter, the mixture was heated. Then, the resulting mixture was heated slowly to 850 °C. It was left at this temperature for 7 hours to activate the chemical reaction and to fix different elements to limit their volatilization. Also, the sample pellets of LiMn0.5Fe2O4 were embedded in the calcined powder to avoid severe lithium evaporation during sintering.Once the reaction was completed, the obtained powder was ground for 1 hour and pressed into a circular disc of 8 mm diameter and 1 mm thickness. To obtain a high-density ceramic with perfect crystallization, the pellet was sintered at 1100 °C for 2 hours in an electric muffle furnace and slowly cooled to room temperature. Finally, the pellet was ready to be characterized.
2.2 Characterization tools
The X-ray powder diffraction pattern of our ferrite was recorded at room temperature using a BRUKER diffractometer with copper anticathode (CuKα radiation λ = 1.5406 Å) in the Bragg range from 10 to 90°. The morphological characterization was performed by a scanning electron microscope (SEM) in order to estimate the particle size. To investigate the chemical compositions, energy-dispersive X-ray (EDX) images and simple mapping were done.The electrical properties of LiMn0.5Fe2O4 were determined by impedance spectroscopy. Two proper thin layers of silver were put on each surface of the synthesized pellet through a circular mask by thermal evaporation. The pellet was placed in a cryostat from Janis Corporation, which allowed the temperature to be varied from 200 to 380 K. The conductance and impedance measurements were done using an Agilent 4294 A analyzer under vacuum over the explored frequency range from 40 Hz to 106 Hz.
3. Results and discussion
3.1 Structural study
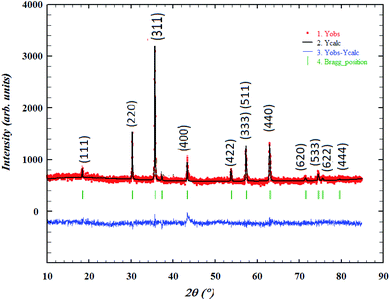
The crystalline structure and the formed phase-purity of LiMn0.5Fe2O4 were characterized through X-ray powder diffraction (XRD) measurement performed at room temperature. The refinement of the XRD pattern was performed by the Rietveld method using the Full PROF program.32 Fig. 1 shows the observed, calculated, and difference diffraction patterns. All Bragg peaks are successfully indexed and satisfactorily modeled without any extra peaks related to hematite (Fe2O3) or any foreign impurity. This confirms the superior purity of the prepared sample. The diffraction results show that our compound is a cubic system with Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group (Oh7 point group), as expected for the ferrite structures, according to the JCPDS card no. 96-152-6193.
m space group (Oh7 point group), as expected for the ferrite structures, according to the JCPDS card no. 96-152-6193.
The strongest reflection comes from the (311) plane, which denotes the spinel phase formation.33 All the Rietveld refinement parameters are reported in Table 1.
| Formula | LiMn0.5Fe2O4 at room temperature |
|---|---|
| Crystalline system | Cubic |
| Space group | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Lattice parameter (Å) | |
| a = b = c | 8.343 |
| α = β = δ (°) | 90 |
| V (Å3) | 580.913 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Reliability factors (%) | |
| Rp (%)/Rwp (%)/Rexp (%) | 3.960/5.090/4 |
| χ2 | 1.620 |
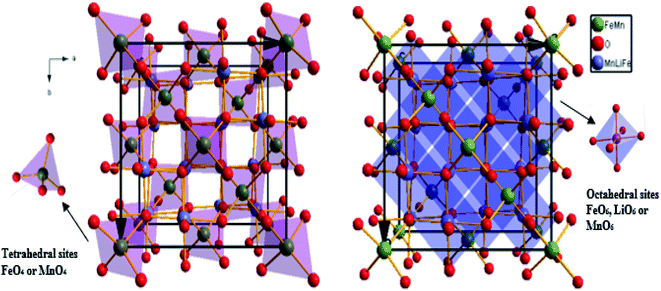
The weak value of the goodness fit parameter (χ2) confirms the rigor of the refining and the precision of the fit. The crystal structure, projected in the (110) plan, of the compound, is schematically depicted in Fig. 2 using the Diamond software.
The average crystallite size (Dsc) shown in Table 1 is determined from the full width at half maximum using the classical Debye–Scherrer equation.34
β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θDsc = Kλ θDsc = Kλ
| (1) |
The link lengths between cations occupying the tetrahedral positions (A) and cations placed in the octahedral positions (B) (LA–A, LB–B, and LA–B) depend only on the lattice parameter (a). They are calculated employing the equations of Standely.34
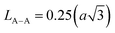 | (2) |
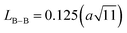 | (3) |
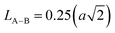 | (4) |
The density (ρX-ray) is fixed, bearing in mind that a cubic spinel structure consists of a unit cell including eight molecules, according to the following formula.34
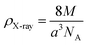 | (5) |
In this expression, M denotes the molecular weight of each compound of the studied spinel ferrite, a denotes the calculated lattice parameter determined from the XRD measurements, and NA (=6.023 × 1023) represents Avogadro's number.
The bulk density of LiMn0.5Fe2O4 is calculated using the following standard relation:34
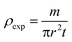 | (6) |
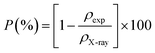 | (7) |
The specific surface area (Sa) is obtained from the following expression.34
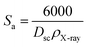 | (8) |
All details deduced from previous analyses are tabulated in Table 2.
| Average crystallite size (nm) | Dsc | 46 |
| Average interionic bond distances between the cations' positions (Å) | LA–A | 3.61 |
| LB–B | 3.27 | |
| LA–B | 2.95 | |
| Tetrahedral (A) site radii (Å) | rA | 0.62 |
| Octahedral (B) site radii (Å) | rB | 0.64 |
| Density (g cm−3) | ρX-ray | 4.81 |
| Bulk density (g cm−3) | ρexp | 4.68 |
| Porosity | P | 3 |
| Specific surface area (m2 g−1) | Sa | 27.11 |
The specific surface and porosity percentage have an important role in controlling the diverse properties of polycrystalline spinel ferrites. They exhibit that the particle size of the spinel is nearly homogeneous, uniformly distributed, and well agglomerated over the whole surface of the studied sample.34
3.2 Morphological study
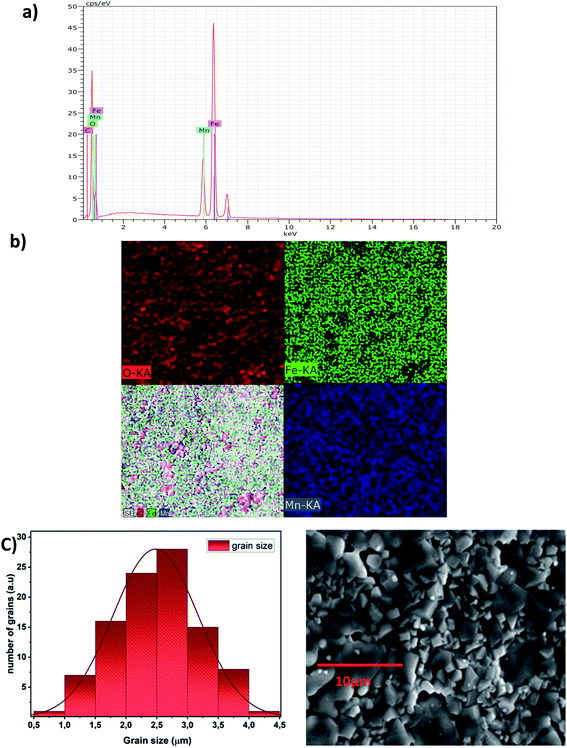
Elemental analysis by EDX is used to characterize the chemical composition of the sample. It gives the qualitative and quantitative analysis of the elements present in the prepared compound. The spectrum obtained is shown in Fig. 3a. The characteristic peaks of the constituent elements, namely, manganese (Mn), iron (Fe), and oxygen (O), are demonstrated without any impurity. This is good evidence of the purity of the synthesized sample. On the other hand, the appearance of the carbon (C) signal can be ascribed to carbon tape on which the sintered pellet is mounted with a holder.35 Nevertheless, the small atomic number (Z) of lithium element, which is less than the sensitivity of EDX to the element's atomic number, explains its invisibility in the spectrum.30Fig. 3b shows the EDX mapping analysis of LiMn0.5Fe2O4. The distribution of the elements is presented with different colors (Mn (royal blue), Fe (green), and O (red)).
It highlights that all elements are approximately uniformly distributed at the micrometer scale in the sample. Small differences can be ascribed to the different crystallographic orientations.
The experimental and theoretical proportions of the constituents obtained as an atomic percentage are recorded in Table 3. The experimental weight and atomic percentages are in agreement with the expected theoretical values. This proves the success of the pathway for the synthesis of LiMn0.5Fe2O4.
| Element | Experimental values | Theoretical values | ||
|---|---|---|---|---|
| Weight (%) | Atom (%) | Weight (%) | Atom (%) | |
| Carbon | 1.66 | 4.17 | — | |
| Oxygen | 31.60 | 59.64 | 30.46 | 53.33 |
| Manganese | 12.08 | 6.64 | 15.69 | 6.66 |
| Iron | 54.66 | 29.55 | 53.17 | 26.66 |
The EDX result indicates that the preparation denotes a homogeneous distribution of iron and manganese cations with high purity.
The micrograph displayed in Fig. 3a illustrates an interesting surface morphology of LiMn0.5Fe2O4. Scanning electron microscopy reveals a high melting or accumulation microstructure with polygonal-shaped and polyhedron-shaped grains. The average grain size of the particles (DSEM) is deduced by fitting the histogram (Fig. 3c) by employing the image analyzer software ImageJ. DSEM is about 2.48 μm. This means that the grains have a polycrystalline structure, compared with the low crystallite size obtained from the XRD study.36
3.3 Electrical results
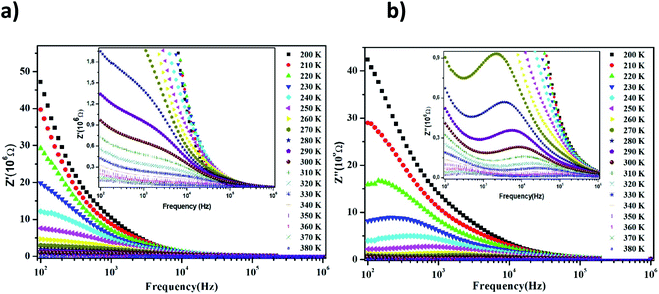
The Nyquist diagram of LiMn0.5Fe2O4 at a chosen temperature is shown in Fig. 4a and b. These diagrams reveal a succession of semicircles that reflect the grain and grain boundary contributions. Two distinct behaviors are observed below (Fig. 5a) and after (Fig. 5b) 270 K.
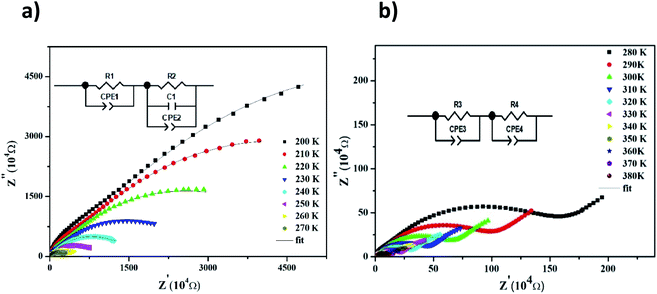 | ||
| Fig. 4 Complex impedance spectra in the Nyquist plane with electrical equivalent circuit (inset), accompanied by theoretical data (solid lines) at 200–270 K (a) and 280–380 K (b). | ||
Two semicircular arcs are observed in Fig. 4a for the temperature range of 200–270 K, which is related to the grain and the grain boundary effects. In order to extract the different electrical parameters, the experimental data are modeled as an equivalent circuit formed by a series of two parallel combinations. The first one consists of resistance (R1) and a constant phase element (CPE1), and the second one is composed of a parallel combination of resistance (R2), capacitance (C1), and a constant phase element (CPE2) (Fig. 4a inset).
The impedance of CPE is given by39
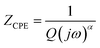 | (9) |
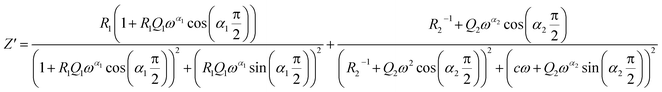 | (10) |
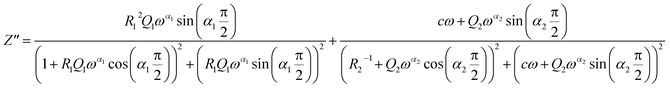 | (11) |
From 280 K to 380 K, the compound can be modeled by an equivalent circuit model. It implies a serial association of grain resistance (R3) associated in parallel with (CPE3) and (R4) resistance grain boundary associated in parallel with (CPE4). The equivalent circuit is deposited, as shown in the inset of Fig. 4b. Based on this model, we can obtain the subsequent expressions:41
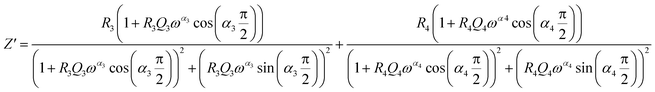 | (12) |
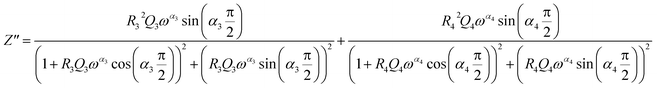 | (13) |
The real and imaginary parts of impedance plots at several temperatures show an ordinary behavior, observed in many materials,42,43 as depicted in Fig. 5. We can observe in Fig. 5a that with a further increase in frequency, the real impedance part comes down to a particular frequency depending on the temperature. Then, all curves of the value Z′ merge into a single line at a higher frequency side for all temperatures. This can be clarified by the release of space charges caused by the reduction of barriers in the investigated material.44 In fact, a decrease in the real part of impedance Z′ at the lower frequency limit region can be accounted by the NTCR (negative temperature coefficient of resistance) nature of the material according to other previous works.45,46 However, other researchers have explained the decreasing trend of Z′ at the lower frequency limit region by the increase in the AC conductivity and the decrease in the trapped charge density guide for an increase in the charge carrier mobility.47 All these suggestions will be discussed in the parts that follow.
Fig. 5b displays the behavior of Z′′, the imaginary part of impedance, with the variation in the frequency at a wide range of temperatures (200–380 K). The value of Z′′ increases gradually with the frequency as the temperature increases, until it reaches a maximum peak Zmax′′. Then, this magnitude decreases. These observations reflect the existence of the electrical relaxation phenomena and describe its type and its strength in our material.48,49
For higher frequencies and for all temperatures, the imaginary part of Z′′ is merged. It can be explained by an accumulation of the space charge effect in the material, as reported in the preceding investigation.50,51 Here, in Fig. 5b, we observe that when the temperature increases, the relaxation peaks shift toward higher frequencies. This behavior indicates an increase in the mobility of the hopping charge carrier, which reveals the drop of the resistive properties in the bulk of the material.52 Also, it indicates the presence of a thermally-activated relaxation process and allows us to estimate its activation energy value in LiMn0.5Fe2O4.
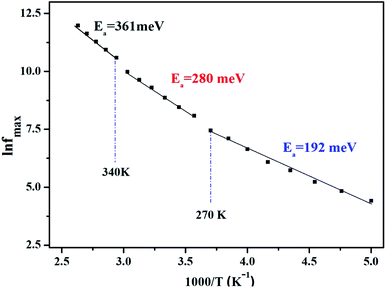
Afterward, we plotted the variation of ln(fmax) vs. 1000/T in Fig. 6, where fmax corresponds to the relaxation frequency at each maximum of Z′′. The determined curve can be described using Arrhenius law53
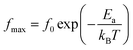 | (14) |
The existence of multivalent cations such as manganese (Mn3+, Mn2+), iron (Fe3+, Fe2+), and their displacement between the A and B sites of the studied sample LiMn0.5Fe2O4 certainly enhanced the electrical proprieties.30 The crystal lattice always tends toward a stable configuration. Therefore, certain ions are obligated to move according to the other new ion position. This jumping ion activates the electron–phonon interaction and the lattice vibration and plays a noteworthy role in the control of the conduction mechanism as a function of temperature.7
All this will be supported through the study of the conductive behavior, which will be discussed in the following part.
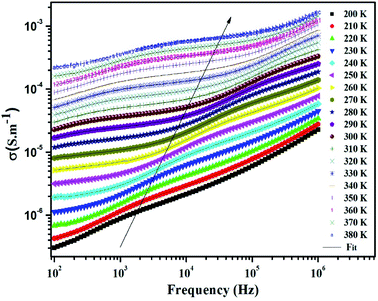
At the lower frequencies (102 –104 Hz), the conductivity spectra have nearly constant values (σdc) because the random distribution of the charges carriers gives rise to frequency-independent conductivity.54 It is clear that dc conductivity is thermally activated, which can display the semiconductor behavior by the leap of the localized load carrier, where the hole jumps between Mn3+ and Mn2+ cation and the electron hops between Fe2+ and Fe3+ ion. The semiconductor nature indicates that these compounds can be promising in certain applications such as optoelectronics, photodetectors, and photovoltaics.7,32
At higher frequencies (>104 Hz), the conductivity increases with increasing frequency. This can be explained by the important contribution of the charge carrier and the jumping mechanism.54 This region is attributed to the alternating conductivity (σac). Generally, the electrical conductivity behavior obeys the common universal power law, as reported by Jonscher.54
| σT = σdc + σac = σdc + Aωs | (15) |
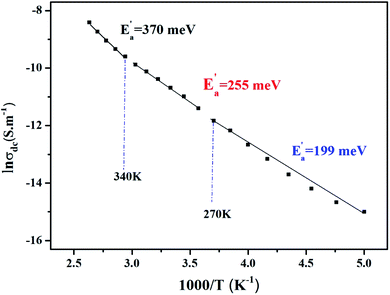
Fig. 8 illustrates the logarithmic variation of the conductivity σdc versus the inverse of the temperature. This curve can be described according to the Arrhenius relation.55
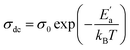 | (16) |
σ0 is the pre-exponential factor, Ea′ is the minimum amount of energy to activate a process, and kB is Boltzmann's constant with a defined value of 8.625 × 10−5 eV K−1.
We acquire three linear regions in the curve, which has thermal activation, where the activation energies are 370 meV, 255 meV, and 199 meV for the first, second, and third region, respectively. These values are close to the obtained from ln(fmax) vs. 1000/T (Fig. 6) with a slight variation, possibly due to the values of frequency taken from the different spectra. This proposes that during relaxation and conduction processes, the mobile charge carriers need to overcome roughly the same energy barrier.34
The experimental curves of conductivity are simulated using eqn (15) to deduce the value of exponent s at different temperatures to determine a suitable conduction mechanism in our material.
Many researchers have proposed several models to explain the behavior of the exponent s such as the correlated barrier hopping CBH model, where the charge carriers hop between sites above the potential barrier between them, as introduced by Elliot,56 similar to the quantum mechanical tunneling mechanism (QMT) by Austin-Mott.57 Further, we find the overlapping large-polaron tunneling (OLPT) and non-overlapping small polaron tunneling (NSPT). The last three models (QMT, NSPT, and OLPT) are related to the carrier motion, which occurs through the tunnel effect between two localized states near the Fermi level.58
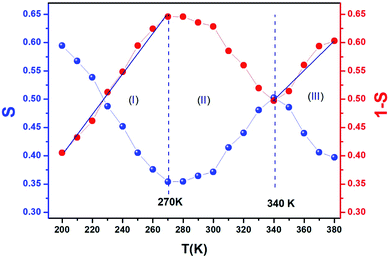
Fig. 9 exhibits that s decreases with increasing temperature in two regions, namely, 200–270 K and 340–380 K. Such a behavior is consistent with correlated barrier hopping,59 whereas the exponent s presents a tendency to increase with increasing temperature in the intermediate region [280–330 K]. Therefore, the NSPT model is an adequate mechanism to characterize the electrical conduction.
For the CBH model, the exponent s is given by60
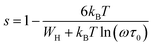 | (17) |
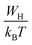 , s can be written as follows.60
, s can be written as follows.60
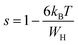 | (18) |
We can extract the value of the potential barrier WH from the slopes of the temperature evolution curve of (1 s). In the range of 200–270 K and 340–380 K, it is equal to 236 and 178 meV, respectively (Fig. 9).
Fig. 10 displays the temperature dependence of the AC conductivity at different frequencies. For each fixed frequency, ln(σac) decreases with rising of the reverse of temperature, showing three linear upright lines with different inclines (regions I, II, and III). The values of the activation energies extracted from the fit of data in the figure are summarized in Table 4. It is plain to see that Ea decreases with the increase in the frequencies at various temperature ranges. This can be associated with the increase in the applied field frequency, which enhances the electronic jump between localized states.61 To put forward, we can affirm that the mobility of charge carriers in the compound is supplied by the hopping conduction mechanism.61
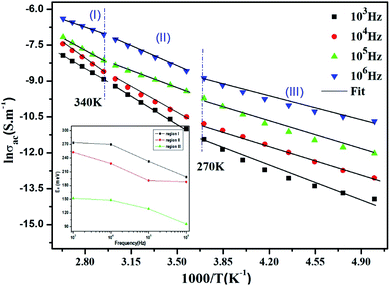 | ||
Fig. 10 Plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σac vs. 1000/T at different frequencies and the variation of the activation energy with the chosen frequencies inset. σac vs. 1000/T at different frequencies and the variation of the activation energy with the chosen frequencies inset. | ||
| Frequency (Hz) | 103 | 104 | 105 | 106 | |
|---|---|---|---|---|---|
| Ea (meV) | Region (I) | 274 | 270 | 233 | 199 |
| Region (II) | 253 | 228 | 191 | 188 | |
| Region (III) | 152 | 148 | 129 | 96 | |
The high annealing temperature (1100 °C) causes the vibration of metal ions present in the ferrite (Li, Mn, Fe). The lithium-oxygen bonds (Li–O) are affected by the fine fraction due to the relatively smaller weight of lithium.7 The breaking of some lithium and oxygen bonds enriches the release of electron and avails free lithium ions.62 Thus, Mn, Fe, O, and mobile Li ions participate in conduction but in varying proportions.
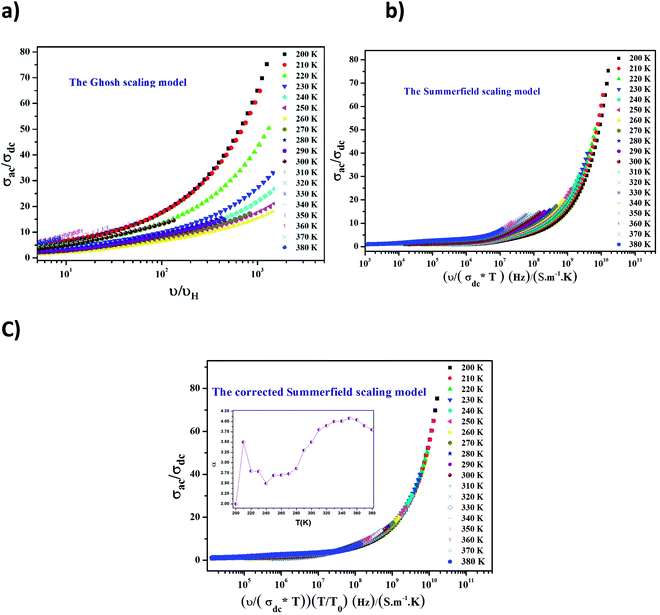
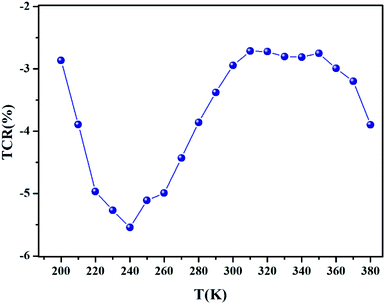
In order to acquire more valuable information on the conduction process and to explore the dynamics of load carriers in LiMn0.5Fe2O4, we were interested in the application of the Ghosh scaling model63 and the Summerfield scaling model.64 To obtain an appropriate scaling mechanism, the conductivity spectra at different temperatures exhibit a single universal master curve.60 Evidently, we presume that the conductivity follows the time–temperature superposition principle (TTSP).65 The plot of the conductivity isotherms is scaled according to the below general expression.65
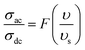 | (19) |
In the abovementioned expression, F denotes the temperature-independent function, σdc is the direct current conductivity, and υs indicates the scaling frequency. In the event of Ghosh scaling, υs is equal to υH, where υH is the hopping frequency obtained from the equation.66
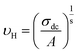 | (20) |
However, in the case of Summerfield scaling, υs = σdcT. In the present section, we study the scaling ac conductivity plot for LiMn0.5Fe2O4 as a function of the latter scaling parameters. Fig. 11a exhibits the Ghosh scaling model and Fig. 11b shows the Summerfield scaling model at the investigated temperature range from 200 to 380 K for our prepared compound. It is observed that the curve shapes did not collapse into a unique master curve. This implies that the conductivity isotherms do not obey the time-temperature superposition principle (TTSP). The failure of the Summerfield scaling approach is due to the dissimilar dynamics of the load carriers over the studied frequency and temperature ranges.67 Such behaviors are possibly related to an alteration in the load carrier density or change in the accessible pathways for the conduction transport number with temperature.67 The presence of various available pathways ensures the conduction transport.67
The Summerfield scaling deviations are corrected using the Random Barrier Model (RBM). Then, the master curves should be restructured and introduced by modifying the scaling frequency axis υs by 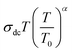 , as depicted in Fig. 11c, where T0 is the initial temperature and α reveals the potency of the interaction force of the coulombic interaction between the charge carriers. The figure shows that all the isotherm conductivity curves are superposed into a master curve. The corrected scaling process holds in the case of the synthesized sample with a positive exponent α.
, as depicted in Fig. 11c, where T0 is the initial temperature and α reveals the potency of the interaction force of the coulombic interaction between the charge carriers. The figure shows that all the isotherm conductivity curves are superposed into a master curve. The corrected scaling process holds in the case of the synthesized sample with a positive exponent α.
The value of α depends on the temperature (inset Fig. 11c), indicating the existence of coulombic interactions between the load carriers.68
It is well known that the temperature coefficient of resistivity (TCR) is important, especially for device performances for ameliorating the sensitivity of uncooled infrared bolometers.34 We checked if our sample can be useful for these device applications. The TCR was calculated by the following equation.69
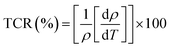 | (21) |
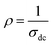 and T refer to the resistivity and temperature, respectively. We plotted the variation of TCR versus temperature in Fig. 12 in order to determine the TCR factor. As it is clear in Fig. 12, the value reaches about −5.5(%) K−1. Comparing the obtained value of TCR to other values collected from previous works, we can consider LiMn0.5Fe2O4 as a good candidate for detecting infrared radiations and infrared bolometric applications.70,71
and T refer to the resistivity and temperature, respectively. We plotted the variation of TCR versus temperature in Fig. 12 in order to determine the TCR factor. As it is clear in Fig. 12, the value reaches about −5.5(%) K−1. Comparing the obtained value of TCR to other values collected from previous works, we can consider LiMn0.5Fe2O4 as a good candidate for detecting infrared radiations and infrared bolometric applications.70,71
4. Conclusion
In view of renewed interest in multifunctional molecular systems, we examine the structural, morphology, and electrical properties of LiMn0.5Fe2O4 prepared via the solid state. The highly crystalline quality of the obtained particles is confirmed by the XRD measurements. The title compound crystallizes in the cubic phase of the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group, and no secondary phase is noted. Furthermore, EDX proves a homogeneous distribution of iron and manganese cations. A detailed analysis of the impedance data reveals the grain and the grain boundary contribution, where the conductivity measurement confirms the semiconducting nature of the sample and examines the charge carrier transport mechanisms. The semiconductor nature indicates that the studied material can be promising in various applications such as optoelectronics, photodetectors, and photovoltaics. Two conduction mechanisms characterize the electrical behavior, which are the correlated barrier hopping model (CBH) and the non-overlapping small polaron tunneling (NSPT). Also, the high value of the resistance coefficient TCR (−5.5 (%) K−1) makes the material a good candidate for detecting infrared radiations and infrared bolometric applications.
m space group, and no secondary phase is noted. Furthermore, EDX proves a homogeneous distribution of iron and manganese cations. A detailed analysis of the impedance data reveals the grain and the grain boundary contribution, where the conductivity measurement confirms the semiconducting nature of the sample and examines the charge carrier transport mechanisms. The semiconductor nature indicates that the studied material can be promising in various applications such as optoelectronics, photodetectors, and photovoltaics. Two conduction mechanisms characterize the electrical behavior, which are the correlated barrier hopping model (CBH) and the non-overlapping small polaron tunneling (NSPT). Also, the high value of the resistance coefficient TCR (−5.5 (%) K−1) makes the material a good candidate for detecting infrared radiations and infrared bolometric applications.
This finding reveals that LiMn0.5Fe2O4 was prepared and characterized as a multifunctional material, which opens up new possibilities for developing molecular functional materials, which is desirable to meet the rapidly increasing demand for technological applications. Nevertheless, the magnetic and dielectric properties as a function of temperature in LiMn0.5Fe2O4 are perspectives in order to complete this work.
Conflicts of interest
Authors declare that they have no conflict of interest or personal relationships that could have appeared to influence the work reported in this paper.References
- N. Amri, J. Massoudi, K. Nouri, M. Triki, E. Dhahri and L. Bessais, RSC Adv., 2021, 11, 13256 RSC.
- J. Massoudi, O. Messaoudi, S. Gharbi, T. Mnasri, E. Dhahri, K. Khirouni, E. Hlil, L. Alfhaid, L. Manai and A. Azhary, J. Phys. Chem. C, 2022, 126, 2857 CrossRef CAS.
- R. Lahouli, J. Massoudi, M. Smari, H. Rahmouni, K. Khirouni, E. Dhahri and L. Bessais, RSC Adv., 2019, 9, 19949 RSC.
- E. Morán, M. C. Blesa, M. E. Medina, J. D. Tornero, N. Menéndez and U. Amador, Inorg. Chem., 2002, 41, 5961 CrossRef PubMed.
- M. Junaid, M. A. Khan, Z. M. Hashmi, G. Nasar, N. A. Kattan and A. Laref, J. Mol. Struct., 2020, 1221, 128859 CrossRef CAS.
- N. Singh, A. Agarwal and S. Sanghi, Curr. Appl. Phys., 2011, 11, 783 CrossRef.
- D. Bouokkeze, J. Massoudi, W. Hzez, M. Smari, A. Bougoffa, K. Khirouni, E. Dhahri and L. Bessais, RSC Adv., 2019, 9, 40940 RSC.
- A. A. Yousif, M. E. Elzain, S. A. Mazen, H. H. Sutherland, M. H. Abdalla and S. F. Mansour, J. Condens. Matter Phys, 1994, 6, 5717 CrossRef CAS.
- D. Ravinder and P. Vijaya Bhasker Reddy, Mater. Lett., 2003, 57, 4344 CrossRef CAS.
- A. Manzoor, M. A. Khan, A. Shahzad, T. I. Al-Muhimeed, A. A. Al Obaid, H. Al balawi, A. M. Afzal, M. Kashif, S. Tahir and T. Munir, Ceram. Int., 2021, 4, 22662 CrossRef.
- J. Jing, L. Liangchao and X. Feng, J. Rare Earths, 2007, 25, 79 CrossRef.
- G. Aravind, M. Raghasudha, D. Ravinder, M. M. Raja, S. S. Meena, P. Bhatt and M. Hashim, Ceram. Int., 2016, 42, 2941 CrossRef CAS.
- M. Srivastava, S. K. Alla, S. S. Meena, N. Gupta, R. K. Mandal and N. K. Prasad, Ceram. Int., 2019, 45, 12028 CrossRef CAS.
- S. H. Chen, S. C. Chang and L. N. Lin, J. Magn. Magn. Mater., 2000, 209, 193 CrossRef CAS.
- S. T. Assar, H. F. Abosheiasha and M. K. El Nimr, J. Magn. Magn. Mater., 2014, 350, 12 CrossRef CAS.
- V. Verma, M. Abdullah dar, V. Pandey, A. Singh, S. Annapoorni and R. K. Kotnala, Mater. Chem. Phys., 2010, 122, 133 CrossRef CAS.
- S. C. Watawe, U. A. Bamne, S. P. Gonbare and R. B. Tangsali, Mater. Chem. Phys., 2007, 103, 323 CrossRef CAS.
- N. Kumar, R. K. Singh and H. K. Satyapal, J. Mater. Sci.: Mater. Electron., 2020, 31, 9231 CrossRef CAS.
- V. Verma, M. A. Dar, V. Pandey, A. Singh, S. Annapoorni and R. K. Kotnala, Mater. Chem. Phys., 2010, 122, 133 CrossRef CAS.
- Z. K. Heiba, M. M. S. Sanad and M. B. Mohamed, Solid State Ionics, 2019, 341, 115042 CrossRef CAS.
- N. Gupta, S. C. Kashyap and D. C. Dube, Phys. Status Solidi A, 2007, 204, 2441 CrossRef CAS.
- P. P. Hankare, R. P. Patil, U. B. Sankpal, S. D. Jadhav, P. D. Lokhande, K. M. Jadhav and R. Sasikala, J. Solid State Chem., 2009, 182, 3217 CrossRef CAS.
- T. N. Pham, T. Q. Huy and A. T. Le, RSC Adv., 2020, 10, 31622 RSC.
- S. Bellad and B. Chougule, Mater. Chem. Phys., 2000, 66, 58 CrossRef CAS.
- S. C. Watawe, U. A. Bamne, S. P. Gonbare and R. B. Tangsali, Mater. Chem. Phys., 2007, 103, 323 CrossRef CAS.
- J. Massoudi, D. Bouekkeze, A. Bougoffa, K. Khirouni, E. Dhahri and L. Bessais, Adv. Powder Technol., 2020, 31, 4714 CrossRef CAS.
- L. Li, X. Zhang, R. Chen, T. Zhao, J. Lu, F. Wu and K. Amine, J. Power Sources, 2014, 249, 28 CrossRef CAS.
- J. Massoudi, M. Smari, K. Khirouni, E. Dhahri and L. Bessais, J. Magn. Magn. Mater., 2021, 528, 167806 CrossRef CAS.
- G. R. Gajula, L. R. Buddiga, K. N. Chidambara Kumar, C. Arun Kumar and M. Dasari, J. Sci.: Adv. Mater. Devices, 2018, 3, 230 Search PubMed.
- R. N. Bhowmik and G. Vijayasri, Int. J. Appl. Phys., 2013, 114, 223701 CrossRef.
- A. Agajanian, IEEE Trans. Magn., 1970, 6, 90 CrossRef CAS.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65 CrossRef CAS.
- M. Kurian, S. Thankachan, D. S. Nair, E. K. Aswathy, A. Babu, A. Thomas and B. K. KT, J. Adv. Ceram., 2015, 4, 199 CrossRef CAS.
- A. Hadded, J. Massoudi, E. Dhahri, K. Khirouni and B. F. O. Costa, RSC Adv., 2020, 10, 1042542 RSC.
- M. Bouzayen, R. Dhahri, A. Benali, S. Chaabouni, K. Khirouni and B. F. O. Costa, Chem. Phys. Lett., 2020, 741, 137106 CrossRef CAS.
- D. Zákutná, J. Vlček, P. Fitl, K. Nemkovski, D. Honecker, D. Nižňanský and S. Disch, Phys. Rev. B, 2018, 98, 064407 CrossRef.
- N. Tawichai, K. Sutjarittangtham, T. Tunkasiri, K. Pengpat, G. Rujijanagul and J. Wang, Ceram. Int., 2013, 39, 145 CrossRef.
- H. Rahmouni, M. Smari, B. Cherif, E. Dhahri and K. Khirouni, Dalton Trans., 2015, 44, 10457 RSC.
- P. Córdoba-Torres, T. J. Mesquita, O. Devos, B. Tribollet, V. Roche and R. P. Nogueira, Electrochim. Acta, 2012, 72, 172 CrossRef.
- A. B. J. Kharrat, N. Moutia, K. Khirouni and W. Boujelben, Mater. Res. Bull., 2018, 105, 75 CrossRef.
- Kh. Ben Brahim, M. Ben gzaiel, A. Oueslati and M. Gargouri, RSC Adv., 2018, 8, 40676 RSC.
- M. Shah, M. Nadeem, M. Idrees, M. Atif and M. J. Akhtar, J. Magn. Magn. Mater., 2013, 332, 61 CrossRef CAS.
- F. S. H. Abu-Samaha and M. I. M. Ismail, Mater. Sci. Semicond. Process., 2014, 19, 50 CrossRef CAS.
- F. B. Abdallah, A. Ben ali, M. Triki, E. Dhahri, M. P. F. Graça and M. A. Valente, Superlattices Microstruct., 2018, 117, 260 CrossRef CAS.
- W. B. Soltan, S. Nasri, M. S. Lassoued and S. Ammar, J. Mater. Sci.: Mater. Electron., 2017, 28, 6356 Search PubMed.
- A. Rouahi, A. Kahouli, F. Challali, M. P. Besland, C. Vallée, B. Yangui, S. Salimy and A. Sylvestre, J. Phys. D: Appl. Phys., 2013, 46, 65308 CrossRef CAS.
- F. I. H. Rhouma, A. Dhahri, N. Farhat, J. Dhahri and K. Khirouni, EPJ Web Conf., 2012, 29, 23 CrossRef CAS.
- S. Chatterjee, P. K. Mahapatra, R. N. P. Choudhary and A. K. Thakur, Phys. Status Solidi A, 2004, 201, 588 CrossRef CAS.
- L, K. Kumari, K. Prasad and R. N. P. Choudhary, J. Alloys Compd., 2008, 453, 325 CrossRef.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341 CrossRef CAS.
- A. Bougoffa, J. Massoudi, M. Smari, E. Dhahri, K. Khirouni and L. Bessais, J. Mater. Sci.: Mater. Electron., 2019, 30, 21018 CrossRef CAS.
- C. Bharti and T. P. Sinha, Phys. Rev. B, 2011, 406, 1827 CrossRef CAS.
- A. Dutta, C. Bharti and T. P. Sinha, Phys. Rev. B, 2008, 403, 3389 CrossRef CAS.
- S. Şenkul, R. Taş, S. Sönmezoğlu and M. Can, Int. J. Polym. Anal. Charact., 2012, 17, 257 CrossRef.
- R. Hanen, A. Mleiki, H. Rahmouni, N. Guermazi, K. Khirouni and A. cheikhrouhou, J. Mater. Sci.: Mater. Electron., 2020, 31, 16830 CrossRef CAS.
- S. R. Elliott, Adv. Phys., 1987, 36, 135 CrossRef CAS.
- N. F. Mott, Philos. Mag. B, 1980, 42, 327 CAS.
- M. Ennefati, B. Louati, K. Guidara, M. Rasheed and R. Barillé, J. Mater. Sci.: Mater. Electron., 2018, 29, 171 CrossRef.
- M. Megdiche, C. Perrin-Pellegrino and M. Gargouri, J. Alloys Compd., 2014, 584, 209 CrossRef CAS.
- P. K. Singh, S. K. Sharma, S. K. Tripathi and D. K. Dwivedi, Results Phys., 2019, 12, 223 CrossRef.
- M. Okutan, E. Basaran, H. I. Bakan and F. Yakuphanoglu, Phys. Rev. B, 2005, 364, 300 CrossRef CAS.
- C. M. Julien and M. A. Camacho-Lopez, Mater. Sci. Eng., B, 2004, 108, 179 CrossRef.
- A. Ghosh and A. Pan, Phys. Rev. Lett., 2000, 84, 2188 CrossRef CAS PubMed.
- S. Summerfield, Philos. Mag. Part B, 1985, 52, 9 Search PubMed.
- Y. Moualhi, H. Rahmouni and K. Khirouni, Phys. B, 2021, 616, 413129 CrossRef CAS.
- S. Singh, P. A Jha, S. Varma and P. Singh, J. Alloys Compd., 2017, 704, 707 CrossRef CAS.
- T. Dabbebi, S. Hcini, B. Alzahrani, H. Rahmouni, E. Dhahri, H. Al Robei and M. L. Bouazizi, J. Mater. Sci.: Mater. Electron., 2021, 56, 1 Search PubMed.
- Y. Moualhi, R. M’nassri, M. M. Nofal, H. Rahmouni, A. Selmi, M. Gassoumi, N. Chniba-Boudjada, K. Khirouni and A. Cheikhrouhou, J. Mater. Sci.: Mater. Electron., 2020, 31, 21046 CrossRef CAS.
- H. Chouaya, M. Smari, I. Walha, E. Dhahri, M. P. F. Graça and M. A. Valente, J. Magn. Magn. Mater., 2018, 451, 344 CrossRef CAS.
- X. Liu, Y. Z. Yan, Q. M. Chen, H. Zhang, M. G. Cao, S. C. Zhang and P. X. Zhang, Appl. Surf. Sci., 2013, 283, 851 CrossRef CAS.
- J. Massoudi, M. Smari, K. Nouri, E. Dhahri, K. Khirouni, S. Bertaina and L. Bessais, RSC Adv., 2020, 10, 34556 RSC.
| This journal is © The Royal Society of Chemistry 2022 |