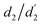Electronic structure, magnetoresistance and spin filtering in graphene|2 monolayer-CrI3₃|graphene van der Waals magnetic tunnel junctions

Abstract

In the pursuit of designing van der Waals magnetic tunneling junctions (vdW-MTJs) with two-dimensional (2D) intrinsic magnets, as well as to quantitatively reveal the microscopic nature governing the vertical tunneling pathways beyond the phenomenological descriptions on CrI₃-based vdW-MTJs, we investigate the structural configuration, electronic structure and spin-polarized quantum transport of graphene|2 monolayer(2ML)-CrI₃|graphene heterostructure with Ag(111) layers as the electrode, using density functional theory (DFT) and its combination of non-equilibrium Green’s function (DFT-NEGF) methods. The in-plane lattice of CrI₃ layers is found to be stretched when placed on the graphene (Gr) layer, and the layer-stacking does not show any site selectivity. The charge transfer between CrI₃ and Gr layers make the CrI₃ layer lightly electron-doped, and the Gr layer hole-doped. Excitingly, the inter-layer hybridization between graphene and CrI₃ layers render the CrI₃ layer metallic in the majority spin channel, giving rise to an insulator-to-half-metal transition. Due to the metallic/insulator characteristics of the spin-majority/minority channel of the 2ML-CrI₃ barrier in vdW-MTJs, Gr|2ML-CrI₃|Gr heterostructures exhibit an almost perfect spin filtering effect (SFE) near the zero bias in parallel magnetization, a giant tunneling magnetoresistance (TMR) ratio up to 2 × 10⁴%, and remarkable negative differential resistance (NDR). Our results not only give an explanation for the observed giant TMR in CrI₃-based MTJs but also show the direct implications of 2D magnets in vdW-heterostructures.

---

I. Introduction

Vertical stacking of distinctive two-dimensional (2D) magnetic van der Waals (vdW) layers enables the creation of diverse vdW heterostructures, which open a new avenue for the development of novel spintronic and magnonic devices such as magnetic tunneling junction (MTJ), spin-filtering MTJ, spin valve, spin tunnel field-effect transistors and spin logic circuit.^1–6 Among these spin-dependent devices, vdW-MTJ as a highly desirable building block for state-of-the-art spintronic devices, has attracted significant interest because the integration of distinctive 2D vdW-layers without chemical bonds can provide promising solutions to the adverse effects of processing technology, e.g., defect/disorder in the electrodes and barrier, interface diffusion and poor thermal stability that lead to low tunnel magnetoresistance (TMR).^1,2 Unlike conventional multilayer MTJ devices where two ferromagnetic layers are separated by a nonmagnetic insulator layer, ferromagnetic vdW-monolayers can serve simultaneously as the tunneling barrier and TMR-related free ferromagnetic layer in vdW-MTJs.^7–10 This functional combination enables spintronic devices to be ultracompact and to be modulated efficiently by electrical means. Their uniform thickness barrier layers should facilitate the all-area tunneling; the sharp atomic interface between spin filters can guarantee the achievement of large TMR. Consequently, a research field around vdW-MTJs has emerged and has been gaining strength over the past two years.^1–6

Inspired by the recent discovery of 2D-vdW ferromagnetic materials of CrI₃,¹¹ Cr₂Ge₂Te₆,¹² VSe₂ (ref. 13) and Fe₃GeTe₂ (FGT),^14,15 together with the fascinating observation of large TMR in CrI₃-based vdW-MTJs,^7–10 numerous vdW-MTJs have been artificially designed and successfully fabricated. These research articles focused on vdW-MTJs with the aforementioned 2D magnets, including Gr|CrI₃|Gr,^16–20 Gr|CrBr₃|Gr,²¹ CrI₃|h-BN|CrI₃,²² Cu|CrI₃|Cu,²³ Cu|CrI₃|h-BN|CrI₃|Cu,²⁴ VSe₂|CrI₃|VSe₂,²⁵ CrI₃|Li_0.5CrI₃|CrI₃,²⁶ FGT|h-BN|FGT,^27,28 FGT|InSe|FGT,²⁹ FGT|MoS₂|FGT,³⁰ MoSe₂|VSe₂|WSe₂|VSe₂|MoSe₂,³¹ VSe₂|MoS₂|VSe₂,³² CrTe₂|Gr|CrTe₂ or CrTe₂|h-BN|CrTe₂,³³ and so on. The graphite|nML-CrI₃|graphite vertical MTJ is the most attractive prototype, because its maximal TMR were experimentally reported to be 0.55 × 10³%,⁷ 1.9 × 10⁴%,⁸ 1 × 10⁴%,⁹ and 1 × 10⁶%,¹⁰ respectively. With the increase of anti-aligned spin filters in MTJs by increasing the CrI₃ barrier from bilayer, trilayer to tetralayer, Klein et al.⁷ have measured a remarkable increase in TMRs of 95, 300, 550%, respectively; while Song et al.⁸ have observed the highest values of 530, 3200, 19 000%, respectively. Generally, CrI₃-based vdW-MTJs exhibit thickness-dependent transports with desirable performance such as a large TMR; the transport mechanism can be qualitatively understood in terms of multi-layer spin-filtering effects.⁸ Nevertheless, as clearly pointed out by Klein et al.,⁷ the transport calculations on CrI₃-based vdW-MTJs should be done to elucidate their precise tunneling pathways by inspecting the electronic structures.

From the computational aspect on CrI₃-based MTJs, DFT-NEGF transport calculations have been performed on the heterojunctions within a few monolayers (MLs), i.e., 1ML-CrI₃ barrier sandwiched between graphite electrodes,¹⁹ 3ML-CrI₃ barrier sandwiched between graphite electrodes,²⁰ 4ML-CrI₃ barrier sandwiched between Cu(111) electrodes.²³ By taking hexagonal boron nitride (h-BN) as the tunneling barrier and CrI₃ layers as the ferromagnetic layer, 1ML-CrI₃|h-BN|nML-CrI₃ heterojunctions sandwiched between noble-metal (Cu, Ag, Au) electrodes have been investigated.^22,24 In the above MTJ models with metal as the electrode, metal layers were directly contacted with CrI₃ layers, which leads to an important feature in electronic structure that is different from the expected one. Furthermore, from the point of view of device fabrication, the contact between metal electrodes and heterostructure material is often realized by the molecular beam epitaxy (MBE) method. If CrI₃ magnetic layers are not protected by graphene, lattice mismatch and chemical bonding with metal atoms during the MBE fabrication would lead to diffusion/disorder/defect and conductivity mismatch at the metal|CrI₃ interfaces, which may result in low spin injection in a realistic scenario.^1,2 To solve the problem of MTJ fabrication, it is necessary to interpolate a Gr layer between metal lead and CrI₃ layers.²

The theoretical MTJ models with graphite as the electrode are different from the experimentally fabricated device structures where the top/bottom few-layer Gr flakes were in contact with the pre-patterned metal electrodes,^7–10,16,17 i.e., few-layer Gr were incorporated in CrI₃-based MTJ. In previously theoretical work, the lattice constants of Gr layers were strained or compressed to match with the CrI₃ layers,^19,20 which would significantly influence the TMR and conductance of MTJ via the variation of the band-gap of Gr layers.¹⁹ In this work, the lattice constants of CrI₃ layers were strained or compressed to match with Gr layers regarding the large Young’s modulus of Gr layer. So far, essentially no theoretical work has been done to investigate the electronic structures and transport properties of Gr|2ML-CrI₃|Gr devices with metal electrodes. It remains to be determined whether the interpolation of Gr layers causes new interesting physical phenomena to appear. This is expected because in CrI₃|2ML-Gr|CrI₃ vdW-type spin valves,³⁴ the band structures of the Gr layer were preserved in the minority spin channel while strong hybridizations at the CrI₃|Gr interface open up a Dirac gap in the majority spin channel.

In this paper, we combine DFT method and quantum ballistic DFT-NEGF transport calculations on Gr|2ML-CrI₃|Gr vdW-MTJ to study interface configurations and electronic structures as well as to reveal the microscopic nature governing the spin-dependent transport properties. This device model consists of face-centered cubic (fcc) Ag(111) electrodes, interpolation Gr monolayer, and magnetic 2ML-CrI₃ barrier layers. Our results reveal that Gr and CrI₃ layers can be stably bonded together through the weak vdW-interaction. The hybridizations between them make 2ML-CrI₃ layers exhibit a half-metallic feature and open a small Dirac-gap in the spin-majority channel for Gr layers. The perfect spin filter effects provided by 2ML-CrI₃ layers, in addition to graphene barrier layers, lead to Gr|2ML-CrI₃|Gr to show a giant TMR ratio reaching up to 2 × 10⁴%. We illustrate the mechanism of quantum transport from two aspects of precise tunneling pathways and electronic structures and give consistent interpretations.

II. Computational methods

The calculations for the structure relaxation, different interfaces, electronic structure and magnetism are performed within the framework of spin-polarized density functional theory (DFT) implemented in Vienna ab initio Simulation Package (VASP).^35–38 We adopt the exchange and correlation function with the Perdew–Burke–Ernzerhof (PBE) parameterization to describe the generalized gradient approximation (GGA).^39,40 The valence electrons of C (2s²2p²), Cr (3d⁵4s¹) and I (5s²5p⁵) atoms are explicitly treated by the plane wave method, and the interactions of valence electrons with ionic cores are described by projected augmented plane wave (PAW) pseudopotentials,^41,42 where the plane-wave cutoff energy is set to 400 eV. For structural optimization and electronic structure analyses, the gamma (G)-centered Monkhorst–Pack k-point grids of 6 × 6 × 1 and 12 × 12 × 1 are employed, respectively. We use the Grimme (DFT-D2) functional to include the vdW interaction.⁴³ For transition metal (TM) atoms, the electron correlation effect is important due to the certain localization of their d electrons.⁴⁴ Thus, the on-site Coulomb interaction U and exchange interaction J ^45,46 are set to be 3.2 eV and 0.7 eV, respectively, and the effective value U_eff = 3.2 − 0.7 = 2.5 eV as reported in the literature.⁴⁷ Spin–orbit coupling (SOC) interactions, known to be important to determine the magnetic anisotropy, are included in the calculation of magnetic moment and magnetic anisotropy energy (MAE). Lattice constants and atomic coordinates are fully relaxed with the criterion 10⁻⁶ eV for the self-consistent field (SCF) procedure, and the maximum residual force on each atom is less than 0.001 eV Å⁻¹.

The unit cell of the CrI₃ layer in the hexagonal 2D structure has the experimental lattice constant of a = b = 6.867 Å.⁴⁸ To make a compromised computational performance between efficiency and precision, the Gr|2ML-CrI₃|Gr heterostructure is built by depositing a (5 × 5) supercell of Gr layer (a = 12.295 Å) on both sides of a 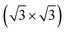supercell of CrI₃ bilayer (a = 11.977 Å), as illustrated in Fig. 1. To obtain the optimal vdW gap and gain the favorable interface between the Gr layer and CrI₃ layer, firstly, we individually relax the Gr|CrI₃ bilayer and 2ML-CrI₃ bilayer to extract their minimum-energy distances. Then, the sandwich-like Gr|2ML-CrI₃|Gr heterostructure is designed by fixing these optimal distances and favorable interfaces. There are 100 C atoms, 36 I atoms and 12 Cr atoms in the heterostructure. The lattice mismatch between graphene and CrI₃ layers is less than 3%, suggesting the possibility of good epitaxy. To avoid the imaging interaction, we add a vacuum region of 15 Å vacuum space layer on both sides of the graphene layers.

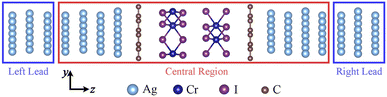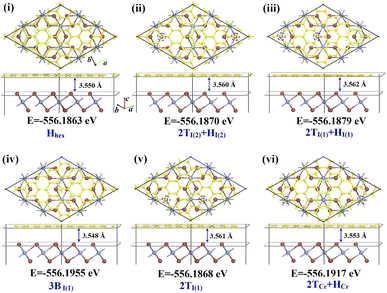
Fig. 1 Schematic sketch of the Gr|2ML-CrI₃(AB)|Gr MTJ. The red dashed rectangle represents the central scattering region. The z-axis is the transport direction.

To study the quantum transport properties of the Gr|2ML-CrI₃|Gr heterostructure, Ag(111) layers as the electrodes are added on both sides of the heterostructure to build a device model. Although (4 × 4) Ag(111) layers are better to directly add on both sides of the heterostructure (lattice mismatch about 6%), there are too many atoms in this structure and the following computational costs are too expensive. A compromising choice with respect to both accuracy and efficiency is to place (3 × 3) graphene on both sides of the (1 × 1) 2ML-CrI₃ layers, followed by adding 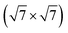Ag(111) layers, where the lattice constant was fixed to the value of the 2ML-CrI₃ layer. About 9% expansion of the lattice constant of Ag(111) layers is reasonable because the metallic characteristic of Ag(111) layers changes little with the variation of lattice constant. More importantly, by analyzing the band structures of the Gr|2ML-CrI₃|Gr heterostructure in the (5 × 5)Gr|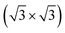2ML-CrI₃|(5 × 5)Gr structure and the realistic space density of states of the (3 × 3)Gr|(1 × 1)2ML-CrI₃|(3 × 3)Gr device structure (Fig. 9), we obtain good consistent transport results. This suggests that the electronic structures of the Gr|2ML-CrI₃|Gr heterostructure are maintained in the device structure. This two-probe MTJ device model can be divided into three regions: left semi-infinite Ag(111) electrode, central scattering region 4ML-Ag|Gr|2ML-CrI₃|Gr|4ML-Ag, and right semi-infinite Ag(111) electrode. The 4ML-Ag(111) layers of the scattering region are the buffer layers to shield the Hartree potential and identify the boundary conditions; two Ag electrodes can extend to z = ±∞ (transport direction). Our proposed structure is like a spin-filter MTJ, where magnetic 2ML-CrI₃ insulators act as a tunneling barrier for vertical transport.^7–10 The calculations of spin-dependent transport properties are performed using state-of-the-art techniques, i.e., the combination of DFT with the NEGF method implemented in Nanodcal package.^49–51 Here, we use a linear combination of atomic orbital basis sets with double-zeta plus polarization basis,^53,54 SCF criteria of 10⁻⁵ eV, cut-off energy of 100 Hartree, G-centered Monkhorst–Pack k-points of 6 × 6 × 1 and 40 × 40 × 1 for density matrix convergence and transmission coefficients, respectively. The spin resolved transmission T^s(E) across the tunnel junction at equilibrium is calculated via the formula of T^s(E) = Tr[Γ_LG^RΓ_RG^A], where s denotes the spin-up or spin-down conduction channels, Γ_L/Γ_R is the coupling matrix of the left/right electrode, G^R/G^A is the retarded/advanced Green’s functions of the center region. The spin-dependent current is calculated by the Landauer–Büttiker formula:⁵² 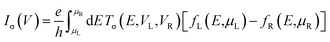where σ ≡ ↑, ↓ means the spin index; μ_L (μ_R) and f_L (f_R) are the electrochemical potential and the Fermi distribution function of the left (right) electrode, respectively; V_L/R are the bias voltages applied on the electrodes. The total current is defined by I = I_↑ + I_↓.

III. Results and discussion

A. Structures and stability

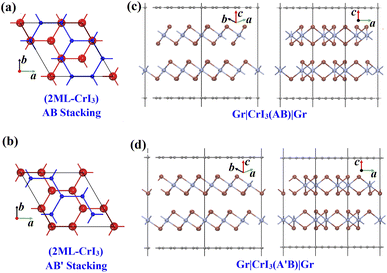
1. CrI₃ monolayer and bilayer. For the monolayer, bilayer and R3̄ bulk of CrI₃, we obtained their in-plane lattice constants of a = b = 6.915 Å, 6.913 Å and 6.909 Å, respectively. Compared with the experimental value of 6.867 Å,⁴⁸ we found that our PBE+U+D2 values are better than the previous PBE value of 7.00 Å,^55,56 PBE+U value of 7.08 Å,⁵⁷ suggesting the importance of the vdW-interaction. We have performed the HSE06 calculation as well as the PBE+U calculation without the D2-type vdW correction, and found that the CrI₃ monolayer has lattice constants of 6.899 Å and 7.071 Å, respectively. Note that the small change in lattice constants have a slight effect on the electronic structure of the CrI₃ layer.⁵⁸ It is well known that the CrI₃ layer has a semiconducting band gap and the single Gr layer is a semi-metal with a zero gap. Our calculated band structures and the partial densities of states of CrI₃ and Gr monolayers are shown in Fig. S1 and S2 (ESI).† The CrI₃ layer has a calculated band gap of 0.97 eV, which is consistent with the previous PBE+U value of 1.05 eV (ref. 57) but is smaller than the measured value of 1.2 eV (ref. 59) due to the intrinsic deficiency of the standard DFT approach.⁶⁰ Typically, the conduction band minimum (CBM) is far from the Fermi level but the valence band maximum (VBM) is close to the Fermi level, both of which are contributed by the majority spin states (Fig. S1 in ESI†). For the Gr layer, its semi-metal character is well preserved owing to the perfect Dirac cone at the Fermi level (Fig. S2 in ESI†).

For the CrI₃ bilayer in AB-stacking (Fig. 2a), the intra-layer Cr–Cr distance of 3.989 Å and the inter-layer spacing of 6.581 Å are consistent with the experimental values of 3.965 Å and 6.602 Å,⁴⁸ respectively, and also comparable to previously theoretical values of 3.98–4.06 Å and 6.68–6.78 Å,⁶¹ respectively. It is found that the inter-layer ferromagnetic ordering is 18 meV more stable than anti-ferromagnetic ordering, which is in line with the previously reported 13 meV.^61,62 Although a recent experiment has reported the antiferromagnetic order of CrI₃ bilayer by exfoliating it from the CrI₃ bulk,¹¹ it is still uncertain whether the experimentally exfoliated CrI₃ bilayer is AB-stacking or AB′-stacking because AB-stacking in a monoclinic phase structure favors the interlayer ferromagnetic order but AB′-stacking in rhombohedral phase structure favors the interlayer antiferromagnetic order.^61–63 The magnetic ground state strongly relies on the initial geometry of the bilayer. For the CrI₃ bilayer in AB′-stacking pattern (Fig. 2b), its lattice constant as well as the band structures are analogous to those of AB-stacking. The AB-stacking is 21 meV and 3 meV more stable than AB′-stacking in ferromagnetic and ferromagnetic orders, respectively. Thus, the CrI₃ bilayer in AB-stacking has been used to calculate the following structural stability, electronic structures and transport properties of the different heterostructures.

Fig. 2 Frame structures of AB (a) and AB′ (b) stacking CrI₃ bilayers are represented by hexagonally connected Cr atoms (red: bottom layer; blue: top layer). Stacking configurations of Gr|2ML-CrI₃(AB)|Gr (c) and Gr|2ML-CrI₃(AB′)|Gr (d) heterostructures.

2. Gr|CrI₃ heterostructure. We now discuss our results for the Gr layer on CrI₃ monolayer, because it permits us to rationalize the results of the Gr|CrI₃ interface-based heterostructure. There are many stacking configurations depending on the lattice symmetries of the individual layer. In Fig. 3, we show six representative interface configurations (i–vi). 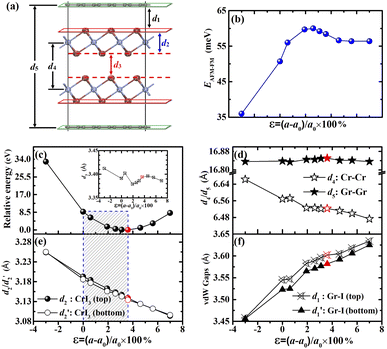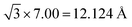After the atomic relaxations at the fixed in-plane lattice , we found that the vdW-gap (distance between Gr and CrI₃ layers) are in a very narrow range of 3.548–3.562 Å for various stacking, and the energy differences between the lowest and highest are less than 0.2 meV per C atom. The equilibrium vdW-gaps using our GGA+U+D2 method are generally in agreement with previous values of 3.53 Å using the GGA+D2 method and 3.57 Å using the GGA+optB86b method.⁵⁸

Fig. 3 Six representative interfaces between Gr and CrI₃ layers in Gr|CrI₃ heterostructures, where yellow, brown and blue balls denote the C, I and Cr atoms, respectively. Total energy and representative indexes are below each configuration. (i) H_hex: a hexagonal C-ring in CrI₃ hollow sites; (ii) 2T_I(2) + H_I(2): two C atoms and one hexagonal C-ring on top of I atoms of the bottom I(2) layer; (iii) 2T_I(1) + H_I(1): similar to (ii) but on top I atoms of top I(1) layer; (iv) 3B_I(1): three C atoms bridged with its neighboring top I(1) atoms; (v) 2T_I(1): two C atoms on top I(1) atoms; (vi) 2T_Cr + H_Cr: similar to (ii) but on Cr atoms.

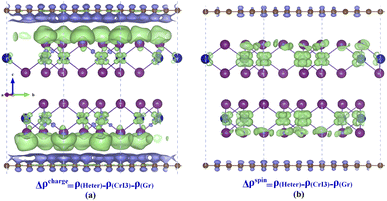
By calculating the interaction energy E_inter, between Gr and CrI₃ layers, via E_inter = (E_CrI3 + E_Gr − E_Heter)/n_C, we obtained E_inter = 38.415 meV for the 3B_I(1) interface configuration, which is comparable to the values found in other vdW systems. Here, total energies E are for the isolated CrI₃ monolayer, Gr monolayer and Gr|CrI₃ heterostructure with the same in-plane lattice of 7.00 Å, respectively, and n_C is the number of C atoms. A small E_inter demonstrates the weak vdW interaction between the Gr layer and CrI₃ layer. Due to small fluctuating magnitudes in inter-layer interaction (2 meV/38.415 meV = 5%) and the vdW-gap (0.014 Å/3.562 Å = 0.4%), we can reasonably deduce that the stability of the Gr|CrI₃ heterostructure is almost independent of stacking types, and the Gr layer can be placed on the CrI₃ layer without any site selectivity.⁵⁸ Therefore, it is advantageous in the process of stacking Gr|2ML-CrI₃|Gr heterostructure with disregard for possible CrI₃|Gr interfaces.

3. Gr|2ML-CrI₃|Gr sandwich-like heterostructure. The supercell of the Gr|2ML-CrI₃|Gr heterostructure was stacked by the AB-type or AB′-type 2ML-CrI₃ bilayer sandwiched between two Gr monolayers with two interfaces (Fig. 3): H_hex (i) and 2T_Cr + H_Cr (vi) interfaces for Gr|2ML-CrI₃(AB)|Gr stacking; 3B_I(1) (iv) and 2T_Cr + H_Cr (vi) interfaces for Gr|2ML-CrI₃(AB′)|Gr stacking. The inter-layer ferromagnetic (FM) and anti-ferromagnetic (AFM) properties have been examined for each stacking type of 2ML-CrI₃ bilayer. To derive the equivalent in-plane lattice and interlayer distance, firstly, we made an equibiaxial compression and expansion of in-plane lattice of Gr|2ML-CrI₃(AB)|Gr heterostructure, and then performed the atomic relaxations by fixing the lattice constants in each strain step. By seeking the lowest energy structure under a series of calculations, we can get the most stable structure within the optimal lattice constant and atomic positions. 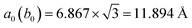The biaxial strain is defined as ε = (a − a₀)/a₀ × 100% = (b − b₀)/b₀ × 100%, where corresponds to the experimental lattice constant of the CrI₃ unit cell.⁴⁸ The positive and negative ε represent the tensile and compressive strain on CrI₃ layers, respectively. From Fig. 4b, we found that FM ordering is always more favorable than AFM ordering for AB stacking; from Fig. 4c, the heterostructure possesses the lowest total energy when the lattice constant is nearly equal to the value of the isolated Gr layer (2.459 × 5 = 12.295 Å; C–C bond-length 1.420 Å). This corresponds to ε = 3.37% lattice stretching of the CrI₃ monolayer and suggests that the CrI₃ layer will suffer larger lattice deformation than the Gr layer. In fact, the Young’s modulus of the CrI₃ monolayer (28 N m⁻²) is significantly lower than that of the Gr monolayer (340 N m⁻²).^64,65 Therefore, the lattice constants and thus the electronic structure of the Gr layer will essentially not be affected in a heterostructure, and the lattice mismatch only provides changing lattice constants and the tuning of magnetic states of CrI₃ layers. Although available experiments have not explicitly indicated the lattice matching information when combined together,^7–10 our findings question the rationality of previous work where MTJ structures were designed by straining or compressing the lattice constants of Gr layers to match with the CrI₃ layers.^19,20

Fig. 4 (a) Schematic structure of Gr|2ML-CrI₂(AB)|Gr heterostructure. Inter-layer distances are represented by different d_n; (b) energy differences between ferromagnetic and anti-ferromagnetic ordering; (c) relative energy with respect to equilibrium structure, 2ML-CrI₃ inter-layer distance d₃ (inset); (d) inter-layer distance d₅ between top and bottom-Gr layers (d₄ between top and bottom-Cr layers); (e) thickness of top/bottom CrI₃ layer ; (f) vdW-gap between Gr and its nearest I layers as a function of biaxial strain ε = (a − a₀)/a₀ × 100% for AB stacking of the CrI₃ bilayer. The ε = 0 corresponds to experimental lattice constant of the pristine CrI₃ layer (a₀ = 6.867 Å); the lowest energy structure (red symbols) correspond to the stretched lattice constant of the CrI₃ layer (a = 7.099 Å; ε = 3.34%) and is equal to the lattice constant of the pristine Gr layer (a₀ = 2.459 Å).

In Fig. 4c–f, we plotted the various interlayer distances (vdW-gaps) as a function of lattice variations for heterostructure with AB stacking consequence in the FM state. With the increase of the in-plane lattice, the interlayer distance between two CrI₃ monolayers (d₃: inset in Fig. 4c) and the thickness of heterostructure (d₅: Fig. 4d) remain nearly constant, while the thicknesses of the CrI₃ monolayer (d₂ and 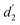; Fig. 4e) decrease monotonously, resulting in a gradual increase of Gr–CrI₃ distance (vdW-gaps d₁ and 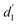; Fig. 4f). These variations demonstrate that the vdW interaction is stronger between CrI₃ bilayers than between Gr and CrI₃ layers. The resultant layer spacing d₄ = 6.52 Å (between CrI₃ layers) as well as the layer separation d₁ = 3.58 Å (between adjacent CrI₃ and Gr layers) are in good agreement with the corresponding values of other studies.^20,23,48,58

B. Electronic structure of Gr|2ML-CrI₃(AB)|Gr

1. Charge (spin) density difference. To check the charge (spin) redistribution between layers in the space of heterostructure, we performed the charge (spin) density difference via Δρ = ρ_Hetero − ρ_CrI3 − ρ_Gr, where ρ_Hetero, ρ_CrI3 and ρ_Gr are charge (spin) densities of the heterostructure, isolated 2ML-CrI₃ and isolated Gr layers, respectively. The densities ρ of the isolated CrI₃ and Gr layers are computed in the same atomic position of the heterostructure under the self-consistent static calculation. In Fig. 5, positive values (green color) represent an accumulation of the charge or spin, while negative values (blue color) depict a depletion of charge or spin as compared to the isolated ones. Five things can be clearly observed and should be emphasized: (i) charge redistribution does occur at the CrI₃|Gr interface with the transferred charges accumulating mostly around the I atoms of the CrI₃ layer positioned close to the Gr layer, indicative of the generation of dipole moment; (ii) all the charges transferred from Gr layers completely occupy the spin-up states of the CrI₃ layer (as visualized in Fig. S3(a) in the ESI†), which will change the band structures of CrI₃ layers and thus impact the transmission probabilities and related quantities; (iii) charge distribution around Cr atoms and the I atoms away from the Gr layer show small changes; (iv) magnetic proximity effect of CrI₃ layers induces a small negative magnetic moment on Gr layers, and these local magnetic moments arise mainly from the out-of-plane p_z orbitals; (v) local magnetic moments of Cr atoms are enhanced due to the charge transfer from spin-down states to spin-up states (Fig. S3(b) in the ESI†). In previous work, when two Cu electrodes were directly stacked on both sides of insulator 2ML-CrI₃ layers, sizable charge transfers from Cu to CrI₃ layers make CrI₃ half-metallic and result in large TMR values.²³ Here, in our studied Gr|2ML-CrI₃(AB)|Gr heterostructure, a graphene layer between metal allows Ag and CrI₃ bilayers not only to play a positive role in avoiding the direct bonding interactions (diffusion/disorder/defect) of CrI₃ magnetic layers with Ag atoms of the electrode for protecting the structural integrity in future experimental preparations, but also provide the access to make CrI₃ magnetic layers be half-metallic by transferring its charges to CrI₃ magnetic layers.

Fig. 5 (a) Charge density difference and (b) spin density difference (isosurface value: 0.0015 e Å⁻³) of Gr|2ML-CrI₃|Gr from side-view. Green and blue colors denote the accumulation and depletion of density area, respectively.

2. FM alignment. For the Gr|2ML-CrI₃(AB)|Gr heterostructure with FM alignment between 2ML-CrI₃ layers, we found that the band structures are basically overlapped by two decoupled Gr monolayers as well as two decoupled CrI₃ layers (Fig. S1 and S2†). Upon close viewing of Fig. 6a, the bands in the energy range 0–0.5 eV are composed of the Gr Dirac-cone states and Cr(3d)-e_g and I-p_z states (Fig. 6b), while the bands in the energy range −1.15 to 0 eV are exclusively contributed by Gr states. Compared with the band structures of the pristine CrI₃ and Gr layers, the spin-majority band of CrI₃ layers was dragged down by the dipolar field while the linear Gr bands were elevated by 0.25 eV, which is consistent with the findings on CrI₃|Gr bilayer.^7,47 It makes 2ML-CrI₃ layers with a metallic feature (CrI₃ majority band is very close to or across the Gr Fermi energy).

Fig. 6 (a) Band structure of Gr|2ML-CrI₃(AB)|Gr with FM alignment between 2ML-CrI₃ layers. Blue and red lines represent spin-up and spin-down channels, respectively; (b) partial density of states (PDOS) resolved to elemental atoms; (c and d) projected band structures of C atoms for spin-up and spin-down channels (green balls). The contribution weight of the p-orbital to each band is represented by the depth of green color (ball color).

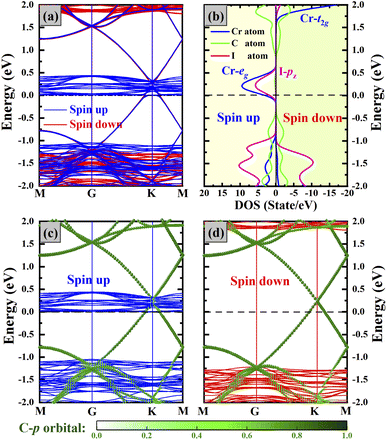
From Fig. 6c for the spin-majority band (blue lines), Cr-e_g and I-p_z states of the CrI₃ bilayer are strongly hybridized with the Gr-Dirac-cones, which opens up 0.2 eV Dirac-gap in a spurious manner (small but nonzero contribution weight). Although there is the Dirac-gap of two side Gr layers, the dispersions of some occupied Dirac states would contribute to the conductance to a degree, and this low barrier can be easily crossed when a small bias voltage is applied. Consequently, the crossing of band structure of 2ML-CrI₃ layers around the E_f in the spin-majority band indicates that the spin-up electrons can transfer from the top Gr layer to 2ML-CrI₃ layer and then through the bottom Gr layer.

In the spin-minority band (Fig. 6d), the Gr-Dirac-cones are basically unaffected and maintain the intactness, and the band structures of 2ML-CrI₃ layers present the wide-gap semiconducting feature (3.0 eV; red lines). Note that the E_f level does not lie at the Dirac-point of Gr due to the dipolar field between Gr and CrI₃ layers. Although the spin-down electrons could pass through the top Gr layer owing to its metallic feature, they will be blocked by the high barrier of the semiconducting 2ML-CrI₃ layers. Therefore, the metallic/semiconducting characteristics of the spin-majority/minority channel of CrI₃ bilayer in FM alignment lead to the result that the spin-up electrons can move vertically through the different layers but the spin-down electrons cannot. On the whole, the hybridization at the CrI₃|Gr interface lowers the conduction band minimum (CBM) of the CrI₃ layers in the spin majority channel while the spin minority band structures remain nearly unchanged, which determines the height of spin-dependent tunneling barriers and controls the transport properties.

3. AFM alignment. For the Gr|2ML-CrI₃(AB)|Gr heterostructure with AFM alignment between 2ML-CrI₃ layers, the overall band-shapes of 2ML-CrI₃ layers are similar to those under FM alignment (Fig. 7a); the Dirac gap-openings appear in the spin-majority channel of the top Gr layer (Fig. 7c) and in the spin-minority channel of the bottom Gr layer (Fig. 7f), respectively. However, the spin-majority channels of the top/bottom CrI₃ layers show the metallic/semiconducting features, respectively; on the contrary, the spin-minority channels of top/bottom CrI₃ layers show the semiconducting/metallic features, respectively. When the spin-up electrons pass through the top Gr layer and Cr₃ layer, they would successively encounter the barrier of the bottom CrI₃ layer due to its wide band-gap in spin-up channel, suggesting that the spin-up electrons will be filtered by the lower-half of the heterostructure; on the contrary, the spin-down electrons can be initially blocked by the top CrI₃ layer even though the transmission channel is open in the bottom Cr₃ layer, suggesting that the spin-down electrons will be filtered by the upper-half of the heterostructure. By examining the band structures of the Gr|2ML-CrI₃(AB′)|Gr heterostructure, we derived very similar results (Fig. S4 and S5 in the ESI†). Therefore, the spin-up and spin-down electrons are filtered simultaneously by the heterostructure for 2ML-CrI₃ in AFM alignment, independent of stacking type of the 2ML-CrI₃ layers. We should emphasize that in Fig. 6 and 7, the t_2g band lies about 1 eV above the e_g band, which is consistent with the findings given by Klein et al.⁷ However, Heath et al. found that the excited minority-spin t_2g band lies just above the excited majority-spin e_g band, different from our results, which is attributed to the lower extent of the dispersion force induced by the large 9% compression strain of graphene layers.²⁰

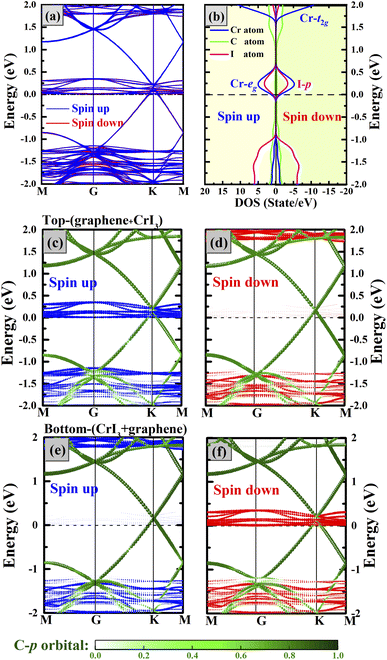Fig. 7 (a and b) are the same as in Fig. 6 but for AFM alignment. (c) and (d) are the spin-majority and spin-minority channels for the upper-half of the heterostructure; (e and f) for the lower-half of the heterostructure. The contribution to each band is divided from the CrI₃ layer (blue/red balls) and Gr layer (green balls), respectively.

C. Transport properties of Ag|Gr|2ML-CrI₃|Gr|Ag

1. Transmission coefficient and TMR at equilibrium. We begin with the transport behavior without the bias voltage to confirm the ground-state properties. Based on the SCF calculation of the center scattering region (Ag@Gr|2ML-CrI₃|Gr@Ag) and two Ag(111) electrodes as illustrated in Fig. 1, we calculated the spin resolved transmission T^s(E). In Fig. 8, we plotted the transmission coefficients as a function of energy. For 2ML-CrI₃ layers in FM alignment, the spin-up values are large over a wide energy window E > −0.03 eV, e.g. there is a sharp peak around E_f; the spin-down values are almost zero in the whole energy window. At the E_f, T^↑(E_f) of the spin-up channel is about 3 orders of magnitude higher than that of the spin-down channel. 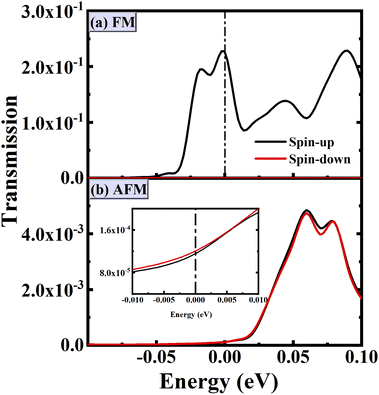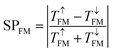Consequently, the spin polarization of tunneling conductance, , is virtually 100%, verifying the perfect SFE in FM state. This evidence is explained by the band structure analyses shown in Fig. 6. For 2ML-CrI₃ layers in AFM alignment, the curves of the spin-up and spin-down transmission coefficients nearly coincide with each other because of the mirror-symmetry of band structure shown in Fig. 7. Although there is a large peak at E = 0.06 eV, it is 2 orders of magnitude smaller than that of FM alignment, not to mention the fact that it’s energy position is far away from the E_f. By amplifying the curves around the E_f, we found a slight difference between the spin-up and spin-down channels, thus resulting in very small SP_AFM and bad spin-filtering effects.

Fig. 8 The transmission coefficients versus electron energy at zero bias for the MTJ in FM (a) and AFM (b) alignment. The inset shows the zoomed-in curve around E = 0 (inset chart). Vertical black-dashed line shows the Fermi level.

TMR is a critical parameter to characterize the performance of the MTJ device. According to the formula 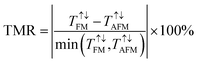, TMR can be calculated by total transmission coefficients at the E_f level, where 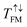and 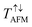refer to total coefficients in FM and AFM alignments, respectively, and 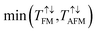is the smaller one of the two values. Our calculate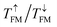d and 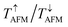are 2.26 × 10⁻¹/9.28 × 10⁻⁷ and 1.16 × 10⁻⁴/1.20 × 10⁻⁴, respectively, giving a large TMR of 1 × 10³%. The remarkably large TMR value originates from the significant transmission coefficient of the spin-majority channel in FM alignment but small transmission coefficients of both spin-majority and spin-minority channels in AFM alignment.

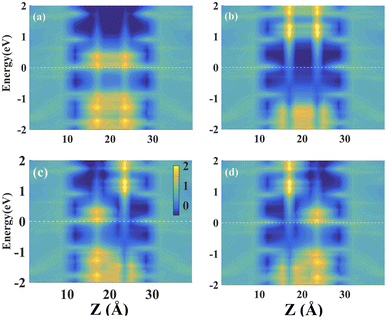
In Fig. 9, we illustrate the realistic PDOS distributions along the transport direction (z) to underline the tunneling transport mechanism. Along the transmission route, the region from 10 Å to 30 Å represents the central scattering region (red box; Fig. 1). For FM alignment, the spin-up electrons suffer from a lower-height barrier and they can easily cross it, and thus the spin-majority transmission channel is opened (Fig. 9a, yellow sparkles join together to form long strings around the E_f); the spin-down electrons encounter a remarkably higher-height barrier due to a wide band gap of 2ML-CrI₃ layers, and thus the spin-minority transmission channel is blocked (Fig. 9b, no yellow sparkles around the E_f). For AFM alignment, the spin-up electrons go across the lower-potential barrier of the left scattering region (Fig. 9c: 10 Å to 20 Å; yellow sparkles around the E_f), and then they meet another potential barrier provided by the bottom CrI₃ layer (20 Å to 30 Å; no yellow sparkle around the E_f); it is reversed for the spin-down electrons (Fig. 9d). This observed transport evidence is consistent with the band structure analyses from Fig. 6 and 7, where the spin-dependent band gaps of CrI₃ layers are responsible for the spin-dependent barrier height.

Fig. 9 Project density of states (PDOS) along the transport direction (z direction) at equilibrium state in realistic space. Spin-majority (a) and spin-minority (b) states in FM alignment; spin-up (c) and spin-down (d) states in AFM alignment. All the sub-figures have the same color coding values, which are given by the vertical bar. The white-dashed lines at energy = 0 eV denote the E_f.

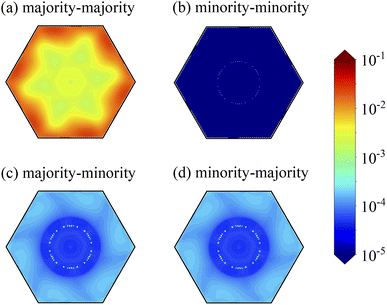
The spin dependent k_‖-resolved transmission coefficients in 2D Brillouin zone (BZ) are calculated at E_f and their contour plots are displayed in Fig. 10, where k_x and k_y are perpendicular to the transport direction z and the k-grid number is set to be 100 × 100. For FM alignment in Fig. 10a and b, the density of hot spots in the spin majority–majority channel are much larger than those in the spin minority–minority channel, indicating that spin-up electrons have higher transport ability than spin-down electrons, in agreement with the transmission curves shown in Fig. 8a. For example, the topmost hot spot presents a large transmission coefficient of 0.24 at the edge of the BZ in FM alignment. In Fig. 10c and d, although there are little hot spots in both contour plots, their strength is 2–3 orders of magnitude weaker than that of FM alignment, meaning that the tunneling current in AFM alignment would be much smaller than that in FM alignment.

Fig. 10 The k_‖-resolved transmission coefficient at the E_f in the 2D BZ of the MTJ. k_x and k_y are perpendicular to the transport direction. (a) and (b) are for the MTJ in FM alignment; (c) and (d) are for MTJ in AFM alignment.

2. I–V curves and TMR at nonequilibrium. Now, we turn our attention to the spin transport properties at non-equilibrium states. The spin polarized currents of the Gr|2ML-CrI₃|Gr heterostructure are calculated and presented as a function of bias voltage (0–0.1 V) in Fig. 11a and b. The black and blue balls represent the spin-up current (I^↑) and the spin-down current (I^↓), respectively. In the FM curve (Fig. 11a), the spin-up current elevates with a bias voltage of up to 0.07 V and then drops to a smaller value at a voltage 0.08 V, exhibiting the negative differential resistance (NDR) effect; the spin-down current is completely filtered and maintains zero value in the whole voltage range. In the AFM curve (Fig. 11b), both of the spin-up and spin-down currents show a similar increasing trend with the increase of bias voltage, however, they are two orders of magnitude smaller than those for FM alignment. Thus, the Gr|2ML-CrI₃|Gr heterostructure possesses a perfect SFE in FM alignment and exhibits 100% spin-up tunneling current; but it will not give a good SFE in AFM alignment because of small and comparable spin currents.

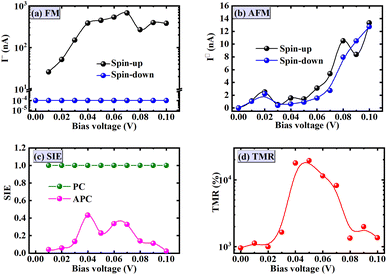Fig. 11 I–V curves in FM alignment (a) and AFM alignment (b); SIE (c) and TMR (d) versus the bias voltage. The solid line is a guide to the trend for the eye.

The spin injection efficiency (SIE) can reveal the degree of spin polarization in transport current, and it can be expressed as: 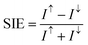. We displayed the SIE of the FM and AFM alignments in Fig. 11c. The heterostructure maintains 100% SIE in FM alignment, but it shows the largest value of about 40% at bias voltage 0.04–0.07 V in AFM alignment. A large SIE in FM alignment is related to a much larger spin-up current than spin-down current, as shown in Fig. 11a. Using the total current of I^↑↓ = I^↑ + I^↓ in FM and AFM alignments, we calculated TMR according to 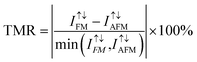, and showed them versus the bias voltage in Fig. 11d. It is less than 1 × 10³% for V < 0.03 V and dramatically increases to 2 × 10⁴% at 0.05 V, followed by a decrease down to 1 × 10³% again. Compared with Cu|2ML-CrI₃|Cu MTJ where 2ML-CrI₃ layers synchronously act as the barrier layer and TMR was reported to be 1500%,²³ the two Gr layers in our designed MTJ can be an additional barrier layer and they also play the spin-filtering roles. As analyzed in Fig. 6 and 7, the spin-up states are blocked to a certain degree but spin-down can easily cross two graphene layers in FM alignment, while the spin-up/spin-down states are blocked/cross the top-graphene but suffer the opposite effect when they meet the bottom-graphene. This may be the reason that our calculated TMR values are larger than those of Cu|2ML-CrI₃|Cu MTJ. The variational trend can be understood with the following reasons: (i) at low bias voltage 0–0.03 V, 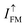and thus 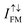are 2 orders larger than 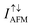due to significant blocked roles of AFM 2ML-CrI₃ layers on the spin-up/down electrons; (ii) as bias voltage increases from 0.03 V to 0.07 V, 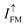increases quickly but 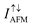increases slowly, due to the small Dirac-gap (0.2 eV) of the spin-majority channel in FM alignment providing a very low barrier, but large spin-up/down band gaps (3.0 eV) of AFM 2ML-CrI₃ layers provide a higher barrier; (iii) further increasing bias voltage (larger than 0.07 V) will assist the spin-down electrons to pass through the barrier of FM 2ML-CrI₃ layers.

IV. Conclusions

In summary, we have constructed a vdW-heterostructure with 2ML-CrI₃ layers sandwiched between two Gr monolayers, and then used Ag(111) layers as the electrodes in building a vdW-MTJ model to explore the spin transport properties. By employing the DFT and DFT-NEGF methods, structural stability, electronic structures, tunneling conductance, k_‖-resolved transmission coefficient, SIE and TMR were investigated. Due to the lattice mismatch between CrI₃ and Gr layers as well as the remarkably large Young’s modulus of Gr layer, CrI₃ layers in the Gr|2ML-CrI₃|Gr heterostructure get stretched. Strong hybridizations of Cr(3d)-e_g and I-p_z states with Gr-Dirac-cone state allow 2ML-CrI₃ layers to show metallic features in the spin-majority channel, for which the Fermi level is located close to the bottom of the upper Hubbard band of the e_g manifold; however, the insulator characteristic in the spin-minority channel of CrI₃ layers is almost unchanged. This renders the 2ML-CrI₃ layers a spin filter for electron tunneling, and consequently, Gr|2ML-CrI₃|Gr MTJs shows a perfect spin filter effect and a giant TMR ratio reaching up to 20 000%. The physical mechanisms behind the phenomenon are given by analyzing the spin-polarized band structure and k_‖-resolved transmission spectra, i.e., large differences of tunneling conductance between FM and AFM alignments are driven by the distinctive electronic structure of two spin transmission channels in 2ML-CrI₃ (unobstructed transmission of spin-up channel for a parallel-aligned configuration vs. suppressed transmission of both spin-channels for an antiparallel-aligned configuration). Based on our calculated results, the CrI₃-device designed in this study is expected to work in a low field and provide important theoretical guidance for further experimental studies of 2D CrI₃-based vdW MTJs, which may gain valuable applications in spintronics.

Author contributions

This manuscript was written through contributions from all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

All authors declare that they have no conflicts of interest.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (11874306, 12174320), and the Natural Science Foundation of Chongqing (CSTC2021jcyj-msxm1946, cstc2022ycjh-bgzxm0127). We gratefully acknowledge HZWTECH for providing computational facilities. Hongkuan Yuan thanks Kui Gong, Yibin Hu and Yin Wang (all from HZWTECH) for help and discussions regarding this study.

References

1. C. Gong and X. Zhang, Two-dimensional magnetic crystals and emergent heterostructure devices, Science, 2019, 363, eaav4450.
2. L. Zhang, J. Zhou, H. Li, L. Shen and Y. P. Feng, Recent progress and challenges in magnetic tunnel junctions with 2D materials for spintronic applications, Appl. Phys. Rev., 2021, 8, 021308.
3. D. L. Cortie, G. L. Causer, K. C. Rule, H. Fritzsche, W. Kreuzpaintner and F. Klose, Two-dimensional magnets forgotten history and recent progress towards spintronic applications, Adv. Funct. Mater., 2020, 30, 1901414.
4. S. J. Liang, B. Cheng, X. Cui and F. Miao, Van der Waals heterostructures for high-performance device applications challenges and opportunities, Adv. Mater., 2020, 32, 1903800.
5. J. Chu, Y. Wang, X. Wang, K. Hu, G. Rao, C. Gong, C. Wu, H. Hong, X. Wang, K. Liu, C. Gao and J. Xiong, 2D polarized materials: Ferromagnetic, ferrovalley, ferroelectric materials, and related heterostructures, Adv. Mater., 2021, 33, 2004469.
6. S. Yang, T. Zhang and C. Jiang, Van der Waals magnets material family, detection and modulation of magnetism, and perspective in spintronics, Adv. Sci., 2021, 8, 2002488.
7. D. R. Klein, D. MacNeill, J. L. Lado, D. Soriano, E. NavarroMoratalla, K. Watanabe, T. Taniguchi, S. Manni, P. Canfield, J. Fernandez-Rossier and P. Jarillo-Herrero, Probing magnetism in 2D van der Waals crystalline insulators via electron tunneling, Science, 2018, 360, 1218–1222.
8. T. Song, X. Cai, M. W. Y. Tu, X. Zhang, B. Huang, N. P. Wilson, K. L. Seyler, L. Zhu, T. Taniguchi, K. Watanabe, M. A. Mcguire, D. H. Cobden, D. Xiao, W. Yao and X. Xu, Giant tunneling magnetoresistance in spin-filter van der Waals heterostructures, Science, 2018, 360, 1214–1218.
9. Z. Wang, I. Gutiérrez-Lezama, N. Ubrig, M. Kroner, M. Gibertini, T. Taniguchi, K. Watanabe, A. Imamoğlu, E. Giannini and A. F. Morpurgo, Very large tunneling magnetoresistance in layered magnetic semiconductor CrI₃, Nat. Commun., 2018, 9, 2516.
10. H. H. Kim, B. Yang, T. Patel, F. Sfigakis, C. Li, S. Tian, H. Lei and A. W. Tsen, One million percent tunnel magnetoresistance in a magnetic van der Waals heterostructure, Nano Lett., 2018, 18, 4885–4890.
11. B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden and W. Yao, Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit CrI₃, Nature, 2017, 546, 270–273.
12. C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang and Z. Q. Qiu, Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals, Nature, 2017, 546, 265–269.
13. M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, M. H. Phan and M. Batzill, Strong room-temperature ferromagnetism in VSe₂ monolayers on van der Waals substrates, Nat. Nanotechnol., 2018, 13, 289.
14. Z. Fei, B. Huang, P. Malinowski, W. Wang, T. Song, J. Sanchez, W. Yao, D. Xiao, X. Zhu, A. F. May, W. Wu, D. H. Cobden, J. Chu and X. Xu, Two-dimensional itinerant ferromagnetism in atomically thin Fe₃GeTe₂, Nat. Mater., 2018, 17, 778.
15. Y. Deng, Y. Yu, Y. Song, J. Zhang, N. Z. Wang, Z. Sun, Y. Yi, Y. Z. Wu, S. Wu, J. Zhu, J. Wang, X. H. Chen and Y. Zhang, Gate-tunable room-temperature ferromagnetism in two-dimensional Fe₃GeTe₂, Nature, 2018, 563, 94.
16. H. H. Kim, B. Yang, S. Tian, C. Li, G. X. Miao, H. Lei and A. W. Tsen, Tailored tunnel magnetoresistance response in three ultrathin chromium trihalides, Nano Lett., 2019, 19, 5739–5745.
17. T. Song, M. W. Y. Tu, C. Carnahan, X. Cai, T. Taniguchi, K. Watanabe, M. A. McGuire, D. H. Cobden, D. Xiao, W. Yao and X. Xu, Voltage control of a van der Waals spin-filter magnetic tunnel junction, Nano Lett., 2019, 19, 915–920.
18. Z. Qiu, M. Holwill, T. Olsen, P. Lyu, J. Li, H. Fang, H. Yang, M. Kashchenko, K. S. Novoselov and J. Lu, Visualizing atomic structure and magnetism of 2D magnetic insulators via tunneling through graphene, Nat. Commun., 2021, 12, 70.
19. B. Yang, X. Zhang, H. Yang, X. Han and Y. Yan, Strain controlling transport properties of heterostructure composed of monolayer CrI₃, Appl. Phys. Lett., 2019, 114, 192405.
20. J. J. Heath, M. Costa, M. Buongiorno-Nardelli and M. A. Kuroda, Role of quantum confinement and interlayer coupling in CrI₃-graphene magnetic tunnel junctions, Phys. Rev. B, 2020, 101, 195439.
21. D. Ghazaryan, M. T. Greenaway, Z. Wang, V. H. Guarochico-Moreira, I. J. Vera-Marun, J. Yin, Y. Liao, S. V. Morozov, O. Kristanovski, A. I. Lichtenstein, M. I. Katsnelson, F. Withers, A. Mishchenko, L. Eaves, A. K. Geim, K. S. Novoselov and A. Misra, Magnon-assisted tunneling in van der Waals heterostructures based on CrBr₃, Nat. Electron., 2018, 1, 344–349.
22. L. Pan, L. Huang, M. Zhong, X. W. Jiang, H. X. Deng, J. Li, J. B. Xia and Z. Wei, Large tunneling magnetoresistance in magnetic tunneling junctions based on two-dimensional CrX₃ (X = Br, I) monolayers, Nanoscale, 2018, 10, 22196.
23. T. R. Paudel and E. Y. Tsymbal, Spin filtering in CrI₃ tunnel junctions, ACS Appl. Mater. Interfaces, 2019, 11, 15781–15787.
24. Z. Yan, R. Zhang, X. Dong, S. Qi and X. Xu, Significant tunneling magnetoresistance and excellent spin filtering effect in CrI₃-based van der Waals magnetic tunnel junctions, Phys. Chem. Chem. Phys., 2020, 22, 14773.
25. F. Li, B. Yang, Y. Zhu, X. Han and Y. Yan, Four distinct resistive states in van der Waals full magnetic 1T-VSe₂/CrI₃/1T-VSe₂ tunnel junction, Appl. Surf. Sci., 2020, 505, 144648.
26. F. Li, B. Yang, Y. Zhu, X. Han and Y. Yan, Ultrahigh tunneling magnetoresistance in van der Waals and lateral magnetic tunnel junctions formed by intrinsic ferromagnets Li_0.5CrI₃ and CrI₃, Appl. Phys. Lett., 2020, 117, 022412.
27. Z. Wang, D. Sapkota, T. Taniguchi, K. Watanabe, D. Mandrus and A. F. Morpurgo, Tunneling spin valves based on Fe₃GeTe₂/hBN/Fe₃GeTe₂ van der Waals heterostructures, Nano Lett., 2018, 18, 4303–4308.
28. X. Li, J. T. Lu, J. Zhang, L. You, Y. Su and E. Y. Tsymbal, Spin-Dependent transport in van der Waals magnetic tunnel junctions with Fe₃GeTe₂ electrodes, Nano Lett., 2019, 19, 5133–5139.
29. L. Zhang, T. Li, J. Li, Y. Jiang, J. Yuan and H. Li, Perfect spin filtering effect on Fe₃GeTe₂-based Van der Waals magnetic tunnel junctions, J. Phys. Chem. C, 2020, 124, 27429–27435.
30. H. Lin, F. Yan, C. Hu, Q. Lv, W. Zhu, Z. Wang, Z. Wei, K. Chang and K. Wang, Spin-Valve effect in Fe₃GeTe₂/MoS₂/Fe₃GeTe₂ van der Waals heterostructures, ACS Appl. Mater. Interfaces, 2020, 12, 43921–43926.
31. W. Yang, Y. Cao, J. Han, X. Lin, X. Wang, G. Wei, C. Lv, A. Bournel and W. Zhao, Spin-filter induced large magnetoresistance in 2D van der Waals magnetic tunnel junctions, Nanoscale, 2021, 13, 862.
32. J. Zhou, J. Qiao, C. G. Duan, A. Bournel, K. L. Wang and W. Zhao, Large tunneling magnetoresistance in VSe₂/MoS₂ magnetic tunnel junction, ACS Appl. Mater. Interfaces, 2019, 11, 17647–17653.
33. H. Zhou, Y. Zhang and W. Zhao, Tunable tunneling magnetoresistance in van der Waals magnetic tunnel junctions with 1T-CrTe₂ electrodes, ACS Appl. Mater. Interfaces, 2021, 13, 1214–1221.
34. C. Cardoso, D. Soriano, N. A. Garc-Martnez and J. Fernndez-Rossier, Van der Waals spin valves, Phys. Rev. Lett., 2018, 121, 067701.
35. G. Kresse and J. Hafner, Norm-conserving and ultrasoft pseudopotentials for first-row and transition elements, J. Phys.: Condens. Matter, 1994, 6, 8245.
36. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
37. D. Hobbs, G. Kresse and J. Hafner, Fully unconstrained noncollinear magnetism within the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 11556.
38. M. Marsman and J. Hafner, Broken symmetries in the crystalline and magnetic structures of γ-iron, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 224409.
39. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671.
40. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865.
41. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
42. A. Dal Corso and A. Mosca Conte, Spin-orbit coupling with ultrasoft pseudopotentials: Application to Au and Pt, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 115106.
43. S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787.
44. L. Wang, T. Maxisch and G. Ceder, Oxidation energies of transition metal oxides within the GGA+U framework, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107.
45. O. Bengone, M. Alouani, P. Blöchl and J. Hugel, Implementation of the projector augmented-wave LDA+U method: Application to the electronic structure of NiO, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 16392.
46. A. Rohrbach, J. Hafner and G. Kresse, Molecular adsorption on the surface of strongly correlated transition-metal oxides: A case study for CO/NiO (100), Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 075413.
47. J. Kim, K. W. Kim, B. Kim, C. J. Kang, D. Shin, S. H. Lee, B. C. Min and N. Park, Exploitable magnetic anisotropy of the two-dimensional magnet CrI₃, Nano Lett., 2020, 20, 929–935.
48. M. A. McGuire, H. Dixit, V. R. Cooper and B. C. Sales, Coupling of crystal structure and magnetism in the layered, ferromagnetic insulator CrI₃, Chem. Mater., 2015, 27, 612–620.
49. J. Taylor, H. Guo and J. Wang, Ab initio modeling of open systems: Charge transfer, electron conduction, and molecular switching of a C-60 device, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 121104.
50. A. P. Jauho, N. S. Wingreen and Y. Meir, Time-dependent transport in interacting and noninteracting resonant-tunneling systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 5528–5544.
51. J. Taylor, H. Guo and J. Wang, Ab initio modeling of quantum transport properties of molecular electronic devices, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245407.
52. Y. Meir and N. S. Wingreen, Landauer formula for the current through an interacting electron region, Phys. Rev. Lett., 1992, 68, 2512.
53. J. M. Soler, E. Artacho, J. D. Gale, A. Garcia, J. Junquera, P. Ordejon and D. Sanchez-Portal, The SIESTA method for ab initio order-N materials simulation, J. Phys.: Condens. Matter, 2002, 14, 2745–2779.
54. H. Wang, J. Zhou, X. Liu, C. Yao, H. Li, L. Niu, Y. Wang and H. Yin, Spin transport through a junction entirely consisting of molecules from first principles, Appl. Phys. Lett., 2017, 111, 172408.
55. W. B. Zhang, Q. Qu, P. Zhu and C. H. Lam, Robust intrinsic ferromagnetism and half semiconductivity in stable two-dimensional single-layer chromium trihalides, J. Mater. Chem. C, 2015, 3, 12457–12468.
56. T. Liu, N. Zhou, X. Li, G. Zhu, X. Wei, J. Cao and Z. Yang, Prediction of colossal magnetocrystalline anisotropy for transition metal triiodides, J. Phys.: Condens. Matter, 2019, 31, 295801.
57. C. X. Huang, J. S. Feng, F. Wu, D. Ahmed, B. Huang, H. J. Xiang, K. M. Deng and E. Kan, Toward intrinsic room-temperature ferromagnetism in two dimensional semiconductors, J. Am. Chem. Soc., 2018, 140, 11519–11525.
58. J. Zhang, B. Zhao, T. Zhou, Y. Xue and C. Ma, Strong magnetization and Chern insulators in compressed graphene/CrI₃ van der Waals heterostructures, Phys. Rev. B, 2018, 97, 085401.
59. J. F. Dillon and C. E. Olson, Magnetization, resonance, and optical properties of the ferromagnet CrI₃, J. Appl. Phys., 1965, 36, 1259–1260.
60. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125, 224106.
61. N. Sivadas, S. Okamoto, X. Xu, C. J. Fennie and D. Xiao, Stacking-dependent magnetism in bilayer CrI₃, Nano Lett., 2018, 18, 7658–7664.
62. P. Jiang, C. Wang, D. Chen, Z. Zhong, Z. Yuan, Z. Y. Lu and W. Ji, Stacking tunable interlayer magnetism in bilayer CrI₃, Phys. Rev. B, 2019, 99, 144401.
63. R. Xu and X. Zou, Electric Field-Modulated Magnetic Phase Transition in van der Waals CrI₃ Bilayers, J. Phys. Chem. Lett., 2020, 11, 3152.
64. F. Zheng, J. Zhao, Z. Liu, M. Li, M. Zhou, S. Zhang and P. Zhang, Tunable spin states in the two-dimensional magnet CrI₃, Nanoscale, 2018, 10, 14298.
65. A. Politano and G. Chiarello, Probing the Young’s modulus and Poissons ratio in graphene/metal interfaces and graphite: a comparative study, Nano Res., 2015, 8, 1847.

---

Footnotes

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra02988j

‡ Equal contribution author.

---