Open Access Article
Open Access ArticleThe nature of metal–metal bonding in Re-, Ru- and Os-corrole dimers†
Mohammed Obies *a and
Aqeel A. Hussein
*a and
Aqeel A. Hussein *b
*b
aCollege of Pharmacy, University of Babylon, 51002, Hillah, Babylon, Iraq. E-mail: phar.mohammed.h.obies@uobabylon.edu.iq
bDepartment of Biomedical Science, College of Science, Komar University for Science and Technology, Qularaisi, Sulaymaniyah, Kurdistan Region, Iraq. E-mail: aqeel.alaa@komar.edu.iq
First published on 28th June 2022
Abstract
Studies of multiple bonding between transition metal complexes offer fundamental insight into the nature of bonding between metal ions and facilitate predictions of the physical properties and the reactivities of metal complexes containing metal–metal multiple bonds. Here we report a computational interrogation on the nature of the metal–metal bonding for neutral, oxidized, and reduced forms of dinuclear rhenium and osmium corrole complexes, [{Re[TpXPC]}2]0/1+/1− and [{Os[TpXPC]}2]0/1+/1−, using a complete active space self-consistent (CASSCF) methodology and density functional theory (DFT) calculations. For [{Re[TpXPC]}2]0, [{Ru[TpXPC]}2]0, and [{Os[TpXPC]}2]0, CASSCF calculations shows that the effective bond order is 3.29, 2.63, and 2.73, respectively. On their oxidized forms, [{Re[TpXPC]}2]1+, [{Ru[TpXPC]}2]1+, and [{Os[TpXPC]}2]1+ molecules, the results indicate an electron removal from a ligand-based orbital, where [{Re[TpXPC]}2]1+ gives slightly different geometry from its neutral form due to populating the δ* orbital. In this regard, the CASSCF calculations give an effective bond order of 3.25 which is slightly lower than in the [{Re[TpXPC]}2]0. On their reduced forms, the electron addition appears to be in the metal-based orbital for [{Re[TpXPC]}2]1− and [{Ru[TpXPC]}2]1− whereas in the ligand-based orbital for the Os-analogue which has no effect on the Os–Os bonding, an effective bond order of 3.18 and 2.17 is presented for the [{Re[TpXPC]}2]1− and [{Ru[TpXPC]}2]1−, respectively, within the CASSCF simulations. These results will further encourage theoreticians and experimentalists to design metalloporphyrin dimers with distinct metal–metal bonding.
Introduction
Corrole1 is a contracted porphyrin analogue that can be bound to transition metals giving so-called metallocorroles. It is known to stabilize transition metals in high oxidation states.2 Metallocorroles are useful in various catalytic reactions, for example, iron and manganese corroles proved to be useful in hydroxylation reactions whereas antimony and rhodium corroles were successfully used in oxidation reactions of hydrocarbons and cyclopropanation reactions, respectively. Furthermore, iron and rhodium corroles have been also used in N–H and C–H insertion reactions, respectively.3 All these molecules have a single transition metal in their structures. However, metalloporphyrin also can be synthesized as dimers with multiple metal–metal bonds in which they have a significant interest.4 Tuning the bond order of the metalloporphyrin/corrole dimers can be achieved by oxidation and reduction of the dimer. Metal–metal-bonded dimeric porphyrin complexes in various accessible oxidation states were studied utilizing resonance Raman scattering, infrared absorption, and absorption spectroscopy.4d,e For instance, Kadish and co-workers5 characterized the one-electron-oxidized forms of ruthenium–ruthenium-bonded dimeric corrole complexes using a combination of UV/Vis spectrophotometry and EPR spectroelectrochemistry. Collman and Arnold conducted experimental (UV/Vis/NIR/EPR spectroelectrochemical) and theoretical (DFT) approaches to establish the electronic nature of the electro-generated species.4Interestingly, transition metal corrole dimer {M[TpXPC]}2 (M = Re or Ru or Os and TpXPC refers to a meso-tris(para-X-phenyl) corrole and X= CF3, H, Me, and OMe) have been synthesized recently by Ghosh and co-workers.6 The cyclic voltammetry measurements of the {Re[TpMePC]}2, the {Ru[TpMePC]}2 and the {Os[TpMePC]}2 exhibit three reversible oxidations and one reversible reduction. The X-ray data is available just for the neutral structure. Thus, there is little information regarding the nature of the metal–metal bonding in the oxidized and reduced species from electrochemistry and DFT calculations.6a,b High level computational calculations offer fundamental insight into the nature of metal–metal bonding in the neutral, oxidized, and reduced species of the [{Re[TpMePC]}2]0/1+/1−, the [{Ru[TpMePC]}2]0/1+/1− and the [{Os[TpMePC]}2]0/1+/1− complexes. However, rationalizing the nature of metal–metal bonding is challengeable from theoretical perspectives.7
The most popular computational method is DFT. It has been used for dealing with large systems, in particular, those that contain transition metals. This method, however, in some cases fails to give a clear description of the nature of the metal–metal bonding because it is inherently a single determinant in nature, and the accuracy of the available exchange-correlation functionals is still open to debate. An alternative approach is multi-configurational self-consistent field (MCSCF) method, specifically, the complete active space self-consistent field (CASSCF) method. Metal–metal bonding forms from the overlap between d orbitals on each metal of the dimer. That leads to forming different types of bonds that are σ, π, and δ with different strengths. CASSCF approach takes into account the different contributions of the σ, π, and δ components of overall bond strength, thus, gives a better description of the nature of the metal–metal bonding. The main challenge in using the CASSCF methodology is the choice of the active space due to its dependence on the chemical intuition of the system under study. The occupation numbers in single determinant methods (DFT) are restricted to integer values whereas in the CASSCF wavefunction can be fractions between zero and two which can capture all points between the strongly bonded limit and the dissociation limit, where occupation numbers of the bonding and antibonding orbitals are 0.5.
The [{M[TpXPC]}2]0 (M = Re or Ru or Os) complexes have similar geometries to the landmark [Re2Cl8]2− molecule.8 Each metal centre of the dimers is bonded to the ligands through four nitrogen atoms. The nitrogen atoms have almost an eclipsed arrangement similar to the chlorine atoms in the [Re2Cl8]2−. Therefore, the metal–metal bonding of the three corrole dimers ([{M[TpXPC]}2] (M = Re or Ru or Os)) can be described similarly to that in the [Re2Cl8]2− molecule. The [Re2Cl8]2− molecule features a metal–metal quadruple bond with a Re–Re distance of only 2.27 Å.8 The structure of this molecule has been described as two rhenium atoms lying within a square prism defined by eight chlorine atoms. The bonding between the two rhenium centres was explained qualitatively using molecular orbital arrays as shown in Fig. 1a. The four d orbitals 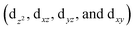 on each metal centers are participated in the Re–Re bonding (σ, π, and δ) while the
on each metal centers are participated in the Re–Re bonding (σ, π, and δ) while the 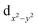 orbitals on each rhenium atom interact with the ligands. Re2-core has eight electrons populating the four bonding orbitals in Fig. 1a (σ2π4δ2) giving a bond order of 4.0. The metal–metal bonding of [Mo2Cl8]4−, [Tc2Cl8]2−, and [Tc2Cl8]3− complexes is described in the same way as that in the [Re2Cl8]2−.9
orbitals on each rhenium atom interact with the ligands. Re2-core has eight electrons populating the four bonding orbitals in Fig. 1a (σ2π4δ2) giving a bond order of 4.0. The metal–metal bonding of [Mo2Cl8]4−, [Tc2Cl8]2−, and [Tc2Cl8]3− complexes is described in the same way as that in the [Re2Cl8]2−.9
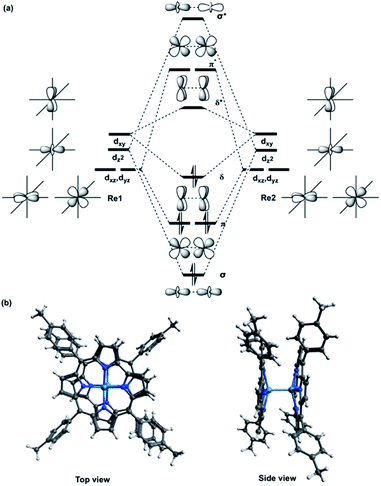 | ||
| Fig. 1 (a) Schematic molecular orbital arrays for D4h-[Re2Cl8]2− molecule and (b) X-ray structure of {M[TpMePC]}2 (M = Re or Ru or Os) complex with two views. | ||
In 2003, Gagliardi and Roos studied the electronic structure of [Re2Cl8]2− using CASSCF/PT2 methodology.10a Their calculations adopted a CAS(12,12) active space that includes the eight metal-based orbitals (Fig. 1a) and the four metal–ligand orbitals and twelve electrons distributed among them. The CASSCF results showed that the ground state occupations of the δ and δ* orbitals are 1.54 and 0.46, respectively. These occupation numbers are very different from the classical values of 2.0 (δ) and 0.0 (δ*) for formally doubly occupied and unoccupied molecular orbitals. For the σ-manifold the natural orbital populations are 1.92 and 0.08 for σ and σ*, respectively, reflecting substantial overlap of the σ orbitals. The natural orbital populations of π-symmetry are intermediate, with values of 3.74 and 0.26 for bonding and antibonding orbitals, respectively. These occupations give a total Re–Re bond order of 3.18, much smaller than the classical value of 4.0. The metal–ligand orbitals remain almost fully occupied in the wavefunction with bonding and antibonding occupations of 1.98 and 0.02, respectively. The effective bond order of the [Re2Cl8]2− molecule was also calculated by Sakaki and co-workers using a CAS(8,8), the metal–ligand orbitals were not included in the calculations.10b The results show that the effective Re–Re bond order of 3.20 is very close to the Roos and co-workers results.
Therefore, we believe that understanding the nature of the metal–metal bonding in the transition metal corrole dimers is still in need of further investigation using computational methods that are beyond the single determinant method (DFT). Here we report a computational study on the {M[TpMePC]}2 (M = Re or Os) complexes and their oxidation and reduction forms to shed some light on the nature of the metal–metal bonding in these important complexes using the complete active space self-consistent field (CASSCF) methodology.
Results and discussions
To analyse the nature of the metal–metal bonding in the [{M[TpXPC]}2] (M = Re or Ru or Os and X = Me or CF3) complexes, all geometries including neutral, oxidized, and reduced species were optimized at the DFT level. Then, the complete active space self-consistent (CASSCF) methodology used those DFT-optimized structures to analyse the nature of the metal–metal bonding. In the following sections, the DFT results will be briefly introduced as required to make the discussions followed easily. The detailed results of the DFT calculations will be introduced in the ESI.†Initial considerations
In this computational study, all geometries including neutral, oxidized, and reduced species were optimized using two different exchange-correlation functionals that are OLYP and B3LYP. The atom-pairwise dispersion correction with the Becke–Johnson damping scheme (D3BJ) was applied on all optimized geometries. To reduce the computational cost, a model of the TpXPC (X= Me or CF3) ligand where used. The phenyl rings of the ligands with their substitutions are replaced by hydrogen atoms as shown in Scheme 1. To validate this simplification on the structure parameters, we have firstly compared the main structure parameters of the complex with the full ligand and with the model ligand. Following this validation, we will then present a detailed analysis of the neutral, oxidized, and reduced species at the CASSCF level using the simplified model of the ligand TpXPC (X= Me or CF3). In the following discussion, we will refer to the simplified complex as M2-Model and M2-Full (M = Re or Ru or Os) for the complex with the whole ligand.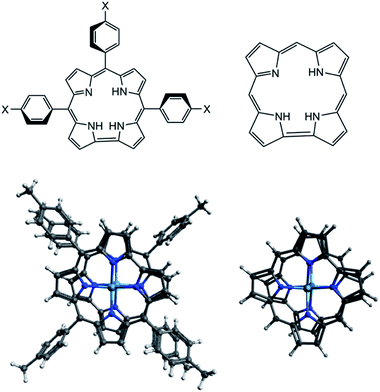 | ||
| Scheme 1 (Top) the actual and model 2D structures of the ligand. (Bottom) the full and model 3D structure of the {M[TpXPC]}20 systems, where M = Re or Ru or Os and X = Me or CF3. | ||
Geometrical comparison
Table 1 illustrates the main geometry parameters of the [M2-Model]0 and the [M2-Full]0 complexes computed with OLYP functional along with the crystallographic data. We need to note here that the [Ru-Full]0 was optimized with the TpCF3PC ligand because the X-ray structure of the [{Ru[TpMePC]}2]0 is unavailable. The Re–Re bond length in the [Re2-Model]0 molecule is computed to be 2.20 Å compared to 2.2364(6) Å of its X-ray counterpart whereas 2.19 Å with the full ligand. The averaged Re–N bond distance of the model ligand is reproduced within 0.01 Å of crystallographic value and within 0.02 Å with the [Re2-Full]0. The computed Ru–Ru bond length of the [Ru2-Model]0 is 2.14 Å which is shorter than that of the [Re2-Full]0 and the X-ray value by 0.01 and 0.04 Å, respectively. The averaged Ru–N bond distance of the [Ru2-Model]0 and [Re2-Full]0 in excellent agreements the X-ray vale (1.97 Å). The Os–Os bond distance is also in good agreement with the X-ray values since the computed value is shorter than the X-ray value by only 0.02 Å of the [Os2-Model]0 and the [Os2-Full]0. The averaged Os–N distance of both [Os2-Model]0 and [Os2-Full]0 is predicted within 0.02 Å compared to the X-ray result. These results show that the simplification has almost no effect on the structure parameters, thus, the model structure will be used in all electronic structure analysis in this paper. Also, these results indicate that the computational methodology is valid for electronic structure analysis of the {Re[TpMePC]}20, {Ru[TpCF3PC]}20 and {Os[TpMePC]}20 molecules, and consequently for the oxidation and reduction forms.| M2-Model | M2-Full | X-ray | |
|---|---|---|---|
| Re–Re | 2.20 | 2.19 | 2.2364(6) |
| Avg. Re–N | 2.02 | 2.03 | 2.01 |
| Ru–Ru | 2.14 | 2.15 | 2.1827(5) |
| Avg. Ru–N | 1.97 | 1.97 | 1.97 |
| Os–Os | 2.22 | 2.22 | 2.2403(5) |
| Avg. Os–N | 1.98 | 1.98 | 1.96 |
The neutral forms of [M2-Model]0 (M = Re, Ru or Os)
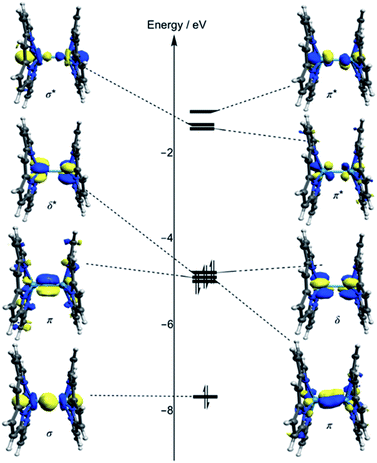
Kohn–Sham molecular orbital array of the [Re2-Model]0 complex is shown in Fig. 2. The eight electrons of the Re2-core populate the bonding orbitals in Fig. 2 giving a low spin ground state with σ2π4δ2 electron configuration and formal bond order of 4.0. Both Ru2-core and Os2-core in the [Ru2-Model]0 and [Os2-Model]0 molecules have ten electrons which are populating the δ* orbital beside the σ, π, and δ orbitals. That gives a σ2π4δ2δ*2 electron configuration with a formal bond order of 3.0. The single configurational description from DFT on the metal–metal bonding does not take into account the different strengths of the M–M bonding components (σ, π, and δ). Therefore, we have turned our attention to the multi-configurational method, namely CASSCF.For the [Re2-Model]0 system, the active space consists of the metal-based orbitals that are σ, 2π, and δ, and their antibonding counterparts (σ*, 2π*, and δ*). The Re2-core has eight electrons which are distributed among the eight orbitals (Fig. 2) giving a CAS(8,8) active space. The CAS(8,8) active space indicates that eight electrons in eight orbitals. The DFT-OLYP geometry is used in the CASSCF calculations with a Re–Re bond length of 2.20 Å. The CASSCF orbitals of the [Re2-Model]0 complex with the occupations are shown in Fig. 3 (top). The ground state wavefunction of the [Re2-Model]0 molecule is dominated by σ2π4δ2 configuration with 0.69 weight of the total wavefunction. The second configuration weights only 0.16 of the total wavefunction is σ2π4δ0δ*2. The rest has a neglectable contribution to the total wavefunction with a contribution less than 0.02. The bond order of the σ manifold is 0.93 and for π and δ manifolds are 1.8 and 0.56, respectively, giving an effective bond order of 3.29 which is very diverge from the formal bond order of 4.0. This bond order is bigger than the Re–Re bond order of [Re2Cl8]2− predicated by Roos and Sakaki to be 3.20 and 3.18, respectively.10 For comparison, the bond order of [Re2-Model]0 was also calculated using natural bond orbitals (NBO) and Mayer bond order (MBO) methodologies (Table 2). The NBO and MBO are 2.96 and 2.27, respectively; these values are less than the CASSCF value by 0.33 and 1.02, respectively.
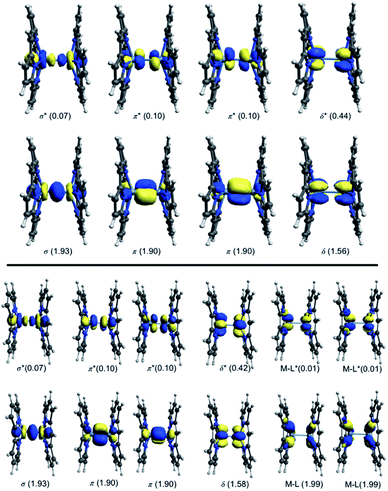 | ||
| Fig. 3 Active space natural orbitals with occupations of the [Re2-Model]0 complex (top: CAS (8,8), bottom: CAS(12,12)). | ||
| EBO | NBO | MBO | ||
|---|---|---|---|---|
| [M2-Model]0 | Re2 | 3.29 | 2.96 | 2.27 |
| Ru2 | 2.63 | 1.81 | 1.66 | |
| Os2 | 2.73 | 1.93 | 2.52 | |
For the [Ru2-Model]0 and [Os2-Model]0, a CAS(10,8) was adopted with ten electrons and eight metal-based orbitals were being included, the active space natural orbitals shown in Fig. ESI1 and ESI2† and the occupations of each orbital is presented in Table 3. The σ2π4δ2δ*2 configuration makes 0.82 and 0.87 of the total wavefunction of the [Ru2-Model]0 and [Os2-Model]0, respectively. In the [Ru2-Model]0 complex, the bond order of the σ is 0.91 and for π is 1.72, these results are different from those in the [Re2-Model]0 molecule. The occupations of the δ and δ* orbitals are 2.0, giving a bond order of zero compared to 0.56 of the [Re2-Model]0 molecule. Those occupations give an effective bond order of 2.63, which is clearly distinct from the formal bond order of 3.0. However, this value is the closest one to the formal bond order of 3.0 compared to the values 1.81 and 1.66 obtained from NBO and MBO, respectively. In the [Os2-Model]0 molecule, the occupations of the σ and π manifolds are identical to those in the [Re2-Model]0 molecule while the occupations of δ manifold are 2.00 for both δ and δ* orbitals (see Table 3). The effective bond order of the [Os2-Model]0 molecule is 2.73, which is slightly different from the bond order of the Ru-analogue (2.63) and much smaller than the bond order of the [Re2-Model]0 (3.29). The NBO of the [Os2-Model]0 of 1.93 is significantly smaller than the effective bond order (2.73), while the MBO is smaller than the effective bond order by just 0.2 (see Table 2). In summary, the EBO-CASSCF gives reasonable bond order compared to that of the NBO- and MBO-DFT.
| σ | σ* | π | π* | δ | δ* | ||
|---|---|---|---|---|---|---|---|
| [M2-Model]0 | Re2 | 1.93 | 0.07 | 3.80 | 0.20 | 1.56 | 0.44 |
| Ru2 | 1.91 | 0.09 | 3.72 | 0.28 | 2.00 | 2.00 | |
| Os2 | 1.93 | 0.07 | 3.80 | 020 | 2.00 | 2.00 | |
| [M2-Model]1+ | Re2 | 1.93 | 0.07 | 3.78 | 0.22 | 1.54 | 0.46 |
| Os2 | 1.93 | 0.07 | 3.80 | 0.20 | 2.00 | 2.00 | |
| [M2-Model]1− | Re2 | 1.93 | 0.07 | 3.82 | 0.18 | 1.93 | 1.07 |
| Ru2 | 1.89 | 0.11 | 3.78 | 1.22 | 2.00 | 2.00 | |
To take into account the effect of the ligand orbitals on the nature of the metal–metal bonding; the active space was expanded to include the metal–ligand orbitals. For all [Re2-Model]0, [Ru2-Model]0 and [Os2-Model]0 complexes, the active space was expanded to include the two M–N δ (M = Re or Ru or Os) bonding orbitals and the corresponding two antibonding molecular orbitals and them four electrons distributing among them. This yields CAS(12,12) for [Re2-Model]0 and CAS(14,12) active space for both [Ru2-Model]0 and [Os2-Model]0 (see Fig. 3 and ESI3†). For [Re2-Model]0, the active space natural orbitals with the occupations are shown in Fig. 3 (bottom). The Re–N δ orbitals are kept fully occupied with the occupation of 1.99 and 0.01 of bonding and antibonding orbitals, respectively. The occupations of the σ and π manifolds are the same to that in the CAS(8,8) whereas the occupations of the δ manifold is slightly different from those of the CAS(8,8) with occupations of 1.58 and 0.42 of δ and δ* orbitals, respectively, compared to 1.56 and 0.44 in CAS(8,8). Resulting in slight increase in the strength of the δ bonding (δ bond order of 0.56 with CAS(8,8) compare to 0.58 with CAS(12,12)) but this has almost no effect on the effective bond order (3.30 vs. 3.29). For [Os2-Model]0, the M–N δ orbitals are preserved fully occupied with occupation number of 1.99 and 0.01 of bonding and antibonding orbitals, respectively, similar to those of Re-analogue. The occupations of these orbitals in the [Ru2-Model]0 are 1.98 and 0.02, respectively. The active space orbitals of the [Os2-Model]0 are shown in Fig. ESI3.† These results show that including the M–N δ orbitals in the active space has no effect on the nature of the metal–metal bonding in these three complexes.
The oxidized forms of [M2-Model]1+ (M = Re, Ru or Os)
One electron removal from the [M2-Model]0 (M = Re or Ru or Os) systems occurs either from the metal-based orbitals or the ligand-based orbitals, giving a [M2-Model]1+ (M = Re or Ru or Os) molecule. Our DFT calculations include Mulliken spin density and geometrical changes suggested that the unpaired electron is removed from the ligand-based orbitals (see ESI† for the details). That was confirmed by the oxidation potentials, where the first oxidation potentials of the three molecules were found experimentally to be nearly identical (0.51 V for Re, 0.52 V for Ru, and 0.55 V for Os).6a,b Our DFT calculations on these potentials are in agreement with the experimental trend, showing that the unpaired electron is removed from the same orbital in all of the three complexes. For the [Re2-Model]0, the δ* metal-based orbital is populated as shown in Scheme 2, one of the δ manifold electron is coupled antiferromagnetically to the electron on the ligand giving a 2A ground state consistent with the finding of Ghosh and co-workers.6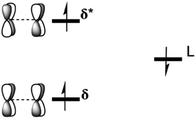 | ||
| Scheme 2 Systematic representation of the configurations of the [Re2-Model]1+ molecule using both OLYP and B3LYP functionals. | ||
To gain insight into the nature of the metal–metal bonding in the [Re2-Model]1+ and the [Os2-Model]1+ systems, we have run CASSCF calculations using the same active spaces as in their neutral forms. The geometry of the [Ru2-Model]1+ is the same as the neutral analogue with Ru–Ru bond length of 2.14 Å; therefore, the CASSCF calculations would give the same results. However, the geometries of both [Re2-Model]1+ and the [Os2-Model]1+ systems are slightly different from the neutral forms. The M–M bond length of 2.21 Å in both [Re2-Model]1+ and [Os2-Model]1+. Furthermore, the δ* orbital in the [Re2-Model]1+ molecule is populated; thus, it needs to consider in the CASSCF calculations. Therefore, σ2π4δ2δ*0 and σ2π4δ1δ*1 will be investigated as they would give different nature of Re–Re bonding. In principle, the σ2π4δ2δ*0 (singlet) configuration gives formal bond order of 4.0 while the σ2π4δ1δ*1 (triplet) configuration gives 3.0. The N-electron valence perturbation theory in combination with the domain-based local pair natural orbital (DLPNO-NEVPT2) results show that the triplet state is 0.5 eV higher in energy than the singlet. The active space natural orbitals with occupations of the singlet and the triplet states are shown in Fig. ESI5† and Table 3. The σ2π4δ2δ*0 configuration makes up 0.67 of the total wavefunction, and the second most predominant configuration is σ2π4δ0δ*2 weights only 0.17 of the total wavefunction. The occupations number of the σ and σ* manifolds are 1.93 and 0.07, respectively, same as those in the [Re2-Model]0. The occupations of the π and δ and them antibonding orbitals are slightly different from those of [Re2-Model]0 due to slightly different geometries. The occupations of the π and π* are 3.78 and 0.22, respectively. The occupations of the δ and δ* are 1.54 and 0.46, respectively. These occupations give an effective bond order of 3.25. The geometry of the [Os2-Model]1+ (2.21 Å vs. 2.22 Å) is very similar to the neutral analogue and also the same active space (CAS(10,8)) would be used in the CASSCF calculations (see Table 3). Therefore, single point CASSCF calculations have the same electrons configuration, the σ2π4δ2δ*2 configuration has also 0.87 weight of the total wavefunction.
The reduced forms of [M2-Model]1− (M = Re, Ru or Os)
The electron addition could occupy a metal-based orbital or a ligand-based orbital. Adding one electron to the [Re2-Model]0 system produces [Re2-Model]1−. DFT calculations show that the single electron is occupied a metal-based orbital in the [Re2-Model]1− and [Ru2-Model]1− complexes. In contrast to the [Re2-Model]1− and [Ru2-Model]1−, the electron is added to the ligand-based orbitals in the [Os2-Model]1− (see ESI† for details). Here, the first reduction potentials of the three complexes were found very different from each other experimentally (−0.55 V for Re, −0.85 V for Ru, and −1.31 V for Os).6a,bCASSCF method was applied to explore the nature of the metal–metal bonding in the [Re2-Model]1− and [Ru2-Model]1− molecules. The geometry of the [Os2-Model]1− molecule predicted to be same to that of the neutral complex, therefore, a CAS(10,8) would give the same results to the isoelectronic neutral molecule. For the [Re2-Model]1−, a CAS(9,8) active space was adopted, including the eight metal-based orbitals and nine electrons distributed among them using the DFT-OLYP geometry (Re–Re bond distance of 2.22 Å). The active space natural orbitals with occupations of the [Re2-Model]1− are appeared in Fig. ESI6† and Table 3. The σ2π4δ2δ*1 configuration makes up 85% of the total wavefunction of the 2A ground state. The occupations of the σ and σ* orbitals are 1.93 and 0.07, respectively, giving a bond order of 0.93. The bond order of the π- and δ-mainfold are 1.82 and 0.43, respectively. Thus, effective bond order in the [Re2-Model]1− molecule is 3.18 compared to 3.29 in the [Re2-Model]0 molecule. For the [Ru2-Model]1−, a CAS(11,8) were adopted using DFT-OLYP geometry with the Ru–Ru bond length of 2.19 Å. The σ2π4δ2δ*2π*1 configuration makes 85% of the total wavefunction of the 2A ground state. The bond order of each manifold is 0.89, 1.28, and zero of σ, π, and δ, respectively, giving an effective bond order of 2.17.
Conclusions
The electronic structure of neutral, oxidized, and reduced species of dinuclear rhenium, ruthenium, and osmium corrole complexes, [{Re[TpXPC]}2]0/1+/1−, [{Ru[TpXPC]}2]0/1+/1− and [{Os[TpXPC]}2]0/1+/1−, were theoretically investigated using state-of-the-art quantum methods including density functional theory (DFT) and complete active space self-consistent field (CASSCF) methodologies. The DFT computed ground state geometry of [{Re[TpXPC]}2]0, [{Re[TpXPC]}2]0 and [{Os[TpXPC]}2]0 complexes are in excellent agreement with the experimental structures determined by single-crystal X-ray diffraction. For the [{Re[TpXPC]}2]0, [{Ru[TpXPC]}2]0, and [{Os[TpXPC]}2]0 molecules, the CASSCF calculations show that the effective bond order is 3.29, 2.63 and 2.73, respectively. These bond orders vastly diverge from the formal bond order of 4.0 and 3.0 for the [{Re[TpXPC]}2]0 and the [{M[TpXPC]}2]0 (M = Ru or Os), respectively; that would expect from a simple molecular orbital picture.For the oxidized species, the oxidation process removes an electron from the ligand-based orbital in [{Re[TpXPC]}2]1+, [{Ru[TpXPC]}2]1+, and [{Os[TpXPC]}2]1+. This has a minimal effect on the structure's parameters and also on the effective bond order of the three complexes. For example, the Re–Re bond distance is slightly elongated compared to that in the neutral molecule (2.20 Å vs. 2.21 Å) due to populating the δ*orbital. The ground state σ2π4δ2 configuration makes 0.67 of the total wavefunction giving effective bond order of 3.25. On the reduction process, the electron was found occupying the metal-based orbital in the [{Re[TpXPC]}2]1− and [{Ru[TpXPC]}2]1− whereas in the ligand-based orbital of the [{Os[TpXPC]}2]1−. Accordingly, that reduction process does not effect on the nature of the Os–Os bonding in the [{Os[TpXPC]}2]1−. These findings show some impact on the nature of the metal–metal bonding in these systems. For instance, the effective bond order of the [{Re[TpXPC]}2]1− complex dropped by 0.11 compared to that in the neutral form.
We envision that using high-level computations will provide a further understanding of the metalloporphyrin dimers with multiple metal–metal bonds to predict the physical properties and the reactivities of such metal complexes.
Computational details
The crystallographic coordinates for metal-corrole dimers were obtained from the structures deposited at the Cambridge Structural Database.6a,b,e All calculations in this paper were performed using ORCA 5.0 package,11,12 otherwise mentioned. Two functionals were used in this work, the OLYP and B3LYP.13,14 The OLYP functional have been extensively used in studying metalloporphyrin-type complexes.6d We have used def2-TZVP basis set to describe the Re, Ru and Os while N, C, and H were described using def2-SVP basis set in combination with the def2/J auxiliary basis set of Weigend.15,16 The atom-pairwise dispersion correction with the Becke–Johnson damping scheme (D3BJ) were applied.17,18 Single point gas-phase CASSCF calculations was carried out using def2-TZVP basis set to describe the Re, Ru and Os and def2-svp/c19 to describe N, C, and H with def2/J auxiliary basis set. To speed up the CASSCF calculations we have used RIJCOSX approximation.20 The N-electron valence perturbation theory (NEVPT2) in combination with the domain-based local pair natural orbital (DLPNO) were used to account for the dynamic correlation.21–23The electrochemical properties were calculated using the Gaussian 16 package,24 in which the Gaussian 09 default integral grid was employed with the OLYP functional being used. The geometry optimization of complexes was done using the def2-TZVP basis set for Re, Ru and Os atoms whereas the def2-SV(P) basis set for the N, C, and H atoms, followed by frequency calculations to generate Gibbs free energy correction to obtain Gibbs free energies for each structure derived from vibrational frequencies at 298.15 K using unscaled frequencies. Single point calculations were performed with the def2-TZVP basis set for all atoms. The implicit solvation based on density (SMD) was employed in both geometry optimization and single point calculations with the dichloromethane as a representative solvent.25 The Grimme's quasi-RRHO correction26 was performed for all structures involved in the electrochemical calculations with a frequency cutoff of 100 cm−1 along with concentration correction (from standard state in gas phase, 1 atm, to standard state in solution, 1 mol l−1) at 298.15 K using the GoodVibes program.27
The relative redox potentials were calculated by using the differences of the free energies of the redox pairs and subtracted from the absolute potential of the reference electrode. The potential of the saturated calomel electrode (SCE), the reference electrode, is 4.67 V. This value is based on the absolute potential of the NHE, which was found to be 4.43 V by Reiss and Heller,28 although this quantity has been reported in the literature to be in the range of 4.2–4.7.29
It is important to mention that the effective bond order (EBO) from CASSCF calculation was computed using the ORCA 5.0 package, whereas natural bond orbitals (NBO) obtained with from DFT-B3LYP and Mayer bond order (MBO) obtained with DFT-OLYP calculations were calculated using the Gaussian 16 package.
Author contributions
The manuscript was written through contribution of both authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the use of the University of Oxford Advanced Research Computing (ARC) facility in carrying out this work.Notes and references
- W. Sinha, M. G. Sommer, L. Hettmanczyk, B. Patra, V. Filippou, B. Sarkar and S. Kar, Chem.–Eur. J., 2017, 23, 2396–2404 CrossRef CAS PubMed.
- (a) H. L. Buckley, L. K. Rubin, M. Chrominski, B. J. McNicholas, K. H. Y. Tsen, D. T. Gryko and J. Arnold, Inorg. Chem., 2014, 53, 7941–7950 CrossRef CAS PubMed; (b) H. L. Zhao, K. Pierloot, E. H. G. Langner, J. C. Swarts, J. Conradie and A. Ghosh, Inorg. Chem., 2012, 51, 4002–4006 CrossRef CAS PubMed.
- (a) H.-Y. Liu, T.-S. Lai, L.-L. Yeung and C. K. Chang, Org. Lett., 2003, 5, 617–620 CrossRef CAS PubMed; (b) I. Nigel-Etinger, I. Goldberg and Z. Gross, Inorg. Chem., 2012, 51, 1983–1985 CrossRef CAS PubMed.
- (a) J. P. Collman and H. J. Arnold, Acc. Chem. Res., 1993, 26, 586–592 CrossRef CAS; (b) J. P. Collman, C. E. Barnes, T. J. Collins, P. J. Brothers, J. Gallucci and J. A. Ibers, J. Am. Chem. Soc., 1981, 103, 7030–7032 CrossRef CAS; (c) F. R. Hopf, T. P. Obrien, W. R. Scheidt and D. G. Whitten, J. Am. Chem. Soc., 1975, 97, 277–281 CrossRef CAS PubMed; (d) J. P. Collman, P. J. Brothers, L. McElweewhite, E. Rose and L. J. Wright, J. Am. Chem. Soc., 1985, 107, 4570–4571 CrossRef CAS; (e) J. P. Collman, H. J. Arnold, J. P. Fitzgerald and K. J. Weissman, J. Am. Chem. Soc., 1993, 115, 9309–9310 CrossRef CAS.
- K. M. Kadish, F. Burdet, F. Jerome, J. M. Barbe, Z. P. Ou, J. G. Shao and R. Guilard, J. Organomet. Chem., 2002, 652, 69–76 CrossRef CAS.
- (a) B. Alemayehu, L. J. McCormick-McPherson, J. Conradie and A. Ghosh, Inorg. Chem., 2021, 60, 8315–8321 CrossRef PubMed; (b) A. B. Alemayehu, L. J. McCormick, H. Vazquez-Lima and A. Ghosh, Inorg. Chem., 2019, 58, 2798–2806 CrossRef CAS PubMed; (c) A. Ghosh, Chem. Rev., 2017, 117, 3798–3881 CrossRef CAS PubMed; (d) S. Nardis, F. Mandoj, M. Stefanelli and R. Paolesse, Coord. Chem. Rev., 2019, 388, 360–405 CrossRef CAS; (e) A. B. Alemayehu, H. Vazquez-Lima, K. J. Gagnon and A. Ghosh, Inorg. Chem., 2017, 56, 5285–5294 CrossRef CAS PubMed; (f) W. Sinha, M. G. Sommer, L. Hettmanczyk, B. Patra, V. Filippou, B. Sarkar and S. Kar, Chem.–Eur. J., 2017, 23, 2396–2404 CrossRef CAS PubMed.
- J. E. McGrady, Introduction and General Survey of Metal–Metal Bonds, in Molecular Metal-Metal Bonds, ed. S. T. Liddle, 2015, pp. 1–22 Search PubMed.
- (a) F. A. Cotton, F. Curtisc, B. Harrisb, F. G. Johnsons, J. Lippardj, T. Maguew, R. Robinsonand and j. S. Wood, Science, 1964, 145, 1305–1307 CrossRef CAS PubMed; (b) F. A. Cotton, Inorg. Chem., 1965, 4, 334–336 CrossRef CAS.
- (a) J. V. Brencic and F. A. Cotton, Inorg. Chem., 1969, 8, 7–10 CrossRef CAS; (b) D. Lawton and R. Mason, J. Am. Chem. Soc., 1965, 87, 921–922 CrossRef CAS.
- (a) L. Gagliardi and B. O. Roos, Inorg. Chem., 2003, 42, 1599–1603 CrossRef CAS PubMed; (b) K. Saito, Y. Nakao, H. Sato and S. Sakaki, J. Phys. Chem. A, 2006, 110, 9710–9717 CrossRef CAS PubMed.
- F. Neese, WIREs Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS; (b) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597 Search PubMed.
- C. Kollmar, K. Sivalingam, B. Helmich-Paris, C. Angeli and F. Neese, J. Comput. Chem., 2019, 40, 1463–1470 CrossRef CAS PubMed.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J. P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS.
- Y. Guo, K. Sivalingam and F. Neese, J. Chem. Phys., 2016, 144, 094111–094116 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Wallingford, CT, 2016 Search PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- S. Grimme, Chem.–Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed.
- G. Luchini, J. V. Alegre-Requena, I. Funes-Ardoiz and R. Paton, F1000Research, 2020, 9, 291 Search PubMed.
- H. Reiss and A. Heller, J. Phys. Chem., 1985, 89, 4207–4213 CrossRef CAS.
- W. A. Donald, R. D. Leib, J. T. O'Brien, M. F. Bush and E. R. Williams, J. Am. Chem. Soc., 2008, 130, 3371–3381 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional calculated electronic studies and Cartesian coordinates for reported structures. See https://doi.org/10.1039/d2ra03004g |
| This journal is © The Royal Society of Chemistry 2022 |