Open Access Article
Open Access ArticleZirconium-based cubic-perovskite materials for photocatalytic solar cell applications: a DFT study
Muhammad Khuram Shahzad *ab,
Syed Taqveem Mujtaba
*ab,
Syed Taqveem Mujtaba c,
Shoukat Hussainab,
Jalil Ur Rehman
c,
Shoukat Hussainab,
Jalil Ur Rehman ab,
Muhammad Umair Farooqd,
Muhammad Aslam Khanab,
Muhammad Bilal Tahirab and
Muhammad Ali Mahmoodef
ab,
Muhammad Umair Farooqd,
Muhammad Aslam Khanab,
Muhammad Bilal Tahirab and
Muhammad Ali Mahmoodef
aInstitute of Physics, Khwaja Fareed University of Engineering and Information Technology, Rahim Yar Khan, Pakistan. E-mail: khuram.shahzad@kfueit.edu.pk
bCenter of Theoretical and Computational Research, Khwaja Fareed University of Engineering and Information Technology, Rahim Yar Khan, Pakistan
cDepartment of Physics, Riphah International University, Faisalabad Campus, Faisalabad, Pakistan
dInstitute of Physics, The Islamia University of Bahawalpur, 63100 Pakistan
eCentre for Mathematical Modeling and Intelligent Systems for Health and Environment (MISHE), Atlantic Technological University Sligo, Ash Lane, F91 YW50 Sligo, Ireland
fDepartment of Computing and Electronic Engineering, Atlantic Technological University Sligo, Ash Lane, F91 YW50 Sligo, Ireland
First published on 27th September 2022
Abstract
The structural, electronic, optical, and mechanical characteristics of the cubic inorganic perovskites XZrO3 (X = Rb and K) based on Rb and K were studied using Cambridge Serial Total Energy Package (CASTEP)-based density functional theory (DFT) via the ultrasoft pseudo-potential (USP) plane wave and generalized gradient approximation (GGA)-Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional. The measured lattice parameters are 3.55 Å and 4.23 Å, and the band gaps of RbZrO3 and KZrO3 are 3.57 eV and 3.78 eV, respectively. Our results indicate that the compounds have indirect and wide bandgaps, making them useful for improving conductivity. It is observed that the compounds have anisotropic, ductile, and brittle natures. The anisotropic factor values of RbZrO3 and KZrO3 are 0.67067 and 0.87224, and their Poisson's ratios are 0.27356 and 0.25853, respectively. In terms of optical properties, they exhibited high optical absorption and conductivity and were active in the visible region for solar cell applications. These results indicate that they could be highly useful for light-emitting diodes (LEDs) and other reflection purposes owing to their indirect bandgap. The results of our investigation of RbZrO3 and KZrO3 present them as favorable materials for solar cell and LED applications.
1. Introduction
Owing to their natural abundance and relatively low cost, hybrid halide perovskites with the basic formula ABX3 (where A, B, and X are inorganic/organic cations, metal cations, and halogen anions, respectively) are frequently utilized with continuing popularity in a variety of fields.1 These materials are suitable for the fabrication of nano-crystals, nano-rods, nanowires, and nanoparticles, and are able to be altered to suit various constructions.1–5 As a result, technology based on perovskites is estimated to be more cost-effective and appropriate than silicon-based technology.6 The scientific community has especially interested in halide hybrid perovskites from 2009 to 2020. So the efficiency has improved from 3.8 percent to 23.7 percent in these era.7,11 In 2022, the highest solar cell efficiency has been recorded in Pb-containing methylammonium lead (Pb) halide materials.8–15 Additionally, the unresolved optoelectronic features, such as way of tall preoccupation and tunable bandgaps, slighter real crowds, leading opinion flaw and comprehensive pre-occupation range, advanced flexibility and lengthy control disperse as extents; and high optical absorption (HOA),16–18 of metallic halide perovskites are highly attractive attention from investigators.16–24 Therefore, as compared to other materials, these resources are abundant and affordable. Consequently, solar cells manufactured from these supplies will be more efficient than silicon-created solar cells.6 This class of semiconductors can also be observed in a variety of other electronic devices, such as LEDs, photo-detectors, and other solar-to-fuel conversion devices.25,26 Perovskites exhibit semiconducting and insulating properties, according to previous research.27,28 For the evaluation and improvement of specific devices, better and more fundamental knowledge of their semiconductor features is essential. Thus, investigating the organizational parameters, electrical and optical properties, and elastic behavior is crucial, as is an understanding of the comprehensive features of the system. Before the development of organic perovskites, various properties of several types of halide perovskites using metallic halides were investigated in recent years for use in applications such as solar cells and diodes.7 However, most existing perovskite complexes contain hazardous lead (Pb), which is undesirable.The present study was performed to examine the organizational, electrical, elastic, and optical aspects of the metallic perovskites RbZrO3 and KZrO3 based on Zr. To understand the electrical characteristics of a material, it is necessary to analyze its solid optical characteristics. The optical properties of materials can also be utilized to determine how the components react to light. Hence, a detailed understanding of the optical properties of materials employed in photocatalytic applications is essential for their advancement. In particular, the compounds RbZrO3 and KZrO3 have yet to be properly characterized in terms of their optical properties. To obtain appropriate perovskites for the above-mentioned purpose, we employed first-principles computations to study the organizational, electrical, elastic, and optical properties of the selected metallic oxide perovskite mixtures. This kind of work is very attractive in the context of photocatalytic solar cell applications.
2. Computational details
The structural, electronic, elastic, and optical properties of the materials were evaluated using an ultra-soft pseudo-potential (USP) plane-wave method. Without considering orbital structure approximation, assessments can be completed quickly and correctly using the USP. The calculations were performed using the density functional theory (DFT)-based Cambridge Serial Total Energy Package (CASTEP) code.29 As it is quicker and better than the other approximations, the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional of the generalized gradient approximation (GGA) was employed in this study.30 The anionic core is formed by the interaction of the nuclei with the inner electrons of the shell. The valence electrons can interact with other atoms. As a consequence, the electron–ion potential converges rapidly. The value of the total energy per atom was considered to be 1.0 × 10−5 eV per atom and 2.0 × 10−5 eV per atom for RbZrO3 and KZrO3 in this situation. As an outcome of the geometry optimization, the comparative temporary arranged atoms were maintained at 0.03 eV Å−1 and 0.05 eV Å−1 for RbZrO3 and KZrO3. The k-integration was performed on a Monk–Horst packing grid with a size of 8 × 8 × 8 and 6 × 6 × 6 for the RbZrO3 and KZrO3 k-point meshes, and the limit cutoff energy was set at 340.0 eV and 300.0 eV for RbZrO3 and KZrO3 throughout the whole Brillouin zone. The all-out ionic movement reserved inside a series of 0.001 Å and 0.002 Å for RbZrO3 and KZrO3 during the geometry optimization procedure. The geometries were then improved using the BFGS approach as the Pulay density mixing methodology. The strain amplitude was set to a maximum value of 0.05 GPa and 0.1 GPa for RbZrO3 and KZrO3 with a total energy of 2 × 10−4 eV and 4 × 10−6 eV per atom for computing the elastic constants. The maximum force was kept constant at 0.06 eV Å−1 and 0.01 eV Å−1 for RbZrO3 and KZrO3, and the maximum ionic displacement was kept at 2 × 10−4 Å and 4 × 10−4 Å for RbZrO3 and KZrO3 during the determination of the elastic constants. The outside stress and relative external hydrostatic pressure were kept at zero during geometry optimization. After creating the unit cell, we optimized the geometry and calculated all of the required characteristics.3. Results and discussion
3.1. Structural analysis
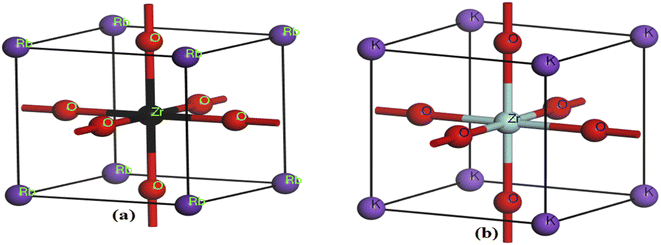
First, the geometries of the built-in unit cell were optimized for our compounds with the space group Pm3m (221). The Rb and K atomic positions stayed fixed at (0.0, 0.0, 0.0); moreover, the Zr atomic positions were kept at (0.5, 0.5, 0.5), whereas the O atoms were kept at (0.0, 0.5, 0.5). Keeping the total energy of the cell at a minimum, the equilibrium lattice parameters were calculated using the Murnaghan equation of state, and the results were obtained over a wide range of lattice constants.31,32 Volume variation exists between the unit and equilibrium cells. A change in the structural characteristics will be noted if different X atoms are used. There are two major types of perovskite materials, oxides and halides, in which X is either an O atom or F, Cl, Br, etc. When the X element is varied in ABX materials (X = O or Cl, Br, and F), the structural characteristics change with the change in the element. The characteristics change based on the atomic variations in the element. That is, if an atom is changed, then the structural and other properties will also change. In the present work, the lattice parameters were modified by substitution of an atom, and the unit cell volume also changed as a result of the changes in the lattice parameters. The lattice parameters for RbZrO3 and KZrO3 were discovered to be 3.55 Å and 4.23 Å, respectively, using the optimized geometry (Fig. 1). As shown in Table 1, these numbers are comparable to previously available statistics in many ways. This illustrates the accuracy of our first-principles calculations.| Compound | Lattice parameter (Å) | Volume (Å3) | Bandgap (eV) | Transition type |
|---|---|---|---|---|
| RbZrO3 | 3.55 | 44.738 | 3.57 | Indirect |
| KZrO3 | 4.23 | 75.818 | 3.78 | Indirect |
| BaSiO3 | 3.76 | 53.15 | 4.1 | Direct33 |
3.2. Band structure and DOS
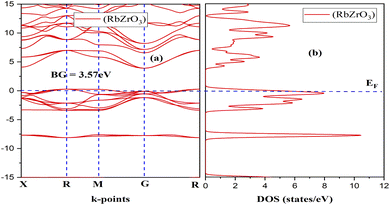
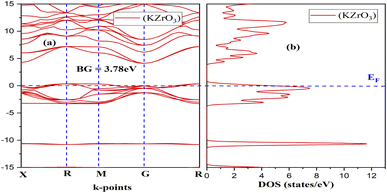
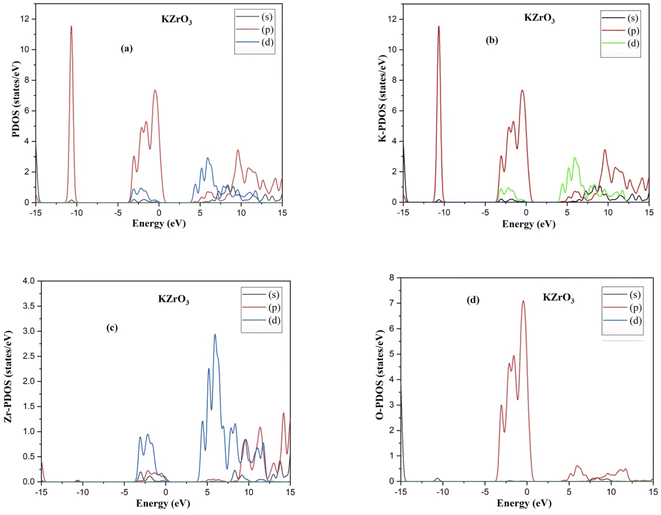
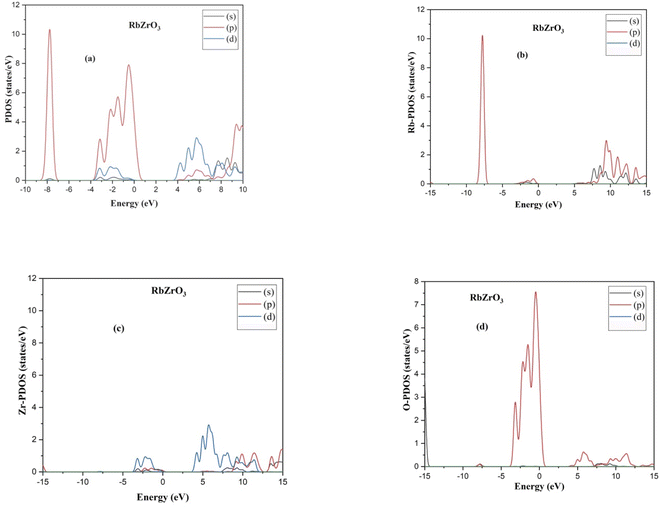
Fig. 2 and 3 depict the band structure and the corresponding total density of states for RbZrO3 and KZrO3, respectively. The electronic band structure reveals the energy range in which electrons can exist (conduction band) as well as the region in which the electron availability is zero (valence band). The EF distinguishes between the conduction and valence bands. The valence bands are located underneath the EF, whereas the conduction band is located above it. The bandgaps were calculated by subtracting the valence band maxima (VBM) from the conduction band minima (CBM). A semiconductor material may possess a direct or an indirect energy bandgap depending upon its band structure. Bandgaps are considered to be direct bandgaps if the maxima of the valence band occur precisely at the minima of the conduction band. When the valence band maxima and conduction band minima are not exactly aligned, an indirect bandgap arises. The VBM and CBM are shown to be different from each other for both materials under investigation, i.e., KZrO3 and RbZrO3. Both the compounds under examination have an indirect bandgap as a result of this.The indirect band gaps of RbZrO3 and KZrO3 are 3.78 eV and 3.57 eV, respectively. The PDOS of the compounds under study are depicted in Fig. 4 and 5. For RbZrO3 and KZrO3, the primary TDOS peak emerges at −0.49 eV with a value of 7.45 and −0.465 eV with a value of 7.94, respectively (Table 2).
| Compound Species | s | p | d | Total | Charge | Bond | Population | Length (Å) | |
|---|---|---|---|---|---|---|---|---|---|
| RbZrO3 | Rb | 1.85 | 5.97 | 0.00 | 7.82 | 1.18 | — | — | — |
| Zr | 2.44 | 6.48 | 1.97 | 10.89 | 1.11 | O–Zr | 0.94 | 2.12 | |
| O | 1.89 | 4.88 | 0.00 | 6.77 | −0.77 | — | — | — | |
| KZrO3 | K | 1.91 | 5.93 | 0.00 | 7.84 | 1.16 | O–K | −0.17 | 2.99 |
| Zr | 2.44 | 6.45 | 1.97 | 10.86 | 1.14 | O–Zr | 0.93 | 2.11 | |
| O | 1.89 | 4.88 | 0.00 | 6.77 | −0.77 | O–O | −0.04 | 2.99 | |
The p-states of both compounds are represented by this primary peak. The d- and p-states make up the valence bands for the two materials in the energy range of −15.0 eV to 0 eV, with the d-state appearing beyond 0 eV. The s- and p-states create the conduction band for RbZrO3 and KZrO3 in the 0 to 15 eV energy range, whereas the d-states are missing. The compound RbZrO3 is effectively presented which is composed of solely s-states beside the p-states, as the d-states exist as an inattentive. At the Fermi level, no sharp peak in the density of states is observed, which indicates that the materials are impure semiconductors.34 However, the materials possess small energy bandgap values, which indicates that these materials will not be insulators. Therefore, these compounds will act as semiconducting materials, which is a critical factor for their use in optoelectronics.
3.3. Optical properties
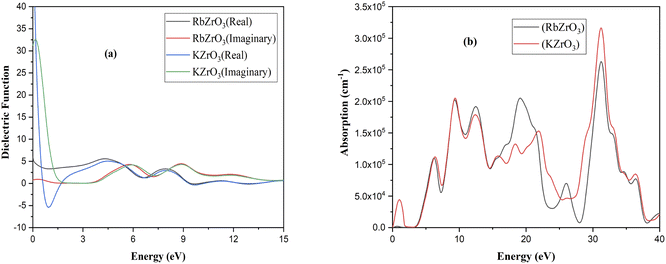
In order to appraise the optical features of RbZrO3 and KZrO3, deflective index, energy loss, conduction, and the non-conductor purposes are analyzed and described in detail. Specific optical characteristics are affected by the frequency. These attributes are the outcomes of the interaction of the material with electromagnetic waves, a phenomenon known as wave–matter interaction. Fig. 6 shows the observed optical properties of RbZrO3 and KZrO3. In photo-sensitive behaviour, the dielectric function ε(ω) is calculated, which is given by the expression:| ε(ω) = ε1(ω) + iε2(ω) |
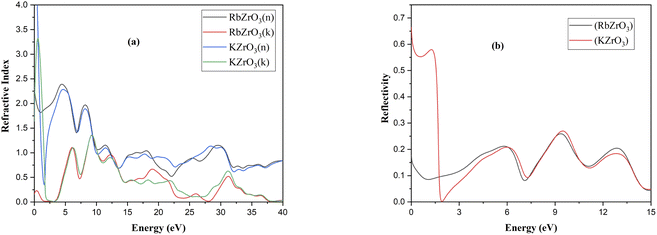
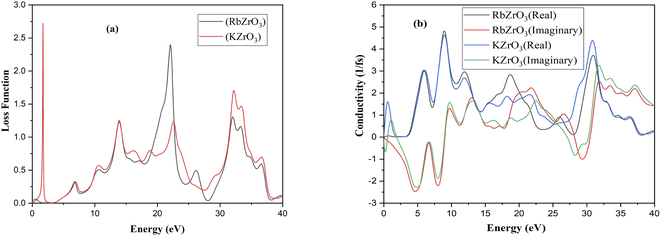
Using the appropriate formulae,35 further optical properties such as the refractive index n(ω), energy loss L(ω), absorption coefficient I(ω), and reflectivity R(ω) can be determined. RbZrO3 shows higher reflectivity at zero eV, with a value of 0.665, and a minimum reflectivity of zero at 1.91 eV (Fig. 7). The reflectivity of KZrO3 is 0.15 at zero eV, and at 9.319 eV, it is 0.259, which is higher than that of RbZrO3 at 9.319 eV. The optical absorption coefficient of the compounds RbZrO3 and KZrO3 are an estimation that specifies the light of a specific wavelengths. Furthermore, it gives information about the ideal solar energy transformation ability, which is crucial for the real-world application of sunlight-based cell materials. RbZrO3 and KZrO3 have absorption peaks located at 0.67 eV and 1.00 eV, respectively. At 2.75 eV, both compounds have absorption values of zero, as shown in the absorption spectrum in Fig. 6, and the maximum peaks occur at 31.35 eV, 19.13 eV and 9.46 eV for RbZrO3, while for KZrO3 the maximum peaks are located at 31.25 eV, 9.22 eV and 12.35 eV. RbZrO3 has a conductivity (real) peak at 0.59 eV and an imaginary peak at 9.61 eV (Fig. 8). The major conductivity (real) peak is located at 8.92 eV, and the major conductivity (imaginary) is located at 31.85 eV for RbZrO3, while for KZrO3, the major conductivity (real) peak is found at 6.03 eV and the major conductivity (imaginary) peak is located at 1.15 eV. At 0 eV, the conductivity (real) approaches 0 for both compounds. RbZrO3 and KZrO3 play a significant role in conductivity for real part; in addition, the situation supper most-worst this 8.92 at 14.12 eV. The real part of the dielectric constant corresponds to the ability of a material to interact with an electronic field (store and transmit energy) without absorbing it, while the imaginary part represents its capacity to permanently absorb energy from a time-varying electric field. The real portion of the dielectric function for RbZrO3 and KZrO3 is located at 4.31 eV and 4.40 eV, respectively; however, the imaginary part of the dielectric function for RbZrO3 and KZrO3 is found at 5.83 eV and 0.15 eV, respectively. RbZrO3 and KZrO3 have dielectric function (real) values of 5.50 and about 50.0, respectively, at 0 eV. Compared to the other compound (KZrO3), RbZrO3 shows a greater dielectric function (real) value. For RbZrO3 and KZrO3, the major peaks of the loss function are located at 22.03 eV and 1.69 eV, respectively. Other major peaks of the loss functions of RbZrO3 and KZrO3 are present at 32.01 eV and 13.95 eV, and 32.32 eV and 13.95 eV, respectively. Both compounds exhibit loss function values of 0 at 0 eV. In the case of RbZrO3, the main refractive index (n) peak is located at 4.35 eV, and the major refractive index (k) peak is located at 9.22 eV. For KZrO3, the main refractive index (k) peak is at 0.47 eV, and the major refractive index (n) peak is located at 0 eV with a value of 6.0. For RbZrO3, the highest refractive index (k) value is 1.34 and the highest refractive index (n) value is 2.38. At 0 eV, the values of refractive index (n) for KZrO3 is 0.0 and 2.26, and for refractive index (k) is 3.29 and 1.34, respectively. As a result, compared to the other compounds, KZrO3 has a greater refractive index (n) values. The transmittance is extremely dependent on the related energies and wavelength. Since the light determination is captivated, it shows no transmittance at higher energies where the wavelength is lower. It is due to irrelevant microelectronic changes by a choice of short energies and fairly out conduction by subordinate through lower wavelengths. Due to irrelevant microelectronic change over by a choice of short energies nearby resolves and fairly out conduction by subordinate energies through slower wavelengths. The studied compounds exhibit remarkable absorption peaks in the energy range of 28–34 eV, with the largest peak at 31.35 eV. It is also identified that a higher maximum absorption value is achieved when K is substituted for Rb, similar to in previous work.36 The optical and electronic properties indicate that these complexes are appropriate for application in the areas of light-emitting semiconductor diodes and solar cells, although RbZrO3 is considered to play a more important role among the two due to its having a narrower band gap. The essential purpose of our research into these DFT methods was to improve the electrical contact, to reduce the defect density and carrier loss during transmission, and to achieve high power conversion efficiency. Hence, it can be concluded that our calculated results are useful in the context of solar cell applications.
3.4. Mechanical properties
The reaction of a crystal with respect to the applied forces can be determined from the elastic properties of a material. Furthermore, these properties are also useful to determine the mechanical behavior of a compound. Subsequently, for deeper examination of the compounds, their mechanical nature and elastic properties were investigated by use of elastic constants. Basically, C11, C12, and C44 are numbers of the three-dimensional structure compounds, and are listed Table 3.| Compounds | C11 | C12 | C44 | A |
|---|---|---|---|---|
| RbZrO3 | 259.71 | 61.81 | 47.62 | 0.67 |
| KZrO3 | 258.24 | 50.26 | 45.40 | 0.87 |
The strength of a substance is a key factor to characterize its nature. Based on the relationships37,38 C11 + 2C12 > 0; C11 − C12 > 0; C44 > 0, both the measured compounds were found to be mechanically stable.
A material is considered isotropic if the adaptable anisotropy factor A is identical to 1, while a value deviating from 1 indicates a substantial anisotropic nature. Because their A values deviate from 1, both these compounds are considered to be anisotropic, as shown in Table 3. To evaluate the hardness of materials, the bulk modulus B is utilized. RbZrO3 has a higher bulk modulus value, which demonstrates that it is the harder of the complexes under observation. The high shear modulus (G) and Young's modulus (E) values confirm the hardness of RbZrO3 and KZrO3. It can be determined whether a compound is ductile or brittle in nature by using Poisson's ratio (σ). A material is ductile if the value of σ is greater than 0.26; otherwise, the material is brittle. The Poisson's ratio values indicated that both compounds under examination are malleable. To determine whether a compound will be malleable or brittle in nature, the B/G38–40 ratio is also utilized. If the ratio is larger than 1.75, the material is said to be ductile; otherwise, it is said to be brittle. The B/G ratio indicates a brittle and ductile nature for KZrO3 and RbZrO3, respectively (Table 4).
| Compounds | B | E | G | σ | B/G |
|---|---|---|---|---|---|
| RbZrO3 | 127.78 | 173.60 | 68.15 | 0.27 | 1.87 |
| KZrO3 | 119.59 | 173.27 | 68.83 | 0.25 | 1.73 |
4. Conclusion
In the modern age, energy production has become a major problem because of energy demand and consumption. Researchers and scientists can play a role in this field and try to produce energy through various experiments and theoretical studies. In this work, perovskite materials were investigated via a DFT study. The structural, electronic, optical, and mechanical characteristics of the cubic inorganic perovskites XZrO3 (X = Rb and K) based on Rb and K were studied using Cambridge Serial Total Energy Package (CASTEP)-based density functional theory (DFT) via the ultrasoft pseudo-potential (USP) plane wave and generalized gradient approximation (GGA)-Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional. The measured lattice parameters and band gaps of KZrO3 and RbZrO3 are 4.23 Å, 3.55 Å and 3.78 eV, 3.57 eV, respectively, which are better than earlier computational research due to high bandgap and low lattice parameters. Our results indicate that these compounds have indirect and narrow band gaps, making them useful for improving conductivity. It is observed that the compounds have anisotropic, ductile, and brittle natures. The anisotropic factor values of RbZrO3 and KZrO3 are 0.67067 and 0.87224, and their Poisson's ratios are 0.27356 and 0.25853, indicating their ductile and brittle nature, respectively. They demonstrated high optical absorption and conductivity, which existed in the visible region for solar cell applications. Our results have potential applications in the field of LEDs.Conflicts of interest
There are no conflicts of interests.References
- J. S. Lee, J. H. Lee and S. H. Hong, Sens. Actuators, B, 2003, 3, 663–668 CrossRef
.
- A. Gherriche, A. Bouhemadou, Y. Al-Douri, S. Bin-Omran, R. Khenata and M. A. Hadi, Mater. Sci. Semicond. Process., 2021, 131, 105890–105896 CrossRef CAS
.
- T. Zhang, L. Yang, C. Zhang, Y. Feng, J. Wang, Z. Shen and Q. Chi, Mater. Horiz., 2022, 9(4), 1273–1282 RSC
.
- X. Chen, D. Wang, T. Wang, Z. Yang, X. Zou, P. Wang and Z. Wei, ACS Appl. Mater. Interfaces, 2019, 11(36), 33188–33193 CrossRef CAS PubMed
.
- M. Wang, C. Jiang, S. Zhang, X. Song, Y. Tang and H. Cheng, Nat. Chem., 2018, 10(6), 667–672 CrossRef CAS PubMed
.
- A. Maho, M. Lobet, N. Daem, P. Piron, G. Spronck, J. Loicq, R. Cloots, P. Colson, C. Henrist and J. Dewalque, ACS Appl. Energy Mater., 2021, 4(2), 1108–1119 CrossRef CAS
.
- X. Zhang, Y. Tang, F. Zhang and C. Lee, Adv. Energy Mater., 2016, 6(11), 1502588 CrossRef
.
- K. Bidai, M. Ameri, I. Ameri, D. Bensaid, A. Slamani, A. Zaoui and Y. Al-Douri, Arch. Metall. Mater., 2017, 5, 1024–1030 Search PubMed
.
- B. Kada, M. Ameri, A. Zaoui, I. Ameri and Y. Al-Douri, Chin. J. Phys., 2016, 54, 678–694 CrossRef
.
- T. Wei, Z. Wang, Q. Zhang, Y. Zhou, C. Sun, M. Wang and S. Qin, CrystEngComm, 2022, 24, 5014–5030 RSC
.
- C. Yu, X. Chen, N. Li, Y. Zhang, S. Li, J. Chen and X. Deng, Environ. Sci. Pollut. Res., 2022, 29(13), 18423–18439 CrossRef CAS PubMed
.
- H. Hiramatsu, H. Yusa, R. Igarashi, Y. Ohishi, T. Kamiya and H. Hosono, Inorg. Chem., 2017, 17, 10535–10542 CrossRef PubMed
.
- F. Yu, Z. Zhu, C. Li, W. Li, R. Liang, S. Yu and Z. Zhang, Appl. Catal., B, 2022, 314, 121467 CrossRef CAS
.
- X. L. Wang, Z. G. Qu, T. Lai, G. F. Ren and W. K. Wang, J. Power Sources, 2022, 525, 231121 CrossRef CAS
.
- N. Guechi, A. Bouhemadou, Y. Medkour, Y. Al-Douri, R. Khenata and S. Bin-Omran, Philos. Mag., 2020, 23, 3023–3039 CrossRef
.
- J. Zhao, Z. Li, M. Wang, Q. Wang and Z. Jin, J. Mater. Chem. A, 2021, 10(9), 6029–6049 RSC
.
- L. Yang, Q. Dai, L. Liu, D. Shao, K. Luo, S. Jamil and X. Wang, Ceram. Int., 2020, 46(8), 10917–10924 CrossRef CAS
.
- K. Deng, Q. Chen and L. Li, Adv. Funct. Mater., 2020, 30(46), 2004209 CrossRef CAS
.
- Y. H. Xu, H. G. Zhang, F. B. Yang, L. Tong, D. Yan, Y. F. Yang, J. Ren, L. L. Ma and Y. Wang, Int. J. Energy Res., 2022, 46, 1–20 CrossRef
.
- D. Shi, Y. Chen, Z. Li, S. Dong, L. Li, M. Hou and N. Zhao, Small Methods, 2022, 2200329 CrossRef CAS
.
- C. W. Huang, W. Ren, V. C. Nguyen, Z. Chen, J. Wang, T. Sritharan and L. Chen, Adv. Mater., 2012, 30, 4170–4174 CrossRef
.
- M. K. Shahzad, Y. Zhang, L. Cui, L. Liu, M. K. Butt and H. Li, RSC Adv., 2018, 8, 19362–19368 RSC
.
- H. Ling-yi and W. R. L. Lambrecht, Phys. Rev. B, 2016, 19, 195211–195216 Search PubMed
.
- M. K. Zoubir, B. Fadila, B. Keltoum, A. Ibrahim, B. Lamia Farah, Y. Al-Douri and A. Mohammed, Mater. Test., 2021, 6, 537–542 CrossRef
.
- E. E. Giles, M. G. Paternò, R. J. Sutton, A. Zampetti, A. A. Haghighirad, F. Cacialli and H. J. Snaith, J. Mater. Chem. A, 2015, 39, 19688–19695 Search PubMed
.
- K. Thirumal, H. Ding, C. Yan, W. L. Leong, T. Baikie, Z. Zhang and M. Sherburne, J. Mater. Chem. A, 2015, 47, 23829–23832 Search PubMed
.
- R. Parthiban, D. H. Lim, B. Kim, S. H. Lee, M. S. Lee and J. S. Lee, Chem. Commun., 2016, 10, 2067–2070 Search PubMed
.
- H. Li, J. Tang, Y. Kang, H. Zhao, D. Fang, X. Fang and Z. Wei, Appl. Phys. Lett., 2018, 113(23), 233104 CrossRef
.
- R. W. Robinson, Y. Han, H. Zhang, T. Ablekim, I. Khan, K. A. Persson and A. Zakutayev, Chem. Rev., 2020, 120(9), 4007–4055 CrossRef
.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef
.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 4A, A1133 CrossRef
.
- R. Padmavathy, A. Amudhavalli, M. Manikandan, R. Rajeswarapalanichamy, K. Iyakutti and A. K. Kushwaha, J. Electron. Mater., 2019, 2, 1243–1251 CrossRef
.
- H. Liu, J. Yang, Y. Jia, Z. Wang, M. Jiang, K. Shen and W. Zhan, Environ. Sci. Technol., 2021, 55(15), 10734–10743 CrossRef CAS PubMed
.
- H. L. yi and W. R. L. Lambrecht, Phys. Rev. B, 2013, 16, 165203 Search PubMed
.
- J. Liu, Y. Yin, K. Wang, P. Wei, H. Lu, C. Song and W. Huang, iScience, 2022, 25(4), 104090 CrossRef CAS PubMed
.
- J. ur Rehman, M. Usman, S. Sajid, M. Sagir, M. B. Tahir, A. Hussain and I. Alam, Comput. Theor. Chem., 2022, 1209, 113624 CrossRef CAS
.
- H. Hiramatsu, H. Yusa, R. Igarashi, Y. Ohishi, T. Kamiya and H. Hosono, Inorg. Chem., 2017, 17, 10535–10542 CrossRef PubMed
.
- D. M. Hoat, J. R. Silva and A. Mendez Blas, Solid State Commun., 2018, 275, 29–34 CrossRef CAS
.
- Z. Huang, P. Luo, H. Zheng and Z. Lyu, J. Alloys Compd., 2022, 908(5), 164599 CrossRef CAS
.
- S. F. Pugh, Philos. Mag., 1954, 45(367), 823–843 Search PubMed
.
| This journal is © The Royal Society of Chemistry 2022 |