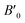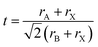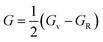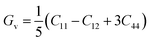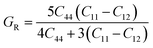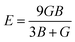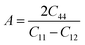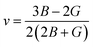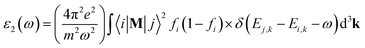Open Access Article
Open Access ArticleStructural, electronic, magnetic and elastic properties of xenon-based fluoroperovskites XeMF3 (M = Ti, V, Zr, Nb) via DFT studies
Abdullaha,
Muhammad Sajjad*a,
Umar Ayaz Khanb,
Hamid Ullahc,
Aiyeshah Alhodaibd,
Mongi Amamief,
Vineet Tirth gh,
Abid Zaman
gh,
Abid Zaman *i and
Shaziab
*i and
Shaziab
aDepartment of Physics, Kohat University of Science and Technology Kohat, 26000, Pakistan. E-mail: sajjadqureshi76@gmail.com
bDepartment of Physics, Government Post Graduate College Karak, 27200, Pakistan
cDepartment of Physics, Riphah International University, Lahore Campus, Pakistan
dDepartment of Physics, College of Science, Qassim University, Buraydah 51452, Saudi Arabia
eDepartment of Chemistry, College of Sciences, King Khalid University, P.O. Box 9004, Abha, Saudi Arabia
fLaboratoire des Matériaux et de l'Environnement pour le Développement Durable LR18ES10, 9 Avenue Dr. Zoheir Safi, 1006, Tunis, Tunisia
gMechanical Engineering Department, College of Engineering, King Khalid University, Abha 61421, Asir, Kingdom of Saudi Arabia
hResearch Center for Advanced Materials Science (RCAMS), King Khalid University, Guraiger, P.O. Box 9004, Abha-61413, Asir, Kingdom of Saudi Arabia. E-mail: zaman.abid87@gmail.com
iDepartment of Physics, Riphah International University Islamabad, 44000, Pakistan
First published on 28th September 2022
Abstract
In this work, the structural, electronic, magnetic and elastic properties of the xenon-based fluoroperovskites XeMF3 (M = Ti, V, Zr, Nb) have been studied using density functional theory. The structural study reveals that all the perovskites have stable structures. A half-metallic nature is observed due to the presence of a band gap in only the spin-down channel. The result indicates that the considered compounds are ferromagnetic materials with integer magnetic moments. The elastic parameters were studied to obtain their elastic properties. It is noted that all compounds have an anisotropic nature and show ductility. The optical characteristics show that these compounds are good optical absorbers at high energy. Furthermore, we suggest that these compounds could be good candidates for spintronic and optoelectronic devices.
1. Introduction
In order to understand the technological importance of a material, the physical properties of that material should first be studied. On the basis of the physical properties, one can demonstrate its technical importance. Among the various classes of materials, perovskites are a most important class; they were discovered in 1839 and have many technological applications. The general formula for a perovskite is ABX3, where A is a cation with a large size, B is a cation with a small size, and X may be a halide or oxygen. When X is fluorine, the resultant perovskite is known as a fluoroperovskite. This class has many applications in various fields due to their large band gaps. They have received attention in the fields of scintillation materials, optical lithography and radiation dosimeters, as well as in the semiconductor industry.1–3 Various applications in these fields have made SrLiF3, RbCaF3, KCaF3, BaLiF3 and other materials of this class of great interest, but to explore the physical properties of this class, theoretical and experimental investigation is required.AgZnF3 and AgMgF3 were studied by G. Murtaza et al.4 They reported that these materials have a large energy absorption range, which may make them useful in numerous devices. F. Hamioud et al. investigated the various properties of TlMnCl3 and TlMnF3 through the FP-LAPW technique.5 They reported that these compounds are elastically stable, ductile and have an anisotropic nature. These compounds are semiconductors with indirect band gaps and have a ferromagnetic nature.
D. Chenine et al. investigated NaVF3 and NaCoF3 for the first time using DFT.6 They concluded that both are mechanically stable. A ferromagnetic nature was reported for NaVF3 and NaCoF3. Furthermore, it was reported that these compounds have a half-metallic nature due to their spin-polarized band structure. Injecting a spin-polarized current into electronic devices is important, and the most applicable materials for this purpose the materials that are fully polarized at the Fermi level, meaning those materials that have no gap in the spin-up channel while a gap is present in the spin-down channel.7,8 The spin-polarized current increases the efficiency of magneto-electronic appliances. Different compounds showing these properties have been studied by researchers, including perovskites,9 magnetic semiconductors,10 and various Heusler compounds.11 These materials are most applicable in the field of spintronics.
Titanium- and zirconium-based perovskites were studied by Waqas Zulfiqar et al.12 and a wide electronic band gap was found for both. The authors noted the good agreement of the theoretical data with the experimental results. Moreover, they suggested that Zr- and Ti-based perovskites would be useful in designing new photo-catalysts.
Due to their power conversion efficiency, perovskite materials in solar cells have gained a great deal of attention recently.13 To improve the power conversion efficiency, different compositions of perovskites have been synthesized. In spite of their advantages, they have some drawbacks, such as their toxic nature and instability to radiation and moisture. These drawbacks have motivated researchers to investigate new perovskites.14–18 To tackle the above-stated problem, in this work, we investigate the xenon-based fluoroperovskites XeMF3 (M = Ti, V, Zr, Nb) and explore their structural, electronic, magnetic and elastic properties. We have report the above properties of the compounds for the first time, as they have not been previously studied. The results presented in this work may provide useful insights regarding the implementation of these materials in the field of spintronics.
2. Computational techniques
Simulation studies for the computation of various properties such as structural, electronic, magnetic and elastic properties were performed using the general framework of DFT within the Wien2k code.19 This is one of the most effective DFT-based computational techniques for examining the ground-state properties of various materials. Simulations were carried out using the GGA+U exchange–correlation potential.20 To represent the crystals, the muffin-tin (MT) model was used. Electrons are grouped as core and valence electrons. The charge density for the valence electrons is found in the interstitial region (IR), but it is restricted to non-overlapping spheres of radius RMT for the core electrons.21 The energy gap between the core and valence bands is taken as 6 Ry. The value of RMT was chosen as 5 for all compounds. The structural parameters were determined through the Birch–Murnaghan equation by fitting the energy versus volume variation to it. The value of Gmax was taken as 12, and the number of K-points was 2000.3. Results and discussion
3.1 Structural properties
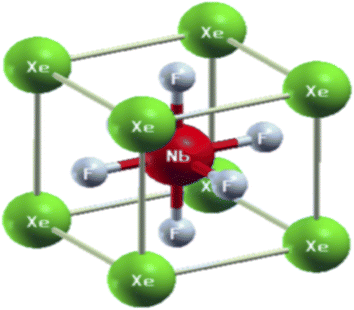
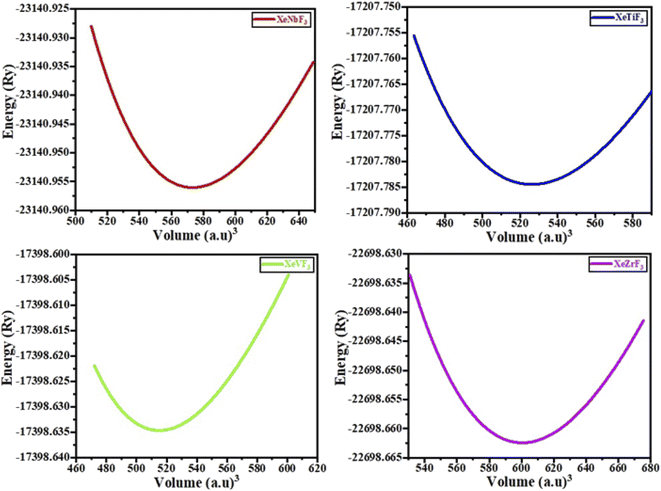
The physical properties of a material depend on its crystal structure. To determine the stability and ground-state properties of the compounds XeMF3 (M = Ti, V, Zr, Nb), their atomic arrangements were studied by considering the positions of the atoms Xe at (0, 0, 0), M at (0.5, 0.5, 0.5) and F at (0, 0.5, 0.5) (Fig. 1). The energy versus volume curves were obtained for the abovementioned compounds and are plotted in Fig. 2. The lattice constant, bulk modulus and pressure derivative of the bulk modulus were determined using the Birch–Murnaghan equation by fitting the energy versus volume variation to it.22 All these parameters are listed in Table 1. From Table 1, it is clear that XeNbF3 is the most stable of the investigated compounds with a minimum energy of −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140.89 Ry. XeNbF3 also has a high bulk modulus value, indicating its hardness and incompressibility.
140.89 Ry. XeNbF3 also has a high bulk modulus value, indicating its hardness and incompressibility.
The perovskite structure of these compounds was confirmed from the tolerance factor. The tolerance factor can be obtained through the following expression:
The thermodynamic stability of a material and whether it can be synthesized experimentally or not can be determined from the formation energy, which is found through the relationship:
| ΔHf = Etot − μA − μB − 3μX |
3.2 Electronic properties
To determine their electronic structure, we calculated the band structure and density of states for all the compounds XeMF3 (M = Ti, V, Zr, Nb). The obtained graphs of the band structure and DOS are plotted in Fig. 3 and 4, respectively. In Fig. 3, both the spin-up and spin-down graphs for all compounds are represented. These graphs show that none of the compounds have a gap between the valence and conduction band in the spin-up channel, while a band gap exists between the valence and conduction band in the spin-down channel, indicating their half metallic nature and 100 percent spin polarization over the Fermi level EF. A direct band gap (Γ–Γ) is present in the spin-down channels for all the investigated compounds. The values of the band gaps for XeMF3 (M = Zr, Ti, V, Nb) are 5.1 eV, 3.4 eV, 5.5 eV, and 4.6 eV, respectively.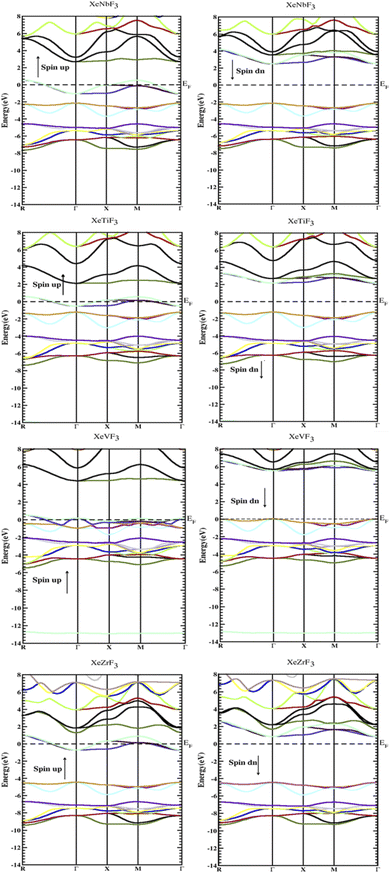 | ||
| Fig. 3 Electronic band gaps of the compounds XeMF3 (M = Ti, V, Zr, Nb) obtained through the GGA+U approximation. | ||
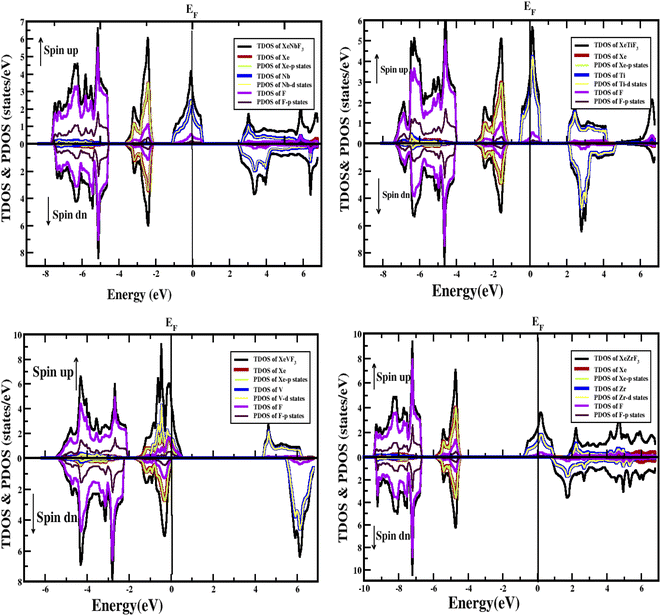
Furthermore, the densities of states were calculated to interpret the interactions among the different states of the compounds. The obtained graphs for the DOS are plotted in Fig. 4. From the DOS graphs, it is also clear that all compounds were spin-polarized and half-metallic. From Fig. 4, we can observe that the Xe-p state has a greater contribution in the energy range of −2 to −3.5 eV, the F-p state has a contribution in the range of −4 to −8 eV, and the M-d states are dominant in the range of −1 to 9 eV. Near the Fermi level, the M atoms are dominant and increase the conductivity of the compounds. In addition, F also has a contribution in the conduction but is not dominant. The energy band gap is inversely proportional to the number of orbitals or number of nucleons, and for all of our compounds, this is confirmed from the density of states and band structure.
3.3 Magnetic properties
The magnetic properties of a material can be explored from its electronic configuration. We can determine the total magnetization from the valence electrons using the relationship Mt = (Zt − 18)μB.25 Here, Mt is the total magnetization, Zt is the number of valence electrons, and μB is the Bohr magneton. The electronic configurations of the studied compounds are [Xe] 4d105s25p6, [F] 2s22p5 and [Ti] 3d24s2, [V] 3d34s2, [Zr] 4d25s2 and [Nb] 4d45s1. From their electronic configurations, it can be observed that they have unpaired electrons, and therefore, they will have some sort of magnetization. The partial and total magnetic moments were computed for the determination of their magnetic natures. The calculated magnetic moments are listed in Table 2. From the values in the table, it is clear that the M site atom has a main role in the magnetization. As niobium and vanadium have more unpaired electrons, they have more magnetization as compared to zirconium and titanium. The values of total magnetization for XeMF3 (M = Ti, V, Zr, Nb) are integers, indicating their ferromagnetic and half-metallic nature.26,27| Magnetic parameter | XeTiF3 | XeVF3 | XeZrF3 | XeNbF3 |
|---|---|---|---|---|
| mint | 0.256 | 0.320 | 0.487 | 0.688 |
| m*1 | 0.001 | 0.0021 | 0.003 | 0.004 |
| m*2 | 0.280 | 1.801 | 0.509 | 1.343 |
| m*3 | −0.024 | −0.084 | −0.001 | −0.0027 |
| mtot | 1.00 | 2.00 | 1.00 | 2.00 |
3.4 Elastic properties
The mechanical properties of materials can be obtained from their elastic constants, as the elastic constants determine the response of the crystal to an applied force. Using the elastic constants, various mechanical properties can be investigated, such as the structural stability, Poisson ratio, bulk modulus, Young's modulus, anisotropy, and bonding nature.All the XeMF3 (M = Ti, V, Zr, Nb) compounds are cubic, and thus the three elastic constants C11, C12, and C44 are sufficient to determine their mechanical properties. These constants were obtained using the IR Elast package in Wien2k and correlated with previous studies. The computed elastic parameters are presented in Table 3. To confirm the mechanical stability of the compounds, the Born criteria were used, according to which:28
| C11, C44 > 0, C12 < B < C11 |
| C11 − C12 > 0, C11 + 2C12 > 0 |
| Compound | C11 | C12 | C44 | B | A | G | E | v | B/G |
|---|---|---|---|---|---|---|---|---|---|
| Generalized Gradient Approximation (GGA) | |||||||||
| XeZrF3 | 167.30 | 33.88 | 24.58 | 77.98 | 0.36 | 4.36 | 12.84 | 0.70 | 17.88 |
| XeTiF3 | 162.51 | 47.66 | 37.50 | 85.80 | 0.65 | 0.98 | 2.92 | 0.74 | 87.55 |
| XeNbF3 | 151.24 | 45.31 | 29.501 | 79.72 | 0.54 | 1.66 | 4.95 | 0.73 | 48.02 |
| XeVF3 | 119.10 | 52.08 | 146.50 | 73.28 | 4.16 | 18.16 | 50.32 | 0.55 | 4.03 |
The elastic constants are positive and fulfill the above criteria, indicating their mechanical stability.
The two important elastic parameters shear modulus and bulk modulus provide detailed information about the stiffness and compressibility of a material, respectively. The bulk modulus indicates the resistance to fracture of a material, while the shear modulus indicates the opposition of the material to plastic deformation. The values of B and G were calculated using the following equation and are presented in Table 3.
| B = (C11 + 2C12)/3 |
The calculated bulk modulus and shear modulus values are presented in Table 3. From the results in Table 3, it can be observed that the bulk modulus value of XeTiF3 is the greatest, showing its high compressibility, while the value of shear modulus is greatest for XeVF3, indicating its stiffness.
The ratio of tensile stress to tensile strain is called Young's modulus. The value of Young's modulus can be obtained through the following expression:
It is an important elastic parameter representing the stiffness of a compound.29 For a greater value of E, the stiffness will be greater. The results in Table 3 confirm that the value of E is greatest for XeVF3, and show consistency with the shear modulus results.
The Zener anisotropic factor A represents the growth of micro-cracks in a material.30 For isotropic materials, the value of A is unity. Deviation from unity indicates the anisotropic nature of a material. The greater the value of A, the greater the chances of micro-cracks in the material. A can be calculated from the following equation:
The computed values of A for XeMF3 (M = Ti, V, Zr, Nb) are presented in Table 3. For all compounds, the value of A is greater than 1, indicating their anisotropic nature.
The Poisson ratio v and Pugh ratio B/G represent the ductility and brittleness of a material.31,32 For materials with a ductile nature, the value of the Poisson ratio should be greater than 0.26, while the value of Pugh ratio should greater than 1.75; otherwise, the material is brittle.33 The value of v can be found using the following expression.
From the results in Table 3, it can be noted that v > 0.26 and B/G > 1.75 for all of the compounds under study, showing that all the investigated materials are ductile. The Poisson ratio v also indicates the bonding nature of materials. Their v values of >0.25 show the presence of inter-atomic bonding between the atoms of the materials.
3.5 Optical properties
The well-known dielectric function ε(ω) = ε1(ω) + iε2(ω) is used to describe the optical response of a medium at different photon energies. The imaginary part ε2(ω) is directly related to the electronic band structure and describes the absorptive behaviour of a material. It can be found through the formula:where M is the dipole matrix, i and j are the initial and final states, respectively, fi is the Fermi distribution function for the i-th state, and Ei is the energy of electron in the i-th state with crystal wave vector k. The real part ε1(ω) of the dielectric function can be extracted from the imaginary part using the Kramers–Kronig relation.34
The imaginary part ε2(ω) gives information on the absorption behavior of these compounds, and the real part ε1(ω) gives information about the electronic polarizability of a material.35 Fig. 5(a) shows that the spectra of XeNbF3, XeTiF3, XeVF3 and XeZrF3 increase to maximum values of 6.9 at 7.51 eV, 5.1 at 4.57 eV, 5.9 at 6.01 eV and 6 at 7.01 eV, respectively. The negative values of the real part ε1(ω) indicate the conducting nature of these materials. The imaginary part of the dielectric function is plotted against energy in Fig. 5(b), show the threshold values of the imaginary part for XeNbF3 (4.6), XeTiF3 (1.0), XeVF3 (13.8) and XeZrF3 (12.0). The spectra decrease and then increase to maximum values of 8.1 at 10.11 eV for XeNbF3, 4.8 at 9.1 eV for XeTiF3, 4.92 at 6.01 eV for XeVF3, and 6.4 at 8 eV for XeZrF3. The systems undergo a fluctuating decrease and end at the saturation values. The fluctuating nature of the imaginary spectra is due to band-to-band transition in these compounds.
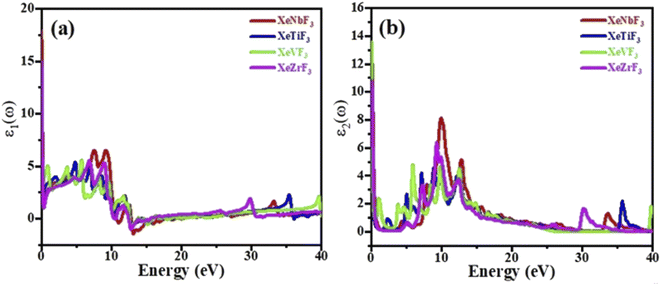 | ||
| Fig. 5 Computed (a) real and (b) imaginary parts of the dielectric functions of XeMF3 (M = Ti, V, Zr, Nb). | ||
Fig. 6(a) shows the relationship between the refractive index and the energy of incident photons. It is clear from the figure that the values of [n(0)] for XeNbF3, XeTiF3, XeVF3 and XeZrF3 are 4.3, 1.99, 2.2 and 3.99, respectively. It can be observed that the refractive index values increase and finally reach maximum values of 2.72 at 9 eV for XeNbF3, 2.35 at 4.9 eV for XeTiF3, 2.4 at 6 eV for XeVF3 and 2.5 at 9.9 eV for XeZrF3. After attaining the maximum values, the refractive indices decrease to minimum values of 0.5, 0.4, 0.4 and 0.5 for XeNbF3, XeTiF3, XeVF3 and XeZrF3, respectively. Their refractive index values greater than one indicate a decrease in the energy of incident photons in the compounds.
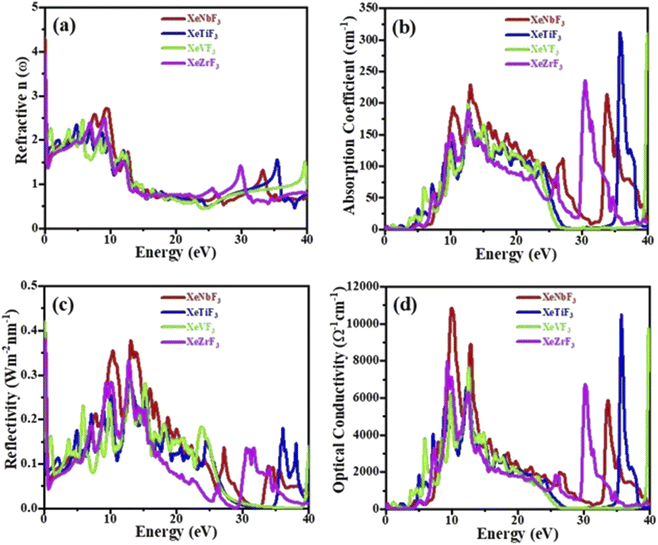 | ||
| Fig. 6 Computed (a) refractive index, (b) absorption coefficient, (c) conductivity and (d) reflectivity of XeMF3 (M = Ti, V, Zr, Nb). | ||
Fig. 6(b) depicts the absorption coefficients of the investigated compounds. It is clear from the spectra that the threshold absorption and maximum absorption are 0.01 and 230 (13.5 eV) for XeNbF3, 0.25 and 322 (37.1 eV) for XeTiF3, 0.2 and 319 (40 eV) for XeVF3 and 0.002 and 348 (32 eV) for XeZrF3, respectively. XeNbF3 has maximum absorption in the visible region while XeTiF3, XeVF3 and XeZrF3 have maximum absorption in the ultraviolet region. Fig. 6(d) shows the optical conductivity of the materials plotted against the energy of the incident photon. It can be observed from the spectra that XeNbF3 has the highest optical conductivity of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 in the visible region while XeTiF3, XeVF3 and XeZrF3 have maximum optical conductivities of 17
000 in the visible region while XeTiF3, XeVF3 and XeZrF3 have maximum optical conductivities of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500, 10
500, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 and 8000, respectively, in the visible region.
900 and 8000, respectively, in the visible region.
Fig. 6(c) shows the reflectivity curves of all four compounds, clarifying that these compounds have a transmitting nature in the energy range of 0 to 6 eV and have their best reflecting nature in the energy range of 6 to 16 eV. From the figure, it is clear that the compounds XeNbF3, XeTiF3, XeVF3 and XeZrF3 have a maximum reflectivity of 0.375 at 14 eV, 0.28 at 13 eV, 0.28 at 15 eV and 0.34 at 12.5 eV, respectively. From this, it can be concluded that XeZrF3 is the best reflector among these compounds.
4. Conclusions
In this study, we examined the structural, electronic, magnetic and elastic properties of XeMF3 (M = Nb, Ti, V, Zr) using the generalized gradient approximation with the Hubbard U term (GGA+U) in the Wien2k package. The stability and formation of these compounds were confirmed from their structural properties. From the study of the structural properties, it was concluded that XeNbF3 is more stable than the other studied compounds. Their electronic structures indicate their half-metallic nature with 100 percent spin polarization. A wide band gap is present in the spin-down channel of all these compounds. The study of their magnetic properties reveals that the materials under study are ferromagnetic in nature. The main contribution to the magnetic moment is made by the M-site atoms. Their elastic properties were determined from the elastic constants obtained using the IR Elast package. All the compounds were found to be mechanically stable and to have an anisotropic nature. XeVF3 was found to be stiffer than the other compounds, while XeTiF3 has high compressibility. The optical characteristics show that these compounds are good optical absorbers at high energy. On the basis of these result, we suggest that these compounds could be good candidates for spintronic and optoelectronic devices.Conflicts of interest
The authors have no conflict of interest.Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Saudi Arabia, for funding this work through the Research Groups Program under grant number R.G.P.2:187/43.References
- T. Nishimatsu, et al., Band structures of perovskite-like fluorides for vacuum-ultraviolet-transparent lens materials, Jpn. J. Appl. Phys., 2002, 41(4A), L365 CrossRef CAS.
- P. Dorenbos, 5d-level energies of Ce3+ and the crystalline environment. IV. Aluminates and ‘simple’ oxides, J. Lumin., 2002, 99(3), 283–299 CrossRef CAS.
- C. Dotzler, G. V. M. Williams and A. Edgar, RbCdF3:Mn2+: A potential ultraviolet dosimeter material, Appl. Phys. Lett., 2007, 91(18), 181909 CrossRef.
- G. Murtaza, et al., First principle study of cubic perovskites: AgTF3 (T = Mg, Zn), Phys. B, 2011, 406(24), 4584–4589 CrossRef CAS.
- F. Hamioud, G. S. AlGhamdi, S. Al-Omari and A. A. Mubarak, Ab initio investigation of the structural, electronic, magnetic and optical properties of the perovskite TlMnX3 (X = F, Cl) compounds, Int. J. Mod. Phys. B, 2016, 30(7), 1650031 CrossRef CAS.
- D. Chenine, et al., Theoretical Investigation of Half-Metallic Ferromagnetism in Sodium-Based Fluoro-perovskite NaXF3 (X = V, Co), J. Supercond. Novel Magn., 2018, 31(1), 285–295 CrossRef CAS.
- S. Datta and B. Das, Electronic analog of the electro-optic modulator, Appl. Phys. Lett., 1990, 56(7), 665–667 CrossRef CAS.
- R. A. De Groot, F. M. Mueller, P. G. Van Engen and K. H. J. Buschow, New class of materials: half-metallic ferromagnets, Phys. Rev. Lett., 1983, 50(25), 2024 CrossRef CAS.
- Z. H. Zhu and X. H. Yan, Half-metallic properties of perovskite BaCrO3 and BaCr0.5Ti0.5O3 superlattice: LSDA+U calculations, J. Appl. Phys., 2009, 106(2), 23713 CrossRef.
- L. Kronik, M. Jain and J. R. Chelikowsky, Electronic structure and spin polarization of MnxGa1−xN, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(4), 41203 CrossRef.
- A. Nourmohammadi and M. R. Abolhasani, First-principle study of full Heusler Co2YSi using PBE0 hybrid functional, Solid State Commun., 2010, 150(33–34), 1501–1504 CrossRef CAS.
- W. Zulfiqar, S. M. Alay-e-Abbas, G. Abbas, A. Laref, J. A. Larsson and A. Shaukat, Revisiting the structural, electronic and photocatalytic properties of Ti and Zr based perovskites with meta-GGA functionals of DFT, J. Mater. Chem. C, 2021, 9(14), 4862–4876 RSC.
- J. I. Gómez-Peralta and X. Bokhimi, Ternary halide perovskites for possible optoelectronic applications revealed by Artificial Intelligence and DFT calculations, Mater. Chem. Phys., 2021, 267, 124710 CrossRef.
- J. A. Christians, et al., Tailored interfaces of unencapsulated perovskite solar cells for >1000 hour operational stability, Nat. Energy, 2018, 3(1), 68–74 CrossRef CAS.
- T. A. Berhe, et al., Organometal halide perovskite solar cells: degradation and stability, Energy Environ. Sci., 2016, 9(2), 323–356 RSC.
- P. V. Balachandran, A. A. Emery, J. E. Gubernatis, T. Lookman, C. Wolverton and A. Zunger, Predictions of new ABO3 perovskite compounds by combining machine learning and density functional theory, Phys. Rev. Mater., 2018, 2(4), 43802 CrossRef CAS.
- Q. Xu, Z. Li, M. Liu and W.-J. Yin, Rationalizing perovskite data for machine learning and materials design, J. Phys. Chem. Lett., 2018, 9(24), 6948–6954 CrossRef CAS PubMed.
- J. Im, S. Lee, T.-W. Ko, H. W. Kim, Y. Hyon and H. Chang, Identifying Pb-free perovskites for solar cells by machine learning, npj Comput. Mater., 2019, 5(1), 1–8 CrossRef CAS.
- D. J. Singh and L. Nordstrom, Planewaves, Pseudopotentials, and the LAPW Method, Springer Science & Business Media, 2006 Search PubMed.
- M. G. Medvedev, I. S. Bushmarinov, J. Sun, J. P. Perdew and K. A. Lyssenko, Density functional theory is straying from the path toward the exact functional, Science, 2017, 355(6320), 49–52 CrossRef CAS PubMed.
- S. Azam, et al., DFT study of the electronic and optical properties of ternary chalcogenides AlX2Te4, Mater. Res. Express, 2019, 6(11), 116314 CrossRef.
- F. D. Murnaghan, The compressibility of media under extreme pressures, Proc. Natl. Acad. Sci. U. S. A., 1944, 30(9), 244 CrossRef CAS PubMed.
- G. Kieslich, S. Sun and A. K. Cheetham, An extended tolerance factor approach for organic–inorganic perovskites, Chem. Sci., 2015, 6(6), 3430–3433 RSC.
- U. A. Khan, N. U. Khan, A. H. Alghtani, V. Tirth, S. J. Ahmed, M. Sajjad and A. Zaman, First-principles Investigation on the Structural, Electronic, Mechanical and Optical Properties of Silver based Perovskite AgXCl3 (X = Ca, Sr), J. Mater. Res. Technol., 2022, 20, 3296–3305 CrossRef CAS.
- I. Galanakis, P. Mavropoulos and P. H. Dederichs, Electronic structure and Slater–Pauling behaviour in half-metallic Heusler alloys calculated from first principles, J. Phys. D: Appl. Phys., 2006, 39(5), 765 CrossRef CAS.
- S. A. Dar, Osmium Containing Double Perovskite Ba2XOsO6 (X = Mg, Zn, Cd): Important Candidates for Half-Metallic Ferromagnetic and Spintronic Applications, in Perovskite Materials, Devices and Integration, IntechOpen, 2019 Search PubMed.
- H. Tokoro, K. Nakabayashi, S. Nagashima, Q. Song, M. Yoshikiyo and S. I. Ohkoshi, Optical properties of epsilon iron oxide nanoparticles in the millimeter- and terahertz-wave regions, Bull. Chem. Soc. Jpn., 2022, 95(3), 538–552 CrossRef CAS.
- G. Grimvall, Thermophysical properties of materials, Elsevier, 1999 Search PubMed.
- C. Jenkins and S. Khanna, Mechanics of materials: a modern integration of mechanics and materials in structural design, Academic Press, 2005 Search PubMed.
- Y. Yang, H. Lu, C. Yu and J. M. Chen, First-principles calculations of mechanical properties of TiC and TiN, J. Alloys Compd., 2009, 485(1–2), 542–547 CrossRef CAS.
- I. N. Frantsevich, Elastic constants and elastic moduli of metals and insulators, Ref. B., 1982 Search PubMed.
- S. F. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45(367), 823–843 CrossRef CAS.
- D. Chenine, Z. Aziz, W. Benstaali, B. Bouadjemi, O. Youb, T. Lantri and S. Bentata, Theoretical Investigation of Half-Metallic Ferromagnetism in Sodium-Based Fluoro-perovskite NaXF3 (X = V, Co), J. Supercond. Novel Magn., 2018, 31(1), 285–295 CrossRef CAS.
- Abdullah, U. A. Khan, I. Ullah, V. Tirth, A. Algahtani, Shazia and A. Zaman, DFT study of the structural, elastic and optoelectronic properties of Cu-based cubic halide-perovskites ACuF3 (A = Mg and Ca), Phys. Scr., 2022, 97(8), 085819 CrossRef.
- M. Lal and S. Kapila, Structural, electronic, optical and mechanical properties of CsCaCl3 and KCdF3 cubic perovskites, Int. J. Mater. Sci., 2017, 12, 137–147 Search PubMed.
| This journal is © The Royal Society of Chemistry 2022 |