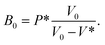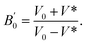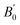Open Access Article
Open Access ArticleMechanics under pressure of gold nanoparticle supracrystals: the role of the soft matrix†
Helen Ibrahim,
Victor Balédent,
Marianne Impéror-Clerc and
Brigitte Pansu *
*
Université Paris-Saclay, CNRS, Laboratoire de Physique des Solides, UMR-8502, 91405, Orsay, France. E-mail: brigitte.pansu@universite-paris-saclay.fr; Tel: +33 169155332
First published on 19th August 2022
Abstract
We report on High Pressure Small Angle X-ray Scattering (HP-SAXS) measurements on 3D face-centered cubic (FCC) supracrystals (SCs) built from spherical gold nanoparticles (NPs). Dodecane-thiol ligands are grafted on the surface and ensure the stability of the gold NPs by forming a protective soft layer. Under a hydrostatic pressure of up to 12 GPa, the SC showed a high structural stability. The bulk elastic modulus of the SC was derived from the HP-SAXS measurements. The compression of the SC undergoes two stages: the first one related to the collapse of the voids between the NPs followed by the second one related to the compression of the soft matrix which gives a major contribution to the mechanical behavior. By comparing the bulk modulus of the SC to that of dodecane, the soft matrix appears to be less compressible than the crystalline dodecane. This effect is attributed to a less optimized chain packing under pressure compared to the free chains, as the chains are constrained by both grafting and confinement within the soft matrix. We conclude that these constraints on chain packing within the soft matrix enhance the stability of SCs under pressure.
Nanocrystals, used as building blocks, may self-assemble in long-range ordered assemblies, so-called supracrystals (SCs). They are a good example of a meta-material as their structural architectures induce collective properties. Due to the plasmonic optical properties of gold nanoparticles (NPs), gold supracrystals are attractive candidates for optical applications. Their optical properties are reported to depend on both the structure and the distance between the particles within the supracrystals.1 The cohesion of these supracrystals is ensured by the interaction between the gold cores, mainly via van der Waals attraction, but it is also related to the stiffness of the soft shell around each gold core.2 Different structures – face-centered cubic (FCC) phases, body-centered cubic (BCC) phases as well as Frank–Kasper phases – have been observed. However, to our knowledge, no experimental study on the role of the soft matrix stiffness on the self-assembly process has been reported yet. In this respect, it is crucial to investigate in depth the stiffness of the ligand shell within SCs. The study of the mechanical properties of gold SCs provides valuable information about the soft matrix: this is the main objective of this paper. The elastic properties of SCs can be determined from nano-indentation measurements performed with an atomic force microscope on films or on bulk domains.3,4 Another way to apply stress is to use diamond-anvil cells (DACs), standard devices for applying high pressure (several GPa) to classical or geoscientific materials, but also to the soft matter field.5 The ordered structures can be probed by in situ High Pressure Small Angle X-ray Scattering (HP-SAXS) measurements under hydrostatic pressure. Due to the thickness of the diamond windows, short X-ray wavelengths and large intensities as provided by synchrotron facilities are required.6 Such experiments have been mainly performed on ordered films of spherical gold NPs organized in an FCC phase, under compression using a diamond anvil cell (DAC).7,8 In situ HP-SAXS measurements showed that gradual elevation of the external pressure from ambient to 8.9 GPa caused reversible shrinkage of the dimensions of the lattice unit cell. As a result, fine tuning of the interparticle spacing could be achieved. While pressures between 8.9 and 13 GPa drove the NPs to coalesce to form 1D nanostructures (nanorods or nanowires) and ordered hexagonal arrays of the nanostructures with P6mm symmetry. Such mechanical behavior has been reported for other types of particles.9–11 Simulations have also been conducted12 to understand the mechanism that induces this structural change and to emphasize the role of the ligands.13 HP-SAXS measurements applied on bulk PbS nanocrystals6 stabilized with oleic acid, between ambient pressure and 12.5 GPa, revealed nearly perfect structural stability of the SCs in an FCC phase.
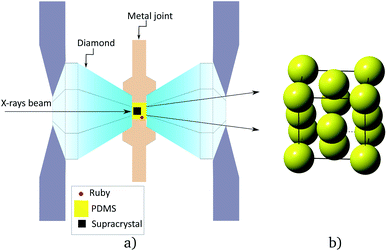
This letter presents experimental results on the mechanical behavior under hydrostatic pressure of an FCC SC built by spherical gold NPs (Fig. 1), similar to those used in a simulation study.12 These NPs consist of a gold core of diameter Dc = 4.88 ± 0.40 nm grafted with dodecane thiols. These particles self assemble into large FCC SCs by a slow evaporation of volatile oil. Then, they are loaded into a DAC cell with transmitting medium (silicon oil). Synchrotron-based HP-SAXS measurements were performed to monitor directly the in situ structural evolution under hydrostatic pressure. When applying a pressure up to 12 GPa, X-ray scattering has revealed a continuous decrease of the parameter of the FCC cell. The bulk modulus of the soft matrix surrounding the gold cores has been measured, showing a large increase upon pressure. The comparison with the bulk modulus of pure dodecane, with the same chain length as that of the ligands (dodecane-thiols) is also made.
Considering the core size of the NPs and the length of the ligands that were used, the expected structure, without any solvent, is FCC.14 The scattered pattern shown in Fig. 2a confirms this structure. Upon applying pressure, a shift of the peaks towards larger q is clearly observed (see Movie in ESI†). In Fig. 2a, four domains with different orientations (see ESI†) have been detected, all containing a three fold axis (111). The domains slightly rotate at least at the beginning as revealed by the change of the relative intensity of spots belonging to different domains. The determination of the structure and the value of the cell parameter was done from the radial integration of the scattered intensity I(q).
 | ||
| Fig. 2 (a) 2D scattered pattern at P = 0 GPa, (b) radial integration of the intensity I(q) for different pressures. | ||
Fig. 2b reports the radially integrated intensity I(q) as a function of the wave vector q for different pressures. One recovers the typical peaks of an FCC phase: 111, 200, 220, 311, 222, 400, 331, 420,…. Upon pressure, all peaks shift towards larger q indicating a decrease of the cell parameter a. No structural transformation has been observed in the investigated pressure range.
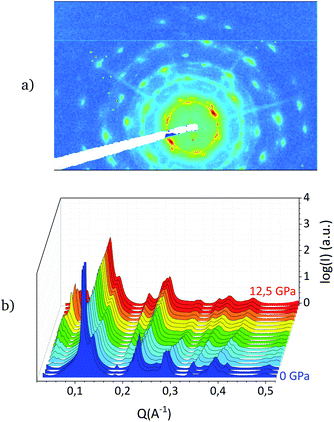
The variation of the FCC cell parameter a as a function of the increasing pressure a(P) is shown in Fig. 3a. When the pressure-transmitting medium PDMS15 is introduced in the cell, a minimum of pressure is applied to fix it in the cell. By increasing the pressure up to 0.2 GPa, one notices that the decreasing slope of the a(P) curve is steep, revealing a drastic decrease in the cell parameter from 96.5 Å to about 94 Å. Then, in a second stage, above 0.2 GPa, the slope of the a(P) curve becomes considerably less steep indicating a slower decrease in the cell parameter.
 | ||
| Fig. 3 (a) FCC cell parameter in Å upon pressure in GPa with insight at low pressure. (b) Sketch of the behavior of the soft particles in the cell upon increasing pressure. | ||
Fig. 3b gives a crude interpretation of this behavior. At null pressure, there is void in between the gold NPs. One can notice that the PDMS gyration radius (2 nm) is too large to let the PDMS penetrate into the supracrystals. When pressure is applied, the soft shell is deformed and the void collapses: this is the first stage. However, below 0.2 GPa, the pressure control is not precise enough in order to measure the bulk modulus in this first stage.
At the end of this first stage, the void between the particles vanishes. In a second stage, the variation of the cell parameter is associated to the compression of the NPs. This behavior, which involves two stages, is predicted through simulation studies.12,13 It shows that voids are present between the NPs, without any trapped solvent.
Extracting the bulk modulus, above 0.2 GPa, from the data requires a defined model. The behaviour and properties of earth materials at high pressure and temperatures have been described by different theoretical equation of state (EOS) P(V), such as the Vinet model.16 These models are based on the interaction between atoms in solids. Several parameters are introduced: the volume at vanishing pressure V0, the bulk modulus at vanishing pressure B0 and its derivative with respect to pressure 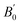 . Even if soft matter systems behave as classical solids, the interaction may be quite different. For polymeric and glass systems, J. Rault17 has proposed another EOS based on three parameters V0, V* and P*. V* is the limit volume at high pressure and P* is related to the bulk modulus at vanishing pressure:
. Even if soft matter systems behave as classical solids, the interaction may be quite different. For polymeric and glass systems, J. Rault17 has proposed another EOS based on three parameters V0, V* and P*. V* is the limit volume at high pressure and P* is related to the bulk modulus at vanishing pressure:
The EOS established by J. Rault is expressed in eqn (1) as follows:
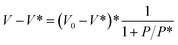 | (1) |
The bulk modulus at pressure P is expressed in eqn (2) as follows:
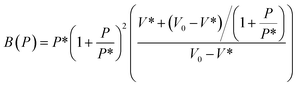 | (2) |
One can deduce from this expression that:
Both models have been tested and the Rault's one clearly gives the better results over the whole pressure range applied in this experiment. This model has been applied on the volume per particle to extract the supracrystal bulk modulus.
The matrix volume per particle, where the matrix is defined as the medium in between the gold cores (ligands + possible void) is clearly an important variable in order to investigate the behavior of the ligands. The matrix volume per particle is obtained by subtracting the core volume from the volume per particle. But the core is also compressed and its volume Vc depends on the pressure. This variation can be estimated using the bulk modulus of the gold core. This bulk modulus has been measured18,19 but for larger particles: BGb = 167 GPa, 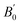 being estimated to 5.72. Recent AFM nanoindentation experiments on small gold nanoparticles20 have revealed an increase of the gold stiffness for particles smaller than 7 nm. But, since the value of the gold bulk modulus for small nanoparticles is not well known, we have used the gold bulk modulus of large particles to estimate the gold core volume upon pressure. Vc(P) has thus been approximated using a linear decrease upon pressure:
being estimated to 5.72. Recent AFM nanoindentation experiments on small gold nanoparticles20 have revealed an increase of the gold stiffness for particles smaller than 7 nm. But, since the value of the gold bulk modulus for small nanoparticles is not well known, we have used the gold bulk modulus of large particles to estimate the gold core volume upon pressure. Vc(P) has thus been approximated using a linear decrease upon pressure: 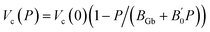 . Then the bulk modulus of the matrix can be determined in the same way as the supracrystal bulk modulus. However, in SI, we show that a larger bulk modulus (300 GPa), as estimated from the AFM experiments, would lead to close values for the matrix stiffness and does not change the main result of this paper.
. Then the bulk modulus of the matrix can be determined in the same way as the supracrystal bulk modulus. However, in SI, we show that a larger bulk modulus (300 GPa), as estimated from the AFM experiments, would lead to close values for the matrix stiffness and does not change the main result of this paper.
The two fits concerning the volume per particle and the matrix volume per particle, obtained by subtracting Vc(P) from the volume per particle, are shown in Fig. 4. The error on the pressure value measured in situ using the fluorescence of small ruby crystals is less than 0.1 GPa.21 The different parameters extracted from the fits are detailed in Table 1.
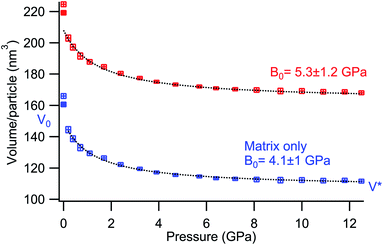 | ||
| Fig. 4 (red) Volume per particle upon pressure, (blue) volume of the matrix only and (black dotted line) the fit using the Rault model. | ||
The relationship between the two bulk modules, B0 for the supracrystal, B0M for the matrix, is given by  , where ϕ0 is the volume fraction occupied by the matrix at room pressure,
, where ϕ0 is the volume fraction occupied by the matrix at room pressure, 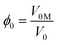 and BGold, the gold core bulk modulus. Since BGold is large compared to B0, one can estimate that B0M ≃ ϕ0B0.
and BGold, the gold core bulk modulus. Since BGold is large compared to B0, one can estimate that B0M ≃ ϕ0B0.
The mechanics of thiol-coated gold NPs supracrystals has already been studied experimentally mainly by AFM, using either AFM tips, colloidal probe or nano-indenter,3 as well as by simulation studies.13 For supracrystals built by gold NPs with approximately the same NPs as studied in this paper (same core diameter coated with dodecane-thiol ligands), the measured bulk modulus is in full agreement with the literature. However, it is about twice as large as that obtained by simulation studies but the error on the experimental value is too large to really compare the two values.
For a better understanding of the ligand behavior (dodecanethiol), pure dodecane mechanics, under isotropic pressure, have been investigated in the same experimental conditions. Pure dodecane crystallizes under pressure at room temperature. The crystalline structure of dodecane is triclinic (see ESI†). The six crystallographic parameters have been measured from the scattering patterns and the volume of the cell upon pressure has been computed. The Rault's model has also been applied in order to determine the bulk modulus (Table 2).
The mechanical behaviour of liquid dodecane below the crystallization pressure (0.2 GPa) has been investigated by Regueira et al.22 By fitting their results with the help of the Rault model, it is possible to compute the bulk modulus of liquid dodecane just before crystallization: Bliq(P = 0.2 GPa) ≈ 3 GPa. At “low” pressure, close to 0.2 GPa, the matrix bulk modulus has an intermediate value between disordered dodecane and crystallized one. At this point, one can notice that no evidence of crystallization inside the ligand matrix was detected in the scattering pattern.
The behavior of the bulk modulus upon hydrostatic pressure of the ligand matrix built with dodecane chains and pure dodecane are compared in Fig. 5. Two different graphs are shown: the ratio V/V0 as a function of P (Fig. 5a) or the bulk modulus B(P) computed with the Rault model (Fig. 5b) for both systems.
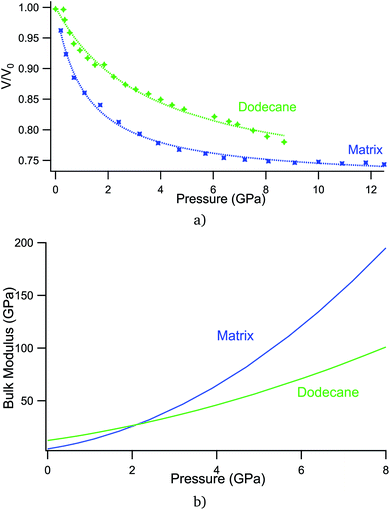 | ||
| Fig. 5 Comparison of the mechanical response of matrix and dodecane under pressure: (a) V/V0(P) (b) B(P). | ||
In Fig. 5, the increase of the matrix bulk modulus upon pressure is larger than the increase of pure dodecane bulk modulus. Surprisingly, the matrix bulk modulus becomes close to that of the gold core upon high pressure. This large increase of the bulk modulus is not predicted by simulations.13 The matrix is built by ligands that are grafted on the NP surface, with a large grafting density (5.2 ligand per nm2), as measured using TGA, in perfect agreement with standard values.23 The ligands are confined between neighboring cores and the matrix is not homogeneously filled. Upon high pressure, the matrix restructuring is more difficult than for crystallized dodecane. In the supracrystals, the ligands are grafted on the NP surface and cannot shift along the backbones. The ligands are also constrained in a confined zone in between the gold cores. This effect of confinement on the matrix bulk modulus is much studied at present.24 Ultrasonic experiments with a broader family of liquids are useful tools to explore how molecular properties affect the compressibility of confined fluids. Nevertheless experiments are needed for fluids that have practical importance for geophysics, i.e., water or hydrocarbons. HP-SAXS experiments on supracrystals give access to information on the solvent compressibility in another pressure range, closer to earth materials conditions.
This large value of the matrix bulk modulus at high pressure prevents from coalescence of the gold cores. From this point of view, the behavior of thin films with similar nanoparticles is totally different since coalescence has been experimentally proved. One may suspect that some ligands may detach from the gold surface under pressure and diffuse to the film surface, which is not possible in a 3D crystal. Therefore, a higher pressure greater than 12 GPa should be applied to potentially promote coalescence between the NPs inside 3D supracrystals.
A 3D FCC supracrystal built by spherical gold nanoparticles grafted with dodecane-thiol has been investigated by HP-SAXS. In a first stage, the voids between the particles collapse, as predicted by Liu et al.,12 leading to a rapid decrease in the cell parameter. In a second stage, the variation of the cell parameter is dominated by the compression of the soft matrix surrounding the gold cores. No structural transitions have been observed, showing a strong structural stability under hydrostatic pressure up to 12 GPa. The mechanical behaviour of the ligands was then compared to that of pure dodecane. A large increase in the matrix bulk modulus has been measured, larger than for pure dodecane. This result is attributed to the fact that it is more difficult to optimize the chain packing under pressure when the chains are constrained by both grafting and confinement compared to free chains. As a result, these constraints on the chain packing inside the soft matrix enhance the stability of the SCs under pressure. In further studies, higher pressure over 12 GPa should be applied in order to promote either structural change or coalescence between the gold cores inside the supracrystals. Since the rearrangement of the thiol ligands under pressure may depend on the gold core interface curvature, changing the gold core size and performing further experiments with smaller or larger particles would be highly valuable.
Author contributions
V. B. built the DAC cell and managed all the technical aspects related to the pressure, B. P. manufactured the gold supracrystals; H. I., V. B. and B. P. performed the measurements, processed the experimental data, performed the analysis, and designed the figures. B. P. drafted the manuscript. M. I. has aided in interpreting the results and worked on the manuscript. All authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge SOLEIL for providing the synchrotron radiation facilities and we thank Thomas Bizien for assistance in using beamline SWING (Run20201484). The TEM images have been obtained by Claire Goldmann (LPS) and the MEB images by Wajdi Chaabani (LPS). This work is funded by the French National Research Agency (SoftQC project; https://softqc.wordpress.com/; ANR grant ANR-18-CE09-0025).Notes and references
- S. Mourdikoudis, A. Colak, I. Arfaoui and M.-P. Pileni, J. Phys. Chem. C, 2017, 121, 10670–10680 CrossRef CAS.
- B. Pansu and J.-F. Sadoc, Eur. Phys. J. E, 2017, 40, 102 CrossRef.
- M.-P. Pileni, Europhys. Lett., 2017, 119, 37002 CrossRef.
- A. Çolak, J. Wei, I. Arfaoui and M.-P. Pileni, Phys. Chem. Chem. Phys., 2017, 19, 23887–23897 RSC.
- K. Pilar, V. Balédent, M. Zeghal, P. Judeinstein, S. Jeong, S. Passerini and S. Greenbaum, J. Chem. Phys., 2018, 148, 30–33 CrossRef PubMed.
- P. Podsiadlo, B. Lee, V. B. Prakapenka, G. V. Krylova, R. D. Schaller, A. Demortière and E. V. Shevchenko, Nano Lett., 2011, 11, 579–588 CrossRef CAS PubMed.
- H. Wu, F. Bai, Z. Sun, R. E. Haddad, D. M. Boye, Z. Wang and H. Fan, Angew. Chem., Int. Ed., 2010, 49, 8431–8434 CrossRef CAS.
- H. Wu, F. Bai, Z. Sun, R. E. Haddad, D. M. Boye, Z. Wang, J. Y. Huang and H. Fan, J. Am. Chem. Soc., 2010, 132, 12826–12828 CrossRef CAS PubMed.
- B. Li, X. Wen, R. Li, Z. Wang, P. G. Clem and H. Fan, Nat. Commun., 2014, 5, 4179 CrossRef CAS PubMed.
- J. Zhu, Z. Quan, C. Wang, X. Wen, Y. Jiang, J. Fang, Z. Wang, Y. Zhao and H. Xu, Nanoscale, 2016, 8, 5214–5218 RSC.
- B. Li, K. Bian, X. Zhou, P. Lu, S. Liu, I. Brener, M. Sinclair, T. Luk, H. Schunk, L. Alarid, P. G. Clem, Z. Wang and H. Fan, Sci. Adv., 2017, 3, e1602916 CrossRef PubMed.
- X. Liu, Y. Wu, G. Li, Y. Zhang and H. Zhai, J. Appl. Phys., 2020, 128, 035109 CrossRef CAS.
- I. Srivastava, B. L. Peters, J. M. D. Lane, H. Fan, K. M. Salerno and G. S. Grest, J. Phys. Chem. C, 2019, 123, 17530–17538 CrossRef CAS.
- B. Pansu, C. Goldmann, D. Constantin, M. Impéror-Clerc and J.-F. Sadoc, Soft Matter, 2021, 6461 RSC.
- N. Tateiwa and Y. Haga, Rev. Sci. Instrum., 2009, 80, 123901 CrossRef PubMed.
- P. Vinet, J. R. Smith, J. Ferrante and J. H. Rose, Phys. Rev. B, 1987, 35, 1945–1953 CrossRef CAS PubMed.
- J. Rault, Eur. Phys. J. E: Soft Matter Biol. Phys., 2014, 37, 113 CrossRef PubMed.
- A. Dewaele, P. Loubeyre and M. Mezouar, Phys. Rev. B, 2004, 70, 094112 CrossRef.
- C. Martín-Sánchez, A. Sánchez-Iglesias, J. A. Barreda-Argüeso, A. Polian, J.-P. Itié, J. Pérez, P. Mulvaney, L. M. Liz-Marzán and F. Rodríguez, ACS Nano, 2021, 15, 19128–19137 CrossRef PubMed.
- H. Li, Y. Han, T. Duan and K. Leifer, Appl. Phys. Lett., 2019, 115, 053104 CrossRef.
- A. D. Chijioke, W. J. Nellis, A. Soldatov and I. F. Silvera, J. Appl. Phys., 2005, 98, 114905 CrossRef.
- T. Regueira, M.-L. Glykioti, E. H. Stenby and W. Yan, J. Chem. Eng. Data, 2018, 63, 1072–1080 CrossRef CAS.
- H. Hinterwirth, S. Kappel, T. Waitz, T. Prohaska, W. Lindner and M. Lämmerhofer, ACS Nano, 2013, 7, 1129–1136 CrossRef CAS.
- C. D. Dobrzanski, B. Gurevich and G. Y. Gor, Appl. Phys. Rev., 2021, 8, 021317 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra03484k |
| This journal is © The Royal Society of Chemistry 2022 |