Open Access Article
Open Access ArticleAll-atom molecular dynamics simulations of the combined effects of different phospholipids and cholesterol content on electroporation
Fei Guo *,
Ji Wang,
Jiong Zhou,
Kun Qian
*,
Ji Wang,
Jiong Zhou,
Kun Qian ,
Hongchun Qu,
Ping Liu and
Shidong Zhai
,
Hongchun Qu,
Ping Liu and
Shidong Zhai
Institute of Ecological Safety, Chongqing University of Posts and Telecommunications, Chongqing 400065, China. E-mail: guofei@cqupt.edu.cn
First published on 30th August 2022
Abstract
The electroporation mechanism could be related to the composition of the plasma membrane, and the combined effect of different phospholipid molecules and cholesterol content on electroporation has rarely been studied nor conclusions drawn. In this paper, we applied all-atom molecular dynamics (MD) simulations to study the effects of phospholipids and cholesterol content on bilayer membrane electroporation. The palmitoyloleoylphosphatidylcholine (POPC) model, palmitoyloleoylphosphatidylethanolamine (POPE) model, and a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixed model of POPC and POPE called PEPC, were the three basic models used. An electric field of 0.45 V nm−1 was applied to nine models, which were the three basic models, each with three different cholesterol content values of 0%, 24%, and 40%. The interfacial water molecules moved under the electric field and, once the first water bridge formed, the rest of the water molecules would dramatically flood into the membrane. The simulation showed that a rapid rise in the Z-component of the average dipole moment of the interfacial water molecules (Z-DM) indicated the occurrence of electroporation, and the same increment of Z-DM represented a similar change in the size of the water bridge. With the same cholesterol content, the formation of the first water bridge was the most rapid in the POPC model, regarding the average electroporation time (tep), and the average tep of the PEPC model was close to that of the POPE model. We speculate that the differences in membrane thickness and initial number of hydrogen bonds of the interfacial water molecules affect the average tep for different membrane compositions. Our results reveal the influence of membrane composition on the electroporation mechanism at the molecular level.
1 mixed model of POPC and POPE called PEPC, were the three basic models used. An electric field of 0.45 V nm−1 was applied to nine models, which were the three basic models, each with three different cholesterol content values of 0%, 24%, and 40%. The interfacial water molecules moved under the electric field and, once the first water bridge formed, the rest of the water molecules would dramatically flood into the membrane. The simulation showed that a rapid rise in the Z-component of the average dipole moment of the interfacial water molecules (Z-DM) indicated the occurrence of electroporation, and the same increment of Z-DM represented a similar change in the size of the water bridge. With the same cholesterol content, the formation of the first water bridge was the most rapid in the POPC model, regarding the average electroporation time (tep), and the average tep of the PEPC model was close to that of the POPE model. We speculate that the differences in membrane thickness and initial number of hydrogen bonds of the interfacial water molecules affect the average tep for different membrane compositions. Our results reveal the influence of membrane composition on the electroporation mechanism at the molecular level.
1 Introduction
When cells are exposed to an electric field, pores form in the cell membranes and increase their permeability, which is known as electroporation.1–3 Technologies based on electroporation have been applied in medicine, biotechnology, and even food processing,4–8 but the electroporation mechanisms are not yet well understood. Various theoretical models have been developed to investigate electroporation at the level of a single cell, multiple cells, and tissues.9–15 However, it is difficult to observe the dynamic process of electroporation from a microscopic perspective using traditional electroporation simulations.All-atom molecular dynamics (MD) simulation is an efficient tool that can directly observe the occurrence of electroporation at the molecular level.16,17 Tieleman found that the water molecules moved with the electric field gradient and continuously entered the cell membrane when a vertical electric field was applied.18 Hu et al. constructed a dipalmitoylphosphatidylcholine (DPPC) bilayer model and found that the phospholipid headgroups on the anodic side of the membrane first shifted and formed voids under the electric field, and water molecules entered the membrane through the voids to form water bridges.19 However, Vernier and Ziegler found that the deflection of the headgroup dipole would not directly lead to the formation of water bridges at the nanoscale, whereas the field-oriented rotation of the headgroup dipole, the water dipole, and the solvation interaction were important factors for the occurrence of electroporation.20,21 Additionally, researchers found that the rearrangement of water molecules at the water/membrane boundary of a POPC phospholipid bilayer, and the magnitude and direction of the average dipole moment of the interfacial water molecules, were key for electroporation to take place, and further revealed the electroporation mechanisms.22–25 Furthermore, some researchers found that, with the movement of water molecules, the hydrogen bonds between the water molecules would change, and the network of hydrogen bonds would vibrate, which affected the occurrence of electroporation.26–28 The variation in hydrogen bonds between the water molecules affected the recombination of peptides on the membrane, and the association between protein peptides and cell membranes has been linked to diseases, such as Alzheimer’s disease.29–31
Most all-atom MD models used to study the electroporation mechanism were based on pure phospholipid membrane models.32–34 However, the presence of different phospholipid molecules in the phospholipid membrane can change its stability and fluidity, which in turn affect the electroporation.35–37 Different phospholipid molecules can influence the shape of the phospholipid membrane and thus regulate the properties of proteins.38 Different lipid enzymes have been enriched with different phospholipid molecules, which changed the physicochemical properties of the membrane.39 These factors led to differences being observed for different phospholipid membranes under an applied electric field to some extent. Gurtovenko applied the same electric field to a POPC phospholipid bilayer and a POPE phospholipid bilayer and found that the POPE model required more time for the occurrence of electroporation, compared to the POPC model.40 Polak et al. found that the architecture of the lipid headgroups and tails affected the propensity for poration in membranes containing fluid-phase lipids.41 Furthermore, they compared a bilayer made from archaeal lipids (with both (glucosyl)inositol and inositol headgroups) with a DPPC lipid bilayer and found that the electroporation threshold for DPPC was larger at the same temperature.42 Hu et al. found that the architecture of the lipid headgroups and tails in coarse-grained Martini membrane models was also the vital reason that determined the propensity for poration, similar to the results for atomistic membrane models, and a higher propensity for poration was found for fully saturated lipids, rather than monounsaturated lipids.43
Cholesterol is also an important component of phospholipid membranes, and the influence of cholesterol content on the electroporation of simple lipid bilayers has been proposed.44–46 In recent years, researchers found that the presence of cholesterol could significantly change the thickness47–52 and the fluidity of the plasma membrane, which in turn affected the breakdown voltage of the membrane.47,53–55 Cholesterol increased lipid cohesion and hardness to prevent peptide-induced damage, reducing the rate of membrane damage, but the effect was even reversed for different phospholipids.56,57 Cholesterol is commonly used in experiments involving vesicles. Researchers used cholesterol to prepare giant unilamellar vesicles, and found that the rupture of the plasma membrane under an electric field would be hindered by cholesterol.37,58–60 Most simulations suggested that cholesterol delayed the occurrence of electroporation, but the effect of cholesterol on the propensity for perforation of the lipid bilayers was strongly dependent on the structure of the lipids. Mauroy et al. reported that the decrease in the propensity for poration for the POPC phospholipid was due to the increased content of cholesterol,61 but Portet found that increasing the content of cholesterol accelerated the occurrence of electroporation in dioleoylphosphocholine (DOPC) vesicles.62 Recently, Kramar added 20%, 30%, 50% and 80% content of cholesterol to the POPC phospholipid, and found that, when the content was too high, the breakdown voltage of the membrane would not increase, but decrease.63 Ruiz-Fernández et al. found that under a nanosecond-pulsed electric field (nsPEF), a phospholipid membrane with high cholesterol content would have significant conformational changes in the voltage-sensing domain (VSD) of the Ga2+ channel, which would affect the movement of the water molecules.64 In conclusion, the influence of cholesterol and different phospholipids on the electroporation mechanism remains to be studied.
The combination of phospholipid molecules and cholesterol enriches plasma membrane diversity. However, most electroporation simulations and experiments with cholesterol did not consider its interaction with different phospholipid molecules. POPC phospholipid molecules exist in the cell membranes of brain cells and erythrocytes, therefore, POPC is one of the most important phospholipids in biophysical experiments.65,66 POPE phospholipid molecules are also widely found in the cell membranes of erythrocytes and in Escherichia coli.67 As the two main phospholipid components in mitochondrial membranes, POPE and POPC phospholipids have often been used in studies under an applied electric field.68,69 These two phospholipids have a similar structure and the same tails, as well as a high sensitivity to electric fields, which facilitated our observation of the dynamic process of electroporation. Therefore, we constructed POPE and POPC models, as well as a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixed model of the two (PEPC), as the three basic models, and then added 24% and 40% content of cholesterol. A constant electric field with a magnitude of 0.45 V nm−1 in the Z-direction was applied in all models. We showed the dynamic process of the formation of a water bridge, and proposed the relationship between the Z-DM and electroporation. The average time for the occurrence of electroporation (tep) for each model was calculated, and it was concluded that the membrane thickness and the initial number of hydrogen bonds in the interfacial water were the main factors affecting the average tep. The number of hydrogen bonds between the interfacial water molecules and phospholipid molecules in the mixed models was also calculated. The entire study provides an efficient basis for future electroporation simulations and experiments.
1 mixed model of the two (PEPC), as the three basic models, and then added 24% and 40% content of cholesterol. A constant electric field with a magnitude of 0.45 V nm−1 in the Z-direction was applied in all models. We showed the dynamic process of the formation of a water bridge, and proposed the relationship between the Z-DM and electroporation. The average time for the occurrence of electroporation (tep) for each model was calculated, and it was concluded that the membrane thickness and the initial number of hydrogen bonds in the interfacial water were the main factors affecting the average tep. The number of hydrogen bonds between the interfacial water molecules and phospholipid molecules in the mixed models was also calculated. The entire study provides an efficient basis for future electroporation simulations and experiments.
2 Models and methods
2.1 Phospholipid membrane models
This study included 9 phospholipid membrane models, all of which were constructed using the CHARMM-GUI.70,71 The water/membrane/water phospholipid bilayer was composed of phospholipid molecules and TIP3P water molecules. The TIP3P water molecule is simple, stable and widely used in the study of electroporation. More importantly, the TIP3P model has an electric charge and the dipole moment can be calculated quickly, which is suitable for our study.33,72 A phospholipid membrane model composed of the single-component of POPC, a phospholipid membrane model composed of the single-component of POPE, and a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixed model of POPC and POPE (PEPC) were the three basic models for our all-atom MD simulations. The positions of the POPC molecules and POPE molecules were randomly distributed in the upper and lower layers of the phospholipid model. Cholesterol molecules were added to the basic models with 24% and 40% content. The total number of phospholipid molecules and cholesterol molecules in all models was 125, and the total number of water molecules was always 8875. The specific parameters, such as the number of molecules within each of the models, are shown in Table 1. All the models were placed in a cuboid box with the same length in the X and Y directions. The initial box size of the POPE model was 6.3 nm × 6.3 nm × 11.2 nm, and the balance, the initial box was slightly changed according to the structure of the different models.
1 mixed model of POPC and POPE (PEPC) were the three basic models for our all-atom MD simulations. The positions of the POPC molecules and POPE molecules were randomly distributed in the upper and lower layers of the phospholipid model. Cholesterol molecules were added to the basic models with 24% and 40% content. The total number of phospholipid molecules and cholesterol molecules in all models was 125, and the total number of water molecules was always 8875. The specific parameters, such as the number of molecules within each of the models, are shown in Table 1. All the models were placed in a cuboid box with the same length in the X and Y directions. The initial box size of the POPE model was 6.3 nm × 6.3 nm × 11.2 nm, and the balance, the initial box was slightly changed according to the structure of the different models.
| Model | NPOPC | NPOPE | NCHL | CHL content (%) | Nwater |
|---|---|---|---|---|---|
| a NPOPC = the number of POPC phospholipid molecules, NPOPE = the number of POPE phospholipid molecules, NCHL = the number of cholesterol molecules, Nwater = the number of water molecules. Model 3, model 6 and model 9 are the mixed model called PEPC. | |||||
| 1 | 125 | 0 | 0 | 0 | 8875 |
| 2 | 0 | 125 | 0 | 0 | 8875 |
| 3 | 63 | 62 | 0 | 0 | 8875 |
| 4 | 95 | 0 | 30 | 24 | 8875 |
| 5 | 0 | 95 | 30 | 24 | 8875 |
| 6 | 48 | 47 | 30 | 24 | 8875 |
| 7 | 75 | 0 | 50 | 40 | 8875 |
| 8 | 0 | 75 | 50 | 40 | 8875 |
| 9 | 38 | 37 | 50 | 40 | 8875 |
2.2 MD simulations
All-atom MD simulations were performed using the NAMD software, and the VMD software was used to observe the dynamic process of the molecular simulations and calculate relevant parameters.73 We referred to the protocol of equilibrium for membranes from the CHARMM-GUI.74 Using 3D periodic boundary conditions, the temperature was set to 310 K. The whole motion formula was integrated using the velocity-Verlet integral method. Long-range electrostatic forces were calculated by the particle-mesh Ewald (PME) method. The space cut-off distance of the van der Waals force and the long-range electrostatic force was set to 1.2 nm, and the switching function was adopted to slowly reduce to zero.33 The CHARMM36 force field was applied to the simulations of the lipid bilayers, and the conjugate gradient method was applied to search for energy successively from the initial gradient until energy minimization. The SHAKE algorithm was used to constrain the lengths of the bonds involving hydrogen atoms and make the water molecules rigid. In order to better balance the entire phospholipid bilayer, the Z-direction position of the heavy atoms and the distance of the dihedral angles were constrained in a short time.75 The Langevin dynamic temperature control method and the Langevin piston Nosé–Hoover pressure control method maintained the temperature and pressure at 310 K and 1 atm, respectively.76The whole simulation process had the following stages: first, after the minimization of energy, a heating process over 250 ps was performed to increase the temperature to 310 K, with a time step of 1 fs. Then, the system was kept at constant temperature and pressure for 1.625 ns under the NPT ensemble, and the time step was changed to 2 fs. Afterwards, the position restriction of the heavy atoms of the phospholipid molecules and the restriction of the dihedral angle distance of the phospholipid molecules were removed, and a 10 ns equilibrium process was performed. Finally, a constant electric field of 0.45 V nm−1 was applied to the models after the 10 ns equilibrium process. As the water bridge became too large, the model became extremely unstable.77 Therefore, the end time of each model simulation was different. The required time of the whole simulation process is shown in Fig. 1.
 | ||
| Fig. 1 Time spent in each stage of the simulation. T stands for temperature, and P stands for pressure. | ||
3 Results and discussion
3.1 The dynamic process of electroporation
We first calculated the potential energy and the area per lipid (APL) of the PEPC model during the 10 ns equilibrium process. Fig. 2 shows that the potential energy curve is relatively stable throughout the 10 ns equilibrium period. The maximum and minimum values of the APL were 0.635 nm2 and 0.58 nm2, respectively, and the curve of the APL was stable, which are similar to results found in previous literature studies.75,78,79 The APL and the potential energy in the other models were also stable like the results shown in Fig. 2 during the 10 ns equilibrium process.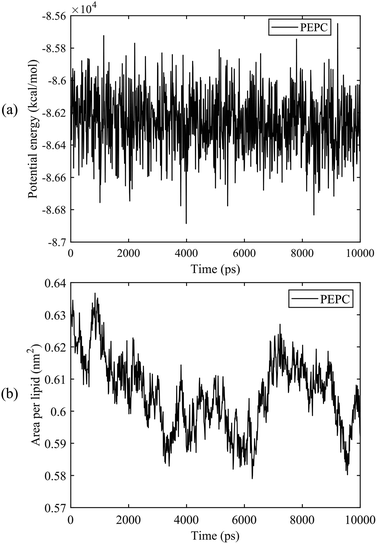 | ||
| Fig. 2 The potential energy and the area per lipid (APL) of the PEPC model during the 10 ns equilibrium process. (a) Potential energy. (b) APL. | ||
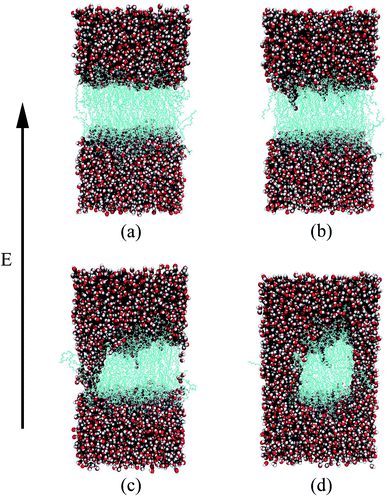
Through all-atom MD simulations, we can observe the dynamic process of electroporation from a microscopic point of view. The process by which water molecules on both sides of the membrane enter the membrane and join to form a water bridge is defined as electroporation.33 Fig. 3 shows the formation of a water bridge in the PEPC model. After the 10 ns equilibrium process, the water/membrane/water interface reached a relative stable state; all water molecules were evenly distributed on the outer sides of the phospholipid bilayer. The heads of the phospholipid molecules moved with the electric field, providing enough space for the water molecules to move, creating a water protrusion. Then, the water molecules continued to move until the water molecules on the upper and lower sides were connected in the interior of the membrane, and the water protrusion changed into a water bridge in this process. It is worth noting that, during the process of the formation of the water bridge, phospholipid molecules will also bend towards the water bridge. When the first water bridge formed, its width increased rapidly. Multiple water bridges appeared one after another, and the water molecules polarized rapidly. The dynamic process of electroporation was similar to that reported in most previous studies.32,80,81 The nanopore formation process in all the other models was similar to that shown in Fig. 3, but varied in the times required for water protrusion and bridge formation among the different models.
3.2 The relationship between dipole moment and electroporation
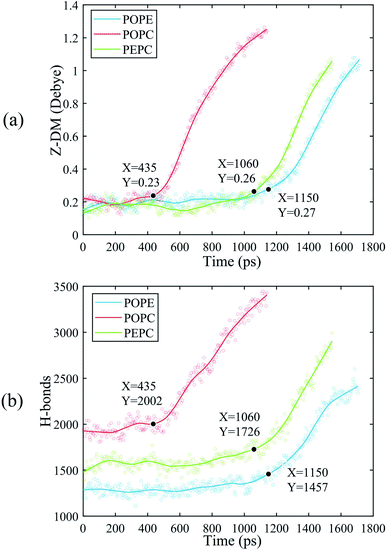
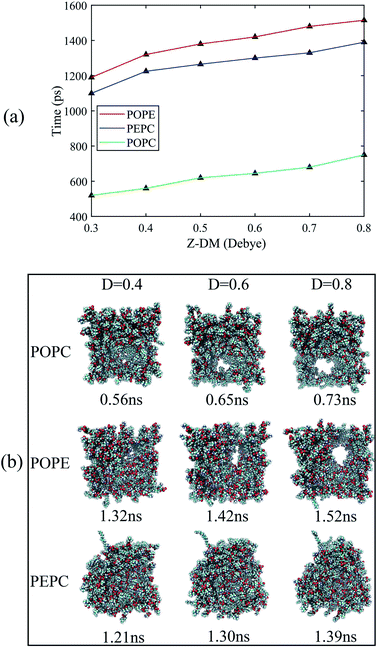
The water molecules within 4 Å of the membrane/water interface were defined as the interfacial water, and the movement of the interfacial water molecules is an important reason for the formation of a water bridge.22 The dipole moment is the most intuitive parameter to reflect the polarization degree of the water molecules.24 When interfacial water moves under the electric field and forms water bridges, the hydrogen bonds between water molecules will also change.27 We calculated the Z-component of the average dipole moment of the interfacial water (Z-DM) and the number of hydrogen bonds between the interfacial water molecules (H-bonds) under the electric field. The Z-DM was given by the Z component of the total dipole moment, then divided by the number of interfacial water molecules. The cut-off angle and the cut-off distance of the H-bonds were 35° and 3.5 Å, respectively. Fig. 4 clearly shows that both the Z-DM and the number of H-bonds increased exponentially, and the models would become extremely unstable when the water bridges were too large, so the end time of each simulation was different.77 From Fig. 4, it can be seen that the first water bridge was formed in the order of the POPC, PEPC, and POPE models, and the time for the first water bridge to be formed with the PEPC model was close to that of the POPE model. The primary amines in the POPE headgroups that were involved in intra- and intermolecular hydrogen bonds had a lower propensity for poration compared with the POPC headgroups. As a result, the POPE model was more compact, which delayed the formation of the first water bridge.40 It is worth noting that the rapid rise in the Z-DM represents the formation of the first water bridge, which is also called the occurrence of electroporation. Once the first water bridge formed, the water molecules rapidly flooded into the membrane, which was the reason for the rapid rise of the Z-DM. When the first water bridge of the three models formed, they had similar dipole-moment values of 0.23 Debye (D), 0.26 D and 0.27 D for the POPC, PEPC and POPE models, respectively. We speculate that the Z-DM is an important parameter that can be used to measure whether the first water bridge is formed or not. More kinds of phospholipid molecules and components will be presented in future work to enrich the complexity of the models and to approach the real cell membrane, and we consider that the Z-DM will also be an indicator to measure the formation of the first water bridge. In Fig. 4(b), the number of H-bonds is seen to increase rapidly after a period of time. At the moment of water bridge formation, the water molecules were in close contact and the number of H-bonds rose. The number of H-bonds in the POPC model rose the fastest, the PEPC model was second, and the POPE model showed the slowest rise. Different from the Z-DM, the initial numbers of H-bonds were quite different. There were about 1900 in the POPC model, 1500 in the PEPC model, and 1300 in the POPE model, and the differences were due to the membrane lipid composition. Therefore, we speculate that the initial number of H-bonds is also a reason affecting the electroporation mechanism, thus, the number of H-bonds in water is an important factor.For Fig. 5, we extracted snapshots of the moments in time that corresponded to the same values of Z-DM for the POPE, POPC and PEPC models The curves showing variation of Z-DM with time were approximately linear and similar in slope. The top views were used to observe the degree of electroporation, which was determined by the size of the water bridge. When the Z-DM was 0.4 D, the corresponding snapshots of the POPE and POPC models were from 1.32 ns and 0.56 ns, respectively, and a tiny water bridge appeared in both models. When the Z-DM was 0.6 D, which corresponded to the snapshots at 1.42 ns and 0.65 ns for the POPE and POPC models, respectively, a similar obvious water bridge outline was observed in both models. When the dipole moment was 0.8 D, the corresponding snapshots of the POPE and POPC models were from 1.52 ns and 0.73 ns, the water bridges have continued to grow, and similar large pores were generated in both models. In addition, we also show top views of the PEPC model. Although a water bridge formed at the edge of the model, it could still be seen that the size of the water bridge increased with the Z-DM. According to the above results, the models had similar sizes of water bridge when the magnitude of Z-DM was the same.
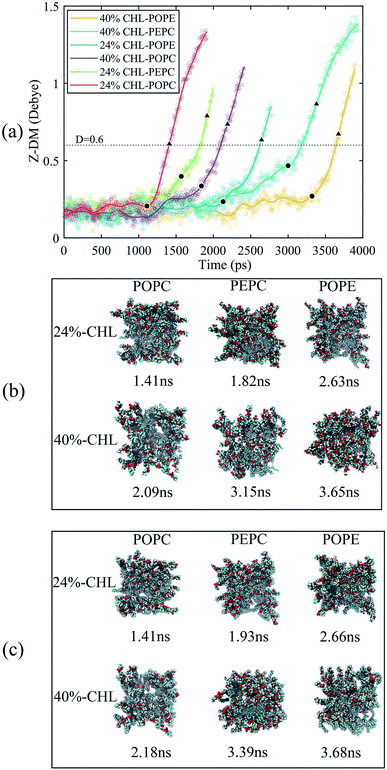
We also analyzed the Z-DM for the models containing cholesterol, as shown in Fig. 6. The Z-DM increased exponentially after the occurrence of electroporation, which was similar to the trend in Fig. 4. At the same cholesterol content, the POPC, PEPC and POPE models successively formed water bridges. The increase in cholesterol content delayed the formation of a water bridge among the same phospholipid models, which was consistent with the simulation result reported by Casciola et al.82 In the models with cholesterol, the moments in time where rapid rises in the Z-DM were observed were close to the times that formation of the water bridges occurred, which was consistent with the result in Fig. 4. We recorded the moments in time when each model had the same Z-DM magnitude of 0.6 D, and extracted snapshots of the corresponding top views. However, when the Z-DM magnitude was the same, the sizes of the water bridges were not similar. Unlike the cholesterol-free phospholipid models, the same Z-DM magnitude hardly reflected the same degree of electroporation. In order to find the relationship between the Z-DM and electroporation, we extracted snapshots and show the top views corresponding to an increment in Z-DM of 0.4 D after the occurrence of electroporation. After the same Z-DM increment of 0.4 D, the sizes of the water bridges of the 6 models were relatively similar. Then, we also looked at the results for increments in the Z-DM of 0.5 D and 0.6 D following electroporation, and the results were the same as for the increment of 0.4 D, which further reflected the relationship between the Z-DM value and the degree of electroporation.
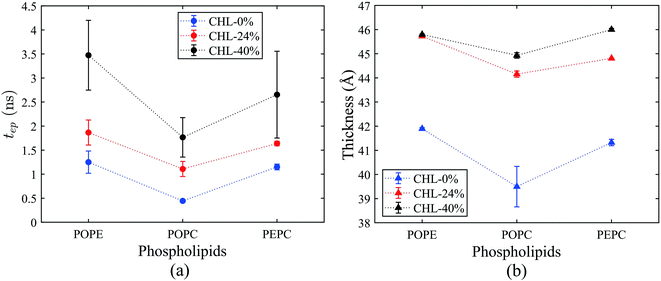
3.3 Effects of initial number of hydrogen bonds and membrane thickness on electroporation
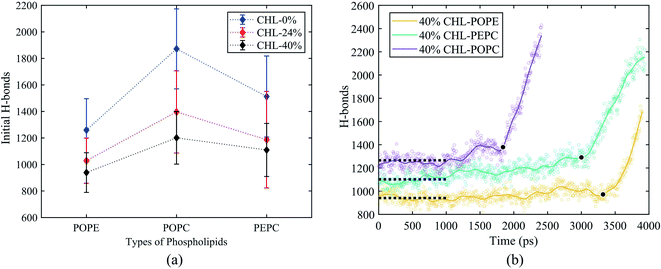
The average tep values were the average values of 10 repeated results for each model, and the membrane thickness of all models was calculated before the electric field was applied. From Fig. 7, it can be seen that, with the same cholesterol content, the average tep of the POPE models were always the biggest, followed by the PEPC models, and the results of the POPC models were the smallest. The average tep values of the PEPC models were consistently close to those of the POPE models, rather than the POPC models, for the three cholesterol content values, but the differences between them rose with the increase in cholesterol. At 0% cholesterol, the average tep of the PEPC model was 0.1 ns faster than that of the POPE model; at 24% cholesterol, the average tep of the PEPC model was 0.23 ns faster than that of the POPE model; and at 40% cholesterol, the average tep of the PEPC model was 0.77 ns faster than that of the POPE model. With the increase in cholesterol content, the average tep of our models increased, and this trend of change was similar to a previous study.82 The average tep values among the three basic models of POPC, PEPC and POPE at 0% cholesterol were 0.45 ns, 1.15 ns and 1.25 ns, respectively; the average tep values at 24% cholesterol were 1.11 ns, 1.57 ns and 1.87 ns, respectively; and the average tep values at 40% cholesterol were 1.84 ns, 2.70 ns and 3.47 ns, respectively. The combination of cholesterol molecules and phospholipid molecules will limit the thermal movement of the phospholipid molecules to a certain extent, thereby affecting their deflection under the electric field. A similar phenomenon is also shown in Fig. 7(b). At the same cholesterol content, the POPE phospholipid model had the largest membrane thickness, the POPC membrane thickness was the smallest, and the PEPC membrane thickness was between the two. The membrane thickness also increased with cholesterol content. The higher the cholesterol content, the lower the influence on the membrane thickness. The influence of cholesterol on the thickness of the membrane was negatively correlated with its concentration. Membrane thickness has been studied for its effect on the electroporation mechanism, as with APL, from a structural perspective of the models.50,52 At the same value of applied electric field, the thinner phospholipid membranes were more likely to form a water bridge,43 and models with a larger membrane thickness required larger transmembrane voltages, resulting in greater average tep values. At the same time, a small membrane thickness corresponds to a large APL,80 which means that the space between the phospholipid molecules widens, and it is easier for water molecules to enter the membrane and electroporation to occur. In our model, the difference in membrane thickness was not particularly large, but it also clearly led to the difference in tep. In the next step in our study, we will compare phospholipid combinations with larger membrane thickness differences, such as POPC and dimyristoylphosphatidylcholine (DMPC), where the membrane thickness of DMPC is much less than that of POPC. This will better confirm our conclusions.Fig. 8(a) shows the initial number of H-bonds for all models. The initial number of H-bonds is the average number of interfacial water H-bonds during the 10 ns equilibrium process, which means that the initial number of H-bonds is only relevant to the composition of the model. With the increase in cholesterol content, the initial number of H-bonds in the three basic phospholipid models decreased. At the same cholesterol content, the initial number of H-bonds in the POPC, PEPC and POPE models decreased successively. According to Table 2, when the cholesterol content increased from 0% to 24%, the average tep, membrane thickness and initial number of H-bonds of the interfacial water changed by 146%, 12% and −25%, respectively. When the cholesterol content increased from 24% to 40%, the average tep, membrane thickness, and initial number of H-bonds of the interfacial water changed by 67%, 2%, and −14%, respectively. From the percentage changes shown, it seems that the initial number of H-bonds is also a factor that affects the average tep, therefore we speculated that both the membrane thickness and the initial number of H-bonds affected the average tep. From Fig. 8(b), it can be seen that, within the first nanosecond of applying the electric field, the average number of H-bonds in the POPC, PEPC, and POPE models with 40% cholesterol content was 1243, 1097, and 939, and the lower the number of H-bonds in the first nanosecond, the later the electroporation occurred. The numbers of H-bonds were relatively stable at first, but when the electroporation occurred, they suddenly rose exponentially. The rapid rise in the number of H-bonds also indicated the formation of a water bridge, which is the same conclusion determined from Fig. 4(b). At 24% cholesterol content, we can also draw a similar conclusion to that with 40% cholesterol content. H-bonds have been applied to describe the process of models from an equilibrium state to the formation of water bridges,27,28 but the initial number of H-bonds was not considered. The combination of other phospholipid molecules (persistent organic pollutants (POPS) and palmitoyloleoylphosphatidylglycerol (POPG)) with cholesterol has also been shown to have an influence on the number of H-bonds,83 which verified our results for different initial numbers of H-bonds. This part of the simulation results is useful for our next stage of work. The combination of different phospholipid molecules and cholesterol content in phospholipid membranes changes the thickness and initial number of H-bonds, all of which influenced the average tep.
| CHL-content (%) | Time (ns) | Membrane thickness (Å) | H-bonds |
|---|---|---|---|
| 0 | 0.45 | 39.49 | 1872 |
| 24 | 1.11 | 44.15 | 1396 |
| 40 | 1.77 | 44.93 | 1200 |
To further understand the influence of different phospholipid molecules on electroporation, we calculated the number of H-bonds between the phospholipid molecules and interfacial water molecules in the PEPC model. As shown in Fig. 9, the number of H-bonds between the phospholipid molecules and interfacial water molecules decreased with the increase in cholesterol content. For 0%, 24%, and 40% cholesterol content, the number of H-bonds between the POPC phospholipid molecules and the interfacial water molecules (H-bonds of POPC–water) was always greater than the number between the POPE phospholipid molecules and the interfacial water molecules (H-bonds of POPE–water). At 0% cholesterol, the difference between the number of H-bonds of POPC–water and that of POPE–water was 103; at 24% cholesterol, the difference between the number of H-bonds of POPC–water and that of POPE–water was 97; at 40% cholesterol, the difference between the number of H-bonds of POPC–water and that of POPE–water was 87. Under the electric field, water molecules are closer to the POPC molecules than they are to the POPE molecules. At the same time, we speculated that this was the reason why the average tep of the POPC model was shorter than that of the POPE model.
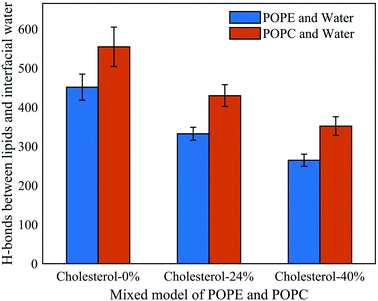 | ||
| Fig. 9 Hydrogen bonds between phospholipid molecules and interfacial water molecules in the PEPC model under the electric field at three cholesterol concentrations. | ||
4 Conclusions
In this study, we used all-atom MD simulations and systematically investigated the influence of different phospholipids and cholesterol content on electroporation. Under an applied electric field, water molecules entered the membrane through the gaps and formed a water protrusion. The water protrusion would become a water bridge after a period of time. Interestingly, the occurrence of electroporation was accompanied by rapid rises in the Z-DM and the number of H-bonds. From the top views of the phospholipid models, we found that the magnitude of the Z-DM could reflect the size of the water bridge, which was also called the degree of electroporation. However, the water bridges of different models were no longer similar with the same Z-DM value after adding the cholesterol, however the sizes of the water bridges in the different models were similar with the same increment in the Z-DM value following the occurrence of electroporation.With the same cholesterol content, the POPC models had the shortest average tep, the POPE models had the longest average tep, and the average tep values of the PEPC models were close to those of the POPE models. The overall average tep decreased with the increase in cholesterol content, but the order of average tep remained unchanged for the three basic phospholipid models with the same cholesterol content. We calculated the parameters that vary with the model composition: the initial number of H-bonds and the membrane thickness. At the same cholesterol content, the POPC model had the smallest membrane thickness, the POPE model had the largest membrane thickness, and the membrane thickness of the PEPC model was between the two. The initial number of H-bonds in the POPC, PEPC and POPE models decreased successively. The presence of cholesterol reduced the initial number of H-bonds and increased the membrane thickness. By combining the variation trends of the initial number of H-bonds and membrane thickness with that of the average tep, we inferred that the membrane thickness and initial number of H-bonds were important factors affecting the average tep. The influence of different phospholipid membranes and cholesterol content on the electroporation mechanism was studied on the molecular level. The effect of the dipole moment on the formation of the water bridge and the effect of the initial number of H-bonds and membrane thickness on the average tep were proposed. In conclusion, this paper provides a reference for future all-atom MD research on the electroporation mechanism.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJQN202100607), in part by the Natural Science Foundation of Chongqing, China (cstc2020jcyj-msxmX0393), and in part by the National Natural Science Foundation of China (No. 51507024).Notes and references
- J. C. Weaver and Y. Chizmadzhev, Bioelectrochem. Bioenerg., 1996, 41, 135–160 CrossRef CAS.
- C. Chen, S. Smye, M. Robinson and J. Evans, Med. Biol. Eng. Comput., 2006, 44, 5–14 CrossRef CAS PubMed.
- A. Muralidharan, L. Rems, M. T. Kreutzer and P. E. Boukany, Biochim. Biophys. Acta, Biomembr., 2021, 1863, 183468 CrossRef CAS PubMed.
- T. Y. Tsong, in Electroporation of Cell Membranes, ed. E. Neumann, A. E. Sowers and C. A. Jordan, Springer US, Boston, MA, 1989, pp. 149–163 Search PubMed.
- S. B. Dev, D. P. Rabussay, G. Widera and G. A. Hofmann, IEEE Trans. Plasma Sci., 2000, 28, 206–223 CrossRef CAS.
- R. V. Davalos, L. Mir and B. Rubinsky, Ann. Biomed. Eng., 2005, 33, 223–231 CrossRef CAS PubMed.
- B. Rubinsky, Technol. Cancer Res. Treat., 2007, 6, 255–259 CrossRef PubMed.
- G. Saulis, Food Eng. Rev., 2010, 2, 52–73 CrossRef.
- W. Krassowska and P. D. Filev, Biophys. J., 2007, 92, 404–417 CrossRef CAS PubMed.
- B. Judkewitz, M. Rizzi, K. Kitamura and M. Häusser, Nat. Protoc., 2009, 4, 862–869 CrossRef CAS PubMed.
- M. Kandušer and D. Miklavčič, Electrotechnologies for extraction from food plants and biomaterials, 2009, pp. 1–37 Search PubMed.
- M. Wang, O. Orwar, J. Olofsson and S. G. Weber, Anal. Bioanal. Chem., 2010, 397, 3235–3248 CrossRef CAS PubMed.
- F. Guo, K. Qian, L. Zhang, X. Liu and H. Peng, Bioelectrochemistry, 2021, 141, 107878 CrossRef CAS PubMed.
- F. Guo, K. Qian, L. Zhang, H. Deng, X. Li, J. Zhou and J. Wang, Electrochim. Acta, 2021, 385, 138426 CrossRef CAS.
- F. Guo, H. Deng, K. Qian and X. Li, Bioelectrochemistry, 2022, 144, 108029 CrossRef CAS PubMed.
- J. C. Weaver, IEEE Trans. Dielectr. Electr. Insul., 2003, 10, 754–768 CrossRef CAS.
- J.-M. Escoffre, T. Portet, L. Wasungu, J. Teissié, D. Dean and M.-P. Rols, Mol. Biotechnol., 2009, 41, 286–295 CrossRef CAS PubMed.
- D. P. Tieleman, BMC Biochem., 2004, 5, 10 CrossRef PubMed.
- Q. Hu, S. Viswanadham, R. Joshi, K. H. Schoenbach, S. J. Beebe and P. Blackmore, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 031914 CrossRef CAS PubMed.
- P. T. Vernier and M. J. Ziegler, J. Phys. Chem. B, 2007, 111, 12993–12996 CrossRef CAS PubMed.
- M. J. Ziegler and P. T. Vernier, J. Phys. Chem. B, 2008, 112, 13588–13596 CrossRef CAS PubMed.
- M. Tokman, J. H. Lee, Z. A. Levine, M.-C. Ho, M. E. Colvin and P. T. Vernier, PLoS One, 2013, 8, e61111 CrossRef CAS PubMed.
- P. T. Vernier, Z. A. Levine, M.-C. Ho, S. Xiao, I. Semenov and A. G. Pakhomov, J. Membr. Biol., 2015, 248, 837–847 CrossRef CAS PubMed.
- J. Tang, J. Ma, L. Guo, K. Wang, Y. Yang, W. Bo, L. Yang, H. Jiang, Z. Wu and B. Zeng, et al., J. Membr. Biol., 2020, 253, 271–286 CrossRef CAS PubMed.
- J. Tang, S. Wang, L. Yang, Z. Wu, H. Jiang, B. Zeng and Y. Gong, Biochim. Biophys. Acta, Biomembr., 2022, 1864, 183811 CrossRef CAS PubMed.
- W. D. Bennett, N. Sapay and D. P. Tieleman, Biophys. J., 2014, 106, 210–219 CrossRef CAS PubMed.
- M.-h. Ji, J.-h. Xu, S.-s. Yuan, Y.-w. Liu, X.-y. Xing, C. Jiang, L. Xue, C.-k. Yang, F.-h. Chu and Y.-h. Jiang, Comput. Theor. Chem., 2022, 1207, 113487 CrossRef CAS.
- P. Marracino, L. Caramazza, M. Montagna, R. Ghahri, M. D’Abramo, M. Liberti and F. Apollonio, Bioelectrochemistry, 2022, 143, 107987 CrossRef CAS PubMed.
- H. Fatafta, B. Kav, B. F. Bundschuh, J. Loschwitz and B. Strodel, Biophys. Chem., 2022, 280, 106700 CrossRef CAS PubMed.
- S. A. Kotler, P. Walsh, J. R. Brender and A. Ramamoorthy, Chem. Soc. Rev., 2014, 43, 6692–6700 RSC.
- S. Y. Cheng, Y. Cao, M. Rouzbehani and K. H. Cheng, Biophys. Chem., 2020, 260, 106355 CrossRef CAS PubMed.
- L. Delemotte and M. Tarek, J. Membr. Biol., 2012, 245, 531–543 CrossRef CAS PubMed.
- J. Tang, H. Yin, J. Ma, W. Bo, Y. Yang, J. Xu, Y. Liu and Y. Gong, J. Membr. Biol., 2018, 251, 681–693 CrossRef CAS PubMed.
- D. Navickaitė, P. Ruzgys, M. Maciulevičius, G. Dijk, R. P. O’Connor and S. Šatkauskas, Bioelectrochemistry, 2021, 142, 107927 CrossRef PubMed.
- A. Sen, Y.-L. Zhao and S. W. Hui, Biophys. J., 2002, 83, 2064–2073 CrossRef CAS PubMed.
- Z. E. Hughes, A. E. Mark and R. L. Mancera, J. Phys. Chem. B, 2012, 116, 11911–11923 CrossRef CAS PubMed.
- T. Rog and I. Vattulainen, Chem. Phys. Lipids, 2014, 184, 82–104 CrossRef CAS PubMed.
- J. C. Bozelli Jr, S. S. Aulakh and R. M. Epand, Biophys. Chem., 2021, 273, 106587 CrossRef PubMed.
- J. C. Bozelli Jr and R. M. Epand, Biophys. Chem., 2020, 265, 106431 CrossRef PubMed.
- A. A. Gurtovenko and A. S. Lyulina, J. Phys. Chem. B, 2014, 118, 9909–9918 CrossRef CAS PubMed.
- A. Polak, D. Bonhenry, F. Dehez, P. Kramar, D. Miklavčič and M. Tarek, J. Membr. Biol., 2013, 246, 843–850 CrossRef CAS PubMed.
- A. Polak, M. Tarek, M. Tomšič, J. Valant, N. P. Ulrih, A. Jamnik, P. Kramar and D. Miklavčič, Bioelectrochemistry, 2014, 100, 18–26 CrossRef CAS PubMed.
- Y. Hu, S. K. Sinha and S. Patel, Langmuir, 2015, 31, 6615–6631 CrossRef CAS PubMed.
- S. Koronkiewicz and S. Kalinowski, Biochim. Biophys. Acta, Biomembr., 2004, 1661, 196–203 CrossRef CAS PubMed.
- P. Shil, S. Bidaye and P. B. Vidyasagar, J. Phys. D: Appl. Phys., 2008, 41, 055502 CrossRef.
- T. Portet, F. C. i Febrer, J.-M. Escoffre, C. Favard, M.-P. Rols and D. S. Dean, Biophys. J., 2009, 96, 4109–4121 CrossRef CAS PubMed.
- S. Bhattacharya and S. Haldar, Biochim. Biophys. Acta, Biomembr., 2000, 1467, 39–53 CrossRef CAS.
- H. Alobeedallah, B. Cornell and H. Coster, J. Membr. Biol., 2018, 251, 153–161 CrossRef CAS PubMed.
- W.-C. Tsai and G. W. Feigenson, Biochim. Biophys. Acta, Biomembr., 2019, 1861, 478–485 CrossRef CAS PubMed.
- D. K. Yadav, S. Kumar, E.-H. Choi, S. Chaudhary and M.-H. Kim, Sci. Rep., 2019, 9, 1–10 CrossRef CAS PubMed.
- H. Alobeedallah, B. Cornell and H. Coster, J. Membr. Biol., 2020, 253, 319–330 CrossRef CAS PubMed.
- D. K. Yadav, S. Kumar, E.-H. Choi and M.-H. Kim, J. Biomol. Struct. Dyn., 2021, 39, 1343–1353 CrossRef CAS PubMed.
- S. Kakorin, U. Brinkmann and E. Neumann, Biophys. Chem., 2005, 117, 155–171 CrossRef CAS PubMed.
- M. L. Fernández and R. Reigada, J. Phys. Chem. B, 2014, 118, 9306–9312 CrossRef PubMed.
- D. Wiczew, N. Szulc and M. Tarek, Bioelectrochemistry, 2021, 141, 107869 CrossRef CAS PubMed.
- A. J. McHenry, M. F. Sciacca, J. R. Brender and A. Ramamoorthy, Biochim. Biophys. Acta, Biomembr., 2012, 1818, 3019–3024 CrossRef CAS PubMed.
- M. F. Sciacca, F. Lolicato, G. Di Mauro, D. Milardi, L. D’Urso, C. Satriano, A. Ramamoorthy and C. La Rosa, Biophys. J., 2016, 111, 140–151 CrossRef CAS PubMed.
- H. Ohvo-Rekilä, B. Ramstedt, P. Leppimäki and J. P. Slotte, Prog. Lipid Res., 2002, 41, 66–97 CrossRef.
- M. A. S. Karal, M. K. Ahamed, N. A. Mokta, M. Ahmed and S. Ahammed, Eur. Biophys. J., 2020, 49, 361–370 CrossRef CAS PubMed.
- M. K. Ahamed, M. Ahmed and M. A. S. Karal, PLoS One, 2022, 17, e0262555 CrossRef CAS PubMed.
- C. Mauroy, I. Rico-Lattes, J. Teissie and M.-P. Rols, Langmuir, 2015, 31, 12215–12222 CrossRef CAS PubMed.
- T. Portet and R. Dimova, Biophys. J., 2010, 99, 3264–3273 CrossRef CAS PubMed.
- P. Kramar and D. Miklavčič, Bioelectrochemistry, 2022, 144, 108004 CrossRef CAS PubMed.
- A. R. Ruiz-Fernández, L. Campos, F. Villanelo, S. E. Gutiérrez-Maldonado and T. Perez-Acle, Membranes, 2021, 11, 473 CrossRef PubMed.
- P. Wydro, Colloids Surf., B, 2013, 103, 67–74 CrossRef CAS PubMed.
- X. Xie, Z. Hou, G. Duan, S. Zhang, H. Zhou, Z. Yang and R. Zhou, Colloids Surf., B, 2021, 203, 111765 CrossRef CAS PubMed.
- S. Karimzadeh, B. Safaei and T.-C. Jen, J. Mol. Liq., 2021, 330, 115698 CrossRef CAS.
- A. N. Stefanovic, S. Lindhoud, S. A. Semerdzhiev, M. M. Claessens and V. Subramaniam, Biochemistry, 2015, 54, 3142–3150 CrossRef CAS PubMed.
- A. A. Oliveira, T. Róg, A. B. da Silva, R. E. Amaro, M. S. Johnson and P. A. Postila, Biomolecules, 2022, 12, 183 CrossRef CAS PubMed.
- S. Jo, J. B. Lim, J. B. Klauda and W. Im, Biophys. J., 2009, 97, 50–58 CrossRef CAS PubMed.
- S. Jo, X. Cheng, J. Lee, S. Kim, S.-J. Park, D. S. Patel, A. H. Beaven, K. I. Lee, H. Rui and S. Park, et al., J. Comput. Chem., 2017, 38, 1114–1124 CrossRef CAS PubMed.
- P. Zarzycki and B. Gilbert, Phys. Chem. Chem. Phys., 2020, 22, 1011–1018 RSC.
- J. E. Stone, A.-P. Hynninen, J. C. Phillips and K. Schulten, International conference on high performance computing, 2016, pp. 188–206 Search PubMed.
- J. Lee, X. Cheng, J. M. Swails, M. S. Yeom, P. K. Eastman, J. A. Lemkul, S. Wei, J. Buckner, J. C. Jeong and Y. Qi, et al., J. Chem. Theory Comput., 2016, 12, 405–413 CrossRef CAS PubMed.
- S. Sun, G. Yin, Y.-K. Lee, J. T. Wong and T.-Y. Zhang, Biochem. Biophys. Res. Commun., 2011, 404, 684–688 CrossRef CAS PubMed.
- K. Kawaguchi, S. Ito, H. Saito and H. Nagao, Mol. Simul., 2022, 1–7 CAS.
- M. L. Fernández, M. Risk, R. Reigada and P. T. Vernier, Biochem. Biophys. Res. Commun., 2012, 423, 325–330 CrossRef PubMed.
- J. Gullingsrud and K. Schulten, Biophys. J., 2004, 86, 3496–3509 CrossRef CAS PubMed.
- S. A. Kirsch and R. A. Böckmann, Biophys. J., 2019, 116, 2131–2148 CrossRef CAS PubMed.
- T. Kotnik, L. Rems, M. Tarek and D. Miklavčič, Annu. Rev. Biophys., 2019, 48, 63–91 CrossRef CAS PubMed.
- S. Mahnič-Kalamiza and D. Miklavčič, Pulsed Electric Fields Technology for the Food Industry, Springer, 2022, pp. 107–141 Search PubMed.
- M. Casciola, D. Bonhenry, M. Liberti, F. Apollonio and M. Tarek, Bioelectrochemistry, 2014, 100, 11–17 CrossRef CAS PubMed.
- N. Kandel, J. O. Matos and S. A. Tatulian, Sci. Rep., 2019, 9, 1–12 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2022 |