Open Access Article
Open Access ArticleGeneration of liquid metal double emulsion droplets using gravity-induced microfluidics†
Qiyue Fana,
Yaohao Guoa,
Shuangliang Zhao ab and
Bo Bao
ab and
Bo Bao *a
*a
aState Key Laboratory of Chemical Engineering and School of Chemical Engineering, East China University of Science and Technology, Shanghai, 200237, China. E-mail: bbao@ecust.edu.cn
bGuangxi Key Laboratory of Petrochemical Resource Processing and Process Intensification Technology and School of Chemistry and Chemical Engineering, Guangxi University, Nanning, 530004, China
First published on 19th July 2022
Abstract
Several microfluidic applications are available for liquid metal droplet generation, but the surface oxidation of liquid metal has placed limitations on its application. Multiphase microfluidics makes it possible to protect the inner droplets by producing the structure of double emulsion droplets. Thus, the generation of liquid metal double emulsion droplets has been developed to prevent the surface oxidation of Galinstan. However, the generation using common methods faces considerable challenges due to the gravity effect introduced from the high density of liquid metal, making it difficult for the shell phase to wrap the inner phase. To overcome this obstacle, we introduce an innovative method – a gravity-induced microfluidic device – to creatively generate controllable liquid metal double emulsion droplets, achieved by altering the measurable inclination angle of the plane. It is found that when the inclination angle ranges from 30° to 45°, the device manages to generate liquid metal double emulsion droplets with perfect double sphere-type configuration. Additionally, the core–shell liquid metal hydrogel capsules present potential applications as multifunctional materials for controlled release systems in drug delivery and biomedical applications. By regulating pH or imposing mechanical force, the hydrogel shell can be dissolved to recover the electrical conductivity of Galinstan for applications in flexible electronics, self-healing conductors, elastomer electronic skin, and tumor therapy.
1 Introduction
Liquid metals, which are usually low melting point metal elements, have recently received wide attention from the scientific community.1,2 Liquid metals show extraordinary properties such as high electrical conductivity3 and superb fluidity because their metallic cores and surfaces are rich in electrons1,4,5 Such extraordinary properties of high surface tension,6,7 low viscosity,3,5 and high electrical and thermal conductivities3,8,9 have enabled their applications in temperature sensing and control devices,4,8 and conductive materials.5,8–10Over a long period of time, one of the most widely used liquid metals is mercury, which has a low melting point of −38.8 °C1 and can readily flow at room temperature, making it an ideal material for batteries, thermometers and barometers.11–14 However, mercury is highly toxic no matter in what forms,1,12,13 imposing irreversible limitations on its practical use.8,15 In contrast to mercury, gallium based liquid metals16–18 such as eutectic gallium indium (EGaIn)11,12 and gallium indium tin18,19 (Galinstan)1,8 have gained widely popularity20 because they exhibit low toxicity,14,17,21 high electrical and thermal conductivities.12,22 Additionally, both of them have low melting points. The melting point of EGaIn is 15.5 °C23,24 while that of Galinstan is −19 °C.1,25,26 Their extraordinary fluidic properties enabling rheological behaviors around room temperature,8,13,14 make them promising for applications in microfluidic systems and soft electronics.3,27
A notable challenge utilizing gallium based liquid metals lies in their scarce resource supplies and associated high expense. As a result, these liquid metals are often utilized in trace amount with typical characteristic lengths around hundreds of microns, which perfectly fall into the regime of microfluidics. Previous studies have indicated successful combination of gallium based liquid metals and microfluidic systems, such as soft and stretchable electronics,5,28 microfluidic electrodes,17,22 conductive microstructures12,14,28,29 and 3D printing.20,21,28 As for the applications in chemical, biochemical30 and pharmaceutical researches,13,24,29,31 droplets play a crucial role in the combination of liquid metals and microfluidics.4,21,32–34
Multiphase flows in microfluidic systems demonstrate unique advantages such as increased interfacial area and improved mixing in comparison with single-phase or two-phase flows.35 In recent years, monodisperse double emulsion droplets, comprised of smaller droplets of a third fluid within the larger droplets,36 have attracted particular attention in microfluidics. Their distinguishing core–shell structure, high stability and distinctive monodispersity unleash great innovations in numerous applications such as biomedicine,1,37 chemical analysis31 and cosmetics38,39 as means of encapsulation and protection of active ingredients.36,40,41 The middle phase serves as a protective shell to insulate the internal material from the outside. Microfluidic chips39,42 and glass capillary devices41,43 with structures like flow focusing44–46 and cross-flowing47–49 are introduced to produce droplets.38,43,50 Conventional methods for the generation of double emulsion droplets principally fall into two categories: one-step and two-step methods.35 One-step method mainly includes dual-coaxial co-flowing41 while two-step methods have various combinations based on dual-coaxial,51,52 two T-junctions,53,54 two cross-junctions.55,56 The double emulsion droplet manages to be generated in a single step by injecting the inner and middle phases into capillary tubes from the same direction simultaneously, while the outer phase is infused from the opposite side by one step.57,58 As for the two-step method, the inner droplets are formed first, followed by the creation of shell droplets.58
The limitation of gallium based liquid metals (such as Galinstan) droplets in microfluidic lies in the instant formation of a self-limiting surface oxide layer4,59 when exposed to air. The thin oxide layer with a thickness of 0.7 to 3 nm,1 imparts its mechanical stability and adhesive property on various substrates, making researches below millimeters difficult.3,24,60 The oxidized liquid metal behaves more like a gel than a liquid, thus hindering its applications. It has been proved that the surface oxide layer can be prevented or removed by applying an electrochemically reductive potential or appropriate chemical treatment, such as hydrochloric acid at proper concentrations.9,21,25,61 However, the addition of external field or chemicals brings a burden to the generation or utilization process.
To our best knowledge, few research adopted the core–shell structure of double emulsion droplets to prevent the oxide layer of Galinstan.
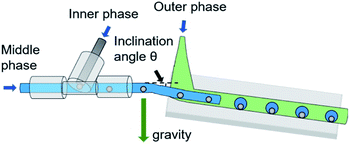
The shell of the double emulsion droplet can isolate liquid metal inner droplets to prevent the oxidation and coalescence, as well as improving the monodispersity and maintaining the stability of the core–shell configuration. As a kind of natural polysaccharide polymer, the shell material sodium alginate possesses high biocompatibility and deceasing oxygen-permeability, imparting high environmental and biologic safety, as well as mechanical robustness and structural stability to the capsule, thus showing great potential in applications.62 The difficulty to generate liquid metal Galinstan double emulsion droplets lies in its great density, which is six times higher than that of water.4,63 Utilizing several apparatuses mentioned in literature41,64,65 seems experimentally unsuccessful, owing to that gravity drives the liquid metal droplets downward deposited on the channel wall. Consequently, an innovative microfluidic device has been developed in this paper. It is composed of a T-shaped junction linked to a co-flowing capillary channel, with an adjustable inclined plane to control the gravity component along the flow direction. Successful generations of liquid metal Galinstan double emulsion droplets are achieved by manipulating the inclination angle and phase flow rates.
Liquid metal micro/nanodroplets can be encapsulated as core–shell capsule by biological macromolecule materials and polymers,66 or modified on the surface by some functional radical groups.67 Functional compound droplets possess new optical, magnetic and transformable properties when applying external stimuli such as pH or temperature changes, presenting exciting opportunities in the fields of flexible electronics, sensors, and catalysts, as well as promoting drug releasing performance in drug delivery systems.18 For example, encapsulating nanodroplets of liquid metal EGaIn or Galinstan into microgels of marine polysaccharides can produce the biocompatible aqueous ink.62 Effective cancer cell elimination can be achieved by exploiting the physicochemical properties of liquid metal droplets, such as NIR (near-infrared) laser exposure, which has a tendency to induce a transformation in the shape liquid metal, destruction of the nanocapsules, contactless controlled release of the loaded drugs, and optical manipulations of a microfluidic blood vessel model.68 The performance of protective hydrogel shell may be optimized through rational combination with environmental stimuli responsive materials or other functional polymer materials to attain liquid metal compound droplets with varying functionalities, or be dissolved to recover the electrical conductivity of Galinstan for controlled release systems in drug delivery and biomedical, or applications in flexible electronics, self-healing conductor, elastomer electronic skin, and tumor therapy.62,66,68,69
2 Theoretical background
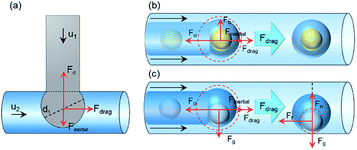
Droplet formation substantially consists of the following two-step process: droplet grows until the equilibrium of forces is disrupted, then the detachment occurs.70,71 Assuming the droplet as a sphere before detachment, the forces acting on a growing droplet in a horizontal T-shaped circular microchannel can be divided into holding and detaching forces.71 As analyzed in Fig. 1(a), the inertial force (Finertial) and drag force (Fdrag) drive the droplet detaching, described as detaching force. The interfacial tension force (Fσ) keeps the droplet attached to the dispersed phase, defined as the holding force.72–74 The magnitude of all forces may be calculated from the following equations:74,75| Finertial = ρ1u1Q1 | (1) |
| Fσ12 = πd1σ12 | (2) |
| Fdrag = 3πμ2μ2d1 | (3) |
The effect of the resultant force of holding and detaching forces is balanced at a critical point where the droplets transform from growth to detachment.71,72,78 When the detaching force exceeds holding force, the forming droplet begins to detach from the neck and pinch off into a droplet. The droplet remains spherical after detaching due to the interfacial tension force. Additionally, the dimensionless numbers related to forces are able to be calculated to manifest the competing phenomena among different forces during the droplet formation process as indicated in Table 1.79–81
| Dimensionless numbers | Equations | Definition |
|---|---|---|
| Reynolds number | Re = ρdu/μ | Inertial/viscous |
| Capillary number | Ca = μu/σ | Viscous/interfacial |
| Weber number | We = ρdu2/σ | Inertial/interfacial |
| Bond number | Bo = (Δρ)gd2/σ | Gravitational/interfacial |
The Reynolds number (Re), served as a criterion dividing fluid flow pattern, is used to quantify the relative importance of inertial and viscous forces, with a low Reynolds number leading to laminar flow.74,82 The capillary number (Ca) denotes the relationship between the viscous and interfacial tension forces acting across the two immiscible liquid interfaces,83 indicating that the interfacial tension force is much more dominant when the capillary number is very small.84,85 The Weber number (We) represents the balance of inertial forces and interfacial tension force,21,79 while the Bond number (Bo) is used as a measure of the relative importance of gravity and interfacial tension force.86,87 When Bo ≪ 1, the interfacial tension force dominates and the effect of gravity can be disregarded.87,88
3 Materials and methods
3.1 Materials
Three phases, i.e., inner phase, middle phase, and outer phase, forms a system to produce double emulsion droplets of liquid metal/water/oil. The inner phase is Galinstan (68.5% Ga+21.5% In+10% Sn) (Changsha Santech Materials Co. Ltd) and the middle aqueous phase is 4% (w/w) sodium alginate solution (Shanghai Macklin Biochemical Technology Co. Ltd). The outer oil phase is composed of paraffin liquid (Shanghai Macklin Biochemical Technology Co. Ltd) and 4 wt% surfactant sorbitan monolaurate (Span 20) (Shanghai Macklin Biochemical Technology Co. Ltd). The purpose of adding surfactant is to reduce the contact angle between the outer continuous phase and the contact wall, as well as improving the wettability of the continuous phase and wall so that to form a more stable water-in-oil droplet.89Additionally, the density and viscosity of the three fluids are measured by densitometer and spinning digital viscometer (Formulaction, Fluidicam RHEO). The interfacial tensions between fluids are determined by a surface tensiometer (Biolin Scientific, Theta Flex) using the pendant drop method. The detailed properties of three liquid phases are shown in Table 2. Experimentally, the middle phase sodium alginate solution is dyed blue while the outer phase liquid paraffin remains colorless transparent to enable clear visualization of different phases. All the experimental progress has been performed at room temperature (25 °C).
| Three-phase | Materials | Density ρ (kg m−3) | Viscosity μ (Pa s) | Interfacial tension σ (N m−1) |
|---|---|---|---|---|
| Inner phase | Galinstan | 6440 | 0.0024 | σ12 = 0.533 |
| Middle phase | Sodium alginate solution (4% w/w) | 1010 | 0.0836 | σ23 = 0.004 |
| Outer phase | Paraffin liquid (4 wt% Span 20) | 850 | 0.0455 | σ13 = 0.509 |
3.2 Microfluidic device
Herein, we exploited a novel and rapid method to perform the generation of liquid metal double emulsion droplets in microfluidic devices with the controllable effect of gravity through an adjustable inclination angle. As sketched in Fig. 2, the detailed microfluidics apparatus is comprised of a T-shaped ETFE tee (OD = 1/16′′ ID = 0.02′′) which is connected with PTFE cylindrical tubes (OD = 1/16′′, ID = 0.02′′). The end of one tube is coaxially inserted into a wider PTFE cylindrical tube (OD = 3.0 mm, ID = 2.0 mm) on an adjustable inclined plane. Three syringe pumps (Harvard Apparatus, Pump 11 Elite) connected with different injection ports are used to inject the three immiscible fluids into the microfluidic channels independently. Each fluid is supplied through a PTFE tube at various flow rates. The flow pattern and frequency of droplet generation are accurately controlled by regulating the flow rates. Experimental images and videos are captured using a portable digital microscope (Dino lite, AM73915MZTL) and automatically imported into a computer. The sizes of the droplets are measured by an open-source image-processing software.4 Results and discussion
In this work we propose a novel method to generate liquid metal double emulsion droplets in two steps, with Galinstan inner droplets first produced at the T-shaped junction, followed by the generation of shell droplets. The second step occurs on the adjustable inclined plane, which manages to control the magnitude of the component of gravity along the flow direction.4.1 Challenge in generation of liquid metal double emulsion droplet
The density difference between liquids of double emulsion droplets usually is not very large, resulting in a stable core–shell configuration of double emulsion droplet with negligible gravity. The inner droplet is totally inside the shell droplet in a state of non-contact with the outer phase and microchannel wall. Similar to those forces considered in the formation of a single droplet generated in the T-shaped microfluidic device, the forces exerting on the whole double droplet at equilibrium in the coaxial tubes are balanced, which can be conveniently divided into directions parallel and vertical to the flow direction as depicted in Fig. 1(b). The inertial force (Finertial), interfacial tension force (Fσ) and drag force (Fdrag) are regarded as the parallel forces, while buoyancy force (Fb) is the vertical force.74,78 The balance of the holding and detaching forces determines the formation of the double emulsion droplets. Assuming the equilibrium shape of the double emulsion droplet to be spherical, the main forces acting on the double emulsion droplet during its detachment are schematically shown in Fig. 1(b).74,76,77In the left half of Fig. 1(b), the inner droplet and the generating shell droplet are analyzed as a whole, subjected to Fb, Fσ, Finertial and Fdrag, while Fb is negligible owing to the small density difference of different fluids.78,90,91 Fdrag serves as detaching force, acting in the flow direction to promote the separation of droplets. Finertial, which is three to four orders of magnitude lower than Fσ, can be ignored in the further calculation. Fσ acts to prevent the droplet separating from the nozzle, which may be described as holding force.74,92 As for the detachment mechanism, double droplet forms at the end of the inner tube, followed by the shrink and detachment when the magnitude of the detaching forces reaches beyond the holding forces. After generating, the inner droplet is totally inside the shell droplet in a state of non-contact with the outer phase and microchannel wall as demonstrated in the right part of Fig. 1(b). The whole double droplet stays stable spherical due to the equal internal interfacial tension force.
However, as for liquid metal Galinstan, which is six times denser than water, the gravity effect is conspicuous, making it difficult to be wrapped by other liquids to form an inner droplet. The force balance analysis of the generated double droplet is not applicable for Galinstan, while the feasibility of preparing Galinstan double emulsion droplets by the normal methods seems very low. Force analysis of the Galinstan double droplet on a horizontal plane is shown in Fig. 1(c). As depicted in the left half of Fig. 1(c), the inner droplet and the generating shell droplet are regarded as a whole, subjected to the gravity Fg, interfacial tension force Fσ, inertial force Finertial of the middle phase, and the drag force Fdrag of the outer phase. After generating, the force analysis on the Galinstan inner droplet is depicted in the right part of Fig. 1(c). As the flow is transverse to Fg on a horizontal plane, Fg drives the Galinstan inner droplet downward on the outer channel, as well as hinders the further flow of itself, due to the sinking of the denser fluid and the sudden expansion of the tube diameter (the ID of inner and outer tubes are 0.5 and 2.0 mm, respectively).87,93 Meanwhile, the calculated value of bond number Bo is 0.431, meaning a nonnegligible effect of gravity. Galinstan droplet comes inevitably into contact with the lower surface of the microchannel wall, causing unavoidable frictional resistance Ff as a holding force during the process of double emulsion droplet formation. Fdrag raises with the increase of the outer phase flow rate, which is capable to accelerate the flow of shell droplets but inner droplets. We called the force or force component consistent with the flow direction as driving force. As the force along the flow direction is not enough to induce the motion of the inner droplet, it is necessary to impose a driving force on the Galinstan droplet. Experimentally, we found that the gravity effect of Galinstan on a horizontal plane is prominent, while part of the gravitational potential energy on an inclined plane manages to be converted into momentum, with the gravity component acting as the driving force to impel the movement of inner droplets.
After adding an inclination angle θ, Fg can be divided into two components parallel and perpendicular to the inclined plane. When the component of Fg in the flow direction gets large exactly enough to overcome Ff, the Galinstan droplet starts to flow forward with a force-balanced configuration.
4.2 Droplet configurations
The inclination angle θ of the plane, which determines the component gravitational force along the flow direction, plays a significant role in the trade-off balance between the gravity and friction force and corresponding droplet morphologies. A larger θ means a larger gravity component along the flow direction, providing greater driving force.94 At a relatively low or high value of θ, the movement of inner droplet and shell droplet is not synchronous, which is inclined to cause the separation. An equilibrium state at the critical point exists where the two droplets are about to separate, as shown in Fig. 3 below. The edge of the inner phase droplet coincides with that of the middle phase droplet in two ways under different inclination angles, constituting different equilibrium configurations of liquid metal Galinstan double emulsion droplet which may be created as follows: (a) push-type, (b) double sphere-type, and (c) pull-type.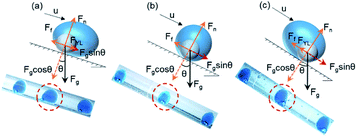 | ||
| Fig. 3 Schematic illustration of three stable configurations of liquid metal double emulsion droplet under different inclination angles. (a) Push-type; (b) double sphere-type; (c) pull-type. | ||
Fig. 3 presents three double droplet morphological configurations under different force conditions, reflecting that the forces acting on the liquid metal Galinstan, especially gravity, predominantly affects the configuration of the double emulsion droplets. For a droplet, the interface with a longer flow distance is signed as the front edge, while that with a shorter flow distance is marked as the rear edge. Fig. 3(b) depicts that at the appropriate inclination angle θ (30°–45°), Fg sinθ raises exactly enough to counterbalance the effect of Ff, while the two forces balance each other to maintain the double droplet flow in a stable double sphere-type configuration (see ESI Movie 1†).
When θ falls in the range of 0° to 30°, the rear edges of the inner and shell droplets coincide, presenting a push-type (see ESI Movie 2†) equilibrium configuration of double droplet with an ellipsoidal shell droplet as shown in Fig. 3(a). On the contrary, if the inclination angle varies between 45° and 60°, the front edges of the inner and shell droplets coincide, constituting a pull-type (see ESI Movie 3†) equilibrium configuration of the double emulsion droplets with an ellipsoidal shell droplet in Fig. 3(c). The inner droplet is maintained inside the shell droplet due to the Laplace pressure of the shell droplet directed to the center of the droplet.
4.3 Effect of flow rates
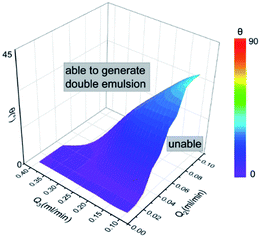
The phase flow rate mainly affects the shell droplets, while the regulation of inclination angle focuses on the inner droplets. Therefore, in addition to the manipulation of the inclination angle θ, the phase flow rate also serves as a particularly eminent study factor during the formation of double droplet. Combined with the adjustment of θ and phase flow rates, liquid metal Galinstan double emulsion droplets with various stable configurations manage to be formulated. The middle shell droplet, sheared off by the outer phase as flowing to the tip of the inner tube, immediately engulfs Galinstan inner droplet, thus producing double emulsion droplets.Fig. 4 drawn from the experimental phenomena schematically shows a three-dimensional illustration of liquid metal double emulsion droplets formation depending on Q2 and Q3 under various inclination angles θ. The surface, colored by the variation of θ, determines the feasibility of the generation of liquid metal double emulsion droplet. Fig. 4 shows that droplets are unable to be generated under the condition below the surface, while they are facile to be formed as θ increases above the surface. The change of Q2 appears inadequate to promote the droplet generation when θ and Q3 both remain relatively small. On the contrary, the influence of Q2 and Q3 on the formation seems not quite notable at larger θ, implying that the gravity of Galinstan plays a decisive role in the formation of liquid metal double emulsion droplets.
Specifically, the results illustrated in Fig. 5 show that the dependency of double emulsion droplet formation and corresponding type on gravity (i.e. inclination angle θ), capillary number (Ca) of the outer phase and the flow rates. Double emulsion droplets manage to be formed within a certain range of θ and phase flow rates. It can be concluded from the theoretical part that the interfacial tension force comes into prominence during the formation of droplet only when Ca and We are both small. Furthermore, flow pattern appears various types at varying flow rates, ranging from squeezing regime (Ca < 0.002) through transient regime (0.002 < Ca < 0.01) to dripping regime (0.01 < Ca < 0.3).95 Experimental results show that the outer phase manages to shear the middle phase into shell droplets when Ca varies in the range of 0.017 to 0.028, so as to produce the liquid metal Galinstan double emulsion droplets.
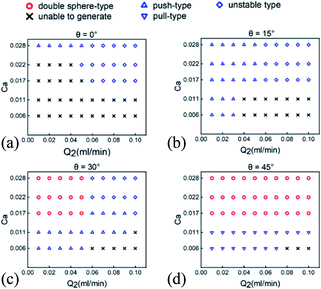 | ||
| Fig. 5 Effect of the middle phase flow rate (Q2) and capillary number (Ca) of the outer phase on the formation of double emulsion droplets at different inclination angles. (a) Double emulsion droplet generation at 0° (horizontal state); (b) 15°; (c) 30°; (d) 45°. The generated double emulsion droplets have many morphological configurations (shown in Fig. 3 above) as signified by different symbols above except that the cross symbol means double emulsion droplets are incapable to be generated. The unstable type refers to the instability during or after the generation. | ||
Double emulsion droplets can hardly be generated under the horizontal state as depicted in Fig. 5(a), owing to the fact that the nonnegligible gravity of Galinstan makes it difficult for the middle phase to wrap the inner phase. The type of “unable to generate” in Fig. 5 represents the following situations (shown in Fig. S1 of the ESI,†). At lower Ca, the middle phase is unable to be sheared off by the outer phase into droplets, while the shell droplets are separated from the inner droplets by a stronger drag force from the outer phase after forming in the case of higher Ca. It is experimentally observed that the middle phase continues to move forward, while the Galinstan droplet is deposited on the channel wall by gravity. Therefore, inclination angle θ are utilized in the microfluidic device to weaken the gravitational action on the horizontal plane. As θ increased from 0° to 45° at 15° intervals (Fig. 5), meaning an increase to 75% of the gravity as driving force along the flow direction, the trend towards double emulsion droplet formation appears to be a little different. Compared to the horizontal state (no inclination angle), double emulsion droplets exhibit a stronger tendency to be generated with more stable configurations when a certain inclination angle such as 15° is added, while the generation seems to be much easier under the high Ca of the outer phase, as shown in Fig. 5(b).
At a relatively high Ca (Ca ≥ 0.017), the morphological configuration appears to be close to perfect double sphere-type shown in Fig. 5(c) and (d) as θ increases to approximately 30° to 45°, meaning that 50–75% of the gravity serves as the driving force. Moreover, 60% double emulsion droplets with perfect double sphere-type are able to be obtained by adjusting the flow rates at about 45°. The morphological configuration has a tendency to change from push-type to pull-type with the increase of θ, as shown in Fig. 5. A relatively large Q2 (Q2 > 0.06 ml min−1) under a small θ (θ ≤ 30°) may lead to an unstable process of the formation of Galinstan double emulsion droplet when Ca ≥ 0.017. In addition, double emulsion droplets may hardly be generated at 30° (Fig. 5(c)) and 45° (Fig. 5(d)) when Q2 is large (Q2 > 0.06 ml min−1) and Ca is relatively small (Ca < 0.017), due to the fact that the outer phase has no ability to shear off the middle phase to form the shell droplets under a relatively low Q3/Q2.
Interestingly, we witness successful and consistent generation, but unstable maintenance of double emulsion droplets given that θ exceeds a threshold value of 60°, regardless of Q2 and Q3. Gravity component along the flow direction (Fg sinθ) serves as the main force acting on the Galinstan droplet, giving rise to the pull-type configuration but easy to separate. It is because that the enhanced Fg sinθ overcomes Ff and brings about an acceleration of the inner droplet, while the drag force of the outer phase exerting on shell droplet is not enough to maintain the synchronous movement, leading to the velocity difference.
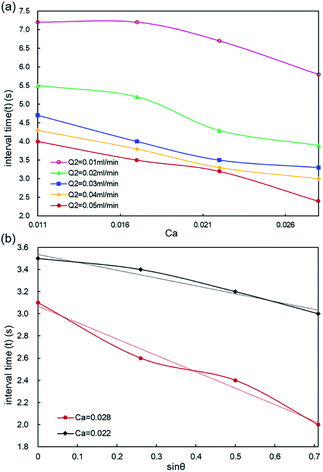
We established a fitting model to predict droplet generation frequency based on our experimental data. In perspectives of practical operations, it is of great significance to optimize droplet generation frequency for the purpose of productivity and quality control. In this work, the droplet generation frequency is indicated by the interval time (t) between two adjacent droplets. The outer phase flow rate is denoted by capillary number (Ca) of the outer phase, as demonstrated in Fig. 6. It is found that the interval time (t) depends on capillary number (Ca) of the outer phase, middle phase flow rate (Q2) and gravity component along the flow direction (denoted by sinθ). As analyzed in Fig. 6(a), we found the interval time (t) decreases linearly with the increasing of Ca and Q2. Especially, a large value of Ca and Q2 results in a short interval time of double emulsion droplets formation. We observed an apparent downward trend of the interval time as Q2 increases from 0.01 to 0.05 ml min−1 at Ca >0.021. Droplet interval time drops sharply under a high Ca by increasing θ, as demonstrated in Fig. 6(b). Conclusively, Ca and θ are inversely proportional to the interval time, signifying a short time to achieve the force balance for droplet generation under a high Ca or θ. The inverse trend can be explained by (i). A large Ca denotes a high shearing force of the outer phase, and (ii). A large θ means a large gravity component along the flow direction serving as the driving force to impel the droplet movement.
A fitting model is built on experimental results to predict the regulation mechanism of interval time (t) through Reynolds number (Re2) and capillary number (Ca), as shown by eqn (4). In this work, Reynolds number (Re2 = ρ2diu2/μ2, di denotes the ID of the outer tube) is used to represent Q2. Ca and Re2 are both logarithmically inversely proportional to the interval time (t) as depicted by eqn (4). Parameters b and c can be interpreted as constants in each case. ta represents the intercept on vertical axis, denoting the interval time at a minimum of Ca. Fitting parameters can be obtained by fitting all the data to the model (see ESI Table S1†).
The effect of gravity (denoted by sinθ) on interval time (t) is analyzed by an empirical linear model as indicated by eqn (5), where m is a positive constant for each case of Ca. Similarly, tb represents the interval time at minimum inclination angle. The detailed parameters are given by ESI Table S1.†
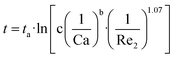 | (4) |
t = − tb·(m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1) θ − 1)
| (5) |
It is worth noting that the interfacial tension force (σ23) and the middle phase viscosity (μ2) are proportional to the droplet formation time, while the gravity component (sinθ), outer phase viscosity (μ3) and velocity (u2 and u3) are inversely proportional. The shearing force increases with the rise of μ3 and u3, and the driving force increases with raising θ, both resulting in a short generation time. High detaching force and long detaching time are required as the holding force (σ23) increases. In a word, the control of droplet generation frequency can be regulated by achieving a delicate balance among interfacial tension, inertial force, viscous force and gravity.
4.4 Droplet solidification
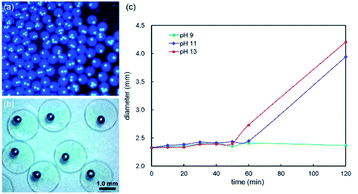
Solidification of the shell droplets to stabilize the double emulsion droplets can be subsequently realized by the crosslinking reaction between sodium alginate solution and calcium ions such as the calcium chloride solution.72,77,79,96 The pH sensitivity of sodium alginate can be used to control the release of its encapsulated content, thus serving as a controlled release system.58 The carboxyl group in the sodium alginate molecule exists mainly in the form of anions that repel each other when the solution is alkaline, facilitating the entry of water molecules, causing an increase in the swelling rate of the gel. It swells further until broken to release the contents. We adapted the direct dropping method to obtain the core–shell liquid metal hydrogel capsules by dropping the double emulsion droplet into calcium chloride solution. The depth of coagulating bath was controlled between 0.8 and 1.0 cm in the experiment. The droplet was solidified to be in the shape of a ball with a tail if the depth is shallower than 0.8 cm, while a gourd shape would be generated when the depth is deeper than 1.0 cm. If the solution is too deep, it produces greater buoyancy than the gravity of Galinstan. On the contrary, the gravity effect of Galinstan is too large in a too shallow solution and thus the droplet has a tendency to float on the surface of the calcium chloride solution. Therefore, an appropriate depth comes into play during the formation of solidified spheres. In addition, the concentrations of calcium chloride and sodium alginate solutions are also crucial in the preparation of calcium alginate gel spheres, which are both 4 wt% owing to the difficulty to form gel completely at a lower concentration. Then the solidified spheres were soaked in solutions of different pH values to test the pH sensitivity due to the PH swelling property of calcium alginate hydrogel.96–98 Fig. 7(a) and (b) exhibit the morphologies of core–shell liquid metal hydrogel capsules obtained in 4 wt% CaCl2 aqueous solution. The diameter variation in alkaline environment is shown in Fig. 7(c).The pH sensitivity of solidified spheres is reflected by diameter in the solutions of variable pH. The solidified spheres exhibit spherical shape with an average diameter of about 2.330 mm (D0), retaining high monodispersity. Experimental results show that the diameters have no discernible difference before and after soaking in acidic and neutral solutions but change in alkaline solution, as shown in Fig. 7(c). Specifically, the generated spheres are soaked in the solution of pH 9, 11 and 13 for 120 min, respectively. Fig. 7(c) shows that diameter increases with the increase of pH. The diameters increase dramatically after soaking in the solution of pH 11 and 13 for 120 min, which are 3.945 mm and 4.207 mm, respectively, indicating a notable swelling degree in the strong alkaline environment. In contrast, the diameter has no significant change in the weak alkaline solution of pH 9, which is 2.369 mm. The swelling rate W can be used to indicate the change of swelling degree and obtained by measuring the diameter change, which may be analyzed by the following equation:
| W/%=(D − D0)/D0 × 100 | (6) |
The swelling rate of soaking for two hours can therefore be obtained according to the experimental data, with values of 1.67% in pH 9, 69.31% in pH 11, and 80.56% in pH 13, respectively, showing that swelling rate is linearly dependent on pH. Additionally, separation of Galinstan inner droplets from the shell gel happens in the strong alkaline environment of pH 11 and 13 after soaking for more than 2 hours experimentally. Experimental phenomenon indicates that strong alkaline environment may destroy the core–shell structure as well as release of contents, thus leading to the disintegration of solidified spheres. Calcium alginate gel exhibits swelling and release properties to the environmental pH, thus extending its potential applications in the field of drug transport and release. Moreover, the swelling characteristic is prone to be regulated by adding environmental stimuli responsive materials to the solution during the preparation of calcium alginate gel to obtain various functional materials.97
Conclusions
A novel type of liquid metal double emulsion droplets has been created by controlling the effect of gravity in microfluidic, which may prevent the surface oxidation of Galinstan, addressing certain application limitations. The effect of gravity is obliged to be taken into consideration in the generation liquid metal double emulsion droplets due to the high density of Galinstan. The most critical and innovative portion of this study is to promote the movement of liquid metal by converting part of gravity into driving force. An adjustable inclination angle to conveniently control the effect of gravity is therefore added to the droplet generation device as the main influence factor for the generation.It can be concluded that the force of gravity, directly reflected by the adjustable inclination angle θ, has a remarkable effect on the droplet formation and morphological configuration. Liquid metal double emulsion droplets with perfect double sphere-type configuration are capable to be generated when θ varies in a range of 30° to 45°, meaning that 50–75% of the gravity serves as the driving force along the flow direction. Furthermore, 60% double emulsion droplets with perfect double sphere-type configuration are able to be obtained by adjusting the flow rates of the middle and outer phases at 45°. Virtually, the relationship between the interfacial tension force and shearing force as well plays a crucial role in the dynamic behaviors of droplet formation, reflecting by the droplet generation interval time.
The stable core–shell liquid metal hydrogel capsules are facile to be obtained by forming calcium alginate hydrogel.72,77,79 Strong alkaline environment has a visible tendency to make the calcium alginate hydrogel swell, enlarging the volume of the solid spheres and releasing inner droplets. By utilizing the pH sensitivity properties of shell material or choosing other shell materials with different characteristics, the core–shell liquid metal capsules promise to be used as multifunctional materials for controlled release systems in drug delivery and biomedical.66,68 Meanwhile, the hydrogel shell is capable to be dissolved by regulating pH or imposing mechanical force to recover the electrical conductivity of Galinstan for applications in flexible electronics, self-healing conductor, elastomer electronic skin, tumor therapy.62,66,69
Author contributions
Qiyue Fan and Yaohao Guo conceived the concept of this work. Qiyue Fan designed and performed the experiments. Qiyue Fan, Yaohao Guo and Bo Bao analyzed the results. Qiyue Fan wrote the manuscript. All the authors participated in revising the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by Natural Science Foundation of the Science and Technology Commission of Shanghai Municipality. (No. 19ZR1472200).Notes and references
- J. Yan, Y. Lu, G. Chen, M. Yang and Z. Gu, Chem. Soc. Rev., 2018, 47, 2518–2533 RSC.
- Z. Wang, H. Gao, J. Niu, C. Zhang and Z. Zhang, ACS Sustainable Chem. Eng., 2019, 7, 3274–3281 CrossRef CAS.
- K. Khoshmanesh, S. Y. Tang, J. Y. Zhu, S. Schaefer, A. Mitchell, K. Kalantar-Zadeh and M. D. Dickey, Lab Chip, 2017, 17, 974–993 RSC.
- T. Daeneke, K. Khoshmanesh, N. Mahmood, I. A. De Castro, D. Esrafilzadeh, S. J. Barrow, M. D. Dickey and K. Kalantar-Zadeh, Chem. Soc. Rev., 2018, 47, 4073–4111 RSC.
- M. Zhang, S. Yao, W. Rao and J. Liu, Mater. Sci. Eng., R, 2019, 138, 1–35 CrossRef.
- A. A. Darhuber, J. P. Valentino, S. M. Troian and S. Wagner, Mater. Sci. Eng., R, 2003, 12, 873–879 CAS.
- B. Gol, M. E. Kurdzinski, F. J. Tovar-Lopez, P. Petersen, A. Mitchell and K. Khoshmanesh, Appl. Phys. Lett., 2016, 108, 164101 CrossRef.
- J. Je and J. Lee, Mater. Sci. Eng., R, 2014, 23, 1156–1163 Search PubMed.
- G. Bo, L. Ren, X. Xu, Y. Du and S. Dou, Adv. Phys.: X, 2018, 3, 412–442 Search PubMed.
- Q. Wang, Y. Yu, J. Yang and J. Liu, Adv. Mater., 2015, 27, 7109–7116 CrossRef CAS PubMed.
- M. Kim and S. Seo, Mol. Cryst. Liq. Cryst., 2019, 685, 40–46 CrossRef CAS.
- M. D. Dickey, R. C. Chiechi, R. J. Larsen, E. A. Weiss, D. A. Weitz and G. M. Whitesides, Adv. Funct. Mater., 2008, 18, 1097–1104 CrossRef CAS.
- S. Y. Tang, I. D. Joshipura, Y. Lin, K. Kalantar-Zadeh, A. Mitchell, K. Khoshmanesh and M. D. Dickey, Adv. Mater., 2016, 28, 604–609 CrossRef CAS PubMed.
- M. D. Dickey, ACS Appl. Mater. Interfaces, 2014, 6, 18369–18379 CrossRef CAS PubMed.
- Y. Hayashi, N. Saneie, G. Yip, Y. J. Kim and J. H. Kim, Int. J. Heat Mass Transfer, 2016, 101, 1204–1216 CrossRef CAS.
- M. R. Khan, C. B. Eaker, E. F. Bowden and M. D. Dickey, Proc. Natl. Acad. Sci. U.S.A., 2014, 111, 14047–14051 CrossRef CAS PubMed.
- T. Hutter, W. A. C. Bauer, S. R. Elliott and W. T. S. Huck, Adv. Funct. Mater., 2012, 22, 2624–2631 CrossRef CAS.
- S. Y. Tang, R. Qiao, S. Yan, D. Yuan, Q. Zhao, G. Yun, T. P. Davis and W. Li, Small, 2018, 14, 1–8 Search PubMed.
- B. Zhang, Q. Dong, C. E. Korman, Z. Li and M. E. Zaghloul, Sci. Rep., 2013, 3, 1–8 Search PubMed.
- A. R. Jacob, D. P. Parekh, M. D. Dickey and L. C. Hsiao, Langmuir, 2019, 35, 11774–11783 CrossRef CAS PubMed.
- Y. Chen, J. L. Wagner, P. A. Farias, E. P. DeMauro and D. R. Guildenbecher, Int. J. Multiphase Flow, 2018, 106, 147–163 CrossRef CAS.
- Y. Jiao, C. W. Young, S. Yang, S. Oren, H. Ceylan, S. Kim, K. Gopalakrishnan, P. C. Taylor and L. Dong, IEEE Sens. J., 2016, 16, 7870–7875 CAS.
- G. J. Hayes, J. H. So, A. Qusba, M. D. Dickey and G. Lazzi, IEEE Trans. Antennas Propag., 2012, 60, 2151–2156 Search PubMed.
- J. Thelen, M. D. Dickey and T. Ward, Lab Chip, 2012, 12, 3961 RSC.
- G. Li, M. Parmar, D. Kim, J. B. Lee and D. W. Lee, Lab Chip, 2014, 14, 200–209 RSC.
- T. Liu, P. Sen and C. J. Kim, Mater. Sci. Eng., R, 2012, 21, 443–450 CAS.
- S. Y. Tang, V. Sivan, P. Petersen, W. Zhang, P. D. Morrison, K. Kalantar-zadeh, A. Mitchell and K. Khoshmanesh, Adv. Funct. Mater., 2014, 24, 5851–5858 CrossRef CAS.
- C. Ladd, J. H. So, J. Muth and M. D. Dickey, Adv. Mater., 2013, 25, 5081–5085 CrossRef CAS PubMed.
- L. Tian, M. Gao and L. Gui, Micromachines, 2017, 8, 1–12 Search PubMed.
- H. Song, D. L. Chen and R. F. Ismagilov, Angew. Chem. Int. Ed., 2006, 45, 7336–7356 CrossRef CAS PubMed.
- Z.-M. Liu, Y. Yang, Y. Du and Y. Pang, Chinese J. Anal. Chem., 2017, 45, 282–296 CrossRef CAS.
- S. Y. Tang, V. Sivan, K. Khoshmanesh, A. P. O'Mullane, X. Tang, B. Gol, N. Eshtiaghi, F. Lieder, P. Petersen, A. Mitchell and K. Kalantar-Zadeh, Nanoscale, 2013, 5, 5949–5957 RSC.
- V. Sivan, S. Y. Tang, A. P. O'Mullane, P. Petersen, N. Eshtiaghi, K. Kalantar-Zadeh and A. Mitchell, Adv. Funct. Mater., 2013, 23, 144–152 CrossRef CAS.
- T. Sannicolo, M. Lagrange, A. Cabos, C. Celle, J. P. Simonato and D. Bellet, Small, 2016, 12, 6052–6075 CrossRef CAS PubMed.
- A. Sattari, P. Hanafizadeh and M. Hoorfar, Adv. Colloid Interface Sci., 2020, 282, 102208 CrossRef CAS PubMed.
- H. Yan and C. Kim, Colloids Surf., A, 2014, 443, 88–95 CrossRef CAS.
- Y. Liu, W. Zhang and H. Wang, Mater. Horiz., 2021, 8, 56–77 RSC.
- S. Okushima, T. Nisisako, T. Torii and T. Higuchi, Langmuir, 2004, 20, 9905–9908 CrossRef CAS PubMed.
- E. Hughes, A. A. Maan, S. Acquistapace, A. Burbidge, M. L. Johns, D. Z. Gunes, P. Clausen, A. Syrbe, J. Hugo, K. Schroen, V. Miralles, T. Atkins, R. Gray, P. Homewood and K. Zick, J. Colloid Interface Sci., 2013, 389, 147–156 CrossRef CAS PubMed.
- N. N. Deng, W. Wang, X. J. Ju, R. Xie, D. A. Weitz and L. Y. Chu, Lab Chip, 2013, 13, 4047–4052 RSC.
- Z.-M. Liu, Y. Du and Y. Pang, Chinese J. Anal. Chem., 2018, 46, 324–330 CrossRef CAS.
- K. L. Lao and G. B. Lee, Transducers 2007 – 2007 Int. Solid-State Sensors, Actuators Microsystems Conf., 2007, pp. 265–268 Search PubMed.
- S. A. Nabavi, G. T. Vladisavljević, S. Gu and E. E. Ekanem, Chem. Eng. Sci., 2015, 130, 183–196 CrossRef CAS.
- N. Wang, C. Semprebon, H. Liu, C. Zhang and H. Kusumaatmaja, J. Fluid Mech., 2020, 895, 1–33 Search PubMed.
- N. Pannacci, H. Bruus, D. Bartolo, I. Etchart, T. Lockhart, Y. Hennequin, H. Willaime and P. Tabeling, Phys. Rev. Lett., 2008, 101, 1–4 Search PubMed.
- M. Seo, C. Paquet, Z. Nie, S. Xu and E. Kumacheva, Soft Matter, 2007, 3, 986–992 RSC.
- C. Cramer, P. Fischer and E. J. Windhab, Chem. Eng. Sci., 2004, 59, 3045–3058 CrossRef CAS.
- A. Perro, C. Nicolet, J. Angly, S. Lecommandoux, J. F. Le Meins and A. Colin, Langmuir, 2011, 27, 9034–9042 CrossRef CAS PubMed.
- M. A. Herrada, A. M. Gañán-Calvo, A. Ojeda-Monge, B. Bluth and P. Riesco-Chueca, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 1–16 Search PubMed.
- T. Nisisako, S. Okushima and T. Torii, Soft Matter, 2005, 1, 23–27 RSC.
- J. H. Xu, R. Chen, Y. D. Wang and G. S. Luo, Lab Chip, 2012, 12, 2029–2036 RSC.
- X. Guan, L. Hou, Y. Ren, X. Deng, Q. Lang, Y. Jia, Q. Hu, Y. Tao, J. Liu and H. Jiang, Biomicrofluidics, 2016, 10, 034111 CrossRef PubMed.
- S. Nawar, J. K. Stolaroff, C. Ye, H. Wu, D. T. Nguyen, F. Xin and D. A. Weitz, Lab Chip, 2019, 20, 147–154 RSC.
- H. Peng, Z. Xu, S. Chen, Z. Zhang, B. Li and L. Ge, Colloids Surf., A, 2015, 468, 271–279 CrossRef CAS.
- B. Cai, T. T. Ji, N. Wang, X. B. Li, R. X. He, W. Liu, G. Wang, X. Z. Zhao, L. Wang and Z. Wang, Lab Chip, 2019, 19, 422–431 RSC.
- M. Samandari, F. Alipanah, S. Haghjooy Javanmard and A. Sanati-Nezhad, Sens. Actuators, B, 2019, 291, 418–425 CrossRef CAS.
- A. Sattari and P. Hanafizadeh, Colloids Surf., A, 2020, 602, 1–14 CrossRef.
- C. X. Zhao, Adv. Drug Delivery Rev., 2013, 65, 1420–1446 CrossRef CAS PubMed.
- A. Zavabeti, J. Z. Ou, B. J. Carey, N. Syed, R. Orrell-Trigg, E. L. H. Mayes, C. Xu, O. Kavehei, A. P. O'Mullane, R. B. Kaner, K. Kalantar-Zadeh and T. Daeneke, Science, 2017, 358, 332–335 CrossRef CAS PubMed.
- X. Sun, B. Cui, B. Yuan, X. Wang, L. Fan, D. Yu, Z. He, L. Sheng, J. Liu and J. Lu, Adv. Funct. Mater., 2020, 30, 1–12 Search PubMed.
- J. Jeon, J. B. Lee, S. K. Chung and D. Kim, Lab Chip, 2017, 17, 128–133 RSC.
- X. Li, M. Li, L. Zong, X. Wu, J. You, P. Du and C. Li, Adv. Funct. Mater., 2018, 28, 1–8 Search PubMed.
- P. J. Geddis, L. Wu, A. M. McDonald, S. W. S. Chen and B. R. Clements, Can. J. Chem., 2020, 98, 1–31 CrossRef.
- S. Farley, K. Ramsay and K. S. Elvira, Lab Chip, 2021, 2781–2790 RSC.
- G. T. Vladisavljevi, R. Al Nuumani and S. A. Nabavi, Micromachines, 2017, 8, 1–34 Search PubMed.
- J. Fu, C. Zhang, T. Liu and J. Liu, Front. Energy, 2020, 14, 81–104 CrossRef.
- Q. Wang, Y. Yu and J. Liu, Adv. Eng. Mater., 2018, 20, 1–21 Search PubMed.
- S. A. Chechetka, Y. Yu, X. Zhen, M. Pramanik, K. Pu and E. Miyako, Nat. Commun., 2017, 8, 1–19 CrossRef PubMed.
- T. Liu, P. Sen and C. J. Kim, Mater. Sci. Eng., R, 2012, 21, 443–450 CAS.
- S. D. Svetlov and R. S. Abiev, Chem. Eng. Sci., 2021, 235, 116493 CrossRef CAS.
- J. H. Xu, G. S. Luo, G. G. Chen and J. D. Wang, J. Membr. Sci., 2005, 266, 121–131 CrossRef CAS.
- A. S. Chaurasia, F. Jahanzad and S. Sajjadi, Chem. Eng. J., 2017, 308, 1090–1097 CrossRef CAS.
- Y. Chen, X. Liu, C. Zhang and Y. Zhao, Lab Chip, 2015, 15, 1255–1261 RSC.
- X. Wang, J. Zhu, T. Shao, X. Luo and L. Zhang, Chem. Eng. Technol., 2019, 42, 1330–1340 CrossRef CAS.
- S. K. Jena, S. S. Bahga and S. Kondaraju, Phys. Fluids, 2021, 33, 032120 CrossRef CAS.
- J. Husny and J. J. Cooper-White, J. Nonnewton. Fluid Mech., 2006, 137, 121–136 CrossRef CAS.
- Y. Gu, H. Kojima and N. Miki, Sens. Actuators, A, 2011, 169, 326–332 CrossRef CAS.
- D. L. Giorgio, P. D. M. Francesco, D. R. Alberto and D. Enrico, Chem. Eng. Process., 2008, 47, 1150–1158 CrossRef.
- C. Chen, Z. Ding, S. S. Tiwari, J. Wang, J. Wang, G. Liu, Y. Li, M. Guo and K. Nandakumar, Can. J. Chem. Eng., 2021, 1–15 Search PubMed.
- Y. Guo, L. Zhang, Y. Yang, Z. Xu and B. Bao, J. Pet. Sci. Eng., 2021, 207, 109107 CrossRef CAS.
- P. Zhu and L. Wang, Lab Chip, 2017, 17, 34–75 RSC.
- T. Gothsch, C. Schilcher, C. Richter, S. Beinert, A. Dietzel, S. Büttgenbach and A. Kwade, Microfluid. Nanofluid., 2015, 18, 121–130 CrossRef CAS.
- M. Azarmanesh, M. Farhadi and P. Azizian, Phys. Fluids, 2016, 28, 032005 CrossRef.
- T.-V. Vu, T. V. Vu, C. T. Nguyen and P. H. Pham, Int. J. Heat Mass Transfer, 2019, 135, 796–810 CrossRef.
- C. Zhou, P. Yue and J. J. Feng, Phys. Fluids, 2006, 18, 092105 CrossRef.
- N. Zhumatay, B. Kabdenova, E. Monaco and L. R. Rojas-Solórzano, European Journal of Mechanics – B/Fluids, 2021, 86, 198–209 CrossRef.
- C. N. Baroud, F. Gallaire and R. Dangla, Lab Chip, 2010, 10, 2032–2045 RSC.
- T. Trantidou, M. S. Friddin, A. Salehi-Reyhani, O. Ces and Y. Elani, Lab Chip, 2018, 18, 2488–2509 RSC.
- N. Teo, C. Jin, A. Kulkarni and S. C. Jana, J. Colloid Interface Sci., 2020, 561, 772–781 CrossRef CAS PubMed.
- V. Schroder, O. Behrend and H. Schubert, J. Colloid Interface Sci., 1998, 340, 334–340 CrossRef.
- D. L. Giorgio and D. Enrico, J. Colloid Interface Sci., 2006, 294, 436–448 CrossRef PubMed.
- W. Wang, K. H. Ngan, J. Gong and P. Angeli, Colloids Surf., A, 2009, 334, 197–202 CrossRef CAS.
- A. Giorello, F. Minetti, A. Nicastro and C. L. A. Berli, Sens. Actuators, B, 2020, 307, 127595 CrossRef.
- S. Verleger, A. Grimm, C. Kreuter, H. M. Tan, J. A. Van Kan, A. Erbe, E. Scheer and J. R. C. Van Der Maarel, Lab Chip, 2012, 12, 1238–1241 RSC.
- Y. H. Geng, S. Da Ling, J. P. Huang and J. H. Xu, Small, 2020, 16, 1–20 Search PubMed.
- K. M. Lee, W. C. Yoong, C. F. Loke, J. C. Juan, K. Yusoff, N. Mohtarrudin and T. H. Lim, ScienceAsia, 2021, 47, 42–50 CAS.
- J. Comaposada, P. Gou, B. Marcos and J. Arnau, LWT-Food Sci. Technol., 2015, 64, 212–219 CrossRef CAS.
- H. Daemi and M. Barikani, Sci. Iran., 2012, 19, 2023–2028 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra04120k |
| This journal is © The Royal Society of Chemistry 2022 |