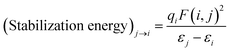Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theoretical study of induced selective N2 binding under an electric field in MOF-74: application for N2/CH4 separations†
Honghui Kim and
Jihan Kim*
and
Jihan Kim*
Department of Chemical and Biomolecular Engineering, Korea Advanced Institute of Science and Technology (KAIST), 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Republic of Korea. E-mail: jihankim@kaist.ac.kr
First published on 19th August 2022
Abstract
In this theoretical study, selective binding of dinitrogen to the coordinatively unsaturated metal site in M-MOF-74 (M = Mg, Mn, Fe, Co, Ni, Cu, Zn) under an external electric field is investigated. Simulation results suggest that an external electric field enhances the π* back-bonding between the transition metal and dinitrogen molecule while weakening the σ bond between the metal and other small gas molecules such as CO2 and CH4. In particular, Co-MOF-74 and Fe-MOF-74 show the highest dinitrogen binding energy in the presence of an electric field, twice as high as that of methane. Our work demonstrates that the asymmetric effect of the electric field on different gas molecules can serve as another dimension of design that can be exploited in small gas molecule separation in metal–organic frameworks.
Introduction
Dinitrogen, the most abundant species in the air, is widely known as a component that needs to be removed for utilization in raw mixtures such as natural gas. Cryogenic distillation is known to be useful for large-scale N2/CH4 separation application, but massive power consumption is one of the drawbacks.1 As such, alternative methods such as pressure swing adsorption and membrane separation have been explored to remedy these concerns.2 Recently, many researchers have used metal–organic frameworks (MOFs) to separate the mixture of N2 and CH4,3–5 and in particular, researchers have reported that the π* back-bonding between a MOF and dinitrogen can enhance the performance for the N2/CH4 separation.6In terms of materials applications, external stimuli and modifications such as pressure, temperature, ligand insertion and electric/magnetic fields provide means to tune the properties of the materials,7–9 and thereby can be used as a “switch” to enhance the performance of the material. In particular, electric fields have been gaining traction as of late as their utility has been explored in many different applications such as gas separation of propene/propane10 and electric field-induced assembly of MOF.11 Moreover, there have been many computational studies regarding electric field that have demonstrated its potential utility in CO2 capture,12 methane C–H bond activation,13 graphene hydrogenation14 and controllable molecular gate.15 However, to the best of knowledge there hasn't been anyone who has investigated how electric field can affect the N2/CH4 separation performance.
Here, we use density functional theory (DFT) to investigate the mechanisms in which the electric field can asymmetrically modify both the N2 and the CH4 binding energies in M-MOF-74 (with M being Mg and 3d transition metals). We hypothesize that since the donation of electron in π* back-bonding is opposite to that of σ bond, there will be disparate effect on the bonds from the external electric field. And this difference will map into unique effects in the N2 and CH4 binding energies, which can lead to synergetic separation performances.
Computational methods
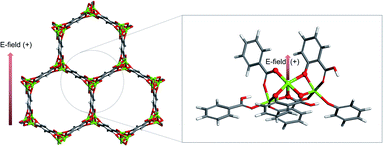
The cluster model of M-MOF-74 is constructed in the same manner as the iron MOF-74 model from Verma et al.,16 that cleaves out the cluster by considering metal node as the center and drawing a circle to include linkers (see the circle in grey dashed line in Fig. 1 left). Periodic unit cell of Mg-MOF-74 from Lee et al.17 is used as a starting material for all the other M-MOF-74 structures. First, the Mg-MOF-74 unit cell is extended to cleave out the cluster model of 88 atoms that consists of three Mg atoms and six organic linkers (see Fig. 1).When the cluster is cleaved out, functional groups such as carboxylate and oxido are terminated with hydrogen atoms to make the cluster neutral in charge. Then, to investigate the MOF-74 system with transition metals, the Mg atom is substituted with transition metal atoms such as Mn, Fe, Co, Ni, Cu, Zn which to the best of our knowledge are the list of experimentally synthesizable M-MOF-74s. Here we only substitute the central Mg atom to the other transition metals, so that the cluster can precisely simulate the environment of targeted M-MOF-74 while lowering computational cost. Spin state of the central transition metal is set to be a high-spin state (S = 5/2 for Mn, 4/2 for Fe, 3/2 for Co), which is deemed to be ground states, experimentally and computationally.17–19
All the DFT calculations in this study is performed using the Gaussian 16 program20 (G16), and M06-L21 exchange–correlation functional and def2tzvp22 basis sets, that are well validated as appropriate functional and basis sets for 3d transition metals by Xu et al.,23 are employed. During the geometrical optimization, the central metal atom and the first coordination shell composed of five oxygen atoms are relaxed and other atoms of the cluster are fixed. External electric field is applied to the cluster in the range of −0.010 a.u. to +0.010 a.u. (where 1 a.u. = 5.142 × 1011 V m−1). The positive direction of the electric field corresponds to the vector with direction as follows (see Fig. 1).
Binding energy of small gas molecules (CH4, CO2, N2) within the M-MOF-74 cluster is computed using the below equation.
| (Binding energy) = |Ecluster+gas − Ecluster − Egas| |
Along with the binding energy, N2 stretching frequency, which is a good indicator of the π* back-bonding, is computed. Also, natural bond orbital (NBO) analysis is performed using the NBO 3.1 program24 (included in the G16). From the NBO analysis, stabilization energy via delocalizing donor NBO (Lewis type) to acceptor NBO (non-Lewis type) is calculated by second order perturbation theory as following
Results and discussion
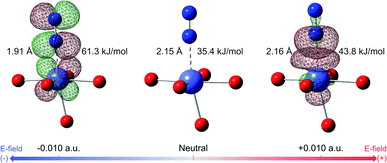
The DFT binding energy of N2 and CH4 under electric field is computed for the M-MOF-74 structures and the results are plotted in Fig. 2 for different metal atoms. As the electric field changes from negative to zero to positive value, binding energy of CH4 shows monotonic increase for all metal types. Since σ bond is the dominant mechanism for CH4 binding in M-MOF-74, positive electric field further induces the electron to move from the CH4 gas molecule towards the coordinatively unsaturated metal site (CUS), thereby strengthening the σ bond. On the contrary, the negative electric field will provide a force that induces electrons away from the metal site and as such weaken the CH4–MOF interactions. On the other hand, N2 binding shows a different trend because of the π* back-bonding via d–π* interaction (3d orbital from transition metal and π* orbital from N2 molecule). For all metal types, positive electric field strengthens the N2 binding energy, similar to the case for CH4. On the other hand, negative electric field weakens N2 binding in Mg, Mn, Ni, and Zn-MOF-74, while it strengthens binding in Fe, Co, and Cu-MOF-74. Similar to CH4, the former can be interpreted as σ bond dominant environment, while for the latter case, π* back-bonding needs to be considered. In the M-MOF-74 systems, the π* back-bonding is formed by donating electrons from the d orbitals of the transition metal to the π* orbital of N2. Therefore, negative electric field induces the electrons to move toward the metal and thereby strengthening the π* back-bonding and increasing the N2 binding energy. Fig. 3 visualizes corresponding NBOs in Co-MOF-74, which showed the largest enhancement in the N2 binding energy for negative electric fields amongst the investigated systems. Similar analysis for CO2 can be seen in Fig. S1† where CO2 acts more like CH4 given that it also lacks the π* back-bonding.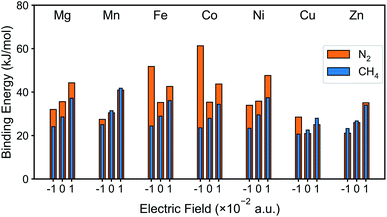 | ||
| Fig. 2 N2 and CH4 binding energy of M-MOF-74 (M = Mg, Mn, Fe, Co, Ni, Cu, Zn) with external electric field (−0.010 a.u., neutral, and +0.010 a.u.). | ||
To further validate our interpretation, NBO analysis is conducted from the binding energy calculations (see Fig. 4). In Fig. 4(a), stabilization energies corresponding to π* back-bonding are calculated and plotted. Similar to the previous interpretation, the stabilization energy increases in the system where the N2 binding energy is increased when an electric field is applied in the negative direction.
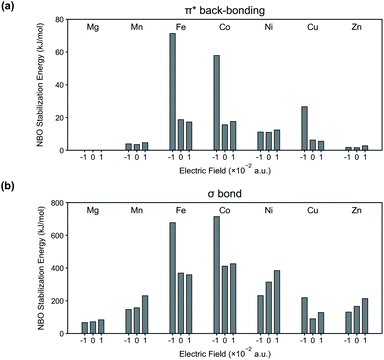 | ||
| Fig. 4 NBO stabilization energies corresponding to (a) π* back-bonding and (b) σ bond in the system of M-MOF-74 (M = Mg, Mn, Fe, Co, Ni, Cu, Zn) and N2. | ||
Along with π* back-bonding, the stabilization energies from σ bond (lone pair electrons (donor) of N atom in N2 → metal's antibonding lone pair orbitals (acceptor)) are computed as well (Fig. 4(b)). According to our previous assumption, we expect the amount of σ bond to increase for positive electric field and to decrease for negative electric field. The stabilization energy in Fig. 4(b) are well explained by this assumption except certain M-MOF-74 (i.e. M = Fe, Co, Cu) at negative electric field. The exceptions have significant increase of the π* back-bonding in common, and this strong π* back-bonding decreases the distance between N2 and CUS (see Fig. 4(a) for increased π* back-bonding and Table S1† for decreased bond length). Consequently, it increases overlap of orbitals participating in σ bond. Fig. S2† shows the increased overlap between orbitals participating in the σ bond and decreased bond length in Co-MOF-74 and N2 system. Therefore, a system with strong π* back-bonding shows synergetic increase for the σ bond at negative electric field. In Fig. S4 and S5,† the reason behind the superior performance of Fe, Co-MOF-74 is explained by considering the d orbitals splitting and the synergetic increase of the σ bond. In addition, NBO analysis for CH4 and CO2 with each M-MOF-74 systems are in ESI (see Fig. S6 and S7†).
For N2/CH4 separation, the DFT binding energies can serve as good predictors especially when comparing structures with the same topology in materials such as M-MOF-74 structures. As such, the difference between the N2 and CH4 binding energies for three test case M-MOF-74 systems (Mg-MOF-74, Co-MOF-74, and Fe-MOF-74) are plotted in Fig. 5 for several values of the electric fields. Mg-MOF-74 represents the MOF-74 system which showcases σ bond dominance, whereas Co-MOF-74 and Fe-MOF-74 are two systems that show the largest enhancement in the N2 binding energy at negative electric field. In Mg-MOF-74, the binding energy difference between N2 and CH4 remains relatively unchanged for different values of the electric field as both the N2 and the CH4 bind to CUS via σ bond, therefore cancelling out the effect of electric field. For Co-MOF-74 and Fe-MOF-74, similar trends can be found for positive electric field values. However, for negative electric fields, negative electric field increases the N2 binding energy while weakening CH4 binding energy because it strengthens the π* back-bonding and weakens the σ bond. Therefore, the binding energy difference between N2 and CH4 starts to increase as electric field becomes more negative. The increased N2 binding energy for negative electric field is accompanied by a decrease in N2 stretching frequency (see Fig. S3†), indicating the increase in the π* back-bonding.
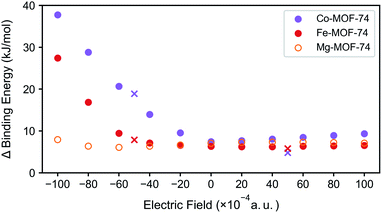 | ||
| Fig. 5 Binding energy difference between N2 and CH4 in M-MOF-74 (M = Co, Fe, Mg) under external electric field. Marker ‘×’ represents the rotated clusters' case. | ||
In all of the aforementioned analysis, the direction of the electric field was purposefully chosen to optimally enhance the N2/CH4 separation. However, in real experiments, it is impossible to control the direction of the electric field with respect to the crystal orientation. As such, we explore the effect of the changes in the direction of the electric field while starting with the assumption that the changes in the binding energy will be equivalent to the component of the electric field that are aligned to the optimal direction. To test this assumption, the electric field is applied at the intensity of 0.01 a.u., but in the direction of the field is tilted to around 60 degrees. The resulting data points (Fig. 5, marked ‘×’) situated in the region that coincides between the inner product between electric field and the vector of unsaturated metal direction, validating our assumption.
Conclusions
The effect of electric field as external stimuli to control the binding property of small gas molecules in MOF have been investigated computationally at the DFT level. Our computational studies indicate that due to the presence of π* back-bonding, certain M-MOF-74 systems show stronger binding for N2 for both positive and negative electric field directions whereas CH4 displays more of a monotonical behavior with respect to electric field. As such, one can theoretically use the electric field to increase the binding energy difference between N2 and CH4 in these systems, and thereby enhance the N2/CH4 separation performances. It remains to be seen how much of this work will be mapped to actual experimental studies given the large magnitudes of the electric field required to see meaningful effects from our computational studies. However, it has been shown in other computational/experimental work10 that electric fields require to see noticeable changes in macroscopic properties can be quite different and as such, it is our opinion that one cannot just dismiss the theoretical studies due to the large magnitude of electric field values.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Basic Science Research Program through the National Research Foundation of Korea funded by the Ministry of Science, ICT, & Future Planning under grant no. 2021R1A2C2003583.Notes and references
- T. E. Rufford, S. Smart, G. C. Y. Watson, B. F. Graham, J. Boxall, J. C. Diniz da Costa and E. F. May, J. Pet. Sci. Eng., 2012, 94–95, 123–154 CrossRef CAS
.
- R. W. Baker and K. Lokhandwala, Ind. Eng. Chem. Res., 2008, 47, 2109–2121 CrossRef CAS
.
- J. W. Yoon, H. Chang, S.-J. Lee, Y. K. Hwang, D.-Y. Hong, S.-K. Lee, J. S. Lee, S. Jang, T.-U. Yoon, K. Kwac, Y. Jung, R. S. Pillai, F. Faucher, A. Vimont, M. Daturi, G. Férey, C. Serre, G. Maurin, Y.-S. Bae and J.-S. Chang, Nat. Mater., 2017, 16, 526–531 CrossRef CAS PubMed
.
- M. Chang, J. Ren, Q. Yang and D. Liu, Chem. Eng. J., 2021, 408, 127294 CrossRef CAS
.
- F. Zhang, K. Li, J. Chen, X. Zhang, K. Li, H. Shang, L. Ma, W. Guo, X. Wu, J. Yang and J. Li, Sep. Purif. Technol., 2022, 281, 119951 CrossRef CAS
.
- K. Lee, W. C. Isley, A. L. Dzubak, P. Verma, S. J. Stoneburner, L.-C. Lin, J. D. Howe, E. D. Bloch, D. A. Reed, M. R. Hudson, C. M. Brown, J. R. Long, J. B. Neaton, B. Smit, C. J. Cramer, D. G. Truhlar and L. Gagliardi, J. Am. Chem. Soc., 2014, 136, 698–704 CrossRef CAS PubMed
.
- Z. Liu, L. Zhang and D. Sun, Chem. Commun., 2020, 56, 9416–9432 RSC
.
- B. L. Suh and J. Kim, RSC Adv., 2020, 10, 22601–22605 RSC
.
- B. L. Suh, T. Hyun, D.-Y. Koh and J. Kim, Chem. Mater., 2021, 33, 7686–7692 CrossRef CAS
.
- A. Knebel, B. Geppert, K. Volgmann, D. I. Kolokolov, A. G. Stepanov, J. Twiefel, P. Heitjans, D. Volkmer and J. Caro, Science, 2017, 358, 347–351 CrossRef CAS PubMed
.
- N. Yanai, M. Sindoro, J. Yan and S. Granick, J. Am. Chem. Soc., 2013, 135, 34–37 CrossRef CAS PubMed
.
- M. Wang, Z. Zhang, Y. Gong, S. Zhou, J. Wang, Z. Wang, S. Wei, W. Guo and X. Lu, Appl. Surf. Sci., 2020, 502, 144067 CrossRef CAS
.
- S. Ketrat, T. Maihom, P. Treesukul, B. Boekfa and J. Limtrakul, J. Comput. Chem., 2019, 40, 2819–2826 CrossRef CAS PubMed
.
- Z. M. Ao and F. M. Peeters, Appl. Phys. Lett., 2010, 96, 253106 CrossRef
.
- B. Tam and O. Yazaydin, J. Mater. Chem. A, 2017, 5, 8690–8696 RSC
.
- P. Verma, X. Xu and D. G. Truhlar, J. Phys. Chem. C, 2013, 117, 12648–12660 CrossRef CAS
.
- K. Lee, J. D. Howe, L.-C. Lin, B. Smit and J. B. Neaton, Chem. Mater., 2015, 27, 668–678 CrossRef CAS
.
- E. D. Bloch, W. L. Queen, R. Krishna, J. M. Zadrozny, C. M. Brown and J. R. Long, Science, 2012, 335, 1606–1610 CrossRef CAS PubMed
.
- A. S. Rosen, M. R. Mian, T. Islamoglu, H. Chen, O. K. Farha, J. M. Notestein and R. Q. Snurr, J. Am. Chem. Soc., 2020, 142, 4317–4328 CrossRef CAS PubMed
.
- M. J. Frisch, et al., Gaussian 16 (Rev A.03), Gaussian Inc., Wallingford, CT, 2016 Search PubMed
.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- X. Xu and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 80–90 CrossRef CAS PubMed
.
- E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1, 2016 Search PubMed
.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView Version 6.1, Semichem Inc., Shawnee Mission, KS, 2019 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra04216a |
| This journal is © The Royal Society of Chemistry 2022 |