Open Access Article
Open Access ArticleA first-principles prediction of novel Janus T′-RuXY (X/Y = S, Se, Te) monolayers: structural properties and electronic structures
Nguyen D. Hien *
*
Institute of Applied Technology, Thu Dau Mot University, Binh Duong Province 750000, Vietnam. E-mail: nguyendinhhien@tdmu.edu.vn
First published on 12th August 2022
Abstract
Due to the breaking of the mirror symmetry, two-dimensional layered Janus materials possess many extraordinary mechanical and electronic properties that cannot exist in symmetric structures. In this paper, we propose and investigate the structural and electronic properties of Janus T′-RuXY (X/Y = S, Se, and Te) monolayers using the first-principles simulations. Our calculated results indicate that the T′-RuXY is found to be dynamically and mechanically stable through the phonon dispersion analysis and examination of elastic properties. The T′-RuXY exhibits high anisotropic elastic characteristics due to its in-plane anisotropic atomic structure. Besides, the vertical asymmetry of T′-RuXY leads to the appearance of a difference in the vacuum level between its two different surfaces. At the ground state, all three structures of the Janus T′-RuXY are semiconductors with indirect bandgaps. The bandgaps of T′-RuXY can be modulated by a biaxial strain. Particularly, the semiconductor-to-metal phase transitions are observed in all studied structures at a large compressive strain. Our calculation results not only provide important structural and electronic features of the Janus T′-RuXY monolayers but also show the prospect of their application in nanoelectromechanical devices.
1 Introduction
With a strong quantum confinement effect, two-dimensional (2D) structures have many interesting physical properties that do not exist in bulk forms. Since graphene was discovered experimentally,1 2D materials with layered structures were of particular interest to the scientific community.2–4 Many 2D structures have been experimentally synthesized and theoretically predicted with anomalous physical properties that differ from their bulk counterparts.5–9 Among them, transition metal dichalcogenides are one of the objects that have been focused on in recent research with many prospects for applications in nanotechnology.10–13The atomic structure of 2D monolayers can exist in many different symmetry forms at the ground state, such as 1T, 2H, and 3R…14,15 Many 2D materials have a stable structure in the 2H phase (hexagonal structure) and this is also the most investigated structure according to our observations. However, RuS2 (and also RuSe2) is one of those unusual materials. Its hexagonal (2H) and octahedral (1T) phases are unstable while it is stable only in the T′ phase with an orthorhombic unit-cell containing six atoms (two Ru and four S atoms).16 Also, 3D RuS2 and RuSe2 materials belong to the Pa3 symmetry space,16 which are different from most other transition metal dichalcogenides. Similarly, the transition metal dioxide RuO2 is also dynamically stable only in the 1T′ phase.17
The discovery of 2D structures is not limited to symmetric compounds such as transition metal dichalcogenides or post-transition monochalcogenides. With advanced experimental techniques, Janus asymmetrical structures have also been reported recently. The two research groups of Lu18 and Zhang18,19 independently reported the experimentally successful synthesis of Janus MoSSe material by different methods. 2D Janus structures have quickly attracted the attention of the scientific community due to their many unusual physical properties with bright prospects for applications in nanotechnology.20–22 The electronic structures of 2D materials are particularly sensitive to the symmetry of their atomic structure. Once the out-of-plane mirror symmetry was broken, many new physical properties were observed in 2D Janus materials.23,24 With the asymmetrical structure, a built-in electric field appeared and resulted in a difference in the electrostatic potential between the two surfaces of the 2D Janus materials.25 This will affect the photocatalytic properties of Janus materials.26 In this paper, we systematically study the structural features and electronic structures of asymmetrical Janus T′-RuXY (X/Y = S, Se, and Te; X ≠ Y) monolayers by the first-principles method. After optimizing the atomic structure, the structural stability of the studied materials was tested and evaluated. We have studied the electronic structure of T′-RuXY using various functionals. Besides, the influence of mechanical strain on electronic properties has also been investigated in this paper.
2 Method and computational details
We use the first-principles calculations based on the density functionals to study the structural and electronic properties of the T′-RuXY (X/Y = S, Se, and Te; X ≠ Y) monolayers. All calculations are performed in the Quantum Espresso simulation package.27 The projector-augmented wave method is adopted to study the ion core–electron interactions.28 We use the generalized gradient approximation with Perdew–Burke–Ernzerhof (PBE) functional29 to investigate the exchange-correlation function. Also, the Heyd–Scuseria–Ernzerhof functional (HSE06)30 is performed to correct the band diagrams of the studied structures. The DFT-D2 with van der Waals (vdW) correction31 is used to consider the weak vdW forces in the layered structures. A plane-wave cut-off is chosen to be 50 Ry and a (15 × 15 × 1) k-grid mesh is set to sample the first Brillouin zone in the present calculations. The atomic structure of the proposed structure is relaxed when the residual forces per atom were smaller than 0.001 eV Å−1. We used a large vacuum distance of 25 Å along the z direction to eliminate interactions between periodic images of slabs. The density functional perturbation theory is performed to evaluate the vibrational spectra of the considered structures.32 A large supercell of (4 × 4 × 1) is set for the phonon calculations to obtain accurate results.3 Calculated results and discussion
3.1 Atomic structures and structural stability
The atomic structures of the Janus T′-RuXY (X/Y = S, Se, Te; X ≠ Y) are presented in Fig. 1. There are six atoms in the orthorhombic unit-cell (rectangular in 2D projection) of the T′ Janus RuXY, including two Ru and four chalcogen atoms (two X and two Y atoms). As presented in Table 1, the optimized lattice constants a and b of RuXY monolayers are in the range from 5.67 to 5.97 Å and from 3.52 to 3.70 Å, respectively. These increments in lattice parameters a and b conform to the radius of atoms in the compounds. The lattice constants of T′-RuSSe are between the values of T′-RuS2 and T′-RuSe2.16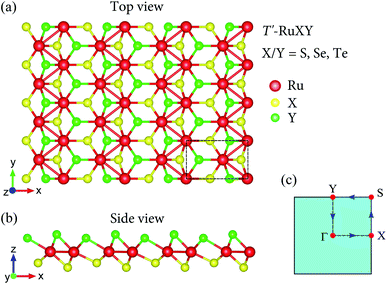 | ||
| Fig. 1 Atomic structure in different views (a and b) and 2D Brillouin zone (c) of Janus T′-RuXY (X/Y = S, Se, and Te; X ≠ Y) monolayers. Unit-cell is indicated by a dashed rectangle in (a). | ||
| a (Å) | b (Å) | C11 (N m−1) | C12 (N m−1) | C22 (N m−1) | C66 (N m−1) | Ecoh (eV per atom) | |
|---|---|---|---|---|---|---|---|
| RuSSe | 5.67 | 3.52 | 101.07 | 20.05 | 96.43 | 40.89 | −5.97 |
| RuSTe | 5.85 | 3.60 | 92.38 | 21.57 | 77.54 | 34.64 | −5.74 |
| RuSeTe | 5.97 | 3.70 | 86.61 | 23.83 | 80.45 | 33.11 | −5.54 |
To test the structural stabilities, we first calculate the cohesive energy of the Janus T′-RuXY to evaluate their chemical bond strength. The cohesive energy Ecoh of the Janus T′-RuXY is given by:
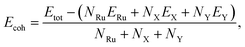 | (1) |
In Table 1, we present the obtained results for Ecoh of the T′-RuXY monolayers. It is found that the cohesive energies of RuSSe, RuSTe, and RuSeTe monolayers are −5.97, −5.74, and −5.54 eV per atom, respectively. From eqn (1), the negative Ecoh suggests that the T′-RuXY monolayers are energetically favorable.
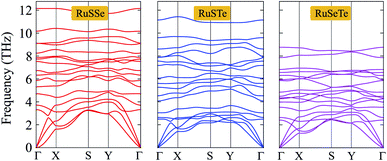
To consider the dynamical stabilities of the T′-RuXY structures, we calculate their phonon dispersions as depicted in Fig. 2. The investigated structure is confirmed to be dynamically stable when no soft modes are available in its vibrational spectrum. The phonon dispersions of the T′-RuX, as presented in Fig. 2, contain 18 vibrational branches (3 acoustic and 15 optical branches). No gap was found between the acoustic and optical vibrational regions in all three investigated structures. This suggests that the acoustic–optical scattering in the studied structures is strong. As a result, the T′-RuXY structures can possess a low thermal conductivity. The vibrational properties depend strongly on the atomic size of elements. The elements with higher atomic mass will vibrate more softly.33 As a result, the phonon frequencies of the investigated structures decrease with the change of the atomic mass of the elements in the compound, specifically, RuSSe has the higher vibrational frequencies and the vibrational frequency of RuSeTe is the lowest as illustrated in Fig. 2. Particularly, no negative frequencies are found in the vibrational spectra of all three studied monolayers, suggesting that they are dynamically stable.
3.2 Mechanical anisotropy
We here examine the mechanical properties of the T′-RuXY monolayers. The elastic constants are considered as decisive parameters that can determine other elastic parameters such as Young's modulus Y2D or Poisson's ratio ν and also the mechanical stability of the investigated structures. We now evaluate the elastic constants Cij of the T′-RuXY. In the 2D monolayers, four elastic constants, including C11, C22, C12, and C66, need to be evaluated. The Cij of the T′ RuXY are tabled in Table 1. It is found that C11 of RuSSe, RuSTe, and RuSeTe is 101.07, 92.38, and 86.61 N m−1, respectively. Obtained values indicate that all four independent elastic constants Cij are positive and C11C22 > C212,34 suggesting that the studied structures are mechanical stable.The direction-dependent 2D Young's modulus Y2D(α) and Poisson's ratio ν(α) are given by35,36
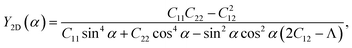 | (2) |
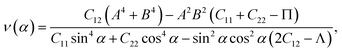 | (3) |
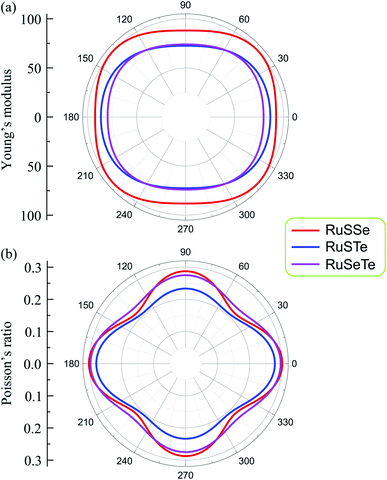
In Fig. 3, we show the dependence of Young's modulus and Poisson's ratio on the examined directions (angular-dependence) of the T′-RuXY. We show that Y2D(α) and ν(α) are directionally anisotropic due to the lattice anisotropy of the T′-RuXY. However, the directional anisotropy of Young's modulus is quite small compared to the anisotropy of Poisson's ratio. The difference in Young's modulus in different directions is not large. For example, the minimum and maximum Young's moduli of RuSSe are 88.09 N m−1 (at α = 90°) and 99.87 N m−1 (at α = 42°), respectively. Meanwhile, Poisson's ratio of the Janus T′-RuXY exhibits high directionally anisotropic as shown in Fig. 3(b). It is found that the Poisson's ratio of T′-RuXY is the highest along the x-axis (α = 0°).
3.3 Electronic properties
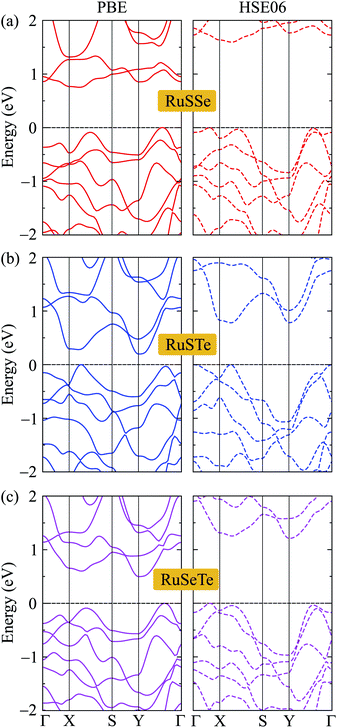
We next consider the electronic structures of the T′-RuXY monolayers. In Fig. 4, we show the band diagrams of the T′-RuXY examined by the PBE/HSE06 method. It is calculated that the T′-RuXY monolayers are indirect bandgap semiconductors. The profiles of the calculated band diagrams by the HSE06 and PBE functionals are almost the same. The evaluated PBE(HSE06) bandgaps of T′-RuSSe, T′-RuSTe, and T′-RuSeTe are 0.75(1.53), 0.20(0.78), and 0.50(1.17) eV, respectively. The HSE06 method is known to be the method that gives more accurate band gap calculation results than the PBE method. The band gaps of T′-RuXY are listed in Table 2.| EPBEg | EHSE06g | EF | ΔΦ | ΦX | ΦY | |
|---|---|---|---|---|---|---|
| RuSSe | 0.75 | 1.53 | −2.10 | 0.72 | 5.75 | 5.02 |
| RuSTe | 0.20 | 0.78 | −1.07 | 1.35 | 5.52 | 4.17 |
| RuSeTe | 0.50 | 1.17 | −1.28 | 0.64 | 5.25 | 4.61 |
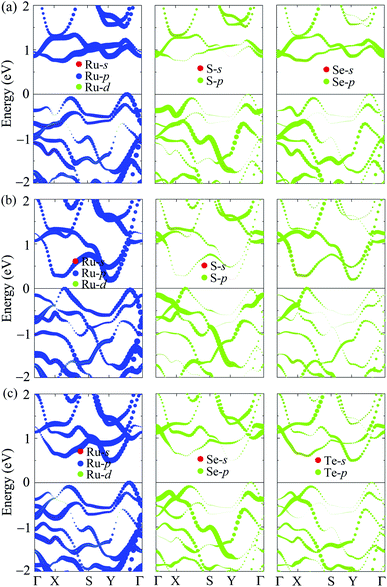
In Fig. 5, we present the PBE weighted bands of T′-RuXY to evaluate the contributions of atomic orbitals to their electronic structures. We can see that, as shown in Fig. 5, the electronic bands of T′-RuXY monolayers are mainly contributed by the p-orbitals of the components in the compound, particularly the Ru-p orbitals. The Ru-p orbitals have a high contribution to both the valence band maximum (VBM) and conduction band minimum (CBM) in the electronic bands of T′-RuXY. Besides, the contributions of the Y-p orbitals to the CBM are also significant.
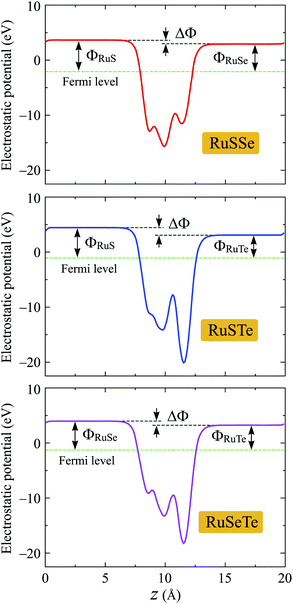
We next evaluate the work functions of the studied structures based on the calculations for their electrostatic potentials as presented in Fig. 6. The work function Φ is the most important parameter, which can estimate the electron's ability to escape from the material surfaces. The work function Φ is defined by:
| Φ = Φv − ΦF, | (4) |
It is well-known that a built-in electric field is found in the 2D layered Janus monolayers due to their vertically asymmetrical structure.25 Then, the dipole correction can be used to eliminate artificial fields caused by periodic boundary conditions.37 When the dipole correction is used, a difference between the vacuum levels ΔΦ on the two sides of Janus T′-RuXY is found as shown in Fig. 6. The value of ΔΦ depends on the atomic number difference between X and Y atoms. The higher the ΔΦ, the larger the atomic number difference. The ΔΦ of RuSTe is the highest (1.35 eV) due to the difference in atomic number between S and Te atoms being the largest compared with others. In Table 2, we list the calculated results for the work functions on the X side ΦX and the Y side ΦY. It is found that the value of ΦX is higher than that of ΦY for all three studied Janus structures. This suggests that the electrons on the Y surface can be escaped more easily than electrons on the X surface.
The electronic structures of 2D materials are generally sensitive to changes in their atomic structure. Mechanical strain is known to be one of the simplest and most effective ways to alter and control the electronic properties of materials. In the following, we will investigate the effect of biaxial strains on the electronic properties of Janus T′-RuXY. Quantitatively, we suggest the definition for the biaxial strain as εb = (t − t0)/t0, where t0 and t are the lengths of the computational cells before and after strain. This also means that a positive value of εb corresponds to the tensile strain while the compressive strain corresponds to its negative value.
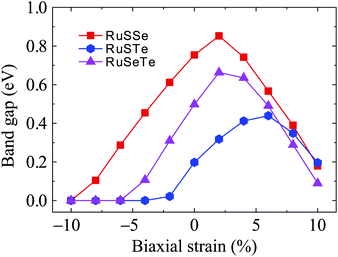
Fig. 7 shows the electronic bands of T′-RuXY at several values of the biaxial strain εb. Our calculated results demonstrate that the band structures of the T′ RuXY depend strongly on the applied strains. The strain significantly changes the band structures of the investigated structures, particularly in the case of compressive strain. The semiconductor-to-metal phase transition was detected when the Janus monolayers were subjected to compressive strain. The band gap changes unpredictably in the presence of strains. Fig. 8 depicts the dependence of the energy gaps on the strain. It is indicated that the shape of the graphs describing the strain-dependence of the energy gaps of the three structures is almost the same. The tensile strain increases slightly in the energy gap and then decreases with increasing tensile strain strength. Meanwhile, compressive strain rapidly reduces the energy gap of the monolayers. As a consequence, semiconductor-to-metal phase transitions were found in all three materials within the strain range from 0 to −10%. The phase transitions are found at −4%, −6%, and −10% for RuSTe, RuSeTe, and RuSSe, respectively. Phase transition is an important characteristic of electronic nanomaterials, which opens up many prospects for their applications in nanoelectromechanical devices.
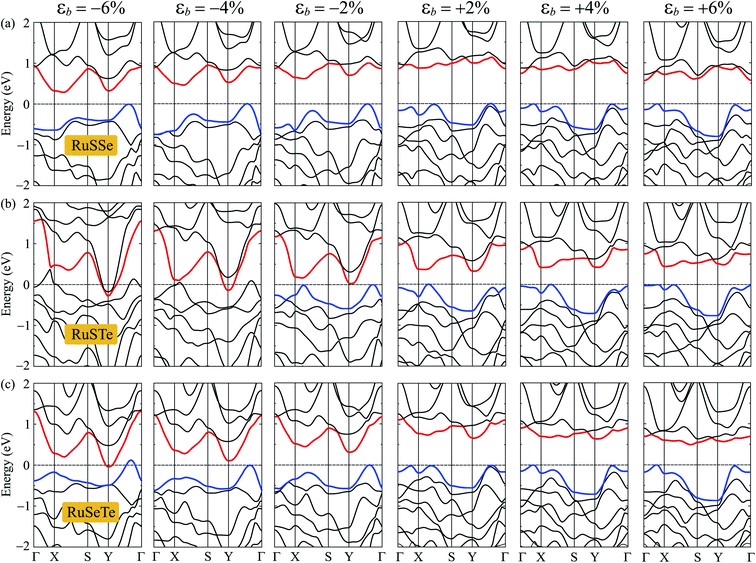 | ||
| Fig. 7 The PBE band diagrams of the T′-RuSSe (a), T′-RuSTe (b), and T′-RuSeTe monolayers under biaxial strains εb (c). | ||
4 Conclusion
In conclusion, we have studied the structural properties and electronic structures of the asymmetric T′ RuXY monolayers by using the DFT calculations. It was calculated that the T′-RuXY are dynamically and mechanically stable in the T′ phase with their phonon spectra containing only positive vibrational frequencies and elastic coefficients satisfying the Born-Huang's criterion. All three monolayers of the T′-RuXY structures are found to be indirect semiconductors and their energy gap can be controlled by the applied strains. In particular, the semiconductor–metal phase transitions were observed when the monolayers were subjected to compressive strain. Our calculation results suggest that the T′-RuXY have potential prospects for applications in nanoelectronic and nanoelectromechanical devices.Conflicts of interest
There are no conflicts of interest to declare.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666 CrossRef CAS.
- N. A. Poklonski, S. A. Vyrko, A. I. Siahlo, O. N. Poklonskaya, S. V. Ratkevich, N. N. Hieu and A. A. Kocherzhenko, Mater. Res. Express, 2019, 6, 042002 CrossRef.
- T. V. Vu, C. V. Nguyen, H. V. Phuc, A. A. Lavrentyev, O. Y. Khyzhun, N. V. Hieu, M. M. Obeid, D. P. Rai, H. D. Tong and N. N. Hieu, Phys. Rev. B, 2021, 103, 085422 CrossRef CAS.
- T. N. Bich, S. S. Kubakaddi, L. Dinh, N. N. Hieu and H. V. Phuc, Phys. Rev. B, 2021, 103, 235417 CrossRef CAS.
- M. E. Dávila, L. Xian, S. Cahangirov, A. Rubio and G. Le Lay, New J. Phys., 2014, 16, 095002 CrossRef.
- B. Lalmi, H. Oughaddou, H. Enriquez, A. Kara, S. Vizzini, B. Ealet and B. Aufray, Appl. Phys. Lett., 2010, 97, 223109 CrossRef.
- Z. Zeng, Z. Yin, X. Huang, H. Li, Q. He, G. Lu, F. Boey and H. Zhang, Angew. Chem., Int. Ed., 2011, 50, 11093–11097 CrossRef CAS.
- D. Muoi, N. N. Hieu, C. V. Nguyen, B. D. Hoi, H. V. Nguyen, N. D. Hien, N. A. Poklonski, S. S. Kubakaddi and H. V. Phuc, Phys. Rev. B, 2020, 101, 205408 CrossRef CAS.
- T. V. Vu, V. T. T. Vi, H. V. Phuc, C. V. Nguyen, N. A. Poklonski, C. A. Duque, D. P. Rai, B. D. Hoi and N. N. Hieu, J. Phys.: Condens. Matter, 2021, 33, 225503 CrossRef CAS PubMed.
- B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147–150 CrossRef CAS PubMed.
- N. D. Hien, C. V. Nguyen, N. N. Hieu, S. S. Kubakaddi, C. A. Duque, M. E. Mora-Ramos, L. Dinh, T. N. Bich and H. V. Phuc, Phys. Rev. B, 2020, 101, 045424 CrossRef.
- C. Ataca, M. Topsakal, E. Aktürk and S. Ciraci, J. Phys. Chem. C, 2011, 115, 16354–16361 CrossRef CAS.
- C. V. Nguyen, N. N. Hieu, N. A. Poklonski, V. V. Ilyasov, L. Dinh, T. C. Phong, L. V. Tung and H. V. Phuc, Phys. Rev. B, 2017, 96, 125411 CrossRef.
- A. Kuc and T. Heine, Chem. Soc. Rev., 2015, 44, 2603–2614 RSC.
- S. M. A. e-Abbas, G. Abbas, W. Zulfiqar, M. Sajjad, N. Singh and J. A. Larsson, Nano Res., 2022 DOI:10.1007/s12274-022-4637-3 in press.
- F. Ersan, S. Cahangirov, G. Gökoğlu, A. Rubio and E. Aktürk, Phys. Rev. B, 2016, 94, 155415 CrossRef.
- F. Ersan, H. D. Ozaydin and O. Ü. Aktürk, Philos. Mag., 2019, 99, 376–385 CrossRef CAS.
- A.-Y. Lu, H. Zhu, J. Xiao, C.-P. Chuu, Y. Han, M.-H. Chiu, C.-C. Cheng, C.-W. Yang, K.-H. Wei, Y. Yang, Y. Wang, D. Sokaras, D. Nordlund, P. Yang, D. A. Muller, M.-Y. Chou, X. Zhang and L.-J. Li, Nat. Nanotechnol., 2017, 12, 744 CrossRef CAS.
- J. Zhang, S. Jia, I. Kholmanov, L. Dong, D. Er, W. Chen, H. Guo, Z. Jin, V. B. Shenoy, L. Shi and J. Lou, ACS Nano, 2017, 11, 8192–8198 CrossRef CAS PubMed.
- L. Seixas, J. Appl. Phys., 2020, 128, 045115 CrossRef CAS.
- T. V. Vu, V. T. T. Vi, H. V. Phuc, A. I. Kartamyshev and N. N. Hieu, Phys. Rev. B, 2021, 104, 115410 CrossRef CAS.
- T. V. Vu, H. D. Tong, D. P. Tran, N. T. T. Binh, C. V. Nguyen, H. V. Phuc, H. M. Do and N. N. Hieu, RSC Adv., 2019, 9, 41058–41065 RSC.
- A. Kandemir and H. Sahin, Phys. Rev. B, 2018, 97, 155410 CrossRef CAS.
- L. Hu and D. Wei, J. Phys. Chem. C, 2018, 122, 27795–27802 CrossRef CAS.
- C.-F. Fu, J. Sun, Q. Luo, X. Li, W. Hu and J. Yang, Nano Lett., 2018, 18, 6312–6317 CrossRef CAS.
- A. Huang, W. Shi and Z. Wang, J. Phys. Chem. C, 2019, 123, 11388 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS.
- T. Sohier, M. Calandra and F. Mauri, Phys. Rev. B, 2017, 96, 075448 CrossRef.
- A. Molina-Sánchez and L. Wirtz, Phys. Rev. B, 2011, 84, 155413 CrossRef.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B, 2014, 90, 224104 CrossRef.
- N. T. Hung, A. R. T. Nugraha and R. Saito, J. Phys. D: Appl. Phys., 2018, 51, 075306 CrossRef.
- P. Xiang, S. Sharma, Z. M. Wang, J. Wu and U. Schwingenschlögl, ACS Appl. Mater. Interfaces, 2020, 12, 30731 CrossRef CAS.
- L. Bengtsson, Phys. Rev. B, 1999, 59, 12301 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |