Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Discovering surface reaction pathways using accelerated molecular dynamics and network analysis tools†
Hirotoshi Hirai * and
Ryosuke Jinnouchi*
* and
Ryosuke Jinnouchi*
Toyota Central R&D Labs., Inc., 41-1, Yokomichi, Nagakute, Aichi 480-1192, Japan. E-mail: hirotoshih@mosk.tytlabs.co.jp
First published on 17th August 2022
Abstract
We present an automated method that maps surface reaction pathways with no experimental data and with minimal human interventions. In this method, bias potentials promoting surface reactions are applied to enable statistical samplings of the surface reaction within the timescale of ab initio molecular dynamics (MD) simulations, and elementary reactions are extracted automatically using an extension of the method constructed for gas- or liquid-phase reactions. By converting the extracted elementary reaction data to directed graph data, MD trajectories can be efficiently mapped onto reaction pathways using a network analysis tool. To demonstrate the power of the method, it was applied to the steam reforming of methane on the Rh(111) surface and to propane reforming on the Pt(111) and Pt3Sn(111) surfaces. We discover new energetically favorable pathways for both reactions and reproduce the experimentally-observed materials-dependence of the surface reaction activity and the selectivity for the propane reforming reactions.
1 Introduction
Identification of surface reaction pathways is essential for mechanistic analysis of catalytic reactions and design of catalytic materials. Based on the identified reaction pathways, micro-kinetic reaction models1 can be constructed to quantitatively predict the reactivity and selectivity of the catalytic reactions under practical operation conditions of industrial reactors. Ab initio calculations are a vital tool for the identification of surface reaction pathways. Due to the significant advances in computational algorithms and computer performance,2 the reaction heats and activation energies of elementary reactions can now be predicted by ab initio calculations. The computed reaction heats and activation energies of a variety of surface elementary reactions exhibit universal linear relations3–7 that can be used to efficiently calculate reaction energies and activation energies of a wide variety of surface reactions. Micro-kinetic simulations using these thermodynamic and kinetic parameters have been successfully used to understand the mechanisms underlying the experimentally-observed material-dependent activity and selectivity trends and to design new catalysts with the desired performance.8–10However, surface reactions are complex, and the number of the relevant chemical species and elementary reactions can become enormous, making it difficult to consider all possible reaction pathways. Therefore, surface reaction modeling studies have been conducted on the assumed reaction pathways that are suggested based on the experimental data and the researcher's intuition.11,12 Although reactants and products can be routinely detected in experiments, it is difficult to fully detect the reaction intermediates adsorbed on surfaces. Thus, experimental identification of reaction pathways is often challenging, and dominant reaction pathways may be overlooked.13 Needless to say, such empirical assumptions cannot be used for unknown reactive systems where experimental data are unavailable.
In the last 10 years, automatic reaction mechanism generation methods have been applied for computational predictions of surface reaction pathways. In particular, the power of automated methods was demonstrated in the studies of hydrocarbon combustion reactions.14–16 This success is due to the regularity of the skeleton of hydrocarbon molecules, where the additivity rule has been well-established, and the generation of the lists of elementary reactions and their rate constants can be automated based on the rule-based methods.17 For example, Zimmerman et al.18,19 proposed a method to generate reaction pathways using predefined heuristic bond-forming rules. Suleimanov and Green20 have proposed a fully automated method for reaction pathway identification where bond electron matrices were used to generate the possible pathways. Maeda et al.21,22 have developed an automated reaction pathway search method based on a geometric search. Habershon et al.23,24 have proposed an automated reaction mechanism generation method using Graph-driven search. Some of these methods have been extended to the surface reactions of hydrocarbon molecules and their oxides.25–28 These methods for the automatic generation of surface reaction pathways require the definition and validation of the rules for the generation of reaction networks. However, the definition and validation of such rules require a sufficiently large dataset and/or accumulated knowledge, and thus, are possible only for well-studied systems. This makes it difficult for such an approach to be applied to new systems.
Combinations of the automated methods with ab initio molecular dynamics (MD) simulations29–31 can provide a purely non-empirical procedure to identify reaction pathways. However, ab initio electronic structure computations are too computationally expensive to run MD simulations. In the previous studies, MD simulations using computationally low-cost quantum chemical calculation methods have been used to discover reactions, and high-precision calculations have been used to refine the discovered chemical reactions to obtain accurate reaction networks. For example, Wang et al.32 used Hartree-Fock level of theory with minimal basis set, and Varela et al.33 used a semi-empirical method for MD simulations to sample reactions. Nevertheless, it is still difficult to cover the required timescale of the chemical reactions, and therefore, direct ab initio MD identification of reaction pathways often necessitates unrealistically high simulation temperatures to accelerate the chemical reactions.34
To solve this problem, van Duin and others have developed the ReaxFF reactive force field that can describe bond formation and breaking while maintaining the speed of classical MD methods.35 In this approach, the force field parameters were determined to optimally reproduce ab initio data on selected relevant systems, and the constructed force field was used in MD simulations to observe the chemical reactions of interest. This approach has been successively applied to surface reaction simulations.36–39 However, the systems used to prepare the training dataset are often selected based on human intuitions, and therefore, the generated training dataset can lack information for important chemical reactions. It should also be noted that the limitations of the functional form of the force field can give rise to non-negligible errors.
An alternative method to solve this problem is to use accelerated MD methods. In these methods, biased potentials are introduced to accelerate the rate of rare events. After the simulations, thermodynamic and kinetic reaction properties of unbiased systems are restored by conversions based on statistical mechanics. Thus, chemical reactions can become observable within the timescale of the ab initio MD simulation. To date, a variety of accelerated MD methods have been proposed40–44 and applied to reactive systems.45–49 These methods have also been applied to surface systems, such as for the modeling of diffusion50 and heteroepitaxy reactions.51 However, to the best of our knowledge, this approach has never been applied to the catalytic reactions composed of a series of adsorption, bond scission, bond generation and desorption steps.
It should be noted that automated reaction identification method has not been established for the surface reactions. Several automated methods have been developed and applied to extract reaction pathways from MD trajectories in gas- and liquid-phase systems.32,52,53 However, no such method applicable to surface systems has been reported to date.
In this study, we present an automated method that can extract reaction pathways from the trajectories provided by accelerated ab initio MD simulations of catalytic reactions on heterogeneous surfaces. In this method, bias forces that promote surface reactions are applied to enable statistical sampling of the surface reactions. An automatic extraction of elementary reactions is realized by extending the method constructed for gas- or liquid-phase reactions.49,54 The extracted elementary reaction data are converted into directed graph data that can be efficiently mapped onto a clearly visible reaction network using a network analysis tool. To demonstrate its power, this method is applied to the steam reforming of methane on the Rh(111) surface and to propane reforming on the Pt(111) and Pt3Sn(111) surfaces. Steam reforming of methane (CH4 + H2O → CO + 3H2) on Rh(111) is a simple but important catalytic reaction that plays a key role in hydrogen production. Its energetics and reaction pathways have been intensively studied,10,55,56 so that the results obtained for this reaction can be verified by comparing to the ab initio computational results reported in previous studies. Pt3Sn(111) is known to have high selectivity for the propane to propylene (CH3CHCH2) conversion.57 Previous static ab initio calculations58 showed that the introduction of Sn activates propylene desorption, enhancing the catalytic selectivity of propane dehydrogenation. However, the propane dehydrogenation reaction involves a variety of elementary reactions that may not be fully examined by the static calculations. The application of our method to these systems demonstrate that our scheme can automatically extract energetically favorable reaction pathways from the accelerated ab initio MD simulations without using any empirical information.
2 Method
2.1 Accelerated MD simulation for surface reaction
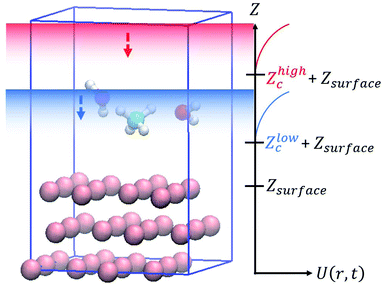
In this study, slab models were used to represent the gas/solid interface. In the slab models, periodic boundary conditions are imposed on the unit cells in order to accurately represent the infinite extent of the single crystal surfaces, where atoms are repeatedly arranged in the surface horizontal directions, and a vacuum layer is inserted between the surface slabs to represent the boundary between the gas phase and the solid surface. The dimensions of the slab model are specified by the number of primitive surface unit cells included in the supercell, the number of slab layers and the thickness of the vacuum layer are chosen so that the model can be used to accurately provide the desired properties. For example, a thicker slab is necessary to accurately describe the interactions of the molecules with bulk surfaces, and a thicker vacuum layer is necessary to avoid artificial interactions with the molecules and slabs in the periodic image cells. A wider unit cell is required to examine adsorbate energetics at low coverage. For molecular dynamics simulations, additional care is also required to prevent the artificial interactions between the periodic images of the slabs. In the simulations, the molecules placed in the gas phase can interact with surfaces located at both upper and lower boundaries of the gas phase even though in reality, the molecule can interact only with a surface at one boundary. Additionally, it is also necessary to ensure efficient sampling. If a thick vacuum layer is placed between the slabs, the molecule can spend most of the simulation time in that layer, making the sampling of the desired interfacial reactions significantly worse.To solve these problems, in this work, wall potentials are imposed to prevent the molecular diffusion to the vacuum layer using the following expression:
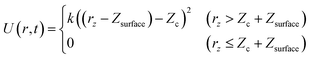 | (1) |
Both wall potentials apply a spring force to the atoms located at z > Zc + Zsurface to ensure that they return to the surface. Since the wall potentials do not act on the atoms located at z ≤ Zc + Zsurface, they do not affect the energetics of surface reactions. The wall potential located at Zhighc acts on atoms continuously to prevent molecular diffusion to the upper boundary of the vacuum layer. By contrast, the wall potential located at Zlowc is periodically turned on and off at constant intervals. When this wall potential is turned on, it promotes the adsorption of the molecule on the surface. The application of this bias force temporarily increases the velocity of the gas phase molecule moving toward the surface, increasing its temperature. This enables efficient sampling of the reactions by the molecules distributed in the high-energy region of the Boltzmann distribution.
In addition to the application of wall potentials (eqn (1)), the accelerated MD method was used to enhance the sampling of surface reactions. We used the adaptive hyperdynamics (AHD) method43 to accelerate the reactions. The AHD method is based on the hyperdynamics method developed by Voter.40 Voter showed that the relative rates of transitions from one state to other states are preserved as long as the original potentials at the transition states are not modified by the bias potential.40 This means that the selectivity of the reaction pathways are preserved if the bias potential is designed so as not to perturb the potential energy surfaces near the transition states. Such a bias potential was proposed by Hamelberg et al.41 as shown below.
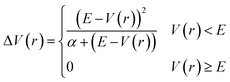 | (2) |
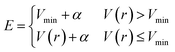 | (3) |
The AHD method was implemented in the Quantum Espresso ab initio simulation package.60 The parameters of the AHD were set to α = 0.13 Ry and τ = 100 MD steps. For the parameters in eqn (1), k = 0.008 Ry Å−2, Zlowc = 2 Å, and Zhighc = 7.5 Å were used. The wall potential corresponding to Zlowc was switched on and off every 250 MD steps. Because of the limited width of the surface unit cell, hydrogen atoms dissociated from the molecules are repeatedly adsorbed on and desorbed from the surface during AHD simulations. These frequent phenomena strongly hinder efficient sampling of other rare events. To prevent repeated hydrogen adsorptions and desorptions, the bias potential located at Zlowc was always switched off for the hydrogen molecules desorbed from the surface. This enables the hydrogen molecules generated by the reactions to diffuse to the vacuum region. Additionally, we deleted the hydrogen molecules that diffuse to the vacuum region.
2.2 Automatic extraction of elementary reactions and visualization of reaction networks
In this study, we assumed that metal atoms in the slab do not evaporate and travel to the gas phase. We also assumed that subsurface oxides are not formed and that the crystal structure of the metal slab is preserved during AHD simulations. Hence, we focus only on the reactions on clean surfaces. To automatically extract elementary reactions, the automatic elementary reaction extraction method49,54 that was developed for gas- and liquid-phase reactions was applied to the group of atoms comprising the reactant molecules located in the gas phase at the beginning of the simulations. In this method, a bond matrix that identifies each atomic pair as either bonding or non-bonding using 1 or 0, respectively, is block-diagonalized to extract the chemical species and elementary reactions from the MD trajectories (see ESI for details†). The bond matrix was updated every 5 MD steps. To distinguish between the surface and gas-phase chemical species, the distances between the atoms located in the gas phase at the beginning of the simulations and the atoms in the slab were calculated. When the distances became shorter than the determined threshold value, these atoms were assigned as surface species and labeled with “(s)”. This procedure was conducted after every evaluation of the bond matrix. Then, we can detect adsorption or desorption reactions based on the changes in these labels. The following threshold values were used to determine whether the atom is assigned to the surface-adsorbed species (Table 1).| Atom pair | Threshold (Å) |
|---|---|
| H–Rh | 2.40 |
| O–Rh | 2.76 |
| C–Rh | 2.76 |
| H–Pt | 2.40 |
| C–Pt | 2.76 |
| H–Sn | 2.40 |
| C–Sn | 2.76 |
The extracted elementary reactions were mapped onto a reaction network using network graph analysis tools that can clearly visualize the reaction pathways and numbers of events. This visualization process was automated using Python with NetworkX modules.61 The constructed graph data were written to a file in the graph modeling language (GML) format and were visualized by the Cytoscape software.62,63
2.3 Models and parameters
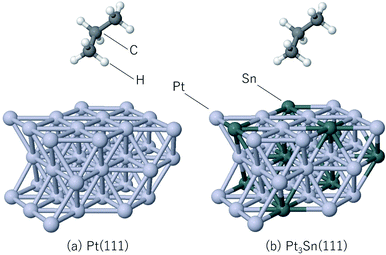
The steam reforming of methane on the Pt(111) surface was simulated using a slab model of 12 atoms with the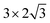 periodicity and with the thickness of 3 atomic layers (see Fig. 1). The atoms in the bottom layer of the slab were fixed at the theoretically calculated positions for the bulk Rh. The vacuum layer was set to 12 Å. A methane molecule and two water molecules acting as reactant molecules were located in the vacuum layer at the beginning of the simulations. Propane dehydrogenation on the Pt3Sn alloy surface was simulated using a three-layer slab model with the
periodicity and with the thickness of 3 atomic layers (see Fig. 1). The atoms in the bottom layer of the slab were fixed at the theoretically calculated positions for the bulk Rh. The vacuum layer was set to 12 Å. A methane molecule and two water molecules acting as reactant molecules were located in the vacuum layer at the beginning of the simulations. Propane dehydrogenation on the Pt3Sn alloy surface was simulated using a three-layer slab model with the 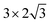 periodicity (Fig. 2).
periodicity (Fig. 2).
The thickness of the vacuum layer was set to 12 Å. The structure of Pt3Sn was constructed according to the previous work.58 A propane molecule was placed in the gas phase as the initial state to simulate the propane reforming reaction. During the simulations, the atoms in the bottom layer were fixed to the bulk positions obtained in the bulk calculations. All simulations were carried out using the Quantum Espresso60 ab initio simulation package that uses the plane wave basis set and pseudopotentials. Vanderbilt ultrasoft pseudopotentials64 were used to describe the electron–ion interaction. The cutoff energy of the plane wave basis set was set to 30 Ry and revPBE65–67 was used as the exchange-correlation energy functional. The time step of the MD calculation was set to 15 Ry a.u. (0.726 fs), and 5000 step MD simulations were conducted 10 times for the steam reforming of methane, 20 times for the propane reforming simulations with each simulation started from different initial positions and velocities in order to sample the reactions. The temperature was set to 1273 K, and the Berendsen thermostat68 was used for temperature control during the MD simulations. Gaussian smearing with the energy width of 0.003 Ry was used to improve the convergence of the electronic structure calculations.69
3 Results and discussion
3.1 Methane steam reforming
A total 32 types of elementary reactions were observed during the 10 independent AHD simulations. The number of events for each elementary reaction is tabulated in Table 2.| Elementary reaction | Count |
|---|---|
| CHO(s) ⇒ CO(s) + H(s) | 1 |
| H2O(s) ⇒ H2O | 37 |
| H(s) + H(s) ⇒ H2(s) | 51 |
| CH(s) + OH(s) ⇒ C(s) + H2O(s) | 1 |
| H2O(s) + O(s) ⇒ OH(s) + OH(s) | 2 |
| H2(s) + OH(s) ⇒ H(s) + H2O(s) | 1 |
| H(s) + OH(s) ⇒ H2O(s) | 25 |
| CH(s) + H(s) ⇒ CH2(s) | 13 |
| CH2(s) + H(s) ⇒ CH3(s) | 3 |
| H2(s) ⇒ H(s) + H(s) | 33 |
| CH4(s) ⇒ CH4 | 11 |
| CH(s) ⇒ C(s) + H(s) | 9 |
| CH2(s) ⇒ CH(s) + H(s) | 23 |
| HO2(s) ⇒ OH(s) + O(s) | 2 |
| OH(s) ⇒ H(s) + O(s) | 10 |
| C(s) + H(s) ⇒ CH(s) | 4 |
| COH(s) + OH(s) ⇒ CO(s) + H2O(s) | 2 |
| CH(s) + OH(s) ⇒ CHOH(s) | 2 |
| CH2(s) + H2O(s) ⇒ CH3(s) + OH(s) | 1 |
| OH(s) + OH(s) ⇒ H2O(s) + O(s) | 4 |
| CH3(s) + H(s) ⇒ CH4(s) | 2 |
| CH4 ⇒ CH4(s) | 21 |
| CH4(s) ⇒ CH3(s) + H(s) | 12 |
| H(s) + OH(s) ⇒ H2(s) + O(s) | 1 |
| H2O ⇒ H2O(s) | 58 |
| OH(s) + O(s) ⇒ HO2(s) | 2 |
| H2O(s) ⇒ H(s) + OH(s) | 47 |
| CH3(s) ⇒ CH2(s) + H(s) | 14 |
| CO(s) + H(s) ⇒ CHO(s) | 1 |
| H2(s) ⇒ H2 | 17 |
| CHOH(s) ⇒ COH(s) + H(s) | 2 |
| H(s) + O(s) ⇒ OH(s) | 4 |
Formation of CO(s) (CO molecule adsorbed on the surface) was observed twice during the simulations while its desorption from the surface was not observed because of the high adsorption energy(1.3 eV) of CO on the Rh(111) surface. By contrast, formation of H2(s) (H2 molecule adsorbed on the surface) through H(s) + H(s) → H2(s) was observed 51 times, and its desorption from the surface was observed 17 times. Thus, the steam reforming of methane to CO and H2 was simulated by our accelerated MD simulations.
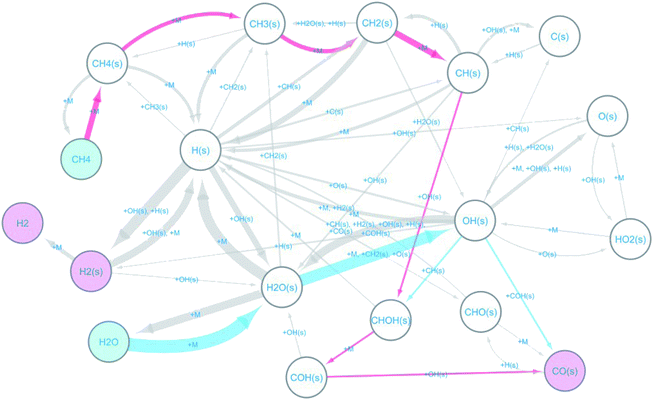
The observed elementary reactions were converted to a directed graph data and were summarized as a reaction network with 18 nodes and 53 edges shown in Fig. 3.
Here, the label “+ M” means an unimolecular reaction. The pathways leading to the formation of CO(s) from CH4 and H2O are colored red and blue, respectively. The reaction network indicates that at the beginning of the reforming, methane and water are decomposed on the surface by the following reactions.
| CH4 ⇒ CH4(s) | (R1) |
| CH4(s) ⇒ CH3(s) + H(s) | (R2) |
| CH3(s) ⇒ CH2(s) + H(s) | (R3) |
| CH2(s) ⇒ CH(s) + H(s) | (R4) |
| H2O ⇒ H2O(s) | (R5) |
| H2O(s) ⇒ OH(s) + H(s) | (R6) |
The formed surface-adsorbed hydrogen atoms quickly associate on the surface to form the hydrogen molecule.
| H(s) + H(s) ⇒ H2(s) ⇒ H2 | (R7) |
The slow CO formation reaction occurs through the following surface reactions.
| CH(s) + OH(s) ⇒ CHOH(s) | (R8) |
| CHOH(s) ⇒ COH(s) + H(s) | (R9) |
| COH(s) + OH(s) ⇒ CO(s) + H2O(s) | (R10) |
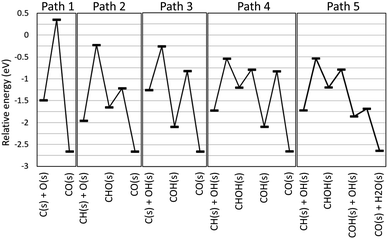
The automatically extracted CO formation pathways R8 and R9 agree with the energetically most favorable pathway suggested by elaborate manual static ab initio calculations.70 However, it should be noted that to the best of our knowledge, reaction path R10 has never been considered in previous work. To verify this newly discovered pathway, we examined its energetics by static ab initio calculations using the Climbing Image-Nudged Elastic Band (CI-NEB) method71 and compared its energetics with those of other pathways as shown in Fig. 4.
Here, the reference energy value was set to the energy of one methane and two water molecules in the gas phase, and all species not shown were assumed to be adsorbed on the surface as H(s) and O(s). Paths 1, 2, and 3 were included in the existing reaction models for the methane steam reforming on Rh surface.56 However, they exhibit high energies for the transition states of C(s) + O(s) ⇒ CO(s) for Path 1, CH(s) + O(s) ⇒ CHO(s) for Path 2 and C(s) + OH(s) ⇒ COH(s) for Path 3, indicating that these pathways are kinetically hindered. As suggested by Lee and co-workers,70 Path 4 exhibits the lower transition state of CH(s) + OH(s) ⇒ CHOH(s). Following this step, COH(s) is formed from CHOH(s). Identical steps appear in our Path 5, however, Paths 4 and 5 differ in the subsequent CO formation step. In Path 4, the unimolecular decomposition reaction of COH(s) occurs to form CO(s) and H(s). This step has a large activation energy of 1.27 eV. By contrast, in Path 5, the hydrogen transfer reaction from COH(s) to OH(s) occurs to form CO(s) and H2O(s). Remarkably, this hydrogen transfer reaction is barrierless while the CI-NEB analysis finds a slight energetic barrier in the subsequent OH(s) diffusion process. Although formation of OH(s) involves activation barriers of 1.15 eV for H2O(s) ⇒ H(s) + OH(H3CH2CH2)(s) ⇒ CH3CHCH2(s) and of 0.87 eV for O(s) + H(s) ⇒ OH(s), both of these are lower than the activation barrier of the unimolecular decomposition reaction (1.27 eV). Hence, static ab initio calculations indicate that Path 5 discovered automatically by our scheme is indeed an energetically more favorable pathway than the pathways reported in previous studies.
3.2 Propane reforming (dehydrogenation) on Pt(111) and Pt3Sn(111) surfaces
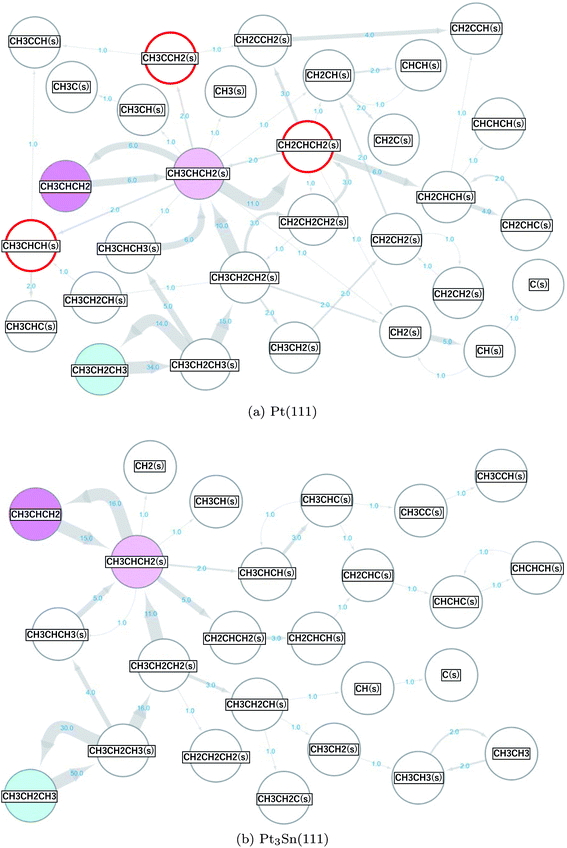
The same scheme was applied to the propane (CH3CH2CH3) reforming reaction on the Pt(111) and Pt3Sn(111) surfaces to elucidate the origin of the high selectivity of the Pt3Sn(111) surface for propylene (CH3CHCH2) production from propane (CH3CH2CH3).57,58 A reaction network with 34 nodes and 77 edges was obtained for Pt(111), and a reaction network with 28 nodes and 53 edges was obtained for Pt3Sn(111). These networks are shown in Fig. 5, where the surface hydrogen atoms (H(s)) are not shown to simplify the networks. The propane in the gas phase (the initial state) is shown in cyan, the propylene in the gas phase (the main target of the reforming reaction) is shown in magenta, and the propylene adsorbed on the surface (CH3CHCH2(s)) is shown in light magenta. The numbers on the arrows indicate the numbers of the occurrences of the corresponding events. More frequent events are shown by thicker arrows. More nodes, edges and arrows appear in the network for the reaction on the Pt(111) than in the network for the reaction on the Pt3Sn(111) surface, indicating that the Pt(111) surface is more reactive than the Pt3Sn(111) surface. On the Pt(111) surface, propane is decomposed to propylene and is further decomposed to CH2CHCH2(s), CH2CHCH(s), and CH2CHC(s) through the following reactions.| CH3CH2CH3 ⇒ CH3CH2CH3(s) | (R11) |
| CH3CH2CH3(s) ⇒ CH3CH2CH2(s) + H(s) | (R12) |
| CH3CH2CH2(s) ⇒ CH3CHCH2(s) + H(s). | (R13) |
| CH3CHCH2(s) ⇒ CH2CHCH2(s) + H(s) | (R14) |
| CH2CHCH2(s) ⇒ CH2CHCH(s)+H(s) | (R15) |
On the other hand, the formed propylene is desorbed to the gas phase on the Pt3Sn(111) surface.
| CH3CHCH2(s) ⇒ CH3CHCH2 | (R16) |
The results are consistent with the experimentally observed low reactivity and high selectivity for selective propylene formation on the PtSn alloy catalyst.57
Fig. 5 shows the presence of a side pathway for the propylene formation on both the Pt(111) and Pt3Sn(111) surfaces.
| CH3CH2CH3(s) ⇒ CH3CHCH3(s) + H(s) | (R17) |
| CH3CHCH3(s) ⇒ CH3CHCH2(s) + H(s) | (R18) |
As indicated by the thickness of the arrows, pathways R12 and R13 occur more frequently than pathways R17 and R18. Static ab initio CI-NEB calculations support the observations in the AHD simulations as shown by the data presented in Table 3.
On the Pt(111) surface, selective formation of propylene is hindered by further dehydrogenation reactions. The decomposition to CH2CHCH2(s) was observed most frequently (11 times), followed by the decomposition to CH3CCH2(s) and decomposition to CH3CHCH(s) that were observed twice each in this study (these 3 products are highlighted by red circles in Fig. 5(a)). These results are different from the conclusions of the previous studies58,72 that reported that the decompositions to CH3CCH2(s) and CH3CHCH(s) rather than to CH2CHCH2(s) are the main pathways. To verify our results, we further conducted CI-NEB analyses. The obtained results are summarized in Table 4.
| Elementary reaction | Activation energy (eV) | Reaction heat (eV) |
|---|---|---|
| ⇒ CH2CHCH2(s) + H(s) | 0.756 | −0.003 |
| ⇒ CH3CCH2(s) + H(s) | 0.846 (0.77) | −0.001 (−0.01) |
| ⇒ CH3CHCH(s) + H(s) | 0.810 (0.76) | 0.007 (0.06) |
The computed activation barriers for the reactions for the formation of CH3CCH2(s) and CH3CHCH(s) suggested in previous work are in good agreement with the reported values albeit with slight differences because of the differences in the computational methods (this study: revPBE/ultrasoft pseudopotentials, the previous study: PBE/projector augmented wave method). The activation barrier of the CH2CHCH2(s) formation reaction is the lowest among the three reactions. Hence, our scheme correctly automatically extracts the energetically favorable pathway.
4 Conclusion
An automated ab initio method was developed to elucidate the reaction pathways of complex surface reactions with no experimental data and with minimal human interventions. The method adopts accelerated MD simulations that enable efficient sampling of rare events at the surface by applying bias potentials without perturbing the selectivity of multiple elementary reactions. By extending the method previously developed for gas- or liquid-phase reactions, elementary reactions are automatically extracted from the MD trajectories. The extracted elementary reactions are converted to directed graph data that can be visualized by a network analysis tool. The method was applied to two surface reactions: the steam reforming of methane on the Rh(111) surface and propane dehydrogenation on the Pt(111) and Pt3Sn(111) surfaces. In both applications, our automated scheme extracted new energetically favorable reaction pathways as well as conventional reaction pathways suggested in past studies that employed manual static ab initio calculations. Moreover, the application of our method to the propane dehydrogenation showed that the high selectivity for propylene formation on the Pt3Sn(111) surface is due to the deactivation of propylene decomposition and the activation of propylene desorption on this surface. These two applications demonstrate that our scheme can indeed automatically extract the dominant reaction pathways of complex heterogeneous surface reactions without making artificial assumptions regarding the reaction pathways.Conflicts of interest
There are no conflicts to declare.References
- J. A. Dumesic, D. F. Rudd, L. M. Aparicio, A. A. Trevino and J. E. Rekoske, The microkinetics of heterogeneous catalysis, Wiley-VCH, 1993 Search PubMed.
- A. Richard, Friesner. Ab initio quantum chemistry: Methodology and applications, Proc. Natl. Acad. Sci. U. S. A., 2005, 102(19), 6648–6653 CrossRef PubMed.
- A. J. Medford, A. Vojvodic, J. S. Hummelshøj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, From the sabatier principle to a predictive theory of transition-metal heterogeneous catalysis, J. Catal., 2015, 328, 36–42 CrossRef CAS.
- G. Jones, F. Studt, F. Abild-Pedersen, J. K. Nørskov and T. Bligaard, Scaling relationships for adsorption energies of C2 hydrocarbons on transition metal surfaces, Chem. Eng. Sci., 2011, 66(24), 6318–6323 CrossRef CAS.
- S. Wang, B. Temel, J. Shen, G. Jones, L. C. Grabow, F. Studt, T. Bligaard, F. Abild-Pedersen, C. H. Christensen and J. K. Norskov, Universal Bronsted-Evans-Polanyi relations for C–C, C–O, C–N, N–O, N–N, and O–O dissociation reactions, Catal. Lett., 2011, 141(3), 370–374 CrossRef CAS.
- F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, J. Rossmeisl and M. T. M. Koper, Physical and chemical nature of the scaling relations between adsorption energies of atoms on metal surfaces, Phys. Rev. Lett., 2012, 108(11), 116103 CrossRef CAS PubMed.
- A. Logadottir, T. Holm Rod, J. K. Nørskov, B. Hammer, S. Dahl and C. J. H. Jacobsen, The Brønsted–Evans–Polanyi relation and the volcano plot for ammonia synthesis over transition metal catalysts, J. Catal., 2001, 197(2), 229–231 CrossRef CAS.
- N. Schumacher, A. Boisen, S. Dahl, A. A. Gokhale, S. Kandoi, L. C. Grabow, J. A. Dumesic, M. Mavrikakis and I. Chorkendorff, Trends in low-temperature water–gas shift reactivity on transition metals, J. Catal., 2005, 229(2), 265–275 CrossRef CAS.
- H. Falsig, T. Bligaard, J. Rass-Hansen, A. L. Kustov, C. H. Christensen and J. K. Nørskov, Trends in catalytic NO decomposition over transition metal surfaces, Top. Catal., 2007, 45(1), 117–120 CrossRef CAS.
- G. Jones, J. G. Jakobsen, S. S. Shim, J. Kleis, M. P. Andersson, J. Rossmeisl, F. Abild-Pedersen, T. Bligaard, S. Helveg and B. Hinnemann, et al., First principles calculations and experimental insight into methane steam reforming over transition metal catalysts, J. Catal., 2008, 259(1), 147–160 CrossRef CAS.
- M. Iannuzzi, A. Laio and M. Parrinello, Efficient exploration of reactive potential energy surfaces using Car-Parrinello molecular dynamics, Phys. Rev. Lett., 2003, 90(23), 238302 CrossRef PubMed.
- B. Ensing, M. De Vivo, Z. Liu, P. Moore and M. L. Klein, Metadynamics as a tool for exploring free energy landscapes of chemical reactions, Acc. Chem. Res., 2006, 39(2), 73–81 CrossRef CAS PubMed.
- Z. W. Ulissi, A. J. Medford, T. Bligaard and J. K. Nørskov, To address surface reaction network complexity using scaling relations machine learning and DFT calculations, Nat. Commun., 2017, 8(1), 1–7 CrossRef PubMed.
- A. Miyoshi, Systematic computational study on the unimolecular reactions of alkylperoxy (RO2), hydroperoxyalkyl (QOOH), and hydroperoxyalkylperoxy (O2QOOH) radicals, J. Phys. Chem. A, 2011, 115(15), 3301–3325 CrossRef CAS PubMed.
- C. W. Gao, J. W Allen, W. H. Green and R. H. West, Reaction Mechanism Generator: Automatic construction of chemical kinetic mechanisms, Comput. Phys. Commun., 2016, 203, 212–225 CrossRef CAS.
- M. R. Harper, K. M. Van Geem, S. P. Pyl, G. B. Marin and W. H. Green, Comprehensive reaction mechanism for n-butanol pyrolysis and combustion, Combust. Flame, 2011, 158(1), 16–41 CrossRef CAS.
- S. W. Benson, Oxygen initiated combustion: Thermochemistry and kinetics of unsaturated hydrocarbons, Int. J. Chem. Kinet., 1996, 28(9), 665–672 CrossRef CAS.
- P. M. Zimmerman, Automated discovery of chemically reasonable elementary reaction steps, J. Comput. Chem., 2013, 34(16), 1385–1392 CrossRef CAS PubMed.
- P. M. Zimmerman, Navigating molecular space for reaction mechanisms: an efficient, automated procedure, Mol. Simul., 2015, 41(1–3), 43–54 CrossRef CAS.
- Y. V. Suleimanov and W. H. Green, Automated discovery of elementary chemical reaction steps using freezing string and berny optimization methods, J. Chem. Theory Comput., 2015, 11(9), 4248–4259 CrossRef CAS PubMed.
- S. Maeda, K. Ohno and K. Morokuma, Automated global mapping of minimal energy points on seams of crossing by the anharmonic downward distortion following method: a case study of H2CO, J. Phys. Chem. A, 2009, 113(9), 1704–1710 CrossRef CAS PubMed.
- S. Maeda, K. Ohno and K. Morokuma, Systematic exploration of the mechanism of chemical reactions: the global reaction route mapping (GRRM) strategy using the ADDF and AFIR methods, Phys. Chem. Chem. Phys., 2013, 15(11), 3683–3701 RSC.
- S. Habershon, Automated prediction of catalytic mechanism and rate law using graph-based reaction path sampling, J. Chem. Theory Comput., 2016, 12(4), 1786–1798 CrossRef CAS PubMed.
- I. Ismail, H. B. V. A. Stuttaford-Fowler, C. O. Ashok, C. Robertson and S. Habershon, Automatic proposal of multistep reaction mechanisms using a graph-driven search, J. Phys. Chem. A, 2019, 123(15), 3407–3417 CrossRef CAS PubMed.
- M. Salciccioli, Y. Chen and D. G. Vlachos, Density functional theory-derived group additivity and linear scaling methods for prediction of oxygenate stability on metal catalysts: adsorption of open-ring alcohol and polyol dehydrogenation intermediates on pt-based metals, J. Phys. Chem. C, 2010, 114(47), 20155–20166 CrossRef CAS.
- V. Vorotnikov and D. G. Vlachos, Group additivity and modified linear scaling relations for estimating surface thermochemistry on transition metal surfaces: Application to furanics, J. Phys. Chem. C, 2015, 119(19), 10417–10426 CrossRef CAS.
- S. Rangarajan, R. R. O. Brydon, A. Bhan and P. Daoutidis, Automated identification of energetically feasible mechanisms of complex reaction networks in heterogeneous catalysis: application to glycerol conversion on transition metals, Green Chem., 2014, 16(2), 813–823 RSC.
- S. Rangarajan, A. Bhan and P. Daoutidis, Identification and analysis of synthesis routes in complex catalytic reaction networks for biomass upgrading, Appl. Catal., B, 2014, 145, 149–160 CrossRef CAS.
- F. Nattino, H. Ueta, H. Chadwick, M. E van Reijzen, R. D. Beck, B. Jackson, M. C. van Hemert and G.-J. Kroes, Ab initio molecular dynamics calculations versus quantum-state-resolved experiments on CHD3+ Pt (111): new insights into a prototypical gas–surface reaction, J. Phys. Chem. Lett., 2014, 5(8), 1294–1299 CrossRef CAS PubMed.
- T. Cheng, H. Xiao and W. A. Goddard, Full atomistic reaction mechanism with kinetics for CO reduction on Cu (100) from ab initio molecular dynamics free-energy calculations at 298 K, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(8), 1795–1800 CrossRef CAS PubMed.
- Y. Wang and P. B Balbuena, Ab initio molecular dynamics simulations of the oxygen reduction reaction on a Pt (111) surface in the presence of hydrated hydronium (H3O)+(H2O) 2: direct or series pathway?, J. Phys. Chem. B, 2005, 109(31), 14896–14907 CrossRef CAS PubMed.
- L.-P. Wang, A. Titov, R. McGibbon, F. Liu, V. S. Pande and T. J. Martínez, Discovering chemistry with an ab initio nanoreactor, Nat. Chem., 2014, 6(12), 1044–1048 CrossRef CAS PubMed.
- J. A. Varela, S. A. Vázquez and E. Martínez-Núñez, An automated method to find reaction mechanisms and solve the kinetics in organometallic catalysis, Chem. Sci., 2017, 8(5), 3843–3851 RSC.
- D. G. Sangiovanni, G. K. Gueorguiev and A. K. Georgieva, Ab initio molecular dynamics of atomic-scale surface reactions: Insights into metal organic chemical vapor deposition of AlN on graphene, Phys. Chem. Chem. Phys., 2018, 20(26), 17751–17761 RSC.
- A. C. T. Van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, ReaxFF: a reactive force field for hydrocarbons, J. Phys. Chem. A, 2001, 105(41), 9396–9409 CrossRef CAS.
- M. F. Russo Jr, R. Li, M. Mench and A. C. T. Van Duin, Molecular dynamic simulation of aluminum–water reactions using the ReaxFF reactive force field, Int. J. Hydrogen Energy, 2011, 36(10), 5828–5835 CrossRef.
- J. E. Mueller, A. C. T. Van Duin and W. A. Goddard III, Development and validation of ReaxFF reactive force field for hydrocarbon chemistry catalyzed by nickel, J. Phys. Chem. C, 2010, 114(11), 4939–4949 CrossRef CAS.
- J. E. Mueller, A. C. T. Van Duin and W. A. Goddard III, Application of the ReaxFF reactive force field to reactive dynamics of hydrocarbon chemisorption and decomposition, J. Phys. Chem. C, 2010, 114(12), 5675–5685 CrossRef CAS.
- S. Hong and A. C. T. Van Duin, Atomistic-scale analysis of carbon coating and its effect on the oxidation of aluminum nanoparticles by reaxff-molecular dynamics simulations, J. Phys. Chem. C, 2016, 120(17), 9464–9474 CrossRef CAS.
- A. F. Voter, Hyperdynamics: Accelerated molecular dynamics of infrequent events, Phys. Rev. Lett., 1997, 78(20), 3908 CrossRef CAS.
- D. Hamelberg, J. Mongan and J. A. McCammon, Accelerated molecular dynamics: a promising and efficient simulation method for biomolecules, J. Chem. Phys., 2004, 120(24), 11919–11929 CrossRef CAS PubMed.
- L. C. T. Pierce, R. Salomon-Ferrer, C. A. F. de Oliveira, J. A. McCammon and R. C. Walker, Routine access to millisecond time scale events with accelerated molecular dynamics, J. Chem. Theory Comput., 2012, 8(9), 2997–3002 CrossRef CAS PubMed.
- H. Hirai, Practical hyperdynamics method for systems with large changes in potential energy, J. Chem. Phys., 2014, 141(23), 234109 CrossRef PubMed.
- K. A. Fichthorn and S. Mubin, Hyperdynamics made simple: Accelerated molecular dynamics with the Bond-Boost method, Comput. Mater. Sci., 2015, 100, 104 CrossRef.
- J.-P. Du, Y.-J. Wang, Yu-C. Lo, L. Wan and S. Ogata, Mechanism transition and strong temperature dependence of dislocation nucleation from grain boundaries: An accelerated molecular dynamics study, Phys. Rev. B, 2016, 94(10), 104110 CrossRef.
- M. A. Nejad and H. M. Urbassek, Functionalized silica surfaces as carriers for monoclonal antibodies in targeted drug delivery systems: Accelerated molecular dynamics study, Chem. Phys. Lett., 2020, 739, 136988 CrossRef CAS.
- M. Lauricella, L. Chiodo, G. Ciccotti and A. Alberto, Ab initio accelerated molecular dynamics study of the hydride ligands in the ruthenium complex: Ru(H2)2H2(P(C5H9)3)2, Phys. Chem. Chem. Phys., 2019, 21(45), 25247–25257 RSC.
- H. Hirai, Molecular Dynamics Simulation of n-Heptane Pyrolysis using Adaptive Hyperdynamics Method. Technical report, SAE Technical Paper, 2015 Search PubMed.
- H. Hirai and R. Jinnouchi, Discovering Chemical Reaction Pathways Using Accelerated Molecular Dynamics Simulations and Network Analysis Tools-Application to Oxidation Induced Decomposition of Ethylene Carbonate, Chem. Phys. Lett., 2021, 138439 CrossRef CAS.
- R. A. Miron and K. A. Fichthorn, Accelerated molecular dynamics with the bond-boost method, J. Chem. Phys., 2003, 119(12), 6210–6216 CrossRef CAS.
- R. A. Miron and K. A. Fichthorn, Heteroepitaxial growth of Co/Cu (001): An accelerated molecular dynamics simulation study, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72(3), 035415 CrossRef.
- J. Liu, X. Li, L. Guo, M. Zheng, J. Han, X. Yuan, F. Nie and X. Liu, Reaction analysis and visualization of ReaxFF molecular dynamics simulations, J. Mol. Graphics Modell., 2014, 53, 13–22 CrossRef CAS PubMed.
- M. Döntgen, M.-D. Przybylski-Freund, L. C. Kröger, W. A. Kopp, A. E. Ismail and K. Leonhard, Automated discovery of reaction pathways, rate constants, and transition states using reactive molecular dynamics simulations, J. Chem. Theory Comput., 2015, 11(6), 2517–2524 CrossRef PubMed.
- H. Hirai, Reaction mechanism generation method and reaction mechanism generation device, US Pat., 15/551,071, February 1 2018 Search PubMed.
- L. Maier, B. Schädel, K. Herrera Delgado, S. Tischer and O. Deutschmann, Steam reforming of methane over nickel: development of a multi-step surface reaction mechanism, Top. Catal., 2011, 54(13–15), 845 CrossRef CAS.
- B. T. Schädel, M. Duisberg and O. Deutschmann, Steam reforming of methane, ethane, propane, butane, and natural gas over a rhodium-based catalyst, Catal. Today, 2009, 142(1–2), 42–51 CrossRef.
- M. S. Kumar, D. Chen, A. Holmen and J. C. Walmsley, Dehydrogenation of propane over Pt-SBA-15 and Pt-Sn-SBA-15: Effect of Sn on the dispersion of Pt and catalytic behavior, Catal. Today, 2009, 142(1–2), 17–23 CrossRef.
- M.-L. Yang, Y.-A. Zhu, X.-G. Zhou, Z.-J. Sui and D. Chen, First-principles calculations of propane dehydrogenation over PtSn catalysts, ACS Catal., 2012, 2(6), 1247–1258 CrossRef CAS.
- H. Hirai, Molecular dynamics simulations for initial formation process of polycyclic aromatic hydrocarbons in n-hexane and cyclohexane combustion, Chem. Phys., 2021, 548, 111225 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21(39), 395502 CrossRef PubMed.
- A. Hagberg, P. Swart and D. S. Chult, Exploring network structure, dynamics, and function using NetworkX, Technical report, Los Alamos National Lab.(LANL), Los Alamos, NM, United States, 2008 Search PubMed.
- P. Shannon, A. Markiel, O. Owen, N. S. Baliga, J. T. Wang, D. Ramage, N. Amin, B. Schwikowski and T. Ideker, Cytoscape: a software environment for integrated models of biomolecular interaction networks, Genome Res., 2003, 13(11), 2498–2504 CrossRef CAS PubMed.
- M. E. Smoot, K. Ono, J. Ruscheinski, P.-L. Wang and T. Ideker, Cytoscape 2.8: new features for data integration and network visualization, Bioinformatics, 2011, 27(3), 431–432 CrossRef CAS PubMed.
- D. Vanderbilt, Soft self-consistent pseudopotentials in a generalized eigenvalue formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41(11), 7892 CrossRef PubMed.
- Y. Zhang and W. Yang, Comment on “generalized gradient approximation made simple”, Phys. Rev. Lett., Jan 1998, 80, 890 Search PubMed.
- K. Yang, J. Zheng, Y. Zhao and D. G. Truhlar, Tests of the RPBE, revPBE, τ-HCTHhyb, ωB9X–D, and MOHLYP density functional approximations and 29 others against representative databases for diverse bond energies and barrier heights in catalysis, J. Chem. Phys., 2010, 132(16), 164117 CrossRef PubMed.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- H. J. C. Berendsen, J. P. M. van Postma, W. F. Van Gunsteren, A. R. H. J. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81(8), 3684–3690 CrossRef CAS.
- P. Kratzer and J. Neugebauer, The basics of electronic structure theory for periodic systems, Front. Chem., 2019, 7, 106 CrossRef CAS PubMed.
- K. Lee, E. Lee, C. Song and M. J. Janik, Density functional theory study of propane steam reforming on Rh–Ni bimetallic surface: Sulfur tolerance and scaling/Brønsted–Evans–Polanyi relations, J. Catal., 2014, 309, 248–259 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113(22), 9901–9904 CrossRef CAS.
- M.-L. Yang, Y.-A. Zhu, C. Fan, Z.-J. Sui, D. Chen and X.-G. Zhou, DFT study of propane dehydrogenation on Pt catalyst: effects of step sites, Phys. Chem. Chem. Phys., 2011, 13(8), 3257–3267 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Methods to identify and extract chemical species and elementary chemical reactions from molecular dynamics trajectories. See https://doi.org/10.1039/d2ra04343b |
| This journal is © The Royal Society of Chemistry 2022 |