Femtosecond coherent anti-Stokes Raman spectroscopy study of vibrational dynamics of liquid chloroform

Abstract

Femtosecond time-resolved coherent anti-Stokes Raman spectroscopy (CARS) was used to study the dynamics of the vibrational modes of liquid chloroform. The vibrational modes were selectively excited and their coherent vibrational dynamics were obtained. Some subtle features that are difficult to distinguish in the ordinary spontaneous Raman spectrum, such as overtones and combinations of some fundamental vibrational modes, were recognized from the CARS transients. Combined with theoretical calculations, the contributions of chlorine isotopes were also confirmed from the CARS transients of the vibrational modes involving the motion of chlorine atoms.

---

1. Introduction

Time-resolved coherent anti-Stokes Raman spectroscopy (tr-CARS) has been widely used to study molecular vibrational dynamics. In tr-CARS, a Raman-active vibrational mode is coherently excited when the energy difference between the simultaneous incident pump and Stokes pulse is tuned to be resonant with the transition of this vibrational mode. The coherently excited vibration is probed by the probe pulse, and the generated anti-Stokes Raman signal is emitted in the phase-matching direction. By scanning the delay time between the probe pulse and the pump/Stokes pulses, coherent vibrational dynamics can be obtained. W. Kiefer and co-workers have carried out a lot of pioneering work in this field.^1–4 They demonstrated the application of femtosecond tr-CARS to study the vibrational dynamics of the electronic ground or excited states of gas- and liquid-phase materials. V. A. Apkarian et al. also carried out a lot of research on vibrational dynamics using femtosecond tr-CARS, in particular the vibrational dynamics of I₂ molecules in solids at low temperature.^5–7 Using tr-CARS, this group then reported the first real-time record of vibrational wave packet motion at the single-molecule limit.⁸ Vibrational dynamics obtained by CARS can help understand the reaction mechanisms in various materials, such as energetic materials.^9–11 In addition to the studies of vibrational dynamics, CARS can also be used for imaging and diagnostics. As a kind of label-free imaging technology, CARS microscopy has been widely used in biology and medicine.^12–15 The CARS transient of nitrogen molecules can be used to measure temperature in reacting flows.^16,17 These remarkable works indicate that CARS is an effective tool for studying the microscopic mechanism of chemical reactions both in organisms and inorganic materials.

When femtosecond laser pulses are used as pump and Stokes, Raman-active vibrational modes in the range of hundreds of wavenumbers can be excited. If two or more vibrational modes are excited simultaneously, polarization beats will be observed in the CARS transients when probed by femtosecond pulses.^1,18–21 Using femtosecond tr-CARS, spectral information can be obtained not only directly from the frequency domain, but also through the analysis of polarization beats, which may have higher precision. With the advances in laser and photodetector technology, femtosecond CARS has achieved higher detection sensitivity and can provide more and more detailed characteristics of vibration dynamics in experiments.

Chloroform is a common organic solvent with the fewest atoms in a single molecule and consequently the fewest normal vibrational modes. It is often chosen as a sample to study the vibration-related processes and the interactions with other molecules. In the early work, the vibrational relaxation of chloroform molecules was obtained by analyzing the Raman line shape.^22–24 In the room-temperature condensed-phase system, the line shape of the spectrum is modified by a variety of homogeneous and inhomogeneous broadening, so it is difficult to access accuracy dynamics parameters from Raman spectra. As a time-domain approach to vibration, CARS was used in some work to get the dephasing time constants of some specific vibrational modes, such as C–H stretching vibration.^25,26 In our previous work, the vibrational dynamics of the CH stretching vibration of chloroform was studied by multiplex CARS.²⁷ Although different modes were simultaneously excited, the application of white-light continuum greatly reduced the intensity of the CARS signal, resulting in large errors in extracting the information of a single mode. To our knowledge, there is little work on the systematic study of the vibrational dynamics of chloroform by direct time-domain detection methods. In this paper, the vibrational dynamics of liquid chloroform was systematically investigated using femtosecond CARS with higher sensitivity. The CARS transients of all the vibrational modes were obtained at room temperature. Compared with the previous results, the signal-to-noise ratio of the CARS curves was greatly improved. Besides the more reliable dynamics derived from the high quality experimental data, many subtle features that are difficult to distinguish in spontaneous Raman spectra were also observed.

2. Experimental

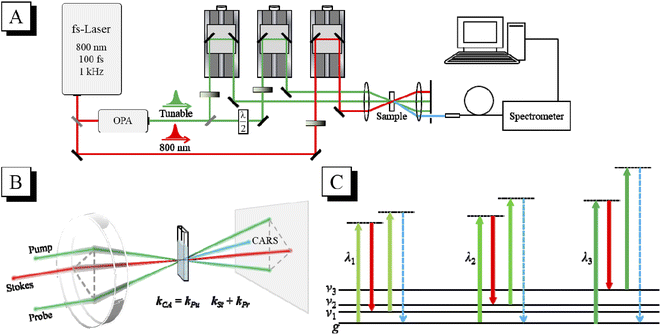
The schematic diagram of the CARS experimental setup is shown in Fig. 1(A). The output laser beam (802 nm, 100 fs, 1 kHz) from a Ti:sapphire regenerative amplifier (Spitfire Ace, Spectra Physics) was divided into two beams by a 9 : 1 beam splitter. The laser beam with 90% energy was used to pump an optical parametric amplifier (OPA) (TOPAS, Light Conversion). The wavelength-tunable laser beam output from the OPA was further divided by a 1 : 1 beam splitter into two beams, which were used as the pump and probe, respectively. The 802 nm laser beam with 10% energy was used as the Stokes beam. The timing of the pump, Stokes and probe laser pulses was adjusted by their respective optical delay lines. The delay time between the pump pulse and the Stokes pulse was adjusted to zero to ensure that they interact with the sample simultaneously, and the delay time between the probe pulse and the other two laser pulses was scanned to get the CARS transient. The three laser beams (after appropriate attenuation) were then focused into the sample in the folded BOXCARS geometry by a lens with a focal length of 300 mm, as shown in Fig. 1(B). The generated CARS signal is naturally separated from the incident laser beams, and can be spatially selected and then directed into a micro optical fiber spectrometer (QE Pro, Ocean Insight). In the tr-CARS experiments in this work, the center wavelength of the Stokes pulses was fixed at 802 nm, and the center wavelength of the pump/probe pulses was tuned by adjusting the OPA to realize the selective excitation of specific vibrational modes. As shown in Fig. 1(C), when the energy difference between the pump pulse and the Stokes pulse is resonant with a certain vibrational mode, this mode will be selectively excited and detected. By scanning the wavelength of the pump laser, all the Raman-active modes can be selectively excited one by one, and their vibrational dynamics can then be obtained. For all the vibrational modes, the laser power of the pump, Stokes and probe beams was all 0.1 mW in the CARS experiments.

Fig. 1 (A) Schematic diagram of the fs-CARS experimental setup. (B) Folded BOXCARS geometry of the three incident laser beams. The generated CARS signal is spatially separated from the incident laser beams. (C) Schematic of selective excitation. The wavelength of the pump pulse is tuned to selectively excite each vibrational mode.

The spontaneous Raman spectrum of chloroform was obtained by a home-built experimental setup, in which a 532 nm single longitudinal mode CW laser (Samba, Cobolt) was used as the excitation source. The excitation laser was focused on the sample through a 10× microscopic objective, and the light power arriving at the sample was about 0.13 mW. A spectrometer with a focal length of 500 mm and a grating of 1800 grooves/mm (SR-500i, Andor) combined with a charge-coupled device (CCD) (DR-316B, Andor) was used to detect the Raman spectrum. The acquired spectrum was calibrated with the standard Raman spectrum of naphthalene. The sample in this work was liquid chloroform (purity ≥ 99%), which was placed in a quartz cuvette with an optical path of 1 mm without further purification. All the experiments were carried out at room temperature.

3. Results and discussion

3.1 Normal vibrational modes of chloroform

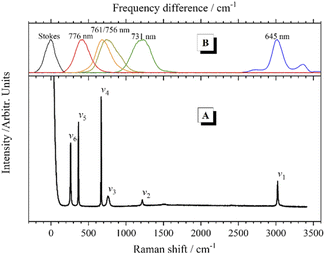
The chloroform molecule has highly symmetrical geometry that belongs to the C_3v point group. A chloroform molecule has 5 atoms and consequent 9 normal vibrational modes, all of which are Raman active. The normal vibrational modes of chloroform were calculated at the B3LYP/6-311++G(d,p) level using Gaussian 03.²⁸ According to the calculation results, 3 pairs of normal vibrational modes are degenerate or have almost identical vibrational energy, so only 6 Raman bands contributed by the fundamental modes can be observed in the Raman spectrum, as shown in Fig. 2(A). The experimental and calculated frequencies of these vibrational modes and their assignments are listed in Table 1.

Fig. 2 (A) Spontaneous Raman spectrum of chloroform at room temperature. (B) Spectra of the Stokes pulse (black line) and the selected pump/probe pulses (colored lines), with frequency difference relative to the Stokes pulse as horizontal coordinate.

Table 1 Vibrations of chloroform

Mode	Vibrational frequency (cm^−1)		Assignment
	Experimental	Calculated
a d here stands for degenerate.b s here stands for symmetric.
v1	3023	3181.56	CH stretching
v2	1218	1245.25/1245.25	CH d^a-bending
v3	761	729.41/729.39	CCl3 d-stretching
v4	669	661.73	CCl3 s ^b-stretching
v5	367	364.74	CCl3 s-deformation
v6	261	261.19/261.18	CCl3 d-deformation

---

In the CARS experiments, the center wavelength of the Stokes pulse was kept unchanged at 802 nm, while the output of the OPA was tuned to 645 nm, 731 nm, 756 nm, 761 nm and 776 nm to selectively excite the corresponding vibrational modes of chloroform molecules, respectively. Fig. 2(B) shows the frequency differences between these pump pulses and the 802 nm Stokes pulse, which match the Raman peaks in the spontaneous Raman spectrum. It should be mentioned that, since the bandwidth (full width at half maximum; FWHM) of the femtosecond laser pulses is about 300 cm⁻¹, the width of the effective excitation band generated by the pump and the Stokes pulses may exceed 600 cm⁻¹. Therefore, only the CH stretching mode can be excited separately. When the other vibrational modes are desired to be excited, multiple vibrational modes within the excitation bandwidth will be excited simultaneously, and obvious polarization beats will emerge in the time domain CARS transient. Besides, considering the output laser pulse with a wavelength near 802 nm from the OPA was not that stable, the direct selective excitation of ν₆ mode with the pump pulse at 784 nm was cancelled. When ν₅ was excited with the pump pulse at 776 nm, ν₆ was also in the effective excitation range. Then the dynamics of ν₆ can be obtained by analyzing the polarization beats generated between them.

3.2 Vibrational dynamics of chloroform

In order to analyze the vibrational dynamics, it is necessary to fit the experimental transient curves to obtain the desired parameters. The following formula is usually used to describe the change of CARS signal intensity with delay time:²⁰Here, I_as(t) is the time-dependent intensity of the CARS signal, and t is the delay time. A_j represents the pre-exponential factor of the j^th mode, and τ_j, ω_j, φ_j are the dephasing time, angular frequency, and initial phase of the j^th mode, respectively. Not only the coherent dynamics of a single vibrational mode, but also the coherent dynamics of multiple vibrational modes that are simultaneously excited can be described by eqn (1).

3.2.1. ν₁ mode (CH stretching). Fig. 3 shows the experimental result of selective excitation of ν₁. It can be seen from the inserted contour map that the CARS signal appears at around 540 nm, as the wavelength of the pump/probe pulse was tuned to 645 nm. (A 600 nm short-pass edge filter was used to filter out the scattered light of the pump/probe.) In CARS experiments, the time when the probe pulse temporally coincides with the pump/Stokes pulse is usually defined as the time zero. A main component of the signal occurs at time zero is the nonresonant background that arises from the response of electrons to the electric field of the incident laser pulses. The signal intensity of the nonresonant background is usually higher than that of the molecular vibrations, and they can even differ by several orders of magnitude in fs-CARS experiments. Nevertheless, because of the ultrafast response of electrons, the duration of the nonresonant background is basically the same as the convolution of the probe and pump/Stokes pulses. Compared with the dephasing of the vibrational modes, the lifetime of the nonresonant background from electrons is usually much shorter, and the skipping of the nonresonant background has little effect on the analysis of the vibrational dynamics. Thus, only the CARS transients at positive delay times that mainly contributed by the vibrational modes are considered in the following analysis.

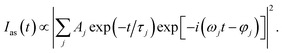Fig. 3 CARS transient of ν₁ at 540 nm. The red line is the single exponential fit to the experimental data (black squares). The upper subgraph shows the fitting residuals. The inserted contour map (left) shows the two-dimensional CARS signal around 540 nm, and the other inserted graph (right) shows the partially enlarged Raman spectrum for ν₁.

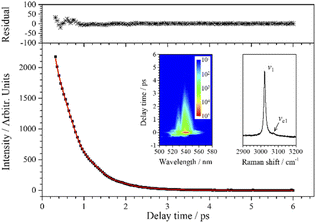
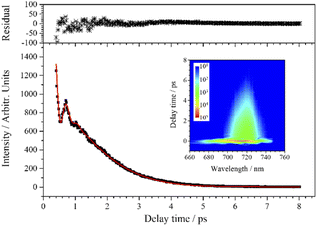
Since the CH stretching mode v₁ (3023 cm⁻¹) appears as a single peak in the spontaneous Raman spectrum, the decay of the CARS signal of v₁ should be an ideal single exponential decay in principle. However, when the experimental data are fitted with a single exponential decay function, there is a weak periodic oscillation emerged in the residuals. That is, some other component contributes to this CARS transient. When two components are considered (j = 2) in the fitting process, the fitted curve (red) obtained by eqn (1) is in good agreement with the experimental data (black squares), and the beat frequency (i.e. the angular frequency difference between two vibrations) is fitted to be 49 cm⁻¹ (to facilitate analysis, the fitted beat frequency is directly given in wavenumbers here and in the following analysis). It means that, besides v₁, there is another component contributing to the oscillation signal with a pre-exponential factor ratio of 0.018 to v₁, and the frequency difference between them is 49 cm⁻¹.

When the spontaneous Raman spectrum around 3000 cm⁻¹ is partially enlarged, shown as an insert in Fig. 3, a weak shoulder can be distinguished at 3072 cm⁻¹, labeled as v_c1. The frequency difference between v₁ (3023 cm⁻¹) and v_c1 is just coincident with beat frequency appearing in the CARS transient. Although the intensity of v_c1 itself is very weak, the high intensity v₁ can be regarded as a local oscillation, and their cross term forms a relatively more obvious oscillation in the CARS transient. Therefore, the parameters of the dynamics of v_c1 can be easily obtained by analyzing the polarization beats. The fitting result shows that the dephasing time constants of v_c1 and v₁ are both about 1.11 ps. Even though the Raman spectrum of chloroform was obtained nearly a hundred years ago, there is no definite assignment about this Raman peak at about 3072 cm⁻¹. The first reporter of this peak believed that the peak was from the residual aliphatic or aromatic impurities in chloroform,²⁹ and some other researchers assigned it to the 2ν₅ + 3ν₃ combination, which appeared due to Fermi resonance mixing with ν₁.³⁰ The almost identical dephasing time constants of ν₁ and ν_c1 obtained in this experiment also suggests a possible coupling between the two vibrational modes. We suggest that ν_c1 may most likely originate from the third overtone of ν₃ (4ν₃), which may be easier to access since the first overtone can directly be observed in the Raman spectrum.

3.2.2. ν₂ mode (CH stretching). ν₂ is the normal mode with the lowest oscillation strength. The CARS signal intensity of ν₂ is much lower than that of the nonresonant background. In order to get a transient curve with a good signal-to-noise ratio (SNR), the exposure time of the detector needs to be increased. Under the circumstance, the nonresonant background signal will saturate the detector. So the acquisition of the CARS transient of ν₂ was started from the delay time of 0.5 ps to avoid the influence of the nonresonant background.

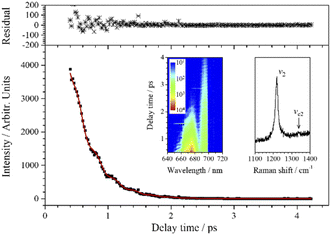
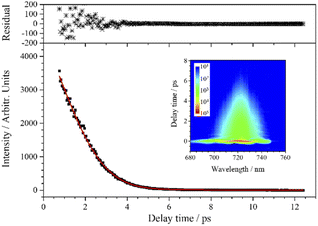
As shown in the inserted contour map in Fig. 4, the CARS signal of ν₂ appears at around 671 nm when the pump/probe light is centered at 731 nm. (A 700 nm short-pass edge filter was used to filter out the scattered light of the pump/probe.) In this inserted contour map with intensity depicted on a logarithmic scale, there is another vibrational signal appearing at around 697 nm (the signal above 700 nm was blocked by a short-pass filter) with lower intensity and longer lifetime. This signal is assigned to ν₄ which is covered by the effective excitation range formed by the pump and Stokes pulses, even though the efficiency is very low. The beat pattern appears (around 685 nm in the inserted contour map in Fig. 4) between the two vibrational signals with a frequency fitted to 550 cm⁻¹ is also evidence for the participation of ν₄. Compared with ν₄, ν₃ is too weak to be distinguished in the CARS signal under this excitation condition.

Fig. 4 CARS transient of ν₂ at 671 nm. The red line is the fit to the experimental data (black squares) when two vibrational modes are involved. The upper subgraph shows the fitting residuals. The inserted contour map (left) shows the two-dimensional CARS signal around 671 nm, and the other inserted graph (right) shows the partially enlarged Raman spectrum for ν₂.

The weak-intensity oscillation in the CARS transient curve indicates the coherence between ν₂ and other vibrational modes. The experimental data are also well fitted when j = 2 using eqn (1) and the fitted beat frequency is 120 cm⁻¹. The pre-exponential factor ratio of the weak component to the strong component is 0.034. When the spontaneous Raman spectrum around ν₂ is partially enlarged, shown as the insert in Fig. 4, a very weak peak can be vaguely distinguished at about 1339 cm⁻¹, which is labeled as ν_c2. ν_c2 may also come from the overtones or combination of some low-frequency normal modes, most possibly the first overtone of ν₄. It is worth noting that unlike the case of v_c1 and v₁, there may be no coupling between v_c2 and v₂, since there is a certain difference between the fitted dephasing time constants of ν_c2 (0.8 ps) and ν₂ (0.69 ps).

3.2.3. ν₃ mode (degenerate CCl₃ stretching). In the low-frequency vibration region of chloroform, the intervals between different vibrations are small, so it is impossible to directly excite a specific vibrational mode with femtosecond laser pulses without affecting the nearby vibrations. When the pump/probe pulse was tuned to 756 nm, the ν₃ mode is excited with the highest efficiency, and correspondingly the CARS signal of ν₃ appears at 715 nm. (A 750 nm short-pass edge filter was used to filter out the scattered light of the pump/probe.) At the same time, the nearby ν₄ mode will also be efficiently excited, and the edge of the effective excitation range even covers the ν₅ mode. The CARS signal of ν₄ appears at 720 nm under this excitation condition, as shown in the insert contour map in Fig. 5. Since the frequency difference between ν₃ and ν₄ is 92 cm⁻¹, polarization beats of 92 cm⁻¹ can be expected. As the Raman intensity of ν₄ is much stronger than that of ν₃, ν₄ is the main component even in the transient curve at 715 nm, and then the short-lived oscillation indicates a fast dephasing of ν₃. Although ν₅ is excited under this condition, it has little effect on the signal at 715 nm, while it contributes to the high-frequency polarization beats with a frequency of 302 cm⁻¹ around 730 nm (as shown in the inserted contour map in Fig. 5) due to its coherence with ν₄.

Fig. 5 CARS transient of ν₃ at 715 nm. The red line is the fit to the experimental data (black squares) when three components are considered. The upper subgraph shows the fitting residuals. The inserted contour map shows the two-dimensional CARS signal around 715 nm.

The experimental transient curve at 715 nm is well fitted when j is taken 3, and the fitting result is shown in Fig. 5. This means that the transient consists of three main components. Although ν₃ is not the dominant component in the transient, reliable dynamic parameters of ν₃ can still be obtained from the fitting process. Besides ν₃, there are two other vibrational modes (with a wavenumber interval of about 4.5 cm⁻¹) participating in the polarization beats at 715 nm, and their assignment will be discussed below.

3.2.4. ν₄ mode (symmetric CCl₃ stretching). In order to excite the ν₄ mode most effectively, the center wavelength of the pump/probe pulse was tuned to 761 nm, and correspondingly the CARS signal of ν₄ is centered at about 724 nm. (A 750 nm short-pass edge filter was used to filter out the scattered light of the pump/probe.) In this case, although ν₃ can also be effectively excited, its intensity is much lower than that of ν₄. While, since ν₅ is at the edge of the effective excitation band, its excitation efficiency is not that high. Thus, ν₃ and ν₅ have little effect on the CARS transient at 724 nm, but contribute to the polarization beats at both wings of the signal spectrum, respectively.

Although the experimental curve of ν₄ seems to exhibit a single exponential decay, the experimental data cannot be fitted by a single exponential decay function. Instead, when two vibrational components are involved in the fitting process (j = 2), the experimental data are well fitted by the red fitting curve, as shown in Fig. 6. It indicates that there are indeed polarization beats in the experimental curve, and the fitted beat frequency is about 4.5 cm⁻¹. This splitting may originate from the isotopes of chlorine. However, because the beat period is too long relative to the dephasing of ν₄, the decay curve cannot even cover a complete period, the fitting results are unreliable and unable to reflect the real polarization beats. As for contribution of chlorine isotopes to the CARS signal, the following analysis of ν₅ will give more reliable results.

Fig. 6 CARS transient of ν₄ at 724 nm. The red line is the fit to the experimental data (black squares) when two components are involved. The upper subgraph shows the fitting residuals. The inserted contour map shows the two-dimensional CARS signal around 724 nm.

In addition, it needs to be explained that the relatively large residuals below 3 ps are not due to the low SNR, but because there is still a weak high-frequency beat pattern from the coherence between ν₄ and ν₅ at 724 nm. The beat amplitude is very small, thus the influence is not considered in the fitting process, which leads to the relatively large residuals.

3.2.5. ν₅ mode (symmetric CCl₃ deformation). For the Raman shift of the ν₅ mode, the corresponding pump wavelength should be centered at 779 nm. However, in the experiment, the pump/probe pulse was tuned to 776 nm to ensure the stability of the OPA output. The corresponding CARS signal appears at around 755 nm, as shown in the inserted contour map in Fig. 7. In this case, ν₄ and ν₆ can also be effectively excited, and their corresponding CARS signals appear at around 738 nm and 761 nm, respectively. ν₄ and ν₆ are coherent with ν₅, producing polarization beats with frequencies of 302 cm⁻¹ and 106 cm⁻¹, respectively. The polarization beats with a frequency of 106 cm⁻¹ appear within the first 5 ps. The time scale shown in Fig. 7 is relatively long, so that the 106 cm⁻¹ polarization beats are not obvious in the contour map. The 302 cm⁻¹ polarization beats show obvious frequency distortion in this experimental result due to undersampling, because the delay step in the experiment of ν₅ was 100 fs, corresponding to a sampling frequency of 10 THz, which is shorter than twice the signal frequency.

Fig. 7 CARS transient of ν₅ at 755 nm. The red line is the fit to the experimental data (black squares) when five components are involved. The upper subgraph shows the fitting residuals. The lower left corner shows the zooming out within 5 ps, and the inserted contour map shows the two-dimensional CARS signal around 755 nm.

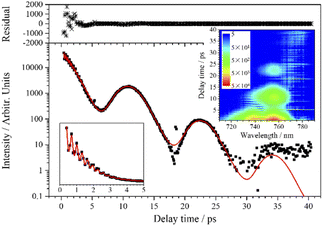
Similar to the transient of the ν₄ mode, there is also a low-frequency polarization beat pattern in the transient of ν₅. The ν₅ mode shows the longest dephasing time, and three oscillation periods can be distinguished in the experimental curve, so a more reliable analysis of the low-frequency polarization beats is allowed. As the decay of the signal spans several orders of magnitude, in order to exhibit the oscillation characteristics more clearly, the signal curve of ν₅ is plotted on a logarithmic scale, as shown in Fig. 7. The transient of ν₅ is also fitted by eqn (1). When five components are involved (j = 5), the experimental curve is well fitted, as shown in Fig. 7.

From the beats with a frequency of 106 cm⁻¹ within the first 5 ps, it can be determined that v₆ is one of the five participating components. The other four components have very close vibrational frequencies, which possibly come from the different combinations of chlorine isotopes. It is known that chlorine has two major isotopes, ³⁵Cl and ³⁷Cl, with natural abundances of 75.77% and 24.23%, respectively. Since the ³⁷Cl atom is heavier than the ³⁵Cl atom, a vibrational mode involving ³⁷Cl has lower frequency than the same mode involving ³⁵Cl. Taking into account these two isotopes, chloroform molecules have four possible combinations (CH³⁵Cl₃, CH³⁵Cl₂³⁷Cl, CH³⁵Cl³⁷Cl₂, CH³⁷Cl₃), and their proportions and the corresponding calculated vibrational frequencies of ν₅ are listed in Table 2. For comparison, the fitting parameters of the four components corresponding to the four combinations of chlorine isotopes are also listed in this table. Comparing the parameters listed in Table 2, the relative proportions of A_j are very close to the calculated proportions of the four combinations. The frequency differences between the fitted frequencies are basically consistent with the calculated frequency differences as well, and they are in good agreement with the fine structure measured under high dispersion.³¹ Therefore, it can be confirmed that the low-frequency polarization beats in the CARS transient of ν₅ originate from the coherence between the symmetric CCl₃ deformation vibrations with different combinations of chlorine isotopes.

Table 2 Upper sub-table: calculated proportions of chloroform molecules with different combinations of chlorine isotopes and the corresponding vibrational frequencies of ν₅. Lower sub-table: fitting parameters using eqn (1) when j = 5 (the parameters belonging to ν₆ mode are not listed)

	CH^35Cl3	CH^35Cl2^37Cl	CH^35Cl^37Cl2	CH^37Cl3
Calculated
Proportion (%)	43.50	41.73	13.35	1.42
Frequency of v5 (cm^−1)	364.74	361.93	359.05	356.10
Fitting parameters when j = 5
Aj (relative proportion in %)	86 (46.5)	72 (38.9)	23 (12.4)	4 (2.2)
ωj (cm^−1)	370.85	368.00	365.15	362.30

---

3.2.6. ν₆ mode (degenerate CCl₃ deformation). The excitation and detection conditions of the ν₆ mode were basically the same as those of ν₅, except that the scanning step of probe was adjusted to 20 fs, for the dephasing time of ν₆ is much shorter than that of ν₅. Under these conditions, ν₄, ν₅ and ν₆ can all be effectively excited, as shown in the insert contour map in Fig. 8. With such a time resolution, the polarization beats of 302 cm⁻¹ formed by ν₄ and ν₅ can be correctly distinguished, and polarization beats of 106 cm⁻¹ formed by ν₅ and ν₆ can be depicted more clearly.

Fig. 8 CARS transient of ν₆ at 761 nm. The red line is the fit to the experimental data (black squares) when three components are involved. The upper subgraph shows the fitting residuals. The inserted contour map shows the two-dimensional CARS signal around 761 nm.

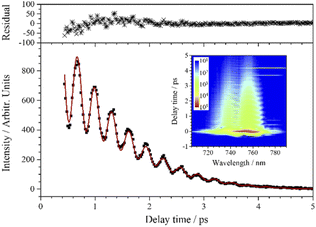
The CARS signal corresponding to ν₆ appears at around 761 nm, and the experimental curve is shown in Fig. 8. The oscillation feature mainly comes from the coherence between ν₅ and ν₆. Taking into account the chlorine isotopes, j should be taken 5 in the fitting, but the dephasing time of ν₆ is relatively short, and the low-frequency oscillation feature introduced by chlorine isotopes cannot be effectively revealed in such a short time scale. In this case, it is not necessary to introduce too many components into the fitting process, as is the case with ν₄. As a component with relatively low intensity, ν₆ contributes more to the frequency and the amplitude decay of the polarization beats, so reducing the number of types of ν₅ will not directly affect the accuracy of the fitting parameters of ν₆. As shown in Fig. 8, the experimental data are well fitted when j = 3, except that the residuals deviate a little from the zero line, which maybe result from insufficient consideration of all the combinations. It is worth noting that the fitting curve well reproduces the oscillation feature in the experimental curve, which means that the fitting parameters belonging to ν₆ are reliable.

It can be noticed that the effects of carbon and hydrogen isotopes are not observed in the present work, because the natural abundances of ¹³C and D are 1.11% and 0.016%, respectively, which are much smaller than that of ³⁷Cl.

3.3 The dephasing times of chloroform vibrational modes

In the above analysis, the transient curves of all the normal vibrational modes are fitted. The fitted dephasing times at room temperature are summarized and listed in Table 3. It is necessary to give some interpretations on the dephasing times. First, two different chlorine isotopic combinations of v₄ are involved in the fit at 724 nm and their fitted dephasing times are very close, so the mean value is listed in Table 3. Second, since the mass difference between different chlorine isotopes is small, the dephasing time differences between the different isotopic combinations of the same vibrational mode are very small, the dephasing time of ν₅ is fixed in the fit processes performed at 755 nm and 761 nm in order to reduce the number of variables. Third, ν₄, ν₅ and ν₆ participate in the transients at different selected wavelengths, their dephasing times given in Table 3 are the mean of the values obtained at different wavelengths.

Table 3 Vibrational components involved in the CARS transients at the selected signal wavelengths and the corresponding fitted dephasing times

Mode	Signal wavelength^a (nm)	Participating component^b	Dephasing time (ps)
a Signal wavelengths where the transient curves are selected to extract the vibrational dynamics.b The vibrational components that contribute to the beat patterns in the transient signals.c The dephasing time of v4 obtained by fitting the transient at 715 nm is covered in the probable range of that obtained by fitting the transient at 724 nm, so the latter is listed here.d Two v4 modes with different chlorine isotopic combinations are involved to obtain a good fit. Their dephasing times are very close, and the mean value is listed here.e Four v5 modes with different chlorine isotopic combinations are considered to participate in the CARS transient, and the mean value is listed.f Only two chlorine isotopic combinations of v5 modes are considered in the fit of the transient, and their mean value is list.
v1	540	v1, vc1	1.110 ± 0.002, 1.105 ± 0.002
v2	671	v2, vc2	0.692 ± 0.003, 0.802 ± 0.003
v3	715	v3, v4	0.22 ± 0.01, 2.5 ± 0.1^c
v4	724	v4^d	2.5 ± 0.1^d
v5	755	v5^e, v6	7.6 ± 0.2^e, 1.28 ± 0.05
v6	761	v5^f, v6	7.6 ± 0.2^f, 1.28 ± 0.05

---

4. Conclusions

Highly sensitive fs-CARS was used to systematically study the vibration of chloroform, and the transients of all the normal vibrational modes at room temperature are detected and analyzed. By fitting the high-quality CARS transients, not only precise dephasing times were obtained, but also some subtle features that were difficult to distinguish in spontaneous Raman spectra were recognized, including the overtones and combinations of some normal vibrational modes, and the vibrational energy splitting induced by chlorine isotopes. The weak subtle features do modulate the CARS transients and their intensities are enhanced by the heterodyne effect in the coupling between adjacent vibrational modes, which makes the subtle features have higher possibility to be extracted from the time-domain CARS signals. Although the complexity will increase for complex molecules under the excitation and probe with femtosecond laser pulses, femtosecond time-resolved CARS has the potential to provide subtle spectra of the species in chemical reactions and may help determine the reaction pathways.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Funding for this work was provided by the National Natural Science Foundation of China (Grant No. 21903075) and National Science and Technology Major Project (Grant No. 2017-III-0005-0030).

References

1. M. Schmitt, G. Knopp, A. Materny and W. Kiefer, J. Phys. Chem. A, 1998, 102, 4059–4065.
2. T. Chen, A. Vierheilig, P. Waltner, W. Kiefer and A. Materny, Chem. Phys. Lett., 2000, 325, 176–182.
3. T. Chen, A. Vierheilig, W. Kiefer and A. Materny, Phys. Chem. Chem. Phys., 2001, 3, 5408–5415.
4. G. Yu, Y. Zeng, W. Guo, H. Wu, G. Zhu, Z. Zheng, X. Zheng, Y. Song and Y. Yang, J. Phys. Chem. A, 2017, 121, 2565–2571.
5. M. Karavitis, R. Zadoyan and V. A. Apkarian, J. Chem. Phys., 2001, 114, 4131–4140.
6. M. Karavitis, T. Kumada, I. U. Goldschleger and V. A. Apkarian, Phys. Chem. Chem. Phys., 2005, 7, 791–796.
7. V. Senekerimyan, I. Goldschleger and V. A. Apkarian, J. Chem. Phys., 2007, 127, 214511.
8. S. Yampolsky, D. A. Fishman, S. Dey, E. Hulkko and V. A. Apkarian, Nat. Photonics, 2014, 8, 650–656.
9. J. Franken, S. A. Hambir and D. D. Dlott, AIP Conf. Proc., 1998, 429, 819–822.
10. G. Yu, Y. Zeng, W. Guo, H. Wu, G. Zhu, Z. Zheng, X. Zheng, Y. Song and Y. Yang, J. Phys. Chem. A, 2017, 121, 2565–2571.
11. N. K. Katturi, S. Dev G, N. Kommu, G. K. Podagatlapalli and V. R. Soma, Chem. Phys. Lett., 2020, 756, 137843.
12. A. Zumbusch, G. R. Holtom and X. S. Xie, Phys. Rev. Lett., 1999, 82, 4142–4145.
13. C. L. Evans and X. S. Xie, Annu. Rev. Anal. Chem., 2008, 1, 883–909.
14. R. Li, L. Wang, X. Mu, M. Chen and M. Sun, J. Biophotonics, 2019, 12, e201900119.
15. L. Cui, R. Li, T. Mu, J. Wang, W. Zhang and M. Sun, Spectrochim. Acta, Part A, 2022, 264, 120283.
16. S. Roy, P. J. Kinnius, R. P. Lucht and J. R. Gord, Opt. Commun., 2008, 281, 319–325.
17. Y. Song, H. Wu, G. Zhu, Y. Zeng, G. Yu and Y. Yang, Combust. Flame, 2022, 242, 112166.
18. P. He, S. Li, R. Fan, Y. Xia, X. Yu, Y. Yao and D. Chen, Opt. Commun., 2011, 284, 4677–4682.
19. T. Kozai, S. Yamashita, K. Hirochi, H. Miyagawa, N. Tsurumachi, S. Koshiba, S. Nakanishi and H. Itoh, Chem. Phys. Lett., 2012, 553, 26–29.
20. R. Leonhardt, W. Holzapfel, W. Zinth and W. Kaiser, Chem. Phys. Lett., 1987, 133, 373–377.
21. J. Faeder, I. Pinkas, G. Knopp, Y. Prior and D. J. Tannor, J. Chem. Phys., 2001, 115, 8440–8454.
22. A. Moradi-Araghi and M. Schwartz, J. Chem. Phys., 1978, 68, 5548–5552.
23. K. Tanabe and J. Hiraishi, Adv. Mol. Relax. Interact. Processes, 1980, 16, 281–297.
24. W. G. Rothschild and R. M. Cavagnat, J. Chem. Phys., 1992, 97, 2900–2908.
25. D. J. Ulness, M. J. Stimson, J. C. Kirkwood and A. C. Albrecht, J. Phys. Chem. A, 1997, 101, 4587–4591.
26. K. Tominaga and K. Yoshihara, J. Phys. Chem. A, 1998, 102, 4222–4228.
27. Y.-H. Wang, Y.-J. Peng, X. He, Y.-F. Song and Y.-Q. Yang, Chin. Phys. B, 2009, 18, 1463–1468.
28. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, and J. A. Pople, Gaussian 03, Gaussian, Inc., Wallingford CT, 2004, Vol. Revision E.01.
29. W. M. Dabadghao, Indian J. Phys., 1930, 5, 207–217.
30. A. Fendt, S. F. Fischer and W. Kaiser, Chem. Phys., 1981, 57, 55–64.
31. D. H. Rank and J. A. Van Horn, J. Opt. Soc. Am. B, 1946, 36, 454–459.

---