Open Access Article
Open Access ArticleConjugated donor–acceptor substituted systems involving the 1,3-indandione-derived electron accepting moieties†
Mark Sigalova,
Royi Mazor‡
a,
Arkady Ellernb,
Nina Larina‡c,
Vladimir Lokshinc and
Vladimir Khodorkovsky *c
*c
aDept. of Chemistry, Ben-Gurion Univ. of the Negev, Beer-Sheva, 84105, Israel
bChemistry Department, Iowa State University, 1711, Ames, IA 50011, USA
cAix Marseille Université, CNRS, CINaM UMR 7325, 13288, Marseille, France. E-mail: vladimir.khodorkovsky@univ-amu.fr
First published on 28th September 2022
Abstract
Conjugated donor–acceptor molecules are the focus of research owing to their unusual photo- and electro-physical properties. At the same time, several unusual features of these compounds are difficult to explain or predict. Here we present our results on the synthesis, X-ray structures and D-NMR spectra providing a deeper insight into the conjugation within the derivatives involving the 1,3-indandione-derived series of compounds with varying electron acceptor strength and conjugating bridge length. The X-ray structures show the presence of several intermolecular short contacts strongly affecting the molecular geometries. In solution, the coalescence temperatures corresponding to the rotation of the phenylamino moiety of all derivatives do not exceed 246 K indicating the unhindered rotation at room temperature. Using B3LYP/aug-cc-pVDZ, the calculated model chemistry barriers to rotation, dipole moments and first hyperpolarizabilities are within experimental error. We conclude that neglecting the electron donating properties of bridges themselves and internal rotation about the single bonds taking part in conjugation can result, for instance, in misinterpretation of their room temperature NMR spectra and overestimation of the computed molecular dipole moments by more than 5 D.
Introduction
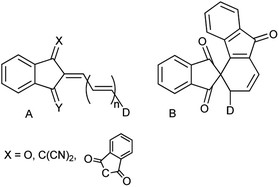
Derivatives involving the indan moiety of general structure A (Chart 1) have been a topic of numerous investigations from the very beginning of the 20th century owing to their unusual properties. The first derivative of this type (n = 0, D = p-dimethylaminophenyl) was prepared as blue crystals by condensation of the respective aldehyde with 1,3-indandione in ethanol or without a solvent.1 The initial interest in these compounds including those with X = C(CN)2, Y = O, X = Y = C(CN)2 and n = 0, 1 was related to their potential use as colorants.2 High photoconductivity of a number of 2-arylidene-1,3-indandiones (A, D = arylamino) was detected in the early 70's. Thus, the ratio of the steady-state photocurrent to the dark current of the pressed pellets of the p-dimethylaminophenyl derivative was as high as 104–105.3The latter discovery laid a start to the studies of type A analogs as potential components of organic diodes, transistors and solar cells.4 Derivatives A, as the majority of conjugated electron donor–acceptor systems, exhibit enhanced second and third order nonlinear optical properties and were extensively studied as components of optical limiting and processing materials.5 It is worth of mentioning that replacing the dicyanomethylene group in structure A (X = C(CN)2, Y = O, n = 1) by the 1,3-indandionylidene moiety (bindone derivatives) extending thus the conjugation pattern, unexpectedly afforded cyclic derivatives of type B. These weakly colored compounds exhibit photochromic behavior and in solution convert reversibly into deeply colored derivatives of type A upon irradiation by visible light up to 640 nm.6
Versatile reactivity of 2-arylidene-1,3-indandiones makes these compounds valuable synthetic precursors of several types of bioactive molecules and their analogs.7
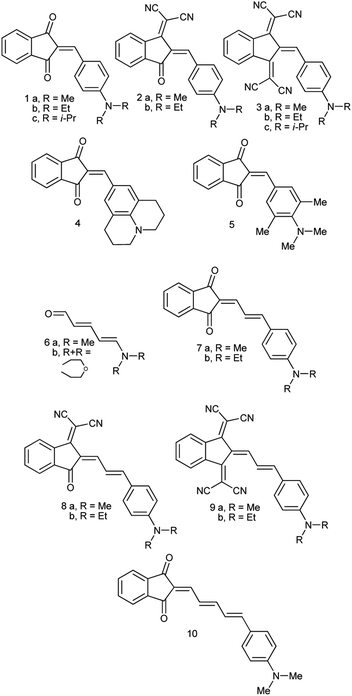
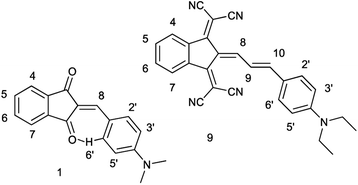
Recently, we demonstrated that the experimental barriers to rotation within push–pull π-conjugated molecules involving strong electron donors (D) and acceptors (A) can be reproduced by quantum mechanical calculations with a reasonable accuracy only when rotation of the conjugated D and A moieties is explicitly taken into account.8 Moreover, we found that this approach allows reproducing the experimental dipole moments and spectroscopic features of these type of compounds.9 Thus, we found that the best computational methods for evaluating the rotational barriers of a series of seven simple push–pull compounds and 10 barriers are B3LYP with the basis sets 6-311+G(2d,p), aug-cc-pVDZ and 6-311++G(2df,2p) (MADs 0.28, 0.26 and 0.19 kcal mol−1, respectively) and APFD. M062X/6-311++G(2df,2p) model chemistry showed MAD of 0.63 kcal mol−1 for the same set of compounds and the largest deviation of −2.19 kcal mol−1.8 A similar trend was observed in calculated dipole moments vs. experimental for a larger set of derivatives.9 The above findings imply that determination of the rotation barrier values by means of the temperature-dependent NMR spectroscopy is an indispensable way of characterizing the degree of conjugation between the D and A moieties. Here we report on preparation, solid-state structures, barriers to rotation determined by the temperature-dependent 1H-NMR spectra and the respective theoretical calculations on a series of type A derivatives (1–10, Chart 2). Derivative 6, which does not involve the indan accepting moiety, is also included as a convenient model.
Experimental
Derivatives 1a–c, 2a,b, 4, 5, 7a,b, 8a,b and 10 (see ESI† and ref. 10 for more details on these compounds) were prepared by refluxing 1,3-indandione or its dicyanomethylene derivative with the equivalent amount of the respective aldehyde in absolute ethanol. Derivative 6 was prepared according to ref. 11 and derivatives 3a,b and 9a,b according to ref. 12 New derivative 1c was isolated as red crystals, m.p. 177–178 °C (from ethanol) and 3c as almost black crystals with green luster, m.p. 240–242 °C (from acetonitrile) (see ESI† for the details). UV-Vis absorption spectra of all compounds were recorded in dichloromethane and toluene solutions in 1 mm and 10 cm cells to confirm that all tested compounds obey Lambert–Beer's Law.Reflections were measured with a Syntex Pī diffractometer with conventional X-ray tube and point detector [λ(MoKα) = 0.71069 Å, graphite monochromator, 2θ/ω scan]. The structures were solved by direct methods and refined by least-squares in anisotropic approximation for non-hydrogen atoms. All hydrogen atoms were placed to calculated positions and were refined using riding model. All calculations were carried out using SHELX-76 and SHELX-86 programs and were recalculated with Bruker APEX II Software Suite to meet modern requirements. The crystallographic data have been deposited at the Cambridge Crystallographic Data Centre. Derivative 5: CCDC 2083073; 7b: CCDC 2083072; 8b: CCDC 2083071, 2193391; 9b: CCDC 2083076; 10: CCDC 2083075.
Variable temperature 1H NMR spectra were recorded on the Bruker AMX-400 spectrometer at 400.1 MHz, in CD2Cl2 and toluene-d8 (6b) in the temperature range 190–300 K. The barriers to rotation were measured as the energy of activation at the coalescence temperature (Tc). The rate constants of exchange Kc were obtained from equation:
| Kc = πΔν/√2 |
The barriers to rotation at the coalescence temperature Tc were calculated by substitution of the Kc values into modified Eyring equation:13
| ΔG≠ = 4.57Tc{9.97 + log(Tc/Δν)}. |
All calculations were carried out using Gaussian 16 software.14 Geometry optimizations of the stationary structures were done using tight conversion criteria and Gaussian 16 defaults. The transition state (TS) geometries were found using Berny algorithm. Harmonic frequency calculations at the same level verified achieving ground states (GS) (zero imaginary frequencies) and TS (one or two imaginary frequencies) and provided the estimates of the free energies G. All calculations were performed using the default self-consistent reaction field (SCRF) model. We used B3LYP/aug-cc-pVDZ//B3LYP/aug-cc-pVDZ (denoted further DZ) and B3LYP/aug-cc-pVTZ//B3LYP/aug-cc-pVTZ (denoted TZ) as the model chemistries.
All calculations were carried out for derivatives 1a–10, R = Me, except for barriers estimation of 6b.
Results and discussion
Syntheses and structures
The synthesis of compounds 1–5 and 7–9 seems to be rather straightforward, the simplest compound 1a (Chart 2) was prepared 120 years ago by the reaction of 1,3-indandione with p-dimethylaminobenzaldehyde in ethanol or without a solvent as blue crystals with metal luster from ethanol, the melting point 99 °C, or as a scarlet solid from benzene.1 The formation of the same blue crystals with the same melting point precipitating from ethanol after a few minutes was reported later.15 However, a series of 2-benzylidene-1,3-indandiones was prepared in ethanol in the presence of piperidine affording in particular, red crystals of 1a, with the melting point 198–200 °C.16 As demonstrated later, in the presence of piperidine, in addition to 2-benzylidene-1,3-indandiones, several other compounds including bindone and derivatives involving two 1,3-indandione and one or two bindone moieties are formed.17The UV-Vis spectrum of 1a was first recorded in ethanol featuring the absorption maximum at 480 nm.18 Later, bronze-red needles of 1a with the melting point 203.5 °C (from AcOH) were prepared by heating the components at 130–140 °C without a solvent19 and in ethanol in the presence of either HCl or piperidine,20 the melting point 198–200 °C, λmax 487 nm (ethanol). Other known preparation procedures employ refluxing the components in acetic acid containing small amount of sulfuric acid affording the product with the melting point 204 °C (ref. 21) and heating in acetic anhydride at 60 °C,12 the melting point 218–220 °C (from acetic anhydride). The addition of a base as a catalyst gives rise to the formation of several by-products including bindone 11 (Chart 3). Bindone also reacts with aldehydes and derivative 1a prepared in the presence of piperidine22 was apparently contaminated with p-dimethylamino-phenylidenebindone judging by the absorption maximum at 610 nm in acetone. The authors erroneously ascribed this absorption band to the intrinsic absorption of compound 1a. A pure bindone derivative as described in ref. 23 exhibits the longest wavelength absorption maximum at 609 nm (acetone).
The confusion about the melting point and the color of compound 1a is at least in part related to its propensity to form polymorphs. Currently, three polymorphs of 1a are known: α (red-violet prisms),24 β (blue prisms with metal luster)25 and γ (bright-red thin needles)26 modifications. Each polymorph exhibits different photoconductivity3 and varying second harmonic generation activity.27 In our hands, all three polymorphs showed the melting points above 200 °C and the blue crystals of 1a prepared initially1,15 with the melting point of 99 °C either involved impurity or presented another example of disappearing polymorphs.28 The propensity of derivatives 2–10 to form polymorphs was never studied systematically, to the best of our knowledge, but it is probably also very high. For instance, single recrystallization of derivative 8b afforded a second polymorph. The selected data on the X-ray crystal structures of compounds 1–10 are collated in Table 1.
| Compd | Experimental | Calculated | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | Ref. | a | b | c | d | ||
| a This work.b TZ. | ||||||||||
| 1a | α | 1.3673 | 1.4387 | 1.3646 | 2.087 | 24 | 1.381 | 1.430 | 1.361 | 2.08 |
| A | 1.372b | 1.424 | 1.356 | 2.09 | ||||||
| α | 1.3624 | 1.4363 | 1.3577 | 2.121 | ||||||
| B | ||||||||||
| γ | 1.3791 | 1.4213 | 1.3519 | 2.219 | 25 | |||||
| β | 1.3641 | 1.4241 | 1.3513 | 2.142 | 26 | |||||
| β | 1.370 | 1.428 | 1.358 | 2.172 | 29 | |||||
| 1b | 1.355 | 1.446 | 1.362 | 2.554 | 30 | 1.382 | 1.428 | 1.362 | 2.08 | |
| 2b | 1.382 | 1.424 | 1.359 | 2.077 | 31 | 1.392 | 1.427 | 1.357 | 2.05 | |
| 3b | 1.387 | 1.422 | 1.357 | — | 32 | 1.392 | 1.425 | 1.355 | — | |
| 4 | 1.362 | 1.429 | 1.363 | 2.190 | 33 | 1.384 | 1.431 | 1.368 | 2.09 | |
| 5 | 1.347 | 1.452 | 1.428 | 2.23 | a | 1.376 | 1.438 | 1.394 | 2.09 | |
| 6b | 1.351 | 1.412 | 1.339 | — | 34 | 1.375b | 1.421 | 1.348 | — | |
| 7a | 1.365 | 1.421 | 1.361 | 2.515 | 29 | 1.379 | 1.417 | 1.364 | 2.43 | |
| 7b | 1.362 | 1.423 | 1.368 | 2.657 | a | |||||
| 8b | α | 1.372 | 1.411 | 1.367 | 2.381 | a | 1.393 | 1.411 | 1.360 | 2.27 |
| A | ||||||||||
| α | 1.374 | 1.413 | 1.363 | 2.385 | ||||||
| B | ||||||||||
| β | 1.364 | 1.427 | 1.351 | 2.344 | a | |||||
| 9b | 1.387 | 1.384 | 1.358 | — | a | 1.399 | 1.405 | 1.358 | — | |
| 10 | A | 1.347 | 1.426 | 1.384 | 2.585 | a | 1.381 | 1.415 | 1.365 | 2.46 |
| B | 1.348 | 1.390 | 1.386 | 2.615 | ||||||
| C | 1.352 | 1.397 | 1.386 | 2.531 | ||||||
| D | 1.368 | 1.424 | 1.404 | 2.591 | ||||||
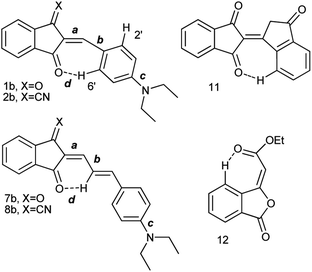
Judging from the data provided in Table 1, no conclusion on the degree of charge transfer from the electron donating dialkylamino group to the electron accepting indan moieties and the resulting bond length alternation (BLA) in the linking conjugated bridge can be driven from the solid state structures. For instance, the double bond ‘a’ (Chart 3) in molecule B in α-polymorph of 1a is 1.362 Å, in γ-polymorph 1.379 Å and the same bond in 1b is considerably shorter: 1.355 Å. The single bonds ‘b’ lengths vary between 1.421 and 1.439 Å (1a) and amounts to 1.446 Å (1b). No systematic variations in the C–N bond lengths ‘c’ are observed within all the series of compounds: for derivative 1a the bond lengths between 1.351–1.365 Å were determined and the lengths of this bond for all other derivatives except derivative 10 fit into this range. Noticeable difference in geometry is observed in the cases when more than one independent molecule is present in the cell (A and B for α 1a and 8b, A, B, C, D for 10). Thus, not depending on the acceptor strength and the bridge length within the series 1–3, 7–9, the C–N bond lengths, both experimental and calculated, in average amount to 1.36 Å. The C–N bond lengths determined for derivative 10 are the longest within the series indicating the weakest through-bond D–A interaction between the 1,3-indandione accepting and the diethylamino donating moieties. A common feature of the structure of all compounds of the series is the presence of the numerous intramolecular and intermolecular >C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–C and C
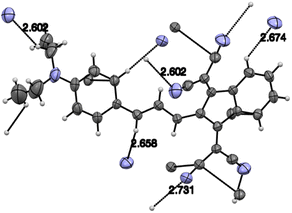
O⋯H–C and C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N⋯H–C hydrogen bonds, see for instance Fig. 1 and S23 in ESI.†
N⋯H–C hydrogen bonds, see for instance Fig. 1 and S23 in ESI.†
The degree of charge transfer from the electron donating toward the accepting moieties can be estimated by the degree of –N< group pyramidalization. Thus, the dihedral angles for the calculated GS structures of derivatives 1–3, 7–10 are practically 0° evidencing the complete charge transfer and about 3.4° in derivative 6a. Thus, the dihedral angles for the calculated GS structures of derivatives 1–3, 7–10 are practically 0° evidencing the complete charge transfer, and about 3.4° in derivative 6a.
The optimized GS geometries of derivatives 1–10 are generally in agreement with the X-ray structures. The observed –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H hydrogen bonds are also reproduced by the calculations. The formal double bond ‘a’ adjacent directly to the accepting moiety is the most sensitive and becomes longer than the bond ‘b’ in derivative 9. However, no bond length alternation is observed within the bridge: the central double bonds in 7–9 are about 1.38 and the C–Ar single bonds are about 1.43 Å. In other words, the intramolecular charge transfer occurs mostly from the bridge, which is a part of the donating moiety along with the conjugated –C6H4–NR2 unit toward the accepting moiety.
O⋯H hydrogen bonds are also reproduced by the calculations. The formal double bond ‘a’ adjacent directly to the accepting moiety is the most sensitive and becomes longer than the bond ‘b’ in derivative 9. However, no bond length alternation is observed within the bridge: the central double bonds in 7–9 are about 1.38 and the C–Ar single bonds are about 1.43 Å. In other words, the intramolecular charge transfer occurs mostly from the bridge, which is a part of the donating moiety along with the conjugated –C6H4–NR2 unit toward the accepting moiety.
1H-NMR spectra and barriers to internal rotation
The room temperature (RT) 1H-NMR spectra of all derivatives of the series are shown in Fig. 2, 3, S1–S21 in the ESI.† Neither the chemical shifts nor the signal splitting patterns of the 1H-NMR spectra recorded for all compounds of the series at room temperature correspond to the expected. Thus, the aromatic protons in compounds 11 and 12 (Chart 3) involved in the C–H⋯O hydrogen bonds of similar geometries according to their X-ray structures, are strongly low-field shifted (above 9 ppm).35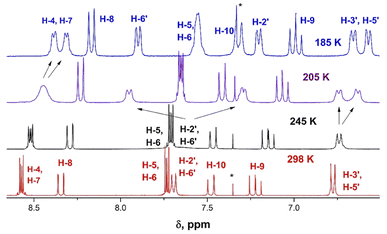 | ||
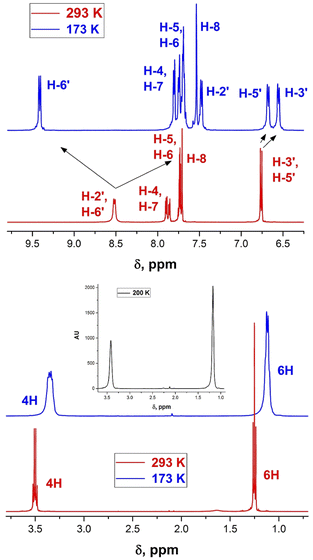
| Fig. 3 Changes in the 1H-NMR spectra of derivative 9b upon varying temperature from 298 (red) to 185 K (blue). | ||
Whereas the similar geometrical features are observed in asymmetrical Γ-shaped solid derivatives 1, 2, 4, 5, 7, 8 and 10, no low-field shifted signals are visible. For instance, the RT spectrum of 1b exhibits a doublet of both H-2′ and H-6′ protons (Chart 4) at 8.52 ppm and a doublet of two protons H-3′, and H-5′ in the o-positions to the 4′-diethylamino substituent at 6.75 ppm (Fig. 2), suggesting a symmetrical configuration of the phenyl group.
This feature evidences unrestricted rotation of the phenyl group in 1b at RT. Indeed, at low temperature the signal of H-6′ is shifted to 9.48 ppm, that of H-2′ appears at 7.5 ppm and the signals of the protons at o-positions to the 4′-diethylamino group are also split and appear at 6.7 and 6.6 ppm.
The 1H NMR spectrum of 9b at 298 K consists of three groups of signals: two doublets at 7.69 and 6.78 ppm (J = 9.0 Hz) of aromatic protons H-2′, H-6′, and H-3′, H-5′ respectively; three signals of the bridge olefin protons at 8.35 ppm (d, J = 12.7 Hz, H-8); 7.48 ppm (d, J = 7.48, H-10) and 7.22 ppm (dd, H-9); two multiplets of indandione aromatic protons forming AA′BB′ spin system at 8.57 ppm (H-4, H-7) and at 7.73 ppm (H-5, H-6). The signals of the first and third groups undergo considerable changes in the line shape with decreasing temperature.
The doublet signal of H-2′, H6′ at 7.69 ppm practically disappears at the coalescence temperature of 245 K and reappears as two doublets with a further decrease in temperature (7.90 and 7.21 ppm at 185 K). Similar, but smaller changes shows the doublet of H-3′, H-5′ which on cooling coalesces and splits into two doublets at 6.67 and 6.58 ppm. These changes reflect the slowing rotation about C–C(Ar) bond and are associated with the different influence of dicyanomethylene groups on the chemical shifts in each proton pair (H-2′ and H-6′, and H-3′ and H-5′), respectively.
The signal of H-4, H-7 under cooling sample broadens, coalesces and splits into two doublets at 8.39 and 8.33 ppm, while the protons H-5 and H-6 that are more distant from 2-substituent experience only a slight broadening. This behavior is explained by slow rotation about the bridge double bond adjacent to bis(dicyanomethylene)indan moiety.
Recently we demonstrated that quantum-mechanical calculations of the barriers to rotation in the D–A conjugated systems should take into account that internal rotations about the hindered conjugated bonds are not independent.8 The weighted average of the barrier heights can be derived from potential energy scans or, simpler, using the extreme energy values calculated for the transition states upon rotation the molecular moieties by about 90°, 180° and 270°. This method provides a reasonable reproduction of the experimental barrier heights, at least in the cases when the force hindering free rotation stems mainly from conjugation between the D and A moieties.8 The barriers to rotation in conjugated systems depend on the relative D and A strengths and the nature of conjugated bridge. Thus, for the aromatic derivatives (p-phenylene bridge) free rotation can typically be observed by D-NMR spectroscopy above the coalescence temperature: 170 K (ΔG≠ about 8.5 kcal mol−1) and 210 K (ΔG≠ about 11 kcal mol−1). For DMF, as an example of a D–A molecule lacking a bridge, free rotation of the amino group is observed above 420 K and in N,N-dimethylaminoacrolein at 310 K in toluene (ΔG≠ about 15.5 kcal mol−1) (see ref. 8, 9 and references therein).
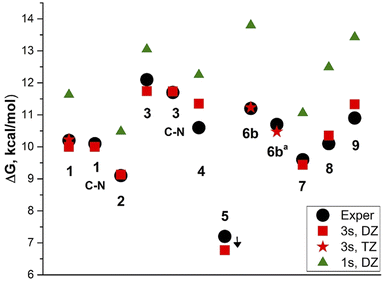
We calculated the barriers to rotation using the three-state (3s) approximation8 and B3LYP/aug-cc-pVDZ model chemistry, reproducing the experimental values very well (Table 2 and Fig. 4).
| Compd | kc (s−1) | Tc (K) | ΔG≠ | Calc. ΔG≠ | Tc (K) | ΔG≠ | Calc. ΔG≠ |
|---|---|---|---|---|---|---|---|
| C–CAr | C–CAr | C–N | C–N | ||||
a Extrapolated to RT.b 2,6-H, 233 K, ΔG≠ = 10.0, 3,5-H, 213 K, ΔG≠ = 10.2.c ΔG≠ = 10.23 at TZ.d 2,6-H, 213 K, ΔG≠ = 9.2, 3,5-H, 195 K, ΔG≠ = 9.4.e 2,6-H, 246 K, ΔG≠ = 11.7.f TZ//TZ.g In toluene.h Calculated ΔG≠ = 9.93 (![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–CH), 14.75 (HC–CH). C–CH), 14.75 (HC–CH). |
|||||||
| 1b | 2150 | 235 | 10.2a,b | 10.00c | |||
| 1c | 1690 | 233 | 10.1 | — | 204 | 9.4 | 9.12 |
| 2b | 1887 | 195 | 9.1a,d | 9.13 | 9.89 | ||
| 3b | 221 | 246 | 12.1a,e | 11.74 | 10.51 | ||
| 3c | 195 | 245 | 11.7 | 11.46 | 210 | 9.6 | 10.11 |
| 4 | 2259 | 248 | 10.6 | 9.98 | |||
| 5 | — | <180 | <7.2 | 6.77 | |||
| 6b | — | — | — | 225 | 11.2 | 11.37f | |
| 6bg | 223 | 10.7 | 10.47f | ||||
| 7b | 722 | 215 | 9.61 | 9.44 | — | — | 8.34 |
| 8b | 570 | 225 | 10.11 | 10.35 | — | — | 9.14 |
| 9b | 770 | 242 | 10.9 | 11.33h | — | 10.09 | |
The exception is derivative 4 for which the rotation barrier about the C–C bond is overestimated by 0.75 kcal mol−1. Derivative 4 involves four CH2 groups scaffold (julolidine moiety), the vibrations of which, passing through the coplanar transition states, cannot be easily modelled by calculations. Using the coordinates for the vibrational average structures at 248 K (Sa) from frequency calculations with anharmonic corrections for both GS and TSC–C we get ΔG≠ = 9.98 kcal mol−1. This value underestimates the experimental by 0.62 kcal mol−1. Carrying out these calculations with TZ basis set is too expensive.
Using the one-state (1s) approximation systematically overestimates the barrier values by 1–2.5 kcal mol−1. The experimental barrier for derivative 5 cannot be determined, as it requires lowering the temperature under 170 K.
Derivatives 6–8 involve three rotors: CH–CH, CH–CAr and C–N and derivative 9 involves four. The barrier height corrections using the weighted-average values were done separately for each couple of barriers corresponding to the coalescence temperature or RT as shown in Fig. S24, ESI.† Noteworthy, the effect of increasing the electron accepting strength of the A substituent is apparently a short-range. The lowest rotation barrier is found to be about the formal double bond ‘a’ in derivative 9: ΔG≠ = 9.93 kcal mol−1 (calculated), broadening the 1H-NMR signals of protons H-4–H-7 from 205 to 185 K. It is also in agreement with the calculated and experimental ‘a’ bond length compared with the ‘b’ bond length.
The experimental barriers to rotation about C–CAr and C–N bonds do not exceed 12.1 kcal mol−1 corresponding to the coalescence temperatures (Tc) below 246 K. It means that several respective rotamers are present in solution at RT at which the dipole moments and hyperpolarizabilities were determined.
Dipole moments and first static hyperpolarizabilities
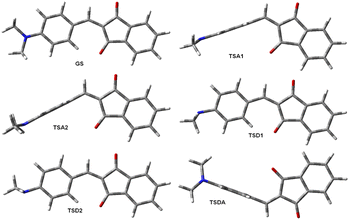
The measurement of the molecular dipole moments as a function of temperature is one of the earliest methods for the internal rotation studies.36 This approach did not find wide application owing to the technical difficulties related to the low barriers to rotation determination of which required very low temperatures.The major part of experiments on the dipole moments and hyperpolarizabilities determination has been carried out at RT. As noted before, the rotation barriers are relatively low for all compounds under discussion here and averaging the dipole moments requires calculating the dipole moments of all possible rotamers that can exist at RT. There are six unique rotamers for derivative 1a shown in Fig. 5.
Taking into account that rotation of the phenylamino group by 180° for conformations GS and TSDA produces the same conformation, the average dipole moment of 1a is (2*DMGS + DMTSA1 + DMTSA2 + DMTSD1 + DMTSD2 + 2*DMTSDA)/8 = 3.79 D. The same averaging produces the average zero-frequency hyperpolarizability of 42.1 × 10−30 esu and μβ0 169.5 × 10−48 esu. These values in a good agreement with the experimental values of μ 3.74 D and β0 37.9 × 10−30 esu in chloroform32 and μβ0 = 130 × 1048 esu of in dichloromethane.38 The calculations using TZ basis set improve the agreement: μ 3.75 D and β0 40.8 × 10−30 esu and μβ0 153 × 1048 esu (Table 3). The structures of the unique rotamers and the averaging patterns for 6a and 7a are given in the ESI, Fig. S25 and S26.† The calculated dipole moments of each rotamer are collated in Tables S10–S12 (ESI).†
Calculations of the dipole moments neglecting internal rotation, i.e., using the optimized GS geometries (one-state approximation) strongly overestimate the electrical properties as shown in Table 3. For longer conjugated D–A substituted molecules the error in estimating the dipole moments can exceed 5 D. For example, the calculated β0 for the GS of derivative 7 is more than three times larger than the experimental (345.9 × 10−30 vs. 110 × 10−30 esu) and μβ0 exceeds the experimental by about 300 times. Using the recommended for this type of calculations M062X functional40 with the same basis set does not improve considerably the resulting dipole moment values (Table 3).
It should be mentioned that the dipole moments of 1 and 7 were determined in chloroform, a solvent well known to be a proton donor strongly interacting with amines: Cl3C–H⋯NR3.41 At the same time, the measurements carried out in solutions of 7 in dichloromethane38 afforded practically the same values of β0 as reported in chloroform (Table 3). Indeed, the rotamers of 1 and 7 as well as their analogues 2, 3, 8 and 9 with the largest CAr–N< dihedral angles are those with the amino groups rotated 90° and 270° (like TSD1 and TSD2, Fig. 5); these angles amount to about 29.5°. The experimental42 (C–N: 1.451 Å, C–N–C: 110.9°) and calculated (C–N: 1.455 Å, C–N–C: 111.5°, –N< 32.08°, TZ, in chloroform) geometries of trimethylamine indicate that the most basic rotamers of 1–3 and 7–9 are weaker proton acceptor. In the case of derivative 6a, the respective optimized at the same level of theory in chloroform transition states geometries gave the following values: ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–N: 1.424 Å, C–N–C: 111.1°, –N< 33.0°, close to the geometry of trimethylamine.
C–N: 1.424 Å, C–N–C: 111.1°, –N< 33.0°, close to the geometry of trimethylamine.
The dipole moment calculated for 6a in chloroform is expectedly larger than in benzene: 8.70 D. These observations can account for the doubtful dipole moment values reported in a paper on the nonlinear optical properties (NLO) properties of D–A polyenes of the type D(CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH)nA.43 The authors were apparently unaware of ref. 39 that provided accurate measurements in benzene for this series: 3.86 ± 0.01 D, n = 0; 6.24 ± 0.02 D, n = 1; 7.67 ± 0.05 D, n = 2; 8.24 ± 0.02 D, n = 3 and 8.50 ± 0.04 D, n = 4. No experimental details were provided in ref. 43 for measurements in chloroform, the results provided in a table were: 3.5 D, n = 0; 6.3 D, n = 1; 6.5 D, n = 2; 6.9 D, n = 3. The results for derivatives n = 0 (DMF) and n = 1 (N,N-dimethylaminoacrolein) are acceptable and do not contradict the values determined in ref. 43 and calculated by us previously.9 The dipole moments of derivatives n = 2 and n = 3 are underestimated at least by 1.2 and 1.3 D, probably, as a result of specific interaction with the solvent, namely the H-bonds formation between strongly basic TSC–N rotamers.§
CH)nA.43 The authors were apparently unaware of ref. 39 that provided accurate measurements in benzene for this series: 3.86 ± 0.01 D, n = 0; 6.24 ± 0.02 D, n = 1; 7.67 ± 0.05 D, n = 2; 8.24 ± 0.02 D, n = 3 and 8.50 ± 0.04 D, n = 4. No experimental details were provided in ref. 43 for measurements in chloroform, the results provided in a table were: 3.5 D, n = 0; 6.3 D, n = 1; 6.5 D, n = 2; 6.9 D, n = 3. The results for derivatives n = 0 (DMF) and n = 1 (N,N-dimethylaminoacrolein) are acceptable and do not contradict the values determined in ref. 43 and calculated by us previously.9 The dipole moments of derivatives n = 2 and n = 3 are underestimated at least by 1.2 and 1.3 D, probably, as a result of specific interaction with the solvent, namely the H-bonds formation between strongly basic TSC–N rotamers.§
Averaging of the calculated values is also useful for interpretation of the NMR spectra. Thus, as mentioned above, the RT 1H-NMR spectrum of 1b (Fig. 2) does not correspond to the spectrum calculated using the GS structure and the signals of H2′ and H6′ appear as a doublet at 8.52 ppm at RT. The averaged calculated chemical shift of both these protons is 8.49 ppm.
Conclusions
Electron D–A conjugated systems (push–pull molecules) represent a very special class of organic compounds. Thus, their identities in the solid state cannot unequivocally be established by the usual means (crystal color, melting points). In solution at room temperature the NMR spectra are also confusing and cannot be reproduced by simple modeling or quantum mechanical calculations considering only their ground states. The experiments in solution aiming at determination of electrical properties (such as dipole moments, etc.) should be accompanied by verification of the absence of specific interactions with the solvent or self-aggregation.We conclude that the temperature-dependent D-NMR spectroscopy is indeed indispensable for investigating and designing such systems. The properties of push–pull molecules can be adequately described when the degree of conjugation and the temperature influence on the possibility of free or hindered rotation is taken into account. The barriers to rotation determined by the D-NMR technique or evaluated using quantum mechanical calculations possess considerably larger values span than the bond length variations. This technique coupled with calculations also allows to determine the nature of free rotating moieties at RT needed to interpret and evaluate the results of measurements traditionally carried out at this temperature, such as electron absorption, fluorescence, IR spectra, dipole moments and others.
We also conclude that using B3LYP/aug-cc-pVDZ model chemistry is a good compromise for evaluating the rotational barriers, dipole moments and NLO properties of larger D–A conjugated molecules involving stronger electron donating and acceptor moieties than investigated previously.
In particular, we find that the conjugated bridge linking the strong D and A moieties cannot be considered as an independent part of such molecules serving only to provide intramolecular charge transfer from D to A, as in the presence of strong accepting substituents the bridge behaves rather as a part of the donating moiety. A stronger acceptor can indeed diminish the linear and nonlinear response by decreasing barriers to rotation of the nearest bonds.
The interpretation of electronic absorption spectra by quantum mechanical calculations requires the same approach taking into account the temperature of the experiments as demonstrated on the example of nitrobenzene.9 The results of these studies involving the D–A conjugated molecules will be published elsewhere.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Centre National de la Recherche Scientifique (CNRS) for financial support. This work was supported by the computing facilities of CRCMM, ‘Centre Régional de Compétences en Modélisation Moléculaire de Marseille. The authors are thankful to Dr G. Berkovic and Dr Z. Kotler for the fruitful discussions.Notes and references
- E. Noelting and H. Blum, Chem. Ber., 1901, 34, 2467 CrossRef CAS.
- (a) R. Merkx, Bull. Soc. Chim. Belg., 1949, 58, 460 CrossRef; (b) G. Irick, Jr. and J. M. Straley, Text. Chem. Color., 1969, 1, 178 Search PubMed; (c) K. A. Bello, L. Cheng and J. Griffiths, J. Chem. Soc., Perkin Trans. 2, 1987, 815 RSC; (d) K. A. Bello, C. M. O. A. Martins and I. K. Adamu, J. Soc. Dyers Colour., 1994, 110, 238 CrossRef CAS.
- N. A. Dimond and T. K. Mukherjee, Discuss. Faraday Soc., 1971, 51, 102 RSC.
- (a) A. Mishra and P. Bäuerle, Angew. Chem., Int. Ed. Engl., 2012, 51, 2020 CrossRef CAS PubMed; (b) S. Jursenas, V. Gulbinas, T. Gustavsson, S. Pommeret, J.-C. Mialocq and L. Valkunas, Chem. Phys., 2002, 275, 231 CrossRef CAS; (c) K. N. Winzenberg, P. Kemppinen, F. H. Scholes, G. E. Collis, Y. Shu, T. B. Singh, A. Bilic, C. M. Forsyth and S. E. Watkins, Chem. Commun., 2013, 49, 6307 RSC; (d) A. Arjona-Esteban, J. Krumrain, A. Liess, M. Stolte, L. Huang, D. Schmidt, V. Stepanenko, M. Gsänger, D. Hertel, K. Meerholz and F. Würthner, J. Am. Chem. Soc., 2015, 137, 13524 CrossRef CAS PubMed; (e) Y. Hao, X. Yang, J. Cong, H. Tian, A. Hagfeldt and L. Sun, Chem. Commun., 2009, 4031 RSC; (f) X. Chen, Y. Sun, Z. Wang, H. Gao, Z. Lin, X. Ke, T. He, S. Yin, Y. Chen, Q. Zhang and H. Qiu, Dyes Pigm., 2018, 158, 445 CrossRef CAS.
- (a) R. Matsushima, M. Tatemura and N. Okamoto, J. Mater. Chem., 1992, 2, 507 RSC; (b) H. Schwartz, R. Mazor, V. Khodorkovsky, L. Shapiro, J. T. Klug, E. Kovalev, G. Meshulam, G. Berkovic, Z. Kotler and S. Efrima, J. Phys. Chem. B, 2001, 105, 5914 CrossRef CAS; (c) S. Acharya, P. Krief, V. Khodorkovsky, Z. Kotler, G. Berkovic, J. T. Klug and S. Efrima, New J. Chem., 2005, 29, 1049 RSC; (d) G. Seniutinas, R. Tomasiunas, R. Czaplicki, B. Sahraoui, M. Daskeviciene, V. Getautis and Z. Balevicius, Dyes Pigm., 2012, 95, 33 CrossRef CAS; (e) A. Bundulis, E. Nitiss, I. Mihailovs, J. Busenbergs and M. Rutkis, J. Phys. Chem. C, 2016, 120, 27515 CrossRef CAS; (f) Y. Qi, H. Li, J. P. Fouassier, J. Lalevee and J. T. Sheridan, Appl. Opt., 2014, 53, 1052 CrossRef CAS PubMed; (g) Y. Liu, Y. Sun, M. Li, H. Feng, W. Ni, H. Zhang, X. Wan and Y. Chen, RSC Adv., 2018, 8, 4867 RSC; (h) F. Lin, K. Jiang, W. Kaminsky, Z. Zhu and A. K. Jen, J. Am. Chem. Soc., 2020, 142, 15246 CrossRef CAS; (i) A. Nowak-Król, R. Wagener, F. Kraus, A. Mishra, P. Bäuerleb and F. Würthner, Org. Chem. Front., 2016, 3, 545 RSC; (j) S. Fusco, M. Barra, L. Gontrani, M. Bonomo, F. Chianese, S. Galliano, R. Centore, A. Cassinese, M. Carbone and A. Carella, Chem.–Eur. J., 2022, 28, e202104552 CrossRef CAS PubMed.
- (a) B. Zinger, P. Schaer, G. Berkovic, G. Meshulam, Z. Kotler, L. Shapiro, R. Mazor and V. Khodorkovsky, Proc. SPIE, 1997, 3135, 71 CrossRef CAS; (b) L. Bekere, N. Larina, V. Lokshin, A. Ellern, M. Sigalov and V. Khodorkovsky, New J. Chem., 2016, 40, 6554 RSC; (c) V. Lokshin, L. Bekere and V. Khodorkovsky, Dyes Pigm., 2017, 145, 570 CrossRef CAS.
- (a) K. Rehse and F. Brandt, Arch. Pharm., 1984, 317, 54 CrossRef CAS; (b) A. Patel, D. Giles, G. Basavarajaswamy, C. Sreedhar and A. Patel, Med. Chem. Res., 2012, 21, 4403 CrossRef CAS; (c) S. Meena, D. Shankar, K. V. Ramseshu, D. Giles, M. S. Prakash and S. Venkataraman, Indian J. Chem., Sect. B: Org. Chem. Incl. Med. Chem., 2006, 45, 1572 Search PubMed; (d) B. Bano, Kanwal, K. M. Khan, F. Begum, M. A. Lodhi, U. Salar, R. Khalil, Z. Ul-Haq and S. Perveen, Bioorg. Chem., 2018, 81, 658 CrossRef CAS PubMed; (e) A. F. C. D. S. Oliveira, A. P. M. de Souza, A. S. de Oliveira, M. L. da Silva, F. M. de Oliveira, E. G. Santos, Í. E. P. da Silva, R. S. Ferreira, F. S. Villela, F. T. Martins, D. H. S. Leal, B. G. Vaz, R. R. Teixeira and S. O. de Paula, Eur. J. Med. Chem., 2018, 149, 98 CrossRef CAS; (f) S. Das, New J. Chem., 2020, 44, 17148 RSC; (g) V. Lokshin and V. Khodorkovsky, Tetrahedron, 2018, 74, 418 CrossRef CAS; (h) V. Lokshin, H. Clavier and V. Khodorkovsky, New J. Chem., 2020, 14373 RSC.
- M. Sigalov, V. Lokshin, N. Larina and V. Khodorkovsky, Phys. Chem. Chem. Phys., 2020, 22, 1214 RSC.
- V. Lokshin, M. Sigalov, N. Larina and V. Khodorkovsky, RSC Adv., 2021, 11, 934 RSC.
- R. Mazor, New strong electron acceptors: potential components for advanced materials, Ph. D. Thesis, Ben-Gurion University of the Negev, 2003 Search PubMed.
- L. Finsen, J. Becher, O. Buchard and R. R. Koganty, Acta Chem. Scand., Ser. B, 1980, 34, 513 CrossRef.
- K. A. Bello, C. M. O. A. Martins and I. K. Adamu, J. Soc. Dyers Colour., 1994, 110, 238 CrossRef CAS.
- M. Oki, Applications of Dynamic NMR Spectroscopy to Organic Chemistry Vol. 4 of Methods in Stereochemical Analysis, VCH Verlags, Deerfield Beach, Basel, Winheim, 1985, p. 423 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.02, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- A. Zaki, J. Chem. Soc., 1930, 1078 RSC.
- M. V. Ionescu, Bull. Soc. Chim. Fr., 1930, 47(4), 210 CAS.
- M. V. Ionescu and H. Slusanschi, Bull. Soc. Chim. Fr., 1932, 51(4), 1109 CAS.
- D. Radulescu and A. Georgescu, Z. Physiol. Chem., 1929, 5BB, 189 CrossRef.
- V. Petrov, J. Saper and B. Sturgeon, J. Chem. Soc., 1949, 2134 RSC.
- R. Merckx, Bull. Soc. Chim. Belg., 1949, 58, 460 CrossRef CAS.
- I. Agranat, R. M. J. Loewenstein and E. D. Bergmann, Isr. J. Chem., 1969, 7, 89 CrossRef CAS.
- M.-A. Tehfe, F. Dumur, B. Graff, D. Gigmes, J.-P. Fouassier and J. Lalevee, Macromolecules, 2013, 46, 3332 CrossRef CAS.
- G. Irick, Jr., J. Chem. Eng. Data, 1971, 16, 118 CrossRef.
- N. S. Magomedova and Z. V. Zvonkova, Kristallografiya, 1978, 23, 281 (Sov. Phys. Crystallogr., 1978, 23, 155) CAS.
- N. S. Magomedova and Z. V. Zvonkova, Kristallografiya, 1980, 25, 1183 (Sov. Phys. Crystallogr., 1980, 25, 677) CAS.
- N. S. Magomedova, Z. V. Zvonkova, M. G. Neigauz and L. A. Novakovskaya, Kristallografiya, 1980, 25, 400 (Sov. Phys. Crystallogr., 1980, 25, 230) CAS.
- R. Matsushima, M. Tatemura and N. Okamoto, J. Mater. Chem., 1992, 2, 507 RSC.
- J. D. Dunitz and J. Bernstein, Acc. Chem. Res., 1995, 28, 193 CrossRef CAS.
- G. Bogdanov, J. P. Tillotson and T. Timofeeva, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2019, 75, 1595 CrossRef CAS.
- V. Khodorkovsky, R. A. Mazor and A. Ellern, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1996, 52, 2878 CrossRef.
- A. Arjona-Esteban, J. Krumrain, A. Liess, M. Stolte, L. Huang, D. Schmidt, V. Stepanenko, M. Gsänger, D. Hertel, K. Meerholz and F. Würthner, J. Am. Chem. Soc., 2015, 137, 13524 CrossRef CAS.
- A. Capobianco, A. Esposito, T. Caruso, F. Borbone, A. Carella, R. Centore and A. Peluso, Eur. J. Org. Chem., 2012, 2012, 2980 CrossRef CAS.
- V. K. Belyakov, P. J. Pastors and A. Tokmakov, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2008, 64, o1200 CrossRef PubMed.
- S. Kulpe and B. Schulz, Krist. Tech., 1976, 11, 707 CrossRef CAS.
- (a) M. Sigalov, A. Vashchenko and V. Khodorkovsky, J. Org. Chem., 2005, 70, 92 CrossRef CAS; (b) M. Sigalov, P. Krief, L. Shapiro and V. Khodorkovsky, Eur. J. Org. Chem., 2008, 2008, 673 CrossRef.
- (a) S. Misushima, Structure of Molecules and Internal Rotation, Academic Press, N. Y., 1954 Search PubMed; (b) E. Bright Wilson, Jr., The problem of barriers to internal rotation in molecules, in Adv. Chem. Phys., vol. 2, ed. I. Prigogine, 1959, p. 367 Search PubMed.
- C. R. Moylan, R. J. Twieg, V. Y. Lee, S. A. Swanson, K. M. Betterton and R. D. Miller, J. Am. Chem. Soc., 1993, 115, 12599 CrossRef CAS.
- (a) G. Meshulam, G. Berkovic, Z. Kotler, A. Ben-Asuly, R. Mazor, L. Shapiro and V. Khodorkovsky, Synth. Met., 2000, 115, 219 CrossRef CAS; (b) G. Meshulam, G. Berkovic, Z. Kotler and A. Sa’ar, Rev. Sci. Instrum., 2000, 71, 3490 CrossRef CAS.
- M. H. Hutchinson and L. E. Sutton, J. Chem. Soc. (Res.), 1958, 4382 RSC.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 Search PubMed.
- (a) K. F. Wong and S. Ng, J. Chem. Soc., Faraday Trans. 2, 1975, 71, 622 RSC; (b) A. T. Lemley, Hydrogen bonding phenomena, in The chemistry of nonaqueous solvents, ed.:J. J. Lagovski, vol. IV, AP, N. Y., 1976, p. 19 Search PubMed.
- (a) B. Beagley and T. G. Hewitt, Trans. Faraday Soc., 1968, 64, 2561 RSC; (b) J. E. Wollrab and V. W. Laurie, J. Chem. Phys., 1969, 51, 1580 CrossRef CAS.
- S. R. Marder, C. B. Gorman, B. G. Tieman and L.-T. Cheng, J. Am. Chem. Soc., 1993, 115, 3006 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: NMR spectra, frequency calculation results, short intermolecular distances, dipole moments of rotamers and tables of Cartesian coordinates for optimized structures. CCDC 2083071, 2083072, 2083073, 2083075, 2083076 and 2193391. For ESI and crystallographic data in CIF or other electronic format see https://doi.org/10.1039/d2ra05335g |
| ‡ Present addresses: R. M.: Dept HERA, ICL Group, Beer Sheva, 84101, Israel; N. L.: Thales DIS France SAS, Avenue du Pic de Bertagne, 13420 Gémenos, France. |
| § We also noticed that derivative 6b in chloroform solutions exhibits noticeable deviations from the Lambert–Beer's Law. |
| This journal is © The Royal Society of Chemistry 2022 |