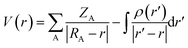Role of O–H⋯O/S conventional hydrogen bonds in considerable C_sp²–H blue-shift in the binary systems of acetaldehyde and thioacetaldehyde with substituted carboxylic and thiocarboxylic acids

Abstract

Stable binary complexes of RCZOH⋯CH₃CHZ (R = CH₃, H, F; Z = O, S) are due to contributions from the O–H⋯O/S and C_sp²–H⋯O/S hydrogen bonds. The strength of C_sp²/O–H⋯O is 1.5 to 2 times greater than that of the C_sp²/O–H⋯S bond. The substitution of H(C_sp²) of HCZOH by CH₃ causes a decrease in complex stability, while the opposite trend occurs for the F atom. A very large red shift of the O–H stretching frequency in O–H⋯O/S bonds was observed. A surprising C_sp²–H blue shift up to 104.5 cm⁻¹ was observed for the first time. It is found that the presence of O–H⋯O/S hydrogen bonds and a decisive role of intramolecular hyperconjugation interactions in the complex cause a significant blue shift of the C_sp²–H covalent bonds. A striking role of O compared to the S atom in determining the blue shift of C_sp²–H stretching vibration and stability of binary complexes is proposed. The obtained results show that the ratio of deprotonation enthalpy and proton affinity could be considered as an index for the classification of the non-conventional hydrogen bond. SAPT2+ results show that the strength of RCSOH⋯CH₃CHS complexes is dominated by electrostatic and induction energies, while a larger contribution to the stability of remaining complexes is detected for the electrostatic component.

---

1. Introduction

Despite exhibiting much lower energy and directionality in comparison to covalent bonds, non-covalent interactions still demonstrate a dominant role owing to their ubiquity in nature and the contribution to the cohesion of chemical systems. The most significant type in non-covalent interactions is the hydrogen bond, which is of great importance in chemistry, biochemistry, and especially in biological systems: DNA, RNA, and proteins.^1–3 The A–H⋯B conventional hydrogen bond is a weak non-covalent interaction, in which A and B are highly electronegative elements, and B usually contains a region of high electron density (a lone pair, a negative charge, or a π-system). Conventional hydrogen bonds (so-called red-shifting hydrogen bonds) characterized by A–H bond elongation along with a decrease in its stretching vibration are well-known, and this frequency shift is due to electrostatic attraction between the H atom and B atom.⁴ The red shift of the A–H stretching vibrational frequency of the A–H bond is proposed from the n(B) → σ*(A–H) intermolecular electron density transfer overcoming the increase in s-character and the A–H bond polarization.⁵ Nonconventional hydrogen bonds with an A–H contraction associated with an increase in its stretching vibration were discovered in complexes of fluoroparaffins with pyridine, acetone, and dioxane by Trudeau et al. in 1980.⁶ Such a nonconventional hydrogen bond is named a blue-shifting hydrogen bond.

Several hypotheses from both theoretical and experimental research works have been proposed to unravel the phenomenon of blue-shifting hydrogen bonds,^2,7–13 however, it has not been deeply understood yet. For instance, Wu et al. indicated that the reason for the shift of A–H stretching vibration arises from the short-range hyperconjugative interaction of n(B) → σ*(A–H) electron density transfer in competition with the long-range electrostatic interaction of the A–H bond and B atom.¹⁴ In another report, based on different physical components of interaction energy, Mao et al. suggested that an enhancement of A–H stretching vibration is encouraged by Pauli repulsion, whereas a combination of electrostatic and dispersion forces causes diminishing of A–H stretching vibration.⁷ The electrostatic and Pauli repulsion energies dominating the sum of polarization and charge transfer interaction define an A–H bond contraction and an increase in its stretching frequency.¹³ An interesting approach that notices the inherent characteristics of proton donor and acceptor monomers to unfold the origin of blue-shifting hydrogen bonds has been proposed.^15–18

The blue-shifting hydrogen bond is mainly discovered in complexes involving C–H bond acting as a proton donor, such as in C–H⋯O/N/halogen/π hydrogen bonds, which are significant due to their abundance and diversity in nature.^19–29 Studies were then further expanded in characterizing the blue-shifting hydrogen bond based on the different hybridization types of the C atom in the C–H bond.^30–32 It is noteworthy that for the demand for elucidating the characteristics and nature of the blue-shifting hydrogen bond, the non-conventional hydrogen bond involving the C_sp³–H bond as a proton donor has been experimentally and theoretically examined much more than the C_sp²–H and C_sp–H one. A few publications suggested that for the same proton acceptor, the lower the polarity of the proton donor, the larger the blue-shift of stretching frequency, and vice versa.^33–35 Consequently, most reports have focused on the C_sp³–H bond with its lowest polarity as compared to both the C_sp²–H and C_sp–H ones. Indeed, in 1999, Hobza et al. used double-resonance infrared ion-depletion (IR-R2PI) spectroscopy to give a predicted blue shift of the C_sp³–H stretching frequency of 14 cm⁻¹ for the chloroform⋯fluorobenzene complex.³⁶ A slight C_sp³–H stretching frequency blue-shift of 8.7 cm⁻¹ in C_sp³–H⋯N nonconventional hydrogen bond was recently observed in the complex between chloroform with acetonitrile in the gas phase using Fourier transform IR (FTIR) spectroscopy by Behera et al.²⁷ Remarkably, a similar change of the C_sp³–H stretching frequency from blue shift in the gas phase to red shift in the argon matrix was also observed in complexes of deuterated chloroform with acetone and cyclohexanone.³⁷

Recently, the blue shift of the stretching frequency was found in the C_sp²–H bond and the extent of stretching frequency was even much higher than that of the C_sp³–H bond as a proton donor, in spite of the larger polarity of the former with respect to the latter one. Indeed, a C_sp²–H significant blue shift by 81 ÷ 96 cm⁻¹ in the C_sp²–H⋯O hydrogen bond formed in the complexes of formic acid with formaldehyde and thioformaldehyde has been recently discovered.³³ An investigation at the B3LYP/6-311++G(d,p) level in the interaction between CH₃CHO with two molecules of water predicted a significant blue shift of the C_sp²–H vibration amounting to 93 cm⁻¹ in the C_sp²–H⋯O hydrogen bond.³⁸ Our group's further reports of the considerable blue shift of C_sp²–H stretching vibration in the C_sp²–H⋯O/S nonconventional hydrogen bonds in XCHO⋯2H₂Z (X = H, F, Cl, Br; Z = O, S, Se, Te) complexes were given in ref. 39. Following complexation, a decrease in the stretching frequency of the O–H bond in the dimers of carboxylic acids^40,41 and an increase in C_sp²–H stretching vibrational frequency in the complexes of acetaldehyde^42–44 were reported. Kaur et al. suggested that the blue shift of C_sp²–H stretching vibrational frequency results from the presence of the O–H⋯O bond in the complexes formed between carbonyl compounds and hydrogen bond donors HOR (R = H, Cl, CH₃, NH₂, C(O)H, C₆H₅).⁴⁵

Although some publications related to the considerable blue shifts of C_sp²–H stretching vibrational frequencies in the complexes containing carbonyl (C_sp²=O) group have been reported,^{33,35,46–48} a systematic investigation of binary complexes stabilized by hydrogen bonds with the C_sp²–H bond acting as the proton donor for having an insight into the nature of blue-shifting hydrogen bonds is desirable. As a consequence, a study of the complexes formed by interactions of acetaldehyde (CH₃CHO) and thioacetaldehyde (CH₃CHS) with the substituted carboxylic and thiocarboxylic acids (RCZOH, with R = F, H, CH_3, and Z = O, S) is performed in this work to acquire a better understanding of the characteristics of conventional and non-conventional hydrogen bonds along with their mutual impact. The impact of the presence of the O–H⋯O/S hydrogen bond on the stability of C_sp²–H⋯O/S nonconventional hydrogen bonds and the blue shift of C_sp²–H stretching vibration is estimated. In addition, the effect of the R substituents of RCZOH (F and CH₃) acting as electron-withdrawing and electron-donating groups on the strength of binary complexes as well as the characteristics and stability of O–H⋯O/S and C_sp²–H⋯O/S hydrogen bonds are evaluated. Furthermore, the role of O compared to S in CH₃CHZ in affecting the characteristics of non-conventional and conventional hydrogen bonds is investigated thoroughly.

2. Computational methods

The optimized geometries of the monomer, the complexes, and their stretching vibrations are determined on the potential energy surface using the Gaussian 09 package⁴⁹ using MP2 (second-order Moller–Plesset perturbation theory)⁵⁰ combined with 6-311++G(3df,2pd).^51,52 Proton affinity (PA) at the O and S sites and deprotonation enthalpy (DPE) of C–H and O–H bonds in the isolated monomers were calculated at the CCSD(T)/6-311++G(3df,2pd) level. Interaction energy (ΔE*) corrected by both zero-point vibrational energy (ZPE) and basis set superposition error (BSSE)⁵³ was carried out at the CCSD(T)/6-311++G(3df,2pd) based on the optimizing geometries at the MP2/6-311++G(3df,2pd) level by the supramolecular method, in which, ΔE* is defined as the difference in total electronic energy between the stable complexes (E_complex) and the sum of two optimized monomers (E_monomer-1, E_monomer-2) given by

ΔE* = E_complex − (E_monomer-1 + E_monomer-2)

AIM (Atom In Molecule) analysis at MP2/6-311++G(3df,2pd) was performed to determine the bond critical points (BCP), electron density (ρ(r_C)), the Laplacian of electron density (∇²ρ(r_C)) using AIMAll package.⁵⁴ The local electron energy density (H(r_C)) at BCP was computed by H(r_C) = G(r_C) + V(r_C), in which V(r_C) and G(r_C) are the electron potential energy density and the electron kinetic energy density, respectively. The individual energy of each hydrogen bond (E_HB)^55–58 was calculated based on the empirical expression revealed by topological analyses of the electron density: E_HB = 0.5 V(r_C).⁵⁸ A natural bond orbital (NBO) analysis at MP2/6-311++G(3df,2pd) using the GenNBO5.G program⁵⁹ for a comprehensive understanding of the nature of hydrogen bond was carried out by calculating the hyperconjugation energies for intramolecular and intermolecular electron density transfer and orbital occupancies. NCI plot description is further utilized to visualize the weak hydrogen bonds.^60,61 Moreover, the Molecular Electrostatic Potential (MEP) analysis^24,62 of the monomers is investigated at the MP2/6-311++G(3df,2pd) level. In particular, electrostatic potential, V(r) has been considered to be an important property for analyzing the nature and predicting the strength of several non-covalent interactions. Herein, we used the maximum and minimum surface electrostatic potentials denoted by V_s,max and V_s,min, respectively, in order to characterize hydrogen-bonded complexes. Generally, V(r) is created by the nuclei and electrons of a molecule at any point r in the surrounding space, given by,

In which, Z_A is the charge on nucleus A, located at R_A, and ρ(r′) is the molecule's total electronic density with r′ as a dummy integration variable.

To evaluate the physically meaningful components contributing to the stability of investigated complexes, the SAPT (Symmetry-Adapted Perturbation Theory) analysis⁶³ using Psi4 program⁶⁴ at the MP2/6-311++G(3df,2pd) level was employed. The total interaction energy (ΔE^SAPT2+) can be divided into the four basic components: exchange-repulsion (E_exch), electrostatic (E_elst), induction (E_ind), dispersion (E_disp) terms, and is defined by the following:

ΔE_SAPT2+ = E_elst + E_exch + E_ind + E_disp + δE^HF_int,r

where δE^HF_int,r is a term containing the third-order and higher-order induction and exchange-induction contributions.

3. Results and discussion

3.1. Structural pattern and stability of complexes

Stable structures of binary complexes of CH₃CHZ and RCZOH (with Z = O, S; R = CH₃, H, F) at the MP2/6-311++G(3df,2pd) level are shown in Fig. 1a. Twelve stable complexes located on potential energy surfaces are presented in detail in Fig. S1 in the ESI.† Some typical parameters in the observed complexes are tabulated in Table S1.† Briefly, investigated complexes are named RZ–Z, in which, R is CH₃, H, and F substitution groups. The O atom or S atom is represented by Z in RCZOH and CH₃CHZ, denoted as Z2 and Z7 in the complexes. The sp²-hybridized carbon atom in CH₃CHZ is labelled hereafter as C_sp². It can be seen that all structures contain a ring formed by two intermolecular interactions: one C_sp²–H⋯Z2 with an obtuse angle (<180°) and one O–H⋯Z7 with an angle of ∼180° (Table S1†). The chalcogen atoms (Z) act as proton-accepting centers and C_sp²–H or O–H bonds in the isolated monomers are proton-donating sites.^40,65,66 Remarkably, a rotational spectrum study of formic acid – isopropylformate by Spada et al. suggested a similar geometry with hydrogen bonds including O–H⋯O and C_sp²–H⋯O.⁶⁷ Besides, as shown in Table S1,† the distances of H⋯O7, H⋯S7, H⋯O2, and H⋯S2 contacts are close to the sum of the van der Waals radii of relevant atoms (this sum is 3.00 Å and 2.72 Å for the corresponding pair of S and H, O, and H atoms). The lengths of H⋯O distances in C_sp²–H⋯O^33,45 and O–H⋯O^33,45,68 interactions are comparable to those in the complexes of this work. Additionally, the H⋯S distances of O–H⋯S7 hydrogen bond in HO–S are close to those obtained at the MP2/aug-cc-pVDZ level.³³ These results roughly suggest the presence of O–H⋯Z7 conventional and C_sp²–H⋯Z2 nonconventional hydrogen bonds in the binary complexes.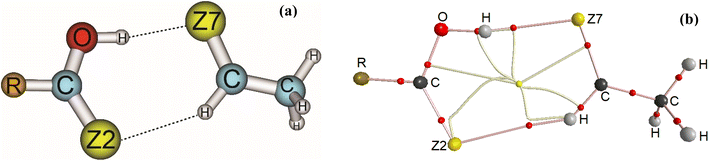

Fig. 1 Geometries (a) and topological features (b) of RCZOH⋯CH₃CHZ complexes (with R = CH₃, H, F; Z = O, S) at MP2/6-311++G(3df,2pd).

Concerning the C_sp²–H⋯Z2 bonds, the H⋯Z2 distance is increased when R is an electron-withdrawing group (F) while the opposite is true for an electron-donating group (CH₃). Meanwhile, a converse trend is obtained with O–H⋯Z7 bonds. To explain this observation, the effect of the proton-donating or -accepting ability of the isolated monomers on the strength of hydrogen bonds is evaluated through deprotonation enthalpy (DPE) of O/C_sp²–H bonds and proton affinity (PA) at the Z sites of CH₃CHZ and RCZOH (Table 1). By changing the R substitution in RCZOH, the O–H⋯Z7 intermolecular distance in complexes increases in the order of F < H < CH₃. This change accompanies a decrease in the polarity of the O–H bond in RCZOH as one goes from F to H to CH₃ substitution (Table 1). Besides, the C_sp²–H⋯Z2 intermolecular distance decreases in the substitution order: CH₃ > H > F, which relates directly to the increasing proton affinity of the Z2 site in RCZOH.

Table 1 Values of proton affinity (PA) and deprotonation enthalpy (DPE) at CCSD(T)/6-311++G(3df,2pd)//MP2/6-311++G(3df,2pd) and the ratios of DPE/PA for C_sp²–H⋯Z2 bonds in the complexes^a

Monomer	CH3CHO	CH3CHS	CH3COOH	CH3CSOH	HCOOH	HCSOH	FCOOH	FCSOH
a Experimental values in parentheses are taken from the NIST webpage (https://webbook.nist.gov/chemistry/).
PA (Z), kJ mol^−1	767.2 (768.5)	807.1	768.2 (783.7)	809.3	722.3 (742.0)	770.3	698.5	744.0
DPE (Csp^2/O–H), kJ mol^−1	1641.0 (1645.1 ± 4.0)	1610.0 (1461.0 ± 17.0)	1454.8 (1457.0 ± 5.9)	1392.7	1440.1 (1449.0 ± 5.0)	1381.9	1366.5	1312.4

---

(1) DPE of Csp^2–H in CH3CHZ	DPE^(1)/PA^(2)	CH3O–O	CH3S–O	HO–O	HS–O	FO–O	FS–O
		2.14	2.03	2.27	2.13	2.35	2.21
(2) PA of Z = O/S in RCZOH	DPE^(1)/PA^(2)	CH3O–S	CH3S–S	HO–S	HS–S	FO–S	FS–S
		2.10	1.99	2.23	2.09	2.30	2.16

---

To evaluate the role of conventional and nonconventional hydrogen bonds in stabilizing the complexes, the second-order perturbative energies E_inter from NBO calculations at the MP2/6-311++G(3df,2pd) level are given in Table 2. The large positive values of electron density transfer (EDT) of ca. 0.039–0.079 e show that the electron density is considerably transferred from CH₃CHZ to RCZOH following complexation. These EDT values are taken from a stronger electron density transfer from n(Z7) to σ*(O–H) orbital versus n(Z2) to σ*(C_sp²–H) one in each binary complex. The values of E_inter[n(Z7) → σ*(O–H)] (ca. 22.6–37.4 kJ mol⁻¹) are indeed 10 ÷ 17 times larger than E_inter[n(Z2) → σ*(C_sp²–H)] (ca. 1.4–3.1 kJ mol⁻¹). It could be thus drawn that the charge-transfer interaction of n(Z7) → σ*(O–H) in the conventional hydrogen bond plays a dominant role in stabilizing each complex, as compared to those of the n(Z2) → σ*(C_sp²–H) electron transfer in the non-conventional ones.

Table 2 Selected NBO results for C_sp²–H⋯Z2 and O–H⋯Z7 hydrogen bonds at MP2/6-311++G(3df,2pd)^a

Complex	EDT (e)	Δ% s (%)		Δσ* (e)		Einter (kJ mol^−1)		ΔEintra (kJ mol^−1)
		O(H)	Csp^2(H)	O–H	Csp^2–H	n(Z7) → σ*(O–H)	n(Z2) → σ*(Csp^2–H)	n(Z7) → σ*(Csp^2–H)
a EDT: electron density transfer; Δ% s: change in s-character percentage; Δσ*: change in electron density of anti-bonding orbital; Einter: intermolecular hyperconjugation interaction energy; ΔEintra: difference of intramolecular hyperconjugation interaction energy in isolated monomer and complex.
CH3O–O	0.039	3.71	1.37	0.041	−0.012	23.1	1.7	−7.6
CH3S–O	0.040	3.99	1.16	0.043	−0.007	26.2	2.5	−7.2
HO–O	0.042	3.81	1.31	0.043	−0.012	25.6	1.7	−7.8
HS–O	0.041	4.14	1.12	0.044	−0.007	27.8	2.4	−7.4
FO–O	0.055	3.82	1.26	0.055	−0.015	35.6	1.4	−8.7
FS–O	0.056	3.99	1.15	0.060	−0.011	37.4	2.2	−8.6
CH3O–S	0.050	3.52	1.62	0.054	−0.004	22.6	2.6	−3.9
CH3S–S	0.054	3.82	1.41	0.061	0.002	26.0	3.1	−3.2
HO–S	0.056	3.73	1.55	0.059	−0.004	25.1	2.6	−3.8
HS–S	0.057	4.03	1.39	0.064	0.002	28.4	3.1	−3.4
FO–S	0.076	3.99	1.50	0.074	−0.006	33.0	2.1	−4.1
FS–S	0.079	4.18	1.39	0.083	−0.001	37.0	2.7	−3.7

---

Interaction energies (ΔE*) including ZPE and BSSE corrections of the studied complexes are listed in Table 3. Generally, the values of the interaction energy range from −27.1 to −46.5 kJ mol⁻¹, implying that the considered complexes are stable. The stability of CH₃CHZ⋯RCZOH complexes lies between that of (CH₃CHZ)₂ and (RCZOH)₂ dimers, with R = CH₃, H, F, and Z = O, S. Particularly, the values of the interaction energy of (HCOOH)₂ and (CH₃COOH)₂ are calculated to be in turn −61.9 and −66.6 kJ mol⁻¹ at the MP2/aug-cc-pVTZ level⁴⁰ or −56.9 and −60.7 kJ mol⁻¹ at the MP2/6-311++G(d,p),⁴¹ respectively. The less negative interaction energy found for (CH₃CHO)₂ dimer was −14.8 kJ mol⁻¹ at the M062X/6-311++G(3df,3pd) level⁴² or −11.6 kJ mol⁻¹ at the MP2/6-311++G(d,p) level.⁴⁴ The investigated complexes are more stable than CH₃CHS⋯HOBr (ΔE* is −22.8 kJ mol⁻¹ at the MP2/aug-cc-pVTZ level)⁶⁹ and CH₃CHO⋯H₂O and CH₃CHS⋯H₂O (ΔE* are −15.3 and −11.7 kJ mol⁻¹, respectively, at CCSD(T)/6-311++G(3df,2pd)//MP2/6-311++G(3df,2pd)).⁷⁰

Table 3 Interaction energy (ΔE*), basis set superposition error (BSSE) at CCSD(T)/6-311++G(3df,2pd)//MP2/6-311++G(3df,2pd) and SAPT2+ analysis at MP2/6-311++G(3df,2pd), all in kJ mol^−1a

Complex	Eelst	Eind	Edisp	δE^HF	Eexch	E^SAPT2+	ΔE*	BSSE
a The values in parentheses for the contribution percentage (%) of energy component on the stability of complexes.
CH3O–O	−70.6(46)	−44.0(29)	−25.4(17)	−12.5(8)	98.9	−53.6	−35.7	5.13
CH3S–O	−72.5(43)	−52.8(31)	−27.8(17)	−15.1(9)	117.8	−50.3	−35.0	5.86
HO–O	−73.3(46)	−46.6(29)	−25.3(16)	−13.5(9)	102.9	−55.9	−36.5	5.14
HS–O	−74.5(43)	−54.6(32)	−27.7(16)	−16.0(9)	120.3	−52.5	−35.3	5.85
FO–O	−81.4(46)	−53.4(30)	−26.0(15)	−16.0(9)	112.3	−64.5	−46.5	5.90
FS–O	−83.3(43)	−60.6(32)	−28.7(15)	−18.8(10)	129.1	−62.3	−46.4	6.50
CH3O–S	−53.0(40)	−43.8(33)	−25.0(19)	−11.0(8)	95.8	−37.0	−28.7	5.42
CH3S–S	−52.8(36)	−52.7(36)	−27.5(19)	−12.8(9)	114.6	−31.2	−27.1	6.00
HO–S	−54.3(40)	−46.5(34)	−24.8(18)	−11.9(9)	99.4	−38.1	−28.8	5.34
HS–S	−54.1(36)	−54.7(36)	−27.4(18)	−13.6(9)	117.3	−32.6	−27.5	6.00
FO–S	−58.5(38)	−54.7(36)	−25.2(17)	−13.9(9)	106.5	−45.8	−36.2	6.01
FS–S	−58.1(36)	−60.7(37)	−27.9(17)	−15.7(10)	124.7	−37.7	−34.7	6.04

---

With the same atoms Z2 and Z7, the interaction energies of complexes tend to decrease from CH₃Z–Z to HZ–Z and finally to FZ–Z. As a result, the substitution of H by F attached to the carboxyl group in HCZOH gives rise to an enhancement of the stabilization energy, while the attachment of the CH₃ group diminishes this value. The E_inter[n(Z7) → σ*(O–H)] values thus increase in the order of CH₃ < H < F substitutions, which are in line with the tendency of enhancement in the polarity of O–H covalent bonds in RCZOH (cf. Table 1). Following this substitution, as observed in Table 2, the E_inter[n(Z2) → σ*(C_sp²–H)] values decrease slightly, which is due to a lower proton affinity at the Z2 site in the isolated isomers. This indicates a dominant role of the O–H⋯O/S compared to C_sp²–H⋯O/S hydrogen bonds in stabilizing the complexes. More negative values of the interaction energy were obtained for CH₃CHO⋯HCOOH (−39.8 kJ mol⁻¹) in comparison with CH₃CHO⋯CH₃COOH (−38.0 kJ mol⁻¹) at the B3LYP-D3/aug-cc-pVTZ level,⁶⁸ which shows that the H substitution of the C_sp²–H group in HCOOH by the CH₃ group causes a decrease in the stability of hydrogen-bonded complexes. This observation is also similar to the obtained result in this work and the complexes of alcohol derivatives and amine.⁷¹

The values of the maximum surface electrostatic potential (V_s,max) at the H atom of –OH groups in substituted carboxylic and thiocarboxylic acids (RCZOH) are displayed in Fig. S2.† As expected, V_s,max of the RCZOH molecule at the H atom decreases with the substitution of the CH₃ group, whereas, it increases in the presence of the F atom, corresponding to the changing trend of the interaction energy in the complexes. Indeed, the F substituted RCZOH having the highest V_s,max is accompanied by the largest negative interaction energy, whereas the CH₃ substitution having the lowest V_s,max is associated with the least negative interaction energy. The linear correlations (R² ≈ 0.9) between the interaction energy of the complexes and the magnitude of V_s,max value are observed in this study, as given in Fig. S3 of ESI.† It shows that the stability of the investigated complexes increases when there is an enhancement of the positive electrostatic potential of the H atom in RCZOH monomers and vice versa.

With the same substituent groups R and Z7, the interaction energy of RO–Z is slightly more negative than that of RS–Z, around 0.1–1.6 kJ mol⁻¹, while E_inter[n(S2) → σ*(C_sp²–H)] is larger than E_inter[n(O2) → σ*(C_sp²–H)]. This indicates that the larger strength of C_sp²–H⋯O2 versus C_sp²–H⋯S2 is caused by the electrostatic attraction between H and Z2 overcoming the charge transfer from n(Z2) to σ*(C_sp²–H) orbital. Indeed, the NBO charges given in Table S1 of ESI† show a larger positive charge of the H atom in the C_sp²–H⋯O2 bond in RO–Z, as compared to that in C_sp²–H⋯S2 in RS–Z. Besides the charge of the O2 atom is also more negative than that of the S2 atom in the complexes. This signifies a stronger electrostatic attraction between O2 and H in the C_sp²–H⋯O2 bond than between S2 and H in the C_sp²–H⋯S2 bond.

With the same R and Z2, the RZ–O is ca. 7.0–11.7 kJ mol⁻¹ in energy, which is more stable than RZ–S, although electron transfer energy from n(S7) to σ*(O–H) orbital is stronger than that from n(O7) to σ*(O–H) (cf. Tables 2 and 3). Consequently, the stability of the complexes is governed by the electrostatic interaction of Z7 and H atoms as opposed to the energy for the charge transfer from n(Z7) to σ*(O–H) orbital. In short, it is apparent that the larger stability of RO–Z versus RS–Z or RZ–O versus RZ–S comes from the contribution of electrostatic attraction between O and H atoms, overwhelming that between S and H atoms. Indeed, as seen from Table S1,† the NBO charges on O7 atoms have large negative values, whereas positive charges are found on S7 atoms. In addition, more positive charges of H of the –OH group in RZ–O, as compared to those in RZ–S are also observed (cf. Table S1†). Accordingly, the electrostatic attraction between O7 and H in O–H⋯O7 bond is stronger than that between S7 and H in O–H⋯S7 bond. Similarly, the larger stability of HCOOH⋯CH₃CHO, as compared to that of HCOOH⋯CH₃CHS at the MP2/aug-cc-pVTZ level studied by Trung et al.³³ indicates a more important role of the O atom in comparison with the S atom in stabilizing hydrogen-bonded complexes.

The energy components⁷² were evaluated by employing the SAPT2+ procedures at the MP2/6-311++G(3df,2pd) basis set (Table 3). The calculated results indicate that the interactions in the investigated complexes are mainly contributed by E_elst (36–46%) and E_ind (29–37%) components, while E_disp and δE^HF only contribute less, half of those, by 15–19% and 8–10%, respectively. As a consequence, the electrostatic and induction components play an important role in stabilizing the complexes, especially, a considerable role of electrostatic energy in complex stabilization. An approximation of the contributions in the percentage of physical energy terms to the stability of the complexes for both electron-donating (CH₃) and electron-withdrawing (F) substituent groups was observed (cf. Fig S4†). A great contribution of the electrostatic term to the complex stability occurs in RZ–O in comparison to RZ–S, making the former to be about 1.3–1.4 times more stable than the latter (Table 3). The high values of E_exch seem to be the additional reason for the less stable RS–Z versus RO–Z. Besides, there are approximate contributions of E_elst and E_ind components, about 36–37% in RS–S.

3.2. AIM and NCI analyses

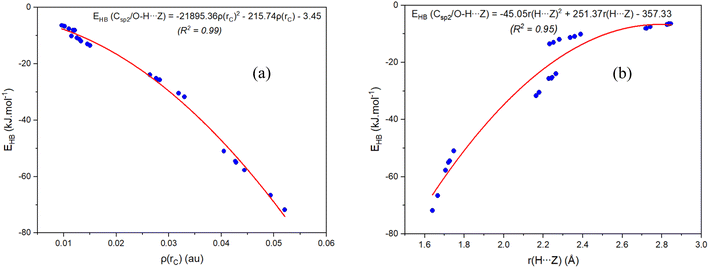
In order to clarify the existence and stability of conventional and nonconventional hydrogen bonds in the binary complexes, an AIM analysis was performed and its results showed the bond critical points (BCP) in red between the lines connecting H atoms with Z7 and H atoms with Z2 for all complexes (cf. Fig. 1b and S1 in ESI†). These BCPs again indicate that the O–H⋯Z7 and C_sp²–H⋯Z2 contacts in the binary complexes of RCZOH and CH₃CHZ are hydrogen bonds. Besides, their existence was confirmed by the values of electron density ρ(r_C) and Laplacian at BCPs ∇²ρ(r_C), which fall within the criteria for the formation of hydrogen bonds.⁷³ All values of ρ(r_C) and ∇²ρ(r_C) at these BCPs (cf. Table S2, ESI†) are indeed in the range of 0.0096–0.0521 au and 0.027–0.105 a.u., respectively. The characteristics of conventional and nonconventional hydrogen bonds in the complexes are emphasized by values of local electron energy densities (H(r_C)) at BCPs.^74,75 The positive values of ∇²ρ(r_C) and negative values of H(r_C) at BCPs of O–H⋯Z7 contacts in the complexes suggest a partly covalent character of the conventional hydrogen bonds.⁴⁵ Meanwhile, the positive ∇²ρ(r_C) and H(r_C) values indicate that the C_sp²–H⋯Z2 nonconventional hydrogen bonds are considered to be weak hydrogen bonds.

The E_HB values from Table S2† suggest that the O–H⋯O7 is twice stabler than O–H⋯S7 and C_sp²–H⋯S2 is about 1.5 times less stable than C_sp²–H⋯O2. This implies that the O–H⋯Z7 hydrogen bonds keep a substantial part in stabilizing further the complexes, in addition to the stabilization by C_sp²–H⋯Z2 hydrogen bonds. This observation is also reported in the hydrogen-bonded complexes between carbonyl derivatives and water.^38,46,70 It is found that the contribution to the RZ–Z stabilization is larger for C_sp²–H⋯O2/O–H⋯O7 hydrogen bonds than that for C_sp²–H⋯S2/O–H⋯S7. With the different substitution of Z2 or Z7 atoms, AIM data shows a larger strength of the C_sp²–H⋯O2 hydrogen bond compared to C_sp²–H⋯S2,^76,77 and a larger strength of the O–H⋯O7 bond in comparison with O–H⋯S7 one.^78,79 The second-order correlations between the individual energy of hydrogen bond (E_HB) with the value of electron density (ρ(r_C)) at the BCP and the distance H⋯Z(r(H⋯Z)) are plotted in Fig. 2. It shows that the more negative the E_HB values are, the larger the ρ(r_C) values and the shorter the r(H⋯Z) at BCPs. In other words, the ρ(r_C) at the BCP of the hydrogen bond is inversely proportional to r(H⋯Z). This result affirms a dominant role of the O–H⋯Z7 bond compared to the C_sp²–H⋯Z2 bond in contributing to complexation.

Fig. 2 The second-order correlations of individual hydrogen bond energies (E_HB) with respect to electron density ρ(r_C) at BCPs (a) and intermolecular distances (b) for RCZOH⋯CH₃CHZ complexes (Z = O, S; R = CH₃, H, F).

For a more obvious understanding of the characteristics of conventional and nonconventional hydrogen bonds in the complexes, NCI (Non-Covalent Interaction) calculations were performed. The reduced density gradient (RDG) isosurfaces and their 2D plots for all complexes are displayed in Fig. S5a and b (in ESI†). In the 2D plots, the low-density and low reduced gradients in the region are where the second eigenvalue (λ₂) of the electron-density Hessian matrix is negative, indicating weak and non-covalent attractive interactions between CH₃CHZ and RCZOH molecules. It can be seen from Fig. S5a and b† that the volume and site of the tail on the horizontal axis of the blue spike and the green spike in all complexes are not the same. However, in all complexes, the O–H⋯Z7 bond is recognized by the blue spike lying at the higher negative region in comparison with the green spike of the C_sp²–H⋯Z2 bond. In RZ–O complexes, the difference in the distance between the tail of the blue spike and the tail of the green spike is larger than that in RZ–S complexes. For instance, with the same site of the tail of the green spike (about −0.01 a.u.), the blue spike for the O–H⋯O7 bond in FS–S lies at about −0.03 a.u., while it lies at −0.05 a.u. for FO–O.

Here, the FO–O complex is chosen as a good example for analysis (Fig. 3). In particular, two spikes (blue and green) are detected in the negative region, confirming again the attendance of O–H⋯Z7 and C_sp²–H⋯Z2 hydrogen bonds in the complexes. The O–H⋯Z7 bond is recognized by the blue spike lying at the high negative region (∼0.05 au). This indicates that the O–H⋯Z7 hydrogen bonds are stronger compared to C_sp²–H⋯Z2 ones in the complexes, in agreement with the results reported by Lei et al.⁸⁰ and Cuc et al.^39,70 Moreover, the spike found at the positive region with only about 0.01 a.u. in the electron density implies a repulsive non-covalent interaction at the RCP interior to the ring.

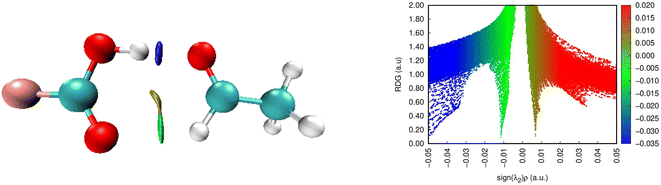Fig. 3 NCI isosurface (3D) and plots of RDG as a function of sign(λ₂)ρ(r_C) (2D) for FCOOH⋯CH₃CHO (the isosurfaces are colored according to the values of sign(λ₂)ρ(r_C) from −0.05 to 0.05 a.u.).

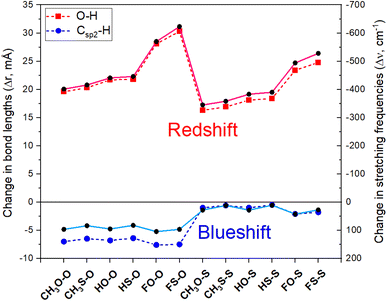
3.3. Changes in lengths and stretching frequencies of C_sp2–H and O–H bonds

The results obtained for the changes in the values of lengths (Δr, mÅ) and stretching frequencies (Δν, cm⁻¹) of O–H and C_sp²–H bonds at MP2/6-311++G(3df,2pd) level are tabulated in Table 4 and displayed in Fig. 4. The C_sp²–H bond length decreases by 0.5 to 7.6 mÅ, accompanied by an increase in its stretching vibration by 11.0 cm⁻¹ to 104.5 cm⁻¹ in comparison with the corresponding values in the isolated monomers. This observation is remarkable, given that, as introduced in Section 1, a considerable contraction of a C_sp²–H bond length has rarely been observed owing to its polarity. The changes in the C_sp²–H stretching frequency indicate that all C_sp²–H⋯Z2 hydrogen bonds in the studied complexes are blue-shifted. For comparison, a concise summary of the theoretical and experimental publications on the changes in stretching frequencies of the C_sp–H, C_sp²–H, C_sp³–H bonds upon complex formation is given in ESI (Table S3).† It is seen that the red shift in the stretching frequency of the C_sp–H bond was found at high levels of theory, while both red or blue shifts of C_sp³–H stretching frequencies with weak and moderate magnitude were observed.

Table 4 Change of bond lengths (Δr, mÅ) and corresponding stretching frequency (Δν, cm⁻¹) in the complexes at MP2/6-311++G(3df,2pd)

Complex	CH3O–O	CH3S–O	HO–O	HS–O	FO–O	FS–O
Δr(O–H)	19.6	20.3	21.7	21.8	28.1	30.3
Δν(O–H)	−401.1	−416.0	−441.4	−445.6	−569.7	−622.8
Δr(Csp^2–H)	−7.0	−6.5	−6.8	−6.4	−7.6	−7.5
Δν(Csp^2–H)	96.6	83.8	95.3	82.5	104.5	96.7

---

Complex	CH3O–S	CH3S–S	HO–S	HS–S	FO–S	FS–S
Δr(O–H)	16.3	16.9	18.1	18.4	23.4	24.8
Δν(O–H)	−344.9	−358.3	−382.7	−389.5	−494.0	−528.3
Δr(Csp^2–H)	−1.0	−0.6	−1.0	−0.5	−2.1	−1.8
Δν(Csp^2–H)	28.1	11.9	28.3	11.0	42.3	27.7

---

Fig. 4 The relationship of changes in C_sp²/O–H bond length (Δr in mÅ, dash line, and symbol) and corresponding stretching frequency (Δν in cm⁻¹, solid line and symbol) with different R, Z substitutions for investigated complexes.

The extent of changes in C_sp²–H stretching frequencies have been observed in several binary hydrogen-bonded systems (Table S3 in ESI†).^{33,38,39,46,81} Moderate and strong C_sp²–H blue shifts were reported in some complexes between carbonyl/thiocarbonyl compounds with water.^38,46,81 Indeed, in complexes between aldehydes and hydrogen chalcogenides (H₂O, H₂S),³⁹ the C_sp²–H stretching frequencies undergo a significant blue shift, amounting to 92 cm⁻¹ for CH₃CHO⋯2H₂O. The strong blue shift of the C_sp²–H stretching frequency (93 cm⁻¹) in the CH₃CHO⋯2H₂O complex was also found by Chandra et al.³⁸ Remarkably, a strong blue shift of the C_sp²–H stretching vibration up to 96 cm⁻¹ in binary complexes between formic acid and acetaldehyde was reported in ref. 33. At the MP2/cc-pVTZ level, Damanjit et al. calculated a significant blue shift of the C_sp²–H bond in NH₂CHO⋯HCOOH to about 93 cm⁻¹.⁴⁵ As seen from Table S3† that the blue-shift of the C_sp²–H stretching frequency in the dimer of (CH₃CHO)₂ (including two C_sp²–H⋯Z hydrogen bonds) is smaller than that in the HCOOH⋯CH₃CHO binary complex (including one C_sp²–H⋯Z bond and one O–H⋯O bond). This result emphasizes the important role of O–H⋯O interaction to the large blue-shift of C_sp²–H stretching vibration.

Comparing C_sp²–H⋯Z types, it is found that the magnitude of the blue shift in the C_sp²–H stretching vibrational frequency in O7 = C_sp²–H⋯Z2 (RZ–O) is larger than that in S7 = C_sp²–H⋯Z2 (RZ–S). This likely relates to the stronger polarity of the C_sp²–H bond in CH₃CHS with respect to CH₃CHO (cf. Table 1). As seen in Fig. 4, a larger contraction of the C_sp²–H bond length accompanied by a larger increase in its stretching vibrational frequency was observed for the C_sp²–H⋯O2 hydrogen bonds in comparison to the C_sp²–H⋯S2. This difference is owing to the larger gas phase Lewis basicity at the S site in RCSOH as compared to that at the O site in RCOOH (cf. Table 1), which denotes a more prominent role of O versus S atom in the larger magnitude of the blue shift of C_sp²–H stretching frequency involving hydrogen bond. Importantly, a good correlation between Δν(C_sp²–H) and DPE(C_sp²–H) along with PA(Z2) is found with R² ≈ 0.98 (illustrated in Fig. S6†). Hence, the results of the present work demonstrate the fact that the blue shift of stretching vibrational frequency is dependent on the inherent property of the monomer, as discussed in some recent works.^{18,33–35,39} As seen from Tables 1 and 4, it is found that the higher the DPE/PA ratio for the C_sp²–H⋯Z2, the larger blue-shift of the C_sp²–H stretching vibration will be, and vice versa. It is also found that the DPE/PA ratio for the C_sp²–H⋯Z2 bonds in the complexes with CH₃CHZ is larger for Z = O than for Z = S. The highest DPE/PA was estimated in FO–O, and the lowest value was obtained in HS–S. Therefore, it could be proposed that the DPE/PA ratio can be used for the evaluation of the category of hydrogen bonds and the extent of the blue shift of stretching frequency.

The C_sp²–H stretching frequency in C_sp²–H⋯Z2 bond experiences a strong enhancement upon F substitution in RCZOH compared to H and CH₃ substitutions, which has been rarely reported before (cf. Table S3†). It is suggested that a contraction in the length of the C_sp²–H bond and a remarkable increase of its stretching vibrational frequencies are affected by the presence of O–H⋯Z7 hydrogen bonds in complexes, especially O–H⋯O hydrogen bonds.⁴⁵ For instance, the highest extent of the blue shift in C_sp²–H⋯Z2 bonds belongs to FO–O (connected by C_sp²–H⋯O and O–H⋯O bonds) with a C_sp²–H contraction of 7.6 mÅ and a strong increase in its stretching vibration of 104.5 cm⁻¹. This result arises from the largest decrease in the electron density of the σ*(C_sp²–H) antibonding orbital (0.015 e), which strengthens the C_sp²–H bond and thereby contributes to a blue shift of the C_sp²–H stretching vibration.

Table 2 points out that the trend in the change of electron density in the σ*(C_sp²–H) orbitals is quite comparable to the change in C_sp²–H stretching frequency. Meanwhile, the increase in the percentage of the s-character of C_sp² in the C_sp²–H covalent bond is not too much different in the complexes. As a consequence, a decrease of electron density in the σ*(C_sp²–H) orbitals, which overwhelms an increase in s character percentage in the hybridization of C_sp²(H), governs the magnitude of the blue shift of C_sp²–H stretching frequency in the complexes. All complexes including CH₃CHO exhibit a large decrease in electron densities in σ*(C_sp²–H) (0.007–0.015 e), while a slight increase of 0.002 e or a slight decrease of 0.001 e in the electron density of the σ*(C_sp²–H) is estimated for RS–S complexes. Besides, the decreases of the electron density in σ*(C_sp²–H) for H or CH₃ substituted complexes are comparable and are much smaller than that for F substitutions, which confirms again the strong blue shift of the C_sp²–H stretching frequency with the F substituent.

Considering the second-order stabilization energy of interaction¹¹ from Table 2, it shows that a larger decrease in intramolecular hyperconjugation energy of the n(Z7) → σ*(C_sp²–H) electron density transfer versus intermolecular hyperconjugation energies of n(Z2) → σ*(C_sp²–H) transfer determines the decrease in σ*(C_sp²–H) orbital population. It is also noted that a decrease in the hyperconjugation energies associated with intramolecular electron density transfer from n(O7) to σ*(C_sp²–H) is twice as large as that from n(S7) to σ*(C_sp²–H). A good linear correlation of the changes in the electron density at σ*(C_sp²–H) with both E_inter[n(Z2) → σ*(C_sp²–H)] and ΔE_intra[n(Z7) → σ*(C_sp²–H)] with R² ≈ 0.98 is found in Fig S7.† The results show a crucial role in decreasing the hyperconjugation interaction of intramolecular electron transfer from the (Z7) to σ*(C_sp²–H) orbital, overcoming the increase in the electron density transfer from the n(Z2) → σ*(C_sp²–H) orbital. This result leads to a large decrease in the σ*(C_sp²–H) occupation in the complexes, which governs a C_sp²–H bond contraction and the associated blue shift. In short, there are two features leading to a significant blue shift of C–H stretching frequency: (i) the presence of O–H⋯Z7 hydrogen bonds in the cyclic structure; and (ii) the decrease in the electron density of σ*(C_sp²–H) orbital.

On the other hand, the changes of Δr(O–H) and Δν(O–H), as shown in Fig. 4, denote a strong red shift of O–H stretching frequencies along with its bond elongation in O–H⋯Z7 hydrogen bonds upon complexation. This observation is accompanied by a large enhancement of σ*(O–H) occupation (ca. 0.041–0.083 e) overcoming an increase in the percentage of s-character at O(H) atom (ca. 3.52–4.18%), which does not favor an O–H bond elongation that accompanies an associated red shift of the stretching vibration. From Table 2, the strong hyperconjugation energy for the intermolecular n(Z7) → σ*(O–H) transfer (amounting to 22.6 ÷ 37.4 kJ mol⁻¹) is the reason for the increase in the occupation of σ*(O–H) orbital in complexes. The remarkable red shift of O–H stretching vibration in the O–H⋯O7 hydrogen bond was also observed in the complexes between HCOOH and HCHO derivatives (363 ÷ 604 cm⁻¹)^45,68,82,83 or between acetic acid and acetaldehyde (436 cm⁻¹).⁶⁸ Similar results were also reported in a recent investigation on HCOOH⋯CH₃CHS and HCOOH⋯CH₃CHO complexes.³³

The red shift of O–H stretching frequency of the O–H bond in O–H⋯Z7 hydrogen bonds follows the ordering of CH₃ < H < F substitutions, in good agreement with the enhancement of the polarity of the O–H bond in RCZOH in going from CH₃ to H and finally to F (Table 1). The red shift of the O–H stretching frequency is greater for RS–Z than for RO–Z, which is in accordance with the higher polarity of the O–H bond in RCSOH, as compared to its value in RCOOH (cf. Table 1). The obtained results indicate that the red shift of O–H stretching frequency in the O–H⋯Z7 hydrogen bond is determined by an increase in σ*(O–H) electron density. From Fig. 4, it is seen that for the same Z2, this O–H stretching frequency red shift in RZ–O is greater than that in RZ–S. Thus, the O–H red-shifting stretching frequency is mainly due to a larger attractive electrostatic force between Z7 and H, which overcomes the n(Z7) → σ*(O–H) charge transfer.

4. Concluding remarks

In this study, twelve stable ring structures of CH₃CHZ⋯RCZOH (R = H, F, CH₃; Z = O, S) stabilized by O–H⋯O/S and C_sp²–H⋯O/S hydrogen bonds, with the interaction energies from −27.1 to −46.5 kJ mol⁻¹ were thoroughly investigated using quantum chemical methods. The substitution of H by the F atom in RCZOH induces an increase in the thermodynamic stability of complexes, while the opposite is true for CH₃, which is due to the overwhelming contribution to complex stability of O–H⋯O/S bonds compared to their C_sp²–H⋯O/S counterparts. Besides, arising from the electrostatic interaction, a larger role of the O atom in comparison with the S atom in affecting the characteristics and strength of hydrogen bonds as well as the stability of complexes is elucidated in these systems. The strength of C_sp²/O–H⋯O is 1.5÷2 times larger than C_sp²/O–H⋯S counterparts. SAPT2+ analysis indicates that the attractive electrostatic term plays a crucial role in stabilizing the complexes containing C_sp²/O–H⋯O hydrogen bonds. Meanwhile, stabilizing the complexes by C_sp²/O–H⋯S hydrogen bonds is due to both electrostatic and induction terms.

The C_sp²–H stretching frequency in the C_sp²–H⋯O/S nonconventional hydrogen bond increases when substituting one H of the –CH group in HCZOH with both, a halogen atom and CH₃ group. The largest blue shift of the C_sp²–H bond up to 104.5 cm⁻¹ in the FO–O binary complex was observed for the first time, which corresponds to the smallest basicity at the O atom in FCOOH, as compared to that in the other monomers. It is realized that with the presence of O–H⋯O/S bonds, a large decrease in the electron density in σ*(C_sp²–H) orbital predominating an increase in the percentage of s-character, causes an abnormal blue-shift of the C_sp²–H stretching vibration by ca. 82.5–104.5 cm⁻¹. Besides, the ratio of DPE/PA can be considered a factor in identifying the type of hydrogen bond and the magnitude of blue shift observed upon complexation. NBO results show that the considerable blue shift of C_sp²–H stretching vibration is governed by an intramolecular hyperconjugation interaction overcoming the intermolecular one. Moreover, the shift of C_sp²–H stretching frequency as a function of net second hyperconjugative energy for the σ*(C_sp²–H) orbital was observed.

All the O–H bonds in the O–H⋯O/S conventional hydrogen bonds are red-shifted. The significant elongation of O–H bonds in O–H⋯O/S hydrogen bonds and the strong decrease of their stretching vibrational frequency come from considerable increases in the σ*(O–H) electron density overcoming an increase in the percentage of the s-character of the O/S hybridized atom. It was found that the red shifting of the O–H⋯O bond is larger than that of the O–H⋯S one, and increases in the ordering of CH₃Z–Z < HZ–Z < FZ–Z binary complexes.

Conflicts of interest

The authors declare that they have no conflict of interest.

Acknowledgements

This research was funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 104.06-2020.28. We are sincerely thankful to Professor Thanh-Tung Nguyen-Dang, Université Laval – Canada for valuable discussions.

References

1. J. Lehn, Supramolecular Chemistry: Concepts and Perspectives, Wiley, 1st edn, 1995.
2. X. Li, L. Liu and H. B. Schlegel, J. Am. Chem. Soc., 2002, 124, 9639–9647.
3. S. Scheiner, J. Phys. Chem. B, 2006, 110, 18670–18679.
4. L. Pauling, J. Am. Chem. Soc., 1931, 53, 1367–1400.
5. I. V. Alabugin, M. Manoharan, S. Peabody and F. Weinhold, J. Am. Chem. Soc., 2003, 125, 5973–5987.
6. G. Trudeau, J. M. Dumas, P. Dupuis, M. Guérin and C. Sandorfy, Top. Curr. Chem., 1980, 93, 91–125.
7. Y. Mao and M. Head-Gordon, J. Phys. Chem. Lett., 2019, 10, 3899–3905.
8. A. Vashchenko and A. Afonin, J. Struct. Chem., 2014, 55, 636–643.
9. M. Domagała and S. J. Grabowski, J. Phys. Chem. A, 2005, 109, 5683–5688.
10. J. Joseph and E. D. Jemmis, J. Am. Chem. Soc., 2007, 129, 4620–4632.
11. F. Weinhold and C. R. Landis, Valency and Bonding: A Natural Bond Orbital Donor-Acceptor Perspective, Cambridge University Press, Cambridge, 2005.
12. O. Donoso-Tauda, P. Jaque and J. C. Santos, Phys. Chem. Chem. Phys., 2011, 13, 1552–1559.
13. C. Wang, D. Danovich, S. Shaik and Y. Mo, J. Chem. Theory Comput., 2017, 13, 1626–1637.
14. Y. Mo, C. Wang, L. Guan, B. Braïda, P. C. Hiberty and W. Wu, Chem.–Eur. J., 2014, 20, 8444–8452.
15. S. Michielssens, N. T. Trung, M. Froeyen, P. Herdewijn, M. T. Nguyen and A. Ceulemans, Phys. Chem. Chem. Phys., 2009, 11, 7274–7285.
16. N. T. Trung, T. T. Hue, M. T. Nguyen and T. Zeegers-Huyskens, Phys. Chem. Chem. Phys., 2008, 10, 5105–5113.
17. N. T. Trung, T. T. Hue and M. T. Nguyen, Can. J. Chem., 2010, 88, 849–857.
18. N. T. Trung, T. T. Hue and M. T. Nguyen, Phys. Chem. Chem. Phys., 2009, 11, 926–933.
19. Y. Gu, T. Kar and S. Scheiner, J. Am. Chem. Soc., 1999, 121, 9411–9422.
20. A. C. Pierce, E. ter Haar, H. M. Binch, D. P. Kay, S. R. Patel and P. Li, J. Med. Chem., 2005, 48, 1278–1281.
21. S. Pingali, J. P. Donahue and F. Payton-Stewart, Acta Crystallogr., Sect. C: Struct. Chem., 2014, 70, 388–391.
22. L. Spada, Q. Gou, M. Vallejo-López, A. Lesarri, E. J. Cocinero and W. Caminati, Phys. Chem. Chem. Phys., 2014, 16, 2149–2153.
23. P. Hobza and Z. Havlas, Chem. Rev., 2000, 100, 4253–4264.
24. S. R. Garde and R. N. Shirsat, Electrostatics of Atoms and Molecules, Sangam Books Ltd, Hyderabad, 2001.
25. P. Hobza, V. Špirko, H. L. Selzle and E. W. Schlag, J. Phys. Chem. A, 1998, 102, 2501–2504.
26. R. Gopi, N. Ramanathan and K. Sundararajan, J. Phys. Chem. A, 2014, 118, 5529–5539.
27. B. Behera and P. K. Das, J. Phys. Chem. A, 2019, 123, 1830–1839.
28. K. S. Rutkowski, S. M. Melikova, M. Rospenk and A. Koll, Phys. Chem. Chem. Phys., 2011, 13, 14223–14234.
29. I. S. Sosulin, E. S. Shiryaeva, D. A. Tyurin and V. I. Feldman, J. Phys. Chem. A, 2018, 122, 4042–4047.
30. X. Chang, Y. Zhang, X. Weng, P. Su, W. Wu and Y. Mo, J. Phys. Chem. A, 2016, 120, 2749–2756.
31. R. H. Crabtree and A. Lei, Chem. Rev., 2017, 117, 8481–8482.
32. P. Khanh, V. Ngan, N. Man, N. T. Ai Nhung, A. Chandra and N. Trung, RSC Adv., 2016, 6, 106662–106670.
33. N. T. Trung, P. N. Khanh, A. J. P. Carvalho and M. T. Nguyen, J. Comput. Chem., 2019, 40, 1387–1400.
34. N. Thi Hong Man, P. Le Nhan, V. Vo, D. Tuan Quang and N. Tien Trung, Int. J. Quantum Chem., 2017, 117, e25338.
35. N. T. Trung, N. P. Hung, T. T. Hue and M. T. Nguyen, Phys. Chem. Chem. Phys., 2011, 13, 14033–14042.
36. P. Hobza, V. Špirko, Z. Havlas, K. Buchhold, B. Reimann, H.-D. Barth and B. Brutschy, Chem. Phys. Lett., 1999, 299, 180–186.
37. I. Bhattacharya, J. Sadhukhan, S. Biswas and T. Chakraborty, J. Phys. Chem. A, 2020, 124, 7259–7270.
38. A. K. Chandra and T. Zeegers-Huyskens, J. At., Mol., Opt. Phys., 2012, 2012, e754879.
39. N. T. T. Cuc, C.-T. D. Phan, N. T. A. Nhung, M. T. Nguyen, N. T. Trung and V. T. Ngan, J. Phys. Chem. A, 2021, 125, 10291–10302.
40. K. Tabayashi, O. Takahashi, H. Namatame and M. Taniguchi, Chem. Phys. Lett., 2013, 557, 1–9.
41. R. W. Gora, S. J. Grabowski and J. Leszczynski, J. Phys. Chem. A, 2005, 109, 6397–6405.
42. T. S. Thakur, M. T. Kirchner, D. Bläser, R. Boese and G. R. Desiraju, Phys. Chem. Chem. Phys., 2011, 13, 14076–14091.
43. Y. Yang and W. Zhang, Acta Chim. Sin., 2009, 67, 599–606.
44. A. Kovács, A. Szabó, D. Nemcsok and I. Hargittai, J. Phys. Chem. A, 2002, 106, 5671–5678.
45. D. Kaur and R. Kaur, J. Chem. Sci., 2015, 127, 1299–1313.
46. A. K. Chandra and T. Zeegers-Huyskens, J. Comput. Chem., 2012, 33, 1131–1141.
47. N. T. Trung, T. T. Hue and M. T. Nguyen, J. Phys. Chem. A, 2009, 113, 3245–3253.
48. D. Voet, J. G. Voet and C. W. Pratt, Fundamentals of Biochemistry, Wiley, New York, Upgrade edn, 2001.
49. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman and J. A. Pople, Gaussian 09 (Revision B.01), Gaussian Inc., Wallingford, CT, 2009.
50. M. Head-Gordon, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1988, 153, 503–506.
51. K. E. Riley, J. A. Platts, J. Řezáč, P. Hobza and J. G. Hill, J. Phys. Chem. A, 2012, 116, 4159–4169.
52. K. E. Riley and P. Hobza, J. Phys. Chem. A, 2007, 111, 8257–8263.
53. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
54. T. A. Keith and T. K. Gristmill, AIMAll (Version 19.10.12) Software, Overland Park, KS, USA, 2019.
55. P. L. Popelier, Atoms in Molecules: An Introduction, Prentice Hall, Harlow, 1 edn, 2000.
56. R. F. W. Bader, Atoms in molecules: a quantum theory, Clarendon Press, Oxford, New York, 1990.
57. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
58. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173.
59. E. D. Glemdeming, J. K. Baderhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, GenNBO5.G, Theoretical Chemistry Institute, University of Wisconsin Madison, WI, 2001.
60. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
61. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
62. P. A. Kollman, in Chemical Applications of Atomic and Molecular Electrostatic Potentials: Reactivity, Structure, Scattering, and Energetics of Organic, Inorganic, and Biological Systems, ed. P. Politzer and D. G. Truhlar, Springer US, Boston, MA, 1981, pp. 243–255.
63. R. Bukowski, W. Cencek, M. Jeziorska, B. Jeziorski, V. F. Lotrich, A. J. Misquitta, R. Moszyński, K. Patkowski, R. Podeszwa, F. Rob, S. Rybak, K. Szalewicz, R. J. Wheatley, E. S. Paul, P. E. S. Wormer and P. S. Żuchowski, SAPT2012.2, Warsaw, Poland, 2013.
64. R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince, E. G. Hohenstein, U. Bozkaya, A. Yu. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 13, 3185–3197.
65. R. Kalescky, E. Kraka and D. Cremer, Mol. Phys., 2013, 111, 1497–1510.
66. W. Qian and S. Krimm, J. Phys. Chem. A, 2002, 106, 11663–11671.
67. L. Spada, L. Evangelisti, W. Li, R. Orlacchio and W. Caminati, J. Phys. Chem. A, 2019, 123, 1785–1789.
68. Q. Zhang and L. Du, Comput. Theor. Chem., 2016, 1078, 123–128.
69. Q.-Z. Li, B. Jing, R. Li, Z.-B. Liu, W.-Z. Li, F. Luan, J.-B. Cheng, B.-A. Gong and J.-Z. Sun, Phys. Chem. Chem. Phys., 2011, 13, 2266–2271.
70. N. T. T. Cuc, N. T. An, V. T. Ngan, A. K. Chandra and N. T. Trung, RSC Adv., 2022, 12, 1998–2008.
71. A. S. Hansen, L. Du and H. G. Kjaergaard, Phys. Chem. Chem. Phys., 2014, 16, 22882–22891.
72. B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930.
73. U. Koch and P. L. A. Popelier, J. Phys. Chem., 1995, 99, 9747–9754.
74. W. D. Arnold and E. Oldfield, J. Am. Chem. Soc., 2000, 122, 12835–12841.
75. I. Rozas, I. Alkorta and J. Elguero, J. Am. Chem. Soc., 2000, 122, 11154–11161.
76. M. Guin, K. Rautela, R. A. Roopa, C. S. Shantharam and S. Begam Elavarasi, Comput. Theor. Chem., 2021, 1196, 113134.
77. B. G. Oliveira, J. Chil. Chem. Soc., 2011, 56, 601–605.
78. S. Bedoura, H.-W. Xi and K. Lim, J. Phys. Org. Chem., 2014, 27, 226–236.
79. D. Kaur, D. Aulakh, S. Khanna and H. Singh, J. Sulfur Chem., 2014, 35, 290–303.
80. J. Lei, S. Alessandrini, J. Chen, Y. Zheng, L. Spada, Q. Gou, C. Puzzarini and V. Barone, Molecules, 2020, 25, 4899.
81. N. T. T. Cuc, H. Q. Dai, N. T. A. Nhung, N. P. Hung and N. T. Trung, Vietnam J. Chem., 2019, 57, 425–432.
82. Q. Gou, L. B. Favero, S. S. Bahamyirou, Z. Xia and W. Caminati, J. Phys. Chem. A, 2014, 118, 10738–10741.
83. E. Sánchez-García, L. A. Montero and W. Sander, J. Phys. Chem. A, 2006, 110, 12613–12622.

---

Footnote

† Electronic supplementary information (ESI) available: Tables and figures list of contact distances, the AIM analysis, MEP analysis, SAPT analysis, NCI plot, length changes, and stretching frequency shifts of the C_sp²–H and O–H bonds in the complexes. See DOI: https://doi.org/10.1039/d2ra05391h

---