Open Access Article
Open Access ArticleParameter estimation of three-parameter Weibull probability model based on outlier detection†
Hang Zhang‡
,
Zhefeng Gao‡,
Chenran Du ,
Shansong Bi,
Yanyan Fang*,
Fengling Yun,
Sheng Fang,
Zhanglong Yu,
Yi Cui and
Xueling Shen
,
Shansong Bi,
Yanyan Fang*,
Fengling Yun,
Sheng Fang,
Zhanglong Yu,
Yi Cui and
Xueling Shen
China Automotive Battery Research Institute Co., Ltd., No. 11 Xingke East Street, Yanqi Economic Development Area, Huairou District, Beijing, 101407, China. E-mail: fangyy@glabat.com
First published on 30th November 2022
Abstract
The Weibull probability model used in statistical analysis has become more popular in the inconsistency evaluation of used Li-ion batteries due to its flexibility in fitting asymmetrically distributed data. However, despite its better fitting of data with a non-zero minimum, the three-parameter Weibull model is less used because of its complicated calculation. Additionally, the Weibull family is likely to overfit and shows inference from outliers. Although conventional estimation methods for Weibull parameters based on dispersion and symmetry of the overall distribution lead to derivation from the actual data features, there is little research into methods to solve the contradiction between estimation accuracy and proper outlier detection. In this study, a Weibull parameter estimation method was proposed that features simplified computation and eliminates the interference from outliers. The outliers were identified based on the obtained Weibull parameters and excluded from the sample data. The method was implemented for fitting the capacity distribution of Li-ion batteries, which was verified by a chi-square test at a confidence of 95% and the Anderson–Darling test. It showed a higher goodness-of-fit and less error than the results of the maximum likelihood estimated Weibull model as well as the normal distribution. The optimal presetting of column number and peak reference point selection were determined by parameter discussion.
Introduction
As Li-ion batteries become promising as power supplies for vehicles, research interest in battery lifetime behavior is rising. To better describe this, probability models have been used, among which the Weibull model is a practical one.The Weibull distribution1 has shown wide applicability since its first appearance. It is used in fields including survival analysis, reliability engineering, and extreme value theory. To amplify the relevance of the Weibull, a regression structure can be added to one of the parameters, i.e., the behavior of the distribution may be explained from covariates (explanatory variables) and unknown parameters can be estimated from the observable data.
The Weibull probabilistic model is applied to the consistency evaluation of lithium-ion batteries. It quantitatively describes the distribution characteristics of battery capacity, internal resistance, voltage and other parameters.2,3 Since lithium-ion batteries are nonlinear systems, the parameter distribution is not always symmetrical.4 When the mean value deviates from the midpoint of the maximum and minimum values, the eigenvalues of the normal model cannot capture this asymmetry. Regardless of whether the batteries are grouped or not, the statistical values of the normal distribution model will lead to deviations in predicting the battery consistency. However, the asymmetric distributions of the battery parameters usually reflect important characteristics of the battery, providing an effective statistical basis for the formation and evolution of the consistency of the battery.5 Therefore, the asymmetric distribution characteristics of the battery give an accurate statistical understanding of the consistency characteristics of the battery and provide a reliable foundation for battery consistency prediction and control.6
In addition to the Weibull model, two other statistical distributions have been used to describe the material data: the normal distribution and the lognormal distribution.7–9 Comparatively, the two-parameter Weibull distribution is mostly used because: (a) it is more accurate in describing glass strength data than the normal distribution,2 and (b) it is always more conservative in the tail of the distribution than the lognormal distribution.3 Conservative estimates are preferred for engineering design applications considering the safety margin. As a result, the Weibull distribution is the established way of describing battery capacity data in both academic studies10,11 and engineering applications.12–14
The normal distribution is also widely used to describe engineering data. Also known as the Gaussian distribution, it is a symmetrical distribution. Some characteristics of Li-ion batteries have been found to follow a normal distribution, especially for newly produced batteries.15 Its usage has also expanded to describe other characteristics of batteries. Specifically, compared with new cells, retired battery cells behave less consistently and have a more left-skewed capacity distribution.16 This asymmetrical tendency is likely to be better described by the Weibull distribution, indicating its potential in describing Li-ion battery data.
Consistency evaluation methods for the asymmetric distribution of batteries are mainly based on the two-parameter Weibull distribution model, because it requires little calculation, and the asymmetry characteristics of the battery consistency distribution can be indicated by the change of shape parameters. The two-parameter Weibull distribution model defaults the minimum value of the distribution as 0, but the values of the capacity, internal resistance, and voltage of batteries are usually non-zero. If 0 is used as the minimum value of the distribution range, the Weibull size parameter and the shape parameter will lose accuracy in describing the distribution characteristics. Adopting a three-parameter Weibull distribution model will effectively avoid this problem. S. J. Harris applied two- and three-parameter Weibull models to consistency studies of battery life.17 The capacity distribution of 24 batteries was statistically analyzed using a Weibull distribution, and the optimal estimation of Weibull parameters was obtained using the great likelihood probability method. It was found that the symmetry of the capacity distribution is constantly changing during the cycling process. The location parameters in the three-parameter Weibull model varied with the distribution range, accurately describing the minimum value of the distribution range.18 Based on the parameter behaviors, the Weibull dimensional and shape parameters will reflect the discrete and symmetrical characteristics of the distribution more accurately.
The symmetry of the Weibull distribution must be verified by statistical inference. In the statistical inference, the Wald test is often performed to test whether the regression parameters are statistically significant. In the case of standard regularity, the null hypothesis of the statistic is asymptotically chi-squared, a consequence of the maximum likelihood estimators (MLE) distribution.19 If the distribution is symmetrical, the skewness coefficient γ equals zero. However, there are asymmetrical distributions with as many zero-odd order central moments as desired,20 so the value of γ must be interpreted with caution.
In statistical studies, several regression models do not have closed-form estimation for the skewness coefficient γ of the MLE.21 Another researcher obtained a general expression for the distribution of the MLE.22 The sample size was also taken into account. Following previous achievements, several studies have been conducted in order to obtain the skewness coefficient. One research study determined the expression for the class of generalized linear models.23 Another defined the coefficient for the varying dispersion beta regression model and showed that this coefficient for the distribution of the MLE of the precision parameter is relatively large in samples of small to moderate size.24 For the three-parameter Weibull distribution, the formula for skewness and the parameters is complicated and relatively difficult to solve together with the estimation of the mean value and the variance. Due to this complexity, numeric experiment methods, such as the Monte Carlo method, have been carried out in the studies, which is relatively costly in terms of computation.25 To reduce the complexity and the computational resource requirements of solving the problem, this work proposes a novel method to estimate the three parameters for a Weibull model used in Li-ion battery data. Another indicator of the asymmetry will be used in this work, which is defined to simplify the computation.
There have been studies using three-parameter Weibull distribution in Li-ion battery data analysis. However, overfitting and failure to capture the features of the data were reported when using the three-parameter model with MLE estimated parameters.17,24 This indicated that the usage of the three-parameter Weibull model for Li-ion battery data required further investigation of other possible parameter estimation methods. To explore the feasibility of the three-parameter Weibull distribution in Li-ion battery analysis, a robust parameter estimation method must be investigated and validated.
The Weibull estimation is extremely sensitive to errors. The properties of a distribution can easily be impacted. Outliers in the data, especially in the censoring data, usually introduce significant error in the estimation algorithm and threaten the accuracy of the estimation. However, only a few studies have focused on error exclusion. One investigation identified outliers using 6σ theory to eliminate data far from the distribution range.26 This method is Gauss-based and is not feasible in Weibull distributions. Another excluded the data with which the MLE value was more sensitive.27 However, the estimation method requires primary knowledge of the number of the outliers and assumes that the outliers occur on one side of the distribution. Thus, it would be helpful to find an outlier detection method that could automatically find the location and number of outliers.28
With the possibility of capturing asymmetrical features and a flexible minimum value of the random variable, the three-parameter Weibull model has the potential to describe and predict the behaviors of Li-ion batteries. It has been used in some investigations to fit the capacity data of Li-ion batteries, and is especially suitable for used battery data. However, due to the complexity between the model skewness and the statistics, the overfitting tendency of the MLE method results, and the possibility of outlier inference, the performance of the three-parameter Weibull model in Li-ion battery inconsistency analysis has been limited. Investigation of a more feasible and robust parameter estimation method for the three-parameter Weibull model is needed.
In this work, a method of parameter estimation was proposed to predict the three-parameter Weibull distribution based on the data excluding possible outliers. The approximately linear feature of the Weibull cumulative distribution was used to derive the parameters of the Weibull distribution of the symmetry, as well as to recognize and exclude outliers in the raw data. Using the simply defined asymmetry indicator avoided the need to solve complex equations or numeric experiments. The proposed method is promising for estimating the three-parameter Weibull model without costly computations or inference from outliers. It aims to provide a reliable and simple way to estimate the three parameters for the Weibull model and then extend the application of this model to Li-ion battery inconsistency evaluation.
In this paper, the above method was implemented in the processing of Li-ion battery capacity data. The relevant three-parameter Weibull model was obtained and validated using the chi-square test and the Anderson–Darling test. The fitting result with the Weibull distribution was compared with the parameters estimated by MLE and the normal distribution.
Theory and methods
Three-parameter Weibull probability model
The Weibull model is constructed by the Weibull probability density function (PDF) and cumulative density function (CDF), which are expressed using the scale parameter A, shape parameter B and location parameter C, as shown in formula (1) and (2).29 The Weibull CDF is the integral of Weibull PDF for x from 0 to 1.
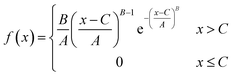 | (1) |
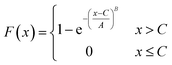 | (2) |
The plots of the Weibull PDF and CDF are presented in Fig. 1, while only the Weibull model with B larger than 1 is discussed and applied in this paper.
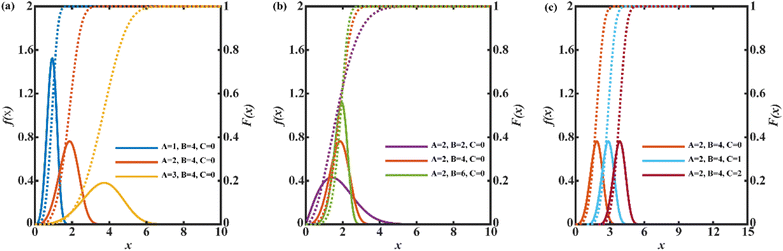 | ||
| Fig. 1 Weibull PDF (solid line) and CDF (dashed line) plots with various values of (a) scale parameter A, (b) shape parameter B and (c) location parameter C. | ||
To be used for the distribution evaluation, the statistical implication of the three Weibull parameters must be clarified. The scale parameter A reflects the dispersion of a distribution. In Fig. 1(a), the PDF and CDF curves are stretched as A increases. The shape parameter B reflects the symmetry characteristic of a distribution. In Fig. 1(b), the PDF curve with a smaller B (B = 2) has a peak closer to the left limit of the x range and a longer tail on the right side, indicating that more random variables are distributed in the low-value region. Given the left-skewed distribution, the CDF slope grows more quickly than the others before x = A and slows down after. As the value of B grows larger, the PDF peak moves to the right and the rapid rise in the CDF occurs later, but it approaches 1 more quickly, which means that the major variables are concentrated on the right side. According to ref. 13, when B is between 3 and 5, the PDF indicates a symmetric distribution. Otherwise, when B is smaller than 3, the distribution is supposed to be left-skewed. When B is larger than 5, the distribution is right-skewed. The location parameter C controls the start point of the x range. It is the lower limit of the random variables. In Fig. 1(c), the PDF and CDF curves move along the x axis without morphing as the C value varies. When C is equal to 0, it is called the two-parameter Weibull model as well, as shown in Fig. 1(a) and (b). Hence, the Weibull parameters are supposed to describe the flexible features of a Weibull distribution. The statistical nature can be quantified using the estimated Weibull parameters.
Weibull parameter deduction
To support a more definite expression for the Weibull distribution, reparameterization was developed by deducing the Weibull function with three parameters. Based on the principle of a symmetry distribution, the exact location of the PDF peak can be obtained. In this paper, the x value corresponding to the Weibull peak is denoted as xp, which can be solved by the derivative of Weibull PDF, as shown in formula (3).
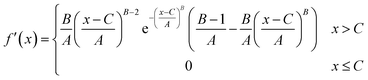 | (3) |
The expression for xp can be obtained when the expression in formula (3) equals 0, as shown in formula (4).
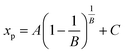 | (4) |
Value of Weibull PDF and CDF at xp:
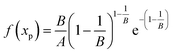 | (5) |
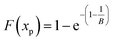 | (6) |
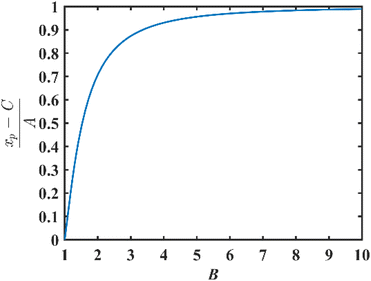
Formula (4) shows that xp is expressed as a variable close to A. The difference between A and xp is determined by a factor related to the shape parameter B, which can be discussed in form of (xp − C)/A as shown in Fig. 2.
Symmetry is quantified as the ratio of cumulative probability on the left and right of xp, denoted as η. This ratio can be deduced from the Weibull CDF and simplified to a function of B, as shown in formula (7), which establishes the direct relationship between the two parameters related to symmetry of the distribution.
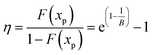 | (7) |
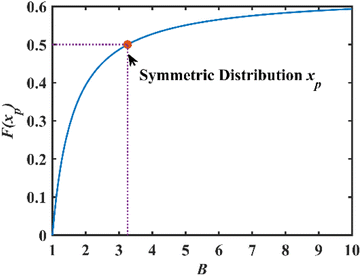
The CDF at xp in formula (6) is only related to shape parameter B, which means that the cumulative probability at xp is an indicator of the distribution symmetry. When F(xp) is 0.5, the Weibull distribution is symmetric and equivalent to a Gaussian distribution. In this case, probability distribution on the left and right side is equal. Thus, the value of B for the symmetric distribution can be calculated to be 3.2589, as shown in Fig. 3.
The shape parameter B can be regarded as an indicator of left-skewed and right-skewed distributions: B < 3.2598, left-skewed distribution; B = 3.2598, symmetric distribution; B < 3.2598, right-skewed distribution.
The PDF at xp in formula (5) is related to A and B. Because of the A in the denominator, the PDF at xp decreases with increasing A, which agrees with the stretching effect of A on the PDF curve.
Out of concern for the symmetry of Weibull distribution, the location of xp is deduced, and the properties of CDF and PDF at xp are discussed. The proposed functions at xp are promising to estimate the Weibull parameters and evaluate the Weibull distribution.
Statistical processing of the distribution
Before estimation of the Weibull parameters, the sample data must be processed statistically. The range of the distribution is separated into n equally spaced subintervals, denoted as {x1, x2, x2, x3, …, xn, xn+1}. For convenience of recording, the position of the ith subinterval is denoted by its mid-value, as shown in formula (8).
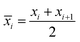 | (8) |
The probability in the ith subinterval is denoted as pi. The cumulative probability density of the ith subinterval is summed from p1 to pi, as shown in formula (9). The probability density of the ith subinterval is the difference of pi with respect to xi, as shown in formula (10).
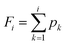 | (9) |
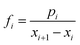 | (10) |
Symmetry based estimation (SBE) of Weibull parameters
For the sake of the estimation of the Weibull parameters, the basic variables must first be obtained from the distribution, such as the location of xp, and the CDF and PDF at xp. The location of xp is determined by three subintervals {![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,1,
p,1, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,2,
p,2, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,3} (denoted as
p,3} (denoted as ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) p) with three maximums of probability {
p) with three maximums of probability {![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) p,1,
p,1, ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) p,2,
p,2, ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) p,3} (denoted as
p,3} (denoted as ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) p). The value of xp is the weighted mean value of
p). The value of xp is the weighted mean value of ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) p, where
p, where ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) p is used as the weighting coefficient, as expressed in formula (11).
p is used as the weighting coefficient, as expressed in formula (11).
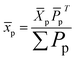 | (11) |
The probability density at ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p is defined as the mean value of {
p is defined as the mean value of {![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p,1,
p,1, ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p,2,
p,2, ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p,3}, which is the probability density of {
p,3}, which is the probability density of {![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,1,
p,1, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,2,
p,2, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,3}, as shown in formula (12).
p,3}, as shown in formula (12).
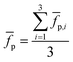 | (12) |
To estimate ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) , the cumulative probability at the peak,
, the cumulative probability at the peak, ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p, is calculated based on the cumulative probability of three probability peaks, as shown in formula (13).
p, is calculated based on the cumulative probability of three probability peaks, as shown in formula (13).
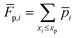 | (13) |
As ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p is the weighted mean value of {
p is the weighted mean value of {![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,1,
p,1, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,2,
p,2, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,3}, there is a tiny distance between
p,3}, there is a tiny distance between ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p and {
p and {![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,1,
p,1, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,2,
p,2, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,3}. As shown in Fig. 1, the relationship between {
p,3}. As shown in Fig. 1, the relationship between {![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,1,
p,1, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,2,
p,2, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,3} and {
p,3} and {![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p,1,
p,1, ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p,2,
p,2, ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p,3} is approximately linear, such as the form in formula (14).
p,3} is approximately linear, such as the form in formula (14).
a·![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p + b = p + b = ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p p
| (14) |
Therefore, a group of linear equations of {![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,1,
p,1, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,2,
p,2, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,3} and {
p,3} and {![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p,1,
p,1, ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p,2,
p,2, ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p,3} are built to obtain the linear relationship of the Weibull CDF at xp, as shown in formula (15).
p,3} are built to obtain the linear relationship of the Weibull CDF at xp, as shown in formula (15).
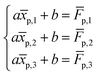 | (15) |
The equations in formula (14) are coupled with each other, and the unknown coefficients a and b can be solved thrice. The mean of three sets of solutions is used to calculate ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p in formula (14). Then
p in formula (14). Then ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) can be calculated by formula (7).
can be calculated by formula (7).
The Weibull parameters are estimated based on the function relationship with the achieved distribution characteristic variables ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p and
p and ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) . Firstly, the shape parameter B is calculated using
. Firstly, the shape parameter B is calculated using ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) , based on formula (7), as shown in formula (16).
, based on formula (7), as shown in formula (16).
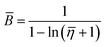 | (16) |
Secondly, the scale parameter A can be obtained based on formula (5) with the calculated ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) and
and ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p, as shown in formula (17).
p, as shown in formula (17).
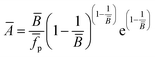 | (17) |
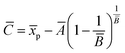 | (18) |
In this way, the Weibull parameters are estimated based on the distribution characteristics. Given the relationship between the Weibull parameters and statistical features of the distribution, the Weibull parameters carry sufficient statistical information. The estimated Weibull distribution reflects the global features of the experimental distribution.
Normal distribution estimation
The normal distribution has the PDF and CDF expressions given in formula (19) and (20).29
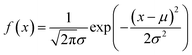 | (19) |
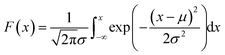 | (20) |
μ is the location parameter of the distribution, which indicates the location of the PDF symmetry axis. It is also the mean value of the random variables following the normal distribution. σ is the dispersion parameter. Variables with larger σ are more concentrated around the symmetric axis. σ2 is also the variance of the random variables.
According to the MLE of the normal distribution parameters, μ and σ2 can be estimated by the mean value and the variance of the sample data, respectively.
Verification of estimation
The Pearson chi-square test was used for distribution verification of the models at the 95% confidence level. The number of degrees of freedom was set as n – 4. It is determined by the number of intervals in distribution, n, and the three parameters. Similarly, in the case of the normal distribution, the number of degrees of freedom is n – 3. When the χ5%2(n − 4) is less than the given upper limiting value, the estimated result is considered to be true and the estimated Weibull distribution is consistent with the experimental distribution. In the opposite case, the estimation is considered to be a false one and the estimated Weibull distribution is considered to deviate from the experimental distribution. Furthermore, since the value of χ5%2(n − 4) stands for the goodness-of-fit of the Weibull distribution to the experimental data, it can be used as an indicator of the estimation error. The p-value is the probability corresponding to a certain χ2 value, suggesting the probability of obtaining an observation the same as the sample when the hypothesis is true. It also shows the acceptance of the hypothesis, as well as the goodness-of-fit of the model.Results and discussion
Pre-processing of data and outlier detection
The SBE estimation method was implemented to evaluate the capacity distribution of a batch of Li-ion batteries. For the sake of sufficient sample data, 122 cells were randomly selected from the population of 3427 cells. The actual capacity was measured at a discharge current of 8.3333 A h. The basic statistical information of the obtained capacity data is listed in Table 1. The capacity of the cells is distributed from 26.9097 A h to 27.7966 A h. The performance of the proposed Weibull estimation method was evaluated based on decreasing the value of χ2(n − 4) to provide reduced fitting error and improved approximation of the distribution of capacity data.| Statistical characteristic | Maximum | Minimum | Mid-value | Mean | Standard variation |
|---|---|---|---|---|---|
| Value | 27.7966 A h | 26.9097 A h | 27.3156 A h | 27.3181 A h | 0.1549 A h |
The distribution range of the capacity data was divided into 20 equally spaced subintervals; the width of each subinterval was 0.0460 A h. The probability, probability density and mid-value in each subinterval are presented in Fig. 4.
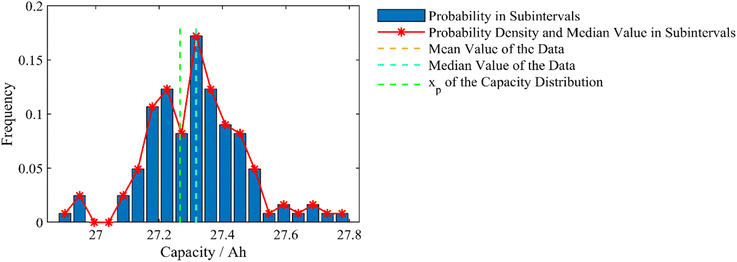 | ||
| Fig. 4 Capacity distribution probability histogram and probability density line chart with mid-value, mean and xp of the capacity distribution. | ||
In Fig. 4, two continuous subintervals with minimal probabilities at the mid-values of 26.9300 A h and 26.9762 A h are distanced from the overall distribution by two blank subintervals. For this reason, the lower boundary (mid-value) was extended from 27.1092 A h to 26.9300 A h, which makes a great impact on the mid-value of the capacity distribution, less impact on the mean value and little impact on xp. The value of xp is 27.2658 A h, as computed using formula (10). As shown in Fig. 4, the mid-value and mean of the capacity distribution are close to each other, which suggests the distribution of the capacity data is symmetric. However, the xp is obviously lower than the mid-value and mean of the capacity distribution, which denotes the distribution is left-skewed. This contradictory conclusion is attributed to the isolated subintervals, and these subintervals cause the type of capacity distribution to be misidentified. Using the SBE method in this study, the Weibull parameters were estimated based on the characteristics of the probability peak, and the interference from the isolated subintervals is eliminated. Furthermore, the estimated parameters can set up the interval consistent with the major characteristics of the distribution, and the stray subintervals can be confirmed to be outliers if they fall outside the correct interval.
Estimation of Weibull parameters
The three subintervals with three maximum probability values were used to determine {![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,1,
p,1, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,2,
p,2, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,3} and {
p,3} and {![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p,1,
p,1, ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p,2,
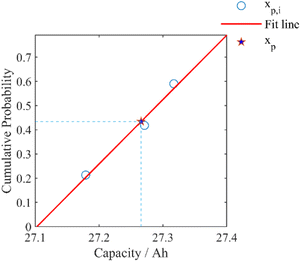
p,2, ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p,3}, as listed in Table 2. The linear system of equations established by any two of the three equations are coupled for one pair of solutions of a and b in formula (14), as presented in Table 3. The mean of three groups of [a b] are set as the coefficients of formula (14).
p,3}, as listed in Table 2. The linear system of equations established by any two of the three equations are coupled for one pair of solutions of a and b in formula (14), as presented in Table 3. The mean of three groups of [a b] are set as the coefficients of formula (14). ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p can then be computed by inserting xp into formula (14), as shown in Fig. 5. The obtained value of
p can then be computed by inserting xp into formula (14), as shown in Fig. 5. The obtained value of ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p is 0.4340, indicating that the peak of the distribution is deflected to the left.
p is 0.4340, indicating that the peak of the distribution is deflected to the left.
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,i
p,i
| i | ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,i p,i |
F(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p,i) p,i) |
|---|---|---|
| 1 | 27.3170 | 0.5902 |
| 2 | 27.1790 | 0.2131 |
| 3 | 27.2710 | 0.4180 |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) p p |
![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p p |
|
| Mean | 27.2658 | 0.4340 |
| i | a | b |
|---|---|---|
| 1, 2 | 2.7326 | −74.0565 |
| 1, 3 | 3.7435 | −101.6704 |
| 2, 3 | 2.2272 | −60.3193 |
| Mean | 2.6601 | −72.0791 |
With the value of ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p, the value of
p, the value of ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) can be obtained based on formula (7), which indicates the symmetry of the capacity distribution. The result of
can be obtained based on formula (7), which indicates the symmetry of the capacity distribution. The result of ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) is 0.7667, which means the capacity distribution is left-skewed.
is 0.7667, which means the capacity distribution is left-skewed.
Based on the intermediate parameters of xp, ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p and
p and ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) , the Weibull parameters can be deduced. To prove the accuracy of the estimation method, MLE was selected to provide a set of comparative results. Given the statistical features of the data including the mean value and the variance, the parameters of the normal distribution can also be obtained. In Table 4, the estimated distribution models are verified by the value of χ2. The χ2 of the above SBE is less than that of the MLE Weibull model and the normal distribution, which means that SBE provides a better fit. Therefore, SBE provides a description of the distribution characteristics closer to the true one. The Ā of the SBE is less than that of MLE, which means that the discreteness of the capacity distribution becomes narrower after the outliers are removed. The
, the Weibull parameters can be deduced. To prove the accuracy of the estimation method, MLE was selected to provide a set of comparative results. Given the statistical features of the data including the mean value and the variance, the parameters of the normal distribution can also be obtained. In Table 4, the estimated distribution models are verified by the value of χ2. The χ2 of the above SBE is less than that of the MLE Weibull model and the normal distribution, which means that SBE provides a better fit. Therefore, SBE provides a description of the distribution characteristics closer to the true one. The Ā of the SBE is less than that of MLE, which means that the discreteness of the capacity distribution becomes narrower after the outliers are removed. The ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) of SBE is found to be smaller, so the capacity distribution becomes more left-skewed after the outliers are removed. The
of SBE is found to be smaller, so the capacity distribution becomes more left-skewed after the outliers are removed. The ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) of SBE is larger than that of MLE, which means that the outliers are on the left side of the distribution. The result show that SBE provides a better recognition of the statistical characteristics of the capacity distribution. Additionally, comparison of the χ2 test p-values among the Weibull models, the normal distribution and a lognormal distribution from ref. 31 are provided in Table 4. It shows that the p-value achieved in this work is relatively significant and the data features are mostly captured by the probability models.
of SBE is larger than that of MLE, which means that the outliers are on the left side of the distribution. The result show that SBE provides a better recognition of the statistical characteristics of the capacity distribution. Additionally, comparison of the χ2 test p-values among the Weibull models, the normal distribution and a lognormal distribution from ref. 31 are provided in Table 4. It shows that the p-value achieved in this work is relatively significant and the data features are mostly captured by the probability models.
| Ā | ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) |
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) |
χ2 (χ5%2(16) = 26.2962) | p value | |
|---|---|---|---|---|---|
| SBE Weibull | 0.3583 | 2.3209 | 27.0277 | 2.4680 | 0.99996 |
| MLE Weibull | 0.5366 | 3.3941 | 26.8341 | 4.4014 | 0.99802 |
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/char_e0cd.gif) |
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/char_e0d2.gif) 2 2 |
χ2 (χ5%2(17) = 27.5871) | p value | ||
| MLE normal | 27.3181 | 0.0228 | 4.0028 | 0.99948 | |
| Reference | p value | ||||
| Lognormal31 | 0.5407 |
Additionally, the fitting of the three-parameter Weibull model in this work is also compared with results in other studies in Table 5 to give a general impression of the goodness-of-fit. The indicators of goodness-of-fit used are the Anderson–Darling value and the Lilliefors test result. The Anderson–Darling test is commonly used to test whether a data sample comes from a certain distribution. The smaller the Anderson–Darling value is, the more confident the claim that the data follow a certain distribution. The Lilliefors test is a two-sided goodness-of-fit test. When the test returns h = 0, it fails to reject the null hypothesis that the data follows the given distribution at a certain significance. Similar to in the chi-square test, the p-value is the probability of observing a test statistic as extreme as, or more extreme than, the observed value under the null hypothesis. It is an indicator of the test validity.30
| Reference | Model | Indicator | |
|---|---|---|---|
| Anderson–Darling value | Lilliefors test | ||
| Ref. 32 | 3-Parameter Weibull | 12.57 | |
| 3-Parameter lognormal | 12.56 | ||
| 3-Parameter loglogistic | 12.49 | ||
| 2-Parameter exponential | 12.68 | ||
| Ref. 16 | Weibull model | h = 0, p = 0.112 | |
| Ref. 33 | Normal | 7.80 | |
| Lognormal | 2.88 | ||
| 3-Parameter Weibull | 35.81 | ||
| 3-Parameter log-Weibull | 13.58 | ||
| Ref. 34 | Normal | 18.16 | |
| Lognormal | 0.97 | ||
| 3-Parameter Weibull | 23.63 | ||
| 3-Parameter log-Weibull | 8.43 | ||
| This work | 1.30 | h = 0, p = 0.5 | |
The results of the comparison suggest the validity and goodness-of-fit of the SBE method in this work. Based on the Lilliefors test, it is safe to say that the data used follows the Weibull distribution. The Anderson–Darling value of the three-parameter Weibull model estimated using the SBE method is also relatively small, indicating a good fitting.
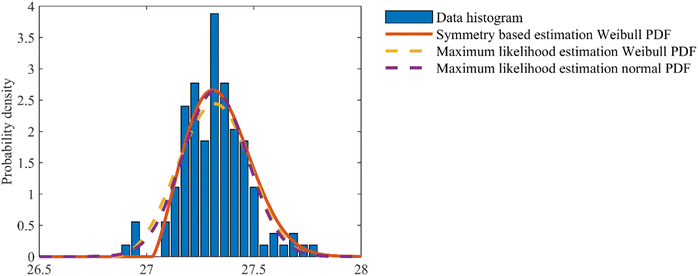
In Fig. 6, the Weibull PDFs are displayed with the estimated parameters by SBE and MLE, as well as the normal distribution. The outliers can be observed on the left of the distribution. With the outliers contained, the MLE estimated Weibull distribution and the normal distribution near the left tail of PDF fail to fit properly. Besides, the estimated PDF of SBE shows left-skewed distribution, which agrees with the capacity distribution without the outlier influence. It is confirmed that the SBE could provide a better fit for an asymmetric distribution. Thus, the SBE method can be implemented in predicting the asymmetric capacity distribution of Li-ion batteries.
Discussion on influence of estimation factors
It is noted that Weibull parameters are sensitive to the presupposition of the estimation algorithm, so we focused on variation in the column number n and xp,i in this paper.Influence of column number
Fig. 7 shows the change in the histogram with increasing number of columns. Fig. 7(a) displays the capacity distribution with only 15 columns, and the characteristics of the distribution are blurred out. Fig. 7(c) shows the capacity distribution with more segmentation, in which the distributions features are hard to distinguish. Thus, a proper number of separation columns, as shown in Fig. 7(b), improves the accuracy of the estimation. For different data distributions, the number n should be determined case-by-case.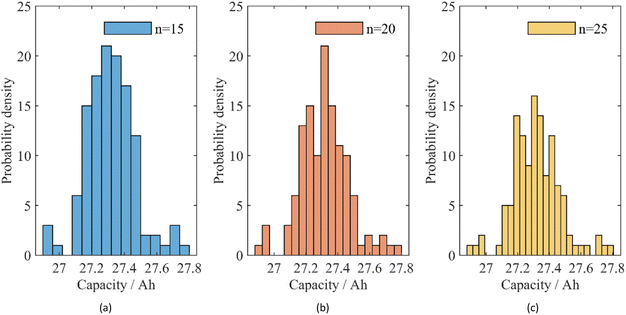 | ||
| Fig. 7 Histogram of capacity distribution separated into different numbers of columns: (a) 15 columns, (b) 20 columns, and (c) 25 columns. | ||
Table 6 lists the estimated Weibull parameters and χ2 with the three numbers of columns shown in Fig. 7. From these results, we can see that the estimations with more or less columns fail to perform better than that with 20. This comparison confirms that the number of columns is relevant for the estimation accuracy. This tendency has been reported in ref. 10.
| Number of columns | Scale parameter | Shape parameter | Location parameter | χ2 |
|---|---|---|---|---|
| 15 | 0.5434 | 3.9973 | 26.8294 | 12.5296 |
| 20 | 0.3583 | 2.3209 | 27.0277 | 2.4680 |
| 25 | 0.3845 | 3.5441 | 26.9903 | 10.6449 |
Influence of number of xp,i
Fig. 8 shows the change in xp with increasing the number of xp,i selected. The linear slope at the distribution peak is determined by the number of reference points. The selection of improper reference points leads to deviation of the fitting line at the peak from the CDF curve. Comparing the three selection modes listed in Table 7, the selections of two or four reference points gives larger errors than using three reference points, according to the values of χ2. When two reference points were chosen, the Weibull distribution is controlled by fewer peak columns, which means the random bias of the peaks can lead to more error. The fitting line corresponding to the four points deviates from the linear range of the CDF as well. Hence, a proper selection of the xp,i should fill but not overflow the linear range of the CDF, which is promising to give a better fitting xp and an accurate symmetry identification.| Number of xp,i | Scale parameter | Shape parameter | Location parameter | χ2 |
|---|---|---|---|---|
| 2 | 0.4310 | 4.2542 | 26.9405 | 4.8677 |
| 3 | 0.3583 | 2.3209 | 27.0277 | 2.4680 |
| 4 | 0.5056 | 3.4215 | 26.8804 | 18.4997 |
Conclusions
In this paper, a novel estimation method for the Weibull parameters (SBE) is proposed. The primary findings are:(1) Based on the approximate linear feature of the Weibull cumulative function, the SBE method establishes the three-parameter model without solving complex equations or numeric experiments.
(2) Outliers in the original data have been detected and excluded.
(3) The SBE result gave a higher p-value (0.99996) and lower Anderson–Darling value (1.30) compared with other models and methods, which suggested better goodness-of fit.
With the SBE method, the Weibull parameters are estimated based on the distribution of the majority of the sample data instead of the whole. The outliers are identified according to the estimated Weibull parameters and excluded from the data automatically. The method was implemented for approximating the capacity distribution of lithium-ion cells, which is one of the battery inconsistency evaluations, and was verified by chi-square test at a confidence of 95%. It gave less error than the results of the maximum likelihood estimation of the Weibull model and the similar normal distribution. Comparison of the p-values suggests that the three-parameter Weibull model captured most of the data information. The goodness-of-fit of the SBE method was demonstrated by comparing the results of the Anderson–Darling test and the Lilliefors test with those from other studies. This showed that the three-parameter Weibull model estimated using the SBE method fit the data well enough. The number of columns n and xp,i selection are key factors for the estimation accuracy. Based on the estimation error, the number of columns and xp,i are considered to be determined by the data features.
In conclusion, the SBE method estimates the parameters of the distribution and is free from the influence of outliers and complex computations. The contradiction between estimation accuracy and data completeness is solved, and the application of the three-parameter Weibull model is expanded. In future studies, feature abstraction and identification will be carried out for adaptive optimization of the estimation algorithm.
Conflicts of interest
There are no conflicts to declare.Nomenclature
| γ | Skewness coefficient |
| A | Scale parameter |
| B | Shape parameter |
| C | Location parameter |
| f | Probability density function (PDF) |
| F | Cumulative density function (CDF) |
| x | Random variable/independent variable |
| xp | x value where the Weibull PDF peaks |
| η | Symmetry ratio |
| n | Number of subintervals into which the raw data is divided |
| i | Index of the subinterval of the data |
| xi | Boundary value of the ith subinterval |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) i i | Mid-value of the ith subinterval |
| pi | Probability in the ith subinterval |
![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) p p | The three largest probabilities pp,1, pp,2, pp,3 |
![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) p p | Location of xi corresponding to ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) p p |
| xp,i | Elements in ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) p p |
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) p p | PDF values at ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) p p |
![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p p | CDF values at ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) p p |
| a | Slope in the linear equation of ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) p and p and ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p p |
| b | Intercept in the linear equation of ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) p and p and ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) p p |
| μ | Location parameter of the normal distribution |
| σ | Dispersion parameter of the normal distribution |
| MLE | Maximum likelihood estimation |
| Probability density function | |
| CDF | Cumulative density function |
| SBE | Symmetry based estimation |
Acknowledgements
Supported by Beijing Natural Science Foundation (2214066) and Youth Fund Project of GRINM.Notes and references
- F. R. Hampel, P. J. Rousseuw and E. M. Ronchetti, et al., Robust Statistics. The Approach Based on Influence Functions, Journal of the Royal Statistical Society Series D (The Statistician), 1986, 35(5), 565–566 Search PubMed
.
- L. S. Wang, Y. Y. Fang, T. Zhao, J. T. Wang, H. Zhang, L. Wang and et al, ., Lithium-ion cell inconsistency analysis based on three-parameter Weibull probability model, Rare Met., 2020, 39(4), 392–401 CrossRef CAS
.
- L. Wang, Y. Fang, L. Wang, F. Yun and S. Lu, Understanding discharge voltage inconsistency in lithium-ion cells via statistical characteristics and numerical analysis, IEEE Access, 2020, 8, 84821–84836 Search PubMed
.
- S. Weisberg, Applied linear regression, John Wiley & Sons, 2005, vol. 528 Search PubMed
.
- T. S. Ferguson, On the rejection of outliers, in Proceedings of the fourth Berkeley symposium on mathematical statistics and probability, University of California Press, Berkeley and Los Angeles, 1961, vol. 1, no. 1, pp. 253–287 Search PubMed
.
- R. J. Beckman and R. D. Cook, Outliers, Technometrics, 1983, 25(2), 119–149 Search PubMed
.
- D. M. Hawkins, Identification of outliers, Chapman and Hall, London, 1980, vol. 11 Search PubMed
.
- P. Taylan, F. Yerlikaya-Oezkurt and G. W. Weber, An approach to the mean shift outlier model by Tikhonov regularization and conic programming, Intell. Data Anal., 2014, 18(1), 79–94 Search PubMed
.
- C. S. Ferreira, T. B. Mattos and N. Balakrishnan, Mean-shift outliers model in skew scale-mixtures of normal distributions, J. Stat. Comput. Simul., 2016, 86(12), 2346–2361 CrossRef
.
- J. Ha, S. Seok and J. S. Lee, A precise ranking method for outlier detection, Inf. Sci., 2015, 324, 88–107 CrossRef
.
- K. Evans, T. Love and S. W. Thurston, Outlier identification in model-based cluster analysis, J. Classif., 2015, 32(1), 63–84 CrossRef PubMed
.
- A. Nardi and M. Schemper, New residuals for Cox regression and their application to outlier screening, Biometrics, 1999, 55(2), 523–529 CrossRef CAS PubMed
.
- S. H. Eo, S. M. Hong and H. Cho, Identification of outlying observations with quantile regression for censored data, arXiv, 2014, preprint, arXiv:1404.7710, DOI:10.48550/arXiv.1404.7710.
- Y. She and A. B. Owen, Outlier detection using nonconvex penalized regression, J. Am. Stat. Assoc., 2011, 106(494), 626–639 CrossRef CAS
.
- S. F. Schuster, M. J. Brand, P. Berg, M. Gleissenberger and A. Jossen, Lithium-ion cell-to-cell variation during battery electric vehicle operation, J. Power Sources, 2015, 297, 242–251 CrossRef CAS
.
- M. Baumann, L. Wildfeuer, S. Rohr and M. Lienkamp, Parameter variations within Li-Ion battery packs – Theoretical investigations and experimental quantification, J. Energy Storage, 2018, 18, 295–307, DOI:10.1016/j.est.2018.04.031
.
- S. J. Harris, D. J. Harris and C. Li, Failure statistics for commercial lithium ion batteries: A study of 24 pouch cells, J. Power Sources, 2017, 342, 589–597 CrossRef CAS
.
- P. Kostoulas, S. S. Nielsen, W. J. Browne and L. Leontides, A Bayesian Weibull survival model for time to infection data measured with delay, Prev. Vet. Med., 2010, 94(3–4), 191–201 CrossRef PubMed
.
- T. Park and G. Casella, The Bayesian Lasso, J. Am. Stat. Assoc., 2008, 103(482), 681–686 CrossRef CAS
.
- G. W. Somes and V. P. Bhapkar, A simulation study on a Wald statistic and Cochran's Q statistic for stratified samples, Biometrics, 1977, 643–651 CrossRef
.
- A. Haldar, and S. Mahadevan, Probability, reliability, and statistical methods in engineering design, John Wiley & Sons Incorporated, 2000 Search PubMed
.
- D. K. Dey and L. R. Jaisingh, Estimation of system
reliability for independent series components with Weibull life distributions, IEEE Trans. Reliab., 1988, 37(4), 401–405 CrossRef
.
- Data modeling for metrology and testing in measurement science, ed. F. Pavese and A. B. Forbes, Springer Science & Business Media, 2008 Search PubMed.
- M. Johnen, C. Schmitz, M. Kateri and U. Kamps, Fitting lifetime distributions to interval censored cyclic-aging data of lithium-ion batteries, Comput. Ind. Eng., 2020, 143, 106418 CrossRef
.
- E. Chiodo, D. Lauria, N. Andrenacci and G. Pede, Accelerated life tests of complete lithium-ion battery systems for battery life statistics assessment, IEEE 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), 2016, pp. 1073–1078 Search PubMed
.
- S. Rothgang, T. Baumhofer and D. U. Sauer, Diversion of aging of battery cells in automotive systems, in 2014 IEEE Vehicle Power and Propulsion Conference (VPPC), IEEE, 2014, pp. 1–6 Search PubMed.
- S. Banerjee and B. Iglewicz, A simple univariate outlier identification procedure designed for large samples, Commun. Stat. – Simul. Comput., 2007, 36(2), 249–263 CrossRef
.
- K. Yuen Fung and S. R. Paul, Comparisons of outlier detection procedures in Weibull or extreme-value distribution, Commun. Stat. – Simul. Comput., 1985, 14(4), 895–917 CrossRef
.
- H. K. T. Ng, L. Luo, Y. Hu and F. Duan, Parameter estimation of three-parameter Weibull distribution based on progressively Type-II censored samples, J. Stat. Comput. Simul., 2012, 82(11), 1661–1678 CrossRef
.
- J. W. Evans, R. A. Johnson and D. W. Green, Two-and three-parameter Weibull goodness-of-fit tests, US Department of Agriculture, Forest Service, Forest Products Laboratory, 1989, vol. 493 Search PubMed
.
- T. Mouais, O. A. Kittaneh and M. A. Majid, Choosing the best lifetime model for commercial lithium-ion batteries, J. Energy Storage, 2021, 41, 102827 CrossRef
.
- Y. Mekonnen, H. Aburbu and A. Sarwat, Life cycle prediction of Sealed Lead Acid batteries based on a Weibull model, J. Energy Storage, 2018, 18, 467–475 CrossRef
.
- M. Tiryakioğlu and D. Hudak, On estimating Weibull modulus by the linear regression method, J. Mater. Sci., 2007, 42(24), 10173–10179 CrossRef
.
- M. Tiryakioğlu, On estimating Weibull modulus by moments and maximum likelihood methods, J. Mater. Sci., 2008, 43(2), 793–798 CrossRef
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra05446a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |