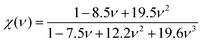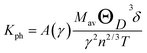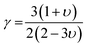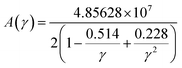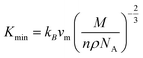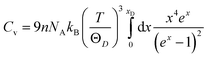Open Access Article
Open Access ArticleMetallic boro-carbides of A2BC (A = Ti, Zr, Hf and W): a comprehensive theoretical study for thermo-mechanical and optoelectronic applications†
R. Islamab,
M. M. Hossain *ab,
M. A. Ali
*ab,
M. A. Ali ab,
M. M. Uddinab and
S. H. Naqib
ab,
M. M. Uddinab and
S. H. Naqib bc
bc
aDepartment of Physics, Chittagong University of Engineering and Technology (CUET), Chattogram-4349, Bangladesh. E-mail: mukter_phy@cuet.ac.bd
bAdvanced Computational Materials Research Laboratory, Department of Physics, Chittagong University of Engineering and Technology (CUET), Chattogram-4349, Bangladesh
cDepartment of Physics, University of Rajshahi, Rajshahi 6205, Bangladesh
First published on 18th November 2022
Abstract
High-hardness materials with ductile deformation behavior have recently piqued interest due to their prospective applications, particularly as hard and protective coatings. The crack formation, especially in metal and ceramic materials, is one of the biggest problems of the surface hard coatings on heavy-duty tools. In this regard, mechanical properties (Vickers hardness, fracture toughness, machinability index, index of brittleness, as well as Pugh's ratio) have been studied for the metallic boro-carbides of A2BC (A = Ti, Zr, Hf, and W) compounds using the state-of-the-art density functional theory in detail. The compounds under investigation are both thermodynamically and mechanically stable. The value of Vickers hardness (in GPa) for A2BC (A = Ti, Zr, Hf, and W) compounds are 28.20, 23.12, 12.44, and 35.70, respectively, which indicates the W2BC could be a member of the hard family (Hv > 30 GPa). Pugh's ratio suggests ductile deformation for the W2BC compound, whereas the other three (Ti2BC, Zr2BC, and Hf2BC) compounds exhibit brittle deformation behavior. The W2BC compounds have the highest ductility among the other metallic boro-carbides (M2BC; M = V, Nb, Mo and Ta) and some other benchmark coating materials (TiN, TiAlN, C-BN, and Cr0.5Al0.5N). The fracture toughness (KIC) values are in the following sequence: Zr2BC < Ti2BC < Hf2BC < W2BC, which indicates that, the highest resistance (KIC = 4.96 MPam1/2) found for W2BC is suitable to prevent the crack propagation within the solid. In addition, the structural, electronic, optical, and thermal properties are also investigated for the A2BC (A = Ti, Zr, Hf, and W) compounds. The Ti2BC (W2BC) reflectivity spectra never fall below 53 (45)% in the 0 to 10.3 eV (0 to 16.70 eV) photon energy range, suggesting that these compounds have promise for usage as coating materials to reduce solar heating. Hf2BC and W2BC compounds could also be exploited as promising thermal barrier coating materials, while Ti2BC could be used as heat sink material based on the results of Debye temperature, melting temperature, thermal conductivity, and thermal expansion coefficient. The electronic properties reveal the metallic behavior of these compounds. The results obtained here are compared with those of some commercially known compounds, where available.
1. Introduction
Despite the numerous benefits of ceramic materials (for example, TiN, TiAlN, c-BN, Ti0.5Al0.5N, Ti0.25Al0.75N, Cr0.5Al0.5N etc.) such as high chemical stability, higher mechanical characteristics and hardness, stiffness, oxidation and corrosion resistance, the usage of these materials as surface hard coatings on cutting tools and other heavy-duty tools in abrasive applications is limited.1–7One of the most serious issues is the formation of cracks in the material's surface, which greatly reduces the tool's lifetime and, as a result, its performance.3 Many researchers, industrialists and investors are working hard to find a solution to this significant problem. The main problem is the brittle characteristics and can be solved by increasing their ductility index via materials engineering. There are two main approaches for increasing ductility: (1) nanostructuring and (2) finding novel materials with high stiffness and innately ductile/damage tolerant properties.3 Pugh proposed that a material's inherent ductility is determined by the shear to bulk modulus ratio being less than a critical value 0.57.8The nanostructure of the Mo2BC compound was grown using magnetron sputtering technique and nanoindentation was used to investigate the mechanical features such as stiffness and level of ductility.4 The Mo2BC has an orthorhombic structure with a space group Cmcm. A combination of boride and carbide subcells make up the crystal structure of Mo2BC. The boron-formed curving chain is positioned in the Mo6B trigonal prism, while the C atoms are located at the octahedral positions in the Mo6C prism.9,10 The experimentally measured Young's modulus and hardness value of Mo2BC was 460 GPa and 29 ± 2 GPa, respectively.4 The bulk modulus value of 324 GPa, which expresses the stiffness of a material, is higher than that of commercially available compounds such as TiN (295 GPa) and Ti0.25Al0.75N (178 GPa) but lower than c-BN (376 GPa).3,4
The Mo2BC crystal with dimensions 10 mm in length and 3 mm in diameter was grown using the Czochralski method.10,11 P. Lejay et al.10 investigated the effect of metal substitution into Mo2−xMxBC (M = Zr, Nb, Rh, Hf, Ta, W) compound and found its superconducting (Type-II) behavior with critical temperature above Tc = 4.2 K. It was envisaged that replacing the Mo atom in the Mo2BC compound with some transition metals could improved physical properties at some specific sectors. The structural, mechanical, and electronic band structures of X2BC (X= Mo, Ti, V, Zr, Nb, Hf, Ta, and W) were investigated by Bolvardi et al.3 They reported that all the compounds are mechanically and thermodynamically stable. Also, X2BC (X= Ta, Mo and W) compounds showed high stiffness and moderate ductility, indicating the application as cutting and forming tools. Specifically, the bulk modulus of W2BC is 350 GPa, which is 93% of the value of commercialized compounds, c-BN. P. Barua et al.1 reported a comprehensive study of structural, mechanical, hardness, electronic, thermal and optical properties of M2BC (M = V, Nb, Mo and Ta) compounds. These compounds show excellent thermal and optical properties that could be helpful in the design of thermo-mechanical and optoelectronic devices. For the usage as thermal barrier coating (TBC) material, researchers are looking for the materials with high hardness and malleable in nature. At present, some materials such as c-BN, TiN, TiAlN, Ti0.25Al0.75N, Ti0.5Al0.5N and Cr0.5Al0.5N are used as hard coating materials but their brittleness is prominent.2–5,12 To partially address this problem and the reported excellent thermal and optical properties in compounds of a similar type such as M2BC (M = V, Nb, Mo and Ta),1 we are strongly motivated to study the physical properties of A2BC (A = Ti, Zr, Hf, and W) compounds. Various vital physical features, such as mechanical (Vickers hardness, fracture toughness, index of brittleness, machinability index) and electronic (band profile, Fermi surface, charge density, Mulliken population analysis) properties of metallic boro-carbides of A2BC (A = Ti, Zr, Hf, and W) compounds are still unexplored from the standpoint of device applications in many areas. Some thermal properties such as Debye temperature, minimum thermal conductivity, Grüneisen parameter, thermal expansion coefficient, specific heat of these compounds are entirely unexplored. Knowledge on these thermophysical properties are prerequisites to any possible thermal device application. Furthermore, numerous optical features that are technologically essential (dielectric function, refractive index, absorption coefficient, photoconductivity, reflectivity, and loss function) have not been adequately researched till date.
Therefore, in the present study, a detailed investigation of structural, electronic, mechanical, optical and thermal properties of A2BC (A = Ti, Zr, Hf, and W) compounds will be reported to understand the physical states of these compounds further. We will also go over some mechanical and electronic parameters again to double-check the accuracy of our findings and provide some extra information. The obtained results suggested that Ti2BC and W2BC compounds have notable promise as coating materials to reduce solar heating. Also, Hf2BC and W2BC compounds can be exploited as promising thermal barrier coating materials.
2. Theoretical methodologies
The first-principles technique was used to explore metallic boro-carbides of A2BC (A = Ti, Zr, Hf, and W) compounds utilizing the state-of-the-art density functional theory.13 The high-throughput calculations are done in the CAmbridge Serial Total Energy Package (CASTEP)14,15 platform. The generalized gradient approximation (GGA) is used for electron exchange correlation function with the Perdew–Burke–Ernzerhof (PBE) functional.16 The obtained results in this study are based on ultrasoft pseudo-potential.1 The cut-off energy is taken to be 500 eV for all the compounds for the plane wave expansion process. Broyden–Fletcher–Goldfarb–Shanno (BFGS) approach has been adopted for atomic configuration optimization. During the optimization process the following additional parameters are used: k-point sampling of 8 × 2 × 8 special points in a Monkhorst–pack grid;17 energy convergence thresholds of 5 × 10−6 eV atom−1; maximum force of 0.01 eV Å−1; maximum stress of 0.02 GPa and maximum displacement of 5 × 10−4 Å. The single crystal stiffness constants, Cij, are calculated using the ‘stress–strain’ approach enabled in the CASTEP code.14 These stiffness constants are then used to obtain the bulk modulus, B, Young modulus, Y, and shear modulus, G. The theory of optical properties and relevant formulae can be found in prior reports.18,19 The analysis of Mulliken population is used to calculate the value of Vickers hardness (Hν) of all the compounds under study.3. Results and discussion
3.1 Structural properties
The metallic boro-carbides of A2BC (A = Ti, Zr, Hf, and W) belong to orthorhombic crystal system with space group: Cmcm (#No.:61).1,3,4 The optimized crystal structure of Ti2BC, as an example, is shown in Fig. S1.† This orthorhombic unit cell contains 16 atoms in total, in which 8 atoms are A-element and each of B and C contains 4 atoms. The stability of the compounds under study was ensured by the calculation of the formation enthalpy which has been reported in ref. 3. The crystal structure (conventional unit cell) is first optimized and then the ground state lattice parameters and volume of the unit cell are obtained. It is noticed that the changes of b-axis lattice parameter for all compounds are significantly increased compared to a- and c-axis when we go from Ti to Zr to Hf. The calculated lattice parameters are well matched with previous report as the variation is less than 1%.3 The value of lattice parameters and volumes of the A2BC (A = Ti, Zr, Hf, and W) compounds are given in Table S1.†3.2 Electronic properties, charge density and Fermi surface
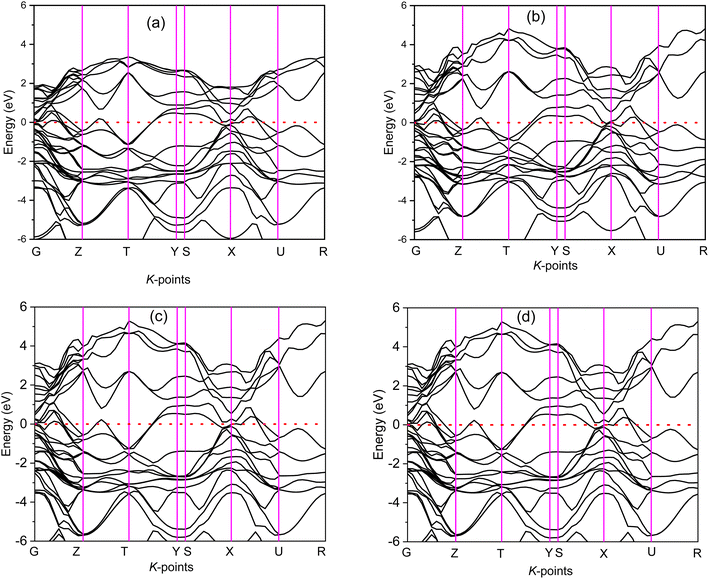
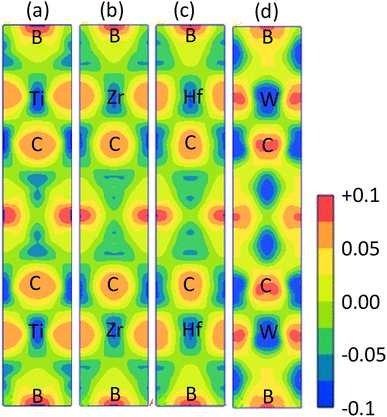
The electronic band structure (BS) are calculated along the high symmetry directions following the paths G-Z-T-Y-S-X-U-R within the Brillouin zone (BZ) and electronic energy density of states (DOS) over the whole BZ of A2BC (A = Ti, Zr, Hf, and W) compounds as shown in Fig. 1(a–d) and Fig. S2(a–d).† These band structure features are closely linked to charge density, atomic bonding and Fermi surface topology. The Fermi level (EF) is denoted by the horizontal dashed line and set at 0 eV. The valence bands (VB) are clearly crossing the EF which is a signature of the metallic behavior of the systems. The total density of states (TDOS) describes the gross contribution to the electronic transport properties while the partial density of states (PDOS) elucidates the individual atomic contribution to the same. The TDOS value of A2BC (A = Ti, Zr, Hf, and W) compounds are 5.80, 5.85, 4.76 and 5.41 states per eV, respectively. It is seen from the BS that the band dispersion along the path Y–S at EF is strongly non-dispersive compared to any other symmetry path in all the studied compounds. This non-dispersive nature could account for a high DOS value. It is noticed that the highest contribution to the TDOS for A2BC (A = Ti, Zr, Hf, and W) comes from the d-orbital electrons of Ti, Zr, Hf and W elements. The DOS spectrum of VB can be divided into two sub-bands, ranging from −15 to −7.5 eV and (−7.5 to 0) eV, based on its composition. It is observed that the formation of total band in the energy range of −15 to −7.5 eV for all title compounds is mainly comprised of the hybridization of C-2p, B-2s and B-2p orbitals. Again, in the range of (−7.5 to 0) eV, the band is formed by the hybridization of C-2p, B-2p and W-5d electronic states. The contribution of 6s and 5p orbitals of the elements Ti/Zr/Hf/W to the composition of the energy bands is minimal.The Fig. 2 depicts the electron density difference (EDD) for A2BC (A = Ti, Zr, Hf, and W) compounds, as well as the adjacent scale bar (+0.1 to −0.1). It has been found that all of the compounds under study have an asymmetric charge distribution at various atomic species. The red hue in the mapping images represents the level of charge accumulation, whereas the blue color represents charge depletion. It is seen that the electron is transferred from A element (Ti, Zr, Hf and W) to B/C element, which is an indication of ionic bonding. On the other hand, the strong covalent bond (due to the accumulation of charge) between the Ti/Zr/Hf/W–B/C is found. It is noted here that the covalent bond between Ti/Zr/Hf/W–C is much stronger than the Ti/Zr/Hf/W–B bond. The charge accumulation at B species was gradually decreased, while the charge depletion at metallic A species was gradually increased in the order of W2BC > Ti2BC > Zr2BC > Hf2BC compounds and accordingly, the bond strength. The non-directional metallic bonding between transition metal A elements can also be found. In summary, the mixture of bonding (ionic, covalent and metallic bond) characteristics has been found in the all the compounds under investigation.
The Fermi surfaces of metals are useful for characterizing and predicting the thermal, electrical as well as optical properties. In Fig. 3, the Fermi surfaces of A2BC (A = Ti, Zr, Hf, and W) compounds are shown. Depending on the composition, the Fermi surface features differ in shape and position. Therefore, it implies that electrons motion on the Fermi surface and accordingly, charge transport properties will be different for the A2BC (A = Ti, Zr, Hf, and W) compounds. The Fermi surface structure of the W2BC compound is completely different from that of the other (Zr2BC, Hf2BC, and W2BC) compounds. In the G-X direction, a cylinder with an octahedral shape can be found as hole pocket. Additionally, five similar-shaped sheets are oriented in the same direction. The Ti2BC and Hf2BC compounds have nearly identical Fermi surfaces. In both these compounds, a rectangle-shaped cylinder is observed along the G-X direction, which can be considered as hole pocket. Furthermore, there are two almost similarly shaped cylinders on either side of it along the G-Z directions. Along the G-Z direction, there are additionally three curvy sheets. The open surfaces positioned in the Y–S direction at the edge of BZ are considered as electron pockets, as shown for the Ti2BC, Zr2BC and Hf2BC compounds. The Fermi surface of Zr2BC is almost similar to those of Ti2BC and Hf2BC, the only exception being that an octahedral cylinder can be found along the G-X direction.
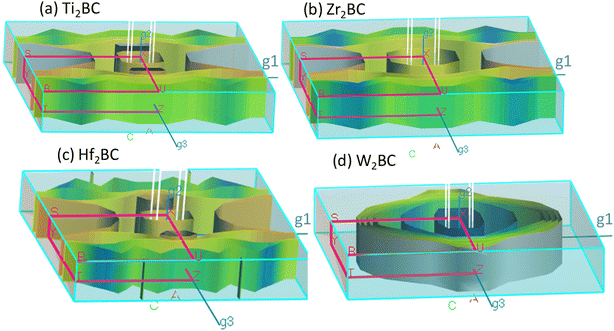 | ||
| Fig. 3 The Fermi surface of the metallic boro-carbides of (a) Ti2BC, (b) Zr2BC, (c) Hf2BC and (d) W2BC compounds. | ||
3.3 Optical properties
Before delving into the optical functions, it is necessary to understand the frequency/energy dependent dielectric function (real and imaginary parts). The optical functions of any homogeneous medium at all photon energies can be described by the dielectric function. The imaginary part of the dielectric function (IDF) is directly related to the electronic band structure and is calculated from the momentum matrix element through a possible electronic transition between two electronic states in the Brillouin zone from the valence band to the conduction band. The real part of the dielectric function (RDF) can be obtained using the Kramers–Kronig relations.15,18 Once an IDF(ε2) and an RDF(ε1) are obtained, all the other optical functions such as photoconductivity, absorption coefficient, refractive index, reflectivity, and loss function can be derived. The details of the theory and the relevant formulae can be found in the literature.14,15,18,19The RDF(ε1) and IDF(ε2) of A2BC (A = Ti, Zr, Hf, and W) compounds are illustrated in Fig. S3(a).† The IDFs for all the compounds are gradually reduced from a positive value as the incident photon energy increases. This is a very common occurrence in metallic systems. However, in the range of 7.0–9.0 eV photon energies, the IDF (ε2) values for all the compounds were zero. The RDF (ε1) spectra for all examined compounds, on the other hand, shows prominent peaks at roughly 1 eV and thereafter goes zero from negative value in the energy range of 9.0–12.0 eV. Both the spectra (RDF and IDF) ensure the Drude like behavior of the compounds.
The refractive index (n) compares the velocity of light in any medium with that in empty space, whereas the extinction coefficient (k) indicates how much light is absorbed by the material. Fig. S3(b)† displays the refractive index (n) and the extinction coefficient (k) for all the compounds under consideration. It is seen that for A2BC (A = Ti, Zr, Hf, and W) compounds, the values of n at zero photon energy/frequency are 20.68, 8.96, 12.12, and 15.95, respectively. For enhancing the visual features of electronic displays, high refractive index materials (typically larger than 1.50) are beneficial in photonic and optoelectronic device applications such as LCDs, OLEDs, and QDLED televisions.18,20,21 Furthermore, materials having a high refractive index are frequently combined with materials with a low refractive index to create transparent components with enhanced anti-reflective qualities.22 It is noted here that, among all the compounds, the highest refractive index (20.68) is found for Ti2BC and the lowest (8.96) for the Zr2BC compound. The spectrum of k shows that the sequence of maximum low-energy light absorption in the studied materials is as follows: Ti2BC > W2BC > Hf2BC > Zr2BC, since the highest peak for each studied compound was obtained at about 1 eV photon energy.
The spectrum of the absorption coefficient (α) of A2BC (A = Ti, Zr, Hf and W) is shown in Fig. 4(a). It can be seen that absorption starts from the zero photon energy. This behavior is a signature of the metallic nature of these compounds, which was also confirmed by the investigations of the electronic band structures. However, the value of the absorption coefficient increases with the incident photon energy. The highest values of α of 2.15 ×105, 2.03 ×105 and 3.0 ×105 (all units are cm−1) at 5.80 eV, 6.80 eV and 6.40 eV for A2BC (A = Ti, Zr and W) compounds are found, while for the Hf2BC compound, a significantly lower absorption occurs with the value of α = 0.8 ×105 cm−1 at photon energy of 6.0 eV. The possible reason can be explained from the TDOS value in Fig. S2.† The TDOS value of the Hf2BC compound at the Fermi level is the lowest among all the compounds under study. The lower the available electronic states, the lower the possibility of photon absorption.
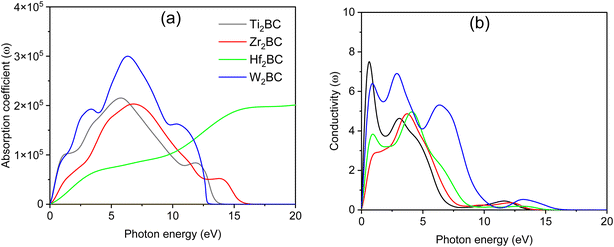 | ||
| Fig. 4 (a) Absorption coefficient and (b) photoconductivity versus photon energy of the A2BC (A = Ti, Zr, Hf, and W) compounds. | ||
Optical conductivity also begins when low-energy electromagnetic radiation (photon energy) is just incident on the material (Fig. 4(b)), further verifying the metallic character. The photoconductivity increases sharply in the IR region and then gradually decreases with several notable peaks. The positions of these peaks are determined by the peaks in the electronic energy density of states. The photoconductivity spectrum of the W2BC compound, for example, has peaks at 0.85, 2.9, and 6.33 eV photon energies, and then drops to zero at 16 eV. However, a significant photoconductivity could be found at least for a wide range of photon energies from 0 to 10 eV. The rest of the compounds under study show qualitatively similar character.
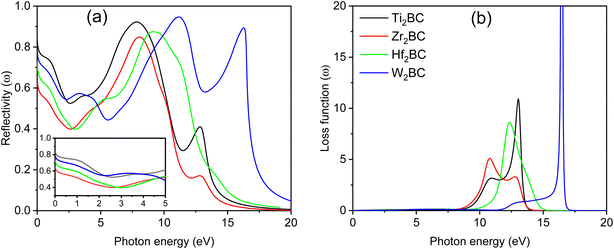
The reflectivity spectra start at 80%, 60%, 70% and 75% for A2BC (A = Ti, Zr, Hf and W) compounds, respectively, as shown in Fig. 5(a). It is also noted that the Ti2BC (W2BC) reflectivity spectra never fall below 53 (45)% in the 0 to 10.3 eV (0 to 16.70 eV) photon energy range, while the spectra for Zr2BC and Hf2BC compounds drop below 40%. Furthermore, the maximum reflectivity for all studied compounds can be found in the UV range within photon energy of 7.5–11.2 eV. The spectra for Ti2BC and W2BC never go below 53% up to 5 eV. This means that 53% or more photons are reflected in the IR, visible and UV (from 3.1 to 5 eV). The value of reflectivity spectra of these two compounds (Ti2BC and W2BC) are much higher than that of other metallic boro-carbides of M2BC (M = V, Nb, Mo and Ta),1 TmCu3S4 (Tm = V, Ta, Nb),23 La2Q2O7 (Q = Ge, Sn),24 some 211 MAX phase compounds25–28 and others29 in the energy region of 0–6 eV. According to prior research, a material with a reflectivity of at least about 44% may be able to avoid solar heating.1,27,30,31 The excellent reflectivity properties of Ti2BC and W2BC, in particular, show promise in coating technology designed to avoid solar heating.
The loss function, L(ω), quantifies the energy lost by charged particles such as electrons passing through a material. It is seen from Fig. 5(b) that there is no loss of energy up to 0–8.55 eV for all the compounds under study due to the comparatively large value of [ε2(ω)]. Maximum energy loss is noticed when a plasma resonance occurs. Prominent peaks (expressing the energy loss of the charged particle) for A2BC (A = Ti, Zr, Hf and W) are found at 13, 10.77, 12.35 and 16.50 eV, respectively. At these particular energies the reflection and absorption spectra exhibit drastic falls and the compounds under investigation are expected to show high transmittance.
3.4 Mechanical properties
| C11 > 0; C44 > 0; C55 > 0; C66>0; |
| C11C22 > C122; (C11C22C33 + 2C12C13C23) > (C11C232 + C22C132 + C33C122) |
As can be seen from Table S2,† the above-mentioned conditions are satisfied by the calculated elastic constants for all the compounds under study. Therefore, the A2BC (A = Ti, Zr, Hf, and W) compounds can be said to be mechanically stable. In addition to the confirmation of mechanical stability, some interesting features can also be evaluated from elastic stiffness constant, Cij. In the present study, all the compounds have C33 > C11, implying that atomic bonding should be stronger along the c-axis than that along the a-axis. The values of C11 and C33 are much higher than C44. This indicates that the linear elastic strain along the [100] and [001] directions is much harder to produce than the shear strain of all the compounds under study. It is also noticeable from Table S2† that the value of the elastic stiffness coefficient C66 is higher than C44 for all the compounds. This reflects that the ability to resist deformation for basal plane and prismatic slip shear along the [110] direction should be higher than that along the [010] direction in the (100) plane. According to previous report,34 the shear constant C44 is one of the best predictors of a material's hardness. Therefore, as seen in the Table S2,† the W2BC compound should have the highest hardness among all the investigated compounds, as its C44 value is the highest.
The Cauchy pressure (CP) explains which type of chemical bond dominates in a compound. The value of CP is determined by the following relation: CP = C12 − C44. The positive sign of CP indicates dominance of ionic bonding, while the negative sign means a dominance of covalent bonding in the material.1,33,35 From the present study (Table S2†), it is worth noting that the covalent bond dominates in the Ti2BC compound, while the ionic bond is dominating in the W2BC. The other two compounds exhibit a good balance of covalent/ionic bonding within the crystals.
The modulus of elasticity for an elastic material is usually assessed as the bond strength among atoms in a solid. The three types of elastic moduli (bulk modulus (B), shear modulus (G), and Young's modulus (Y)) can be computed from the single crystal elastic constants utilizing the Viogt–Reuss–Hill (VRH) approximation.36,37 These moduli mainly reveal the mechanical behavior of solids under stress and reflect the capability of materials to resist elastic deformations of various types. The associated formulas and theories can be found in previous literatures.1,18,21,33 The results of calculations of the moduli of elasticity for A2BC (A = Ti, Zr, Hf, and W) compounds are given in Table 1. It is seen from Table 1 that the highest value of elastic moduli (B = 353, G = 188 and Y = 479; all are in GPa) is found for the W2BC compound, which should show the highest resistance to elastic deformation compared to other studied compounds. It is instructive to compare the elastic constants of W2BC with a well-known commercial compound, TiAlN, that is normally used as a surface hard coating on various tools. The values of B, G and Y for W2BC are higher by 27.20%, 5.30% and 9.40% from those of TiAlN,2,5 and higher by 49.57%, 34.57% and 37.36% from those of Ti0.25Al0.75N.4 Also those values are higher by 29.17%, 20.21% and 21.71% from Cr0.5Al0.5N.7 However, these elastic moduli of W2BC are much lower than those of commercialized compound c-BN. It should be noted here that the B value, which expresses the resistance to volume deformation, is only 6.50% lower than that of the c-BN compound.4
| Compound | B | G | Y | G/B | ν | Ref. |
|---|---|---|---|---|---|---|
| a Calculated from the elastic constants. | ||||||
| Ti2BC | 214 | 163 | 390 | 0.76 | 0.20 | This |
| 208 | 158 | 378 | 0.76 | 3 | ||
| Zr2BC | 193 | 136 | 330 | 0.70 | 0.22 | This |
| 187 | 128 | 312 | 0.68 | 3 | ||
| Hf2BC | 218 | 153 | 372 | 0.70 | 0.22 | This |
| 207 | 150 | 362 | 0.72 | 3 | ||
| W2BC | 353 | 188 | 479 | 0.53 | 0.27 | This |
| 350 | 184 | 468 | 0.52 | 3 | ||
| V2BC | 254 | 177 | 431 | 0.69 | 0.22 | 1 |
| 260 | 178 | 435 | 0.68 | 3 | ||
| Nb2BC | 263 | 169 | 418 | 0.64 | 0.23 | 1 |
| 259 | 163 | 404 | 0.63 | 3 | ||
| Mo2BC | 317 | 187 | 469 | 0.59 | 0.25 | 1 |
| 324 | 187 | 470 | 0.58 | 0.26 | 4 | |
| 313 | 181 | 455 | 0.58 | 3 | ||
| Ta2BC | 275 | 165 | 412 | 0.60 | 0.25 | 1 |
| 286 | 168 | 421 | 0.59 | 3 | ||
| TiN | 295 | 213 | 514 | 0.72 | 0.22 | 5 |
| TiAlN | 257 | 178 | 434 | 0.69 | 0.22 | 5 |
| Ti0.5Al0.5N | 280 | 210 | 504a | 0.75 | 0.20a | 6 |
| Ti0.25Al0.75N | 178 | 123 | 300a | 0.69 | 0.22a | 4 |
| Cr0.5Al0.5N | 250 | 150a | 375 | 0.60a | 0.25 | 7 |
| c-BN | 376 | 382 | 856 | 1.01 | 0.12 | 4 |
The malleability/brittleness of a solid can be predicted by Poisson's ratio (ν) and Pugh ratio (G/B). A value G/B > 0.571 and ν < 0.26, is an indication of brittleness, otherwise implies malleability of solid.8,18,21,27,35 In this study, it is seen from Table 1 that the W2BC compound meets the criteria (G/B = 0.53) for malleability or ductility behavior, while the other three compounds (Ti2BC, Zr2BC and Hf2BC) show brittle behavior. Interestingly, the W2BC compounds have the highest ductility among all the metallic boro-carbides (X2BC; X= Mo, Ti, V, Zr, Nb, Hf, Ta, and W). The hardness of this compound is also the highest. It should be noted that the available benchmark coating material, c-BN, shows a brittle nature with a G/B value of 1.02, which is an indication of extreme brittleness.4 Despite the fact that Ti2BC, Zr2BC, and Hf2BC are brittle, their G/B values are remarkably similar to those of other known coating materials.2–5,7 A combination of high hardness and ductility is very attractive for engineering applications and in this respect W2BC has significant potential in industrial sector.
The elastic moduli and elastic stiffness constants of A2BC (A = Ti, Zr, Hf, and W) compounds are used to calculate the anisotropy indicators to evaluate the degree of anisotropy. The related theory and formulae can be found elsewhere.1,33 All results are summarized in Table S3.† It can be seen in the Table S3† that the values of the shear anisotropy factors Ai (i = 1, 2 and 3) for the crystal planes (100), (010), and (001), respectively, are off from the unity. This shows that the compounds under study have anisotropic character. The values of bulk modulus Ba, Bb, and Bc (all in GPa) along the a, b, and c axes, respectively, show that the degree of axial bulk modulus follows the following sequence: Bc > Ba > Bb. Additionally, the percentage (%) of elastic anisotropy in compressibility (AB) and shear (AG) for the orthorhombic crystal structure can also be estimated using the following formulas: 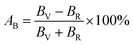 ,
, 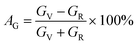 . Among various anisotropy performance indicators, the universal anisotropy index (AU) is the most versatile and acceptable indicator, which was developed by Ranganathan et al.44 as
. Among various anisotropy performance indicators, the universal anisotropy index (AU) is the most versatile and acceptable indicator, which was developed by Ranganathan et al.44 as 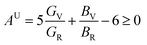 , which may be used to all crystal symmetries to express crystal anisotropy as well. Here the subscripts, V stands for Voigt and R indicates Reuss bounds. According to the results of AB, AG and AU, it can be concluded that the A2BC (A = Ti, Zr, Hf, and W) compounds are elastically anisotropic. The anisotropies in elastic stiffness constants as well as elastic moduli are primarily caused by the anisotropic character of chemical bonds along different crystallographic axes.
, which may be used to all crystal symmetries to express crystal anisotropy as well. Here the subscripts, V stands for Voigt and R indicates Reuss bounds. According to the results of AB, AG and AU, it can be concluded that the A2BC (A = Ti, Zr, Hf, and W) compounds are elastically anisotropic. The anisotropies in elastic stiffness constants as well as elastic moduli are primarily caused by the anisotropic character of chemical bonds along different crystallographic axes.
The resistance of a solid material to localized plastic deformation is measured by its hardness. The hardness of the material is important to understand the behavior in their practical applications. There are several methods to measure the hardness experimentally. For instance, the most popular methods are Brinell hardness, Rockwell hardness, Knoop hardness, and Vickers hardness.41 The theoretical calculation of the hardness is not easy, rather complex. There are various proposed schemes to theoretically calculate the hardness as a function of bulk modulus and shear modulus. The formulae by X. Chen et al.,42 Y. Tian et al.43 and D. M. Teter44 are based on either G or both G and B while N. Miao et al.45 and E. Mazhnik et al.41 formulae are mainly dependent on the Young's modulus and Poisson's ratio. These formulas are as follows:
| (HV)Chen = 2[(G/B)2G]0.585 − 3 | (1) |
| (HV)Tian = 0.92(G/B)1.137G0.708 | (2) |
| (HV)Teter = 0.151G | (3) |
| (HV)Miao = (1 − 2ν)Y/6(1 + ν) | (4) |
| (HV)Mazhnik = γ0χ(ν)Y | (5) |
In eqn (5), χ(ν) is a function of Poisson's ratio and can be written as:
It can be seen from Table 2, that according to Chen and Tian formulae, the highest hardness value was obtained for Ti2BC and the lowest value for the W2BC compound. The intermediate values were obtained for the Zr2BC and Hf2BC compounds. On the other hand, using the Teter formula, the highest value (28.32 GPa) was for the W2BC compound and the lowest value (20.53 GPa) was for the Zr2BC compound. Based on these results, it is very difficult to predict the actual hardness of these compounds. It is reported that hardness differs from the elastic moduli of materials. The B and G cannot predict the hardness of some class of materials with high level of accuracy especially the materials having very low or negative value of Poisson's ratio (ν). Further details on this matter can be found in ref. 41. The hardness values of all the compounds under study obtained using the formula by N. Miao et al.45 are much higher but follow almost the similar tendency of those found by using the Chen and Tian formulae.42,43 Comparatively the most popular and acceptable method at present, is developed by E. Mazhnik et al.41 This approach employs the Young moduli (Y) and Poisson's ratio (ν) to predict hardness. To calculate the hardness, the choice of Y and ν is reasonable because the B and G correlate highly with each other.41 As indicated from the Table 2 that the hardnesses values due to the Mazhnik method are in the following order: W2BC > Ti2BC > Hf2BC > Zr2BC. It's worth noting that, with the exception of Hf2BC, the results of electron density difference and Mulliken population analysis are quite similar with the order of hardness given above [see Section 3.2]. The Vickers hardness, which is a prominent theoretical approach to calculating intrinsic hardness was introduced by F. Gao46 and H. Gou et al.47 The computed Vickers hardness is mostly dependent on the Mulliken overlap population, which quantifies the degree of covalency of the bond and thus determines individual bonding strength. Again the strength of the bond is determined by the mean value of overlap populations per unit volume. However, the intrinsic hardness of a metallic material can be calculated by the following equation:27,47
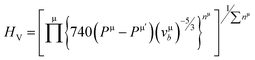 | (6) |
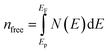 where N(E) is the density of state value at an energy E, Ep is the energy position of the pseudogap which is situated at the left of Fermi energy (EF). Above Ep the nature of electrons should be delocalized. In the present study, as shown in Table 3, the value of Vickers hardness (in GPa) for A2BC (A = Ti, Zr, Hf and W) compounds are 28.20, 23.12, 12.44 and 35.70, respectively. It is noticed here that the hardness values have increased with the sequence of A-element in A2BC compound from Hf to Zr to Ti to W. The hardness value of W2BC compares well with some well known compounds such as SiC, SiO2, B6O, B6S and B6Se.18,21,41 The high valence electron concentration could be the possible reason of the highest value of Vickers hardness of the W2BC compound.3 It should be noted here that the shear elastic constant (C44) and elastic moduli (B, G and Y) were also the highest for this particular compound. Moreover, the results of hardness are also compatible with the findings of electron density difference and Mulliken population analysis. Despite these predictions implying high hardness, the W2BC compound should not be considered as a superhard (Hv > 40 GPa) material,41,48 but at least, could be a member of the hard family. In summary, the hardness values of all the compounds under consideration varied since the hardness formulae (Chen, Tian, Teter, Mazhnik and Miao) have different functional forms and put emphasis on different elastic moduli. On the other hand, the Vickers hardness calculation depends on individual bond strength. For example, the elastic modulus (shear modulus) values of B6O and TiN are almost the same, but the Vickers hardness (Hv) (experimental) of B6O (38 GPa) is more than two times than that (17.6 GPa) of TiN. Again, the Hv (experimental) value for the OsB2 compound is 29.4 GPa, while the hardness using Chen's formula is 17.8 GPa.41 Therefore, our hardness results require experimental verification for further confirmation. Roughly speaking, theoretical analyses under different schemes predict W2BC as the hardest among all the A2BC (A = Ti, Zr, Hf and W) ternaries considered herein.
where N(E) is the density of state value at an energy E, Ep is the energy position of the pseudogap which is situated at the left of Fermi energy (EF). Above Ep the nature of electrons should be delocalized. In the present study, as shown in Table 3, the value of Vickers hardness (in GPa) for A2BC (A = Ti, Zr, Hf and W) compounds are 28.20, 23.12, 12.44 and 35.70, respectively. It is noticed here that the hardness values have increased with the sequence of A-element in A2BC compound from Hf to Zr to Ti to W. The hardness value of W2BC compares well with some well known compounds such as SiC, SiO2, B6O, B6S and B6Se.18,21,41 The high valence electron concentration could be the possible reason of the highest value of Vickers hardness of the W2BC compound.3 It should be noted here that the shear elastic constant (C44) and elastic moduli (B, G and Y) were also the highest for this particular compound. Moreover, the results of hardness are also compatible with the findings of electron density difference and Mulliken population analysis. Despite these predictions implying high hardness, the W2BC compound should not be considered as a superhard (Hv > 40 GPa) material,41,48 but at least, could be a member of the hard family. In summary, the hardness values of all the compounds under consideration varied since the hardness formulae (Chen, Tian, Teter, Mazhnik and Miao) have different functional forms and put emphasis on different elastic moduli. On the other hand, the Vickers hardness calculation depends on individual bond strength. For example, the elastic modulus (shear modulus) values of B6O and TiN are almost the same, but the Vickers hardness (Hv) (experimental) of B6O (38 GPa) is more than two times than that (17.6 GPa) of TiN. Again, the Hv (experimental) value for the OsB2 compound is 29.4 GPa, while the hardness using Chen's formula is 17.8 GPa.41 Therefore, our hardness results require experimental verification for further confirmation. Roughly speaking, theoretical analyses under different schemes predict W2BC as the hardest among all the A2BC (A = Ti, Zr, Hf and W) ternaries considered herein.
| Compound | (HV)Chen | (HV)Tian | (HV)Teter | (HV)Miao | (HV)Mazhnik |
|---|---|---|---|---|---|
| Ti2BC | 25.63 | 24.86 | 24.61 | 33.00 | 21.23 |
| Zr2BC | 20.51 | 20.02 | 20.53 | 25.86 | 16.05 |
| Hf2BC | 22.07 | 21.66 | 23.10 | 29.00 | 17.99 |
| W2BC | 17.47 | 18.31 | 28.38 | 28.34 | 23.49 |
| Compound | Bond | dμ | Pμ | Pμ′ | vbμ | HVμ | HV | KIC | HV/KIC |
|---|---|---|---|---|---|---|---|---|---|
| Ti2BC | B–B | 1.78777 | 1.47 | 0.0348 | 2.9369 | 175.5807 | |||
| C–Ti(I) | 2.07903 | 0.25 | 4.6190 | 12.3286 | |||||
| C–Ti(II) | 2.10977 | 0.24 | 4.8269 | 10.9200 | 28.20 | 2.81 | 10.00 | ||
| C–Ti(III) | 2.19435 | 1.51 | 5.43105 | 64.65076 | |||||
| B–Ti(I) | 2.32277 | 0.89 | 6.4414 | 28.1776 | |||||
| Zr2BC | C–Zr(I) | 2.29162 | 0.35 | 0.0262 | 5.98995 | 12.1076 | |||
| C–Zr(II) | 2.29402 | 0.30 | 6.0079 | 10.18093 | |||||
| C–Zr(III) | 2.3656 | 1.42 | 6.5881 | 44.52817 | 23.12 | 2.38 | 9.71 | ||
| B–Zr(I) | 2.52756 | 0.94 | 8.0360 | 20.95955 | |||||
| B–B | 1.87731 | 1.42 | 3.29265 | 141.469 | |||||
| Hf2BC | C–Hf(I) | 2.27847 | 0.41 | 0.0060 | 7.1606 | 11.212 | |||
| C–Hf(II) | 2.30038 | 0.48 | 10.2939 | 12.544 | |||||
| C–Hf(III) | 2.36171 | 1.51 | 7.9744 | 34.94404 | 12.44 | 2.85 | 4.37 | ||
| B–Hf(II) | 2.50748 | 1.14 | 9.5440 | 19.52519 | |||||
| B–Hf(III) | 3.16178 | 0.21 | 19.1344 | 1.09774 | |||||
| B–B | 1.90007 | 1.43 | 4.1526 | 98.1533 | |||||
| W2BC | B–B | 1.82386 | 1.20 | 0.0176 | 2.4491 | 195.9051 | |||
| C–W(I) | 2.10329 | 0.14 | 3.7560 | 9.8833 | 35.70 | 4.96 | 7.19 | ||
| C–W(II) | 2.16423 | 0.22 | 4.0921 | 14.1907 | |||||
| C–W(III) | 2.19304 | 1.54 | 4.25773 | 100.1959 | |||||
| B–W(I) | 2.31895 | 0.98 | 5.0942 | 46.9345 |
The crack formation, especially in metals and ceramic materials is one of the biggest problems of the surface hard coatings on heavy-duty tools. Fracture toughness, KIC is a parameter, which can evaluate the resistance of a material to crack/fracture initiation. The formula for KIC of a material is as follows:41
| KIC = α0−1/2V01/6[ξ(ν)Y]3/2 | (7) |
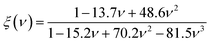
As presented in Table 3, the values of KIC of the A2BC (M = Ti, Zr, Hf and W) compounds are 2.81, 2.38, 2.85 and 4.96 MPam1/2, respectively. It is found that the highest resistance to crack formation and propagation is offered by the W2BC compound. The KIC value of W2BC is well matched with those of some of the commercialized compounds, namely, WC, BN, diamond, and Si3N4.49,50The hardness and fracture toughness ratio is called an index of brittleness (Bi) of a solid.49 The Bi expresses the degree of damage tolerance. The lower value of Bi indicates higher damage tolerance of materials. In the present study, the value of Bi for A2BC (A = Ti, Zr, Hf, and W) compounds are 10.00, 9.71, 4.37, and 7.19, respectively. It is seen that the Hf2BC shows the highest damage tolerance among all the compounds under consideration. Noted here that the hardness value (Hv = 35.70 GPa) of W2BC is much higher than that (Hv = 12.44 GPa) of Hf2BC, even though it is somewhat less damage tolerant.
The machinability index is considered to evaluate the machinability of A2BC (A = Ti, Zr, Hf and W) compounds. The machinability may differ depending on the cutting technique. The greater a material's machinability index value, the more machinable it is.21 The value of machinability index (B/C44) is 1.45, 1.59, 1.65, 1.91 for Ti2BC, Zr2BC, Hf2BC and W2BC respectively. As a result, it is obvious that the W2BC compound is more machinable than the other compounds. High hardness together with high machinability once again makes W2BC an attractive compound for machine tools applications.
3.5 Thermal properties
Thermal properties measure the response of a material to the applied heat. Study of thermal properties such as Debye temperature (ΘD), thermal conductivity (K), specific heats (Cv, Cp), thermal expansion coefficient (α), and melting temperature (Tm) are essential to comprehend the temperature dependent behaviors of A2BC (A = Ti, Zr, Hf and W) ternaries. For many high temperature device applications, thermal barrier coating (TBC) materials are an important requisite. A popular application of TBC is the coating on turbine blades in gas-turbine engines which facilitates its use at elevated operating temperature, resulting in the high efficiency of the engines.35In the sub-sections to follow, we will study the various thermal properties such as Debye temperature, lattice thermal conductivity, minimum thermal conductivity, specific heat and thermal expansion coefficient of A2BC (A = Ti, Zr, Hf and W) in detail.
| Compounds | ρ (gm cm−3) | vl (m s−1) | vt (m s−1) | vm (m s−1) | ΘD (K) | Kmin (W mK−1) | kpha (W mK−1) | γ | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| a Calculated at 300 K. | |||||||||
| Ti2BC | 4.66 | 9616 | 5915 | 6527 | 886 | 1.87 | 48.30 | 1.29 | This |
| Zr2BC | 6.33 | 7692 | 4637 | 5127 | 642 | 1.25 | 30.23 | 1.37 | This |
| Hf2BC | 11.85 | 5964 | 3590 | 3971 | 499 | 0.97 | 26.17 | 1.36 | This |
| W2BC | 15.51 | 6240 | 3482 | 3877 | 528 | 1.12 | 20.79 | 1.60 | This |
| V2BC | 05.63 | 9331 | 5608 | 6202 | 881 | 1.95 | — | 1.36 | 1 |
| Nb2BC | 07.50 | 8068 | 4746 | 5260 | 693 | 1.42 | — | 1.40 | 1 |
| Mo2BC | 08.60 | 8116 | 4664 | 5180 | 707 | 1.50 | — | 1.50 | 1 |
| Ta2BC | 13.33 | 6094 | 3518 | 3906 | 508 | 1.03 | — | 1.51 | 1 |
The thermal conductivity of a material plays an important role to design power-dissipating device and/or thermoelectric device. A high value of thermal conductivity of a material is used as heat sink while its low value is helpful to increase the figure of merit of a thermoelectric device. The lattice thermal conductivity (Kph) of a solid originates from the conduction of heat due to the lattice vibrations. The total thermal conductivity is a combination of lattice thermal conductivity and electronic thermal conductivity. The thermal conductivity of a material plays an important role to design many useful devices like power-dissipating device, thermoelectric device, thermal barrier coating (TBC) materials etc. As an example, a high value of thermal conductivity of a material is used as heat sink while its low value is helpful to increase the figure of merit of a thermoelectric device and TBC materials.21 Here, we will discuss only the lattice thermal conductivity (kph). In all materials, the lattice thermal conductivity dominates at high temperatures. The kph of a material is measured by the heat conduction due to lattice vibration. Slack derived an empirical formula to estimate the kph theoretically as follows:54
where, γ is the acoustic Grüneisen parameter which measures the degree of anharmonicity of phonons. A material with small value of Grüneisen parameter indicates low anharmonicity of phonons which results in high thermal conductivity. The coefficient A(γ) is evaluated by the following equation:
The kph for the A2BC (A = Ti, Zr, Hf and W) compounds are a decreasing function of temperature given by: 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 491.33/T, 9071.07/T, 7851.76/T and 6237.72/T, respectively. The value of kph is almost constant after ∼1000 K as shown in Fig. 6. The lattice thermal conductivity, kph at temperature 300 K and Grüneisen parameter, γ are tabulated in Table 4. At room temperature (300 K), the kph value (in W mK−1) for the A2BC (A = Ti, Zr, Hf and W) compounds follow the following order: 48.30 > 30.23 > 26.17 > 20.79. It is noted here that the compound, Ti2BC contains the highest value of lattice thermal conductivity due to high value of ΘD. This value is comparable with B6X (X = S, Se), MAX phase compounds, bronze, brass and aluminum bronze, but is much lower than SiC, copper, diamond, aluminium nitride etc.21,55–57 It is well known that high thermal conductivity materials can be used as heat sink materials in laptops or any other microelectronic devices as heat dissipating agency. The value of minimum thermal conductivity can be calculated based on the modified Clarke's model and the equation can be represented as follows:58
491.33/T, 9071.07/T, 7851.76/T and 6237.72/T, respectively. The value of kph is almost constant after ∼1000 K as shown in Fig. 6. The lattice thermal conductivity, kph at temperature 300 K and Grüneisen parameter, γ are tabulated in Table 4. At room temperature (300 K), the kph value (in W mK−1) for the A2BC (A = Ti, Zr, Hf and W) compounds follow the following order: 48.30 > 30.23 > 26.17 > 20.79. It is noted here that the compound, Ti2BC contains the highest value of lattice thermal conductivity due to high value of ΘD. This value is comparable with B6X (X = S, Se), MAX phase compounds, bronze, brass and aluminum bronze, but is much lower than SiC, copper, diamond, aluminium nitride etc.21,55–57 It is well known that high thermal conductivity materials can be used as heat sink materials in laptops or any other microelectronic devices as heat dissipating agency. The value of minimum thermal conductivity can be calculated based on the modified Clarke's model and the equation can be represented as follows:58
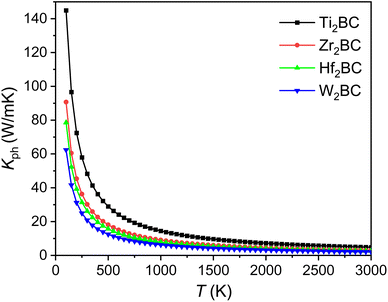 | ||
| Fig. 6 The lattice thermal conductivity (Kph) as a function of temperature of the A2BC (A = Ti, Zr, Hf, and W) compounds. | ||
The value of minimum thermal conductivity, Kmin can be found in Table 4. It is found that the values of ΘD and Kmin for Hf2BC and W2BC are much lower and these values are comparable with well known commercialized TBC material, Y4Al12O9 (Kmin = 1.13 W mK−1; ΘD = 564 K).59,60 The Kmin (W mK−1) value for Hf2BC (0.97) and W2BC (1.12) compounds are also comparable with some other compounds such as metallic boro-carbides, Ta2BC (1.03),1 MAB phase Hf3PB4 (1.14),31 MAX phase Ti2SnC (0.99)61 and so on. The melting temperatures (Tm in K) for A2BC (A = Ti, Zr, Hf and W) compounds are calculated using the formula in ref. 31, 40 and 62 and are found to be 2073 K, 1884 K, 2054 K and 2615 K, respectively. It is found that the maximum Tm value is attained for W2BC owing to the high hardness and bond strength of this compound.
where,
 ; and n is the number of atoms per formula unit, NA is the Avogadro's number and kB is the Boltzmann constant. The linear thermal expansion coefficient (α) and specific heat at constant pressure (Cp) can be determined from the following equations:21,35
; and n is the number of atoms per formula unit, NA is the Avogadro's number and kB is the Boltzmann constant. The linear thermal expansion coefficient (α) and specific heat at constant pressure (Cp) can be determined from the following equations:21,35where, BT is the isothermal bulk modulus, vm is the molar volume, and γ is the Grüneisen parameter.
Fig. 7(a–b) and Fig. 8 display the temperature dependence of Debye specific heats, Cv, Cp and α for A2BC (A = Ti, Zr, Hf and W) compounds in the temperature range of 0–1500 K where the quasi-harmonic Debye model is expected to be valid.
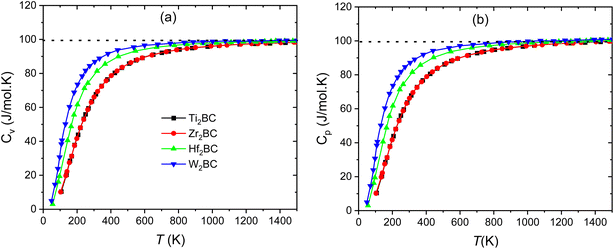 | ||
| Fig. 7 Specific heats (a) Cv, and (b) Cp of the A2BC (A = Ti, Zr, Hf and W) compounds as a function of temperature. The dashed line marks the classical Dulong–Petit limit. | ||
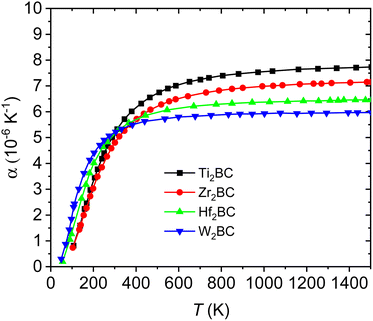 | ||
| Fig. 8 Linear thermal expansion coefficient for the A2BC (A = Ti, Zr, Hf and W) compounds as a function of temperature. | ||
The phononic thermal softening occurs with increasing temperature. As a result the heat capacity also increases with increasing temperature. Both heat capacities and linear thermal expansion coefficient have an increasing tendency with temperature. The temperature dependences are steep at low temperature region, indicating to an increased ability of the lattice waves to enhance their average energy with ascending temperature. At low temperature, the relationship between heat capacities and temperature meets the Debye-T3 power-law.67 It is noticed that at high temperature the heat capacities approach the Dulong–Petit (DP) (3nNAkB) limit.68 The value of Cv (J mol−1 K−1) at room temperature (300 K) is found to be different for different compounds and followed the sequence: W2BC (86.9) > Hf2BC (81.4) > Zr2BC (66.08) > Ti2BC (65.7).
The thermal expansion coefficient (α) of solids can be estimated from the difference between Cp and Cv. Temperature dependences of α are illustrated in Fig. 8 for the A2BC (A = Ti, Zr, Hf and W) compounds. It is found that like Cp and Cv, the values of α also increase rapidly up to the room temperature (300 K) and then gradually goes to a constant value at higher temperatures. At room temperature, the values of α are as follows: Ti2BC (5.33 × 10−6 K−1), Zr2BC (4.81 × 10−6 K−1), Hf2BC (5.10 × 10−6 K−1) and W2BC (5.21 × 10−6 K−1).
To summarize, to predict a compound as an efficient TBC material, the following characteristics should be considered. The solid should have damage tolerant behavior, low value of Kmin, comparatively high Tm, comparatively low ΘD and low thermal expansion coefficient (α). In our case, we have found favorable data sets for Hf2BC and W2BC compounds. So we can suggest that these two compounds can be used as promising TBC materials. The high value of lattice thermal conductivity (kph), Kmin, α and ΘD for the Ti2BC compound, on the other hand, give strong indication of its use as a heat sink material.
4. Conclusions
The first-principles approach has been adopted to perform a comprehensive theoretical study on ternary metallic boro-carbides A2BC (A = Ti, Zr, Hf, and W) using the state-of-the-art density functional theory. The study focuses on these compounds' physical aspects such as structural, electronic, optical, mechanical, and thermal properties. Characterizing parameters for orthorhombic unit cells, such as lattice parameters and volume, are clearly justified in the light of prior research. Because there is no band gap between the valence and conduction bands, all of the compounds tested are metallic in nature. The total density of states at the Fermi level of A2BC (A = Ti, Zr, Hf, and W) compounds are 5.80, 5.85, 4.76, and 5.41 states per eV, respectively. Relatively high values of TDOS at the Fermi level result from some flat bands crossing this particular energy. The compounds under study are mechanically stable. These compounds are also predicted to be anisotropic in nature. The compound W2BC shows ductile deformation, but the deformation characteristic is brittle for the other three compounds (Ti2BC, Zr2BC, and Hf2BC). The hardness of the materials is evaluated using the approach of Chen, Tian, Teter, Mazhnik, Miao, and Vickers hardness. It is found that the W2BC compound has the highest Vickers hardness rating among all the compounds under investigation. The predicted Vickers hardness value is increased for the metallic element in the following sequence: Hf2BC < Zr2BC < Ti2BC < W2BC, which also followed the shear elastic constant, C44, and elastic moduli (B, G, and Y) except for Hf2BC. The value of the machinability index is 1.45, 1.59, 1.65, and 1.91 for Ti2BC, Zr2BC, Hf2BC, and W2BC, respectively, indicating that W2BC compounds are more machinable than the other compounds. Various optical properties (such as dielectric function, refractive index, absorption coefficient, photoconductivity, reflectivity and loss function) are computed based on Kramer–Kronig relation and discussed in detail. Reflectivity spectra show for Ti2BC (>53%) and W2BC (>45%) in the IR, visible, and UV regions (<10 eV, at least), indicating the possible use as of these as coating materials to avoid solar heating. The study of various thermal properties such as Debye temperature, melting temperature, thermal conductivity, and thermal expansion coefficient suggest that Ti2BC could be used as heat sink material, whereas Hf2BC and W2BC possess significant promise as TBC materials.Data availability
The datasets generated during the current study are available from the corresponding authors on a reasonable request.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This work was carried out with the aid of a grant (No. 21-378 RG/PHYS/AS_G-FR3240319526) from UNESCO-TWAS and the Swedish International Development Cooperation Agency (Sida). The views expressed herein do not necessarily represent those of UNESCO-TWAS, Sida or its Board of Governors. Authors are also grateful to the Department of Physics, Chittagong University of Engineering & Technology (CUET), Chattogram-4349, Bangladesh, for providing the computing facilities for this work.References
- P. Barua, M. M. Hossain, M. A. Ali, M. M. Uddin, S. H. Naqib and A. K. M. A. Islam, J. Alloys Compd., 2019, 770, 523–534 CrossRef CAS
.
- S.-Y. Yoon, J.-K. Kim and K. H. Kim, Surf. Coat. Technol., 2002, 161, 237–242 CrossRef CAS
.
- H. Bolvardi, J. Emmerlich, M. to Baben, D. Music, J. von Appen, R. Dronskowski and J. M. Schneider, J. Phys.: Condens. Matter, 2012, 25, 045501 CrossRef PubMed
.
- J. Emmerlich, D. Music, M. Braun, P. Fayek, F. Munnik and J. M. Schneider, J. Phys. D: Appl. Phys., 2009, 42, 185406 CrossRef
.
- K. Chen, L. R. Zhao, J. Rodgers and J. S. Tse, J. Phys. D: Appl. Phys., 2003, 36, 2725–2729 CrossRef CAS
.
- P. H. Mayrhofer, D. Music and J. M. Schneider, J. Appl. Phys., 2006, 100, 094906 CrossRef
.
- P. H. Mayrhofer, D. Music, Th. Reeswinkel, H.-G. Fuß and J. M. Schneider, Acta Mater., 2008, 56, 2469–2475 CrossRef CAS
.
- S. F. Pugh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45, 823–843 CrossRef CAS
.
- J.-O. Bovin, M. O'Keeffe and L. Stenberg, J. Solid State Chem., 1977, 22, 221–231 CrossRef CAS
.
- P. Lejay, B. Chevalier, J. Etourneau and P. Hagenmuller, J. Less-Common Met., 1981, 82, 193–200 CrossRef CAS
.
- B. Bressel, B. Chevalier, J. Etourneau and P. Hagenmuller, J. Cryst. Growth, 1979, 47, 429–433 CrossRef CAS
.
- P. H. Mayrhofer, D. Music, Th. Reeswinkel, H.-G. Fuß and J. M. Schneider, Acta Mater., 2008, 56, 2469–2475 CrossRef CAS
.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef
.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. - Cryst. Mater., 2005, 220, 567–570 CrossRef CAS
.
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef
.
- Md. M. Hossain, Md. A. Ali, Md. M. Uddin, S. H. Naqib and A. K. M. A. Islam, ACS Omega, 2021, 6, 33899–33913 CrossRef CAS PubMed
.
- M. A. Hadi, R. V. Vovk and A. Chroneos, J. Mater. Sci.: Mater. Electron., 2016, 27, 11925–11933 CrossRef CAS
.
- M. M. Hossain, M. A. Hossain, S. A. Moon, M. A. Ali, M. M. Uddin, S. H. Naqib, A. K. M. A. Islam, M. Nagao, S. Watauchi and I. Tanaka, J. Mater. Sci.: Mater. Electron., 2021, 32, 3878–3893 CrossRef CAS
.
- M. M. Hossain, M. A. Ali, M. M. Uddin, A. K. M. A. Islam and S. H. Naqib, J. Appl. Phys., 2021, 129, 175109 CrossRef CAS
.
- What are High Refractive Index Materials?, https://avantama.com/what-are-high-refractive-index-materials/, accessed May 27, 2022 Search PubMed.
- Z. Abbas, K. Fatima, M. Abubakr, I. Gorczyca, T. Alshahrani, S. Muhammad and A. G. Al-Sehemi, Optik, 2022, 250, 168289 CrossRef CAS
.
- K. Fatima, Z. Abbas, A. Naz, T. Alshahrani, Y. Chaib, S. H. A. Jaffery, S. Muhammad, S. Hussain, J. Jung and H. Algarni, J. Solid State Chem., 2022, 313, 123305 CrossRef CAS
.
- M. S. Hossain, M. A. Ali, M. M. Hossain and M. M. Uddin, Mater. Today Commun., 2021, 27, 102411 CrossRef CAS
.
- M. A. Ali, M. M. Hossain, M. M. Uddin, M. A. Hossain, A. K. M. A. Islam and S. H. Naqib, J. Mater. Res. Technol., 2021, 11, 1000–1018 CrossRef CAS
.
- A. Chowdhury, M. A. Ali, M. M. Hossain, M. M. Uddin, S. H. Naqib and A. K. M. A. Islam, Phys. Status Solidi B, 2018, 255, 1700235 CrossRef
.
- F. Sultana, M. M. Uddin, M. A. Ali, M. M. Hossain, S. H. Naqib and A. K. M. A. Islam, Results Phys., 2018, 11, 869–876 CrossRef
.
- Z. Abbas, K. Fatima, S. H. A. Jaffery, A. Ali, H. H. Raza, S. Muhammad, H. Algarni, S. Hussain and J. Jung, J. Comput. Sci., 2022, 63, 101791 CrossRef
.
- S. Li, R. Ahuja, M. W. Barsoum, P. Jena and B. Johansson, Appl. Phys. Lett., 2008, 92, 221907 CrossRef
.
- M. A. Ali, M. M. Hossain, A. K. M. A. Islam and S. H. Naqib, J. Alloys Compd., 2021, 857, 158264 CrossRef CAS
.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef
.
- M. A. Ali, M. A. Hadi, M. M. Hossain, S. H. Naqib and A. K. M. A. Islam, Phys. Status Solidi B, 2017, 254, 1700010 CrossRef
.
- S.-H. Jhi, J. Ihm, S. G. Louie and M. L. Cohen, Nature, 1999, 399, 132–134 CrossRef CAS
.
- M. M. Hossain, M. A. Ali, M. M. Uddin, M. A. Hossain, M. Rasadujjaman, S. H. Naqib, M. Nagao, S. Watauchi and I. Tanaka, Mater. Today Commun., 2021, 26, 101988 CrossRef CAS
.
- W. Voigt, Lehrbuch Der Kristallphysik, Vieweg + Teubner Verlag, Wiesbaden, 1966 Search PubMed
.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349–354 CrossRef
.
- C. M. Kube, AIP Adv., 2016, 6, 095209 CrossRef
.
- D. H. Chung and W. R. Buessem, J. Appl. Phys., 1967, 38, 2010–2012 CrossRef CAS
.
- Md. M. Rahaman, M. H. K. Rubel, Md. A. Rashid, M. A. Alam, K. M. Hossain, Md. I. Hossain, A. A. Khatun, Md. M. Hossain, A. K. M. A. Islam, S. Kojima and N. Kumada, J. Mater. Res. Technol., 2019, 8, 3783–3794 CrossRef CAS
.
- E. Mazhnik and A. R. Oganov, J. Appl. Phys., 2019, 126, 125109 CrossRef
.
- X.-Q. Chen, H. Niu, D. Li and Y. Li, Intermetallics, 2011, 19, 1275–1281 CrossRef CAS
.
- Y. Tian, B. Xu and Z. Zhao, Int. J. Refract. Hard Met., 2012, 33, 93–106 CrossRef CAS
.
- D. M. Teter, MRS Bull., 1998, 23, 22–27 CrossRef CAS
.
- N. Miao, B. Sa, J. Zhou and Z. Sun, Comput. Mater. Sci., 2011, 50, 1559–1566 CrossRef CAS
.
- F. Gao, J. He, E. Wu, S. Liu, D. Yu, D. Li, S. Zhang and Y. Tian, Phys. Rev. Lett., 2003, 91, 015502 CrossRef PubMed
.
- H. Gou, L. Hou, J. Zhang and F. Gao, Appl. Phys. Lett., 2008, 92, 241901 CrossRef
.
- R. A. Andrievski, Int. J. Refract. Hard Met., 2001, 19, 447–452 CrossRef CAS
.
- B. R. Lawn and D. B. Marshall, J. Am. Ceram. Soc., 1979, 62, 347–350 CrossRef CAS
.
- H. Niu, S. Niu and A. R. Oganov, J. Appl. Phys., 2019, 125, 065105 CrossRef
.
- O. L. Anderson, J. Phys. Chem. Solids, 1963, 24, 909–917 CrossRef CAS
.
- A. J. Slifka, B. J. Filla, J. M. Phelps, G. Bancke and C. C. Berndt, J. Therm. Spray Technol., 1998, 7, 43–46 CrossRef CAS
.
- M. S. Ali, A. K. M. A. Islam, M. M. Hossain and F. Parvin, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 407, 4221–4228 CrossRef CAS
.
- G. A. Slack, Phys. Solid State, 1979, 34, 1–71 CAS
.
- J. Haines, J. Léger and G. Bocquillon, Annu. Rev. Mater. Res., 2001, 31, 1–23 CrossRef CAS
.
- E. Haque, ACS Appl. Energy Mater., 2021, 4, 1942–1953 CrossRef CAS
.
- L.-F. Zhu, B. Grabowski and J. Neugebauer, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 224202 CrossRef
.
- D. R. Clarke, Surf. Coat. Technol., 2003, 163–164, 67–74 CrossRef CAS
.
- X. Zhan, Z. Li, B. Liu, J. Wang, Y. Zhou and Z. Hu, J. Am. Ceram. Soc., 2012, 95, 1429–1434 CrossRef CAS
.
- Y. Zhou, H. Xiang, X. Lu, Z. Feng and Z. Li, J. Adv. Ceram., 2015, 4, 83–93 CrossRef CAS
.
- M. A. Hadi, N. Kelaidis, S. H. Naqib, A. Chroneos and A. K. M. A. Islam, J. Phys. Chem. Solids, 2019, 129, 162–171 CrossRef CAS
.
- M. E. Fine, L. D. Brown and H. L. Marcus, Scr. Mater., 1984, 18, 951–956 CrossRef CAS
.
- M. A. Blanco, E. Francisco and V. Luaña, Comput. Phys. Commun., 2004, 158, 57–72 CrossRef CAS
.
- O. Delaire, A. F. May, M. A. McGuire, W. D. Porter, M. S. Lucas, M. B. Stone, D. L. Abernathy, V. A. Ravi, S. A. Firdosy and G. J. Snyder, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 184302 CrossRef
.
- T. Plirdpring, K. Kurosaki, A. Kosuga, T. Day, S. Firdosy, V. Ravi, G. J. Snyder, A. Harnwunggmoung, T. Sugahara, Y. Ohishi, H. Muta and S. Yamanaka, Adv. Mater., 2012, 24, 3622–3626 CrossRef CAS PubMed
.
- L. Xue, Y.-M. Ren, J.-R. He and S.-L. Xu, Chin. Phys. B, 2017, 26, 067103 CrossRef
.
- P. Debye, Ann. Phys., 1912, 344, 789–839 CrossRef
.
- R. Fox, Br. J. Hist. Sci., 1968, 4, 1–22 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra05448e |
| This journal is © The Royal Society of Chemistry 2022 |