Open Access Article
Open Access ArticleGraph–sequence attention and transformer for predicting drug–target affinity
Xiangfeng Yan and
Yong Liu*
and
Yong Liu*
School of Computer Science and Technology, Heilongjiang University, Harbin, China. E-mail: 2010023@hlju.edu.cn
First published on 14th October 2022
Abstract
Drug–target binding affinity (DTA) prediction has drawn increasing interest due to its substantial position in the drug discovery process. The development of new drugs is costly, time-consuming, and often accompanied by safety issues. Drug repurposing can avoid the expensive and lengthy process of drug development by finding new uses for already approved drugs. Therefore, it is of great significance to develop effective computational methods to predict DTAs. The attention mechanisms allow the computational method to focus on the most relevant parts of the input and have been proven to be useful for various tasks. In this study, we proposed a novel model based on self-attention, called GSATDTA, to predict the binding affinity between drugs and targets. For the representation of drugs, we use Bi-directional Gated Recurrent Units (BiGRU) to extract the SMILES representation from SMILES sequences, and graph neural networks to extract the graph representation of the molecular graphs. Then we utilize an attention mechanism to fuse the two representations of the drug. For the target/protein, we utilized an efficient transformer to learn the representation of the protein, which can capture the long-distance relationships in the sequence of amino acids. We conduct extensive experiments to compare our model with state-of-the-art models. Experimental results show that our model outperforms the current state-of-the-art methods on two independent datasets.
1 Introduction
Drug discovery is a complicated process, which has the risks of long research cycles, high costs, and low success rates. It takes billions of dollars and more than ten years to develop a new drug from development to approval.1,2 The effective prediction of drug–target binding affinity (DTA) is one of the significant issues in drug discovery.3–5 Drugs are usually represented as a string obtained from the simplified molecular-input line-entry system (SMILES)6 or represented by a molecule graph with atoms as nodes and chemical bonds as edges. Targets (or proteins) are sequences of amino acids. Binding affinity indicates the strength of drug–target pair interaction. Through binding, drugs can have a positive or negative influence on functions carried out by proteins, affecting the disease conditions.7 By understanding drug–target binding affinity, it is possible to find out candidate drugs that can inhibit the target/protein and benefit many other bioinformatics applications.8,9Early computational attempts were focused on biologically intuitive methods, such as ligand-similarity based approaches and docking simulations.10 Ligand-similarity based methods predict interactions by comparing a new ligand to known ligands of proteins. However, ligand-similarity methods perform poorly when the number of known ligands is insufficient. Docking simulation methods require the 3D structures of the target proteins hence becoming inapplicable when there are numerous proteins with unavailable 3D structures.11 In the past few years, some research has begun predicting DTAs from a network perspective.12–14 However, the prediction qualities of network-based approaches are strongly limited by available linked information. Thus, these methods do not perform very well on association predictions for new drugs or targets with scarce linked information. Additionally, some useful information, such as drug and target feature information, cannot be fully utilized to improve prediction accuracy for these methods.
With the development of artificial intelligence, deep learning approaches for DTA prediction have become popular and can be categorized into two main groups according to the input data: sequence-based and graph-based methods. The sequence-based methods learned the representations from sequential data, which are SMILES sequences of drugs and amino acid sequences of proteins. The graph-based methods represented drugs as molecular graphs, which learned the representations from molecular graphs and amino acid sequences of proteins. Although deep learning models show excellent performance improvement in DTA prediction, two main challenges remain to study. First, these methods consider either SMILES sequences or molecular graphs, which failed to capture comprehensive representations of drugs. A SMILES sequence can offer the following features as a representation: (i) ionic groups and atomic groups are represented in the canonical way, which avoids confusion with their surrounding atomic groups. For instance, ammonium is denoted as [NH4+] rather than HHNHH; (ii) some specially defined symbols are used to preserve chemical properties such as chemical valence, isotopes, etc. However, merely taking drugs with sophisticated internal connectivity as simple sequential data lacks sufficient interpretable and expressive capabilities. Molecular graph brings two unique benefits as compared to SMILES sequence: (i) molecular graph can capture the spatial connectivity of different atoms, especially for star structures and ring structures (e.g., alkyl and benzene ring); (ii) chemical molecular bonds are well preserved, which might influence the molecular properties. For instance, carbon dioxide has divalent bonds between carbon and oxygen. However, similar to sequence modeling in SMILES, simply using molecular graphs to model molecules cannot enable methods to comprehensively learn molecular representations. It is difficult to capture information on some specific molecular properties, such as atoms’ chirality, using molecular graphs. Second, most existing methods utilized convolutional neural networks (CNNs) to learn low-dimensional feature representations of proteins from the sequence of amino acids, which ignored the long-distance relationships in the protein sequences.
To overcome the mentioned challenges of current methods for DTA prediction, we propose a novel triple-channel model, named Graph–Sequence Attention and Transformer for Predicting Drug–Target Affinity (GSATDTA), to predict the binding affinity between drugs and targets. Recently, Guo et al.15 proposed that integrating the capabilities of both molecular graphs and SMILES sequences can further enhance molecule representation expressive power. Enlightened by this work, we use a graph neural network to learn the graph representation from molecular graphs and a BiGRU to learn the SMILES representation from SMILES sequences. Then, we propose a graph–sequence attention mechanism to capture significant information from both the SMILES sequence and molecular graph. For the protein representations, we replace CNN with an efficient transformer to learn the representation of the protein, which can capture the long-distance relationships in the sequence of amino acids.16 The main contributions of this paper are summarized as follows:
• We leveraged both the graph and sequence information and proposed a graph–sequence attention mechanism to learn effective drug representations for DTA prediction.
• We utilized an efficient transformer to learn the representation of the protein, which can capture the long-distance relationships in the sequence of amino acids.
• We conduct extensive experiments on two benchmark datasets to investigate the performance of our proposed model. The experimental results show that our proposed model achieves the best performance in the drug–target binding affinity prediction task.
2 Related work
2.1 Simulation methods
Most previous works have focused on simulation-based methods (i.e., molecular docking and descriptors). For example, Li et al.17 proposed a docking method based on random forest (RF). The RF model was also adopted in KronRLS,18 which uses the similarity score obtained by the Kronecker product of the similarity matrix to improve the predictive performance. To alleviate the limitation of linear dependence in KronRLS, a gradient boosting method is proposed in SimBoost19 to construct the similarity between drugs and targets. While classical methods have shown rational performance in DTA prediction, they are usually computationally expensive or rely on external expert knowledge or the 3D structure of the target/protein.2.2 Sequence-based methods
The sequence-based methods learned the representations from sequential data, which are SMILES sequences of drugs and amino acid sequences of proteins. For example, DeepDTA20 uses the 1D representation of the drug and protein, and uses convolutional neural networks (CNNs) to learn representations from the raw protein sequences and SMILES strings. Then, they combined these representations to feed into a fully connected layer to predict the drug–target affinity scores. Similarly, WideDTA21 also relies only on the 1D representation, but different from DeepDTA, the SMILES and protein sequence were represented as words (instead of characters) that correspond to an eight-character sequence and a three-residual sequence, respectively. In addition, WideDTA utilized the ligand maximum common substructure (LMCS)22 of drugs and motifs and domains of proteins (PDM),23 which formed a four-branch architecture together with the ligand SMILES and protein sequence branches. The WideDTA model is an extension of DeepDTA, which also used CNN to learn the representations of drugs and proteins. GANsDTA24 utilized a generative adversarial networks (GAN) to learn beneficial patterns within labeled and unlabeled sequences and used convolutional regression to forecast binding affinity scores. MATT_DTI3 also utilizes the 1D representation, it proposed a relation-aware self-attention block to model the relative position between atoms in drugs, considering the correlation between atoms. As for the protein, it utilizes three convolutional layers as the feature extractor, followed by a max pooling layer. Then, a multi-head attention block is built to model the similarity of drug–target pairs as the interaction information for DTA prediction.2.3 Graph-based methods
The graph-based methods represented drugs as molecular graphs, and learned the representations from molecular graphs and amino acid sequences of proteins. Tsubaki et al.25 proposed the application of the graph neural network (GNN) to DTA (or compound–protein interaction, CPI) prediction. In their model, the chemical structures of drugs (provided in SMILES notation) are represented as graphs. Therefore, they propose the use of GNN and CNN, which can learn low-dimensional real-valued vector representations of molecular graphs and protein sequences. Similarly, Gao et al.26 utilized the GNN for drug representation, whereas the protein descriptors were obtained using long short-term memory (LSTM). GraphDTA5 also introduced graph representation to take advantage of the topological structure information of the molecular graph. GraphDTA used a three-layer GCN as an alternative for drug representation while utilizing the CNN to learn protein representation as in DeepDTA. Among the research on deep learning for drug discovery, DeepGS27 is the most relevant to our work. DeepGS considers both the molecular graphs and SMILES sequences of drugs, however, they directly contacted the two representations, which failed to capture comprehensive information about drugs. Furthermore, DeepGS and other deep learning methods utilized CNN to learn local representations of protein sequences, which ignored the long-distance relationships in the protein sequences.Compared with these deep learning models, we designed a graph–sequence attention mechanism, which can capture significant information from both SMILES sequences and molecular graphs. As for the protein, we replace CNN with an efficient transformer to extract the long-distance relationships in the sequence of amino acids.
3 Materials and methods
We regard DTA prediction as a regression task to predict the binding affinity value between a drug–target pair. We denote the SMILES sequence set as D = {Di}|D|i=1 and the protein sequence set as P = {Pj}|P|j=1. We use RDKit to convert the SMILES set D into a molecular graph set G = {Gi}|G|i=1, where Gi = (Vi, Ei) denotes a molecular graph. Specifically, a node on a molecular graph represents an atom, and an edge represents a chemical bond between two atoms. Formally, the problem of drug–target binding affinity prediction is defined as follows.Given a SMILES set D and a protein set P, and their interaction labels Y = {Yi,j|1 ≤ i ≤ |D|, 1 ≤ j ≤ |P|, Yi,j ∈ R}, the binding affinity prediction problem is to learn a function f: D × P → Y such that f(Di, Pj) → Yi,j.
3.1 Overview
We proposed a triple-channel model, called GSATDTA; the overall architecture of the model is shown in Fig. 1. It takes the symbolic sequences of the target/protein and drug as inputs, as well as the molecular structure of the drug, and outputs the binding affinity of the drug to the target. For the drug representations, we use a graph neural network to learn the topological structure information from molecular graphs and BiGRU to learn contextual information about drugs represented by SMILES sequences. Then, we utilized the graph–sequence attention mechanism to capture significant information from both the SMILES sequence and molecular graph. For the protein representations, we employed an efficient transformer to capture the long-distance relationships in the sequence of amino acids. Thus, we obtained the target representation and the fusion drug representation. The connection of two representations is inputted into several dense layers and ends with a regression layer to predict the drug–target binding affinity value. Next, we will present the details of our model.3.2 Representation learning of drug
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CC(
CC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)…” for a drug in Fig. 1 is a sequence of atoms and chemical bonds. SMILES rules can cover atoms, ions, chemical bonds, valences, and chemical reactions, which can accurately express branched, cyclic, tetrahedral, aromatic, and chiral structures, as well as the expression of isomers and isotopes.
O)…” for a drug in Fig. 1 is a sequence of atoms and chemical bonds. SMILES rules can cover atoms, ions, chemical bonds, valences, and chemical reactions, which can accurately express branched, cyclic, tetrahedral, aromatic, and chiral structures, as well as the expression of isomers and isotopes.Most previous studies adopted one-hot encoding to encode the symbols in the SMILES sequence. However, one-hot encoding ignores the contextual value of the symbol, and thus cannot reveal the functionality of the symbol within the context.28,29 To address this problem, we utilized Smi2Vec,30 a method similar to Word2Vec,31 to encode the tokens in the SMILES sequences. According to DeepGS,27 we fixed maximum lengths of 100 for SMILES sequences. We cut the SMILES sequence if the length of the SMILES sequence is longer than 100. Otherwise, we use zero-padding at the end of the SMILES sequence. In a typical case, a fixed-length SMILES string, for example, C, is partitioned into individual atoms or symbols. It is then mapped to atoms by seeking out each atom embedded from a pretrained dictionary, and if not in the dictionary, it is obtained from randomly generated values.32,33 Then, atom embedding vectors are aggregated to form the final embedding matrix. Enlightened by the gate function in GRU,34 we applied the three layers technique of BiGRU to the generated matrix to obtain a latent representation of the drug, which allows us to model the local chemical context. Finally, we obtain the SMILES representation Si ∈ RN through the max-pooling layer and the fully connected layer, where N is the output dimensional of the fully connected layer.
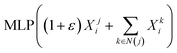 | (1) |
 | (2) |
| F = sigmoid(WG·dHi + WS·dSi) | (3) |
| Md = F⊙Hi + (1 − F)⊙Si | (4) |
3.3 Representation learning of protein
The protein sequence is a string of ASCII characters, which represents amino acids. Mathematically, a protein sequence is expressed as Pj = {p1, p2, …, pi, …}, where pi ∈ N* and the length of Pj depends on the proteins. We fix the length of the input protein sequence as Lp to ensure the same size of inputs. According to the token embedding and position embedding in the transformer,16 the input of the efficient transformer is the sum of token embedding and position embedding of protein sequences. The token embedding Tptok ∈ RLp×M has a trainable weight Wm ∈ Rvp×M, where vp is the vocabulary size of proteins and M is the embedding size of proteins. The position embedding Tppos ∈ RLp×M has a trainable weight Wp ∈ RLp×M. The output of the embedding operations is| Tp = Tptok + Tppos, | (5) |
 | (6) |
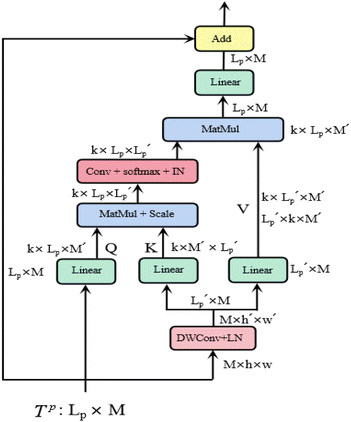
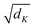 is a scaling factor depending on the layer size.
is a scaling factor depending on the layer size.However, the memory and computation for multi-head self-attention in the traditional transformer scale quadratically with spatial or embedding dimensions (i.e., the number of channels), causing vast overheads for training and inference. Thus, we replace the multi-head self-attention with Efficient Multi-head Self-Attention (EMSA).37 The architecture of the efficient multi-head self-attention is shown in Fig. 2.
Similar to MSA, EMSA first adopts a set of projections to obtain query Q. To compress memory, the 2D input Tp ∈ RLp×M is reshaped to a 3D one along the spatial dimension (i.e., 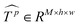 ) and then fed to a depth-wise convolution operation to reduce the height and width dimension by a factor s. To make it simple, s is an adaptive set by the feature map size or the stage number. The kernel size, stride and padding are s + 1, s, and s/2, respectively. The new token map after spatial reduction
) and then fed to a depth-wise convolution operation to reduce the height and width dimension by a factor s. To make it simple, s is an adaptive set by the feature map size or the stage number. The kernel size, stride and padding are s + 1, s, and s/2, respectively. The new token map after spatial reduction 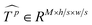 is then reshaped to a 2D one, i.e.,
is then reshaped to a 2D one, i.e., 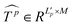 ,
,  . Then
. Then  is fed to two sets of projection to get key K and value V. After that, we adopt eqn (7) to compute the attention function on query Q, K and value V.
is fed to two sets of projection to get key K and value V. After that, we adopt eqn (7) to compute the attention function on query Q, K and value V.
 | (7) |
3.4 Drug–target binding affinity prediction
In this paper, we treat the drug–target binding affinity prediction task as a regression task. With the representation learned from the previous sections, we can integrate all the information about the drug and target to predict the binding affinity value. Firstly, we concatenated the drug representation Md and the protein representation Tj. Secondly, we feed it into three dense fully connected layers to predict the binding affinity value. Besides, we use ReLU as the activation function for increasing the nonlinear relationship. Given the set of drug–target pairs and the ground-truth labels, we use the mean squared error (MSE) as the loss function.4 Experiments and results
4.1 Datasets
Following previous works, we employ two widely used datasets dedicated to DTA prediction:• Davis:20 the Davis dataset, which contains 68 drugs and 442 targets, with 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 056 drug–target interactions. Affinity values range from 5.0 to 10.8.
056 drug–target interactions. Affinity values range from 5.0 to 10.8.
• Kiba:20 the Kiba dataset, which contains 2111 drugs and 229 targets, with 118![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 254 drug–target interactions. Affinity values range from 0.0 to 17.2.
254 drug–target interactions. Affinity values range from 0.0 to 17.2.
For both datasets, we use the same training/testing data ratio as MATT_DTA,3 DeepDTA,20 and GraphDTA5 in our experiments, making the comparison as fair as possible. That is, 80% of the data is used for training and the remaining 20% is used for testing the model. For the same purpose, we use the same evaluation metrics as MATT_DTA, GraphDTA, and DeepDTA for evaluating model performance: the mean squared error (MSE, the smaller the better), rm2 (the larger the better), and the concordance index (CI, the larger the better). Table 1 summarizes the details of the Davis and Kiba datasets.
| Davis | Kiba | |
|---|---|---|
| Compounds | 68 | 2111 |
| Proteins | 442 | 229 |
| Interactions | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 056 056 |
118![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 254 254 |
| Training data | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 046 046 |
98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 545 545 |
| Test data | 5010 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 709 709 |
4.2 Evaluation metrics
MSE is a common metric to measure the difference between the predicted value and the real value:
 | (8) |
CI is used to measure whether the predicted binding affinity values of two random drug–target pairs were predicted in the same order as their true values:
 | (9) |
 | (10) |
The metric rm2 is used to evaluate the external prediction performance of QSAR (Quantitative Structure–Activity Relationship) models. A model is acceptable if and only if  , where r2 and r02 are the squared correlation coefficient values between the observed and predicted values with and without intercept, respectively.
, where r2 and r02 are the squared correlation coefficient values between the observed and predicted values with and without intercept, respectively.
4.3 Baseline methods
We compare our model with the following state-of-the-art models:• KronRLS:18 this baseline formulates the problem of learning a prediction function f as finding a minimizer of the following objective function:
 | (11) |
• SimBoost:19 this baseline is a gradient-boosting machine-based method that constructs features of drug, target, and drug–target pairs. These features are fed into a supervised learning method named gradient boosting regression trees, which is derived from the gradient boosting machine model. Using a gradient regression tree, for a given drug–target pair dti, the binding affinity score ŷi is calculated as follows:
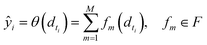 | (12) |
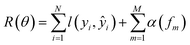 | (13) |
• DeepDTA:20 this baseline trains two 3-layer CNNs using label/one-hot encoding to encode drug and protein sequences for DTA prediction. The CNN model contains two independent CNN blocks that capture features from SMILES sequences and protein sequences, respectively. The drug and target representations are concatenated and passed to a fully connected layer for DTA prediction.
• WideDTA:21 this baseline represents SMILES strings and protein sequences as word sequences and represents the corresponding drugs and proteins through the most common subsequence. In particular, drugs are described by the most common subsequences as Ligand Maximum Common Substructures (LMCS); proteins are represented by the most conserved subsequences that are Protein Domain profiles or Motifs (PDM) retrieved from the PROSTE database. WideDTA contains four independent CNN blocks that learn features from SMILES sequences, LMCS, protein sequences, and PDM. The drug and target representations are all concatenated and passed to a fully connected layer for DTA prediction.
• GANsDTA:24 this baseline proposes a semi-supervised generative adversarial networks (GANs)-based method to predict binding affinity. This method comprises two types of networks, two partial GANs for the feature extraction from the raw protein sequences and SMILES strings separately, and a regression network using convolutional neural networks for prediction.
• DeepGS:27 DeepGS considers both the molecular graphs and SMILES sequences of drugs, and uses BiGRU to extract the local chemical context of SMILES sequences and GAT to capture the topological structure of molecular graphs. For the protein sequences, the CNN module is utilized to learn protein representations from the sequences of amino acids. Then, the representations of drugs and targets are concatenated and passed to a fully connected layer for DTA prediction.
• GraphDTA:5 this baseline converts drugs from SMILES sequences to molecular graphs. GraphDTA consists of two separate modules, a GNN module for modeling molecular graphs to obtain drug representations, and a CNN module for modeling protein sequences to obtain target representations. The drug and target representations are concatenated and passed to a fully connected layer for DTA prediction.
• MATT_DTI:3 this baseline use SMILES sequences and protein sequences as inputs. Unlike DeepDTA, MATT_DTI proposes a relation-aware self-attention module to model SMILES sequences. The relative self-attention module can enhance the relative position information between atoms in a compound while considering the relationship between elements. After the drug and target representations are obtained, a multi-head attention mechanism is used to model the interaction of drug representations and protein representations for DTA prediction.
4.4 Results and discussion
To examine the competitiveness of our proposed model, we compared the model with the current state-of-the-art models on the DTA prediction task. Tables 2 and 3 show the performance of different models on the Davis and Kiba datasets based on MSE, CI, and rm2 metrics. As shown in Tables 2 and 3, those classical methods such as SimBoost19 perform worse than deep learning methods. This is because classical methods rely heavily on manually annotated features provided by a domain expert and drug–target similarity matrices. In comparison, deep learning methods can capture more hidden features by using the automatic feature extraction ability of CNN and GNN.| Method | CI | MSE | rm2 |
|---|---|---|---|
| KronRLS | 0.871 | 0.379 | 0.407 |
| SimBoost | 0.872 | 0.282 | 0.644 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Sequence-based approaches | |||
| DeepDTA | 0.878 | 0.261 | 0.630 |
| WideDTA | 0.886 | 0.262 | 0.633 |
| GANsDTA | 0.881 | 0.276 | 0.653 |
| MATT_DTI | 0.890 | 0.229 | 0.682 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Graph-based approaches | |||
| DeepGS | 0.882 | 0.252 | 0.686 |
| GraphDTA | 0.893 | 0.229 | 0.649 |
| GSATDTA (ours) | 0.906 | 0.200 | 0.732 |
| Method | CI | MSE | rm2 |
|---|---|---|---|
| KronRLS | 0.782 | 0.411 | 0.342 |
| SimBoost | 0.836 | 0.222 | 0.629 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Sequence-based approaches | |||
| DeepDTA | 0.863 | 0.194 | 0.673 |
| WideDTA | 0.875 | 0.179 | 0.675 |
| GANsDTA | 0.866 | 0.224 | 0.675 |
| MATT_DTI | 0.889 | 0.150 | 0.756 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Graph-based approaches | |||
| DeepGS | 0.860 | 0.193 | 0.684 |
| GraphDTA | 0.889 | 0.147 | 0.674 |
| GSATDTA (ours) | 0.902 | 0.126 | 0.790 |
First, we consider a few recent textual representation approaches such as: DeepDTA,20 WideDTA,21 GANsDTA,24 and MATT_DTI.3 Among these approaches, MATT_DTI achieved the best results in terms of CI and MSE. MATT_DTI achieved CI of 0.890, and MSE of 0.229 on the Davis dataset; also, on the Kiba dataset, it achieved CI of 0.889 and MSE of 0.150. This explains the effectiveness of the attention mechanism in learning drug information in the case of MATT_DTI.
Second, we also consider some graph network approaches, GraphDTA and DeepGS. These graph representation approaches can effectively capture topological relationships of drug molecules, which enable further performance improvement. Amongst them, the GraphDTA shows a higher CI value of 0.893 and a lower MSE of 0.229 on the Davis dataset; and on the Kiba dataset, GraphDTA achieved 0.889 in terms of CI and 0.147 in terms of MSE. From Tables 2 and 3, we can find that although DeepGS considers both the molecular graphs and SMILES sequences of drugs, it performs worse than GraphDTA in terms of CI, MSE, and rm2. The reason is that DeepGS directly contacted the SMILES representation and graph representation, which failed to capture comprehensive information about drugs.
As shown in Tables 2 and 3, our proposed GSATDTA has a robust performance on both datasets. For the Davis dataset, our model achieved 0.906 (0.013 improvement), 0.200 (reduced by 0.029), and 0.732 (0.046 improvement) for CI, MSE, and rm2, respectively. For the Kiba dataset, we achieved 0.902 for CI (0.013 improvement), 0.126 for MSE (reduced by 0.021), and 0.790 for rm2 (0.034 improvement). We observe that our model outperforms existing deep-learning methods on three measures, which can be explained due to two factors:
(1) Compared with these models, we replaced CNN with an efficient transformer to learn the representation of the protein, which can capture the long-distance relationships in the sequence of amino acids.
(2) We adopted the GIN architecture to learn the structural information of the molecular graphs and employed BiGRU to obtain extra contextual information for the SMILES sequences. Then, we utilized the graph–sequence attention mechanism to capture significant information from both SMILES representation and graph representation.
4.5 Ablation experiment
To further validate the effect of the different components in GSATDTA, we designed two variants: GSATDTA-a and GSATDTA-b. GSATDTA-a is mainly for investigating the graph–sequence attention, while GSATDTA-b is used to demonstrate the effectiveness of the efficient transformer.• GSATDTA-a used BiGRU to learn the SMILES representation and GIN to learn the graph representation. Then, it directly contacted the two representations without graph–sequence attention. For the protein, GSATDTA-a utilized the efficient transformer to learn the protein representation.
• GSATDTA-b used BiGRU to learn the SMILES representation and GIN to learn the graph representation. Then, it utilized the graph–sequence attention to fuse the SMILES representation and the graph representation. For the protein, GSATDTA-b replaced the efficient transformer with CNN to learn the protein representation.
From Table 4, we can find that in the DTA prediction task, the performance of GSATDTA-a is worse than GSATDTA. These results demonstrate that the graph–sequence attention applied in GSATDTA is beneficial to learning a comprehensive representation of the drugs. Furthermore, we can also observe that GSATDTA-b performs worse than GSATDTA. The result of ablation experiments indicates that the efficient transformer is efficient and effective to learn a good representation of proteins.
| Method | Davis | Kiba | ||||
|---|---|---|---|---|---|---|
| CI | MSE | rm2 | CI | MSE | rm2 | |
| GSATDTA | 0.906 | 0.200 | 0.732 | 0.902 | 0.126 | 0.790 |
| GSATDTA-a | 0.899 | 0.211 | 0.712 | 0.894 | 0.133 | 0.764 |
| GSATDTA-b | 0.894 | 0.216 | 0.697 | 0.890 | 0.136 | 0.752 |
Further, in an attempt to verify our hypothesis about the effectiveness of BiGRU in capturing contextual information from input SMILES, we evaluated the performance of the proposed GSATDTA on the Davis dataset using different versions of RNNs as presented in Fig. 3. We find that simple RNN attains the highest MSE value with 0.224, and there is 0.006 improvement achieved when using GRU. Also, BiLSTM achieved an extra improvement of 3.7%, while BiGRU obtained the lowest MSE value with 0.200, which outperformed the BiLSTM performance by 4.8%. This experiment demonstrates the effectiveness of using BiGRU for modeling the SMILES sequence input.
 | ||
| Fig. 3 The MSE value attained by implementing GSATDTA using different types of RNN on the Davis dataset. | ||
In the molecular property prediction task, Guo et al.15 proposed that integrating the capabilities of both molecular graphs and SMILES sequences can further enhance the model performance. To verify this work in the DTA prediction task, we also conduct an ablation experiment to investigate whether integrating the capabilities of both molecular graphs and SMILES sequences can further enhance the model performance in the drug–target binding affinity prediction task. We designed another two variants: GSATDTA-G and GSATDTA-S. GSATDTA-G uses GIN to learn the graph representation while GSATDTA-S utilizes BiGRU to learn the SMILES representation. For the protein, these two variants both employ the efficient transformer to learn the protein representation. To make the comparison as fair as possible, we chose GSATDTA-a to compare with them. Furthermore, for the evaluation metrics of GSATDTA-G and GSATDTA-S, we use the same metrics as our proposed method, which are the MSE, rm2, and CI.
Fig. 4 and 5 illustrate the predicted against measured (actual) binding affinity values for the Kiba dataset. A perfect model is expected to provide a p = y line where predictions (p) are equal to the measured (y) values. From Fig. 4 and 5, we can observe that compared with GSATDTA-S and GSATDTA-G, GSATDTA-a is denser around the p = y line. More specifically, in regions ① and ④, GSATDTA-S performed better than GSATDTA-G, while in regions ②, ③, and ⑤, GSATDTA-G performed better than GSATDTA-S. For GSATDTA-a, only a few points are spread in these areas. From Fig. 4 and 5, we can also find that the overall trend of GSATDTA-a is more similar to GSATDTA-G, but in regions ① and ④, GSATDTA-a is more similar to GSATDTA-S and performs better than GSATDTA-G. We believe that the topological structure information of the molecular graph is critical to the DTA prediction task, but the local context features in SMILES sequences can be used as supplemental information to predict drug–target binding affinity. In conclusion, the results of visualization indicate that integrating the capabilities of both molecular graphs and SMILES sequences indeed can further enhance the model performance in the drug–target binding affinity prediction task, which is consistent with the viewpoint of Guo et al.15
 | ||
| Fig. 4 Predictions of the GSATDTA-a and GSATDTA-G model against measured (real) binding affinity values for the Kiba dataset. | ||
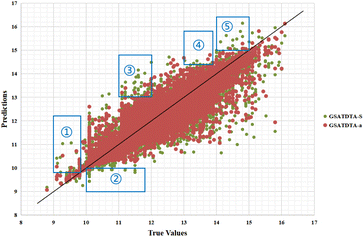 | ||
| Fig. 5 Predictions of the GSATDTA-a and GSATDTA-S model against measured (real) binding affinity values for the Kiba dataset. | ||
Fig. 6 and 7 show the visualization of predicted against measured (actual) binding affinity values for the Davis dataset. We can find similar performance in Fig. 6 and 7. In region ①, GSATDTA-G performed better than GSATDTA-S, while in region ②, GSATDTA-S performed better than GSATDTA-G. GSATDTA-a performed better than GSATDTA-G and GSATDTA-S in region ③ and there are only a few points spread in these areas for GSATDTA-a.
 | ||
| Fig. 6 Predictions of the GSATDTA-a and GSATDTA-G model against measured (real) binding affinity values for the Davis dataset. | ||
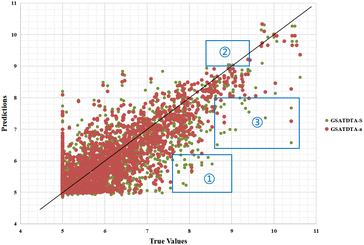 | ||
| Fig. 7 Predictions of the GSATDTA-a and GSATDTA-S model against measured (real) binding affinity values for the Davis dataset. | ||
Furthermore, we also represent the prediction performance of our proposed model based on the predicted value and measured (actual) value (Fig. 8 and 9).
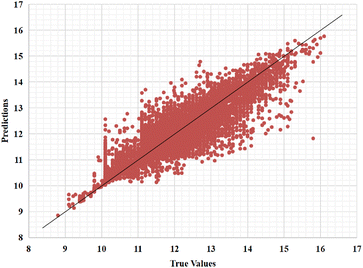 | ||
| Fig. 8 Predictions of the GSATDTA model against measured (real) binding affinity values for the Kiba dataset. | ||
 | ||
| Fig. 9 Predictions of the GSATDTA model against measured (real) binding affinity values for the Davis dataset. | ||
In the Kiba dataset, we analyzed the samples with large errors on the test set and found that when the protein sequence length exceeds 1000, there will be large errors. This is because we fixed the length of the protein sequence to 1000 according to DeepDTA20 and DeepGS,27 which leads to information loss when extracting protein features. There are 4086 samples in the test set with protein sequence lengths longer than 1000. We calculated that the MSE of these samples is 0.174, which is higher than the overall MSE (0.126) of the test set. The MSE of the remaining 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 623 samples in the test set is 0.120, which is lower than the overall MSE of the test set. Therefore, when the sequence length of the protein is longer than 1000, our model suffers from large prediction errors.
623 samples in the test set is 0.120, which is lower than the overall MSE of the test set. Therefore, when the sequence length of the protein is longer than 1000, our model suffers from large prediction errors.
We can find the same performance in the Davis dataset. In the Davis test set, there are 1333 samples with protein sequence lengths longer than 1000. We calculate that the MSE of these samples is 0.214, which is higher than the overall MSE (0.200) of the test set. The MSE of the remaining 3677 samples in the test set is 0.192, which is lower than the overall MSE of the test set.
5 Conclusions
In this paper, we proposed a novel model based on self-attention, called GSATDTA, to predict the binding affinity between drugs and targets. We leveraged both the graph and sequence information and proposed a graph–sequence attention mechanism to learn effective drug representations for DTA prediction. Furthermore, we utilized an efficient transformer to learn the representation of proteins, which can capture the long-distance relationships in the sequence of amino acids. Extensive experimental results show that our model outperforms the state-of-the-art models in terms of MSE, CI, and rm2 on two independent datasets. Since the transformer has achieved great success in various tasks, in the future, we will consider investigating the graph transformer to learn the representations of the drug to predict drug–target binding affinity.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 61972135), the Natural Science Foundation of Heilongjiang Province in China (No. LH2020F043).Notes and references
- J. A. DiMasi, H. G. Grabowski and R. W. Hansen, J. Health Econ., 2016, 47, 20–33 CrossRef PubMed.
- A. D. Roses, Nat. Rev. Drug Discovery, 2008, 7, 807–817 CrossRef CAS PubMed.
- Y. Zeng, X. Chen, Y. Luo, X. Li and D. Peng, Briefings Bioinf., 2021, 22, bbab117 CrossRef.
- Q. Zhao, H. Zhao, K. Zheng and J. Wang, Bioinformatics, 2022, 38, 655–662 CrossRef CAS PubMed.
- T. Nguyen, H. Le, T. P. Quinn, T. Nguyen, T. D. Le and S. Venkatesh, Bioinformatics, 2021, 37, 1140–1147 CrossRef CAS PubMed.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- J. You, B. Liu, Z. Ying, V. Pande and J. Leskovec, Adv. Neural Inf. Process. Syst., 2018, 31, 6412–6422 Search PubMed.
- X. Lin, Z. Quan, Z.-J. Wang, H. Huang and X. Zeng, Briefings Bioinf., 2020, 21, 2099–2111 CrossRef.
- Z. Quan, Y. Guo, X. Lin, Z.-J. Wang and X. Zeng, 2019 IEEE International Conference on Bioinformatics and Biomedicine, BIBM, 2019, pp. 717–722 Search PubMed.
- A. C. Cheng, R. G. Coleman, K. T. Smyth, Q. Cao, P. Soulard, D. R. Caffrey, A. C. Salzberg and E. S. Huang, Nat. Biotechnol., 2007, 25, 71–75 CrossRef CAS PubMed.
- G. M. Morris, R. Huey, W. Lindstrom, M. F. Sanner, R. K. Belew, D. S. Goodsell and A. J. Olson, J. Comput. Chem., 2009, 30, 2785–2791 CrossRef CAS PubMed.
- X. Chen, M.-X. Liu and G.-Y. Yan, Mol. BioSyst., 2012, 8, 1970–1978 RSC.
- F. Cheng, C. Liu, J. Jiang, W. Lu, W. Li, G. Liu, W. Zhou, J. Huang and Y. Tang, PLoS Comput. Biol., 2012, 8, e1002503 CrossRef CAS PubMed.
- X.-Y. Yan, S.-W. Zhang and S.-Y. Zhang, Mol. BioSyst., 2016, 12, 520–531 RSC.
- Z. Guo, W. Yu, C. Zhang, M. Jiang and N. V. Chawla, Proceedings of the 29th ACM International Conference on Information & Knowledge Management, 2020, pp. 435–443 Search PubMed.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser and I. Polosukhin, Adv. Neural Inf. Process. Syst., 2017, 30, 5998–6008 Search PubMed.
- H. Li, K.-S. Leung, M.-H. Wong and P. J. Ballester, Molecules, 2015, 20, 10947–10962 CrossRef CAS PubMed.
- T. Pahikkala, A. Airola, S. Pietilä, S. Shakyawar, A. Szwajda, J. Tang and T. Aittokallio, Briefings Bioinf., 2015, 16, 325–337 CrossRef CAS PubMed.
- T. He, M. Heidemeyer, F. Ban, A. Cherkasov and M. Ester, SimBoost: a read-across approach for predicting drug-target binding affinities using gradient boosting machines, J. Cheminf., 2017, 9, 24 Search PubMed.
- H. Öztürk, A. Özgür and E. Ozkirimli, Bioinformatics, 2018, 34, i821–i829 CrossRef PubMed.
- H. Öztürk, E. Ozkirimli and A. Özgür, arXiv, 2019, preprint, arXiv:1902.04166, DOI:10.48550/arXiv.1902.04166.
- M. Woźniak, A. Wołos, U. Modrzyk, R. L. Górski, J. Winkowski, M. Bajczyk, S. Szymkuć, B. A. Grzybowski and M. Eder, Sci. Rep., 2018, 8, 1–10 CrossRef PubMed.
- C. J. Sigrist, L. Cerutti, E. De Castro, P. S. Langendijk-Genevaux, V. Bulliard, A. Bairoch and N. Hulo, Nucleic Acids Res., 2010, 38, D161–D166 CrossRef CAS PubMed.
- L. Zhao, J. Wang, L. Pang, Y. Liu and J. Zhang, Front. Genet., 2020, 10, 1243 CrossRef PubMed.
- M. Tsubaki, K. Tomii and J. Sese, Bioinformatics, 2019, 35, 309–318 CrossRef CAS PubMed.
- K. Y. Gao, A. Fokoue, H. Luo, A. Iyengar, S. Dey and P. Zhang, et al., Int. Joint Conf. Artif. Intell., 2018, 3371–3377 Search PubMed.
- X. Lin, K. Zhao, T. Xiao, Z. Quan, Z.-J. Wang and P. S. Yu, ECAI 2020, IOS Press, 2020, pp. 1301–1308 Search PubMed.
- T. Song, J. Jiang, W. Li and D. Xu, IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens., 2020, 13, 2853–2860 Search PubMed.
- T. Song, F. Meng, A. Rodriguez-Paton, P. Li, P. Zheng and X. Wang, IEEE Access, 2019, 7, 166823–166832 Search PubMed.
- Z. Quan, X. Lin, Z.-J. Wang, Y. Liu, F. Wang and K. Li, 2018 IEEE International Conference on Bioinformatics and Biomedicine, BIBM, 2018, pp. 728–733 Search PubMed.
- T. Mikolov, I. Sutskever, K. Chen, G. S. Corrado and J. Dean, Adv. Neural Inf. Process. Syst., 2013, 26, 3111–3119 Search PubMed.
- T. Song, S. Pang, S. Hao, A. Rodríguez-Patón and P. Zheng, Neural Process. Lett., 2019, 50, 1485–1502 CrossRef.
- F. Gong, C. Li, W. Gong, X. Li, X. Yuan, Y. Ma and T. Song, Comput. Intell. Neurosci., 2019, 2019, 1939171 Search PubMed.
- J. Chung, C. Gulcehre, K. Cho and Y. Bengio, International conference on machine learning, 2015, pp. 2067–2075 Search PubMed.
- K. Xu, W. Hu, J. Leskovec and S. Jegelka, 7th International Conference on Learning Representations, ICLR, 2019, p. 2019 Search PubMed.
- Z. Xiong, D. Wang, X. Liu, F. Zhong, X. Wan, X. Li, Z. Li, X. Luo, K. Chen and H. Jiang, et al., J. Med. Chem., 2020, 63, 8749–8760 CrossRef CAS PubMed.
- Q. Zhang and Y.-B. Yang, Adv. Neural Inf. Process. Syst., 2021, 34, 15475–15485 Search PubMed.
- D. Ulyanov, A. Vedaldi and V. Lempitsky, arXiv, 2016, preprint, arXiv:1607.08022, DOI:10.48550/arXiv.1607.08022.
| This journal is © The Royal Society of Chemistry 2022 |