Open Access Article
Open Access ArticleDFT and COSMO-RS studies on dicationic ionic liquids (DILs) as potential candidates for CO2 capture: the effects of alkyl side chain length and symmetry in cations†
Mehrangiz Torkzadeh and
Majid Moosavi *
*
Department of Physical Chemistry, Faculty of Chemistry, University of Isfahan, Isfahan 81746-73441, Iran. E-mail: m.mousavi@sci.ui.ac.ir; Fax: +98-313-668-9732; Tel: +98-313-7934942
First published on 9th December 2022
Abstract
A few studies on CO2 capture using dicationic ionic liquids (DILs) show that they are more promising absorbents for CO2 capture than monocationic ILs (MILs). Ion–ion, ion–CO2 and DIL molecule–CO2 interactions are important for understanding the performance–structure–property relationships for the rational design of DILs for CO2 capture applications. However, the role of these interactions in determining CO2 solubility in DILs is unclear. In this study, we used DFT methods to understand these interactions in three selected DILs)considering the effects of alkyl side chain length and symmetry in cations (by exploring different aspects, such as the electronic and geometrical structures, topological properties and the strength and nature of interactions, charge transfer, etc. The results showed that the most suitable solvent for CO2 is the symmetric DIL with a longer side chain length, i.e. [Bis(mim)C5-(C4)2][NTf2]2. In addition, we used the COSMO-RS calculations to obtain the macroscopic solubility of CO2 in the studied DILs, which was in good agreement with the DFT results. Gas selectivity results calculated using COSMO-RS theory indicated that the selectivity of CO2 from H2, CO and CH4 gases decreases slightly with increasing the length of side alkyl chains.
1. Introduction
The burning of fossil fuels for production of electricity and heat is the most important source of greenhouse gas emissions, especially carbon dioxide (CO2), which causes climate changes and global warming. Consequently, various scientific efforts have been made to capture CO2 and protect the environment from its dangerous effects. In the last decade, several methods have been developed for CO2 capture, for example adsorption,1 absorption,2 membrane separation3 and electrochemical separation.4 At present, industries use aqueous amine solutions because of their high tendency to adsorb gas, specifically for CO2 capture. However, these solvents have disadvantages such as high volatility, poor stability, high cost, high energy demand for regeneration, corrosion of equipment, environmental damage associated with amines, etc.5,6 During the past years, ionic liquids (ILs), composed of inorganic/organic anions and organic cations, have been receiving more attention as potential alternatives to conventional amine solutions due to their desirable properties such as negligible vapor pressure, high thermal stability, fine gas solubility and so on.7,8 They can be designed and assembled by altering the structure of their cations and anions to develop functional ILs for selective and effective CO2 capture.9 Dicationic ionic liquids (DILs) are a special class of ILs composed of a doubly charged cation which have two singly charged constituents linked by an alkyl chain paired with two anions.10 It is found that DILs possess wider liquid range, higher melting point, and better thermal stability compared to conventional monocationic ILs (MILs). The physicochemical properties of DILs are more tunable than the corresponding MILs due to the higher combinations of anions and cations.11 From the structural point of view, additional variability of DILs arise from the nature of the cation or from the type and length of their linkage chain. Therefore, DILs present several advantages over traditional MILs in their applications as solvents,12 lubricants,13 and separation media,14 etc. Although, a noticeable quantity of experimental and theoretical works has been invested in studying CO2 capture using ILs, most of them have focused on conventional imidazolium-,15,16 pyridium-17 and phosphonium-based MILs18 and DILs have received very little attention of researchers. Few studies on CO2 capture using DILs show that they are more promising absorbents for CO2 capture than MILs.19–22 Zhang et al.19 showed that the CO2 absorption capacities of six DILs, including four amino acid-functionalized DILs (AADILs) and two traditional DILs (T-DILs), were enhanced heavily compared to MILs. Hojniak et al.20 reported that DILs-incorporated membranes showed the increased CO2/N2 selectivity and adsorption capability compared to MILs-incorporated membrane, which was attributed to the increased CO2 interaction sites in DILs. Similarly, Zhang et al.22 observed the enhanced CO2 capture by imidazolate-based DILs, ([Bis(mim)C2]-[Im]2) and ([Bis(mim)C4]-[Im]2) in which the CO2 capture by DILs is twice that of their MIL analogues. Therefore, the broader and deeper knowledge of structural and electronic properties of ions of DILs is important for designing new DILs for CO2 capture.Theoretical studies are a powerful tool in the insight of nanoscopic features in controlling CO2 absorption by ILs.23–27 The computational studies of gas phase structure of ILs–CO2 systems are of great importance, since the ionic interactions in ILs are often strong to maintain gas-phase structure in liquid phase as well.28 On the other hand, charge distributions are important in describing the structural and dynamical properties in liquid phase, and the partial atomic charges in the force fields of molecular dynamics (MD) simulations of liquid phase are obtained using electronic density and molecular electrostatic potential in gas phase.29 Quantum mechanical methods have proven capable in characterizing IL-CO2 systems, providing valuable information on various aspects such as structural changes, charge transfer, intermolecular hydrogen bonding, etc.30–34 The quantum studies on large systems containing large numbers of ions and CO2 molecules are not possible due to computational constraints. However, studies on anion–cation and ion–CO2 pairs and the analysis of the short-range interactions in these systems are useful and provide valuable information about these systems. In general, in previous quantum studies on MILs–CO2 systems, the interactions have been calculated from placing CO2 molecules around individual ions or IL molecules.35–37 In summary, for common MILs, the CO2 solubility depends more on the cation–anion interactions rather than the CO2–anion or CO2–cation interactions. However, the correlations are more complicated for DILs, which deserve much further analyses.
Although, several studies have been investigated the properties of pure DILs by quantum methods,38–48 to the best of our knowledge, no research has been performed on the structural and electronic properties of DILs in the presence of CO2 gas using quantum mechanical methods. Therefore, in this work, in order to identify the main sites effective in CO2 capture, the structures of three selected DILs (considering the effects of alkyl side chain length and symmetry in cations) in the absence and presence of CO2 are investigated. For each system, the interaction sites, the electronic and geometrical structures, topological properties and the strength and nature of intercations, charge transfer, etc. have been explored. Furthermore, some previous studies, have been also shown that COSMOthermX49 is able to predict the solubility of a gas in the ILs.50–52 Therefore, at the end of this work, the predicted gas absorption in the studied DILs is determined using COSMOthermX based on the absorption isotherms and the results compared with the corresponding quantum mechanical findings.
2. Computational details
2.1 Quantum mechanical calculations
At first, in order to investigate the molecular structure and cation–anion interactions in the selected DILs, one charge-neutral DIL molecule consisting of one cation and two anions (ion triplet) was further investigated by density functional theory (DFT) calculations. The structures of the selected cations and anions along with the labeling of the atoms are shown in Fig. 1. Since the size of a cation in a DIL is large, one DIL molecule (one cation and two anions) may has hundreds of relatively stable configurations. As a result, to find the most stable conformation for each DIL, each DIL was simulated in a big simulation box for 2 ns using NVT ensemble at 298 K. The conformations obtained from simulations were optimized using M06-2X functional and the cc-pVDZ basis set53,54 with Gaussian 09 package.55 Also, the presence of true minima was confirmed by the absence of imaginary frequencies in the calculated vibrational spectra. Recently, researchers have used the M06-2X functional to investigate the physicochemical properties of ILs. M06-2X has been shown remarkable success in predicting reliable structures of the complexes56 and describes the non-covalent interactions better than density functional which are commonly used.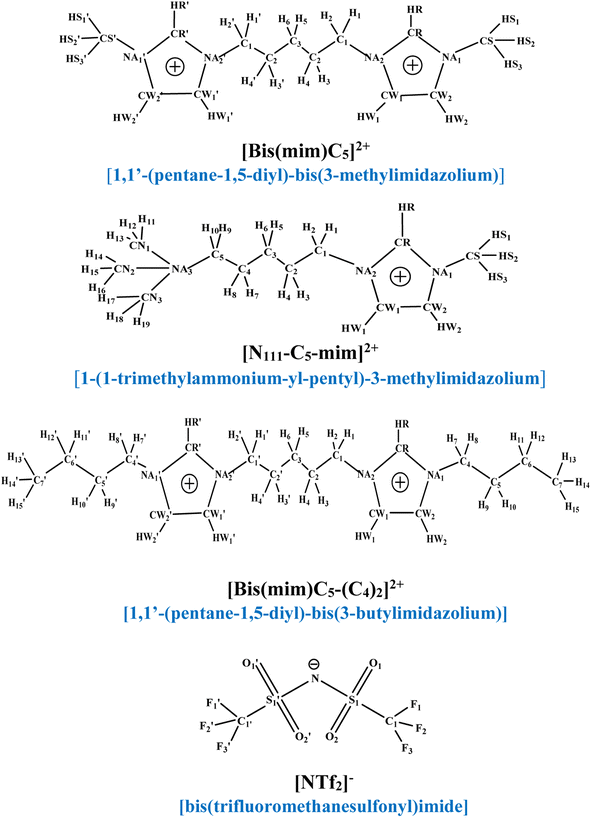 | ||
| Fig. 1 Structures of [Bis(mim)C5]2+, [N111-C5-mim]2+, [Bis(mim)C5-(C4)2]2+ cations and [NTf2]− anion along with their atomic labeling schemes. | ||
After exploring DILs in pure state, their interaction with CO2 was studied by considering isolated ions–CO2 and DIL–CO2 systems. For this purpose, in the second step, after the separate optimization of ions and CO2 molecule, the cation–CO2, anion–CO2 and DIL–CO2 complexes were optimized at the same theoretical level of the optimization of pure DILs (i.e. M06-2X/cc-pVDZ). For each complex, different orientations of CO2 in interaction with isolated ions and DILs were considered and the most stable structures have been chosen to carry out further calculations. The total electronic energies for all the studied systems were corrected using Grimme's DFT-gCP-D3 correction method in which empirical dispersion correction (D3) has been developed by Grimme57 and also the basis set superposition error (BSSE)58 corrections were applied. Charge transfer in all systems was calculated by charges from the electrostatic potential using a grid-based method (CHELPG)59 and natural bonding orbital (NBO) methods at the same theoretical level. Furthermore, to gain further insight into the nature of interactions within the studied systems, NBO analysis has been carried out.60 In order to analyze bond critical point (BCP) data in the studied systems, the quantum theory of atoms in molecules (QTAIM)61 was done using AIM2000 package.62 HOMO–LUMO band gap of all systems were calculated using MultiWFN program.63 Moreover, for identification of non-covalent interactions (NCIs), the reduced density gradient (RDG) was calculated using NCIPLOT program64 and RDG plots were generated through the visual molecular dynamics program (VMD).65
2.2 COSMO-RS theory calculations
It has been verified experimentally that the conductor-like screening model for real solvents (COSMO-RS) theory is a reliable solubility prediction method for ILs systems that combines statistical thermodynamics and quantum chemical calculations.49 Therefore, to obtain the solubility of CO2 in DILs macroscopically, COSMO-RS theory of molecular thermodynamics was used to get macroscopic gas solubility data. In this work, BP functional and TZVP basis set from Turbomole program66 were used for COSMO calculations. Then, the generated COSMO files were imported into COSMOtherm program67 to compute CO2 solubility in the studied DILs.3. Results and discussion
3.1 DFT calculations
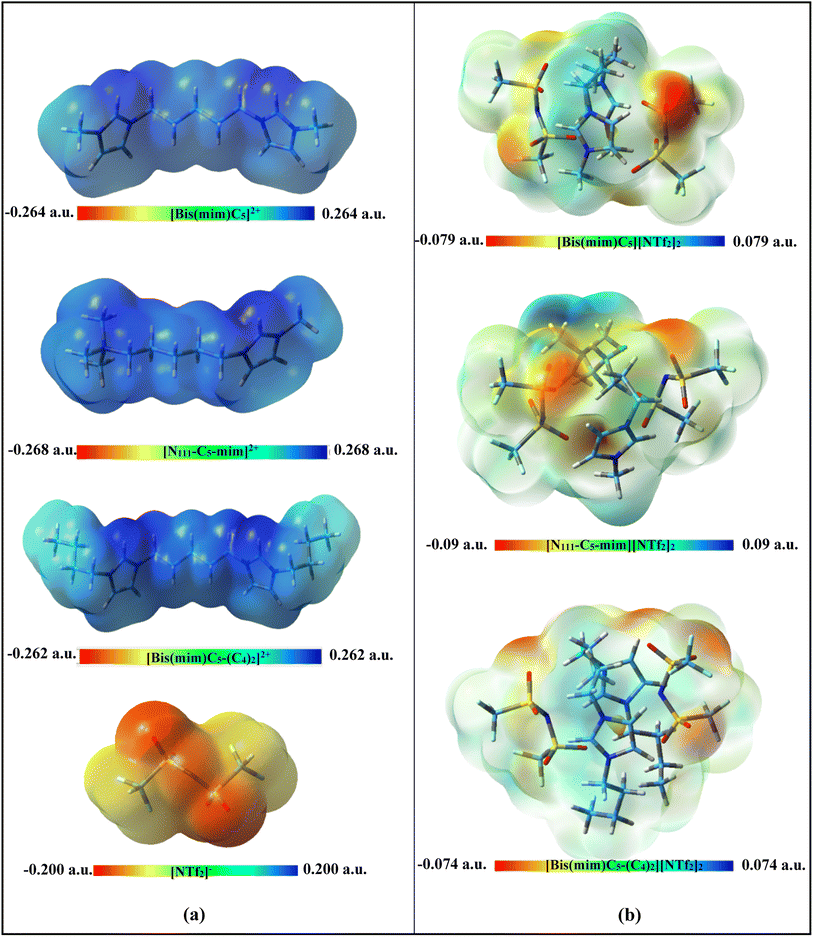 | ||
| Fig. 2 Calculated ESP maps (isovalue = 0.0004) of (a) isolated ions and (b) the studied DILs at M06-2X/ccpVDZ level of theory. | ||
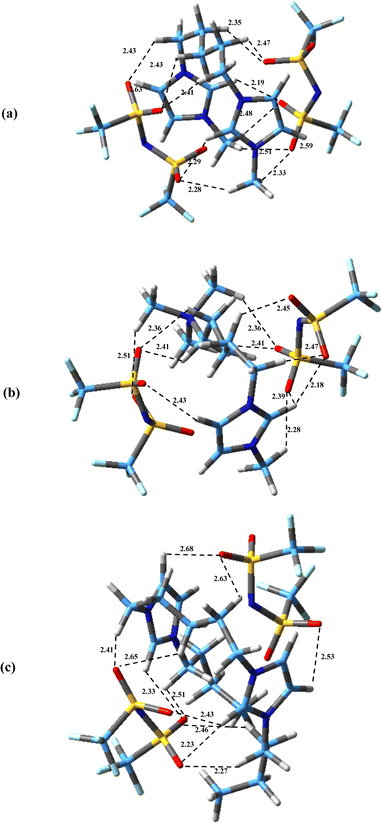
The possible configurations of anions around cation have many effects on hydrogen bondings, interaction energies and physicochemical properties of DILs.45 The most stable structures obtained for the studied DILs have been represented in Fig. 3. It can be found that in all these structures, there exist multiple hydrogen bonds between the cations and the anions, which play an important role for stabilizing the DILs. As it can be seen, in all three structures, the linkage chain entangles in order to maximize the interactions of the two heads of DILs with two anions. Compared with asymmetric [N111-C5-mim][NTf2]2, in two symmetric DILs, the middle chain folding is more and two imidazolium rings are almost parallel to each other. Bodo et al.39 and Sun et al.38 showed that the stability of ion pairs increase as two imidazolium rings become more compact for [Cndmim][NTf2]2 with n = 3, 9 and for [C3(mim)2]Br2 DILs, respectively. Also, Soltanabadi and Bahrami47 showed that the two rings bend towards each other and two halides are placed in the middle of two rings for imidazolium-based DILs. This situation allows the halide anions to have better interaction with special sites of cation. As it can be seen in Fig. 3, the minimum observed distance in the studied DILs is between the anion atoms and the HR (HR′) atoms of the rings which is in agreement with the observed results for imidazolium based MILs,69 DILs70 and tricationic ILs (TILs).71 The minimum distances between the oxygen atoms of anions and HR (HR′) atoms are 2.19, 2.18 and 2.23 Å for [Bis(mim)C5][NTf2]2, [N111-C5-mim][NTf2]2 and [Bis(mim)C5-(C4)2][NTf2]2, respectively.
Interaction energy (ΔEint) is one of the most powerful tools for estimating the strength of non-covalent interactions, which is defined as difference between electron energy of DIL molecule and sum of the energies of cation and anion species:
| ΔEint = EDIL − (EC + 2EA) | (1) |
The values of interaction energies, and also BSSE and D3 corrections for the most stable structures observed in studied DILs (Fig. 3) are reported in Table 1. According to this table, the trend of interaction energy values (with corrections) is as follows: [N111-C5-mim][NTf2]2 > [Bis(mim)C5][NTf2]2 > [Bis(mim)C5-(C4)2][NTf2]2. It seems that in asymmetric DIL [N111-C5-mim][NTf2]2, by replacing a imidazolium group with the ammonium group, the interaction energy between the cations and anions increases due to the more localized charge in the ammonium group. Similarly, Fernandes et al.72 showed that aromatic-based ILs (pyridinium- and imidazolium-based) due to charge delocalization in aromatic rings have lower relative interaction strength values compared with their saturated counterparts (pyrrolidinium- and piperidinium-based). Also, by increasing “side” chain length in [Bis(mim)C5-(C4)2][NTf2]2, the interaction energy decreases. A similar trend of decrease of interaction energies with increasing the length of “linkage” alkyl chain between rings in DILs has been reported.70
| System | ΔEint | D3 | ΔEBSSE | ΔEc |
|---|---|---|---|---|
| “Entangled” configuration | ||||
| [Bis(mim)C5][NTf2]2 | −253.22 | −6.67 | 29.08 | −230.81 |
| [N111-C5-mim][NTf2]2 | −254.47 | −6.40 | 26.40 | −234.47 |
| [Bis(mim)C5-(C4)2][NTf2]2 | −248.41 | −9.17 | 33.47 | −224.11 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| “Stretched” configuration | ||||
| [Bis(mim)C5][NTf2]2 | −224.10 | −5.87 | 43.10 | −186.87 |
| [N111-C5-mim][NTf2]2 | −229.22 | −5.43 | 39.10 | −195.55 |
| [Bis(mim)C5-(C4)2][NTf2]2 | −208.03 | −5.86 | 36.40 | −177.49 |
In Table 1, the interaction energies of the most stable stretched structures have been also tabulated. As it can be seen, the structures with a “stretched” configuration of the linkage chain have higher energies than the “entangled” structures. The “stretched” configurations of [Bis(mim)C5][NTf2]2, [N111-C5-mim][NTf2]2 and [Bis(mim)C5-(C4)2][NTf2]2 have about 43.94, 38.92, 46.62 kcal mol−1 higher than the entangled ones, respectively. Similarly, Bodo et al.39 reported that the energy of “stretched” chain structure is about 40 kcal mol−1 higher than the “entangled” one for [C9dmim][NTf2]2. In general, the calculated interaction energies between cation and two anions in the studied DILs are much higher than reported interaction energies between ion pairs in MILs.73,74 This can be due to the stronger coulombic anion–cation attractions in DILs compared to the interaction between ions in MILs which is responsible for higher thermal stability and melting point in DILs. This result is in agreement with those obtained by Soltanabadi and Bahrami for TILs.47 They reported that the interaction energies of TILs are more than three times of their corresponding MILs. Also, Farmanzadeh et al.40 reported the following trend for the interaction energies in comparison among several MILs and DILs with halide anions: C6(mim)2Cl2 > C6(mim)2Br2 > C6(mim)2I2 > C6(mim)Cl > C6(mim)Br > C6(mim)I.
The frontier molecular orbitals including the lowest unoccupied molecular orbital (LUMO) and the highest occupied molecular orbital (HOMO) are key factors in chemical stability of a system.75 Generally, LUMO as an electron acceptor represents the ability of molecule to capture an electron; whereas HOMO represents the ability of molecules to donate an electron. The electronic properties of a chemical species may be described in terms of global quantum molecular descriptors such as HOMO–LUMO gap (ΔEgap), chemical hardness (η) and chemical potential (μ) which are calculated as:76
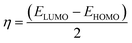 | (2) |
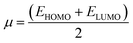 | (3) |
The calculated values of the HOMO, LUMO energies, ΔEgap, η and μ for the isolated cations, anions and the studied DILs have been reported in Table 2. The magnitude of band gaps (ΔEgap) implies the strength of interactions in an IL, that is, stronger interactions between cations and anions lead to a further reduction in energy gap. As it can be seen, the HOMO–LUMO energy gap follows the order of [N111-C5-mim][NTf2]2 (−5.91 eV) < [Bis(mim)C5][NTf2]2 (−5.99 eV) < [Bis(mim)C5-(C4)2][NTf2]2 (−6.33 eV) which is in agreement with trend of interaction energies. Chemical hardness is a measure of inhibition of charge transfer to the molecule, and species with less polarizability have higher hardness values. Considering chemical hardness, if a molecule has a large ΔEgap, it is a hard molecule, and if it has a small ΔEgap, it is a soft molecule. Also, the stability of a molecule can be related to its hardness, as a small ΔEgap leads to high chemical reactivity.
| System | EHOMO/eV | ELUMO/eV | Egap/eV | η/eV | μ/eV |
|---|---|---|---|---|---|
| [Bis(mim)C5]2+ | −13.24 | −6.92 | −6.31 | 3.16 | −10.08 |
| [N111-C5-mim]2+ | −13.54 | −6.92 | −6.62 | 3.31 | −10.23 |
| [Bis(mim)C5-(C4)2]2+ | −12.93 | −6.67 | −6.25 | 3.13 | −9.80 |
| [NTf2]− | −3.90 | 3.54 | −7.44 | 3.72 | −0.18 |
| [Bis(mim)C5][NTf2]2 | −7.16 | −1.17 | −5.99 | 2.99 | −4.16 |
| [N111-C5-mim][NTf2]2 | −7.21 | −1.29 | −5.91 | 2.96 | −4.25 |
| [Bis(mim)C5-(C4)2][NTf2]2 | −7.28 | −0.94 | −6.33 | 3.17 | −4.11 |
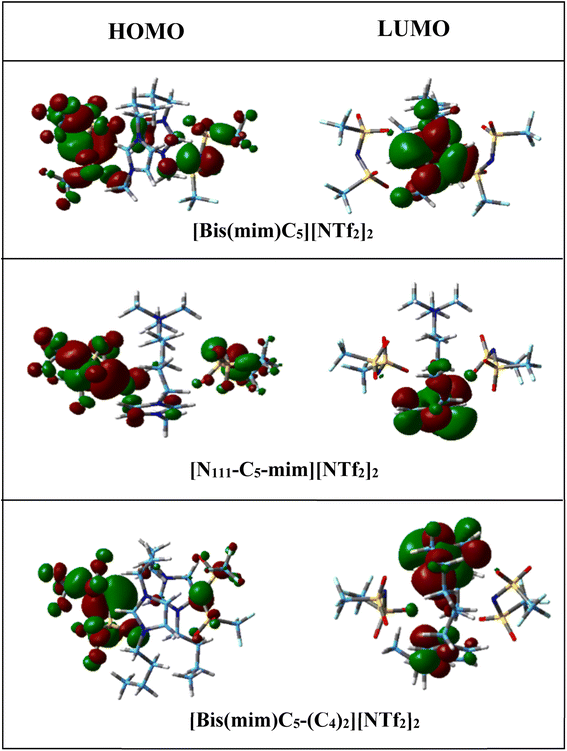
According to the values in Table 2, the calculated chemical hardness has the trend [N111-C5-mim][NTf2]2 < [Bis(mim)C5][NTf2]2 < [Bis(mim)C5-(C4)2][NTf2]2 for the studied DILs. Furthermore, electronic chemical potential describes tendency of the electron to escape from a stable system. The observed trend for the chemical potential of DILs is the reverse of the chemical hardness trend. Therefore, it is plausible to say that with increasing symmetry and increasing side chain length of cations, the stability of DILs increases. The spatial distribution of frontier molecular orbitals is important in describing electrical properties of ILs. Thus, spatial distribution of HOMO and LUMO for isolated cation, anions and the studied DILs are visualized in Fig. S1† and 4, respectively. From these figures, it can be seen that HOMOs are mainly concentrated on two anions, while LUMOs are mainly located on the imidazolium rings of cations. Thus, the charge transfer can be occurred from HOMO of [NTf2] anion to the LUMO of the imidazolium rings in all DILs.
As seen in Fig. 3, there are several intermolecular interactions between cations and anions. The nature of these interactions in DILs may be analyzed by Bader's topological QTAIM analysis using topological parameters such as electron density (ρ(r)), Laplacian of electron density (∇2ρ(r)), kinetic energy density (G(r)), potential energy density (V(r)), the total energy density (H(r)) (where H(r) = G(r) + V(r)) and −(G(r)/V(r)) ratio at bond critical point (BCP) between the cation and anions of DILs. The topological graphics of the lowest energy structures of studied GDILs have been shown in Fig. S2.† Also, the values of mentioned parameters at M06-2X/ccpvDZ level have been summarized in Table S1.† The hydrogen bonding is characterized from ρ(r) values in the range of 0.002–0.035 a.u and with corresponding ∇2ρ(r) in the range of 0.024–0.139 a.u. For all of the studied DILs, values of ρ(r) and ∇2ρ(r) are in the mentioned ranges. ρ(r) is used to describe the strength of a bond, the stronger the bond, the larger the value of ρ(r). As it can be seen, interaction of oxygens of anions with HR (or HR′) atoms of the rings is stronger than interaction with the rest of hydrogens and there are at least two interactions between the HR (or HR′) atoms and the anions in DILs. The hydrogen bonds in ILs are classified as medium and weak (∇2ρ(r) > 0, and H(r) > 0) and strong (∇2ρ(r) > 0, and H(r) < 0) in nature. Therefore, according to the values in the table, hydrogen interactions in studied DILs are often of the type of weak and medium interactions. In asymmetric [N111-C5-mim][NTf2]2 DIL, total electron density (∑ρ(r)) at all critical points of the bond is higher than the other two symmetric DILs. Also, increasing the side chain length in [Bis(mim)C5-(C4)2][NTf2]2 DIL reduces the electron density in the system which is in agreement with the results of interaction energies. The −(G(r)/V(r)) ratio serves as a useful descriptor for separation of various interactions in ILs.77 As it can be seen, the −(G(r)/V(r)) ratio turns out to be between 0.99 a.u and 1.27 a.u, which suggests that the studied DILs are stabilized by van der Waals (vdW) and weak hydrogen bonding interactions. It has been shown that hydrogen bond interactions may not reveal its signature with the emergence of BCP. Extension of the QTAIM theory introduces the G(r) component corresponding to Smin (equivalent to BCP in QTAIM theory) that is directly proportional to the electron density mobility in BCP. Thus, G(r) component offers certain advantages over conventional method used to probe the electron density properties and is useful to characterize the hydrogen bondings. Saleh et al.78 demonstrated that there is a correlation between OH stretching frequencies and the G(r) in substituted amino alcohols that have intramolecular hydrogen bonds. Lane et al.79 showed that the strength of intermolecular hydrogen bonds which reflect in frequency down (red) shift of the OH-stretching vibration can be estimate with G(r) component. A plot of G(r) as a function of interaction energies has been shown in Fig. 5(a) turns out to be almost linear. Espinosa et al.80 showed that hydrogen bond energy (EHB) can be estimated from V(r) at the corresponding BCP, through EHB = −0.5 V(r) which a larger energy indicates a stronger bond. A plot of EHB as a function of G(r) displayed in Fig. 5(b) turns out to be linear. As it can be seen, the asymmetric [N111-C5-mim][NTf2]2 possesses stronger cation–NTf2 binding.
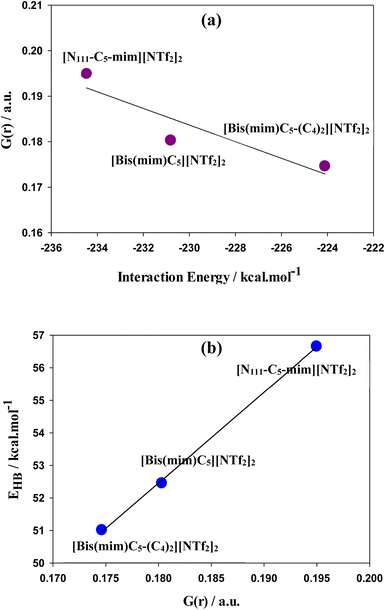 | ||
| Fig. 5 (a) Kinetic energy density, G(r), as a function of interaction energies and (b) EHB as a function of G(r). | ||
Charge transfer is the process in which a fraction of electron charge is transferred within a molecule or between different molecules. Generally, the charge is transferred from the HOMO to LUMO orbitals. In this section, NBO and CHELPG methods have been used to study charge transfer in the studied DILs. The results of both methods have been reported in Table S2.† According to this table, in both methods, the charge transfer for DILs has the following trend: [N111-C5-mim][NTf2]2 > [Bis(mim)C5][NTf2]2 > [Bis(mim)C5-(C4)2][NTf2] which is in agreement with decreasing the HOMO–LUMO energy gap from [Bis(mim)C5-(C4)2][NTf2]2 to [N111-C5-mim][NTf2]2 reported in Table 2.
In DILs, multiple hydrogen bonds are able to form. For example, an anion can interact simultaneously with two hydrogens which both of them can belong to alkyl chains or one hydrogen belongs to the alkyl chains and one hydrogen belongs to the ring. The NBO analysis (according to second order perturbation theory) has been extensively employed in studying hydrogen bonding.77 The NBO analysis of DILs considering second-order perturbation energy (E(2)), the energy difference between donor and acceptor (ΔEij), and Fock matrix element between donor and acceptor (Fij) has been reported in Table S3.† E(2) describes the strength of interactions between anti-bonding orbitals (BD*) of C–H bonds of cations and lone pair electrons (LP) of N, F and O atoms of anion. Strong hydrogen bonding in the studied DILs, are characterized by large E(2) values which are produced by low ΔEij and large Fij. The E(2) values in Table S3† show that there is a high stabilization energy corresponding to charge transfers between oxygen atoms of anions and HR atoms of rings. The trend for these strong hydrogen bonds follows the order of [N111-C5-mim][NTf2]2 > [Bis(mim)C5][NTf2]2 > [Bis(mim)C5-(C4)2][NTf2]2, which is in agreement with the trend of AIM and interaction energies. In the studied DILs, alkyl chains bend and more atoms of alkyl chains are able to form hydrogen bonds (see Fig. 3). Besides the strong hydrogen bonds forming between HR atoms of the rings and anions, some of the weaker hydrogen bonds with lower E(2), which form between the hydrogens of alkyl chains and anions, are shown in Table S3.†
| ΔEint = Ecomplexes − (Eion or DIL + ECO2) | (4) |
The values of interaction energies, BSSE and D3 corrections for the structures shown in Fig. S3 and S4† have been reported in Table 5. Fig. 6 and 7 show the most stable structures for ion–CO2 and DIL–CO2 complexes, respectively, which were selected according to the values of interaction energies for further analyses. Due to the presence of two different heads in the asymmetric cation, for [N111-C5-mim]2+–CO2 and [N111-C5-mim][NTf2]2–CO2 complexes, two stable structures were considered to investigate the differences between two heads in the performance of CO2 absorption.
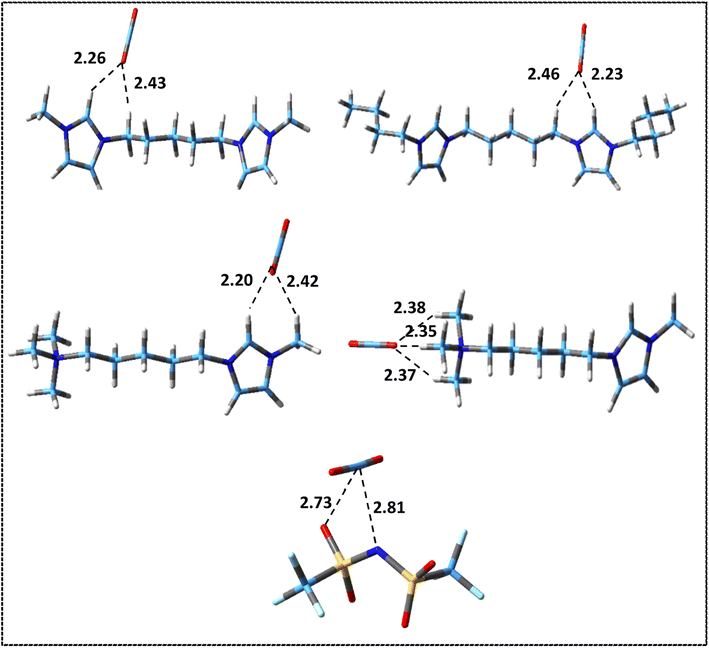 | ||
| Fig. 6 Most stable structures of isolated ion–CO2 complexes at M06-2X/ccpVDZ level. Broken lines show the most important intermolecular interactions (distances are in Å). | ||
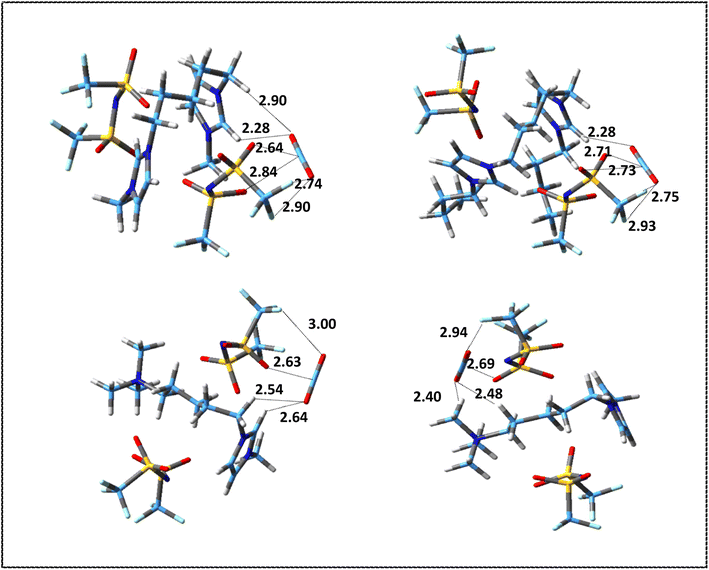 | ||
| Fig. 7 Most stable structures of DIL–CO2 complexes at M06-2X/ccpVDZ level. Broken lines show the most important intermolecular interactions (distances are in Å). | ||
As it can be seen in Fig. 6, based on intermolecular cation–CO2 distances, the most stable sites for CO2 absorption in the symmetric cations are mainly the co-absorbing position by HR hydrogen in imidazolium ring and methylene group attached to the ring. This result is consistent with previous studies on the interaction of imidazolium-based MILs with CO2 molecules.81 However, in the asymmetric [N111-C5-mim]2+ cation, the most stable structure is related to the placement of the CO2 molecule in front of the ammonium head (structure no. 3 in Fig. S3†) probably due to the more localized charge in the ammonium group. As it can be seen, for [NTf2] anion, the most stable sites for CO2 absorption are nitrogen and oxygen atoms of anion. Comparing the interactions of anions and cations with the CO2 molecule shows that, with the exception of the structure in which the CO2 molecule interacts with the asymmetric cation from the ammonium head, the interaction energy of the anion–CO2 is higher than that for the cation–CO2. It can be said that the main intermolecular interactions of anion–CO2 are due to the strong electrostatic interactions, while for cation–CO2 are the weak hydrogen bonds.
According to the values of energies reported in Table S4,† in symmetric DIL–CO2 complexes, the most stable structure is obtained from the orientation of the CO2 molecule on top of the HR hydrogen of ring, and the interaction energy decreases as the CO2 molecule moves away from the ring. In the [N111-C5-mim][NTf2]2–CO2 complexes, the most stable structure is related to the placement of the CO2 molecule in the vicinity of the ammonium head. In the [N111-C5-mim]2+–CO2 complexes, we saw that the most stable structure is formed by the orientation of one of the oxygen atoms of CO2 in front of the ammonium head. However, in [N111-C5-mim][NTf2]2–CO2 complex due to the presence of anion, CO2 molecule is oriented in the ammonium head in such a way that it has the most interaction with the anion and cation at the same time and presents a more accurate picture of reality.
The trend of interaction energies for DIL–CO2 complexes is as follows: [N111-C5-mim][NTf2]2–CO2 < [Bis(mim)C5][NTf2]2–CO2 < [Bis(mim)C5-(C4)2][NTf2]2–CO2 which is the reverse of the trend of interaction energies for pure DILs. It seems that with decreasing interaction energy between anions and cations, the CO2 capture in DILs increases. This result is in agreement with the studies of Babarao et al.82 and Gupta et al.83 on MILs–CO2 systems. They showed that CO2 solubility is governed by the binding energy of cation–anion rather than anion–CO2.
In Table 3, the values of charge transfer in ion–CO2 and DIL–CO2 complexes with NBO and CHELPG methods have been reported. As it can be seen, the CHELPG method predicts higher values of charge transfer, and as expected in cation–CO2 complexes the charge transfer is from the CO2 molecule to cations and in the anion–CO2 complex the charge transfer is from anion to CO2 molecule. Charge transfer calculated by both methods indicates higher charge transfer in the anion–CO2 complex compared to cation–CO2, which shows stronger electrostatic interactions in this complex. Also, in both methods, the asymmetric cation–CO2 complex shows higher charge transfer compared to the two symmetric cations. Another interesting feature presented in Table 3 is the bending of O–C–O angle in the CO2 molecule for anion–CO2 system, which is significant compared to cation–CO2 complexes.
| System | Charge transfer | Δϕ/deg | ||
|---|---|---|---|---|
| CHELPG | NBO | |||
| Ion–CO2 complexes | ||||
| [Bis(mim)C5]2+–CO2 | 0.048 | 0.011 | 0.26 | |
| [N111-C5-mim]2+–CO2 | Imidazolium head | 0.050 | 0.012 | 0.18 |
| Ammonium head | 0.053 | 0.014 | 0.04 | |
| [Bis(mim)C5-(C4)2]2+–CO2 | 0.030 | 0.011 | 0.19 | |
| [NTf2]−–CO2 | −0.063 | −0.018 | 4.77 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| DIL–CO2 complexes | ||||
| [Bis(mim)C5][NTf2]2–CO2 | −0.033 | −0.0039 | 2.88 | |
| [N111-C5-mim][NTf2]2–CO2 | Imidazolium head | −0.019 | −0.0023 | 2.3 |
| Ammonium head | −0.023 | −0.0037 | 2.69 | |
| [Bis(mim)C5-(C4)2][NTf2]2–CO2 | −0.038 | −0.0039 | 3.13 | |
In DIL–CO2 complexes, the negative charge of CO2 molecule shows that more charge from the anion has been transferred to CO2 molecule. According to the results presented in the table, charge transfer by both CHELPG and NBO methods for DIL–CO2 complexes obeys the following order: [N111-C5-mim][NTf2]2–CO2 < [Bis(mim)C5][NTf2]2–CO2 < [Bis(mim)C5-(C4)2][NTf2]2–CO2
This trend is in agreement with interaction energies reported in Table S4.† In some studies, the bending of O–C–O angle is considered as a criterion of the tendency to adsorb CO2 in the ILs.27,32 By comparing the values of the angle deviation for CO2 molecules in different DIL–CO2 complexes, it seems that the interactions between CO2 molecule and the studied DILs have an enhanced tendency as side chains extend.
The values of the HOMO, LUMO energies, ΔEgap, η and μ calculated for systems containing CO2 have been listed in Table 4. Comparing the values of ΔEgap in Table 2 and its values in this table (after interaction with CO2), it is observed that the ΔEgap of anion–CO2 complexes decreases from 7.44 eV to 6.57 eV, but no significant change is observed in the cation–CO2 complexes. It can be said that the magnitude of the decrease in the ΔEgap is due to the increase in the strength of the interactions between the anion and CO2, and stronger interactions between the orbitals lead to a more stable anion–CO2 complex. For DIL–CO2 complexes, the [Bis(mim)C5-(C4)2][NTf2]2–CO2 system has the smallest energy gap compared to other systems which is in agreement with interaction energy and charge transfer results. Fig. S5† shows the spatial distribution of HOMO and LUMO orbitals for studied complexes. As it can be seen, similar to pure DILs, the HOMO orbitals are mainly located on two anions, while the LUMO orbitals for all systems are mainly located on the imidazolium rings.
| System | EHOMO/eV | ELUMO/eV | Egap/eV | η/eV | μ/eV | |
|---|---|---|---|---|---|---|
| Ion–CO2 complexes | ||||||
| [Bis(mim)C5]2+–CO2 | −13.10 | −6.83 | −6.27 | 3.13 | −9.96 | |
| [N111-C5-mim]2+–CO2 | Imidazolium head | −13.31 | −6.66 | −6.65 | 3.32 | −9.98 |
| Ammonium head | −13.48 | −6.87 | −6.61 | 3.30 | −10.17 | |
| [Bis(mim)C5-(C4)2]2+–CO2 | −12.81 | −6.59 | −6.22 | 3.11 | −9.70 | |
| [NTf2]−–CO2 | −3.22 | 3.35 | −6.57 | 3.28 | 0.06 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| DIL–CO2 complexes | ||||||
| [Bis(mim)C5][NTf2]2–CO2 | −7.15 | −1.09 | −6.05 | 3.03 | −4.12 | |
| [N111-C5-mim][NTf2]2–CO2 | Imidazolium head | −7.25 | −0.87 | −6.34 | 3.19 | −4.06 |
| Ammonium head | −7.29 | −0.96 | −6.33 | 3.16 | −4.12 | |
| [Bis(mim)C5-(C4)2][NTf2]2–CO2 | −7.20 | −1.25 | −5.94 | 2.97 | −4.22 | |
In Table 5, the NBO analysis for studied complexes containing CO2 molecules has been reported. In the case of cation–CO2 complexes, interactions are characterized with charge transfer from one of the lone pairs of oxygen atoms in CO2 molecule to anti-bonding orbitals in the C–H bonds of cations and in the case of anion–CO2 complexes, interactions are characterized with charge transfer from nitrogen and oxygen atoms to the anti-bonding orbital in CO2 molecules. As mentioned before, the larger value of E(2) indicates the stronger interaction, which may result from a lower ΔEij or a larger Fij (i.e. better symmetry between the electron donor and electron acceptor). In agreement with previous results, the largest value of E(2) in cations arises from the charge transfer of CO2 molecule to anti-bonding orbitals in C–HR bond of the rings. The trend of E(2) for this charge transfer in cation–CO2 complexes is as follows: > [Bis(mim)C5]2+–CO2 [N111-C5-mim]2+–CO2 > [Bis(mim)C5-(C4)2]2+–CO2
| System | Donor NBO(I) | Acceptor NBO (j) | E(2)/kJ mol−1 | ΔEij/a.u | Fij/a.u |
|---|---|---|---|---|---|
| Ion–CO2 complexes | |||||
| [Bis(mim)C5]2+–CO2 | LP(1) O in CO2 | BD*(1) C–HR | 7.78 | 1.38 | 0.045 |
| LP(1) O in CO2 | BD*(1) C–H1 | 3.51 | 1.38 | 0.03 | |
| [N111-C5-mim]2+–CO2 | LP(1) O in CO2 | BD*(1) C–HR | 11.40 | 1.36 | 0.057 |
| Imidazolium head | LP(1) O in CO2 | BD*(1) C–HS | 4.06 | 1.38 | 0.036 |
| Ammonium head | LP(1) O in CO2 | BD*(1) C–H13 | 5.61 | 1.37 | 0.038 |
| LP(1) O in CO2 | BD*(1) C–H15 | 5.85 | 1.37 | 0.039 | |
| LP(1) O in CO2 | BD*(1) C–H18 | 5.77 | 1.37 | 0.039 | |
| [Bis(mim)C5-(C4)2]2+–CO2 | LP(1) O in CO2 | BD*(1) C–HR | 9.66 | 1.37 | 0.05 |
| LP(1) O in CO2 | BD*(1) C–H1 | 4.35 | 1.37 | 0.034 | |
| [NTf2]−–CO2 | LP(1) N in [NTf2]− | BD*(3) C–O in CO2 | 11.51 | 0.58 | 0.036 |
| LP(2) O1′ in [NTf2]− | BD*(3) C–O in CO2 | 6.61 | 0.41 | 0.024 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| DIL–CO2 complexes | |||||
| [Bis(mim)C5][NTf2]2–CO2 | LP(1) O in CO2 | BD*(1) CR–HR | 3.68 | 1.39 | 0.031 |
| LP(2) O in CO2 | BD*(1) CR–HR | 4.85 | 0.90 | 0.032 | |
| LP(1) O1′ in [NTf2]− | BD*(3) C–O in CO2 | 5.61 | 0.99 | 0.035 | |
| LP(3) O1′ in [NTf2]− | BD*(3) C–O in CO2 | 5.86 | 0.45 | 0.023 | |
| [N111-C5-mim][NTf2]2–CO2 | LP(2) O in CO2 | BD*(1) CR–HR | 1.13 | 0.9 | 0.015 |
| LP(3) O in CO2 | BD*(1) C1–H1 | 1.09 | 0.9 | 0.015 | |
| Imidazolium head | LP(1) O1′ in [NTf2]− | BD*(3) C–O in CO2 | 5.61 | 0.98 | 0.034 |
| LP(2) O1′ in [NTf2]− | BD*(3) C–O in CO2 | 4.64 | 0.44 | 0.021 | |
| Ammonium head | LP(1) O in CO2 | BD*(1) CN1–H11 | 4.48 | 1.37 | 0.038 |
| LP(2) O in CO2 | BD*(1) C4–H7 | 4.02 | 0.91 | 0.031 | |
| LP(1) O1′ in [NTf2]− | BD*(3) C–O in CO2 | 4.69 | 0.98 | 0.032 | |
| LP(3) O1′ in [NTf2]− | BD*(3) C–O in CO2 | 5.69 | 0.74 | 0.025 | |
| [Bis(mim)C5-(C4)2][NTf2]2–CO2 | LP(1) O in CO2 | BD*(1) CR–HR | 3.81 | 1.39 | 0.032 |
| LP(2) O in CO2 | BD*(1) CR–HR | 5.35 | 0.9 | 0.033 | |
| LP(1) O1 in [NTf2]− | BD*(2) C–O in CO2 | 3.68 | 0.98 | 0.028 | |
| LP(1) O1 in [NTf2]− | BD*(3) C–O in CO2 | 3.30 | 1.00 | 0.027 | |
| LP(1) O1 in [NTf2]− | BD*(3) C–O in CO2 | 4.93 | 0.98 | 0.030 | |
| LP(2) O1′ in [NTf2]− | BD*(3) C–O in CO2 | 4.48 | 0.46 | 0.021 | |
The larger E(2) value in the [N111-C5-mim]2+–CO2 arises from larger Fij value, which shows strong donor–acceptor symmetry in this complex. Also, the stronger interaction energy and more charge transfer in anion–CO2 complexes with respect to cation–CO2 complexes (see Tables S4† and 3, respectively) can be explained based on larger E(2) values which in turn arises from low ΔEij coupled with suitable donor–acceptor symmetry and lead to more effective interactions for anions than cations.
For DIL–CO2 complexes, the largest E(2) in all systems arises from the charge transfer of the anions in DILs to CO2 molecules. Compared to cations, anions have a stronger interaction with CO2 molecules which is in agreement with previous results. Furthermore, according to E(2) values, the strongest interactions in the cations of all DILs (including imidazolium head for asymmetric DIL) are due to the charge transfer from CO2 molecule to anti-bonding orbitals in C–HR bond of the rings. The trend of the E(2) (charge transfer from CO2 molecule to C–HR bond) for cations of DILs in the presence of anions is as follows:
[N111-C5-mim]2+–CO2 < [Bis(mim)C5]2+–CO2 < [Bis(mim)C5-(C4)2]2+–CO2. The different trend of E(2) for isolated cations and for cations in the presence of anions can be attributed to the effect of the interaction energy between cations and anions on CO2 capture. The weaker interaction energy between the anions and cations, the stronger interaction of CO2 molecule with cation. It should be noted that since the interaction energy of cation–anion in MILs is lower than that of DILs, it is expected that MILs have higher gas solubility. While, experimental studies show the opposite.19,20,22 In fact, in addition to the interaction energy between ions, other factors such as the number of interaction sites, free volume fraction, types of ions, etc. are effective in the amount of CO2 absorption by ILs and should be taken into consideration.84,85
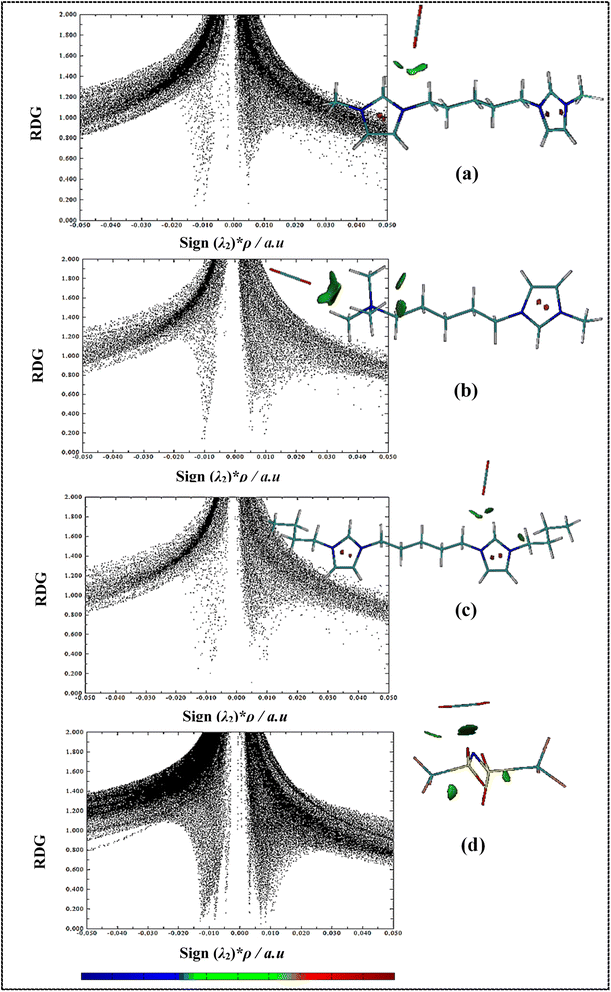
RDG isosurfaces and 2D scatter plots for studied complexes have been displayed in Fig. 8 and S6.† Non-covalent interactions (NCIs) such as hydrogen bonding, vdW interactions and steric effects can be evaluated using RDG analysis. RDG plots can be provided information about the type and strength of interactions in IL–CO2 systems.86 The sign of λ2 (second eigenvalues of the electron-density of Hessian matrix) and electron density ρ(r) value determine the type and strength of the interactions, respectively, where negative and positive sign (λ2) values describe the attractive and repulsive interactions, respectively. In 2D scatter RDG plots, spikes in large negative values of sign (λ2)*ρ (ρ > 0, λ2 < 0) are indicative of hydrogen bond interactions, whereas the spikes located at large positive values sign (λ2)*ρ (ρ > 0, λ2 > 0) are the steric effects. In addition, spikes situated at sign (λ2)*ρ values approach zero (ρ ∼ 0, λ2 ∼ 0) indicate very weak vdW interactions. Also, the colored RDG isosurfaces can be used for qualitative understanding of the nature and the strength of NCIs. The blue, red, and green regions are used for hydrogen bondings, strong repulsion interactions, and attractive vdW interactions, respectively.
In 2D scatter plots for symmetric cation–CO2 complexes (Fig. 8(a) and (c)), two spikes at about −0.01 a.u. and −0.12 a.u. related to the interaction of oxygen of CO2 molecule with H1 and HR atoms of cations, respectively. For the asymmetric cation–CO2 complex (Fig. 8(b)), a strong single spike at −0.01 a.u. indicates the interaction of oxygen of CO2 molecule with methyl groups at the ammonium head of cation. Furthermore, it is observed that in areas close to zero, the number of spikes and their intensity for anion–CO2 system increase compared to the cation–CO2 systems, which indicates an increase in vdW interactions in the anion–CO2 system. In the RDG isosurfaces, the extension of green region shows the local character of an interaction. A larger size of green region for asymmetric cation shows that CO2 has stronger interactions with the ammonium head of the asymmetric cation than the imidazolium head which is in agreement with the previous analyses. In RDG isosurfaces of DIL–CO2 complexes (Fig. S6†), the green areas are formed more between anion and CO2, which indicates the greater contribution of anions in interaction with CO2 molecules. Also, for asymmetric DIL–CO22 system (Fig. S6(b) and (c)†), the size of green region between CO2 and DIL is less than the other two symmetric DILs–CO2 systems (Fig. S6(a) and (d)†). Comparing the scatter plots, it can be seen that in the [Bis(mim)C5-(C4)2][NTf2]2–CO2 system, a strong spike in −0.03 a.u. indicates the existence of stronger hydrogen bond interactions and the more tendency of this DIL for interaction with CO2 molecule. In general, the green region between DILs and CO2 indicates that vdW interactions are driving force to CO2 capture in DILs.
The AIM analysis of isolated ion–CO2 and DIL–CO2 interactions has been reported in Table 6 and Fig. S7 and S8,† respectively. As it can be seen, according to the values of ρ(r), in all systems, the interactions of oxygens of CO2 molecules with HR atoms of rings are stronger than other hydrogens. In DIL–CO2 complexes, the number of interactions between the CO2 molecules and the anions is more than that for cations, and CO2 molecules interact with the anions through the oxygen and fluorine atoms. In accordance with the results of previous analyses, the trend of ∑ρ(r) at BCPs between DILs and CO2 molecules is as follows: [N111-C5-mim][NTf2]2–CO2 < [Bis(mim)C5][NTf2]2–CO2 < [Bis(mim)C5-(C4)2][NTf2]2–CO2
| Structure | BCP | ρ(r) (a.u.) | ∑ρ(r) (a.u.) | ∇2ρ(r) (a.u.) | G(r) (a.u.) | V(r) (a.u.) | H(r) (a.u.) | −(G(r)/V(r)) |
|---|---|---|---|---|---|---|---|---|
| Ion–CO2 complexes | ||||||||
| [Bis(mim)C5]2+–CO2 | b1 O1–HR | 0.0124 | 0.0219 | 0.0436 | 0.0102 | −0.0094 | 0.0008 | 1.0851 |
| b2 O1–H1 | 0.0095 | 0.0344 | 0.0079 | −0.0072 | 0.0007 | 1.0972 | ||
| [N111-C5-mim]2+–CO2 | b1 O1–HR | 0.0132 | 0.0225 | 0.0482 | 0.0111 | −0.0101 | 0.0009 | 1.0990 |
| Imidazolium head | b2 O1–HS1 | 0.0093 | 0.0316 | 0.0074 | −0.0069 | 0.0005 | 1.0725 | |
| Ammonium head | b1 O1–H13 | 0.0102 | 0.0312 | 0.0351 | 0.0082 | −0.0077 | 0.0005 | 1.0649 |
| b2 O1–H15 | 0.0107 | 0.0366 | 0.0086 | −0.0081 | 0.0005 | 1.0618 | ||
| b3 O1–H18 | 0.0103 | 0.0356 | 0.0084 | −0.0078 | 0.0006 | 1.0769 | ||
| [Bis(mim)C5-(C4)2]2+–CO2 | b1 O1–HR | 0.0130 | 0.0221 | 0.0466 | 0.0108 | −0.0099 | 0.0009 | 1.0909 |
| b2 O1–H1 | 0.0091 | 0.0299 | 0.0068 | −0.0061 | 0.0007 | 1.114 | ||
| [NTf2]−–CO2 | b1 C–N | 0.0120 | 0.0292 | 0.0470 | 0.0101 | −0.0084 | 0.0017 | 1.2024 |
| b2 C–O1′ | 0.0127 | 0.0521 | 0.0115 | −0.0099 | 0.0015 | 1.1616 | ||
| b3 O1–F1′ | 0.0045 | 0.0251 | 0.0052 | −0.0041 | 0.0011 | 1.2683 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| DIL–CO2 complexes | ||||||||
| [Bis(mim)C5][NTf2]2–CO2 | b1 O1–HR | 0.0131 | 0.0571 | 0.0446 | 0.0105 | −0.0099 | 0.0006 | 1.0606 |
| b2 O1–H1 | 0.0035 | 0.0154 | 0.0030 | −0.0022 | 0.0008 | 1.3636 | ||
| b3 C–O1 | 0.0089 | 0.0411 | 0.0085 | −0.0066 | 0.0018 | 1.2878 | ||
| b4 C–O1 | 0.0144 | 0.0626 | 0.0139 | −0.0121 | 0.0018 | 1.1487 | ||
| b5 O2–F2′ | 0.0100 | 0.0451 | 0.0105 | −0.0097 | 0.0008 | 1.0824 | ||
| b6 O2–F1′ | 0.0072 | 0.0338 | 0.0074 | −0.0064 | 0.0009 | 1.1562 | ||
| [N111-C5-mim][NTf2]2–CO2 | b1 O1–HR | 0.0082 | 0.0345 | 0.0289 | 0.0065 | −0.0058 | 0.0007 | 1.1206 |
| b2 O1–H1 | 0.0069 | 0.0295 | 0.0061 | −0.0047 | 0.0013 | 1.2978 | ||
| Imidazolium head | b3 C–O1 | 0.0143 | 0.0636 | 0.0139 | −0.0119 | 0.0019 | 1.1680 | |
| b4 O2–F1 | 0.0051 | 0.0271 | 0.0057 | −0.0047 | 0.0010 | 1.2127 | ||
| Ammonium head | b1 O1–H11 | 0.0094 | 0.0429 | 0.0353 | 0.0080 | −0.0072 | 0.0008 | 1.1111 |
| b2 O1–H7 | 0.0088 | 0.0278 | 0.0066 | −0.0063 | 0.0003 | 1.0476 | ||
| b3 O1–N | 0.0039 | 0.0166 | 0.0034 | −0.0027 | 0.0007 | 1.2592 | ||
| b4 C–O1′ | 0.0133 | 0.0562 | 0.0124 | −0.0107 | 0.0017 | 1.1588 | ||
| b5 O2–F1′ | 0.0075 | 0.0368 | 0.0077 | −0.0061 | 0.0015 | 1.2622 | ||
| [Bis(mim)C5-(C4)2][NTf2]2–CO2 | b1 O1–HR | 0.0132 | 0.0580 | 0.0454 | 0.0107 | −0.0099 | 0.0007 | 1.0808 |
| b2 C–O1 | 0.0119 | 0.0543 | 0.0116 | −0.0096 | 0.0019 | 1.2083 | ||
| b3 C–O1′ | 0.0121 | 0.0522 | 0.0113 | −0.0096 | 0.0017 | 1.1770 | ||
| b4 O2–F2′ | 0.0111 | 0.0439 | 0.0102 | −0.0093 | 0.0008 | 1.0967 | ||
| b5 O2–F1′ | 0.0097 | 0.0424 | 0.0081 | −0.0056 | 0.0025 | 1.4464 | ||
Which indicates that DILs with symmetric cation and a longer side alkyl chain are more desirable for interaction with CO2 molecules. Whereas in isolated ion–CO2 systems, ∑ρ(r) for [N111-C5-mim]2+–CO2 is more and the replacement of the ammonium group has a greater effect on the interaction with CO2 molecule compared to increasing the length of side alkyl chain. Therefore, the results indicate the important effect of anion in the interaction of CO2 with cations of DILs, which cannot be ignored.
3.2 COSMO-RS calculations
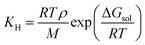 | (5) |
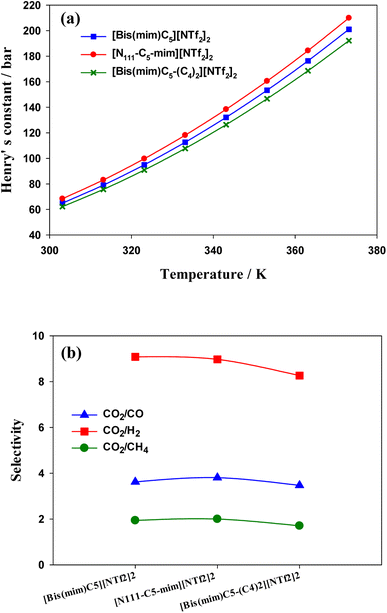 | ||
| Fig. 10 (a) Henry's constant versus temperature for the studied DILs. (b) Selectivity of CO2 from CO, H2 and CH4 in the studied DILs at 303.15 K calculated by COSMO-RS theory. | ||
Separation of CO2 from gas mixture is very common and necessary in the chemical industry. For example, in the production of natural gas, in addition to the main component CH4, in most cases CO2 is also present in the mixed gas. The presence of CO2 reduces the combustion efficiency of natural gas and can cause pipeline corrosion.89 Therefore, separation of CO2 from some gases is very important. In this work, in order to investigate the effect of side chain length and symmetry in cations on gas separation, in Fig. 10(b), the selectivities of CO2/CO, CO2/CH4 and CO2/H2 mixtures were calculated using COSMO-RS theory. The ideal gas selectivity, Sm/n, can be obtained by eqn (6):90
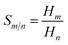 | (6) |
4. Conclusion
In summary, we have investigated three selected DILs (considering the effects of alkyl side chain length and symmetry in cations) in the absence and presence of CO2 using quantum mechanical methods. The results showed that for all three structures, the linkage chain entangles in order to maximize interactions of two heads of DILs with two anions. The trend of interaction energy values was as follows: [N111-C5-mim][NTf2]2 > [Bis(mim)C5][NTf2]2 > [Bis(mim)C5-(C4)2][NTf2]2. It seems that in asymmetric DIL [N111-C5-mim][NTf2]2, by replacing a imidazolium group with the ammonium one, the interaction energy between the cations and anions increases due to the more localized charge in the ammonium group. Furthermore, AIM and NBO analyses for all three DILs, in addition to confirming the trend of interaction energies, showed that interaction of oxygens of anions with HR (or HR′) atoms of the rings is stronger than interaction with the rest of hydrogens.In ion–CO2 complexes, it was observed that the most stable sites for CO2 absorption in the symmetric cations are mainly the co-absorbing positions by HR hydrogen in the imidazolium ring and methylene group attached to the ring. However, in the asymmetric [N111-C5-mim]2+ cation, the most stable structure is related to the placement of CO2 molecule in front of the ammonium head probably due to the more localized charge in the ammonium group. The results of charge transfer values, O–C–O angle deviations in the CO2 molecule, AIM and NBO showed that, with the exception of the structure in which the CO2 molecule interacts with the asymmetric cation from the ammonium head, the tendency of the anions to CO2 is more than cations. It can be said that the intermolecular interactions of the anion–CO2 are due to the strong electrostatic interactions, while for cation–CO2 are the weak hydrogen bonds.
For DIL–CO2 complexes, the trend of interaction energies was as follows: [N111-C5-mim][NTf2]2–CO2 < [Bis(mim)C5][NTf2]2–CO2 < [Bis(mim)C5-(C4)2][NTf2]2–CO2 which is the reverse of the trend of interaction energies for pure DILs. It seems that with decreasing the interaction energy between ions, the CO2 capture in DILs increases. The results of NBO and AIM analyses indicated that DIL with symmetric cation and longer side chain is more favorable for CO2 absorption which was in agreement with the results of interaction energies and charge transfers. Moreover, the green regions between DILs and CO2 showed that the vdW interactions are driving force to CO2 capture in DILs.
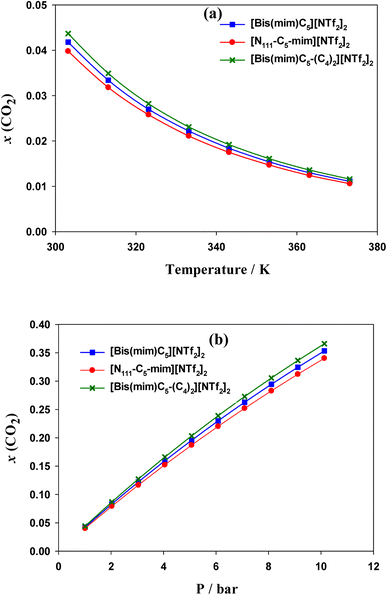
COSMO-RS results indicated that the solubility of CO2 in the DILs has the following trend: [N111-C5-mim][NTf2]2 < [Bis(mim)C5][NTf2]2 < [Bis(mim)C5-(C4)2][NTf2]2. Indeed, both symmetric DILs tend to accommodate a little more CO2 molecules and the solubility of CO2 slightly increases as side alkyl chains of a DIL extends longer, which is in agreement with quantum results. Also, results showed that the selectivity of CO2 from H2, CO and CH4 gases decreases slightly with increasing the length of side alkyl chains.
Author contributions
Mehrangiz Torkzadeh: software, investigation, methodology, visualization, data curation, writing – original draft. Majid Moosavi: supervision, conceptualization, methodology, validation, writing – review & editing.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This research was supported financially by Iran national science Foundation (INSF) and the Research Council of University of Isfahan [grant number 4002409].References
- C. A. Trickett, A. Helal, B. A. Al-Maythalony, Z. H. Yamani, K. E. Cordova and O. M. Yaghi, Nat. Rev. Mater., 2017, 2, 1–16 CrossRef.
- I. Sreedhar, T. Nahar, A. Venugopal and B. Srinivas, Renewable Sustainable Energy Rev., 2017, 76, 1080–1107 CrossRef CAS.
- Z. Dai, R. D. Noble, D. L. Gin, X. Zhang and L. Deng, J. Membr. Sci., 2016, 497, 1–20 CrossRef CAS.
- B. Gurkan, F. Simeon and T. A. Hatton, ACS Sustainable Chem. Eng., 2015, 3, 1394–1405 CrossRef CAS.
- E. Masiren, N. Harun, W. Ibrahim and F. Adam, Int. J. Eng. Sci. Res. Technol., 2016, 3, 43–51 Search PubMed.
- F. Moosavi, F. Abdollahi and M. Razmkhah, Int. J. Greenhouse Gas Control, 2015, 37, 158–169 CrossRef CAS.
- M. J. Earle and K. R. Seddon, Pure Appl. Chem., 2000, 72, 1391–1398 CrossRef CAS.
- X. Zhang, X. Zhang, H. Dong, Z. Zhao, S. Zhang and Y. Huang, Energy Environ. Sci., 2012, 5, 6668–6681 RSC.
- G. Cui, J. Wang and S. Zhang, Chem. Soc. Rev., 2016, 45, 4307–4339 RSC.
- B. Bhargava and M. L. Klein, J. Phys. Chem. B, 2011, 115, 10439–10446 CrossRef CAS PubMed.
- H. Shirota, T. Mandai, H. Fukazawa and T. Kato, J. Chem. Eng. Data, 2011, 56, 2453–2459 CrossRef CAS.
- X. Han and D. W. Armstrong, Org. Lett., 2005, 7, 4205–4208 CrossRef CAS PubMed.
- M. Mahrova, F. Pagano, V. Pejakovic, A. Valea, M. Kalin, A. Igartua and E. Tojo, Tribol. Int., 2015, 82, 245–254 CrossRef CAS.
- M. Qi and D. W. Armstrong, Anal. Bioanal. Chem., 2007, 388, 889–899 CrossRef CAS PubMed.
- C. Cadena, J. L. Anthony, J. K. Shah, T. I. Morrow, J. F. Brennecke and E. J. Maginn, J. Am. Chem. Soc., 2004, 126, 5300–5308 CrossRef CAS PubMed.
- S. Tanaka, K. Kida, H. Fujimoto, T. Makino and Y. Miyake, Langmuir, 2011, 27, 7991–7995 CrossRef CAS PubMed.
- S. Supasitmongkol and P. Styring, Energy Environ. Sci., 2010, 3, 1961–1972 RSC.
- Y. Zhang, S. Zhang, X. Lu, Q. Zhou, W. Fan and X. Zhang, Eur. J. Chem., 2009, 15, 3003–3011 CrossRef CAS PubMed.
- Y. Zhang, P. Yu and Y. Luo, Chem. Eng. J., 2013, 214, 355–363 CrossRef CAS.
- S. D. Hojniak, A. L. Khan, O. Holloczki, B. Kirchner, I. F. Vankelecom, W. Dehaen and K. Binnemans, J. Phys. Chem. B, 2013, 117, 15131–15140 CrossRef CAS PubMed.
- S. Li, W. Zhao, G. Feng and P. T. Cummings, Langmuir, 2015, 31, 2447–2454 CrossRef CAS PubMed.
- Y. Zhang, Z. Wu, S. Chen, P. Yu and Y. Luo, Ind. Eng. Chem. Res., 2013, 52, 6069–6075 CrossRef CAS.
- X. Liu, J. E. Bara and C. H. Turner, J. Phys. Chem. B, 2021, 125, 8165–8174 CrossRef CAS PubMed.
- X. Liu, K. E. O'Harra, J. E. Bara and C. H. Turner, Phys. Chem. Chem. Phys., 2020, 22, 20618–20633 RSC.
- X. Liu and C. H. Turner, Chem. Phys. Lett., 2022, 786, 139204 CrossRef CAS.
- J. Ma, Y. Wang, M. Zhu, X. Yang and B. Wang, J. Mol. Liq., 2020, 320, 114408 CrossRef CAS.
- V. Sanz, R. Alcalde, M. Atilhan and S. Aparicio, J. Mol. Model., 2014, 20, 1–14 CrossRef CAS PubMed.
- G. E. Logotheti, J. Ramos and I. G. Economou, J. Phys. Chem. B, 2009, 113, 7211–7224 CrossRef CAS PubMed.
- H. Li and M. N. Kobrak, J. Chem. Phys., 2009, 131, 194507 CrossRef PubMed.
- B. E. Gurkan, J. C. de la Fuente, E. M. Mindrup, L. E. Ficke, B. F. Goodrich, E. A. Price, W. F. Schneider and J. F. Brennecke, J. Am. Chem. Soc., 2010, 132, 2116–2117 CrossRef CAS PubMed.
- M. I. Cabaço, M. Besnard, Y. Danten and J. Coutinho, J. Phys. Chem. B, 2011, 115, 3538–3550 CrossRef PubMed.
- S. Aparicio and M. Atilhan, J. Phys. Chem. B, 2012, 116, 9171–9185 CrossRef CAS PubMed.
- J.-J. Chen, W.-W. Li, X.-L. Li and H.-Q. Yu, Phys. Chem. Chem. Phys., 2012, 14, 4589–4596 RSC.
- C. Wu, T. P. Senftle and W. F. Schneider, Phys. Chem. Chem. Phys., 2012, 14, 13163–13170 RSC.
- A. Indarto and J. Palgunadi, Ionics, 2012, 18, 143–150 CrossRef CAS.
- J. A. Steckel, J. Phys. Chem. A, 2012, 116, 11643–11650 CrossRef CAS PubMed.
- H. Tang and C. Wu, ChemSusChem, 2013, 6, 1050–1056 CrossRef CAS PubMed.
- H. Sun, D. Zhang, C. Liu and C. Zhang, J. Mol. Struct.: THEOCHEM, 2009, 900, 37–43 CrossRef CAS.
- E. Bodo and R. Caminiti, J. Phys. Chem. A, 2010, 114, 12506–12512 CrossRef CAS PubMed.
- D. Farmanzadeh, A. Soltanabadi and S. Yeganegi, J. Chin. Chem. Soc., 2013, 60, 551–558 CrossRef CAS.
- P. L. Verma, L. J. Bartolotti and S. P. Gejji, J. Phys. Chem. A, 2016, 120, 7732–7744 CrossRef CAS PubMed.
- S. M. Alavi and S. Yeganegi, J. Mol. Liq., 2018, 256, 330–343 CrossRef CAS.
- P. L. Verma and S. P. Gejji, J. Mol. Graphics Modell., 2018, 85, 304–315 CrossRef CAS PubMed.
- L. Guglielmero, L. Guazzelli, A. Toncelli, C. Chiappe, A. Tredicucci and C. S. Pomelli, RSC Adv., 2019, 9, 30269–30276 RSC.
- H. Roohi, S. F. G. Gildeh, K. Ghauri and P. Fathei, Ionics, 2020, 26, 1963–1988 CrossRef CAS.
- H. Roohi, S. F. G. Gildeh, M. Mehrdad and K. Ghauri, J. Mol. Liq., 2020, 310, 113060 CrossRef CAS.
- A. Soltanabadi and M. Bahrami, J. Mol. Graphics Modell., 2020, 96, 107529 CrossRef CAS PubMed.
- P. L. Verma and S. P. Gejji, J. Mol. Struct., 2020, 1201, 127112 CrossRef.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- J. E. Sosa, R. Santiago, A. E. Redondo, J. Avila, L. F. Lepre, M. C. Gomes, J. o. M. Araújo, J. Palomar and A. B. Pereiro, Environ. Sci. Technol., 2022, 56, 5898–5909 CrossRef CAS PubMed.
- N. A. Manan, C. Hardacre, J. Jacquemin, D. W. Rooney and T. G. Youngs, J. Chem. Eng. Data, 2009, 54, 2005–2022 CrossRef.
- M. K. Hadj-Kali, M. Althuluth, S. Mokraoui, I. Wazeer, E. Ali and D. Richon, Chem. Eng. Commun., 2020, 207, 1264–1277 CrossRef CAS.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364–382 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- M. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, Revision D.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- M. Walker, A. J. Harvey, A. Sen and C. E. Dessent, J. Phys. Chem. A, 2013, 117, 12590–12600 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373 CrossRef CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- R. F. Bader and T. Nguyen-Dang, Adv. Quantum Chem., 1981, 14, 63–124 CrossRef CAS.
- F. Biegler-Konig, J. Schonbohm and D. Bayles, J. Comput. Chem, 2001, 22, 545–559 CrossRef.
- T. Lu and F. Chen, J. Comput. Chem, 2012, 33, 580–592 CrossRef CAS PubMed.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput, 2011, 7, 625–632 CrossRef PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph, 1996, 14, 33–38 CrossRef CAS PubMed.
- R. Ahlrichs, M. Bar and M. Ha, Chem. Phys. Lett, 1989, 162, 165–169 CrossRef CAS.
- F. Eckert and A. C. Klamt, COSMOTherm, Version C3. 0, Release 12.01, COSMOlogic GmbH & Co. KG, Leverkusen, Germany, 2013 Search PubMed.
- P. Politzer, P. R. Laurence and K. Jayasuriya, Environ. Health Perspect., 1985, 61, 191–202 CrossRef CAS PubMed.
- W. Li, C. Qi, H. Rong, X. Wu and L. Gong, Chem. Phys. Lett, 2012, 542, 26–32 CrossRef CAS.
- M. Moosavi, F. Khashei and E. Sedghamiz, Phys. Chem. Chem. Phys, 2018, 20, 435–448 RSC.
- E. Sedghamiz, F. Khashei and M. Moosavi, J. Mol. Liq., 2018, 271, 96–104 CrossRef CAS.
- A. M. Fernandes, M. A. Rocha, M. G. Freire, I. M. Marrucho, J. A. Coutinho and L. M. Santos, J. Phys. Chem. B, 2011, 115, 4033–4041 CrossRef CAS PubMed.
- K. Dong, S. Zhang, D. Wang and X. Yao, J. Phys. Chem. A, 2006, 110, 9775–9782 CrossRef CAS PubMed.
- P. A. Hunt, I. R. Gould and B. Kirchner, Aust. J. Chem., 2007, 60, 9–14 CrossRef CAS.
- K. Fukui, Frontier orbitals and reaction paths: selected papers of Kenichi Fukui, World Scientific, 1997 Search PubMed.
- S. Armaković, S. J. Armaković, M. Vraneš, A. Tot and S. Gadžurić, J. Mol. Liq., 2016, 222, 796–803 CrossRef.
- D. Cremer and E. Kraka, Angew. Chem., Int. Ed. Engl., 1984, 23, 627–628 CrossRef.
- G. Saleh, C. Gatti and L. L. Presti, Comput. Theor. Chem., 2015, 1053, 53–59 CrossRef CAS.
- J. R. Lane, S. D. Schrøder, G. C. Saunders and H. G. Kjaergaard, J. Phys. Chem. A, 2016, 120, 6371–6378 CrossRef CAS PubMed.
- E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. lett., 1998, 285, 170–173 CrossRef CAS.
- B. Li, C. Wang, Y. Zhang and Y. Wang, Green Energy Environ., 2021, 6, 253–260 CrossRef.
- R. Babarao, S. Dai and D.-e. Jiang, J. Phys. Chem. B, 2011, 115, 9789–9794 CrossRef CAS PubMed.
- K. M. Gupta and J. Jiang, J. Phys. Chem. C, 2014, 118, 3110–3118 CrossRef CAS.
- M. S. Shannon, J. M. Tedstone, S. P. O. Danielsen, M. S. Hindman, A. C. Irvin and J. E. Bara, Ind. Eng. Chem. Res., 2012, 51, 5565–5576 CrossRef CAS.
- E. J. Beckman, Chem. Commun., 2004, 1885–1888 RSC.
- B. A. Marekha, O. N. Kalugin and A. Idrissi, Phys. Chem. Chem. Phys., 2015, 17, 16846–16857 RSC.
- T. Payagala, J. Huang, Z. S. Breitbach, P. S. Sharma and D. W. Armstrong, Chem. Mater., 2007, 19, 5848 CrossRef CAS.
- T. Su, Z. Tang, C. Yin, Y. Yang, H. Wang, L. Peng, Y. Su, P. Su and J. Li, J. Mol. Liq., 2021, 327, 114857 CrossRef CAS.
- J. Adewole, A. Ahmad, S. Ismail and C. Leo, Int. J. Greenhouse Gas Control, 2013, 17, 46–65 CrossRef CAS.
- Y. Zhao, R. Gani, R. M. Afzal, X. Zhang and S. Zhang, AIChE J., 2017, 63, 1353–1367 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1. Calculated spatial distribution of HOMO and LUMO for isolated ions; Fig. S2. Topological graphics of studied DILs obtained from QTAIM calculations; Fig. S3 and S4. Optimized structures of isolated ion–CO2 and DIL–CO2 complexes; Fig. S5. Calculated spatial distribution of HOMO and LUMO for DIL–CO2 complexes; Fig. S6. Color-filled RDG isosurfaces and scatter graphs of RDG for DIL–CO2 complexes; Fig. S7 and S8. Topological graphics of isolated ion–CO2 and DIL–CO2 complexes obtained from QTAIM calculations; Table S1. Obtained parameters from QTAIM calculations in the studied DILs. Table S2. Charge transfer calculated in the studied DILs using CHELPG and NBO methods. Table S3. NBO analysis of the studied DILs; Table S4. Interaction energies, empirical dispersion and basis set superposition errors for studied ion–CO2 and DIL–CO2 complexes. See DOI: https://doi.org/10.1039/d2ra05805g |
| This journal is © The Royal Society of Chemistry 2022 |