Open Access Article
Open Access ArticleFormation and evolution of C–C, C–O, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h2_char_e001.gif) O and C–N bonds in chemical reactions of prebiotic interest†
O and C–N bonds in chemical reactions of prebiotic interest†
Alejandro Arias a,
Sara Gómez
a,
Sara Gómez *b,
Natalia Rojas-Valencia
*b,
Natalia Rojas-Valencia ac,
Francisco Núñez-Zarur
ac,
Francisco Núñez-Zarur d,
Chiara Cappelli
d,
Chiara Cappelli b,
Juliana A. Murillo-López
b,
Juliana A. Murillo-López e and
Albeiro Restrepo
e and
Albeiro Restrepo *a
*a
aInstituto de Química, Universidad de Antioquia UdeA, Calle 70 No. 52-21, Medellín, Colombia. E-mail: albeiro.restrepo@udea.edu.co
bScuola Normale Superiore, Classe di Scienze, Piazza dei Cavalieri 7, Pisa, 56126, Italy. E-mail: sara.gomezmaya@sns.it
cEscuela de Ciencias y Humanidades, Departamento de Ciencias Básicas, Universidad Eafit, Medellín, AA 3300, Colombia
dFacultad de Ciencias Básicas, Universidad de Medellín, Carrera 87 No. 30-65, Medellín, 050026, Colombia
eDepartamento de Ciencias Químicas, Facultad de Ciencias Exactas, Universidad Andres Bello, Autopista, Concepción-Talcahuano, Talcahuano 7100, Chile
First published on 10th October 2022
Abstract
A series of prebiotic chemical reactions yielding the precursor building blocks of amino acids, proteins and carbohydrates, starting solely from HCN and water is studied here. We closely follow the formation and evolution of the pivotal C–C, C–O, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, and C–N bonds, which dictate the chemistry of the molecules of life. In many cases, formation of these bonds is set in motion by proton transfers in which individual water molecules act as catalysts so that water atoms end up in the products. Our results indicate that the prebiotic formation of carbon dioxide, formaldehyde, formic acid, formaldimine, glycolaldehyde, glycine, glycolonitrile, and oxazole derivatives, among others, are best described as highly nonsynchronous concerted single step processes. Nonetheless, for all reactions involving double proton transfer, the formation and breaking of O–H bonds around a particular O atom occur in a synchronous fashion, apparently independently from other primitive processes. For the most part, the first process to initiate seems to be the double proton transfer in the reactions where they are present, then bond breaking/formation around the reactive carbon in the carbonyl group and finally rupture of the C–N bonds in the appropriate cases, which are the most reluctant to break. Remarkably, within the limitations of our non-dynamical computational model, the wide ranges of temperature and pressure in which these reactions occur, downplay the problematic determination of the exact constraints on the early Earth.
O, and C–N bonds, which dictate the chemistry of the molecules of life. In many cases, formation of these bonds is set in motion by proton transfers in which individual water molecules act as catalysts so that water atoms end up in the products. Our results indicate that the prebiotic formation of carbon dioxide, formaldehyde, formic acid, formaldimine, glycolaldehyde, glycine, glycolonitrile, and oxazole derivatives, among others, are best described as highly nonsynchronous concerted single step processes. Nonetheless, for all reactions involving double proton transfer, the formation and breaking of O–H bonds around a particular O atom occur in a synchronous fashion, apparently independently from other primitive processes. For the most part, the first process to initiate seems to be the double proton transfer in the reactions where they are present, then bond breaking/formation around the reactive carbon in the carbonyl group and finally rupture of the C–N bonds in the appropriate cases, which are the most reluctant to break. Remarkably, within the limitations of our non-dynamical computational model, the wide ranges of temperature and pressure in which these reactions occur, downplay the problematic determination of the exact constraints on the early Earth.
1 Introduction
Abiogenesis, or the origins of life starting from non living matter, is a rich, interdisciplinary field of research encompassing work from areas as diverse as chemistry, physics, biology, astronomy, geology, among others;1–3 its ultimate goal is to determine the conditions and mechanisms that allow life to emerge. Prebiotic chemistry, specifically, seeks to determine what type of chemical compounds and chemical reactions are necessary to produce the constituent components of life, such as biomolecules, and also studies the set of networks of chemical reactions capable of sustaining life as we know it, whether these processes took place on the early Earth, or elsewhere in the interstellar medium.4,5 One progressive reductionist view (life → biology → chemistry → physics → mathematics) is that the emergence of life is a deterministic process, governed by scientific laws, which only needs long times and appropriate local conditions so that isolated events with tiny probabilities do eventually occur and by virtue of local evolution (molecular or otherwise), accumulate and originate highly improbable systems.There are several hypotheses on how life originated, prioritizing either metabolism, self-replication, or a combination of both.6–10 In the RNA world hypothesis, RNA acted as information storage, replicator, and as an active catalyst.11–13 Other views argue in favor of RNA cooperating with peptides and other biomolecules.14 The metabolism-first hypothesis posits that the first living organisms appeared as the final steps of the evolution towards increasing complexity of networks of sequential chemical reactions aided by simple metal catalysts.10,15 The molecules of life (water, carbohydrates, proteins, nucleic acids, ATP, etc.) contain only a few types of atoms, most prominently hydrogen, carbon, oxygen, nitrogen, sulfur, phosphorous. Consequently, any rationalization of how those large biomolecules came to be, at least on Earth, must include detailed descriptions of the formation of C–C, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, C–O and C–N bonds and of the formation of the small molecules that act as the initial building blocks in the series of chemical reactions affording such complicated primary sequences from primitive environments, presumably rich in one carbon (C1) molecules.1 One of those C1 molecules, abundant in extreme environments such as the interstellar medium, planetary and lunar atmospheres within our own solar system, comets, and in the conditions of the primitive Earth is HCN,16–19 which is a favorite target for the ultimate precursor of biomolecules.20–23 Recently, Das and coworkers,15 starting with binary mixtures of water and HCN, offered via molecular dynamics simulations in ab initio nanoreactors, a detailed picture of the myriad of chemical reactions leading to small molecules that are the building blocks of most large biomolecules, i. e., carbon dioxide CO2, formaldehyde CH2O, formic acid H2CO2, formaldimine CH3N, glycolaldehyde C2H4O2, glycine C2H5NO2, glycolonitrile C2H3NO, oxazole C3H3NO derivatives, among many others.
O, C–O and C–N bonds and of the formation of the small molecules that act as the initial building blocks in the series of chemical reactions affording such complicated primary sequences from primitive environments, presumably rich in one carbon (C1) molecules.1 One of those C1 molecules, abundant in extreme environments such as the interstellar medium, planetary and lunar atmospheres within our own solar system, comets, and in the conditions of the primitive Earth is HCN,16–19 which is a favorite target for the ultimate precursor of biomolecules.20–23 Recently, Das and coworkers,15 starting with binary mixtures of water and HCN, offered via molecular dynamics simulations in ab initio nanoreactors, a detailed picture of the myriad of chemical reactions leading to small molecules that are the building blocks of most large biomolecules, i. e., carbon dioxide CO2, formaldehyde CH2O, formic acid H2CO2, formaldimine CH3N, glycolaldehyde C2H4O2, glycine C2H5NO2, glycolonitrile C2H3NO, oxazole C3H3NO derivatives, among many others.
The scientific literature cited above has provided detailed mechanistic pathways identifying reactants, transition states, intermediates, and products as well as estimating the energetics of the chemical reactions that result in the formation of the target molecules building biochemical complexity. Sadly, crucial knowledge describing the formation of the all important C–C, C–O, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, and C–N bonds from the perspective of primitive changes is found nowhere. Consequently, in this work, building on the results of Das,15 we have studied a network of reaction mechanisms yielding the experimentally reported precursor molecules of RNA and proteins. To that end, we closely follow the evolution of bonding interactions leading to formal bonds along the intrinsic reaction coordinates using the tools provided by the Quantum Theory of Atoms in Molecules (QTAIM)24–26 and the Natural Bond Orbitals (NBO).27–29 At this point, it is important to mention that we use QTAIM and NBO as formal analysis tools and make no attempt at discussing their merits and flaws, for which the reader is referred to the extensive literature. The combination of NBO, QTAIM, and other descriptors of bonding allows a detailed dissection of reaction mechanisms and has proven to be an enormously valuable tool to gain insight into the evolution of chemical bonds. A variety of reactions has been successfully studied in the past by our group using this methodology.30–37
O, and C–N bonds from the perspective of primitive changes is found nowhere. Consequently, in this work, building on the results of Das,15 we have studied a network of reaction mechanisms yielding the experimentally reported precursor molecules of RNA and proteins. To that end, we closely follow the evolution of bonding interactions leading to formal bonds along the intrinsic reaction coordinates using the tools provided by the Quantum Theory of Atoms in Molecules (QTAIM)24–26 and the Natural Bond Orbitals (NBO).27–29 At this point, it is important to mention that we use QTAIM and NBO as formal analysis tools and make no attempt at discussing their merits and flaws, for which the reader is referred to the extensive literature. The combination of NBO, QTAIM, and other descriptors of bonding allows a detailed dissection of reaction mechanisms and has proven to be an enormously valuable tool to gain insight into the evolution of chemical bonds. A variety of reactions has been successfully studied in the past by our group using this methodology.30–37
2 Computational methods
Reaction paths starting with HCN and H2O and linking the set of molecular precursors of large biomolecules listed above, i. e., carbon dioxide, formaldehyde, formic acid, formaldimine, glycolaldehyde, glycine, glycolonitrile, and oxazole derivatives, were determined both in gas phase and in aqueous medium, as modelled by the Polarizable Continuum Model (PCM) approach38,39 via intrinsic reaction coordinate (IRC) calculations using second order Moller–Plesset perturbation theory at the MP2/6-311++G(d, p) level. The latter is chosen so that the ambiguity and non systematic problems in the treatment of electron correlation and dispersion proper of Density Functional Theory (DFT) methods are eliminated. All stationary points within a given Potential Energy Surface (PES) were characterized as true minima or saddle points via harmonic vibrational analysis at the same level.We study the energetics of the entire set of 23 reactions listed in Table 1 and characterized every single reactant, product, intermediate, and transition state. However, because of the large number of intermediates and chemical reactions, in order to study the evolution of chemical bonding, we chose a set of five reactions that are particularly relevant in the complex reacting system. These reactions happen to be essential in the pathway towards the target products, which can not be obtained unless those reactions are considered. The point is, the formation of formic acid from HCN and water is the common root from where chemistry branches out into several other intermediates and products according to the following sequence of reactions:
| Label | Reaction | ΔG†act | ΔGrxn | ||
|---|---|---|---|---|---|
| In gas phase | In solution | In gas phase | In solution | ||
| a See Table S1 in the ESI for the intrinsic barriers. An asterisk attached to a label means that HNC is involved instead of HCN. Notice that reaction 14 leads to different products than those reported by Das and coworkers15 in gas phase. | |||||
| 1 | HCN + H2O → CH3NO | 57.2 | 63.8 | 14.3 | 17.0 |
| 2 | CH3NO → CH3NO | 12.9 | 15.9 | −12.0 | −14.1 |
| 3 | CH3NO + H2O → NH3 + CH2O2 | 55.9 | 58.5 | 2.4 | 5.3 |
| 4* | CH2O2 + HNC → C2HNO + H2O | 69.9 | 68.2 | 28.6 | 27.9 |
| 5* | C2HNO → CO + HCN | 34.6 | 27.3 | −38.0 | −38.2 |
| 6 | CO + H2O → CH2O2 | 75.7 | 76.2 | 54.6 | 53.7 |
| 7 | HCN → HNC | 58.0 | 48.8 | 18.4 | 17.7 |
| 8 | CH2O2 → CO2 + H2 | 52.9 | 53.1 | −21.8 | −16.0 |
| 9 | CH2O2 + H2 → CH4O2 | 64.3 | 61.1 | 4.9 | 6.9 |
| 10 | CH4O2 → CH2O + H2O | 35.6 | 37.4 | −5.9 | −8.5 |
| 11* | CH2O + HNC → C2H3NO | 31.9 | 32.4 | −20.8 | −19.8 |
| 12 | CH2O + NH3 → CH5NO | 44.6 | 39.1 | 4.4 | 6.6 |
| 13 | CH5NO → CH3N + H2O | 40.8 | 39.6 | −2.8 | −5.4 |
| 14* | CH3N + HNC → C2H4N2 | NA | 10.6 | NA | −27.2 |
| 14 | CH3N + HCN → C2H4N2 | 39.8 | NA | 11.2 | NA |
| 15 | C2H4N2 + H2O → C2H6N2O | 57.5 | 63.8 | 14.8 | 19.0 |
| 16 | C2H6N2O → C2H6N2O | 11.4 | 14.5 | −12.8 | −14.8 |
| 17 | C2H6N2O + H2O → C2H5NO2 | 53.7 | 57.3 | 1.4 | 1.2 |
| 18 | C2H3NO + CH2O → C3H5NO2 | 64.5 | 60.4 | −2.8 | −1.5 |
| 19* | C3H5NO2 → C2H4O2 +HNC | 37.1 | 31.5 | 19.6 | 17.2 |
| 20 | C2H3NO + CH3NO → C3H6N2O2 | 40.4 | 47.3 | 20.6 | 24.8 |
| 21 | C3H6N2O2 +HCN → C4H7N3O2 | 59.3 | 58.4 | 15.2 | 14.0 |
| 22 | C4H7N3O2 → C4H7N3O2 | 44.5 | 40.0 | −9.4 | −9.0 |
| 23 | C4H7N3O2 → C4H5N3O + H2O | 35.3 | 37.0 | −9.8 | −13.1 |
1. HCN + H2O →⋯→ HCOOH (formic acid). Reaction 3 is the last step of this series.
2. HCOOH →⋯→ H2CO (formaldehyde). Reaction 10 is the last step of this series.
3. H2CO + NH3 → CH5NO (methanol amine via reaction 12).
4. CH5NO →⋯→ C2H5NO2 (glycine). Reaction 17 is the last step of this series.
5. CH2O + HNC → C2H3NO (glycolonitrile via reaction 11).
Notice that all those intermediates (formic acid (reaction 10), formaldehyde (reaction 3), glycolonitrile (reaction 11), amino methanol (reaction 12)) have been experimentally reported to be precursors en route to the target molecules. Glycine is quite important because it is the only amino acid obtained in the entire reacting system. The chosen reactions enable the analysis of the formation and breaking of the very important C–O, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, C–C and C–N bonds starting from C1 molecules. These bonds dictate the chemistry in all the molecules of life. Scheme 1 summarizes the reasons for choosing the set of five reactions listed above as follows: formic acid leads to the formation of formaldehyde. Formaldehyde triggers competitive reactions towards glycine (Strecker synthesis of amino acids) in one channel and glycolonitrile in another. Glycolonitrile yields two further reaction paths, one leading to the oxazole derivative and the other to the glycolaldehyde sugar.
O, C–C and C–N bonds starting from C1 molecules. These bonds dictate the chemistry in all the molecules of life. Scheme 1 summarizes the reasons for choosing the set of five reactions listed above as follows: formic acid leads to the formation of formaldehyde. Formaldehyde triggers competitive reactions towards glycine (Strecker synthesis of amino acids) in one channel and glycolonitrile in another. Glycolonitrile yields two further reaction paths, one leading to the oxazole derivative and the other to the glycolaldehyde sugar.
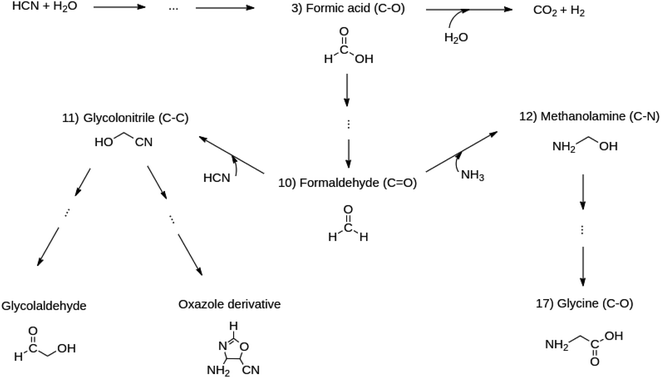 | ||
Scheme 1 The set of five reactions (reactions 3, 10, 11, 12, 17) branching out from formic acid, chosen from Table 1, to study the formation and evolution of the C–C, C–N, C–O and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds. O bonds. | ||
IRCs are conveniently dissected by the critical points of the reaction force, defined, as for any conservative system, as the points for which the negative derivative of the potential energy along the reaction coordinate vanishes (F = −dV/dξ = 0).40–43 For a given elementary step, three critical points are obtained, corresponding to reactants (ξR), transition state (ξTS), and products (ξP); the critical points of the reaction force yield the activated reactants (ξR*) and activated products (ξP*). These five points along the IRC are the limits of three well defined regions, namely, the reactants region, associated to the structural changes needed to bring the reactants into the geometries needed for the reaction to occur and covering the ξR → ξR* interval, the transition state region, the region where most of the electron activity needed for bond breaking/formation takes place, covering the ξR → ξP* interval, and the products region, where the activated products suffer further structural changes to finally release the products, covering the ξP → ξP* interval. The chemical potential along the reaction path is obtained as half the sum of the energies of the HOMO and LUMO orbitals at each point of the IRC,44,45 and the reaction electron flux (REF), is calculated as the derivative of the chemical potential along the entire reaction path.46–48
The evolution of bonding interactions was followed using the set of descriptors provided by QTAIM and by NBO and the recently developed GGR synchronicity index.35 In lieu of a detailed description and to spare the technical details of how QTAIM and NBO descriptors are related to bonding, the interesting reader is directed to the specialized literature,24–29 more explicitly, to the work of Rojas-Valencia et al.49 (their Table 2 and the ensuing description) and references within. All electronic structure calculations including optimization, vibrational frequencies, solvent effects and IRCs were conducted using the Gaussian09 suite of programs.50 QTAIM quantities were derived from the AIMAll suite.51 NBO descriptors were obtained from NBO6 (ref. 52) as implemented in Gaussian.
3 Results and discussion
3.1 Reaction profiles
Starting from HCN and H2O, production of carbon dioxide, formaldehyde, formic acid, formaldimine, glycolaldehyde, glycine, glycolonitrile and oxazole derivatives involves a total of 23 elementary steps detailed in Table 1. Subtle differences between our results and those reported by Das and coworkers15 emerge in the HCN/HNC exchange in reactions 4, 5, 11, 19 and 14, these, however, have little consequences for the prebiotic chemistry because both species are thought to have existed in the primitive Earth reacting environment. Every single step involving more than one reactant starts with a barrier-less formation of a long range reactive complex. In this context we refer to intrinsic (reactive complex → TS) and absolute (isolated reactants → TS) activation barriers. Discrepancies between gas phase and continuum solvent activation energies are due to a stabilizing/destabilizing effect of the solvent without drastically changing the structure.There is a high degree of uncertainty on the conditions of Hadean Earth,53–57 with estimates ranging from very low pressures to well in excess of 20 atm and with equally unconfirmed temperatures, thus, in this work, the energetic balance of the reactions as well as the associated full and intrinsic barriers are reported as changes in the Gibbs free energies within bidimensional grids of pressure and temperature. Accordingly, an exhaustive study of the dependency of activation energies with temperatures and pressures over a grid of [293![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 373] K and [0.5,20] atm was carried out, the results for elementary steps 3 and 11 leading to formic acid and glycolonitrile (Table 1) are shown in Fig. 1, additional plots are provided in the in the ESI (Fig. S1 and S2†). A few important points are immediately drawn. First, only moderate changes in activation energies as a function P, T are observed. This is a very important observation because given the current poor knowledge of primitive conditions, our calculations indicate that once the thresholds for these conditions are overcome,9 then the chemical reactions will occur under a wide variety of conditions. Second, activation energies are relatively high and not too far from the DFT calculations of Das and coworkers, nonetheless, a few of the calculated energy barriers are low enough to be encouraging about the feasibility of these processes to occur.58–60 In any case, all these processes would greatly benefit from natural catalysts such as clays and metal surfaces, which have been postulated to be pivotal components of prebiotic chemistry.61–64
373] K and [0.5,20] atm was carried out, the results for elementary steps 3 and 11 leading to formic acid and glycolonitrile (Table 1) are shown in Fig. 1, additional plots are provided in the in the ESI (Fig. S1 and S2†). A few important points are immediately drawn. First, only moderate changes in activation energies as a function P, T are observed. This is a very important observation because given the current poor knowledge of primitive conditions, our calculations indicate that once the thresholds for these conditions are overcome,9 then the chemical reactions will occur under a wide variety of conditions. Second, activation energies are relatively high and not too far from the DFT calculations of Das and coworkers, nonetheless, a few of the calculated energy barriers are low enough to be encouraging about the feasibility of these processes to occur.58–60 In any case, all these processes would greatly benefit from natural catalysts such as clays and metal surfaces, which have been postulated to be pivotal components of prebiotic chemistry.61–64
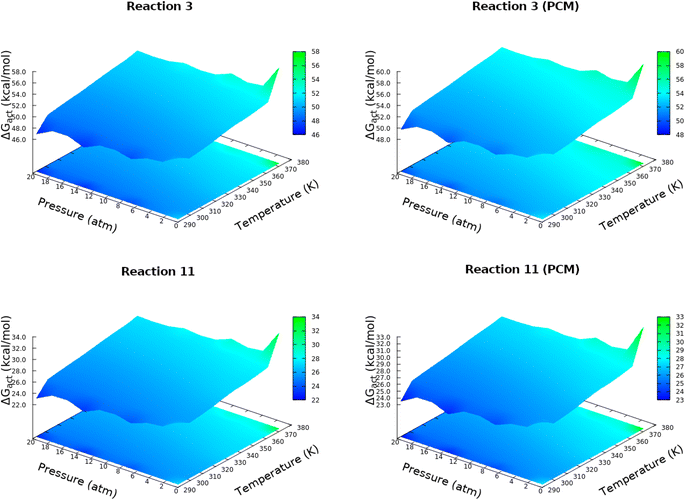 | ||
| Fig. 1 Absolute activation energies for elementary steps 3 and 11 (Table 1), in vacuo (left) and in solution (right), over a grid of temperatures in [293, 373] K and pressures in [0.5, 20] atm. | ||
The Gibbs activation barriers listed in Table 1 lead to slow processes, yet these reactions must be thermodynamic and kinetically viable to be considered as part of likely mechanisms for the formation of life building blocks in prebiotic conditions. These energetic and kinetic observations, in addition to the extreme complexity offered by the ab initio nanoreactor, suggest a more efficient production of the precursors studied in this work under catalytic environments, which are not considered in this work. Notwithstanding, our approach offers valuable insight to understand the bonding interactions driving the reaction mechanisms and should be considered a stepping stone to explicitly deal with the role of catalysts, work that is already in progress in our group.
Several of the reactions under discussion have been already studied with various forms of catalysts, which have proven to significantly reduce activation barriers. For example, Krug et al. studied the hydrolysis of formamide (reaction 3) under basic and acidic catalysis, and obtained a 6 kcal mol−1 barrier for the N-protonated case, 19 kcal mol−1 for the basic promoted case, and a stepwise mechanism for the O-protonated case, with two barriers of 24 and 16 kcal mol−1 for the nucleophilic addition to C and the breaking of the C–N bond respectively.65 Thus, significant reductions of the barriers were found when compared to the neutral case, which afforded a 44 kcal mol−1 barrier. These environment dependent catalysis are relevant since the exact pH under prebiotic conditions is unknown, with estimates pointing to non-neutral scenarios.66 Ice has also been suggested as a proper catalyst in prebiotic conditions. Despite the lack of a universally accepted geochemical model for the primitive earth, well grounded geochemical models that call for the presence of stable icy environments have been proposed.67–70 The icy protons allow the so called “proton-relay” mechanism to take place,71,72 in which a network of hydrogen bonded water molecules present in the ice surface assist in the proton transfer required in most of the set of 23 reactions listed in Table 1. Rimola et al. successfully assessed the catalytic effect of ice in the well known Strecker synthesis of amino acids, reporting barriers of 9.6, 21.3, and 8–9 kcal mol−1 for reactions 12, 13 and 14 respectively.73 Our isolated gas phase calculations are in agreement with their results.
Reaction 3, the neutral hydrolysis of formamide, which we will use to dissect and highlight mechanistic trends in the set of studied prebiotic reactions, has been studied before in the gas phase and in solution with explicit consideration of either one single water molecule as reactant or assisted by an extra water molecule as catalyst.65,74–76 Stepwise and concerted mechanisms have been reported. After refinement by the highly correlated model chemistry used in this work, our mechanism, based on the initial reactive trajectory obtained from the ab initio nanoreactor of Das et al. seeking to satisfy a set of likely prebiotic conditions of temperature, absence of metal catalyst, etc.,15 consists of a concerted water assisted reaction involving two water molecules in the transition state. For the gas phase, concerted, water assisted hydrolysis, Antonczak et al.77 reported a Gibbs free energy of activation of 49.6 kcal mol−1 computed at the MP2/6-31G**//HF/3-21G level at 298 °C and 1 atm, which is consistent with our computed values, 50.5 kcal mol−1 (absolute) and 45.7 kcal mol−1 (intrinsic). Later, using an improved theoretical framework (MP2/6-311+G**//B3LYP/6-31G*), Gorb et al.78 studied the mechanism in solution through different solvent models considering, in all of them, five explicit water molecules. They obtained for the assisted concerted reaction, a Gibbs activation energy of 47.6 kcal mol−1 at the same conditions. Our mechanism in solution, computed with the substantially improved MP2/6-311++G(d, p) yields activation free energies of 53.2 kcal mol−1 (absolute) and 42.8 kcal mol−1 (intrinsic). The energies computed at 298 °C and 1 atm that we use to compare against previous studies are covered in the grids of temperature and pressure presented in Fig. S1 and S2†.
3.2 Dissection of the IRC
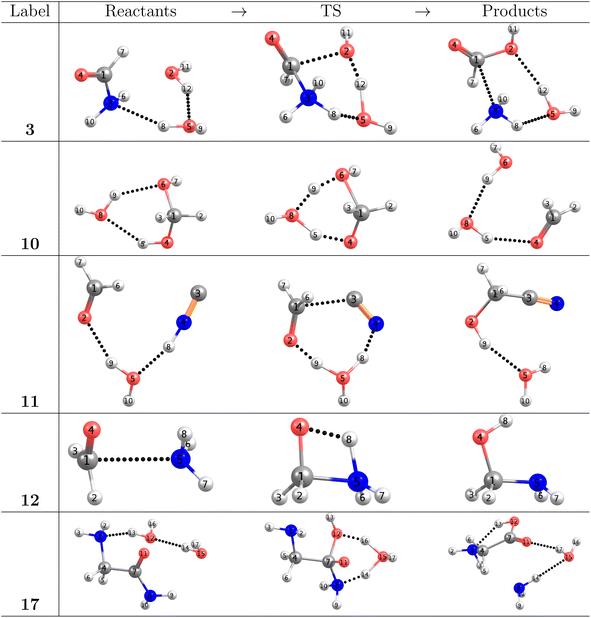
As stated in the Computational methods section, we chose reactions 3, 10, 11, 12, 17 from Table 1 to analyze the pivotal proton transfer processes as well as the breaking/formation of the all important C–C, C–N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, and C–O bonds. The associated intermediates, transition states, and products are depicted in Fig. 2.
O, and C–O bonds. The associated intermediates, transition states, and products are depicted in Fig. 2.
On the grounds of purely electronic energies, the profiles shown in Fig. 3 indicate that reactions 3, 10 and 17 consume energy while reactions 11 and 12 release energy, however, Gibbs energies predict reaction 10 to be exergonic and reaction 12 to be endergonic. Notice that purely electronic energies describe only intrinsic processes (intermediate⋯products) while changes in Gibbs energies are calculated with the isolated reactants as reference. Thus, it is clear that in reaction 10, accounting for entropy and internal degrees of freedom results in a strongly stabilized intermediate while in reaction 12 the intermediate is strongly destabilized. Table 1 reveals only slight changes in activation energies in going from gas phase to solution.
 | ||
| Fig. 3 Relative energies in the IRC (top row), reaction forces (second row), chemical potential (third row), and reaction electron flux (bottom row) corresponding to elementary steps leading to the formation of formic acid (reaction 3, Fig. 2), formaldehyde (reaction 10, Fig. 2), glycolonitrile (reaction 11, Fig. 2), methanolamine (reaction 12, Fig. 2) and glycine (reaction 17, Fig. 2). Solid vertical lines define the reactants ξR → ξR*, transition state ξR → ξP*, and products ξP → ξP* regions. The position of the TS is marked by a dashed vertical line. | ||
Most reactions involve large regions of structural changes before reaching the activated reactants, that is,  are far away from the reactants and comparatively closer to the transition states. The consequences for the reactions in the primitive Earth are that the environment needs to provide the means for the reactions to occur, in other words, that somewhat extreme conditions of temperature and pressure (especially temperature) are needed for the molecules to undergo the required structural changes leading to positive collision events. Transition states are neither earlier nor late, rather, transition state regions are well separated from reactants and products via large regions of a priori structural changes. Thus, as a general trend (there are exceptions), |ΔG†| > |ΔGrxn|.
are far away from the reactants and comparatively closer to the transition states. The consequences for the reactions in the primitive Earth are that the environment needs to provide the means for the reactions to occur, in other words, that somewhat extreme conditions of temperature and pressure (especially temperature) are needed for the molecules to undergo the required structural changes leading to positive collision events. Transition states are neither earlier nor late, rather, transition state regions are well separated from reactants and products via large regions of a priori structural changes. Thus, as a general trend (there are exceptions), |ΔG†| > |ΔGrxn|.
The reaction force, defined as the negative derivative of the potential energy with respect to the reaction coordinate along the reaction path provides a useful dissection of the entire mechanism: negative regions are associated with retarding forces while positive regions are associated with driving forces, thus, the local extrema of the force, corresponding to the second derivative of the IRC, or in other words, the inflection points of the IRC determine the progress of the chemical reaction as comprising a region of structural changes ξR → ξR* opposing the chemical transformation, a region of mostly electronic rearrangements, ξR* → ξTS → ξP* in which the force sharply switches from retarding (before TS) to driving (after TS), and a final structural relaxation ξP → ξP* region that finally yields the corresponding products. There is an apparent inverse correlation between the length of the transition state region ξR* → ξTS → ξP* and activation energies, namely, the smaller the TS region, the larger the activation energy. This observation is consistent with saying that larger activation energies are associated to larger TS regions, thus, most of the energy from the environment is transferred to the reacting system to overcome structural changes.
Steps 3 and 17 – both hydrolysis reactions – deviate from the typical behavior of the reaction force for an elementary step, characterized by a global maximum and global minimum connected through the transition state at ξ = 0. For these two reactions we observe two additional stationary points in the force plot, a local maximum and local minimum. This observation suggests that both reactions occur via a single, complex, concerted, borderline two-step mechanism, i.e., there are two well differentiated regions along the IRC path where electronic activity predominates, and it also serves as an early indication of a formation/breaking of bonds taking place in a non-synchronous fashion. Further evidence for borderline two-step characterization of reactions 3, 17 comes from the maximum of the chemical potential for both reactions in the region products, way past the transition state region. The electron flux plots accentuate the visualization of heavy electron activity outside the transition state region for reactions 3, 17, thus providing additional support for all the previous observations.
4 Evolution of bonding
4.1 Wiberg bond index, its derivative and synchronicity
The collection of plots in Fig. 4 reveals a picture of highly non synchronous concerted reactions. This is a striking observation because, except for reaction 12, all other reactions involve double proton transfers, processes that are notoriously synchronous when they are the only chemical transformations.79 However, that is not the case here since the double proton transfers are accompanied, within the same concerted step, by breaking and formation of other largely covalent bonds. Remarkably, for all reactions involving double proton transfer, the formation and breaking of O–H bonds around a particular O atom occur in a synchronous fashion, apparently independently from other primitive processes (a small discrepancy occurs in reaction 11).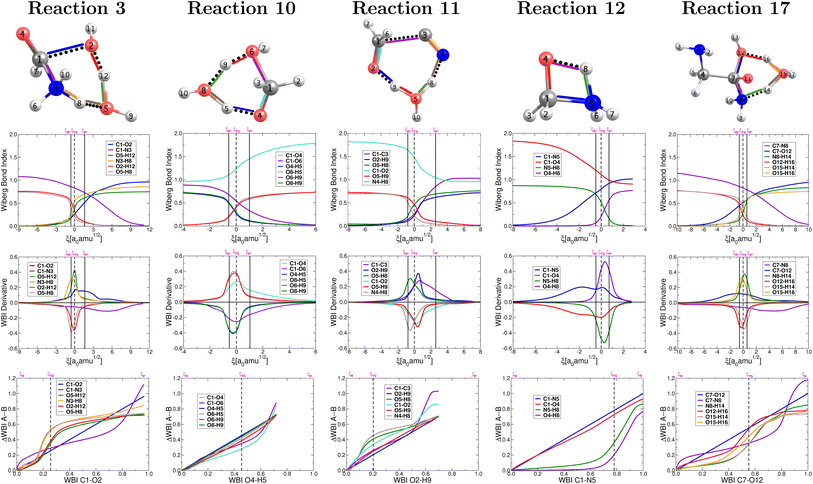 | ||
| Fig. 4 Descriptors of the evolution of bonding as a function of the reaction coordinate for the one step concerted reactions leading to the formation of formic acid (reaction 3, Fig. 2), formaldehyde (reaction 10, Fig. 2), glycolonitrile (reaction 11, Fig. 2), methanolamine (reaction 12, Fig. 2) and glycine (reaction 17, Fig. 2). Wiberg bond indexes (first row), their derivatives (second row) and GGR synchronicity35 (third row). Solid vertical lines define the reactants ξP → ξR*, transition state ξR → ξP*, and products ξP → ξP* regions. The position of the TS is marked by a dashed vertical line. | ||
For the set of five reactions shown in Fig. 2 a general mechanistic trend may be established from the plots in Fig. 4 in the context of a single step concerted reaction in each case. For the most part, the first process to initiate seems to be the double proton transfer in the reactions where they are present, then bond breaking/formation around the reactive carbon in the carbonyl group and finally rupture of the C–N bonds in the appropriate cases, which are the most reluctant to break. The reluctance of the C–N bond to break is clear from the fact that this rupture occurs far behind all other primitive processes, which have significantly progressed at the late stages of the reaction (this is true if reaction 12 is inverted). This is a pivotal point that highlights the importance of water not only as the medium in which all these reactions occur but also as a non innocent spectator catalyzing and actively taking part in most reactions (hydrogen atoms in water molecules end up in the products). In all cases, the double proton transfer process occurs mostly within the boundaries of the given TS region. Conversely, it is not uncommon for the breaking/formation of C–N, C–O, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and N–H bonds to anticipate or to extend beyond the TS region. In other words, besides the structural changes needed to bring reactants to the activated form and to deactivate the activated products, a sensible degree of electronic activity is still needed in the reactants and products regions.
O and N–H bonds to anticipate or to extend beyond the TS region. In other words, besides the structural changes needed to bring reactants to the activated form and to deactivate the activated products, a sensible degree of electronic activity is still needed in the reactants and products regions.
Maximization of the chemical potential (Fig. 3) occurs ahead of the TS region for reaction 12 and beyond the TS region for reactions 3, 17. This is consistent with all descriptors in Fig. 4 which show high electron activity involved in the early formation of the C–N bond (reaction 12) and in the late breaking of the C–N bond in reactions 3, 17. Reaction 10 is a well known dehydration reaction involving the transformation of methanediol into formaldehyde under the catalytic action of one water molecule that enables double proton transfer in our mechanism. This reaction deviates from other perfectly synchronous double proton transfers (i.e. in the dimer of formic acid79) because the two protons transferred in reaction 10 originate from different O–H bonds, C–O–H from methanediol and O–H from water.
4.2 Electron densities, virial ratios and NBO orbital interactions
The collection of plots in Fig. 5 provide a comprehensive picture of the evolution of the nature of bonding interactions for the set of reactions in Fig. 2, which is not only fully consistent with the conclusions drawn from the above analysis of the plots in Fig. 4 but also offers additional evidence and insight. All descriptors are derived from the topological properties of the electron densities at bond critical points as afforded by QTAIM and by the shapes, overlap, and interaction energies in the donor → acceptor orbital paradigm as afforded by NBO.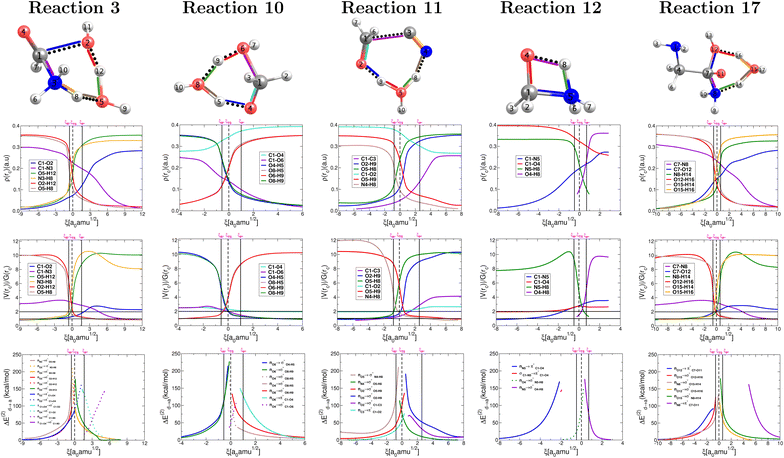 | ||
| Fig. 5 Descriptors of the evolution of bonding as a function of the reaction coordinate for the one step concerted reactions leading to the formation of formic acid (reaction 3, Fig. 2), formaldehyde (reaction 10, Fig. 2), glycolonitrile (reaction 11, Fig. 2), methanolamine (reaction 12, Fig. 2) and glycine (reaction 17, Fig. 2). Electron densities at bond critical points (first row), virial ratios at bond critical points (second row), and representative intermolecular donor → acceptor orbital interactions (third row). Solid vertical lines define the reactants ξR → ξR*, transition state ξR → ξP*, and products ξP* → ξP regions. The position of the TS is marked by a dashed vertical line. | ||
Without a single exception, all broken/formed bonds are formally covalent, as characterized by virial ratios larger than 2 and large accumulations of electron density at bond critical points and by well defined σ, π bonds. This means that there are no ionic reactions and that all reactants and products have well defined bonds. As suggested above, hydrogen transfer seems to kick off the reacting system in the appropriate cases, that is, changes in electron density and virial ratios for the associated bonds seem to initiate ahead of all other primitive changes followed by the breaking/formation of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, C–O, and C–C bonds and mostly independent of the chemical transformation of C–N bonds.
O, C–O, and C–C bonds and mostly independent of the chemical transformation of C–N bonds.
In Fig. 5, bottom panel, all curves correspond to donor → acceptor interactions within the NBO paradigm. For those special cases in which a third lone pair on a given O atom arises, the corresponding interactions are followed via dotted lines. In general, breaking and formation of sigma bonds is due to a maximization in charge transfer following the nO → σ*, nO → π*, nN → σ*, nN → π* rule. In agreement with all other descriptors, in the NBO context, both proton transfers occur very early during the reaction while the bonds associated with heavy atoms are transformed later within the same concerted step. Notice that for each one of the proton transfers, the formation of one σO–H orbital occurs simultaneously with the breaking of a second σO–H orbital associated with the transferred proton. Opposite to the double proton transfer, the bonds involving heavy atoms, i.e., formation of C1–O2 and breaking of C1–N3, do not occur simultaneously. In fact, the formation of the σC1–O2 is completed at the activated products coordinate and precedes the breaking of σC1–N3, which is not finalized until the very end of the reaction, at the coordinate of the products. Although after the reaction has taken place the πC1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O4 orbital remains intact, it is by no means (just like the catalytic water) an innocent spectator for the reaction to occur: reorganizing its electron density is essential during the ξTS → ξP* interval in which a π → σ transformation occurs, inducing the subsequent breaking of the C1–N3 orbital followed by the restoring of the πC1
O4 orbital remains intact, it is by no means (just like the catalytic water) an innocent spectator for the reaction to occur: reorganizing its electron density is essential during the ξTS → ξP* interval in which a π → σ transformation occurs, inducing the subsequent breaking of the C1–N3 orbital followed by the restoring of the πC1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O4 orbital in the formic acid of the final products.
O4 orbital in the formic acid of the final products.
5 General description of the mechanism of reaction 3
It is worth emphasizing two important factors at this point of our discussion. First, each one of the 23 reactions in Table 1 (including those in Fig. 2), occurs via a one step concerted process, that is, all the primitive changes we are about to discuss occur during the same step. Second, although the previous QTAIM, NBO analyses detail the mechanism for reactions 3, 10, 11, 12, 17, all the features and conclusions are mostly transferable to all other reactions because they involve the formation and breaking of the same types of bonds under the same conditions. Accordingly, we provide next a detailed mechanistic sequence of the events leading to the formation of formaldehyde and ammonia from formamide and two water molecules along the lines of reaction 3 (Fig. 2). In addition to the descriptors of the evolution of bonding interactions provided in Fig. 4, 5, further evidence to support our claims is found in Fig. 6, which follows the specific orbitals involved in the intermolecular interactions resulting in the breaking/formation of bonds during the course of reaction 3. As a reference to compare the strength of intermolecular interactions, we recall the values for the archetypal H–O⋯H–O hydrogen bond in the water dimer:80,81 E(2)![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0064_20d1.gif) a = −7.09 kcal mol−1, ρ(rc) = 2.3 × 10−2 a.u.,
a = −7.09 kcal mol−1, ρ(rc) = 2.3 × 10−2 a.u., 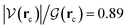 , where rc stands for the bond critical point. The general features for the formation of formic acid (FA) and ammonia (A) from formamide (F1) and two water molecules (W1, W2) are summarized in Scheme 2.
, where rc stands for the bond critical point. The general features for the formation of formic acid (FA) and ammonia (A) from formamide (F1) and two water molecules (W1, W2) are summarized in Scheme 2.
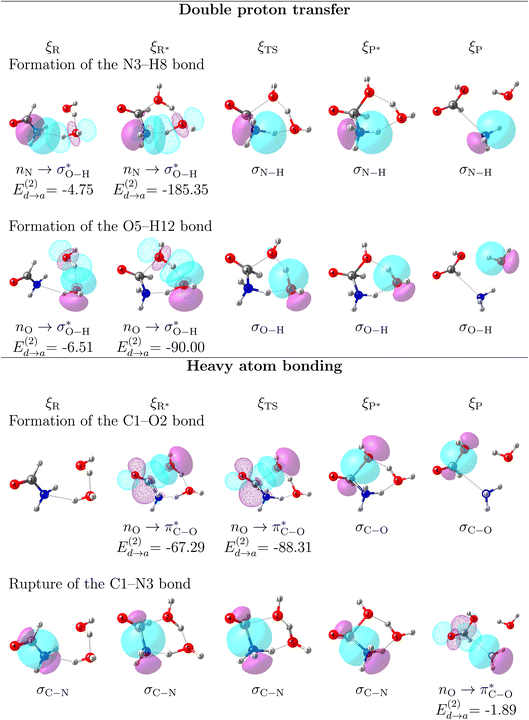 | ||
| Fig. 6 Orbital interactions leading to the breaking/formation of bonds driving the production of formic acid and ammonia from formamide and two water molecules along the lines of the one step, concerted mechanism of reaction 3 (Fig. 2). All donor → acceptor interaction energies in kcal mol−1. | ||
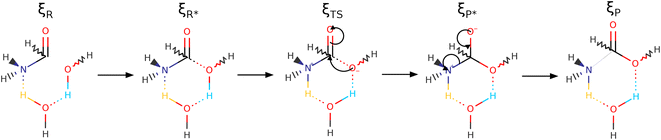 | ||
| Scheme 2 Reaction mechanism covering the entire ξR → ξR* → ξTS → ξP* → ξP IRC, as dissected by the reaction force (Fig. 3), for the one step concerted formation of formic acid from formamide and two water molecules. Notice that one of the water molecules is incorporated into the final formic acid and that the other is not an innocent spectator as indicated by the colors associated to the double proton transfer. See Fig. S3 in the ESI† to follow the natural charges at all oxygen atoms justifying the assignment of formal negative charges at specific points. | ||
As discussed before, every single reaction begins by forming a stabilized long range complex, ξR in Scheme 2. ξR is the starting point of the one step concerted reaction. In the case of reaction 3, this complex involves two specific intermolecular hydrogen bonds of strengths comparable to the isolated water dimer: H–N⋯H–O E(2)![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0064_20d1.gif) a = −4.75 kcal mol−1, ρ(rc) = 1.7 × 10−2 a. u,
a = −4.75 kcal mol−1, ρ(rc) = 1.7 × 10−2 a. u, 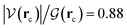 in F1⋯W1, and H–O⋯H–O E(2)
in F1⋯W1, and H–O⋯H–O E(2)![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0064_20d1.gif) a = −6.51 kcal mol−1, ρ(rc) = 2.4 × 10−2 a. u,
a = −6.51 kcal mol−1, ρ(rc) = 2.4 × 10−2 a. u, 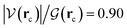 in W1⋯W2. The formation of these complexes leads to somewhat shallow, purely electronic energy wells which may be overcome simply by correcting for the ZPE energies or by accounting for temperature, entropy, and internal degrees of freedom (i.e., using Gibbs energies) as concluded above during the discussion of the energetics of the reaction profiles. The formation of these complexes requires minimal distortion of the electron densities from the isolated reactants, and thus the shallow wells. The regions within the IRC are conveniently analyzed in a separate fashion as follows:
in W1⋯W2. The formation of these complexes leads to somewhat shallow, purely electronic energy wells which may be overcome simply by correcting for the ZPE energies or by accounting for temperature, entropy, and internal degrees of freedom (i.e., using Gibbs energies) as concluded above during the discussion of the energetics of the reaction profiles. The formation of these complexes requires minimal distortion of the electron densities from the isolated reactants, and thus the shallow wells. The regions within the IRC are conveniently analyzed in a separate fashion as follows:
ξR →ξR* region: two important developments characterize this region: first, somewhere within this interval (at ξ = −14.97 a0 a.m.u1/2), a critical point for the C1⋯O2 interaction appears, this interaction strengthens steadily up to the coordinate of the activated reactants, however, not at the same rate as the interactions involved in the double proton transfer as consistently shown by all synchronicity, QTAIM, and NBO descriptors in Fig. 4, 5 and 6, respectively. Second, all orbital interactions associated to intermolecular contacts increase by large factors (from 4.75 to 185.35 kcal mol−1, etc., Fig. 6). These observations are consistent with the sensible structural changes needed to accommodate all reacting fragments in the positions required for the reaction to occur. Notice that although structural changes dominate this region of the IRC, it is not void of electronic activity.
ξR* →ξTS region: the double proton transfer is so early for this reaction that both protons have completely migrated at ξTS. Multiple evidence supports this claim: virial ratios larger than 2 thus indicating covalent bonding (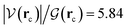 for σN3–H8 and
for σN3–H8 and 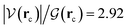 for σO5–H12), large bond orders, and the clear presence of well defined σN–H, σO–H orbitals for the newly formed bonds (Fig. 6). This reorganization of the electron density yields formal negative and positive charges at O2 and N3 respectively (Scheme 2), which are major players driving the progress of the reaction beyond the TS. The asynchronous character of this reaction is clearly seen in the fact that up to ξTS, two O–H bonds have been broken, one O–H and one N–H bond have been formed, while C1⋯O2 remains a long range contact and C1–N3 remains a well defined σ bond (for additional support, see the evolution of all bonds in the GGR synchronicity index, bottom panel in Fig. 4).
for σO5–H12), large bond orders, and the clear presence of well defined σN–H, σO–H orbitals for the newly formed bonds (Fig. 6). This reorganization of the electron density yields formal negative and positive charges at O2 and N3 respectively (Scheme 2), which are major players driving the progress of the reaction beyond the TS. The asynchronous character of this reaction is clearly seen in the fact that up to ξTS, two O–H bonds have been broken, one O–H and one N–H bond have been formed, while C1⋯O2 remains a long range contact and C1–N3 remains a well defined σ bond (for additional support, see the evolution of all bonds in the GGR synchronicity index, bottom panel in Fig. 4).
ξTS →ξP* region: this region is mostly devoted to the formation of the σC1–O2 bond via a classic nucleophilic attack from the negatively charged H–O:− to the carbon atom in the carbonyl group. The formation of the σC1–O2 bond results in a reorganization of the electron density of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond to produce a formally charged C–O− fragment (Scheme 2), beautifully supported by the emergence of a third lone pair on the carbonyl oxygen (O4) right at (ξP*). There is a progressive weakening of the soon to be broken C–N bond in going from ξTS to (ξP*) as seen in the steady decrease of the bond order, electron density, and virial ratio.
O bond to produce a formally charged C–O− fragment (Scheme 2), beautifully supported by the emergence of a third lone pair on the carbonyl oxygen (O4) right at (ξP*). There is a progressive weakening of the soon to be broken C–N bond in going from ξTS to (ξP*) as seen in the steady decrease of the bond order, electron density, and virial ratio.
ξP* →ξP Region: this step involves separation of the fragments, restoring of the πC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, and final rupture of the C1–N3 bond to liberate ammonia and formic acid. Evidence for the rupture of the C1–N3 bond: the virial ratio goes from 2.92 (covalent bond) to 0.82 (long range interaction); the bond order goes from 0.73 to 0.03; the derivative of the bond order decreases substantially; the σC1–N3 orbital ceases to exist; a lone pair is formed in N3. The driving force for the breaking of the C1–N3 bond is unveiled by NBO in the form of
O bond, and final rupture of the C1–N3 bond to liberate ammonia and formic acid. Evidence for the rupture of the C1–N3 bond: the virial ratio goes from 2.92 (covalent bond) to 0.82 (long range interaction); the bond order goes from 0.73 to 0.03; the derivative of the bond order decreases substantially; the σC1–N3 orbital ceases to exist; a lone pair is formed in N3. The driving force for the breaking of the C1–N3 bond is unveiled by NBO in the form of 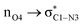 destabilizing charge transfer from the formally charged C–O− fragment freshly formed at (ξP*), as clearly shown by the dotted purple line at the leftmost bottom panel in Fig. 6. Notice that the breaking of the C1–N3 bond occurs very late in the reaction, way past the activated products, just beyond the point in which the C1
destabilizing charge transfer from the formally charged C–O− fragment freshly formed at (ξP*), as clearly shown by the dotted purple line at the leftmost bottom panel in Fig. 6. Notice that the breaking of the C1–N3 bond occurs very late in the reaction, way past the activated products, just beyond the point in which the C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O4 carbonyl is restored and the third lone pair is no longer available after doing its job of weakening C1–N3.
O4 carbonyl is restored and the third lone pair is no longer available after doing its job of weakening C1–N3.
6 Connection to prebiotic chemistry
We now venture an analysis of our results in the context of prebiotic chemistry. Albert Szent-Györgi famously stated that “Life is nothing but an electron looking for a place to rest”. This argument may be readily applied to essential processes for the sustainability of life, such as oxidative metabolism. What we can see from our work and from the scientific literature15,82 is that this argument may be extended to prebiotic chemistry as well. Indeed, the set of 23 reactions studied here was not designed with any purpose in mind, rather, they were obtained from ab initio nanoreactors fed with HCN and water by Das and coworkers,15 nonetheless, they constitute a progressive network of oxidation reactions from the beginning to the actual production of carbon dioxide, formaldehyde, formic acid, formaldimine, glycolaldehyde, glycine, glycolonitrile, oxazole derivatives, etc., and could be seen as a set of “electron accumulator processes”. Another important aspect in our calculations is that water does not simply act as the medium in which all reactions occur, but in many instances, besides working as a catalyst and a non-innocent spectator, it is actually involved in the chemical reactions to the point that water atoms end up in the products. HCN is thought to have existed both in the oceans and in the atmosphere, which also contained water vapor, gratifyingly, the reactions studied here have shown to be plausible in both phases.Until the discovery of the actual causes and mechanisms of the origin of life, we may assert in a pragmatic although speculative way, that a set of conditions are necessary. Namely, a network of chemical reactions capable of producing the building blocks of the molecules of life (such as the ones studied in this work) in local environments that further facilitate their combination to produce large molecules of such astonishing diversity and complexity as proteins and DNA. Our calculations unveil only moderate changes in activation energies as a function of pressure and temperature for the set of reactions studied here (Fig. 1, S1 and S2†), this observation supports the perspective of life just exposed because given the current poor understanding of the conditions of the Hadean earth, these small changes in reaction barriers indicate that above those thresholds, the chemical reactions producing the building blocks for the molecules of life will occur under a wide variety of conditions. The local favorable environments are the product of large scale cumulative changes in the course of billions of years brought about by deterministic molecular processes, that is, chemical reactions, and the consequential physical and chemical changes of the environment (slow building of a tolerable atmosphere, regulation of temperatures and acidic conditions, etc.) that allow the emergence and evolution of life under a particular set of local environmental evolution pressures.
The ever increasing entropy of the universe, as stated by the second law of thermodynamics, is the ultimate reason behind the molecular scale evolution (deterministic, not random, because of the need to satisfy the equilibration of chemical potentials in reacting systems) that changes the chemical landscape and then the environment itself. A second factor contributing to the increase in entropy of the universe in the process of originating life is the complexity of the multitude of reaction channels accessible to produce the small molecules needed to make large biomolecules, as is clearly the case in the present work. Furthermore, proteins are built upon primary sequences of just 20 amino acids, thus, there are on the order of 2.4 × 1018 possible different primary sequences for even the smallest proteins.83 Under this perspective, any local environment (a planet, a moon, or regions within) capable of undergoing the necessary changes under periods of time long enough to avoid major catastrophes caused by external agents, is poised to originate and sustain life. There is a high probability that once set in motion, many of these evolution patterns may not succeed in creating life, but by virtue of the immense dimensions of our observable universe, the emergence of life is not only deterministic, but should be a rather common place.
7 Conclusions
The reaction mechanisms for a set of 23 reactions leading to the formation of carbon dioxide, formaldehyde, formic acid, formaldimine, glycolaldehyde, glycine, glycolonitrile, and oxazole derivatives, among other precursors of large biomolecules in gas phase and in solution are presented in this work. All reactions occur via single step highly non synchronous processes. Given the presence of the substrates and of large amounts of water in the early Earth oceans and atmosphere,84,85 it is highly likely that this set of prebiotic reactions took place in the primitive Earth and should have been rather common. Indeed, relatively high energy barriers are obtained in each case, however, the role of catalysts (clays, icy surfaces, etc.), the different sources of energy associated with the likely prebiotic conditions of the primitive earth, such as oceans with temperatures between 80–100 °C,15,86 shock heating,87 vulcanism, electric discharges, impacts of extraterrestrial objects,88 among others, cannot be ignored as potential triggers for these networks of reactions and may account for the need for significant concentrations of these building blocks for the subsequent formation of larger biomolecules to be effective. The set of 23 reactions studied here constitutes a progressive network of oxidation reactions from the beginning to the actual production of the precursors of large biomolecules. Our results are consistent with the finding of Das et al.15 in that in many cases, water does not act simply as the medium in which all reactions occur, working not just as a catalyst or as an innocent spectator, but it is actually involved in the chemical reactions to the point that water atoms end up in the products.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Internal support from Universidad de Antioquia via “Estrategia para la sostenibilidad” is acknowledged. J. A. M. L. was supported by a grant from ANID (FONDECYT Regular 1221936), Chile.References
- J. D. Sutherland, The origin of life—out of the blue, Angew. Chem., Int. Ed., 2016, 55, 104–121 CrossRef PubMed.
- B. Palmer, A review on the spontaneous formation of the building blocks of life and the generation of a set of hypotheses governing universal abiogenesis, Int. J. Astrobiol., 2013, 12, 39–44 CrossRef.
- A. Pérez-Villa, F. Pietrucci and A. M. Saitta, Prebiotic chemistry and origins of life research with atomistic computer simulations, Phys. Life Rev., 2020, 34, 105–135 CrossRef PubMed.
- M. W. Powner and J. D. Sutherland, Prebiotic chemistry: a new modus operandi, Philos. Trans. R. Soc., B, 2011, 366, 2870–2877 CrossRef CAS PubMed.
- J. L. Bada, New insights into prebiotic chemistry from Stanley Miller's spark discharge experiments, Chem. Soc. Rev., 2013, 42, 2186–2196 RSC.
- A. Lazcano and S. L. Miller, The origin and early evolution of life: prebiotic chemistry, the pre-RNA world, and time, Cell, 1996, 85, 793–798 CrossRef CAS.
- L. E. Orgel, The origin of life—a review of facts and speculations, Trends Biochem. Sci., 1998, 23, 491–495 CrossRef CAS PubMed.
- H. J. Cleaves, Prebiotic chemistry: what we know, what we don't, Evol.: Educ. Outreach, 2012, 5, 342–360 Search PubMed.
- C. Jeancolas, C. Malaterre and P. Nghe, Thresholds in origin of life scenarios, Iscience, 2020, 23, 101756 CrossRef CAS.
- M. Tessera, Is pre-Darwinian evolution plausible?, Biol. Direct, 2018, 13, 1–18 CrossRef.
- E. O. Leslie, Prebiotic chemistry and the origin of the RNA world, Crit. Rev. Biochem. Mol. Biol., 2004, 39, 99–123 CrossRef.
- T. R. Cech, The RNA worlds in context, Cold Spring Harbor Perspect. Biol., 2012, 4, a006742 Search PubMed.
- A. Jandura and H. M. Krause, The new RNA world: growing evidence for long noncoding RNA functionality, Trends Genet., 2017, 33, 665–676 CrossRef CAS PubMed.
- R. Krishnamurthy, Giving rise to life: transition from prebiotic chemistry to protobiology, Acc. Chem. Res., 2017, 50, 455–459 CrossRef CAS PubMed.
- T. Das, S. Ghule and K. Vanka, Insights into the origin of life: Did it begin from HCN and H2O?, ACS Cent. Sci., 2019, 5, 1532–1540 CrossRef CAS PubMed.
- A. Tokunaga, S. Beck, T. Geballe, J. Lacy and E. Serabyn, The detection of HCN on Jupiter, Icarus, 1981, 48, 283–289 CrossRef CAS.
- S. Aalto, S. Garcia-Burillo, S. Muller, J. Winters, P. Van Der Werf, C. Henkel, F. Costagliola and R. Neri, Detection of HCN, HCO+, and HNC in the Mrk 231 molecular outflow-Dense molecular gas in the AGN wind, Astron. Astrophys., 2012, 537, A44 CrossRef.
- E. Lellouch, M. Gurwell, B. Butler, T. Fouchet, P. Lavvas, D. Strobel, B. Sicardy, A. Moullet, R. Moreno and D. Bockelée-Morvan, et al., Detection of CO and HCN in Pluto's atmosphere with ALMA, Icarus, 2017, 286, 289–307 CrossRef CAS.
- B. Fegley, R. G. Prinn, H. Hartman and G. H. Watkins, Chemical effects of large impacts on the Earth's primitive atmosphere, Nature, 1986, 319, 305–308 CrossRef CAS.
- J. P. Ferris and W. J. Hagan Jr, HCN and chemical evolution: the possible role of cyano compounds in prebiotic synthesis, Tetrahedron, 1984, 40, 1093–1120 CrossRef CAS.
- A. W. Schwartz, A. Voet and M. Van der Veen, Recent progress in the prebiotic chemistry of HCN, Origins Life, 1984, 14, 91–98 CrossRef CAS.
- C. N. Matthews, Origins, Springer, 2004; pp pp 121–135 Search PubMed.
- S. Nandi, D. Bhattacharyya and A. Anoop, Prebiotic chemistry of HCN tetramerization by automated reaction search, Chem.–Eur. J., 2018, 24, 4885–4894 CrossRef CAS PubMed.
- R. F. Bader, A quantum theory of molecular structure and its applications, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- P. L. Popelier, Atoms in Molecules: An Introduction, Prentice Hall, London, 2000 Search PubMed.
- S. J. Grabowski, What Is the Covalency of Hydrogen Bonding?, Chem. Rev., 2011, 111, 2597–2625 CrossRef CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- F. Weinhold and C. R. Landis, Discovering Chemistry with Natural Bond Orbitals, Wiley-VCH, Hoboken NJ, 2012, p. 319 Search PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, Natural bond orbital methods, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42 CAS.
- S. Gómez, A. Restrepo and C. Hadad, Theoretical tools to distinguish O-ylides from O-ylidic complexes in carbene–solvent interactions, Phys. Chem. Chem. Phys., 2015, 17, 31917–31930 RSC.
- S. Gomez, D. Guerra, J. G. Lopez, A. Toro-Labbe and A. Restrepo, A detailed look at the reaction mechanisms of substituted carbenes with water, J. Phys. Chem. A, 2013, 117, 1991–1999 CrossRef CAS.
- P. Tobón, S. Gomez, A. Restrepo and F. Núñez-Zarur, Role of Substrate Substituents in Alkene Metathesis Mediated by a Ru Alkylidene Catalyst, Organometallics, 2021, 40, 119–133 CrossRef.
- P. Farfán, S. Gómez and A. Restrepo, Dissection of the Mechanism of the Wittig Reaction, J. Inorg. Chem., 2019, 84, 14644–14658 Search PubMed.
- P. Farfán, S. Gómez and A. Restrepo, On the origins of stereoselectivity in the Wittig reaction, Chem. Phys. Lett., 2019, 728, 153–155 CrossRef.
- C. Giraldo, S. Gómez, F. Weinhold and A. Restrepo, Insight into the Mechanism of the Michael Reaction, ChemPhysChem, 2016, 17, 2022–2034 CrossRef PubMed.
- S. Gómez, H. Ramírez-Malule, W. Cardona-G, E. Osorio and A. Restrepo, Double-ring epimerization in the biosynthesis of clavulanic acid, J. Phys. Chem. A, 2020, 124, 9413–9426 CrossRef PubMed.
- S. Gómez, E. Osorio, E. Dzib, R. Islas, A. Restrepo and G. Merino, Revisiting the Rearrangement of Dewar Thiophenes, Molecules, 2020, 25, 284 CrossRef PubMed.
- B. Mennucci, Polarizable continuum model, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 386–404 Search PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Quantum Mechanical Continuum Solvation Models, Chem. Rev., 2005, 105, 2999–3094 CrossRef PubMed.
- A. Toro-Labbé, S. Gutiérrez-Oliva, M. C. Concha, J. S. Murray and P. Politzer, Analysis of two intramolecular proton transfer processes in terms of the reaction force, J. Chem. Phys., 2004, 121, 4570–4576 CrossRef PubMed.
- A. Toro-Labbé, S. Gutiérrez-Oliva, J. Murray and P. Politzer, A new perspective on chemical and physical processes: the reaction force, Mol. Phys., 2007, 105, 2619–2625 CrossRef.
- J. Martínez and A. Toro-Labbé, The reaction force. A scalar property to characterize reaction mechanisms, J. Math. Chem., 2009, 45, 911–927 CrossRef.
- S. Gómez, D. Guerra, J. G. López, A. Toro-Labbé and A. Restrepo, A Detailed Look at the Reaction Mechanisms of Substituted Carbenes with Water, J. Phys. Chem. A, 2013, 117, 1991–1999 CrossRef.
- R. G. Parr, Horizons of quantum chemistry, Springer, 1980, pp 5–15 Search PubMed.
- R. G. Parr and Z. Zhou, Absolute hardness: unifying concept for identifying shells and subshells in nuclei, atoms, molecules, and metallic clusters, Acc. Chem. Res., 1993, 26, 256–258 CrossRef CAS.
- E. Echegaray and A. Toro-Labbé, Reaction electronic flux: a new concept to get insights into reaction mechanisms. Study of model symmetric nucleophilic substitutions, J. Phys. Chem. A, 2008, 112, 11801–11807 CrossRef CAS.
- M. L. Cerón, E. Echegaray, S. Gutiérrez-Oliva, B. Herrera and A. Toro-Labbé, The reaction electronic flux in chemical reactions, Sci. China: Chem., 2011, 54, 1982–1988 CrossRef.
- C. Morell, V. Tognetti, E. Bignon, E. Dumont, N. Hernandez-Haro, B. Herrera, A. Grand, S. Gutierrez-Oliva, L. Joubert and A. Toro-Labbé, et al., Insights into the chemical meanings of the reaction electronic flux, Theor. Chem. Acc., 2015, 134, 1–7 Search PubMed.
- N. Rojas-Valencia, S. Gómez, D. Guerra and A. Restrepo, A detailed look at the bonding interactions in the microsolvation of monoatomic cations, Phys. Chem. Chem. Phys., 2020, 22, 13049–13061 RSC.
- M. J. Frisch; G. W. Trucks; H. B. Schlegel; G. E. Scuseria; M. A. Robb; J. R. Cheeseman; G. Scalmani; V. Barone; B. Mennucci; G. A. Petersson et al., Gaussian 09 Revision E.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- T. Keith, AIMALL (version 13.05.06), TK Gristmill Software, Overland Park KS, USA, 2013, http://aim.tkgristmill.com Search PubMed.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, 2013 Search PubMed.
- J. F. Kasting and T. P. Ackerman, Climatic consequences of very high carbon dioxide levels in the Earth's early atmosphere, Science, 1986, 234, 1383–1385 CrossRef CAS PubMed.
- D. P. Summers and S. Chang, Prebiotic ammonia from reduction of nitrite by iron (II) on the early Earth, Nature, 1993, 365, 630–633 CrossRef CAS PubMed.
- J. W. Valley, W. H. Peck, E. M. King and S. A. Wilde, A cool early Earth, Geology, 2002, 30, 351–354 CrossRef CAS.
- P. von Paris, H. Rauer, J. L. Grenfell, B. Patzer, P. Hedelt, B. Stracke, T. Trautmann and F. Schreier, Warming the early Earth-CO2 reconsidered, Planet. Space Sci., 2008, 56, 1244–1259 CrossRef CAS.
- J. F. Kasting and M. T. Howard, Atmospheric composition and climate on the early Earth, Philos. Trans. R. Soc., B, 2006, 361, 1733–1742 CrossRef PubMed.
- L. Song and J. Kästner, Formation of the prebiotic molecule NH2CHO on astronomical amorphous solid water surfaces: accurate tunneling rate calculations, Phys. Chem. Chem. Phys., 2016, 18, 29278–29285 RSC.
- Y. Yung and M. McElroy, Fixation of nitrogen in the prebiotic atmosphere, Science, 1979, 203, 1002–1004 CrossRef.
- V. Barone, C. Latouche, D. Skouteris, F. Vazart, N. Balucani, C. Ceccarelli and B. Lefloch, Gas-phase formation of the prebiotic molecule formamide: insights from new quantum computations, Mon. Not. R. Astron. Soc.: Lett., 2015, 453, L31–L35 CrossRef CAS.
- P. V. Coveney, J. B. Swadling, J. A. Wattis and H. C. Greenwell, Theory, modelling and simulation in origins of life studies, Chem. Soc. Rev., 2012, 41, 5430–5446 RSC.
- J. Hao, M. Mokhtari, U. Pedreira-Segade, L. J. Michot and I. Daniel, Transition metals enhance the adsorption of nucleotides onto clays: Implications for the origin of life, ACS Earth Space Chem., 2018, 3, 109–119 CrossRef.
- C. Ponnamperuma, A. Shimoyama and E. Friebele, Clay and the origin of life, Origins Life, 1982, 12, 9–40 CrossRef CAS PubMed.
- A. Rimola, M. Sodupe and P. Ugliengo, Role of mineral surfaces in prebiotic chemical evolution. In silico quantum mechanical studies, Life, 2019, 9, 10 CrossRef CAS.
- J. Krug, P. Popelier and R. Bader, Theoretical study of neutral and of acid and base-promoted hydrolysis of formamide, J. Phys. Chem., 1992, 96, 7604–7616 CrossRef CAS.
- J. Krissansen-Totton, G. N. Arney and D. C. Catling, Constraining the climate and ocean pH of the early Earth with a geological carbon cycle model, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 4105–4110 CrossRef CAS.
- J. L. Bada, C. Bigham and S. L. Miller, Impact melting of frozen oceans on the early Earth: implications for the origin of life, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 1248–1250 CrossRef CAS.
- A. W. Schwartz, H. Joosten and A. Voet, Prebiotic adenine synthesis via HCN oligomerization in ice, Biosystems, 1982, 15, 191–193 CrossRef CAS PubMed.
- J. L. Bada, How life began on Earth: a status report, Earth Planet. Sci. Lett., 2004, 226, 1–15 CrossRef CAS.
- C. Menor-Salván and M. R. Marín-Yaseli, Prebiotic chemistry in eutectic solutions at the water–ice matrix, Chem. Soc. Rev., 2012, 41, 5404–5415 RSC.
- J. W. Gauld, H. Audier, J. Fossey and L. Radom, Water-catalyzed interconversion of conventional and distonic radical cations: methanol and methyleneoxonium radical cations, J. Am. Chem. Soc., 1996, 118, 6299–6300 CrossRef CAS.
- J. W. Gauld and L. Radom, Effects of neutral bases on the isomerization of conventional radical cations CH3X˙ + to their distonic isomers ˙CH2X+ H (X= F, OH, NH2): Proton-transport catalysis and other mechanisms, J. Am. Chem. Soc., 1997, 119, 9831–9839 CrossRef.
- A. Rimola, M. Sodupe and P. Ugliengo, Deep-space glycine formation via Strecker-type reactions activated by ice water dust mantles. A computational approach, Phys. Chem. Chem. Phys., 2010, 12, 5285–5294 RSC.
- S. Antonczak, M. Ruiz-López and J.-L. Rivail, The hydrolysis mechanism of formamide revisited: comparison between ab initio, semiempirical and DFT results, J. Mol. Model., 1997, 3, 434–442 CrossRef.
- T. Oie, G. H. Loew, S. K. Burt, J. S. Binkley and R. D. MacElroy, Quantum chemical studies of a model for peptide bond formation: formation of formamide and water from ammonia and formic acid, J. Am. Chem. Soc., 1982, 104, 6169–6174 CrossRef CAS.
- J. H. Jensen, K. K. Baldridge and M. S. Gordon, Uncatalyzed peptide bond formation in the gas phase, J. Phys. Chem., 1992, 96, 8340–8351 CrossRef CAS.
- S. Antonczak, M. Ruiz-Lopez and J. Rivail, Ab initio analysis of water-assisted reaction mechanisms in amide hydrolysis, J. Am. Chem. Soc., 1994, 116, 3912–3921 CrossRef CAS.
- L. Gorb, A. Asensio, I. Tuñón and M. F. Ruiz-López, The mechanism of formamide hydrolysis in water from ab initio calculations and simulations, Chem.–Eur. J., 2005, 11, 6743–6753 CrossRef CAS PubMed.
- P. Farfán, A. Echeverri, E. Diaz, J. D. Tapia, S. Gómez and A. Restrepo, Dimers of formic acid: Structures, stability, and double proton transfer, J. Chem. Phys., 2017, 147, 044312 CrossRef.
- S. Gómez, N. Rojas-Valencia, S. A. Gómez, C. Cappelli, G. Merino and A. Restrepo, A molecular twist on hydrophobicity, Chem. Sci., 2021, 12, 9233–9245 RSC.
- L. Uribe, S. Gómez, T. Giovannini, F. Egidi and A. Restrepo, An efficient and robust procedure to calculate absorption spectra of aqueous charged species applied to NO2−, Phys. Chem. Chem. Phys., 2021, 23, 14857–14872 RSC.
- J. Ferris, J. Wos, T. Ryan, A. Lobo and D. Donner, Biomolecules from HCN, Origins Life, 1974, 5, 153–157 CrossRef CAS.
- J. David, S. Gómez, D. Guerra, D. Guerra and A. Restrepo, A Comprehensive Picture of the Structures, Energies, and Bonding in the Alanine Dimers, ChemPhysChem, 2021, 22, 2401–2412 CrossRef CAS.
- M. Ferus, P. Kubelík, A. Knížek, A. Pastorek, J. Sutherland and S. Civiš, High energy radical chemistry formation of HCN-rich atmospheres on early Earth, Sci. Rep., 2017, 7, 1–9 CrossRef CAS PubMed.
- J. L. Bada and H. J. Cleaves, Ab initio simulations and the Miller prebiotic synthesis experiment, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E342 CrossRef CAS.
- J. W. Morse and F. T. Mackenzie, Hadean ocean carbonate geochemistry, Aquat. Geochem., 1998, 4, 301–319 CrossRef CAS.
- H. Follmann and C. Brownson, Darwin's warm little pond revisited: from molecules to the origin of life, Naturwissenschaften, 2009, 96, 1265–1292 CrossRef CAS.
- Y. Furukawa, T. Sekine, M. Oba, T. Kakegawa and H. Nakazawa, Biomolecule formation by oceanic impacts on early Earth, Nat. Geosci., 2009, 2, 62–66 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Cartesian coordinates for all isolated reactants, long range complexes, transition states, and products. Gibbs activation and reaction energies in gas phase and in solution for the set of 23 reactions are provided. Plots of absolute and intrinsic activation energies for reactions 10, 12, 17 over grids of temperature and pressure. Plots of the natural charges at all oxygen atoms for followed along the entire IRC of reaction 3. See https://doi.org/10.1039/d2ra06000k |
| This journal is © The Royal Society of Chemistry 2022 |