Ab initio insight into the electrolysis of water on basal and edge (fullerene C₂₀) surfaces of 4 Å single-walled carbon nanotubes

Abstract

The extreme surface reactivity of 4 Å single-walled carbon nanotubes (SWCNTs) makes for a very promising catalytic material, however, controlling it experimentally has been found to be challenging. Here, we employ ab initio calculations to investigate the extent of surface reactivity and functionalization of 4 Å SWCNTs. We study the kinetics of water dissociation and adsorption on the surface of 4 Å SWCNTs with three different configurations: armchair (3,3), chiral (4,2) and zigzag (5,0). We reveal that out of three different configurations of 4 Å SWCNTs, the surface of tube (5,0) is the most reactive due to its small HOMO–LUMO gap. The dissociation of 1 H₂O molecule into an OH/H pair on the surface of tube (5,0) has an adsorption energy of −0.43 eV and an activation energy barrier of 0.66 eV at 298.15 K in pure aqueous solution, which is less than 10% of the activation energy barrier of the same reaction without the catalyst present. The four steps of H⁺/e⁻ transfer in the oxygen evolution reaction have also been studied on the surface of tube (5,0). The low overpotential of 0.38 V indicates that tube (5,0) has the highest potential efficiency among all studied carbon-based catalysts. We also reveal that the armchair edge of tube (5,0) is reconstructed into fullerene C₂₀. The dangling bonds on the surface of fullerene C₂₀ result in a more reactive surface than the basal surface of tube (5,0), however the catalytic ability was also inhibited in the later oxygen reduction processes.

---

1 Introduction

Since their first introduction in 1991, carbon nanotubes (CNTs) have been extensively used in various applications ranging from gas separation to battery electrodes.¹ CNTs are advanced materials obtained by rolling graphene sheets into a tube. The directions and angles at which the graphene sheets are rolled are specified by chiral indices (n,m), which thus define CNT configurations. Based on different integer combinations of (n,m) indices, three different configurations of CNTs are plausible: zig-zag, armchair and chiral. On the other hand, the properties of CNTs are determined by their curvature, which is a function of the tube’s diameter. For example, CNTs with a very small curvature (i.e. large tube diameter) akin to a flat graphene sheet possess very different properties from CNTs with a very high degree of curvature.^2,3

Out of all CNT classes, single-walled carbon nanotubes (SWCNTs) are the most extensively studied due to their intrinsic simplicity. Experimental investigations have confirmed that for SWCNTs the smallest tube diameter possible is 4 Å, which is present in all three different configurations: armchair (3,3), chiral (4,2) and zigzag (5,0).^4–6 The very big curvature of 4 Å SWCNTs allows for strong σ* and π* orbital mixing⁷ between C atoms that results in very active surfaces. Many unexpected and outstanding features are observed in 4 Å SWCNTs, such as superconductivity properties.⁸ It has been reported that in some cases the edges of 4 Å SWCNTs fold up over themselves forming fullerene C₂₀ spontaneously.^6,9–11 It is also interesting that 4 Å SWCNTs are reported as metallic,¹¹ as this contradicts the common belief that the metallicity of CNTs is dependent on their specific configurations, and that CNTs are metallic when n − m is a factor of three.^12,13

The surface reactivity of SWCNTs with larger diameter is similar to that of graphene and graphite,^14–18 thus indicating that the curvature of tubes of larger diameter is insufficient to steer their reactivity behavior away from graphene’s and graphite’s. In practice, graphene, graphite and other carbon based materials (including CNTs and fullerenes) with similar surface reactivity undergo surface treatments to enhance their reactivity. These surfaces are treated by either N-doping or surface oxidation by adsorption of various small molecules, such as –OH and =O.^19–22 However, the extent of surface reactivity provided by the maximum curvature of 4 Å SWCNTs is not yet known. In theory, the large curvature of 4 Å SWCNTs should lead to a very reactive surface, even without subjecting the tubes to any surface treatment. However, the lack of research done on this subject proves that the surface reactivity issue of 4 Å SWCNTs is a double-edged sword that currently limits the amount of research and curtails its widespread applications. The extremely ultrasmall size brings about the extremely reactive surface of 4 Å SWCNTs.¹¹ To date, there is still no record of 4 Å SWCNTs’ functionalization, even through the adsorption of small molecules. Within this perspective, theoretical investigations where the environment that the 4 Å SWCNTs are exposed to can be tightly specified are crucial to shed light on the stability limit of the oxidized surface of 4 Å SWCNTs.

Here, we study the surface reactivity of 4 Å SWCNTs by adsorbing H₂O molecules, that are abundantly present in both liquid and vapor forms, on both basal and edge surfaces of the three configurations of 4 Å SWCNTs. We investigate the energy and activation barrier of H₂O adsorption, its dissociation, and the extent of surface adsorption as a representation of surface functionalization of 4 Å SWCNTs. The understanding of how surface functionalization affects the stability of 4 Å SWCNTs is therefore essential for progressing 4 Å SWCNT research and its potential implementation in various applications, especially to assist water dissociation reactions in fuel cells.

2 Computational details

The unit cells of 4 Å SWCNTs with three different configurations of (3,3), (4,2) and (5,0) consist of 12, 56 and 20 carbon atoms, respectively. To study the reactivity of basal surfaces, the three different configurations of SWCNTs were placed in a box of 15.0 Å × 12.8 Å × 12.8 Å. The unit cells of tubes (3,3) and (5,0) were repeated 5 and 3 times in the axial direction to fill up the box. Edge surfaces were modeled by increasing the size of the box in the axial direction from 12.8 Å to 22.8 Å. In all cases, a vacuum gap of at least 10 Å was employed to avoid interactions between adjacent tubes. Static calculations were carried out within the plane-wave density functional theory (DFT) framework as implemented in the NWChem code.²³ The exchange and correlation energies were calculated using the Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA).²⁴ The PBE functional was corrected for van der Waals interactions by using the Grimme approach (PBE-D3 with BJ damping).²⁵ The norm-conserving Hamann pseudopotentials^26,27 were used on all atoms. Kinetic cutoff energies of 100 and 200 Ry were applied to expand the Kohn–Sham electronic wave functions and charge density, respectively.

To predict the spontaneity of the water dissociation reaction on the surfaces of tube (5,0) in pure aqueous solution at 298.15 K, Car–Parrinello molecular dynamics (CPMD)²⁸ simulations were performed. The basal box was filled with 67 water molecules while the edge box was filled with 136 water molecules so that the water density in both types of boxes was approximately 1 g cm⁻³. The Nose–Hoover thermostat^29,30 was employed to maintain the system temperature at 298.15 K. Each aqueous system was initially pre-equilibrated by using a QM/MM potential³¹ for 6 ps followed by additional CPMD equilibration for at least 10 ps. Hydrogen atoms were replaced with deuterium to facilitate numerical integration. A fictitious electronic mass of 600 au and a simulation time step of δt = 5 au (0.121 fs) were set. Configurations from the post-equilibration CPMD simulations used for further analysis were saved at time intervals of 10δt.

Evaluation of the activation energy barrier of the water dissociation reaction on the surfaces of tube (5,0) in pure aqueous solution at 298.15 K was done by using equilibrated geometries picked from the last block of CPMD production runs. The bond distance of C–O was used as the collective variable (CV) to export the free energy profiles of the water dissociation reaction on the surface of tube (5,0). Repulsive Gaussian hills of height and weight 0.001 a.u. (0.63 kcal mol⁻¹) and 0.1 a.u., respectively, were added for every 100δt.

3 Results and discussion

3.1 Properties of 4 Å SWCNTs

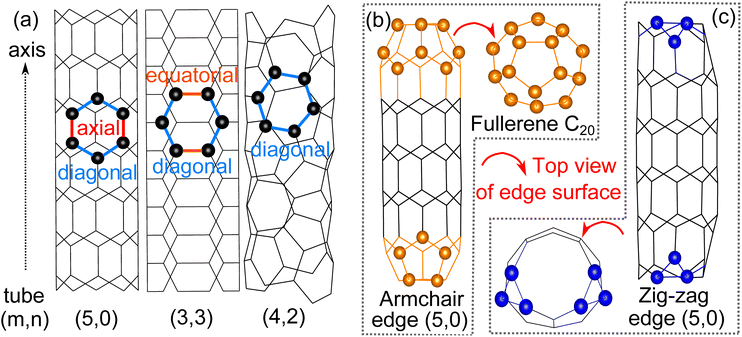
We start our investigation by comparing the three different configurations of 4 Å tubes (Fig. 1(a)). The average cohesive energy of C–C bonds is ∼4.9 eV for all three tubes, suggesting the relative stability of these three tubes of different configurations.⁷ The diameters of the tubes we obtained through structural optimizations agree with previous experimental and theoretical studies.^6,7 Both the diameter and the cohesive energy for all tube configurations are given in Table 1.

Fig. 1 (a) Stick model of 4 Å SWCNTs: tube (5,0), (3,3) and (4,2) with the carbon atoms of one hexatomic ring represented by balls for clarity, (b) ball and stick model of tube (5,0) with armchair edges that fold into half fullerene C₂₀ and (c) ball and stick model of tube (5,0) with zig-zag edges that have an irregular edge surface.

Table 1 Diameter, cohesive energy and the HOMO–LUMO gap for each 4 Å SWCNT

Tube configurations	Diameter (Å)		Ecohesive (eV)	HOMO–LUMO gap (eV)
	This work	Experimental^6
(3,3)	4.17	4.07	4.97	1.51
(4,2)	4.24	4.14	4.97	1.24
(5,0)	4.02	3.93	4.94	0.28

---

As for the edge surfaces, we first considered both the armchair and zigzag edges of tube (5,0) and found that during the optimization, the armchair edge folds up and each edge forms half a fullerene C₂₀ (Fig. 1(b)). This fullerene formation by the armchair edge of tube (5,0) is also observed in experiments.^6,9 The fullerene formation is not observed on the zigzag edge of tube (5,0) however, due to the irregular termination of the zig-zag edge that prevents the formation of fullerene (Fig. 1(c)). The zigzag edge of tube (5,0) is also less stable by 0.15 eV per carbon atom than the now fullerene armchair edge. Then, for the case of tube (3,3), only the armchair edge is feasible on the plane perpendicular to the axis. Further optimization shows that its edge surface will maintain circularity without any reconstruction. The edge structure is energetically unstable by 0.37 eV per C compared with the related basal tube. It’s also notable that previous experimental studies report that the armchair tube (3,3) can also be exactly capped by half fullerene C₂₀;¹¹ we confirmed the validity of the structure because of the anastomosing diameter, however the half fullerene C₂₀ cannot be directly rolled up by the edge surface of pure tube (5,0) because the six-atomic edge surface cannot provide the necessary penta-atomic ring in fullerene C₂₀. Finally, moving to the edge surface of tube (4,2), there are no conventional armchair and zig-zag edges due to the chiral structure; also no stable edge structure has been detected experimentally so far. Therefore, the most stable and feasible edge surface of 4 Å SWCNTs is half fullerene C₂₀ constructed from the armchair edge of tube (5,0).

3.2 Water dissociation on the surface of 4 Å SWCNTs

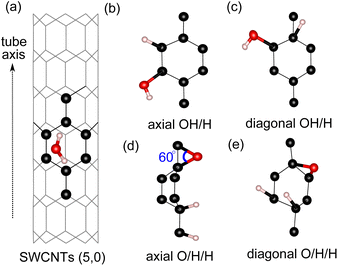
For water adsorption on the surfaces of 4 Å SWCNTs, three different scenarios are considered: (1) adsorption of an H₂O molecule, (2) adsorption of dissociated water as an OH/H pair and (3) adsorption of dissociated water as O/H/H atoms (Fig. 2). The adsorption energy of the H₂O molecule and its constituents in the form of either an OH/H pair or O/H/H atoms is calculated in the following way:

E_ads = E_tube-ads − E_tube − E_H2O (1)

where E_tube-ads is the energy of the tube with H₂O or OH/H or O/H/H adsorbed on its surface, E_tube is the energy of a pristine tube and E_H2O is the DFT energy of a single water molecule.

Fig. 2 Surface sites on SWCNT (5,0) for adsorption of: (a) an H₂O molecule, (b) OH/H on the axial C–C site, (c) OH/H on the diagonal C–C site, (d) O/H/H on the axial C–C site and (e) O/H/H on the diagonal C–C site (e).

We find that the adsorption of the H₂O molecule on the surface of all tube configurations is slightly exothermic with an adsorption energy of ∼−3.0 kcal mol⁻¹ (Table 2). These values are similar to the adsorption of water molecules on basal graphene/graphite surfaces,^14,32 therefore suggesting that the adsorption on 4 Å SWCNTs of a neutral molecule exhibits similar activity behavior to that of basal graphene/graphite. The adsorption of O/H/H atoms on three different C sites with the O atom adsorbed on 2 neighboring C sites has a very strained C–O–C angle of 60° (Fig. 2(d)). This type of adsorption is very energetically unfavorable on the surfaces of all configurations. Even worse, adsorption of either O/H/H or OH/H on the equatorial C–C sites of tube (3,3) results in the breaking of the tube into a graphene sheet. The breaking of the (3,3) tube is the result of its weaker structure in the equatorial direction, where the effect of curvature is experienced the most by equatorial C–C bonds. The already weakened equatorial bond cannot sustain further disruption to its electronic cloud caused by surface adsorption on multiple sites, which results in the breaking of the tube. At the other end, the adsorption of the OH/H pair on tube (5,0) is energetically favorable regardless of its adsorption sites, with the OH/H adsorption on the axial site being the most favorable and exhibiting a highly negative adsorption energy of −10.7 kcal mol⁻¹. By evaluating the HOMO–LUMO gap in all three tubes, we explain the favorability of OH/H adsorption on tube (5,0) using the HOMO–LUMO gap of tube (5,0), which is only 6.5 kcal mol⁻¹ (as shown in Table 1). The HOMO–LUMO gap of tube (5,0) is much smaller in comparison to the HOMO–LUMO gaps of tubes (3,3) and (4,2), resulting in higher chemical reactivity of tube (5,0) as electron transfer between a high-lying LUMO and low-lying HOMO is easily affordable in chemical reactions.

Table 2 Calculated adsorption energies of H₂O as a molecule, an OH/H pair and O/H/H atoms on the basal surfaces of three different configurations of 4 Å SWCNTs (unit: eV)

SWCNTs	Molecular H2O	OH/H			O/H/H
		Axial	Diagonal	Equatorial	Axial	Diagonal	Equatorial
(3,3)	−0.13	N/A	−0.01	Tube break	N/A	1.52	Tube break
(4,2)	−0.16	N/A	1.71	N/A	N/A	1.04	N/A
(5,0)	−0.13	−0.43	−0.09	N/A	0.51	0.13	N/A

---

It has been reported that in carbon based materials, the edge surfaces are more active than their basal surfaces.^32–34 Seeing the highly active basal surface of tube (5,0), we then turn our attention to its edge surfaces of half fullerene C₂₀. The adsorption of the OH/H constituents onto fullerene C₂₀ has an adsorption energy of −49.9 kcal mol⁻¹, which is five times more exothermic than the adsorption onto the basal surface of tube (5,0). This highly negative adsorption energy should be attributed to the presence of extremely reactive dangling bonds on the spherical surface of fullerene C₂₀.³⁵ Adsorption of OH/H allows elimination of dangling bonds and thus stabilizes the surface.

Equipped with the thermodynamic favourability of H₂O dissociation on both tube (5,0) and fullerene C₂₀ surfaces, we start to consider the activation barriers of the above-mentioned H₂O dissociation reactions. Here, CPMD equilibration and CPMD-based metadynamics simulation are employed to estimate the activation barrier for the splitting of a water molecule (the first step of the OER, discussed below) at both tube (5,0) and fullerene C₂₀ surfaces in pure aqueous solution. Fig. 3 shows the free energy profile of H₂O → OH + H⁺ + e⁻ at tube (5,0). We found that the free proton will stay in this aqueous solution as H₃O⁺, which is different from the static DFT prediction. The activation energy barrier for this particular reaction is found to be 0.66 eV, which demonstrates the high surface catalytic ability of tube (5,0). It is just over 10% of the activation barrier for the same dissociation reaction in the absence of tube (5,0) (∼5.11 eV),^36–38 and also much lower in comparison to the same H₂O dissociation on graphene (∼3.04 eV).³⁹ Further, our CPMD simulations show that the H₂O dissociation into OH/H on fullerene is spontaneous at T = 298.15 K.

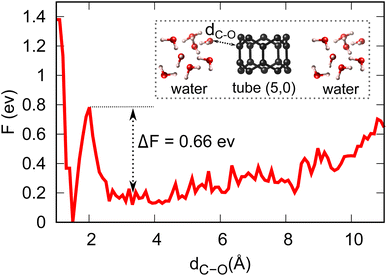Fig. 3 Energy profile and activation barrier of H₂O splitting on the surface of tube (5,0) obtained from metadynamics simulations at T = 298.15 K.

3.3 Oxygen evolution reaction under the catalysis by tube (5,0) and fullerene C₂₀

Here, the oxygen evolution reaction is studied as a common four-step water splitting process, and the reaction mechanism in an acidic environment is as follows:

* + H₂O ⇌ *OH + H⁺ + e⁻

*OH ⇌ *O + H⁺ + e⁻

*O + H₂O ⇌ *OOH + H⁺ + e⁻

*OOH ⇌ * + O₂ + H⁺ + e⁻

In order to evaluate the potential-determining performances for the above OER steps, a thermochemistry method was employed, which has been widely used for various catalyst-based water splitting reactions.^40–43 The ΔG for the above reactions is calculated based on the following equations:

ΔG = ΔG⁰ − eU_RHE + ΔG_field (2)

with: ΔG⁰ = ΔE + ΔZPE − TΔS (3)

and: U_RHE = U_SHE − k_BT ln10 pH/e (4)

where ΔG⁰ is the standard Gibbs energy for a system in its standard state at 298.15 K and 100 kPa. ΔG⁰ is calculated by adding the zero point energy (ΔZPE) correction to the DFT energies (ΔE) and taking into consideration the entropy (ΔS) of the system at a certain temperature (T). U_RHE and U_SHE represent the theoretical reversible hydrogen electrode (RHE) and standard hydrogen electrode (SHE), respectively, and k_B is the Boltzmann constant. ΔG_field is the change in the adsorption energy due to the electric field at the electrode, which usually can be neglected.^43,44 Since the computational SHE was used, the ΔG calculation of proton and electron pairs in the reactions can be replaced by half a hydrogen molecule at U_SHE = 0 V. Moreover, the analysis of free energies is set at standard conditions (pH = 0, T = 298.15 K), the same as calculations in other previous papers for the OER and ORR.^40–43

Fig. 4 shows the Gibbs free energy diagram for the OER on the tube (5,0) and half fullerene C₂₀ cage catalysts. The ideal catalysts will induce all four steps to have a ΔG = 1.23 eV increment at zero potential, namely, no energy loss at the equilibrium voltage (1.23 V) of the OER. At tube (5,0), it’s clear that the potential-determining step is the dissociation of the second water molecule (*O → *OOH), where the Gibbs free energy increment is 1.61 eV. Therefore, at least 1.61 V potential is required to make all steps downhill in operation. However, at the fullerene C₂₀ catalyst, the potential demand becomes very high at 2.41 V to make all steps downhill. The limited potential appears at the step of O₂ desorption (*OOH → O₂), which indicates that the dangling bonds of fullerene C₂₀ are a double-edged sword. On the one hand, they cause the surface to be so active that the first H₂O will be split spontaneously based on negative ΔG even at U = 0 V. On the other hand, the desorption of adsorbates will also be severely prohibited. The shorter 1.39 Å bond distance of C–O also indicates that the OOH intermediate is adsorbed more tightly on the fullerene C₂₀ surface compared with the 1.46 Å C–O bond distance at tube (5,0). Therefore, although the surface of fullerene C₂₀ favours greater extent of oxidation, the catalytic ability in the OER is poor due to the larger potential demand.

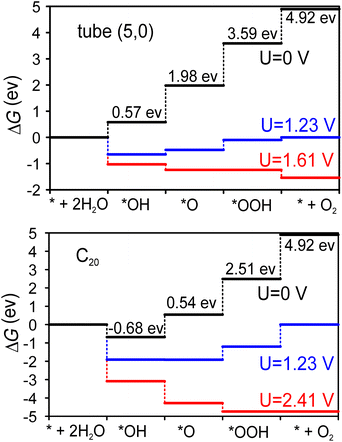Fig. 4 The evolution of H₂O adsorption energy at different coverage density on the basal and armchair edge surfaces of SWCNT (5,0), where both edges are capped by half fullerene C₂₀.

In order to better evaluate the catalytic ability of our tube (5,0), we obtained the theoretical overpotential (η = ΔG^OER/e − 1.23 V). The ΔG^OER represents the reaction Gibbs free energy of the potential-determining step at standard conditions. The overpotentials for the OER at tube (5,0), fullerene C₂₀ and other popular catalysts are summarized in Table 3. As we can see, the overpotential (0.38 V) for tube (5,0) is one of the lowest of all listed candidates, including different carbon-based, metal oxide, and metal materials. Previously, the adsorption of intermediate *OH was confirmed to be energetically unfavorable.³² Hence, various dopants, especially N, have been studied in the graphene matrix, and the potential performance shows that N-doped graphene can also be a promising catalyst for the OER. As such, we considered pyridinic-N-doped tube (5,0) and its fullerene C₂₀ cage, and found that the overpotentials are increased to 0.87 V and 12.4 V for N-doped tube (5,0) and N-doped C₂₀ respectively. This finding is quite different from previous calculations on N-doped graphene. Actually, the N dopants do activate the first water electrolysis and make the first two intermediates (*OH/*O) much more stable on the surface, but also increase the potential demand of the second water hydrolysis and oxygen desorption on our smallest tube and fullerene. Overall, the lower overpotential supports SWCNT (5,0) as a promising catalyst in the OER. To further reduce the overpotential, we suggest reading ref. 45 in which polymer assistance and Stone–Wales defects are used to reduce the overpotential from 0.73 V to 0.38 V at larger diameter (15 nm) carbon nanotubes.

Table 3 The overpotential (η) for the OER on tube (5,0), fullerene C₂₀ and other popular catalysts

	Catalysts	η (V)
Carbon-based	SWCNT (5,0)	0.38
	Fullerene C20	1.18
	SWCNT (100,100)^45	0.73
	N-doped graphene^46,47	0.41
	P-doped graphene^47	0.49
	N,P co-doped graphene^47	0.39
	FeNi@C^48	0.49
Metal oxides	RuO2 (ref. 49)	0.37
	IrO2 (ref. 49)	0.56
	TiO2 (ref. 49)	1.19
	LaMnO3 (ref. 50)	1.27
	LaCuO3 (ref. 50)	1.27
	SrCoO3 (ref. 50)	0.25
Metal	Pt(111) (ref. 51)	1.22

---

3.4 Surface coverage determination for the oxygen evolution reaction on tube (5,0) and fullerene C₂₀

To gain insight into the density of surface active sites for multiple H₂O dissociation (first step of the OER), we adsorb OH/H on tube (5,0) with increasing surface percentage coverage. On the basal surface of the tube, we consider OH/H adsorption in 2 different directions: along the length of the tube (axial direction) and across the same ring section (equatorial direction). We determine the favorability of the surface towards certain coverage percentages of the OH/H group by calculating the adsorption energy at each increment of surface percentage coverage in the following way:

E_ads = E_tube-(OH/H)n − (E_{tube-(OH/H)(n−1)} + E_H2O) (5)

where E_tube-(OH/H)n is the adsorption energy for tubes that are covered by a percentage of OH/H at a certain increment, E_{tube(OH/H)(n−1)} is the adsorption energy for tubes that are covered by a percentage of OH/H at the previous increment and E_H2O is the DFT energy of a single water molecule.

As can be seen in Fig. 5, the adsorption of OH/H in the axial direction is favorable all the way up to 100% coverage. We also reveal that the basal surface of tube (5,0) prefers to have a large amount of functionalization in the axial direction, as the adsorption of the OH/H pair in large numbers (≥50% of the surface) is more stable than if the surface is only sparsely functionalized (≤50% surface adsorption). However, OH/H adsorption on the C atoms of the same penta-atomic ring is only energetically favorable for up to 40% of the surface (i.e. a maximum of 2 C atoms per ring can be functionalized). The 2 adsorption sites in the equatorial direction are located on every other C atom in an alternating fashion, where the symmetry of the structure is still maintained as an oval tube. The adsorption of a third OH/H pair (60% coverage) destabilizes the tube by +1.42 kcal mol⁻¹, as this removes the alternating sequence of adsorption sites. However, the presence of half fullerene at the edges of tube (5,0) allows the adsorption of a third OH/H pair across the equatorial ring section which increases the surface coverage to 60%. On fullerene itself, OH/H can adsorb on each of the 5 atoms that constitute the ring, implying that 100% of the fullerene surface can be active for water dissociation.

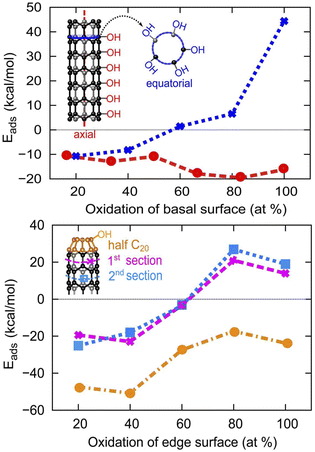Fig. 5 The evolution of H₂O adsorption energy at different coverage density on the basal and armchair edge surfaces of SWCNT (5,0), where both edges are capped by half fullerene C₂₀.

4 Conclusions

In this work, we investigate the surface reactivity of 4 Å SWCNTs by studying water dissociation and adsorption on three different configurations of 4 Å SWCNTs: armchair (3,3), chiral (4,2) and zigzag (5,0). We found that the adsorption of water molecules on the basal surfaces of the three 4 Å SWCNT configurations is slightly exothermic with adsorption energy of −0.13 eV, while the adsorption of O/H/H atoms on all tube configurations is highly unfavourable due to the formation of the very strained C–O–C bond. The adsorption energy of OH/H is highly negative on tube (5,0) with adsorption energy of −0.43 eV, which is due to its small HOMO–LUMO gap. The basal surface of tube (5,0) also prefers 100% functionalization along the axial length of the tube, however OH/H adsorption in the equatorial direction across the same penta-atomic ring section on the basal surface of tube (5,0) is only energetically favorable for adsorption of up to 2 pairs of OH/H, which gives 40% surface coverage. Adsorption of a third OH/H pair destabilizes the basal surface by +0.06 eV. Structural optimization of the armchair edge of tube (5,0) results in the terminating carbon atoms folding up and forming a fullerene C₂₀ structure. The presence of the fullerene results in a more exothermic adsorption energy (−2.16 eV) for the OH/H pair at the edge surface, and 20% more functionalized coverage on the tube surface.

The catalytic ability of tube (5,0) and its fullerene C₂₀ edge has also been studied in the OER. The small overpotential (0.38 V) supports tube (5,0) as the most promising carbon-based catalyst for oxygen evolution. However, the larger overpotential (1.18 V) denies the catalytic ability of fullerene C₂₀, although its surface is highly active in the single water splitting reaction. Further CPMD-based metadynamics simulations show that the activation barrier and solvation effect didn’t change the activity trend of intermediates at T = 298.15 K. Overall, the fullerene C₂₀ is super active in water splitting due to the dangling bonds on the surface, meanwhile, the overpotential is high for further steps, especially desorption of intermediates in the whole OER. The ultrasmall tube (5,0) is an active catalyst in water splitting and potential efficient in the OER.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Z. J., N. I. and Q. Y. gratefully acknowledge the support and computing resources from Prof. Vitaly Alexandrov. The Holland Computing Center at the University of Nebraska-Lincoln is acknowledged for computational support.

Notes and references

1. S. Iijima and T. Ichihashi, Nature, 1993, 363, 603–605.
2. A. G. Nasibulin, P. V. Pikhitsa, H. Jiang and E. I. Kauppinen, Carbon, 2005, 43, 2251–2257.
3. Z. G. Fthenakis, G. Kalosakas, G. D. Chatzidakis, C. Galiotis, K. Papagelis and N. N. Lathiotakis, Phys. Chem. Chem. Phys., 2017, 19, 30925–30932.
4. Z. Tang, H. Sun, J. Wang, J. Chen and G. Li, Appl. Phys. Lett., 1998, 73, 2287–2289.
5. H. Sun, Z. Tang, J. Chen and G. Li, Solid State Commun., 1999, 109, 365–369.
6. C.-R. Wang, T. Kai, T. Tomiyama, T. Yoshida, Y. Kobayashi, E. Nishibori, M. Takata, M. Sakata and H. Shinohara, Nature, 2000, 408, 426–427.
7. H. Liu and C. T. Chan, Phys. Rev. B, 2002, 66, 115416.
8. Z. Tang, L. Zhang, N. Wang, X. Zhang, G. Wen, G. Li, J. Wang, C. T. Chan and P. Sheng, Science, 2001, 292, 2462–2465.
9. L. Guan, K. Suenaga and S. Iijima, Nano Lett., 2008, 8, 459–462.
10. S. A. Siadati, M. S. Amini-Fazl and E. Babanezhad, Sens. Actuators, B, 2016, 237, 591–596.
11. L.-C. Qin, X. Zhao, K. Hirahara, Y. Miyamoto, Y. Ando and S. Iijima, Nature, 2000, 408, 50.
12. R. Saito, G. Dresselhaus and M. S. Dresselhaus, Physical properties of carbon nanotubes, World Scientific, 1998.
13. J. Svensson and E. E. Campbell, J. Appl. Phys., 2011, 110, 111101.
14. G. Levita, P. Restuccia and M. Righi, Carbon, 2016, 107, 878–884.
15. A. Impellizzeri, P. Briddon and C. Ewels, Phys. Rev. B, 2019, 100, 115410.
16. Z. Jiang and V. Alexandrov, J. Phys. Chem. C, 2019, 123, 30335–30340.
17. Z. Jiang, K. Klyukin and V. Alexandrov, ACS Appl. Mater. Interfaces, 2018, 10, 20621–20626.
18. Z. Jiang and V. Alexandrov, ACS Appl. Energy Mater., 2020, 3, 7543–7549.
19. J. T. Robinson, F. K. Perkins, E. S. Snow, Z. Wei and P. E. Sheehan, Nano Lett., 2008, 8, 3137–3140.
20. K. A. Mkhoyan, A. W. Contryman, J. Silcox, D. A. Stewart, G. Eda, C. Mattevi, S. Miller and M. Chhowalla, Nano Lett., 2009, 9, 1058–1063.
21. S. Saxena, T. A. Tyson and E. Negusse, J. Phys. Chem. Lett., 2010, 1, 3433–3437.
22. R. A. Soler-Crespo, W. Gao, P. Xiao, X. Wei, J. T. Paci, G. Henkelman and H. D. Espinosa, J. Phys. Chem. Lett., 2016, 7, 2702–2707.
23. M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. Van Dam, D. Wang, J. Nieplocha, E. Apra and T. L. Windus, et al., Comput. Phys. Commun., 2010, 181, 1477–1489.
24. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
25. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
26. D. Hamann, M. Schlüter and C. Chiang, Phys. Rev. Lett., 1979, 43, 1494.
27. D. Hamann, Phys. Rev. B, 1989, 40, 2980.
28. R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471.
29. S. Nosé, Mol. Phys., 1984, 52, 255–268.
30. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695.
31. E. Cauët, S. Bogatko, J. H. Weare, J. L. Fulton, G. K. Schenter and E. J. Bylaska, J. Chem. Phys., 2010, 132, 194502.
32. Z. Jiang, K. Klyukin and V. Alexandrov, Phys. Chem. Chem. Phys., 2017, 19, 14897–14901.
33. Y. Cao, B. Li, G. Zhong, Y. Li, H. Wang, H. Yu and F. Peng, Carbon, 2018, 133, 464–473.
34. J. Wei, W. Sun, W. Pan, X. Yu, G. Sun and H. Jiang, Chem. Eng. J., 2017, 312, 167–179.
35. A. Du, Z. Pan, Y. Ho, Z. Huang and Z. Zhang, Phys. Rev. B, 2002, 66, 035405.
36. T. P. Jungkamp and J. H. Seinfeld, J. Chem. Phys., 1997, 107, 1513–1521.
37. J. Montgomery Jr, J. Ochterski and G. Petersson, J. Chem. Phys., 1994, 101, 5900–5909.
38. J. W. Ochterski, G. A. Petersson and K. B. Wiberg, J. Am. Chem. Soc., 1995, 117, 11299–11308.
39. S. Xu, S. Irle, D. Musaev and M. Lin, J. Phys. Chem. A, 2005, 109, 9563–9572.
40. H. Dau, C. Limberg, T. Reier, M. Risch, S. Roggan and P. Strasser, ChemCatChem, 2010, 2, 724–761.
41. J. Rossmeisl, A. Logadottir and J. K. Nørskov, Chem. Phys., 2005, 319, 178–184.
42. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
43. H. A. Hansen, J. Rossmeisl and J. K. Nørskov, Phys. Chem. Chem. Phys., 2008, 10, 3722–3730.
44. J. Rossmeisl, J. K. Nørskov, C. D. Taylor, M. J. Janik and M. Neurock, J. Phys. Chem. B, 2006, 110, 21833–21839.
45. Y. Zhang, X. Fan, J. Jian, D. Yu, Z. Zhang and L. Dai, Energy Environ. Sci., 2017, 10, 2312–2317.
46. M. Li, L. Zhang, Q. Xu, J. Niu and Z. Xia, J. Catal., 2014, 314, 66–72.
47. J. Zhang, Z. Zhao, Z. Xia and L. Dai, Nat. Nanotechnol., 2015, 10, 444.
48. X. Cui, P. Ren, D. Deng, J. Deng and X. Bao, Energy Environ. Sci., 2016, 9, 123–129.
49. J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89.
50. I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165.
51. W. T. Hong, M. Risch, K. A. Stoerzinger, A. Grimaud, J. Suntivich and Y. Shao-Horn, Energy Environ. Sci., 2015, 8, 1404–1427.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra06123f

---