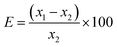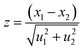DOI:
10.1039/D2RA06163E
(Paper)
RSC Adv., 2022,
12, 32684-32692
Optimization of external (in air) particle induced gamma-ray emission (PIGE) methodology for rapid, non-destructive, and simultaneous quantification of fluorine, sodium, and phosphorus in nuclear waste immobilization matrices†
Received
30th September 2022
, Accepted 25th October 2022
First published on 14th November 2022
Abstract
External (in air) PIGE methodology has been optimized for rapid quantification of fluorine, sodium, and phosphorus in fluorapatite waste immobilization matrices for Molten Salt Reactor (MSR). The present methodology addresses the issue of distinguishing hydroxyapatite and fluorapatite phases through XRD patterns. Fluctuations in proton beam current have been monitored by prompt γ-ray from nitrogen (2312 keV) through 14N(p,p′γ)14N nuclear reaction and have successfully been applied as a new method of current normalization, for the first time, in external PIGE method with lower Compton background and negligible spectral interference. The proposed method was also compared with the earlier method of current normalization using 165 keV (181T(p,p′γ)181Ta) from the Tantalum window used for obtaining “in air” beam. For the fluctuation of beam current within 5–10 nA, nitrogen from air can be used as an effective current normalizer. Moreover, the uncertainty (within ±3%) was also improved in the present method of current normalization. Fluorine can be estimated from trace to major concentrations using 197 keV (19F(p,p′γ)19F) γ-ray with highest sensitivity as compared to other prompt γ-rays (110 keV and 1236 keV). The matrix effect in PIGE was also eliminated by diluting the sample in cellulose. The method was validated using the synthetic samples (Ca10(PO4)6F2, Na2Eu2Ca6(PO4)6F2, Na1.5Eu1.5Ca7(PO4)6F2, Na1Eu1Ca8(PO4)6F2, Na0.5Eu0.5Ca9(PO4)6F2, and Sr10(PO4)6F2). The results were found to be satisfactory and in good agreement with stoichiometric amounts. Elements such as Na, P, and Ca were determined in the fluorapatite samples using PIGE and EDXRF, respectively, as a part of chemical quality control. Moreover, in external PIGE, 1266 keV γ-ray (31P(p,p′γ)31P) provides more accurate P concentrations in the samples.
Introduction
Synthesis of nuclear waste immobilization matrices is always a challenging task and is environmentally important for the safe disposal of radioactive wastes. Several research activities on radioactive waste disposal have been pursued by eminent scientists over the last few decades. The development of molten salt fueled nuclear reactor (MSR) is an interesting area of research.1 In MSR, the fuel is conventionally dissolved in a fluoride salt coolant, having melting points between 315 to 500 °C and thermal stability in the range of 700 to 1000 °C.2,3 However, the high level radioactive waste generated during reactor operation should be immobilized in inert matrices until the level of radioactivity and thermal energy diminishes with time. In MSR, the high level nuclear wastes are in halide form, which is not suitable to be encapsulated in borosilicate glasses due to the high reactivity of halides towards silicon and boron (glass elements). Hence, various ceramic matrices such as apatite, monazite, zircon, thorite, britholite, pyrochlore, perovskite, and zirconolite are proposed as alternatives to conventional borosilicate glass matrix.4 Fluorapatite, phosphate, and fluoride based ceramics are the most promising fluoride based materials for nuclear waste due to their high chemical stability and durability.4 The substitution of divalent calcium in fluorapatite by different trivalent cations can be explained by Cheralite (or Brabantite) type substitution, where Ca2+ is substituted by trivalent ions along with monovalent cations for charge compensations.5 However, during the synthesis of fluorapatite, the fluorine content needs to be fixed. If there is substantial fluorine loss during solid state reaction, the crystallinity of the produced apatite phase may vary largely.6 Due to poor crystallinity, there is a chance that fluorine can be migrated in volatile fluoride form, which is highly dangerous for the environment. Hence, for the safe disposal of radioactive waste, the fluorine content of such phases needs to be ascertained. The simulated XRD patterns of Ca10(PO4)6F2 and Ca10(PO4)6(OH)2, as shown in Fig. 1, clearly state the difficulty in distinguishing these two phases. Hence, elemental quantification plays a crucial role in such a scenario.
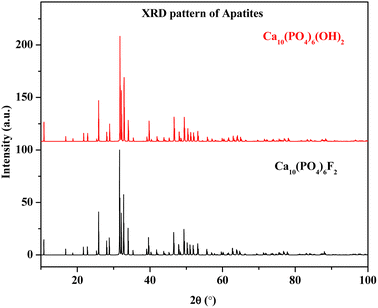 |
| | Fig. 1 Simulated XRD pattern of Ca10(PO4)6F2 and Ca10(PO4)6(OH)2. | |
Determination of low Z elements (fluorine, oxygen, phosphorus) in solid matrices is always a challenging task. Over the years, analytical chemists have come out with several scientific innovations for the determination of fluorine in solid matrices. Fluoride determinations in samples using ion chromatography, UV-visible spectroscopy or Ion Selective Electrodes (ISE) are some of the common analytical techniques involving extraction procedures using hazardous chemicals.7–10 Non-destructive analyses of solid samples are always preferred for not only being rapid enough with less turnaround time of analysis but also eco-friendly without utilizing cumbersome chemicals. One such instrumental technique is Wavelength Dispersive X-ray Fluorescence (WDXRF) spectrometry, which was applied for quantifying fluorine in soil samples.11,12 Nowadays, several improvements have been made in high resolution molecular absorption spectrometry for the estimation of fluorine in biological samples involving animal tissues.13,14 Low Z elements, like phosphorus, have been quantified directly on solid samples by electrothermal vaporization-inductively coupled plasma atomic emission spectrometry.15 In recent years, Particle Induced Gamma-ray Emission (PIGE)16,17 or Micro-PIGE18 is a well-known nuclear analytical technique for fluorine determination in solid matrices. PIGE is such an online nuclear analytical technique where accelerators are used for nuclear reactions like (p,p′γ), (p,αγ) or (p, nγ).19 It involves nuclear de-excitation to emit prompt-γ rays, followed by its assay using High Purity Germanium (HPGe) detector. Conventional PIGE methods were utilized in our laboratory using in situ current normalization/current normalization from the Tantalum window for fluorine determination in coal, soil, and several geological samples.20–22 In the course of time, the external (in air) PIGE method has also been developed by researchers, thereby making the method simpler, rapid, and promising for analyzing samples with non-standard geometry.23–26 Current normalization is always a challenging task in PIGE. Earlier, a complicated structural setup for Rutherford Back Scattering (RBS)27 was used for beam current measurement. In the external PIXE-PIGE setup, Ar Kα X-ray line was used for beam current integration.28 In the literature, it is also reported that prompt γ-rays at 770 keV from atmospheric Ar (40Ar(p,n γ)40K) have been used for external beam current normalization.29 Light emission from excited N2 molecules in air was also monitored for indirect charge measurement in external PIGE.30 Recently, we have developed an external PIGE methodology, where prompt γ-rays from the tantalum window were used for beam current normalization.22 The reaction involved in utilizing Ta as beam current normalization is 181Ta(p,p′γ)181Ta with prominent prompt γ-ray at 165 keV. However, higher γ-ray yield (intensity) of 165 keV gives higher Compton background, leading to erroneous concentration result with current normalization. One such example is fluorine determination with two prompt lower energy γ-rays like 110 keV and 197 keV (19F(p,p′γ)19F).16,31 Earlier, phosphorus was estimated in borosilicate glass samples by in situ current normalized external PIGE, which involved in situ mixing of the sample with a current normalizer (CaF2).32 In such a case, the determination of F (which is already present as an analyte in the sample) is not possible. Hence, the present investigation is focused on the synthesis of fluorapatites and its quality control for the rapid determination of fluorine, sodium and phosphorus by optimizing the external (in air) PIGE method with the proposed current normalization.
Experimental and calculation details
Synthesis of fluorapatites and X-ray diffraction experiment
Both the fluorapatite compounds; Ca10(PO4)6F2 and Sr10(PO4)6F2 were synthesized by conventional solid state reactions of a mixture of CaCO3/SrCO3, NH4H2PO4, and NH4HF2 with mole ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5, respectively. The chemical ingredients, calcium carbonate (CaCO3) (>99% pure), strontium carbonate (SrCO3) (>99.9% pure), ammonium dihydrogen phosphate (NH4H2PO4) (>99.5% pure) and ammonium bifluoride (NH4HF2) (>99.999% pure), used for the synthesis were purchased from E Merck, Germany. The salt mixture was taken in an agate mortar and ground thoroughly. Subsequently, the mixture was heated in a stepwise manner at 773 K for 24 h in a platinum crucible, followed by natural cooling to room temperature. Repeated grinding and heating at 973 K for 24 h was carried out till the pure phase compound was formed, as identified by XRD analysis. For the synthesis of NaxEuxCa10−2x(PO4)6F2 (x = 0.5, 1.0, 1.5, and 2.0), CaCO3, NH4H2PO4, NaNO3, Eu2O3, and NH4HF2 (slightly excess above stoichiometry) were mixed thoroughly in an agate mortar in the above stoichiometric ratio with few drops of acetone for homogenization. The mixture was heated at 773 K for 12 h and again ground in mortar pestles with additional heating for 24 h at 1223 K. The products obtained were again ground and stored in desiccators for further characterization. The phase purity of the samples was ascertained by the X-ray diffraction pattern recorded on the Rigaku SmartLab diffractometer using Cu Kα target. The XRD patterns were recorded in the range of 10–80° in a continuous mode with a scan rate of 1° per min.
2.5, respectively. The chemical ingredients, calcium carbonate (CaCO3) (>99% pure), strontium carbonate (SrCO3) (>99.9% pure), ammonium dihydrogen phosphate (NH4H2PO4) (>99.5% pure) and ammonium bifluoride (NH4HF2) (>99.999% pure), used for the synthesis were purchased from E Merck, Germany. The salt mixture was taken in an agate mortar and ground thoroughly. Subsequently, the mixture was heated in a stepwise manner at 773 K for 24 h in a platinum crucible, followed by natural cooling to room temperature. Repeated grinding and heating at 973 K for 24 h was carried out till the pure phase compound was formed, as identified by XRD analysis. For the synthesis of NaxEuxCa10−2x(PO4)6F2 (x = 0.5, 1.0, 1.5, and 2.0), CaCO3, NH4H2PO4, NaNO3, Eu2O3, and NH4HF2 (slightly excess above stoichiometry) were mixed thoroughly in an agate mortar in the above stoichiometric ratio with few drops of acetone for homogenization. The mixture was heated at 773 K for 12 h and again ground in mortar pestles with additional heating for 24 h at 1223 K. The products obtained were again ground and stored in desiccators for further characterization. The phase purity of the samples was ascertained by the X-ray diffraction pattern recorded on the Rigaku SmartLab diffractometer using Cu Kα target. The XRD patterns were recorded in the range of 10–80° in a continuous mode with a scan rate of 1° per min.
External (in air) PIGE method at FOTIA, BARC
External (in air) PIGE method was developed at FOlded Tandem Ion Accelerator (FOTIA), BARC with 3.5 MeV collimated proton beam after extracting from 25 μm Ta window.21 The details of the experimental setup have been given in our previous publication.20 The entire radioactive assay was carried out using a p-type coaxial HPGe detector (crystal ∼60 mm dia and 50 mm thickness, relative efficiency ∼50% and resolution ∼2.0 keV at 1332 keV of 60Co). The detector was coupled with 8 k MCA (Multichannel Analyzer) for simultaneous detection of multiple γ-rays from low Z elements. The electronics setup was procured from Baltic Scientific Instruments (BSI). Energy calibration of the detector was performed using standard sources like 152Eu and 60Co. CaF2 and SrF2 standards were prepared in a cellulose matrix with varying concentrations (0.6–6.3%). Ca3(PO4)2 was taken as the standard for phosphorus estimation in Ca based fluorapatites. Varying masses of stoichiometric compounds (CaF2, SrF2) were mixed homogenously with cellulose using mortar and pestle, followed by its pellet formation using a 2 ton hydraulic press. 50 mg each of Certified Reference Materials (CRM), USGS G2 and USGS STM-1, were taken and homogenously mixed with 650 mg of cellulose and pelletized. 25 mg each of the synthesized fluorapatites (Ca10(PO4)6F2, Na2Eu2Ca6(PO4)6F2, Na1.5Eu1.5Ca7(PO4)6F2, Na1Eu1Ca8(PO4)6F2, Na0.5Eu0.5Ca9(PO4)6F2, Sr10(PO4)6F2) were taken and homogenously mixed with 675 mg of cellulose followed by pelletization, resulting in a total mass of 700 mg. During sample preparation, all the components are mixed together in mortar and pestle for a constant (∼1 h) duration of time. Cellulose was added to the samples for its dilution, thereby eliminating the matrix effects (stopping powers became similar for samples and standards). In our present work, a relative method of concentration calculation has been followed where samples and standards were irradiated in similar positions and geometry with respect to the detector. Particle sizes were assumed to be the same for the sample and standard, and it did not have any effect on the results. The CaF2 standards in pellet forms were irradiated in a 3.5 MeV proton beam for 15–20 min. The proton beam current was changed from 5 nA to 20 nA and monitored by the current integrator circuit. CaF2 standards were also irradiated in varying beam currents. All the synthesized fluorapatites were irradiated for 15 min in 3.5 MeV (7–8 nA) proton beam. A proper analytical procedure was followed by irradiating the samples and standards in similar geometry with respect to the detector. All the prompt γ-ray spectra were recorded in APTEC software. The peak areas were analyzed by the peak-fit method (Gaussian shape and low exponential tail model) using Pulse Height Analysis (PHAST)33 software developed by BARC, India. Radiological safety was maintained during the experiments.
Calculation details for fluorine and phosphorus determination using the proposed methodology of current normalization
In the present investigation, we have used the relative method of calculations (quantification of the element in the sample using standards of known composition). The concentration of F/P in the sample is given by the expression (1) below,| |
 | (1) |
Here, ‘C’ is the concentration of the analyte (fluorine or phosphorus) in the sample (samp) and standards (std), CPS is the counts per second of the prompt γ-ray peaks of the analytes. The details of the nuclear reactions along with the prompt γ-ray energies are given in Table 1. The symbol ‘φ’ denotes the proton beam current at the target. During the spectrum acquisition, there are always fluctuations in beam current leading to errors in peak area calculations for the analytes. A complicated structural setup like RBS/Faraday cup was utilized to resolve the issue associated with the direct measurement of ‘φ’ from the samples. However, our laboratory has come up with simple current normalization methods like the in situ method (constant amount of Li or F added in the sample),17 and external use of prompt γ-rays (165 keV) from the tantalum window.22 In the present work, prompt γ-ray peak (2312 keV) from nuclear reaction (14N(p,p′γ)14N) has been proposed as a new method for current normalization. Earlier, both the nuclear reactions 14N(p,p′γ)14N (Eγ = 2312 keV) and 15N(p,αγ)12C (Eγ = 4439 keV) have been utilized for determination of nitrogen in blood serum samples by PIGE method.34 However, it has been reported that the analytical sensitivity for the determination of nitrogen is 4.2 times higher for (p,p′γ) resonant scattering reaction as compared to (p,αγ) reaction.34 Prompt γ-ray peak (2312 keV) in the subsequent γ-ray spectra (given in later sections) arises from the nitrogen (∼78%) present in air and thus can be utilized as beam current normalization. Moreover, the γ-ray (2312 keV) is a high energy γ-ray and does not have any spectral interference with the other γ-rays of the analytes. Therefore, the ratio of φstd/φsamp can be expressed as given below,| |
 | (2) |
Table 1 Relevant nuclear data for determination of F, Na, and P by PIGE method
| Element |
Nuclear reactions |
Prompt γ-ray energies, keV |
Gamma-ray yield (counts/μC/Sr)35 |
| Ep = 2.4 MeV |
Ep = 3.1 MeV |
Ep = 3.8 MeV |
| F |
19F(p,p′γ)19F |
110 |
3.5 × 105 |
7.2 × 106 |
1.1 × 107 |
| 19F(p,p′γ)19F |
197 |
2.9 × 106 |
2.0 × 107 |
3.7 × 107 |
| 19F(p,p′γ)19F |
1236 |
1.5 × 105 |
3.0 × 106 |
5.4 × 106 |
| N |
14N(p,p′γ)14N |
2312 |
NA |
NA |
5.5 × 104 |
| 15N(p,αγ)12C |
4439 |
5.0 × 103 |
5.0 × 104 |
6.0 × 104 |
| Na |
23Na(p,p′γ)23Na |
440 |
3.4 × 106 |
9.6 × 106 |
1.6 × 107 |
| 23Na(p,p′γ)23Na |
1636 |
1.5 × 106 |
9.9 × 106 |
1.9 × 106 |
| P |
31P(p,p′γ)31P |
1266 |
3.8 × 104 |
1.6 × 106 |
5.2 × 106 |
| 31P(p,αγ)28Si |
1779 |
2.0 × 103 |
2.1 × 105 |
6.5 × 105 |
Prompt γ-rays of both Ta (165 keV (181Ta(p,p′γ)181Ta))) and N (2312 keV (14N(p,p′γ)14N) have been recorded simultaneously using the HPGe detector coupled to a multichannel analyzer. The measurement time was 600 s, and peak areas of 2312 keV and 165 keV are around 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 counts (for N) and 12
000 counts (for N) and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (for Ta) counts, respectively, which indicates that the peak area uncertainty of N is less as compared to Ta within the same measurement time. Thus, in addition to Ta, N is a good external current normalizer in the external (in air) PIGE method.
000 (for Ta) counts, respectively, which indicates that the peak area uncertainty of N is less as compared to Ta within the same measurement time. Thus, in addition to Ta, N is a good external current normalizer in the external (in air) PIGE method.
EDXRF experiment for quality control assessment
Ca in fluorapatites was determined using the EDXRF method. The Jordan valley EX 3600 M spectrometer procured from Israel was used in the experiment.36,37 The spectrometer contains a Rh source and Be window. Samples were irradiated with X-rays at room temperature. The semiconductor detector Si(Li) coupled with a multichannel analyzer was used for detecting X-ray fluorescence from the samples. The maximum resolution of the instrument is 0.139 keV at Mn-Kα (5.9 keV).38 Pellets of fluorapatites were put inside the Teflon cup having transparent Mylar foil for irradiation in the X-ray beam. A relative method of calculation was followed for the determination of Ca. CaF2 was used as the reference standard. The same pellets used for PIGE analysis were directly used for EDXRF. The X-ray energy (Kα) for Ca is 3.61 keV, used for its estimation.
Results and discussion
X-ray diffraction experiment
The XRD patterns of the synthesized compounds (Ca10(PO4)6F2, Na2Eu2Ca6(PO4)6F2, Na1.5Eu1.5Ca7(PO4)6F2, Na1Eu1Ca8(PO4)6F2, Na0.5Eu0.5Ca9(PO4)6F2, Sr10(PO4)6F2) are shown in Fig. 2, confirming the formation of single phase (hydroxyapatites/fluorapatites). The XRD patterns were compared with the literature (ICDD files).
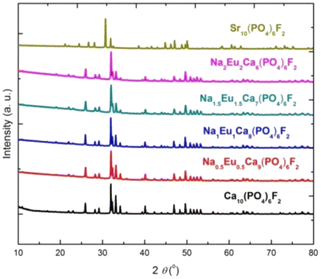 |
| | Fig. 2 The XRD patterns of the synthesized compounds. | |
Optimization of the external PIGE method for fluorine quantification
After irradiation of several fluorine standards in a proton beam (∼3.5 MeV), the count rate without beam current normalization showed an unusual trend, which is not suitable for analytical determination (Fig. 3(a)). Using both the methods of current normalization, it was observed that the analytical sensitivity of 197 keV prompt γ-ray was higher than that of 110 keV and 1236 keV (slope of the calibration plots in Fig. 3(b) and (c)). This might be due to the higher yield for the γ-ray (197 keV) from 19F(p,p′γ)19F. Prompt γ-ray (110 keV) has comparatively lesser sensitivity than 197 keV and can be utilized for quantitative purposes with a slightly higher beam current. However, the 1236 keV γ-ray is not suitable for the quantitative application owing to its poor analytical sensitivity. In the present work, 197 keV prompt γ-ray was utilized for quantification purposes with varying beam currents (5–10) nA. Monitoring the variation in beam current is a challenging task in these analytical measurements. Similar calibration plots were obtained for both Ta and N as current normalizers. Current normalization using N from air via the nuclear reaction 14N(p,p′γ)14N is an innovative idea explored in this scientific report. Utilizing N from air as a current normalizer has several advantages over the conventional method of current normalization (e.g., in situ current normalization). There is no spectral interference from the analytes since 2312 keV (14N(p,p′γ)14N) is a high energy prompt γ-ray peak with a very less Compton background. Prompt γ-rays from the tantalum window (135 keV and 165 keV) have been optimized for current normalization in our previous works and applied to various environmental and forensic samples. The 135 and 165 keV γ-rays are lower energy γ-rays with higher Compton background, thereby causing significant spectral interference for the analytes (for e.g., fluorine). It was also observed that the current normalized cps (CNCPS using 14N(p,p′γ)14N for current normalization) was a linear function of fluorine concentrations over a wide range (0.6–6)% (Fig. 3(c)). However, in the case of 181Ta(p,p′γ)181Ta as the current normalizer, the linearity deviated at higher fluorine concentrations (Fig. 3(b)). Moreover, proton beam currents were changed from 5 nA to 20 nA, and variations in counts (cps) were observed for both Ta and N2 as current normalizers (Fig. 4). For (5–20) nA change in proton current, cps (181Ta(p,p′γ)181Ta) varied linearly within a small range (5–60 cps), whereas for 14N(p,p′γ)14N, cps increases with increasing beam current up to 10 nA, after which no such significant variation in cps was observed. This ensured that N2 from air could be used as effective current normalizer in the external PIGE method with fluctuations in proton current from (5–10) nA. The ratio of peak area at 165 keV (Ta) to peak area at 2312 keV (N) was found to be the same for all the samples, which clearly indicates that there was no change in ambient air pressure during our experiment.
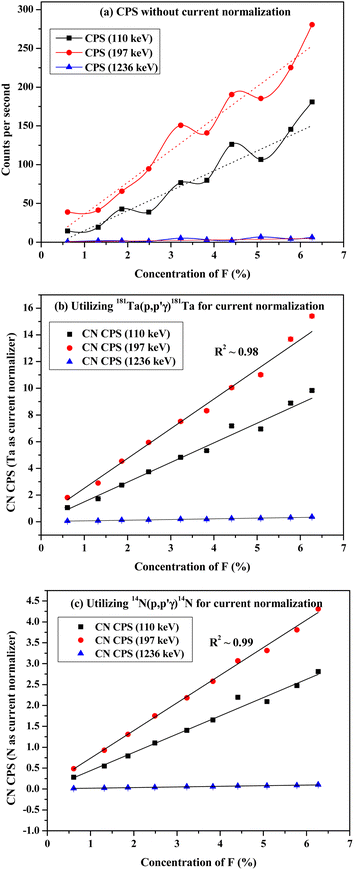 |
| | Fig. 3 Calibration plots with CaF2 standards utilizing (a) without current normalization (b) 181Ta(p,p′γ)181Ta and (c) 14N(p,p′γ)14N for current normalization. | |
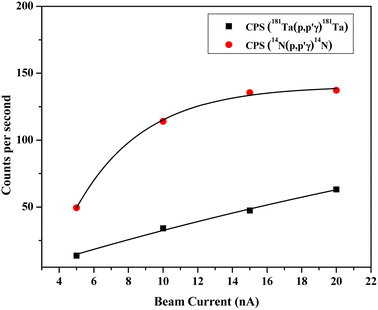 |
| | Fig. 4 Variation of cps for both Ta and N2 as current normalizer with respect to the beam current. | |
Method validation for F determination using synthetic fluorapatites
For method validation, certified reference materials (USGS G2 and USGS STM-1) were chosen. USGS STM-1 was analyzed, considering USGS G2 as the standard. The certificates of both CRMs are given in ESI.† The results obtained are shown in Table 2. The values obtained using 197 keV γ-ray are in good agreement with the certified one (percentage error within ±3% and zeta-score within ±0.5). Using 110 and 1236 keV γ-rays gives less accuracy with percentage deviations varying from ±(7–15)% and zeta score varying from ±(1–2). This showed the capability of the optimized method for the quantification of trace and minor quantities of fluorine. Homogeneity assessment was done by irradiating the sample pellet at different positions using the proton beam. Since the size of the proton beam is ∼3 mm, we get a good result. The concentration results obtained after irradiation at separate positions are reproducible (within ±0.5%). However, it was also observed that with Ta as the current normalizer, results gave more uncertainty (±5%) as compared to current normalization utilizing N2 from air (±3%). This might be due to the higher peak area of 2312 keV (14N(p,p′γ)14N) as compared to 165 keV (181Ta(p,p′γ)181Ta). The uncertainty calculated here was the propagated one considering uncertainties in mass, peak areas of samples, standards, and current normalizers. The external PIGE method with the proposed current normalization procedure was applied for quality control of synthesized fluorapatites (Table 3). SrF2 and CaF2 chemical standards were taken for fluorine determination in Sr10(PO4)6F2 and Ca10(PO4)6F2. Peak areas were taken from the prompt γ-ray spectra of the fluorapatites and analyzed by PHAST software. Fig. 5 shows the γ-ray spectrum for Ca10(PO4)6F2. However, the same CaF2 standards were taken for Na and Eu doped fluorapatites (Na2Eu2Ca6(PO4)6F2, Na1.5Eu1.5Ca7(PO4)6F2, Na1Eu1Ca8(PO4)6F2, Na0.5Eu0.5Ca9(PO4)6F2).
Table 2 Determination of F (ppm) in USGS STM-1 for method validation
| Reactions utilized for beam current normalization |
Prompt γ-ray energy taken (keV) |
Experimental value (x1 ± u1) |
Certified value (x2 ± u2) |
Relative bias (E) (%) 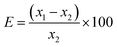
|
Zeta score (z) 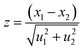
|
| 181Ta(p,p′γ)181Ta |
110 |
984 ± 49 |
910 ± 50 |
8.1 |
1.0 |
| 197 |
880 ± 40 |
910 ± 50 |
−3.3 |
−0.5 |
| 1236 |
1048 ± 52 |
910 ± 50 |
15.2 |
1.9 |
| 14N(p,p′γ)14N |
110 |
980 ± 39 |
910 ± 50 |
7.7 |
1.1 |
| 197 |
890 ± 27 |
910 ± 50 |
−2.2 |
−0.4 |
| 1236 |
1035 ± 41 |
910 ± 50 |
13.7 |
1.9 |
Table 3 Determination of F mass fraction (%) in synthesized fluorapatite samples
| Fluorapatite samples |
Expected concentration value (%) as per stoichiometry of compounds |
Determined concentration of fluorine |
| Using Ta as current normalizer using 165 keV from 181Ta(p,p′γ)181Ta |
Using N2 as current normalizer using 2312 keV from 14N(p,p′γ)14N |
| Conc (%) |
Relative bias (%) |
Conc (%) |
Relative bias (%) |
| Ca10(PO4)6F2 |
3.76 |
3.74 ± 0.18 |
−0.5 |
3.74 ± 0.10 |
−0.5 |
| Na2Eu2Ca6(PO4)6F2 |
3.17 |
3.10 ± 0.15 |
−2.2 |
3.11 ± 0.08 |
−1.9 |
| Na1.5Eu1.5Ca7(PO4)6F2 |
3.30 |
3.33 ± 0.17 |
0.9 |
3.32 ± 0.09 |
0.6 |
| Na1Eu1Ca8(PO4)6F2 |
3.44 |
3.45 ± 0.18 |
0.3 |
3.46 ± 0.10 |
0.6 |
| Na0.5Eu0.5Ca9(PO4)6F2 |
3.60 |
3.63 ± 0.20 |
0.8 |
3.62 ± 0.11 |
0.6 |
| Sr10(PO4)6F2 |
2.56 |
2.65 ± 0.13 |
3.5 |
2.50 ± 0.07 |
−2.3 |
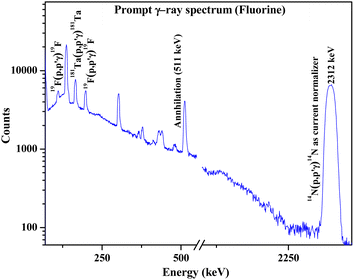 |
| | Fig. 5 Prompt γ-ray spectrum for fluorine determination in synthesized Ca10(PO4)6F2 sample. | |
Results showed the accuracy of the optimized method by using cellulose for dilution, thereby neglecting the matrix effect (Table 3). PIGE being a surface analytical technique exhibits a significant matrix effect, which has been overcome by mixing large quantities of cellulose. Fluorine contents in fluorapatites have been accurately determined by optimizing the external PIGE method with the proposed current normalization (percentage error within ±4%). The results were compared for both Ta and N2 current normalization. It revealed more accurate results with lower uncertainty using N2 as the current normalizer. Both XRD patterns and PIGE results revealed that the compounds synthesized were stoichiometric in nature. The little variation in the determined concentration of fluorine in fluorapatites from the expected one (by stoichiometry) might be due to the unavoidable random error associated with the technique.
Determination of Na, P, and Ca in synthesized fluorapatites
As a part of the chemical control exercise, Na, P and Ca were determined in synthesized fluorapatites. Here, we have chosen 1266 and 1779 keV prompt γ-rays for the quantification of P (Fig. 6). Since Si was absent as an analyte in the synthetic samples, there is no spectral interference from 1779 keV (28Si(p,p′γ)28Si) in external PIGE. Ca was quantified in the samples using EDXRF. However, in external PIGE, P was determined using both the current normalization techniques (Ta and N2 as current normalizer). It was observed that with N2 as the current normalizer, the results were more accurate with lower uncertainty (within ±3%) (Table 4). The energy of 1266 keV for P gave more accurate results as compared to 1779 keV. Hence, 1266 keV prompt γ-ray was used for all calculations. Although the uncertainty is lowered with N2 as the current normalizer in external PIGE, it is difficult to distinguish between Na1.5Eu1.5Ca7(PO4)6F2, Na1Eu1Ca8(PO4)6F2 and Na0.5Eu0.5Ca9(PO4)6F2 in terms of P content. The obtained results in mass fraction (%) from PIGE and EDXRF were also in good agreement with theoretically measured stoichiometric contents of Ca and P in the samples (Ca10(PO4)6F2 (18.44% P and 39.69% Ca), Na2Eu2Ca6(PO4)6F2 (15.51% P and 20.04% Ca), Na1.5Eu1.5Ca7(PO4)6F2 (16.16% P and 24.34% Ca), Na1Eu1Ca8(PO4)6F2 (16.85% P and 29.02% Ca), Na0.5Eu0.5Ca9(PO4)6F2 (17.61% P and 34.11% Ca)). Theoretically, the atomic percentage of an element (X) in a chemical compound (XY) is given by eqn (3), as shown below,| |
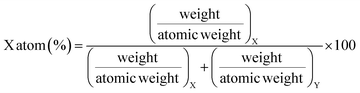 | (3) |
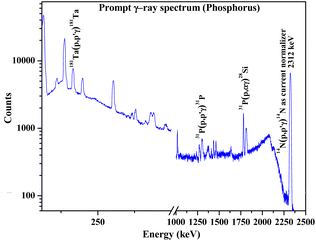 |
| | Fig. 6 Prompt γ-ray spectrum for phosphorus determination in synthesized Ca10(PO4)6F2 sample. | |
Table 4 Determination of P mass fraction (%) and Ca mass fraction (%) in synthesized fluorapatite samples
| Fluorapatite samples |
PIGE P mass fraction (%) |
EDXRF Ca mass fraction (%) |
| Using Ta as current normalizer using 165 keV from 181Ta(p,p′γ)181Ta |
Using N2 as current normalizer using 2312 keV from 14N(p,p′γ)14N |
| Ca10(PO4)6F2 |
18.5 ± 0.9 |
18.4 ± 0.6 |
40.0 ± 1.1 |
| Na2Eu2Ca6(PO4)6F2 |
15.1 ± 0.8 |
15.2 ± 0.5 |
19.7 ± 0.6 |
| Na1.5Eu1.5Ca7(PO4)6F2 |
16.3 ± 0.8 |
16.2 ± 0.5 |
24.2 ± 0.7 |
| Na1Eu1Ca8(PO4)6F2 |
16.9 ± 0.9 |
17.0 ± 0.5 |
28.4 ± 0.8 |
| Na0.5Eu0.5Ca9(PO4)6F2 |
17.4 ± 1.0 |
17.7 ± 0.6 |
34.2 ± 0.7 |
From the measured concentration values of Ca and P in Table 4, the atom percentages are calculated as shown in Table 5. The measured atom (%) from experimentally measured weight (%) is in good agreement with the stoichiometric values. The relative bias is within ±12% in Ca determination by EDXRF. The deviation from stoichiometry may be due to the high experimental uncertainty associated with EDXRF, which cannot be avoided. In external PIGE, relative bias was found to be within +7% (Na0.5Eu0.5Ca9(PO4)6F2), which is mainly due to random error associated with the technique while quantifying mass fractions (%) of the elements.
Table 5 .Determination of P and Ca in atom (%) from the measured mass fraction (%) using N2 as current normalizer as shown in Table 4
| Fluorapatite samples |
P (PIGE) |
Ca (EDXRF) |
| Measured atom (%) |
Calculated atom (%) from stoichiometry |
Relative bias (%) |
Measured atom (%) |
Calculated atom (%) from stoichiometry |
Relative bias (%) |
| Ca10(PO4)6F2 |
14.2 ± 0.5 |
14.3 |
−0.7 |
24.0 ± 1.0 |
23.8 |
0.8 |
| Na2Eu2Ca6(PO4)6F2 |
14.1 ± 0.5 |
14.3 |
−1.4 |
14.1 ± 0.6 |
14.3 |
−1.4 |
| Na1.5Eu1.5Ca7(PO4)6F2 |
13.9 ± 0.5 |
14.3 |
−2.8 |
18.7 ± 0.7 |
16.7 |
12.0 |
| Na1Eu1Ca8(PO4)6F2 |
13.7 ± 0.5 |
14.3 |
−4.2 |
20.5 ± 0.7 |
19.0 |
7.9 |
| Na0.5Eu0.5Ca9(PO4)6F2 |
13.3 ± 0.5 |
14.3 |
−7.0 |
22.7 ± 0.6 |
21.4 |
6.1 |
Na has been quantified in the Na doped fluorapatites as a part of chemical quality control immediately after the synthesis of the compounds. Prompt γ-rays at 440 keV and 1636 keV (Table 1) are monitored with the help of HPGe to determine Na (Fig. 7). The results are shown in Table 6 with relative bias (within ±3%). The current normalizer with N2 showed lower uncertainty (within ±3%) in the measured concentration as compared to the Ta current normalizer.
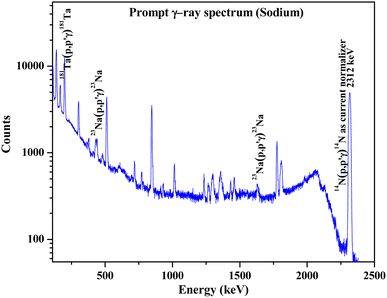 |
| | Fig. 7 Prompt γ-ray spectrum for sodium determination in synthesized Na2Eu2Ca6(PO4)6F2 sample. | |
Table 6 Determination of Na mass fraction (%) in Na doped fluorapatites
| Fluorapatite samples |
Expected concentration value (%) as per stoichiometry of compounds |
Determined concentration of Na |
| Using Ta as current normalizer using 165 keV from 181Ta(p,p′γ)181Ta |
Using N2 as current normalizer using 2312 keV from 14N(p,p′γ)14N |
| Conc (%) |
Relative bias (%) |
Conc (%) |
Relative bias (%) |
| Na2Eu2Ca6(PO4)6F2 |
3.84 |
3.82 ± 0.18 |
−0.5 |
3.85 ± 0.11 |
0.3 |
| Na1.5Eu1.5Ca7(PO4)6F2 |
3.00 |
3.02 ± 0.15 |
0.7 |
3.02 ± 0.08 |
0.7 |
| Na1Eu1Ca8(PO4)6F2 |
2.08 |
2.06 ± 0.09 |
−1.0 |
2.07 ± 0.06 |
−0.5 |
| Na0.5Eu0.5Ca9(PO4)6F2 |
1.09 |
1.11 ± 0.06 |
1.8 |
1.12 ± 0.03 |
2.8 |
Conclusions
The external (in air) PIGE method has been optimized for the first time for rapid determination of Na, F, and P in fluorapatite based nuclear waste immobilization matrices. The innovative idea of using nitrogen (from air) as a current normalizer has been explored in this article for the first time using 14N(p,p′γ)14N nuclear reaction. Nitrogen can be used as an effective current normalizer for beam current fluctuations within (5–10) nA. Moreover, utilizing nitrogen as a current normalizer gives lower uncertainty in concentration calculations as compared to current normalization using the tantalum window. Direct quantification of fluorine in solid samples is always a challenging task, which has been optimized by external PIGE showing 197 keV with the highest sensitivity as compared to other γ-rays (110 and 1236 keV). The method was successfully applied to the synthesized fluorapatites with high accuracy and lower uncertainty. The method was validated using certified reference materials. Even Na, P, and Ca were also quantified in the samples by PIGE and EDXRF as a part of chemical quality control. The prompt γ-ray energy (1266 keV from 31P(p,p′γ)31P) was chosen for P quantification, and the PIGE method was optimized with N2 as the current normalizer.
Author contributions
S. K. Samanta: planning, optimization, and execution of PIGE experiments, manuscript preparation. P. Das: synthesis of fluorapatite compounds and XRD experiments, characterization. A. Sengupta: EDXRF experiment and manuscript preparation. R. Acharya: planning, experiment, and manuscript preparation.
Conflicts of interest
There are no conflicts to declare in this article.
Acknowledgements
The authors thank Dr P. K. Mohapatra, Head, RCD, Dr S. C. Parida, Head, PDD, Dr S. Kannan, Director, RC & I Group, BARC, for the support and encouragement. The authors also thank Dr S. Krishnagopal, Head, IADD, Mr A. Agarwal, OIC, FOTIA, IADD and FOTIA operation crews for their support and co-operation during the PIGE experiment. Mr S. K. Samanta is thankful to Homi Bhabha National Institute (HBNI) and Doctoral Committee, HBNI, for pursuing this work as a part of PhD thesis.
References
- L. H. Ortega, R. J. Livingston and S. M. McDeavitt, Nucl. Mater. Energy, 2022, 32, 101223 CrossRef.
- G. Chen, M. Li, Y. Zou and H. Xu, Prog. Nucl. Energy, 2022, 150, 104308 CrossRef CAS.
- Z. Cheng, Z. Zhao, J. Geng, W. Li, Q. Dou and Q. Li, J. Nucl. Mater., 2022, 566, 153807 CrossRef CAS.
- P. Das, B. G. Vats, P. Samui, S. Kesari, M. Shafeeq, S. C. Parida and S. Dash, ChemistrySelect, 2021, 6, 13817–13831 CrossRef CAS.
- N. Pathak, B. Chundawat, P. Das, P. Modak and B. Modak, RSC Adv., 2021, 11, 31421–31432 RSC.
- L. M. Rodríguez-Lorenzo, J. N. Hart and K. A. Gross, Biomaterials, 2003, 24, 3777–3785 CrossRef.
- Y. Miyake, N. Yamashita, P. Rostkowski, M. K. So, S. Taniyasu, P. K. S. Lam and K. Kannan, J. Chromatogr. A, 2007, 1143, 98–104 CrossRef CAS PubMed.
- F. Polat, Chem. Pap., 2022, 76, 6215–6221 CrossRef CAS.
- J. Li, Y. Guan, L. Wang, J. Guo, Y. Liu and J. Wang, Yejin Fenxi, 2021, 41, 84–90 Search PubMed.
- A. M. Mahmoud, M. H. Mahnashi, S. S. Abu-Alrub, S. A. Alkahtani and M. M. El-Wekil, J. Electrochem. Soc., 2021, 168, 126525 CrossRef CAS.
- W. Zhao, T. Zhang, B. Lu and S. Lü, Yejin Fenxi, 2021, 41, 27–33 Search PubMed.
- J. An, K. H. Kim, H. O. Yoon and J. Seo, Spectrochim. Acta, Part B, 2012, 69, 38–43 CrossRef CAS.
- B. Welz, F. G. Lepri, R. G. O. Araujo, S. L. C. Ferreira, M. D. Huang, M. Okruss and H. Becker-Ross, Anal. Chim. Acta, 2009, 647, 137–148 CrossRef CAS PubMed.
- A. Gawor, A. Tupys, A. Ruszczyńska and E. Bulska, Appl. Sci., 2021, 11, 5493 CrossRef CAS.
- P. Masson, J. Anal. At. Spectrom., 2011, 26, 1290–1293 RSC.
- P. S. Dhorge, P. S. Girkar, A. D. Sharma, T. Keesari, N. S. Rajurkar, R. Acharya and P. K. Pujari, Geochemistry, 2020, 80, 125551 CrossRef CAS.
- S. Chhillar, R. Acharya, S. Sodaye and P. K. Pujari, Anal. Chem., 2014, 86, 11167–11173 CrossRef CAS PubMed.
- K. Yagi, R. Uemura, H. Yamamoto, T. Ishimoto, K. Naito, S. Itoh, Y. Matsuda, K. Okuyama, T. Nakano and M. Hayashi, Dent. Mater. J., 2021, 40, 1142–1150 CrossRef CAS PubMed.
- L. Beck, L. Pichon, B. Moignard, T. Guillou and P. Walter, Nucl. Instrum. Methods Phys. Res., Sect. B, 2011, 269, 2999–3005 CrossRef CAS.
- S. K. Samanta, A. Sengupta, S. Ghorui, R. Acharya and P. K. Pujari, J. Anal. At. Spectrom., 2022, 37, 296–305 RSC.
- S. K. Samanta, S. W. Raja, V. Sharma, P. S. Girkar, R. Acharya and P. K. Pujari, J. Radioanal. Nucl. Chem., 2020, 325, 923–931 CrossRef CAS.
- V. Sharma, R. Acharya, H. K. Bagla and P. K. Pujari, J. Anal. At. Spectrom., 2021, 36, 630–643 RSC.
- F. Mathis, G. Othmane, O. Vrielynck, H. Calvo del Castillo, G. Chêne, T. Dupuis and D. Strivay, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 2078–2082 CrossRef CAS.
- T. Calligaro, Y. Coquinot, L. Pichon and B. Moignard, Nucl. Instrum. Methods Phys. Res., Sect. B, 2011, 269, 2364–2372 CrossRef CAS.
- F. Lucarelli, G. Calzolai, M. Chiari, M. Giannoni, D. Mochi, S. Nava and L. Carraresi, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 318, 55–59 CrossRef CAS.
- F. Lucarelli, G. Calzolai, M. Chiari, S. Nava and L. Carraresi, Nucl. Instrum. Methods Phys. Res., Sect. B, 2018, 417, 121–127 CrossRef CAS.
- D. Sokaras, E. Bistekos, L. Georgiou, J. Salomon, M. Bogovac, E. Aloupi-Siotis, V. Paschalis, I. Aslani, S. Karabagia, A. Lagoyannis, S. Harissopulos, V. Kantarelou and A.-G. Karydas, Nucl. Instrum. Methods Phys. Res., Sect. B, 2011, 269, 519–527 CrossRef CAS.
- X. F. Li, G. F. Wang, J. H. Chu and L. D. Yu, Nucl. Instrum. Methods Phys. Res., Sect. B, 2012, 289, 1–4 CrossRef CAS.
- J. T. Wilkinson, S. R. McGuinness and G. F. Peaslee, Nucl. Instrum. Methods Phys. Res., Sect. B, 2020, 484, 1–4 CrossRef CAS.
- J. O. Lill, Nucl. Instrum. Methods Phys. Res., Sect. B, 1999, 150, 114–117 CrossRef CAS.
- P. S. Dhorge, R. Acharya, N. S. Rajurkar, V. Chahar, V. Tuli, A. Srivastava and P. K. Pujari, J. Radioanal. Nucl. Chem., 2017, 311, 1803–1809 CrossRef CAS.
- A. D. Prakash, R. K. Mishra, T. P. Valsala, V. Sharma, R. Acharya, A. K. Tyagi, P. K. Pujari and C. P. Kaushik, J. Radioanal. Nucl. Chem., 2021, 328, 519–526 CrossRef CAS.
- S. K. Samanta, T. N. Nag, V. Sharma, R. Tripathi, R. Acharya and P. K. Pujari, Nucl. Instrum. Methods Phys. Res., Sect. A, 2021, 1006, 165429 CrossRef CAS.
- T. Kupila-Rantala, M. Hyvönen-Dabek, J. T. Dabek and J. Räisänen, J. Radioanal. Nucl. Chem., 1995, 196, 145–152 CrossRef CAS.
- A. Z. Kiss, E. Koltay, B. Nyakó, E. Somorjai, A. Anttila and J. Räisänen, J. Radioanal. Nucl. Chem., 1985, 89, 123–141 CrossRef CAS.
- S. Jayabun and A. Sengupta, ChemistrySelect, 2021, 6, 376–388 CrossRef CAS.
- A. Sengupta, B. Rajeswari and R. Mahadeo Kadam, ChemistrySelect, 2020, 5, 3763–3769 CrossRef CAS.
- J. Sk, M. Sunita Pathak and A. Sengupta, ChemistrySelect, 2021, 6, 1911–1919 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ac,
P. Das
*ac,
P. Das bc,
A. Sengupta
bc,
A. Sengupta ac and
R. Acharya*ac
ac and
R. Acharya*ac
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5, respectively. The chemical ingredients, calcium carbonate (CaCO3) (>99% pure), strontium carbonate (SrCO3) (>99.9% pure), ammonium dihydrogen phosphate (NH4H2PO4) (>99.5% pure) and ammonium bifluoride (NH4HF2) (>99.999% pure), used for the synthesis were purchased from E Merck, Germany. The salt mixture was taken in an agate mortar and ground thoroughly. Subsequently, the mixture was heated in a stepwise manner at 773 K for 24 h in a platinum crucible, followed by natural cooling to room temperature. Repeated grinding and heating at 973 K for 24 h was carried out till the pure phase compound was formed, as identified by XRD analysis. For the synthesis of NaxEuxCa10−2x(PO4)6F2 (x = 0.5, 1.0, 1.5, and 2.0), CaCO3, NH4H2PO4, NaNO3, Eu2O3, and NH4HF2 (slightly excess above stoichiometry) were mixed thoroughly in an agate mortar in the above stoichiometric ratio with few drops of acetone for homogenization. The mixture was heated at 773 K for 12 h and again ground in mortar pestles with additional heating for 24 h at 1223 K. The products obtained were again ground and stored in desiccators for further characterization. The phase purity of the samples was ascertained by the X-ray diffraction pattern recorded on the Rigaku SmartLab diffractometer using Cu Kα target. The XRD patterns were recorded in the range of 10–80° in a continuous mode with a scan rate of 1° per min.
2.5, respectively. The chemical ingredients, calcium carbonate (CaCO3) (>99% pure), strontium carbonate (SrCO3) (>99.9% pure), ammonium dihydrogen phosphate (NH4H2PO4) (>99.5% pure) and ammonium bifluoride (NH4HF2) (>99.999% pure), used for the synthesis were purchased from E Merck, Germany. The salt mixture was taken in an agate mortar and ground thoroughly. Subsequently, the mixture was heated in a stepwise manner at 773 K for 24 h in a platinum crucible, followed by natural cooling to room temperature. Repeated grinding and heating at 973 K for 24 h was carried out till the pure phase compound was formed, as identified by XRD analysis. For the synthesis of NaxEuxCa10−2x(PO4)6F2 (x = 0.5, 1.0, 1.5, and 2.0), CaCO3, NH4H2PO4, NaNO3, Eu2O3, and NH4HF2 (slightly excess above stoichiometry) were mixed thoroughly in an agate mortar in the above stoichiometric ratio with few drops of acetone for homogenization. The mixture was heated at 773 K for 12 h and again ground in mortar pestles with additional heating for 24 h at 1223 K. The products obtained were again ground and stored in desiccators for further characterization. The phase purity of the samples was ascertained by the X-ray diffraction pattern recorded on the Rigaku SmartLab diffractometer using Cu Kα target. The XRD patterns were recorded in the range of 10–80° in a continuous mode with a scan rate of 1° per min.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 counts (for N) and 12
000 counts (for N) and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (for Ta) counts, respectively, which indicates that the peak area uncertainty of N is less as compared to Ta within the same measurement time. Thus, in addition to Ta, N is a good external current normalizer in the external (in air) PIGE method.
000 (for Ta) counts, respectively, which indicates that the peak area uncertainty of N is less as compared to Ta within the same measurement time. Thus, in addition to Ta, N is a good external current normalizer in the external (in air) PIGE method.