Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The radical scavenging activity of glycozolidol in physiological environments: a quantum chemical study†
Le Trung Hieua,
Mai Van Bayb,
Nguyen Thi Hoac,
Adam Mechler d and
Quan V. Vo
d and
Quan V. Vo *c
*c
aUniversity of Sciences, Hue University, Thua Thien Hue 530000, Vietnam
bThe University of Danang, University of Science and Education, Danang 550000, Vietnam
cThe University of Danang, University of Technology and Education, Danang 550000, Vietnam. E-mail: vvquan@ute.udn.vn
dDepartment of Biochemistry and Chemistry, La Trobe University, Victoria 3086, Australia
First published on 17th November 2022
Abstract
Glycozolidol was isolated from the root of Glycosmis pentaphylla (6-hydroxy-2-methoxy-3-methylcarbazole, GLD). This molecule attracted considerable interest due to its beneficial biological activities that likely stem from its antioxidant activity; yet, the radical scavenging action of GLD has not been investigated thus far. In this study, DFT calculations were used to estimate the radical scavenging activity of GLD against a variety of biologically significant radical species in physiological environments. The findings demonstrated that GLD exerts significant antiradical activity in water at pH = 7.40 and in pentyl ethanoate (as a model of lipidic media) with koverall = 8.23 × 106 and 3.53 × 104 M−1 s−1, respectively. In aqueous solution, the sequential proton-loss electron transfer mechanism made the highest contribution to the activity, whereas in nonpolar solvents the formal hydrogen transfer mechanism dominated the activity. GLD is predicted to have strong antiradical activity against CH3O˙, CH3OO˙, CCl3OO˙, NO2, SO4˙−, DPPH and ABTS+˙ kapp ≈ 109 M−1 s−1 and kf ≈ 106 M−1 s−1. The results suggest that GLD is a good radical scavenger in physiological environments.
1. Introduction
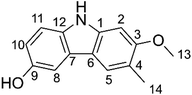
Antioxidants attract considerable interest owing to their roles in important biological processes, and therefore their preferential inclusion in food and pharmaceutical products.1,2 They protect against oxidative deterioration in the body and thus against oxidative stress-induced pathological processes such as cancer, aging, hypo sexuality, hyperlipidemia, cardiovascular disease, inflammation, and many others.1,3,4It is estimated that more than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 individual phytochemicals have been identified in plants, including polysaccharides, phenolics, triterpenoids, steroids, carotenoids, vitamins, essential oils, and alkaloids. Among the great structural diversity of phytochemicals, alkaloid components have attracted considerable attention for known or suspected activity in treating various diseases.4,5 Thus, highly substituted carbazole alkaloids are active against e.g. neurodegenerative diseases, cancer, tuberculosis and Human Immunodeficiency Virus infections.6,7 Among these compounds, glycozolidol (6-hydroxy-2-methoxy-3-methylcarbazole) (Fig. 1) was isolated from the roots of Glycosmis pentaphylla and since confirmed to exert antibacterial (against both Gram-positive and Gram-negative bacteria) and antifungal activities.8,9 Glycozolidol belongs to a class of natural aromatic nitrogen heterocyclic alkaloids. Based on the oxygenation pattern of tricyclic carbazole alkaloids, glycozolidol could provide robust antioxidant activity due to the presence of amine and quinone groups, however, there are no reports on the mechanism and/or kinetics of the radical scavenging activity of glycozolidol. Herein, we explore the effects of solvent environments and molecular structures on the antioxidant activity and oxidation resistance of glycozolidol against a range of free radicals by using thermodynamic and kinetic calculations.
000 individual phytochemicals have been identified in plants, including polysaccharides, phenolics, triterpenoids, steroids, carotenoids, vitamins, essential oils, and alkaloids. Among the great structural diversity of phytochemicals, alkaloid components have attracted considerable attention for known or suspected activity in treating various diseases.4,5 Thus, highly substituted carbazole alkaloids are active against e.g. neurodegenerative diseases, cancer, tuberculosis and Human Immunodeficiency Virus infections.6,7 Among these compounds, glycozolidol (6-hydroxy-2-methoxy-3-methylcarbazole) (Fig. 1) was isolated from the roots of Glycosmis pentaphylla and since confirmed to exert antibacterial (against both Gram-positive and Gram-negative bacteria) and antifungal activities.8,9 Glycozolidol belongs to a class of natural aromatic nitrogen heterocyclic alkaloids. Based on the oxygenation pattern of tricyclic carbazole alkaloids, glycozolidol could provide robust antioxidant activity due to the presence of amine and quinone groups, however, there are no reports on the mechanism and/or kinetics of the radical scavenging activity of glycozolidol. Herein, we explore the effects of solvent environments and molecular structures on the antioxidant activity and oxidation resistance of glycozolidol against a range of free radicals by using thermodynamic and kinetic calculations.
2. Computational details
All density functional theory (DFT) computations in this work were performed with the Gaussian 16 suite of programs10 using the M06-2X functional and the 6-311++G(d,p) basis set.11 The M06-2X functional is one of the most reliable methods for computing the thermodynamics and kinetics of radical reactions.12,13 This method is often used to evaluate the radical scavenging activity of natural and synthesized compounds12,14–17 due to its reliable predictions when compared to experimental data.18–22 The solvent effects of water and pentyl ethanoate were predicted using the SMD technique,23 following a well-established practice in modelling the radical scavenging activity of antioxidants.12,21,24The proton affinity (PA), bond dissociation enthalpy (BDE), and ionization energy (IE) values were calculated as follows.21
| PA = H(GLD−) + H(H+) − H(GLD–H) | (1) |
| BDE = H(GLD˙) + H(H˙) − H(GLD–H) | (2) |
| IE = H(GLD–H+˙) + H(e−) − H(GLD–H) | (3) |
The quantum mechanics-based test for overall free radical scavenging activity (QM-ORSA) protocol20 was used to complete the kinetic calculations. The rate constants (k) were calculated using conventional transition state theory (TST) at 1 M standard state, 298.15 K, following eqn (4).21,25–31
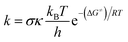 | (4) |
The Marcus theory was used to calculate the reaction barriers of single electron transfer (SET) reactions in media.35,36 The eqn (5) and (6) were used to compute the Gibbs free energy change of reaction ΔG≠ for the SET reaction.
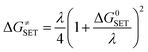 | (5) |
| λ ≈ ΔESET − ΔG0SET | (6) |
For rate constants around the diffusion limit, a modification was made.20 Collins–Kimball theory was used to calculate the apparent rate constants (kapp) for an irreversible bimolecular diffusion-controlled reaction in solvents at 298.15 K,39 and the literature was used to estimate the steady-state Smoluchowski rate constant (kD).20,40
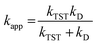 | (7) |
| kD = 4πRABDABNA | (8) |
DAB = DA + DB (denotes the mutual diffusion coefficient of A and B),39,41 where DA or DB is obtained using the Stokes–Einstein formulation eqn (9).42,43
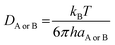 | (9) |
η is the viscosity of the solvents (i.e. η(pentyl ethanoate) = 8.62 × 10−4 Pa s, η(H2O) = 8.91 × 10−4 Pa s) and a is the radius of the solute.
The existence of just one imaginary frequency served as a distinguishing feature across all of the transition stages. Intrinsic coordinate calculations were carried out to ensure that each transition state has an accurate connection to both the pre- and post-complexes.
To avoid over-penalizing entropy losses in solution, Okuno's corrections were applied,44 which were then updated with the free volume theory utilizing the Benson correction.20,45–47
Values for pKa are computed in accordance with Galano et al. pKa = mΔG(BA) + C0, where m and C0 are fitted parameters taken directly from ref. 48 (the M06-2X/6-311++G(d,p) approach), and ΔG(BA) is the difference in Gibbs free energy between the conjugated base (B) and the corresponding acid (A).
3. Results and discussion
3.1 The thermodynamic study
The GLD (GLD–H) can react with free radicals (R˙) via either of the three main pathways:- Formal hydrogen transfer (FHT)21,49,50
| GLD–H + R˙ → GLD˙ + RH | (10) |
- Sequential electron transfer–proton transfer (SETPT)51,52
| GLD–H → GLD–H+˙ + e− | (11) |
| GLD–H+˙ + R− → GLD˙ + RH | (12) |
- Sequential proton loss electron transfer (SPLET)52–55
| GLD–H → GLD− + H+ | (13) |
| GLD− + R˙ → GLD˙ + RH | (14) |
In the initial step, the characteristic thermodynamic parameters (BDE, PA, IE) that define the energy barrier of the first step of each mechanism were calculated for all bonds in the HOO˙ radical scavenging activity of GLD in the gas phase (the standard medium for computational chemistry), in pentyl ethanoate for a lipid medium, and in water at pH 7.4 for an aqueous physiological environment. Table 1 provides an overview of the findings.
| Positions | BDE | PA | IE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| G | P | W | G | P | W | G | P | W | |
| C2–H | 136.7 | 116.0 | 132.0 | 165.2 | 122.1 | 99.2 | |||
| C5–H | 114.4 | 114.9 | 115.3 | ||||||
| C8–H | 115.6 | 116.3 | 129.2 | ||||||
| C10–H | 116.6 | 138.6 | 116.7 | ||||||
| C11–H | 141.9 | 115.9 | 132.8 | ||||||
| C13–H | 99.9 | 101.4 | 101.9 | ||||||
| C14–H | 92.7 | 92.8 | 92.6 | ||||||
| O9–H | 85.2 | 83.1 | 82.8 | 343.6 | 116.2 | 84.7 | |||
| N–H | 91.6 | 92.5 | 90.4 | ||||||
The BDEs ranged from 82.8 to 141.9 kcal mol−1, whereas the PA and IE values were in the range of 84.7–343.6 and 99.2–165.2 kcal mol−1, respectively. The BDE values varied somewhat randomly, while the PAs and IEs reduced in correlation to the dielectric constant of solvents. The lowest BDE of C–H bond was observed at C14–H (BDE = 92.7, 92.8 and 92.6 kcal mol−1 in the gas phase, pentyl ethanoate and water, respectively) that is still higher than BDEs of N–H and O9–H by about 0.3–9.8 kcal mol−1. The lowest BDE was found at the O9–H bond (85.2, 83.1 and 82.8 kcal mol−1 in the gas phase, pentyl ethanoate and water, respectively). The SPLET and SETPT mechanisms are not favorable in the gas phase or pentyl ethanoate solvent due to the higher PA and IE values compared with the BDE(O9–H). Thus it is expected that the O9–H bond will play a dominant role in the radical scavenging activity of GLD following the FHT reaction in all of the studied media; however, in the aqueous solution, the SPLET mechanism may have a major contribution in the radical scavenging activity if the spontaneous dissociation of the acidic protons eliminates the energy barrier of the first step.
The Gibbs free energies of the GLD + HOO˙ reaction following the proton loss (PL-the first step of SPLET), the FHT, and single electron transfer (SET-the first step of SETPT) mechanisms were calculated in order to eliminate pathways that are not spontaneous thermodynamically, and rate constants were only calculated for the spontaneous reactions. The results are shown in Table 2. The results showed that the process was spontaneous only according to the FHT mechanism, especially at the O9–H bond (ΔG0 = −7.3 to −3.6 kcal mol−1). The ΔG0 values of the H-abstraction of the N–H bond were 3.0, 3.7 and 0.1 kcal mol−1 in the gas phase, pentyl ethanoate and water, respectively, while the lowest ΔG0 for the C–H bonds was observed at the C14–H bond with 4.1, 4.8 and 1.7 kcal mol−1 in the gas phase, pentyl ethanoate and water, respectively. The FHT reactions of the other C–H bonds were not spontaneous (ΔG0 = 10.6–53.1 kcal mol−1). Similarly, neither the proton loss nor SET reactions were spontaneous in any of the investigated solvents. Thus, in nonpolar environments the HOO˙ radical scavenging activity follows the FHT pathway, however in polar media such as water at pH = 7.40, the deprotonation of GLD needs also be addressed.
| Positions | FHT | PL | SET | ||||||
|---|---|---|---|---|---|---|---|---|---|
| G | P | W | G | P | W | G | P | W | |
| C2–H | 48.3 | 25.8 | 41.3 | 143.1 | 60.7 | 54.3 | |||
| C5–H | 24.4 | 25.9 | 23.7 | ||||||
| C8–H | 26.5 | 26.5 | 38.6 | ||||||
| C10–H | 27.2 | 51.5 | 25.2 | ||||||
| C11–H | 53.1 | 27.1 | 42.0 | ||||||
| C13–H | 10.9 | 12.9 | 10.6 | ||||||
| C14–H | 4.1 | 4.8 | 1.7 | ||||||
| O9–H | −3.6 | −4.3 | −7.3 | 188.4 | 130.2 | 89.3 | |||
| N–H | 3.0 | 3.7 | 0.1 | ||||||
3.2 The kinetic study
| R2NH2+ ⇆ R2NH + H+ | (15) |
| ROH ⇆ RO− + H+ | (16) |
The computed pKa values for the amine were pKa1 = −2.56 (for the cation form of the N–H bond) and pKa2 = 10.64 (for the O9–H bond). In an aqueous solution with a pH of 7.4, GLD exists in two states: neutral (HA, 99.9%) and anion (A−, 0.1%). As a consequence of this, both states were considered during the kinetic analysis of the HOO˙ radical activity of GLD in water at a pH value of 7.4, whereas in nonpolar media (i.e. the gas phase and pentyl ethanoate) the neutral state was used to compute the rate constants of the HOO˙ + GLD reaction.
| Solv. | Mechanisms | ΔG≠ | κ | kEck | kapp | kfa | koverall | Γ | |
|---|---|---|---|---|---|---|---|---|---|
| a kf = f.kapp; f(A−) = 0.001, f(HA) = 0.999.b The nuclear reorganization energy (λ, in kcal mol−1). | |||||||||
| G | FHT | N–H | 15.8 | 570.5 | 9.64 × 103 | 8.53 × 105 | 1.1 | ||
| O9–H | 12.0 | 82.3 | 8.43 × 105 | 98.9 | |||||
| P | FHT | N–H | 18.8 | 2915 | 2.90 × 102 | 3.53 × 104 | 0.8 | ||
| O9–H | 13.8 | 76.4 | 3.50 × 104 | 99.2 | |||||
| W | SET (A−) | 1.6 | 15.3b | 7.90 × 109 | 7.90 × 106 | 8.23 × 106 | 96.0 | ||
| FHT | N–H | 17.6 | 4218 | 3.04 × 103 | 3.03 × 104 | 0.0 | |||
| (HA) | O9–H | 12.8 | 116.5 | 3.30 × 105 | 3.30 × 105 | 4.0 | |||
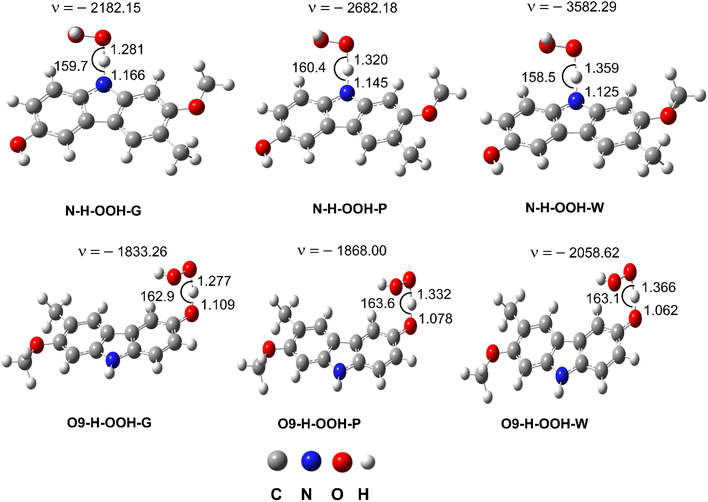 | ||
| Fig. 3 The TS structures of the HOO˙ + GLD reaction following the FHT pathway; imaginary frequencies given in cm−1, bond lengths in Å and bond angles in °. | ||
Nonpolar environments:
| koverall = kapp(FHT(O9–H)-neutral) + kapp(FHT(N–H)-neutral) | (17) |
Water at physiological pH:
| koverall = kf(SET-anion) + kf(FHT(O9–H)-neutral) + kf(FHT(N–H)-neutral) | (18) |
Gas-phase kinetic computations revealed that the HOO˙ antiradical activity of GLD mainly proceeds via H-abstraction of the O9–H bond (k(O9–H) = 8.43 × 105 M−1 s−1, Γ = 98.9%). The contribution of FHT reactions of the N–H bond was negligible (Γ = 1.1%). This is in agreement with thermodynamic data (Table 1). Similar trend was also observed in the lipid medium, H-abstraction at the O9–H bond contributed 99.2% (k(O9–H) = 3.50 × 104 M−1 s−1) to the overall rate constant (koverall = 3.53 × 104 M−1 s−1), whereas, the contribution of the N–H bond was only 0.8% (k(N–H) = 2.90 × 102 M−1 s−1) in the koverall. In aqueous solution, SPLET was the predominant mechanism with kf = 7.90 × 106 M−1 s−1 (ΔG≠ = 1.6 kcal mol−1), however, the FHT reaction of the O9–H and N–H bond still contributed approximately 4.0% of the koverall. Thus in the polar environment the HOO˙ antiradical activity of GLD is roughly 233 times faster than in the lipid environment (koverall = 8.23 × 106 vs. 3.53 × 104 M−1 s−1, respectively). Nevertheless, in the lipid environment the HOO˙ radical scavenging activity of GLD is still higher than that of typical antioxidants such as BHT (koverall = 1.70 × 104 M−1 s−1),14 trolox (koverall = 3.40 × 103 M−1 s−1),19 ascorbic acid (koverall = 5.71 × 103 M−1 s−1),20 or resveratrol (koverall = 1.31 × 104 M−1 s−1).24 In the polar environment, GLD is about 33 and 92 times more active than BHT (koverall = 2.51 × 105 M−1 s−1),14 and trolox (k = 8.96 × 104 M−1 s−1),19 respectively, but less active than ascorbic acid (k = 9.97 × 107 M−1 s−1),20 and resveratrol (k = 5.62 × 107 M−1 s−1).24 Thus GLD is a promising radical scavenger in physiological environments.
3.3 The antiradical activity of GLD against ordinary free radicals in aqueous solution following the SET reaction
Although HOO˙ scavenging activity is a valuable comparative metric, the antiradical activity against different radicals often vary in a broad range. Therefore, the radical scavenging activity of GLD was subsequently modeled against a variety of common free radicals, including HOO˙, CH3OO˙, CCl3OO˙, HO˙, CH3O˙, CCl3O˙, NO, NO2, O2˙−, SO4˙−, N3˙, ABTS+˙ and DPPH. The hydroperoxyl radical scavenging activity of GLD (Γ = 96.0%) is determined by the SET mechanism. Consequently, in this investigation, the antiradical activity against these radicals in water at pH = 7.4 was evaluated using the SET mechanism and the findings are shown in Table 4.| Radicals | ΔG≠ | λ | kD | kapp | kf |
|---|---|---|---|---|---|
| a kf = f.kapp; f(A−) = 0.001. | |||||
| HO˙ | 42.5 | 3.4 | 8.40 × 109 | 4.30 × 10−19 | 4.30 × 10−22 |
| CH3O˙ | 2.1 | 4.5 | 7.90 × 109 | 7.60 × 109 | 7.60 × 106 |
| CCl3O˙ | 24.1 | 21.2 | 7.50 × 109 | 1.30 × 10−5 | 1.30 × 10−8 |
| HOO˙ | 1.6 | 15.3 | 8.10 × 109 | 7.90 × 109 | 7.90 × 106 |
| CH3OO˙ | 2.2 | 14.7 | 8.00 × 109 | 7.60 × 109 | 7.60 × 106 |
| CCl3OO˙ | 1.4 | 16.8 | 7.60 × 109 | 7.50 × 109 | 7.50 × 106 |
| NO | 71.8 | 14.3 | 8.20 × 109 | 1.50 × 10−40 | 1.50 × 10−43 |
| NO2 | 0.0 | 27.7 | 8.00 × 109 | 8.00 × 109 | 8.00 × 106 |
| O2˙− | 36.8 | 17.1 | 8.00 × 109 | 7.10 × 10−15 | 7.10 × 10−18 |
| SO4˙− | 14.1 | 17.6 | 7.70 × 109 | 2.90 × 102 | 2.90 × 10−1 |
| N3˙ | 52.3 | 2.4 | 7.90 × 109 | 3.00 × 10−26 | 3.00 × 10−29 |
| DPPH | 0.8 | 18.8 | 7.40 × 109 | 7.40 × 109 | 7.40 × 106 |
| ABTS˙+ | 0.0 | 11.8 | 7.40 × 109 | 7.40 × 109 | 7.40 × 106 |
GLD should have high activity against CH3O˙, CH3OO˙, CCl3OO˙, NO2, SO4˙−, DPPH and ABTS+˙ radicals with kapp ≈ 109 M−1 s−1 and kf ≈106 M−1 s−1, whereas NO, O2˙− HO˙, CCl3O˙, and N3˙ radicals cannot be eliminated by GLD under the studied conditions. By the SET reaction, GLD is less active against CCl3O˙, and N3˙ radicals than fraxin55 or usnic acid,56 but more effective against HOO˙ and CH3OO˙ radicals. For HO˙, however, the prediction of low activity suggests that SET is not the correct mechanism; highly reactive radicals are known to follow alternative pathways (FHT or radical adduct formation to the neutral species) that for these radicals are essentially barrierless in aqueous media. Thus our results also highlight the limits of generalizations from one detailed study.50
4. Conclusion
The antiradical activity of GLD against HOO˙, CH3OO˙, CCl3OO˙, HO˙, CH3O˙, CCl3O˙, NO, NO2, O2˙−, SO4˙−, N3˙, ABTS˙+ and DPPH was studied using DFT calculations. In the physiological environments GLD exhibited significant antiradical activity. The overall rate constants for the antiradical trapping of GLD in water at pH = 7.40 and pentyl ethanoate were koverall = 8.23 × 106 and 3.53 × 104 M−1 s−1, respectively. The SPLET mechanism made contributions to the activity in water at pH 7.40, however, the FHT mechanism characterized the activity in nonpolar solvents. Additionally, it was found that GLD has strong antiradical activity against CH3O˙, CH3OO˙, CCl3OO˙, NO2, SO4˙−, DPPH and ABTS+˙ kapp ≈ 109 M−1 s−1 and kf ≈ 106 M−1 s−1. According to the computed results, GLD is more effective at trapping HOO· than reference antioxidants like trolox and BHT in the physiological environment. The results suggest that GLD can join the long list of phytochemicals with good radical scavenging activity in physiological environments, emphasizing yet again the importance of varied plant sources in diets and in dietary supplements to maintain health and prevent disease.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by Funds for Science and Technology Development of the University of Danang under project number B2020-DN03-47 (M. V. B.)References
- A. Bensid, N. El Abed, A. Houicher, J. M. Regenstein and F. Özogul, Crit. Rev. Food Sci. Nutr., 2022, 62, 2985–3001 CrossRef CAS PubMed.
- C. Nirmala, M. S. Bisht, H. K. Bajwa and O. Santosh, Trends Food Sci. Technol., 2018, 77, 91–99 CrossRef CAS.
- İ. Gulcin, Arch. Toxicol., 2020, 94, 651–715 CrossRef PubMed.
- L. Khandokar, M. S. Bari, V. Seidel and M. A. Haque, J. Ethnopharmacol., 2021, 278, 114313 CrossRef CAS PubMed.
- P. K. Teja, P. Patel, D. Bhavsar, C. Bindusri, K. Jadhav and S. K. Chauthe, Phytochemistry, 2021, 190, 112865 CrossRef CAS PubMed.
- M. A. Tan, N. Sharma and S. S. A. An, Antioxidants, 2022, 11, 493 CrossRef CAS PubMed.
- R. S. Ramsewak, M. G. Nair, G. M. Strasburg, D. L. DeWitt and J. L. Nitiss, J. Agric. Food Chem., 1999, 47, 444–447 CrossRef CAS PubMed.
- P. Bhattacharyya, P. Chakrabartty and B. Chowdhury, Phytochemistry, 1985, 24, 882–883 CrossRef CAS.
- H. Greger, O. Hofer, H. Kählig and G. Wurz, Tetrahedron, 1992, 48, 1209–1218 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, G. Z. J. Bloino, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2014, 35, 2019–2026 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2008, 112, 1095–1099 CrossRef CAS PubMed.
- H. Boulebd, Int. J. Chem. Kinet., 2021, 1–8 Search PubMed.
- H. Boulebd, D. M. Pereira, I. A. Khodja, N. T. Hoa, A. Mechler and Q. V. Vo, J. Mol. Liq., 2022, 346, 118277 CrossRef CAS.
- M. Carreon-Gonzalez, A. Vivier-Bunge and J. R. Alvarez-Idaboy, J. Comput. Chem., 2019, 40, 2103–2110 CrossRef CAS PubMed.
- Q. V. Vo, N. T. Hoa, P. C. Nam, D. T. Quang and A. Mechler, ACS Omega, 2020, 5, 24106–24110 CrossRef CAS PubMed.
- J. R. l. Alvarez-Idaboy and A. Galano, J. Phys. Chem. B, 2012, 116, 9316–9325 CrossRef CAS PubMed.
- M. E. Alberto, N. Russo, A. Grand and A. Galano, Phys. Chem. Chem. Phys., 2013, 15, 4642–4650 RSC.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2013, 34, 2430–2445 CrossRef CAS PubMed.
- H. Boulebd, A. Mechler, N. T. Hoa and Q. V. Vo, New J. Chem., 2020, 44, 9863–9869 RSC.
- Q. V. Vo, N. T. Hoa and A. Mechler, Polym. Degrad. Stab., 2021, 185, 109483 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- C. Iuga, J. R. l. Alvarez-Idaboy and N. Russo, J. Org. Chem., 2012, 77, 3868–3877 CrossRef CAS PubMed.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- D. G. Truhlar, W. L. Hase and J. T. Hynes, J. Phys. Chem. A, 1983, 87, 2664–2682 CrossRef CAS.
- T. Furuncuoglu, I. Ugur, I. Degirmenci and V. Aviyente, Macromolecules, 2010, 43, 1823–1835 CrossRef CAS.
- E. Vélez, J. Quijano, R. Notario, E. Pabón, J. Murillo, J. Leal, E. Zapata and G. Alarcón, J. Phys. Org. Chem., 2009, 22, 971–977 CrossRef.
- E. Dzib, J. L. Cabellos, F. Ortíz-Chi, S. Pan, A. Galano and G. Merino, Int. J. Quantum Chem., 2019, 119, e25686 CrossRef.
- E. Dzib, J. L. Cabellos, F. Ortiz-Chi, S. Pan, A. Galano and G. Merino, Eyringpy 1.0.2, Cinvestav, 2018, Mérida, Yucatán Search PubMed.
- E. Pollak and P. Pechukas, J. Am. Chem. Soc., 1978, 100, 2984–2991 CrossRef CAS.
- A. Fernández-Ramos, B. A. Ellingson, R. Meana-Pañeda, J. M. Marques and D. G. Truhlar, Theor. Chem. Acc., 2007, 118, 813–826 Search PubMed.
- C. Eckart, Phys. Rev., 1930, 35, 1303 CrossRef CAS.
- R. A. Marcus, Annu. Rev. Phys. Chem., 1964, 15, 155–196 CrossRef CAS.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599 CrossRef CAS.
- S. F. Nelsen, S. C. Blackstock and Y. Kim, J. Am. Chem. Soc., 1987, 109, 677–682 CrossRef CAS.
- S. F. Nelsen, M. N. Weaver, Y. Luo, J. R. Pladziewicz, L. K. Ausman, T. L. Jentzsch and J. J. O'Konek, J. Phys. Chem. A, 2006, 110, 11665–11676 CrossRef CAS PubMed.
- F. C. Collins and G. E. Kimball, J. Colloid Sci., 1949, 4, 425–437 CrossRef CAS.
- M. Von Smoluchowski, Z. Phys. Chem., 1917, 92, 129–168 CAS.
- D. G. Truhlar, J. Chem. Educ., 1985, 62, 104 CrossRef CAS.
- A. Einstein, Ann. Phys., 1905, 17, 549–560 CrossRef CAS.
- G. G. Stokes, Mathematical and Physical Papers, University Press, Cambridge, 1905 Search PubMed.
- Y. Okuno, Chem.–Eur. J., 1997, 3, 212–218 CrossRef CAS PubMed.
- S. Benson, The Foundations Of Chemical Kinetics, Malabar, Florida, 1982 Search PubMed.
- C. Iuga, J. R. Alvarez-Idaboy and A. Vivier-Bunge, J. Phys. Chem. B, 2011, 115, 12234–12246 CrossRef CAS PubMed.
- J. R. Alvarez-Idaboy, L. Reyes and N. Mora-Diez, Org. Biomol. Chem., 2007, 5, 3682–3689 RSC.
- A. Galano, A. Pérez-González, R. Castañeda-Arriaga, L. Muñoz-Rugeles, G. Mendoza-Sarmiento, A. Romero-Silva, A. Ibarra-Escutia, A. M. Rebollar-Zepeda, J. R. León-Carmona, M. A. Hernández-Olivares and J. R. Alvarez-Idaboy, J. Chem. Inf. Model., 2016, 56, 1714–1724 CrossRef CAS PubMed.
- A. Galano and J. Raúl Alvarez-Idaboy, Int. J. Quantum Chem., 2019, 119, e25665 CrossRef.
- Q. V. Vo, M. V. Bay, P. C. Nam, D. T. Quang, M. Flavel, N. T. Hoa and A. Mechler, J. Org. Chem., 2020, 85, 15514–15520 CrossRef CAS PubMed.
- K. U. Ingold and D. A. Pratt, Chem. Rev., 2014, 114, 9022–9046 CrossRef CAS PubMed.
- A. Galano, G. Mazzone, R. Alvarez-Diduk, T. Marino, J. R. Alvarez-Idaboy and N. Russo, Annu. Rev. Food Sci. Technol., 2016, 7, 335–352 CrossRef CAS PubMed.
- G. Wang, Y. Xue, L. An, Y. Zheng, Y. Dou, L. Zhang and Y. Liu, Food Chem., 2015, 171, 89–97 CrossRef CAS PubMed.
- L. Estévez, N. Otero and R. A. Mosquera, J. Phys. Chem. B, 2010, 114, 9706–9712 CrossRef PubMed.
- P. C. Nam, N. M. Thong, N. T. Hoa, D. T. Quang, L. P. Hoang, A. Mechler and Q. V. Vo, RSC Adv., 2021, 11, 14269–14275 RSC.
- N. T. Hoa, M. Van Bay, A. Mechler and Q. V. Vo, ACS Omega, 2020, 5, 17715–17720 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra05907j |
| This journal is © The Royal Society of Chemistry 2022 |