Open Access Article
Open Access ArticleA broad range and piezoresistive flexible pressure sensor based on carbon nanotube network dip-coated porous elastomer sponge†
Yuyang Caia,
Linpeng Liu *a,
Xiancun Mengb,
Jingxiang Wangb,
Changchao Zhangb,
Jianhao Li
*a,
Xiancun Mengb,
Jingxiang Wangb,
Changchao Zhangb,
Jianhao Li b,
Zhilai Lua and
Ji-an Duan
b,
Zhilai Lua and
Ji-an Duan a
a
aThe State Key Laboratory of High Performance and Complex Manufacturing, College of Mechanical and Electrical Engineering, Central South University, Changsha 410012, China. E-mail: linpengliu@csu.edu.cn
bKey Laboratory of Bionic Engineering, Ministry of Education, Jilin University, Changchun 130022, China
First published on 29th November 2022
Abstract
Flexible pressure sensors have provided an attractive option for potential applications in wearable fields like human motion monitoring or human–machine interfaces. For the development of flexible pressure sensors, achieving high performance or multifunctions are popular research tendencies in recent years, such as improving their sensitivity, working range, or stability. Sponge materials with porous structures have been demonstrated that they are one of the potential substrates for developing novel and excellent flexible pressure sensors. However, for sponge-based pressure sensors, it is still a great challenge to realize a wide range of pressures from Pa level to hundreds kPa level. And how to achieve mechanical robustness remains unsolved. Here, we develop a flexible pressure sensor based on multicarbon nanotubes (MWCNTs) network-coated porous elastomer sponge with a broad range and robust features for use in wearable applications. Specifically, polyurethane (PU) sponge is used as the substrate matrix while dip-coated PU/MWCNTs composites as a conductive layer, achieving a highly bonding effect between the substrate and the conductive material, hence a great mechanical robust advantage is obtained and the working range also is improved. The pressure sensor show range of up to 350 kPa, while the minimum detection threshold is as low as 150 Pa. And before and after rolling by a bicycle or electric motorcycle, the sensor has the almost same responses, exhibiting great robustness.
Introduction
Pressure sensors are one of the main components of mechanical sensors, which matters a lot in a variety of applications like pressure measurement in flow fields, weighing measurement and surgical treatment fields.1–6 Over the last decade, flexible pressure sensors are often reported due to their capability in applications on not only planes but also curved surfaces and other advantages like high sensitivity and low cost when compared with traditional silicon-based MEMS pressure sensors. Recently, most developed flexible pressure sensors focus on wearable fields, such as electronic skin, human motion monitoring and human–machine interfaces.7–12 In general, pressure sensors are divided into types including piezoresistive,13,14 capacitive,8,15 piezoelectric,16,17 triboelectric18,19 and other ones,20,21 while piezoresistive pressure sensors show great merits like high sensitivity to both pressure and deformation, simple working mechanism and design, easy signal collection and so on. External mechanical signals like pressures or strains will be transducing into internal resistance change and then it can be detectable in the forms of current or even voltage.It is known that performance indexes determine the pros and cons of the sensor. Among the performance parameters, sensitivity, working range and stability always matter much.22–24 Sensitivity affects the accuracy of sensors to some extent while the working range determines the working conditions in which the sensor can be used. And stability is also important because it influences the service life and reliability. However, sensitivity typically has a contradictory relationship with working range and stability. In other words, sensors with high sensitivity usually have a narrow working range and low stability, and vice versa. For example, Chen et al. developed a planar structured pressure sensor without size restrictions of a dielectric layer, which shows an equivalent sensitivity of 3.75 × 105 kPa−1 in the range of 0–0.05 Pa, and its working range is 0.1 Pa.25 Li et al. designed a coplanar pressure sensor with sharp micro pyramids and a short-channel coplanar device structure that exhibits an ultrahigh sensitivity near 2000 kPa−1 in the range of 0–100 Pa, while its working range reaches up to 1 kPa.26 Therefore, how to develop flexible pressure sensors with high sensitivity, wide working range and excellent stability remain a great challenge. Basically, sensitivity, working range and stability of sensors depend on the micro/nanostructures that responded to external stimuli and the electromechanical signal conversion capability of constituent materials.23,27,28 For example, micro/nanostructures like cracks,29,30 wrinkles,31,32 pyramids33,34 and domes35,36 could be popularly found in flexible pressure sensors which have a positive impact in realizing ultrahigh sensitivity. And sensing functional materials like MXene, Ag/Au/Cu nanowires, graphene are also frequently employed to develop pressure sensors with high sensitivity,37–40 which are well known that they are much expensive. Although these structures indeed improve sensors' sensitivity, they have a negative influence in stability. Because cracks are a kind of destructive structure that can easily be extended, while pyramids and domes are fabricated on surfaces to assemble with other surfaces (like interdigital electrodes) to form sensors with double or multilayers which exist interlaminar gaps, leading to low stability and poor reliability.
However, porous structures can solve the problem of destructive extension and interlayer gaps, which has stronger structural deformation stability, leading to a more sensitive ability to external mechanical signals.41–44 Herein, we use a polyurethane (PU) sponge as the basic framework of the pressure sensor, and a layer of PU/MWCNTs overlaid the framework by a dip-coated method. Due to the mixed solution containing polymer material of PU that is the same as the sponge, hence the coated PU/CNTs layer has a very strong bonding effect with the porous network, which enhances the stability and robustness of sensors greatly. The fabricating procedure of the sponge-based pressure sensor is simple, other advantages like low cost and capability of mass production are obvious. The pressure sensor is demonstrated that it has a wide working range up to 350 kPa, and a sensitivity of ∼0.125% kPa−1 within 200 kPa, a sensitivity of ∼0.017% kPa−1 in the range of 200 to 350 kPa. The minimum detection threshold of the sensor to pressures is as low as 150 Pa. And a cycling test over 5000 times shows that the sensor also has great stability. The sponge-based pressure sensor can be used to monitor human motions like walking, jumping, or finger touching. When the sensor is rolled by a bicycle or motorcycle, the sensor behaviors almost the same under pressures, exhibiting great robustness to large mechanical stimulus.
Experimental
Materials
Polyurethane sponge (40 ppi) with a height of 10 mm was bought from Kunshan Shangte New Material Co. LTD, China. MWCNTs with a purity of >95 wt% (ID: 3–5 nm, OD: 8–15 nm, length: 3–12 μm) were purchased from TANFENG Graphene Technology Co., LTD, China. Aqueous polyurethane dispersion with a concentration of 30% and density of 1.04 g cm−3 bought from ZhengMeiSuJiao Co., LTD, China, was used as the dispersion matrix of MWCNTs.Preparation of the pressure sensor
First, the polyurethane sponge was cut into a size of 20 mm in length and 20 mm in width by laser cutting. Then the MWCNTs and aqueous polyurethane dispersion were mixed at a weight ratio of 6%, followed by an ultrasonic oscillating process lasting around 30 min and a continuous magnetic stirring process for 4 h, to make the CNTs disperse uniformly in the polyurethane matrix. Subsequently, the PU foam sample was immersed in the mixed solution to make the PU/CNTs materials adhere to the foam network. The sample was then dried at room temperature after being taken out. Ag paste and conductive copper foil tape were used to insert electrodes at the top and bottom of PU foam sample respectively, and PET tapes were also employed as the package of the pressure sensor.Characterization
The cross-sectional morphology of the foam-based pressure sensor was carefully observed by super-depth-of-field microscope (VH-5000, KEYENCE). A positioning-controlled electric linear stage was used to apply pressure to the sensor for basic performance tests. A multimeter (DMM6500, Agilent) was used to measure the real-time resistance of the pressure sensor. A strain gauge (HP-1 kN, Handpi Instruments) was used to measure the applied mechanical force to the pressure sensor.Results and discussion
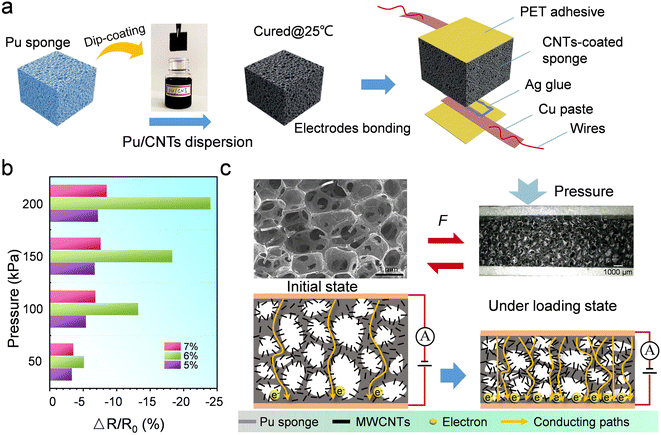
Fig. 1a shows a schematic illustration of the overall fabrication procedures of a flexible resistive pressure sensor, which is composed of a CNT network-coated porous foam and two up and bottom electrodes. Specifically, a polyurethane sponge with a porous density of 40 ppi and a thickness of 10 mm was used as the deformation bulk when suffering from external pressures, while a mixture consisting of aqueous polyurethane solution and multi-carbon nanotubes was prepared as the sensitive functional materials to convert mechanical stimuli to electric signals. Since the sponge and the conductive solution has the same polymer molecular material of PU, thus the PU/CNTs layer would be coated well on the framework of PU sponge, namely, there is hard to occur separation between PU and PU/CNTs layer. After the PU sponge was immersed in the uniformed PU/CNTs solution for 5 min, another drying process under room temperature was followed to cure the PU/CNTs layer. Then, Ag glue, Cu paste, wires and PET tape were used to make the up and bottom electrodes.Different carbon concentrations may cause distinct sensitivity of the pressure sensor. Comparative experiments of pressure sensors with a different mass ratio of CNTs in the PU/CNTs solution (including 5%, 6%, and 7%) have been conducted to select the appropriate ratio to prepare the pressure sensor. Results show that the pressure sensors with a CNTs mass ratio of 6% have a higher relative resistance change (ΔR/R0) than pressure sensors with other mass ratios while the applied pressure is 50 kPa, 100 kPa, 150 kPa, 200 kPa, respectively, exhibiting a more excellent pressure sensing sensitivity (Fig. 1b). Thus, the pressure sensor is further prepared after the mass ratio of CNTs to PU is determined to be 6%. The initial resistance of the fabricated sensor with a CNTs to PU ratio of 6% averages at ∼220 Ω, as shown in Fig. S1.†
The working mechanism of the pressure sensor is shown in Fig. 1c. Firstly, surface and side morphology characterization is conducted by using scanning electron microscope. Porous structures can be clearly observed, showing regular shapes with almost consistant size in skeleton units (Fig. S2†). Many holes are distributed in the direction of the cross-section of the pressure sensor after the PU/CNTs layer is coated. When the pressure sensor is suffered from pressure, the sensor exhibits a compressive deformation, that is to say, a decreasing phenomenon in the height of the pressure sensor occurs, as shown in the optical image in Fig. 1c. During this deformation, the distance between adjacent CNTs changes so that the resistance of the pressure sensor varies too. It is well known that the CNTs are a kind of conductive material with a high aspect ratio tubular shape, hence the distribution pattern of the CNTs embedded in the sponge-based pressure sensor can be divided into two types. One is the CNTs totally embedded in the PU matrix without terminals exposure, and the other is the CNTs distributed along the edges of holes with one terminal inserted into the PU matrix and the other suspended in the hole, just like a cantilever. Therefore, when external pressure applied to the pressure sensor, the distances between CNTs that totally embedded in the PU matrix would be decrease and some of them trigger electron tunneling effect. However, due to the compressive deformation of the holes, the suspended CNTs that are distributed along the edges of the holes trend to close to each other until contact once the applied pressure exceeds a certain threshold. Basically, holes within the sponge-based pressure sensor have a negative impact on the motion of electrons, forming obstacles to the conducting paths. As the pressure is applied, more conducting paths form due to the tunneling effect and the contact of suspended CNTs, resulting in a decrease in the resistance of the sponge-based pressure sensor. And to some extent, the more the pressure applies, the more conducting paths form.
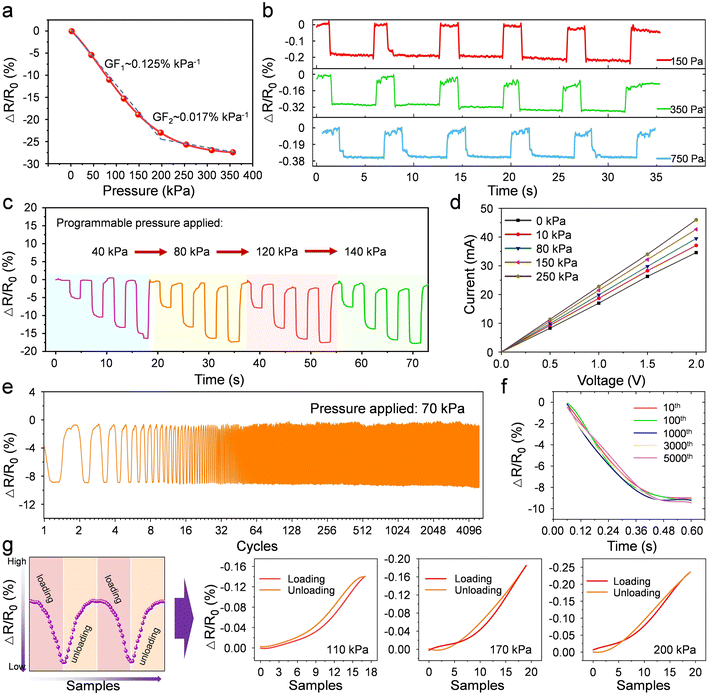
Then the sensing performance of the sponge-based pressure sensor is tested. First of all, the sensing sensitivity of the pressure sensor is measured. A homemade device with a controllable stepper motor and force gauge is used to apply pressure to the sensor. Fig. 2a shows a nonlinear relationship between the relative resistance change and the applied pressure. Therefore, the calculation of the sensitivity of the pressure sensor is finished by using a linear fitting method in two segments. Specifically, when the pressure is lower than 200 kPa, the relative resistance increases with the pressure with a sensitivity of ∼0.125% kPa−1, while a sensitivity of ∼0.017% kPa−1 is obtained in the pressure range from 200 kPa to 350 kPa. The result shows that the sponge-based pressure sensor has a wide working range up to ∼350 kPa, which is higher than some reported sponge-based pressure sensors (Table S1†).
Normally, pressure sensors with wide working range are always not sensitive to external tiny stimuli. But the pressure sensor developed here could be responded to small load as low as 150 Pa. As shown in Fig. 2b, the sponge-based pressure sensor has a relative resistance change of ∼−0.2% when a pressure of 150 Pa was applied. Once the applied pressure increases to 350 Pa or 750 Pa, the relative resistance change of sensor corresponds to ∼−0.32% and ∼−0.38%, respectively, which shows that the sensor has a great response to tiny pressure stimuli. Then the response of the pressure sensor under a cycling step pressure loading (including 4 sub-steps: from 0 to 40 kPa, 40 to 80 kPa, 80 to 120 kPa, 120 to 140 kPa) is tested (Fig. 2c). The result shows that the sensor has an obvious step response to the step load, and the peak level under each sub-step load exhibits regular decrease trends as prediction, that is to say, the absolute value of the relative resistance change (ΔR/R0) increases when the applied pressure grows. Generally, stability is another one of the most important performance indexes except sensitivity for developing sensors, since it determines reliability and calibration interval if they are put into practical applications. Based on this, the stability of the sponge-based pressure sensor is evaluated. First of all, the stability of the real-time resistance of the sensor is assessed by using a volt–ampere characteristic test method. When a constant load of 0 kPa, 10 kPa, 80 kPa, 150 kPa and 250 kPa is applied to the sensor respectively, the resistance of the sensor keeps stable due to a linear relationship between the voltage and the current (Fig. 2d). It means that no matter how much load is applied, the real-time resistance output of the sensor would keep stable, without significant resistance drift. And the result of the sensor under cycling loading–unloading test also matches that conclusion, as shown in Fig. 2e.
When a load of 70 kPa is applied to the sensor, after ∼5000 cycles, no obvious change in signal amplitude is observed, exhibiting that the sensor has great stability when it is used repeatedly under a fixed working condition. Also, there is no obvious change in the real-time resistance signal waveform. As Fig. 2f shows, the curves corresponding to the stages of pressure unloading at the 10th, 100th, 1000th, 3000th, 5000th cycles are extracted, to illustrate that the waveforms always keep samely. Besides, we further observe the resistance change plots that reflect the sensor's electric signals under different cycling pressures. And we extract one loading–unloading cycle arbitrarily among the cycling tests under applied pressures of 110 kPa, 170 kPa and 200 kPa, respectively, to evaluate the loading-response and unloading-recovery of the sensors. The collecting samples vs. relative-resistance-change plots corresponding to loading and unloading show that the loading plot coincides well with the unloading plot (Fig. 2g), while slight space exists which may contribute to the difference between response and recovery time of sensors.
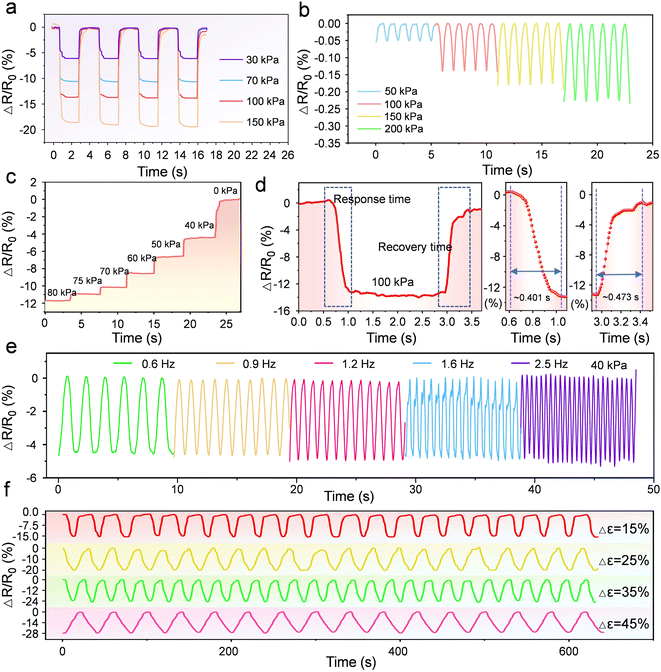
Fig. 3 shows the results of the sensor to dynamic stimuli. Cycling tests of the sponge-based pressure sensor under a pressure of 30 kPa, 70 kPa, 100 kPa, 150 kPa respectively with a same loading frequency of 0.5 Hz, are conducted (Fig. 3a). It should be noted that the process of the experiment is to apply a certain load to the pressure sensor by controlling the stepper motor at a certain speed and then maintaining the load unchanged before removing the load. It could be observed that the corresponding curves overlapped well in terms of the jumping and climbing stages, except for the levels of the peak values. In the maintaining period of the peak load, the curve relating to the relative resistance change of the sensor also keeps almost horizontal, which matches well with the previous conclusion that the sensor has great stability considering the real-time resistance of the sensor under constant pressure. However, if the applied load is removed immediately from the pressure sensors without any remaining time, the real-time signal waveform of the sensor would exhibit a triangular wave pattern, rather than an inverted trapezoidal shape. As shown in Fig. 3b, the curves illustrate the corresponding relative resistance change under different loads including 50 kPa, 100 kPa, 150 kPa and 200 kPa. There is a ∼−0.05% of relative resistance change when a 50 kPa of pressure is applied to the sensor, while a ∼−0.14% of relative resistance change when applied with 100 kPa pressure. There is a decrease of ∼0.09% for the relative resistance change of sensor when the applied pressure grows from 50 kPa to 100 kPa. However, when the applied pressure increases from 100 kPa to 150 kPa, the ΔR/R0 of sensor has a drop of ∼−0.04%. As the applied pressure increases up to 200 kPa, the ΔR/R0 of sensor has a drop of ∼−0.04% too. It demonstrates that with the increase of load, the varying rate of the relative resistance change of the sensor shows a trend of increasing fastly and then slowing down, which is consistent with the sensitivity characterization result in Fig. 2a.
Besides, a decreasing step load from 80 kPa to 0 kPa is also applied to the sponge-based pressure sensor. Fig. 3c reflects the response of the sensor, also showing a step change characteristic. And it could be observed that the heights of the steps increase as the applied pressure decreases. It is known that response and recovery speed are other important sensing parameters for flexible sensors, which are mainly determined by the composed viscoelastic materials and the architectures of sensors.45 For example, flexible polymer materials like PDMS, ecoflex always endow sensors with low response and recovery speed due to their high viscosity and stickiness. Accordingly, we measured the response time and recovery time of the sensor by applying, holding, and removing a pressure of ∼100 kPa to the sensor (Fig. 3d). The results are measured to be ∼0.401 s for the response time and ∼0.473 s for the recovery time. The sensor's response to dynamic stimuli with different frequencies also matters when evaluating newly developed sensors because the frequency response range judges the application scenarios of sensors. For example, mechanical sensors with a wide frequency range up to kHz level could be used to monitor vibrations generated in rotating machinery with high speed like engines or other objects like rails, whereas sensors with a narrow frequency range lower to several Hz level are inappropriate in the above fields but could be used in wearable applications. Fig. 3e shows the responses of sensor under a pressure of 40 kPa with a frequency of 0.6 Hz, 0.9 Hz, 1.2 Hz, 1.6 Hz, 2.5 Hz, respectively. It can be concluded that the sensor has similar output peak levels under the load with different frequencies, demonstrating that there is no distortion in the output signals when the frequency increases. Also, the highest frequency the pressure sensor can be sensed is explored too. As shown in Fig. S3,† when a pressure with a frequency of 200 Hz is applied to the sensor, the response of the sensor is then recorded. After FFT process, the relationship between frequency and amplitude shows that the frequency corresponding to the peak value is 200 Hz too, which means that the sensor has a bandwidth of 200 Hz. However, when the applied frequency increased, the sensor could not recognize the input signal after FFT anymore. Finally, we used the comparative strains to replace the applied load, to evaluate the sponge-based sensor's responses. As we illustrated before, the intrinsic working mechanism is that the sensor deforms with compressive strain when pressure is applied to the sensor. Therefore, the responses of the sensor under different compressive strains were recorded. As Fig. 3f shows, when the compressive strain is 15%, the relative resistance change is ∼−15%. Once the compressive strain increases to 45%, the relative resistance change grows up to ∼−28%, which means that the height of the sponge-based sensor is almost compressed half to ∼5 mm.
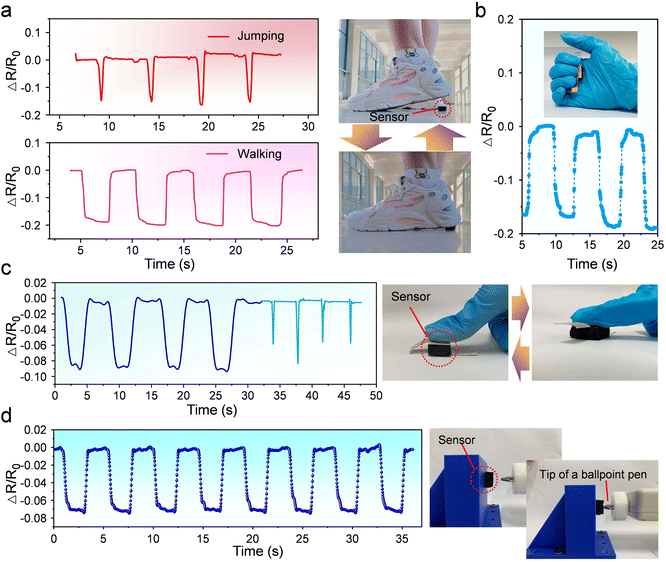
Then comes to characterization of practical wearable applications for the sponge-based pressure sensor. Flexible pressure sensors are often reported to be used to monitor human's gait. As Fig. 4a shows, an adult volunteer performed motions including jumping and walking to simulate daily activities. When the volunteer jumps, the fixed pressure sensor is in contact with heel for a very short time. In other words, an instantaneous load is applied to the pressure sensor and removed quickly. Therefore, triangle-shaped signal waves can be observed when the volunteer is in a jumping mode, while inverted trapezoidal-shaped signal waves correspond to normal walking motions (Fig. 4a).
Besides, the pressure sensor is also used to monitor making a fist behavior. The images inserted in Fig. 4b shows that the sensor is fixed in the position of nearly the center of palm of hand. Once making a fist, fingers press the pressure sensor, resulting in a compressive load to it. When fingers release from it, the compressed sensor would be recovered. Therefore, the change of resistance is first decreasing and then increasing (Fig. 4b). Aside from that, the sponge-based pressure sensor is also used to monitor fingers' motions. Similarly, in terms of the responding curves of the sensor, there are significant differences between pressing and clicking the pressure sensor with finger (Fig. 4c). More sharp troughs can be seen while finger clicks the sensor than when pressing the sensor. The above experiments are finished have a common feature that the surface area of the object which applied forces to sensor is greater than or approximately that of the upper surface area of the sensor. It leads to a phenomenon that the entire surface of the pressure sensor is shifted downward a certain distance, similarly to the deformation of a spring under load. However, sometimes a point-like load might be applied to the sensor, whose contact area is much smaller than the upper surface area of the sensor. It would surprise few to imagine that the position where point load is applied has the most serious invagination, and the concave degree of other positions is centered at this position and gradually decreases outward. Different forms of applied forces might influence the response of pressure sensor. Hence, we carried out a test by using a tip of a ballpoint pen as applying object to press the sensor regularly. Concretely, the tip of a ballpoint pen is installed in the front end of the push rod of the force gauge, and the force gauge is fixed on the top of a stepper motor. When the stepper motor is controlled to do a linear reciprocating motion, the tip of a ballpoint pen applied load to the sensor. The recorded result of the sensor's response is shown in Fig. 4d, regular curves are observed which demonstrates that the pressure sensor responds well to point-like loads too.
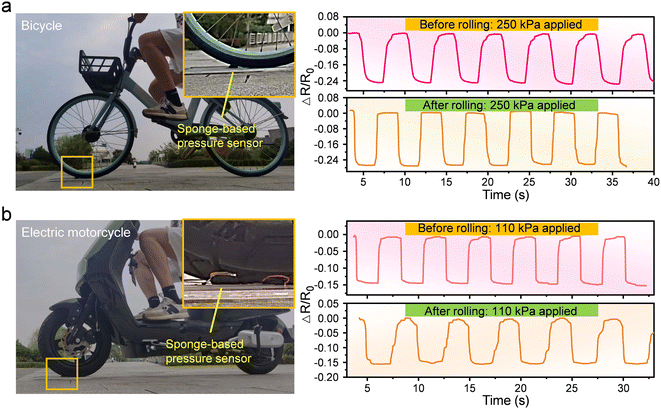
Since the dip-coated conductive composites have polymer material of PU that is the same as the sponge substrate, so the coated layer has strong adhesion to the porous sponge which leads to great stability and robustness theoretically. To demonstrate that, the sponge-based pressure sensor was rolled by bicycle and electric motorcycle respectively, and then compared the sensor's response rolled before and after under a certain pressure. As shown in Fig. 5a, the sensor was first tested its response by applying a cycling pressure of 250 kPa, and the data plot in the upper right corner of Fig. 5a shows that the sensor has regular fluctuation and a peak value of ∼−0.24 in relative resistance change. After the sensor was fixed on the ground and followed by being rolled by a bicycle with a volunteer (∼65 kg) on, the sensor was then applied a cycling pressure of 250 kPa again after a rest time of ∼5 min, to record its real-time response. As the data plot in the lower right corner of Fig. 5a shows, the sensor still exhibits regular fluctuation and has a peak value of ∼−0.24 in relative resistance change. Similarly, when the sponge-based pressure sensor was rolled by an electric motorcycle with an adult volunteer on, the sensor displays a same peak value of ∼−0.15 in relative resistance change which is consistent with the response before rolling under an applied cycling pressure of 110 kPa (Fig. 5b). Accordingly, the sponge-based pressure sensor has great stability and exhibits well robustness.
Conclusions
In summary, we report an efficient and low-cost dip-coating methodology for fabricating flexible piezoresistive sponge-based pressure sensor. In virtue of the porous structures, the sensitivity can be improved due to the great change of conductive paths under external stimulus. The sensor could sense a minimum applied pressure of 150 Pa, while its maximum reaches up to 350 kPa. Specifically, the sensor shows a sensitivity of ∼0.125% kPa−1 within 200 kPa, a sensitivity of ∼0.017% kPa−1 in the range of 200 to 350 kPa. Contributing to the same material used in sponge substrates and conductive composites, the sensor has great robustness and a broad working range. Thus, the sensor can not only resist the crushing of a bicycle but also a motorcycle, while monitoring human motions like walking, jumping, or finger touching is also its potential application.Author contributions
Y. C. and L. L. designed the experiments. Y. C. and L. L. performed the experiments. X. M., C. Z. and J. L. helped with data analysis. L. L. and J. D. wrote the manuscript.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 52205320), National Postdoctoral Program for Innovative Talents (BX20220353), China Postdoctoral Science Foundation (No. 2021M703632), and supported by Opening Project of the Key Laboratory of Bionic Engineering (Ministry of Education), Jilin University (No. K200202).Notes and references
- J. Zhang, Y. Zhang, Y. Li and P. Wang, Polym. Rev., 2022, 62, 65–94 CrossRef CAS.
- O. Gul, K. Kim, J. Gu, J. Choi, D. Del Orbe Henriquez, J. Ahn and I. Park, ACS Appl. Electron. Mater., 2021, 3, 4027–4036 CrossRef CAS.
- Y. Jeong, J. Park, J. Lee, K. Kim and I. Park, ACS Sens., 2020, 5, 481–489 CrossRef CAS PubMed.
- Z. Luo, X. Hu, X. Tian, C. Luo, H. Xu, Q. Li, Q. Li, J. Zhang, F. Qiao, X. Wu, V. Borisenko and J. Chu, Sensors, 2019, 19, 1250 CrossRef CAS.
- Y. Zang, F. Zhang, C. Di and D. Zhu, Mater. Horiz., 2015, 2, 140–156 RSC.
- S. Mishra, S. Mohanty and A. Ramadoss, ACS Sens., 2022, 7, 2495–2520 CrossRef CAS.
- K. Meng, X. Xiao, W. Wei, G. Chen, A. Nashalian, S. Shen, X. Xiao and J. Chen, Adv. Mater., 2022, 34, 2109357 CrossRef CAS.
- H. Wang, Z. Li, Z. Liu, J. Fu, T. Shan, X. Yang, Q. Lei, Y. Yang and D. Li, J. Mater. Chem. C, 2022, 10, 1594–1605 RSC.
- K. Meng, X. Xiao, Z. Liu, S. Shen, T. Tat, Z. Wang, C. Lu, W. Ding, X. He, J. Yang and J. Chen, Adv. Mater., 2022, 34, 2202478 CrossRef CAS PubMed.
- Y. Gao, H. Ota, E. W. Schaler, K. Chen, A. Zhao, W. Gao, H. M. Fahad, Y. Leng, A. Zheng, F. Xiong, C. Zhang, L.-C. Tai, P. Zhao, R. S. Fearing and A. Javey, Adv. Mater., 2017, 29, 1701985 CrossRef.
- F. Ji, Z. Sun, T. Hang, J. Zheng, X. Li, G. Duan, C. Zhang and Y. Chen, Compos. Commun., 2022, 35, 101351 CrossRef.
- B. Chen, L. Zhang, H. Li, X. Lai and X. Zeng, J. Colloid Interface Sci., 2022, 617, 478–488 CrossRef CAS.
- K. Kumari, R. Reeshma, D. S. ArunKumar, S. Meti and M. R. Rahman, Phys. B, 2020, 597, 412386 CrossRef.
- L. Gao, C. Zhu, L. Li, C. Zhang, J. Liu, H.-D. Yu and W. Huang, ACS Appl. Mater. Interfaces, 2019, 11, 25034–25042 CrossRef CAS.
- X. Yang, S. Chen, Y. Shi, Z. Fu and B. Zhou, Sens. Actuators, A, 2021, 324, 112629 CrossRef CAS.
- E. S. Hosseini, L. Manjakkal, D. Shakthivel and R. Dahiya, ACS Appl. Mater. Interfaces, 2020, 12, 9008–9016 CrossRef CAS.
- J. Jiang, S. Tu, R. Fu, J. Li, F. Hu, B. Yan, Y. Gu and S. Chen, ACS Appl. Mater. Interfaces, 2020, 12, 33989–33998 CrossRef CAS.
- D. Yang, H. Guo, X. Chen, L. Wang, P. Jiang, W. Zhang, L. Zhang and Z. L. Wang, J. Mater. Chem. A, 2020, 8, 23827–23833 RSC.
- X. Huo, Mater. Lett., 2022, 320, 132339 CrossRef CAS.
- X. Lin, F. Li, Y. Bing, H. Zhao and T. Zhang, IEEE Electron Device Lett., 2021, 42, 1857–1860 CAS.
- H. Cheng, Y. Du, B. Wang, Z. Mao, H. Xu, L. Zhang, Y. Zhong, W. Jiang, L. Wang and X. Sui, Chem. Eng. J., 2018, 338, 1–7 CrossRef CAS.
- Y. Gao, T. Xiao, Q. Li, Y. Chen, X. Qiu, J. Liu, Y. Bian and F. Xuan, Nanotechnology, 2022, 33, 322002 CrossRef.
- S. R. A. Ruth, V. R. Feig, H. Tran and Z. Bao, Adv. Funct. Mater., 2020, 30, 2003491 CrossRef CAS.
- S. Ma, J. Tang, T. Yan and Z. Pan, IEEE Sens. J., 2022, 22, 7475–7498 CAS.
- S. Chen, S. Xin, L. Yang, Y. Guo, W. Zhang and K. Sun, Nano Energy, 2021, 87, 106178 CrossRef CAS.
- H. Li, K. Wu, Z. Xu, Z. Wang, Y. Meng and L. Li, ACS Appl. Mater. Interfaces, 2018, 10, 20826–20834 CrossRef CAS.
- H. Huang, J. Zhong, Y. Ye, R. Wu, B. Luo, H. Ning, T. Qiu, D. Luo, R. Yao and J. Peng, Polymers, 2022, 14, 3670 CrossRef CAS.
- G. Hu, F. Huang, C. Tang, J. Gu, Z. Yu and Y. Zhao, Nanomaterials, 2022, 12, 3417 CrossRef CAS PubMed.
- Y. Guo, Z. Guo, M. Zhong, P. Wan, W. Zhang and L. Zhang, Small, 2018, 14, 1803018 CrossRef.
- Q. Zhang, L. Shen, P. Liu, P. Xia, J. Li, H. Feng, C. Liu, K. Xing, A. Song, M. Li, X. Yang and Y. Huang, Composites, Part B, 2021, 226, 109365 CrossRef.
- X. Tang, W. Yang, S. Yin, G. Tai, M. Su, J. Yang, H. Shi, D. Wei and J. Yang, ACS Appl. Mater. Interfaces, 2021, 13, 20448–20458 CrossRef CAS.
- X. Zeng, Z. Wang, H. Zhang, W. Yang, L. Xiang, Z. Zhao, L.-M. Peng and Y. Hu, ACS Appl. Mater. Interfaces, 2019, 11, 21218–21226 CrossRef CAS.
- S. H. Cho, S. W. Lee, S. Yu, H. Kim, S. Chang, D. Kang, I. Hwang, H. S. Kang, B. Jeong, E. H. Kim, S. M. Cho, K. L. Kim, H. Lee, W. Shim and C. Park, ACS Appl. Mater. Interfaces, 2017, 9, 10128–10135 CrossRef CAS PubMed.
- G. Li, D. Chen, C. Li, W. Liu and H. Liu, Adv. Sci., 2020, 7, 2000154 CrossRef CAS PubMed.
- Y. Jung, J. Choi, W. Lee, J. S. Ko, I. Park and H. Cho, Adv. Funct. Mater., 2022, 32, 2201147 CrossRef CAS.
- J. Wang, Y. Zhong, S. Dai, H. Zhu, L. Wu, F. Gu, G. Cheng and J. Ding, ACS Appl. Nano Mater., 2022, 5, 13227–13235 CrossRef CAS.
- H. Guan, J. Meng, Z. Cheng and X. Wang, ACS Appl. Mater. Interfaces, 2020, 12, 46357–46365 CrossRef CAS.
- Z. Wu, L. Wei, S. Tang, Y. Xiong, X. Qin, J. Luo, J. Fang and X. Wang, ACS Nano, 2021, 15, 18880–18894 CrossRef CAS PubMed.
- T. Li, L. Chen, X. Yang, X. Chen, Z. Zhang, T. Zhao, X. Li and J. Zhang, J. Mater. Chem. C, 2019, 7, 1022–1027 RSC.
- M.-Y. Liu, C.-Z. Hang, X.-F. Zhao, L.-Y. Zhu, R.-G. Ma, J.-C. Wang, H.-L. Lu and D. W. Zhang, Nano Energy, 2021, 87, 106181 CrossRef CAS.
- W. Li, X. Jin, X. Han, Y. Li, W. Wang, T. Lin and Z. Zhu, ACS Appl. Mater. Interfaces, 2021, 13, 19211–19220 CrossRef CAS PubMed.
- J. C. Yang, J.-O. Kim, J. Oh, S. Y. Kwon, J. Y. Sim, D. W. Kim, H. B. Choi and S. Park, ACS Appl. Mater. Interfaces, 2019, 11, 19472–19480 CrossRef CAS.
- Q. Yu, B. Zhao, X. Ren, C. Zhu, Q. Wang, Y. Lin, W. Zeng, Z. Chen and S. Wang, Langmuir, 2022, 38, 5494–5501 CrossRef CAS.
- Y. Pang, H. Tian, L. Tao, Y. Li, X. Wang, N. Deng, Y. Yang and T.-L. Ren, ACS Appl. Mater. Interfaces, 2016, 8, 26458–26462 CrossRef CAS PubMed.
- J. Byun, Y. Lee, J. Yoon, B. Lee, E. Oh, S. Chung, T. Lee, K.-J. Cho, J. Kim and Y. Hong, Sci. Robot., 2018, 3, eaas9020 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra06487a |
| This journal is © The Royal Society of Chemistry 2022 |