DFT/TD-DFT study of electronic and phosphorescent properties in cycloplatinated complexes: implications for OLEDs

Abstract

High level density functional and time-dependent density functional (DFT, TD-DFT) theoretical methods have been employed to investigate the photophysical properties of 5 inorganic compounds resulting from Pt(II) and ppy (2-phenyl-pyridine) ligands. This study is intended to provide insight into the capability of the selected systems to be used in OLED devices. In addition to an exploration of their ground and excited state geometry and electronic structures, the electronic transitions responsible for their absorption and spectra, as well as other photophysical properties, have been analyzed. To this end, their charge transfer parameters, the triplet exciton generation, phosphorescence quantum yield, and radiative decay rates have been studied. Overall, the results confirm that the selected systems are promising candidates to be used in OLED devices. Moreover, the results of this study assist in understanding the photophysical properties of Pt(II) complexes with ppy ligands.

---

1 Introduction

A significant fraction of the world's electric energy supply is used for lighting and powering display devices. This concern becomes more evident when thinking about the electricity usage in displays.¹ In this regard, the efficiency of optical devices that converts electricity into light is of great importance.

Research and development of organic light-emitting diodes (OLEDs), as the next generation of light-emitting diodes, is being actively pursued. An OLED is a light-emitting tool that makes use of excitons extracted by recombination of the holes and electrons injected into the emitting layer.¹

Nowadays, phosphorescent transition metal complexes with platinum(II), iridium(III),^2–4 ruthenium(I), osmium(II), rhenium(I)^5,6 and gold(III) have received a great deal of attention due to their versatile application in OLEDs.⁷ These compounds are well known as efficient phosphorescent emitters applied in OLEDs, owing to strong spin–orbit coupling (SOC), which enables them to have the potential capability to achieve singlet-triplet excitons resulting in 100% internal quantum efficiency.⁸

The luminescent square planar platinum(II) complexes, as one of the most promising subsets of this class of materials, exhibit a wide variety of optoelectronic properties that have been exploited for sensor materials.⁹ It is known that these systems have the capability of showing a variety of emissive excited states, such as LLCT (ligand-to-ligand charge transfer), ILCT (intra-ligand charge transfer), MLCT (metal-to-ligand charge transfer), and so on.^10–14 Similarly, by the rational design of their ligands, Pt(II) complexes can exhibit extensive emission color tuning.¹² Interesting π–π stacking or axial interactions of Pt that can alter the emission properties arising from their planar geometry, results in unique emissive characteristics.¹⁵

The ligands of cyclometallated Pt(II) complexes can be bidentate, tridentate, or tetradentate, and this variability enormously influences the phosphorescence properties of the resulting complexes.^{11,13,16–19} The main feature that can be taken to enhance the effectiveness of the electroluminescent emitters is improving the spin–orbit coupling scheme, which results in strong intersystem crossing and consequently extending their radiative decay rates.¹⁹

Recent studies have shown that the phosphorescence properties can be easily adjusted by altering the cyclometallated ligands, whereas the change of auxiliary ligands has a minor impact.²⁰ In this regard, heteroleptic C^N ligands such as phenyl-pyridine (ppy) have been widely used in synthesizing transition metal complexes. When C^N ligands coordinate to metal ions, they form a five-membered chelate through the N atom of the pyridine ring and a C atom of the phenyl moiety. The anionic carbon atom connected to the metal center is a strong σ-donor, whereas the pyridyl ring plays the role of a π-acceptor. Hence, a strong ligand field will be applied over the metal center via the C^N ligands resulting in a higher energetic gap between the d–d states inhibiting thermal quenching processes.

The present study is focused on several recently synthesized and characterized Pt(II) complexes based on the C^N (ppy) ligand and the DFT and TD-DFT methodologies have been employed to determine their electronic structures as well as photophysical and optoelectronic properties. For simplicity, the selected systems have been called as the complexes 1–5 (see Scheme 1 and Fig. 1). These are: (1) [Pt(ppy) (p-MeC₆H₄) (SMe₂)],^21,22 (2) [Pt(ppy)(Me)(PPh₂allyl)],²³ (3) [Pt(ppy)(PPh₂ allyl)(py)],^24,25 (4) [Pt(ppy)(SMe₂)(CF₃COO)],^26,27 and (5) [Pt(ppy)(Me)(SMe₂)].^21,22

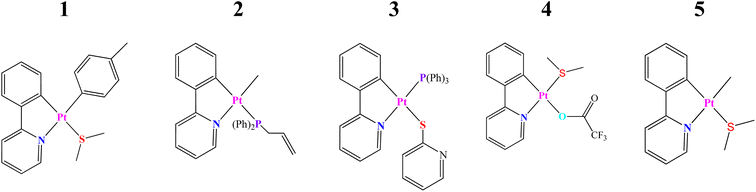Scheme 1 Schematic structures of cycloplatinated(II) complexes, denoted 1–5, and studied in this work (H atoms are omitted for clarity).

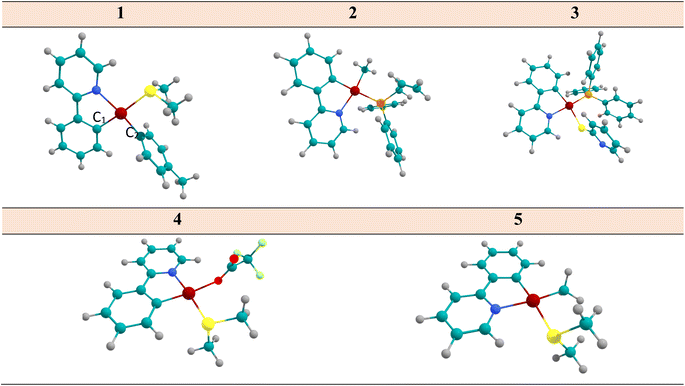Fig. 1 The optimized structure of complex 1–5 considered in this study, determined at the DFT/B3LYP/cc-pVDZ/def2-TZVP.

There is substantial experimental information regarding the chemical and spectroscopy properties such as structural properties determined by X-ray diffraction methods and UV-vis spectra of selected systems.^{21–24,26,28–32} In this work, we focus on the suitability of 1–5 to be used in OLED devices.

2 Methodology

DFT and TD-DFT methods were respectively employed to investigate the ground and excited state properties of the selected systems.³³ In this regard, the Becke, 3-parameter and Lee–Yang–Parr exchange-correlation functional (B3LYP) has been used. In addition, the cc-pVDZ³⁴ basis set was employed for all atoms except Pt, for which the def2-TZVP³⁵ basis set was used. This method has been previously utilized for determination of photophysical and optoelectronic properties of transition metal Ir(III) and Pt(II) complexes and yielded reliable results.^11–14

All calculations were done using the Turbomole program package (V 6.3).^36,37 Based on the selected theoretical methods, the following physical properties have been investigated:

(i) The ionization potential (IP)

(ii) The electron affinity (EA)

(iii) The hole extraction potential (HEP) and electron extraction potential (EEP)

(iv) The reorganization energy (λ).

A brief description of each of the abovementioned properties has been presented in ESI.†

To understand the nature of the excited states involved in the absorption and emission processes, a natural bond orbital (NBO)³⁸ analysis was performed using the Gaussian 16 and Chemissian³⁹ programs. Furthermore, the NBO analysis was carried out to obtain the coefficients of the natural atomic orbitals for the evaluation of spin–orbital coupling (SOC), k_r, k_nr (radiative and non-radiative rate constants) and the phosphorescence quantum yield (Φ).

3. Results and discussion

3.1. Optimized geometries of the ground state (S₀) and lowest-lying triplet state (T₁)

The optimized geometry of the ground (S₀) and the first triplet excited (T₁) of all complexes have been determined at the B3LYP/cc-pVDZ/def2-TZVP level of theory. We have presented the optimized structures in the ESI.† In addition, the selected geometric parameters of the five complexes in the ground and the lowest excited states are listed in Table 1.

Table 1 Selected optimized geometry parameters of 1–5 complexes in the S₀ and the T₁ states at B3LYP/def2-TZVP/cc-pVDZ level of theory. The experimental values obtained from the XRD structures are from the literature (cited appropriately)

Molecular system	States	Bond length (Å)				Bond angle (deg)
1		Pt–C1	Pt–C2	Pt–N	Pt–S	C1–Pt–C2	N–Pt–C1	N–Pt–S	C2–Pt–S
	S0	2.017	2.028	2.167	2.468	94.43	79.91	94.52	91.14
	T1	2.105	2.048	2.019	2.513	94.24	81.05	94.18	90.51
	Exp.^22	2.006	2.000	2.118	2.357	93.56	80.48	95.30	90.66
2		Pt–C1	Pt–C2	Pt–N	Pt–P	C1–Pt–C2	N–Pt–C1	N–Pt–P	C2–Pt–P
	S0	2.054	2.077	2.181	2.386	90.70	79.00	104.00	86.40
	T1	2.016	2.083	2.167	2.416	92.70	79.40	101.50	87.50
	Exp.^23	2.037	2.040	2.136	2.301	92.20	78.70	105.20	83.90
3		Pt–C1	Pt–S	Pt–N	Pt–P	P–Pt–S	N–Pt–C1	C1–Pt–P	S–Pt–N
	S0	2.069	2.445	2.127	2.305	91.10	79.50	97.70	91.90
	T1	2.035	2.452	2.096	2.318	90.50	80.80	97.42	91.45
	Exp.^25	2.065	2.361	2.073	2.244	90.95	81.90	97.25	90.20
4		Pt–C1	Pt–O	Pt–N	Pt–S	C1–Pt–S	N–Pt–C1	N–Pt–O	O–Pt–S
	S0	2.004	2.138	2.054	2.333	94.54	81.14	90.57	93.69
	T1	1.983	2.114	2.039	2.359	95.65	81.22	91.05	92.05
	Exp.^27	1.972	2.118	2.043	2.260	92.50	81.90	89.60	96.10
5		Pt–C1	Pt–C2	Pt–N	Pt–S	C1–Pt–C2	N–Pt–C1	N–Pt–S	C2–Pt–S
	S0	2.017	2.060	2.171	2.447	93.31	79.86	94.56	92.25
	T1	1.198	2.072	2.165	2.514	97.71	80.53	94.04	91.38
	Exp.^21	2.014	2.064	2.195	2.497	93.66	79.70	94.36	92.28

---

In this section, the structural parameters of the selected complexes at the B3LYP/cc-pVDZ/def2-TZVP computational level has been inspected. The difference in bond lengths and bond angles Pt–C₁, Pt–N, and C₁–Pt–N (see Fig. 1 for numbering) at the optimized geometries of S₀ state is about 0.065 Å, 0.127 Å and 1.14 degrees, respectively. Both the S₀ and T₁ states have an almost a planar structure. The Pt–S bond length in complexes 1, 3, 5, (located in the cis-position with respect to the Pt–N bond) are almost the same with a deviation of 0.023 Å. The Pt–N and Pt–C₂ bonds in systems 1, 2, and 5 have been predicted to be 2.028, 2.077, and 2.060 Å, respectively. Also, the N–Pt–S bond angle in complexes 1, 3, and 5 have been predicted to be 94.5, 91.9 and 94.5 degree, respectively. In complex 3, this angle decreases by 3 degree as a result of the N-py substitution connecting to the S atom. In three complexes of 1, 2, and 5, the C₁–Pt–C₂ angles were predicted to be 94.4°, 90.7°, and 93.3°, respectively, which is due to the presence of phenyl substitution attached to C₂ in complex 2 (a deviation of ∼4° has been predicted). Furthermore, the difference in the optimized geometry parameters at the ground and the first triplet excited state of the selected systems is insignificant, which indicates that the planarity of these systems are preserved in the T₁ state. This is an important feature of the phosphorescence emitting systems.

Comparing the close agreement between the structural data obtained from the calculations and considering the experimental results for 1–5 is indicative of the reliability of selected theoretical model.

3.2. Valance molecular orbital (MO) properties

The energetic level of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of the selected systems are presented in Fig. 2; more details can be found in Table 2 (and also in the ESI†).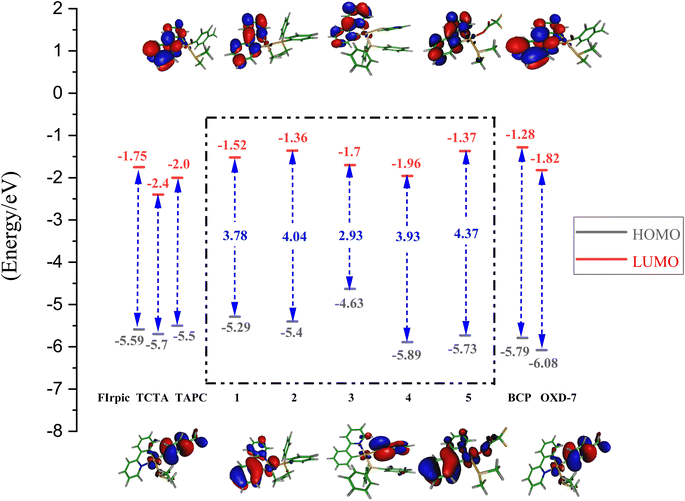

Fig. 2 Molecular orbitals and energetic levels of HOMO and LUMO in complexes 1–5. The values on the arrows give the HOMO–LUMO energetic gap in eV.

Table 2 Frontier molecular orbital compositions (%) in the ground state for complex 1

Orbital	Contribution (%)				Contributions
	Pt	ppy	S(Me)2	p-MeC6H4
H−6	22	20	50	8	n(S) + d(Pt) + π(ppy)
H−5	25	70	—	5	π(ppy) + d(Pt)
H−4	6	2	1	91	π(p-MeC6H4)
H−3	59	35	—	6	d(Pt) + π(ppy)
H−2	85	6	—	9	d(Pt)
H−1	36	62	2	—	π(ppy) + d(Pt)
HOMO	21	2	2	75	π(p-MeC6H4) + d(Pt)
LUMO	7	91	1	1	π*(ppy)
L+1	1	98	1	—	π*(ppy)
					π*(ppy) + n(S) +σ(Me)2 + d(Pt)
L+2	21	44	31	4	π*(p-MeC6H4)
L+3	2	7	2	89	π*(p-MeC6H4) + d(Pt)
L+4	19	9	6	66	π*(p-MeC6H4) + d(Pt)
L+5	26	26	14	34	+ π*(ppy) + n(S)

---

The HOMO in complex 1, is mainly located on Me–C₆H₄-ligand (75%, assigned as a π orbital) and 21% 5d (Pt). The electron density distributions of HOMO for complexes 2, 4, and 5 are rather similar, which are located mainly over the ppy ligand (as the π orbitals) and at the metal center of Pt (5d). The HOMO orbital in complex 3 is predominantly localized as the π orbitals over the S-pyridine (Spy) ligand.

In addition, the LUMO of all complexes has been mostly assigned as a π* orbital, localized on the ppy ligand. In complexes 2, 4, and 5, the metal (Pt) 5d orbitals and π orbitals of ppy ligand significantly contribute to the HOMO, while the π* orbitals of ppy constitutes the majority of the LUMO, demonstrating that the transition from the HOMO to LUMO would mainly have a metal-to-ligand charge transfer (MLCT) character mixed with ILCT (the intra-ligand charge transfer). For complex 1, the 5d orbitals of platinum and the π orbitals of the MeC₆H₄-ligand make a significant contribution to the HOMO, while the π* orbitals of the ppy ligand make the most important contributions to the LUMO, indicating the transition nature of MLCT mixed with ligand-to-ligand charge transfer (LLCT).

As shown in Fig. 2, the energetic level of the HOMOs (in 1, 2, 4, 5) lies within the range of −5.3 to −5.8 eV and are comparable with the HOMO levels of the host materials. The energetic levels of LUMO orbitals also are comparable with the corresponding values of the host. Therefore, in terms of the energetic levels of relevant MOs, our selected systems could be suitable for electron, hole transfer. Nevertheless, in complex 3, the HOMO energy is −4.63 eV, which is higher than that in other systems, which suggest system 3 would not be suitable for this purpose.

According to our calculations, the secondary ligand substitution over the Pt(II) cation has a significant effect on the electron distributions over the MOs, consequently altering the HOMO–LUMO energy gap and phosphorescence quantum yield.

Moreover, a main concern about the efficiency of guest materials in the OLED devices could be non-radiative and thermal quenching processes. This issue could be addressed by considering the d–d* and d-orbital splitting, as stated by Yersin et al.^40,41 The Δdd_occ and Δdd* respectively stands for the energy difference between the highest occupied d-orbitals and the splitting between the HOMO and the LUMO d-orbitals. The calculated Δdd_occ and Δdd* values of 1–5 at both S₀ and T₁ optimized geometries at the B3LYP level are presented in Table 3.

Table 3 Frontier molecular energetic levels and calculated magnitudes of Δdd_occ and Δdd* (eV) determined at the B3LYP/def2-TZVP/cc-pVDZ level of theory

Complex	EHOMO	ELUMO	ΔEgap	S0		T1
				Δddocc	Δdd*	Δddocc	Δdd*
1	−5.29	−1.52	3.78	0.19	5.93	0.21	5.92
2	−5.40	−1.36	4.04	0.04	5.70	0.12	3.85
3	−4.63	−1.70	2.93	0.15	4.88	0.32	4.73
4	−5.89	−1.96	3.93	0.37	5.48	0.51	5.51
5	−5.73	−1.37	4.37	0.04	6.27	0.12	3.44

---

According to the literature, a large splitting between the highest occupied and the lowest unoccupied d-orbitals, Δdd* leads to thermally inaccessible metal-centered (MC) d–d excited states.¹¹ Furthermore, smaller Δdd_occ indicates stronger SOC and a faster radiative decay rate.

The values of Δdd_occ, at S₀ and T₁ optimized-geometry (0.04–0.32 eV) indicate strong SOC and subsequently large radiative deactivation process. In addition, the Δdd* values of 5.48–6.27 eV indicate a large energetic gap between occupied and unoccupied d orbitals. The Δdd* variation between S₀ and T₁ indicates slight structural distortions from the S₀ to the T₁ state. Therefore, from this physical aspect, the considered complexes would have less access to thermally d–d* states and thus difficult d–d* thermal-transitions.

3.3. Charge transportation and triplet exciton generation fraction (χ_T)

The balance between hole and electron transport is another important factor affecting the efficiency of optical devices, especially those applied in OLEDs, indicating the charge carrier mobility. This issue could be evaluated by ionization-potential and electron affinity (IP and EA respectively) of the host materials. It is well known that the smaller ionization potential (IP) would be accompanied with the easier hole injection. In addition, larger electron affinity (EA) facilitates the electron injection feature. Thus, the smaller IP and the larger EA, would be accompanied with the better charge transport.

The calculated IP, EA (IP_v & IP_a where v and a, respectively stand for vertical and adiabatic), the reorganization energy (λ) and the hole/electron extraction potentials (HEP, EEP) are presented in Table 4. All these values have been determined using eqn (2) and (3) presented in the ESI† based on the Marcus theory.^42–44

Table 4 Ionization potential (IP), electron affinities (EA) and reorganization energies (eV) for selected complexes calculated at the B3LYP/def2-TZVP/cc-pVDZ level of theory

Complex	IPv (eV)	IPa (eV)	HEP	λh	EAv (eV)	EAa (eV)	EEP	λe	Δλ
1	6.74	6.57	6.34	0.39	0.08	0.21	0.34	0.26	0.12
2	6.76	6.28	5.50	1.26	0.02	0.13	0.25	0.23	1.02
3	6.05	5.92	5.79	0.26	0.40	0.56	0.71	0.30	−0.04
4	7.34	7.20	6.93	0.46	0.47	0.64	0.80	0.32	0.13
5	6.42	6.31	6.66	0.24	0.35	0.49	0.16	0.19	−0.05

---

It is well known that a lower IP of an emitter results in the easier entrance of holes from the HTL (hole transport layer) to the emitter. Also the greater the EA of an emitter material, the faster the entrance of electrons from the electron transfer layer (ETL) to the emitter layer (ETL). As shown in Table 4, the calculated IP_v values increase in the order 4, 2, 1, 5, 3. This arrangement indicates that the hole transport character is in an increasing trend of 4, 2, 1, 5, 3. On the other hand, concerning the electron accepting properties, it could be noted that 1, and 2, are on the top of the list, having the best electron accepting rates, and the other systems are listed thereafter.

Moreover, in emitting layer materials, the balance between hole and electron injection is another important characteristic, which could be addressed by consideration of the reorganization energy (λ_e and λ_h where e and h, respectively stand to the electron and hole). A lower value of reorganization energy is indicative of a smaller barrier of receiving the hole or electron.

The values of λ determined for complexes 1–5 are presented in Table 4. In contrast to complex 3, in the complexes 1, 2, 4 and 5, λ_e < λ_h, suggesting that the electron-transfer rate is better than the hole transfer rate in these systems; although in complex 3 the trend is reversed (being better in so far as the hole transfer rate is concerned). This indicates that all selected complexes are suitable materials in phosphorescent OLEDs with a good carrier transfer rate. The charge transport properties can also be related to the spatial distribution of the HOMOs and LUMOs. The hole/electron transport is always easier for a more delocalized HOMO/LUMO, as it will allow better overlapping of the intermolecular orbitals.⁴⁵

In addition, the triplet exciton generation fraction (χ_T) is known to be an important parameter dealing with the ISC. The χ_T value approaching unity is indicative of a maximum ISC rate.¹⁴ The values determined for χ_T of all selected systems are tabulated in Table 5, which are in range of 76–84%. This high χ_T property indicates that all the selected Pt(II) compounds are promising to generate great triplet excitons and thus a fast ISC process.

Table 5 Optical properties and exciton generation fractions χ_T (%) of selected systems determined by TD-DFT level. All of energetic values are in eV and the notations are defined as: “p, v, a” respectively stands to phosphorescence, vertical and adiabatic

Complex	ΔEg	T1p	T1v	T1a	S1v	ΔES1–T1	Eg − ES1v	Eg − ET1v	δS/δT	χT (%)
1	3.78	2.47	2.67	2.62	3.14	0.48	0.64	1.11	0.57	84
2	4.04	2.57	2.71	2.71	3.23	0.53	0.81	1.33	0.61	83
3	2.93	1.99	2.27	2.26	2.29	0.02	0.64	0.66	0.96	76
4	3.93	2.40	2.65	2.56	3.17	0.52	0.76	1.28	0.59	83.5
5	4.37	2.25	2.67	2.30	3.16	0.49	1.21	1.70	0.71	83

---

3.4. Performance in OLEDs

Several requirements must be considered for the effective host material to achieve efficient electro phosphorescence:

(i) The relatively long lifetime of phosphorescent heavy metal complexes (scale of microseconds) may lead to dominant triplet–triplet (T₁–T₁) annihilation at high currents, and may also cause a long-range exciton diffusion (>100 nm) that could get quenched in the adjacent layers of materials in OLEDs.⁴⁶ Therefore, phosphorus-heavy metal complexes have to be widely dispersed into the host matrix to reduce these competitive factors. A wide variety of materials have been proposed as the host material in the emitting layer of OLEDs (for instance the ref. 14 and 46–49). However, the matching between the host and dopant material has been a subject of concern in phosphorescent emitting devices. Therefore, in the present study, in order to examine the suitability of the proposed materials for OLED devices, OXD-7, BCP, TCTA, TAPC and FIrpic have been taken as common host materials to compare the efficiency of the studied complexes (see Fig. 3). TCTA and TAPC are typical hole transport (HT) host materials and OXD-7 and BCP are mostly used as electron transport (ET) host in emissive layers. There is a good match between the HOMO and LUMO energy levels of the complexes 1, 2 and 3, as dopant and FIrpic, TCTA and TAPC host materials (Fig. 2). Thus, the selected molecules are suitable for hole injection in OLED systems.

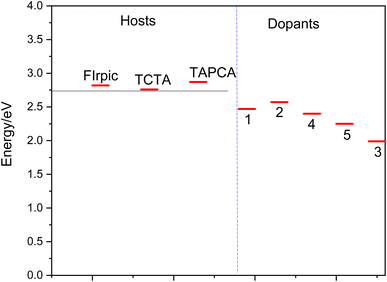Fig. 3 Triplet excitation energy levels of the host (FIrpic, TCTA, TAPC, BCP and OXD-7) and the studied dopant materials (1–5).

Moreover, complex 5 as a guest, shows a good MO energy matching with OXD-7 as a host, indicating to the good electron injecting nature of 5.

(ii) It is well known that the host materials should possess higher triplet excited state energies than those of the dopant emitters to confine the triplet excitons in the emissive layer and prevent reverse energy transfer from the dopant back to the host and consequently blocking T₁–T₁ annihilation. The later effect is an important reason for a decrease in the phosphorescence efficiency in the emissive layer, and hence an important reason for using organometallic dopants in this layer.^2,4 T₁ excitation energies of the selected systems and those of common host materials are presented in Fig. 3. As seen, the vertical T₁ values for the 1–5 has been determined to lie in range of 2.27–2.71 eV, which are significantly lower than those of the host materials (the FIrpic, TCTA and TAPC). The lower T₁ values of these guest materials, compared to the mentioned host materials, indicates that the back electron transfer from the guest to the host would be effectively prohibited; hence, the holes and electrons would be able to be transported from the host to the guest more effectively.¹⁴ Most importantly, this effective hole–electron transport, results in more triplet exciton generation and consequently a higher efficient phosphorescence process.¹⁴

3.5. The absorption and emission spectra

To understand the nature of electronic transitions, the absorption spectra of the complexes 1–5 have been determined based on the optimized S₀ geometry by TD-DFT method. The simulated UV spectrum of complex 1 is presented in Fig. 4, and other relevant information have been given in the ESI.† In Fig. 4, the experimental spectrum recorded by Jamshidi et al.²⁸ has been presented for comparison with our simulated results. To consider the environment effect, we have included the implicit solvent effect (here CH₂Cl₂) to simulate the UV spectrum. As shown in Fig. 4, the experimental spectrum contains two intense bands at 290 and 326 nm, which have been simulated by 290 and 320 nm in our calculation respectively. From theoretical perspective, these two intense bands could be assigned to S₉–S₀ and S₄–S₀ electronic transitions, having significant oscillator strengths of 0.160 and 0.095. There is also a lower intensity band at 365 nm in the experimental spectrum which corresponds to our S₂–S₀ transition at 369 nm (see Table 6).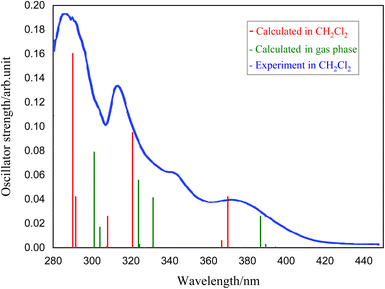

Fig. 4 Simulated absorption spectrum of complex 1 determined at the optimized S₀ geometry in the gas phase (green) and in CH₂Cl₂ solution (red)²⁸ compared to corresponding experimental spectrum (in blue), adapted from ref. 28.

Table 6 Selected the ten lowest lying vertical transition energies of complex 1 determined at the TD-DFT/B3LYP/def2-TZVP/cc-pVDZ level of theory in CH₂Cl₂ solvent. H and L respectively stand to HOMO and LUMO orbitals

Excited state	MO contribution (%)	f	E (eV)	λ (nm)	Assignment
S1	H−L (97.2%)	0.0001	3.27	378	^1MLCT/^1LLCT
S2	(H−1)–L (95.0%)	0.0420	3.35	369	^1MLCT/^1LLCT
S3	(H−2)–L (98.5%)	0.0059	3.38	366	^1MLCT/^1LLCT
S4	(H−3)–L (84.3%)	0.0950	3.86	320	^1MLCT/^1ILCT//^1LLCT
S5	(H−1)–(L+1) (63.2%)	0.0259	4.02	308	^1MLCT/^1ILCT//^1LLCT
	(H−5)–L (18.2%)
S6	H–(L+1) (94.1%)	0.0009	4.032	307	^1MLCT/^1LLCT
S7	(H−2)–(L+1) (97.9%)	0.0001	4.124	301	^1MLCT/^1LLCT
S8	(H−4)–L (85.3%)	0.0420	4.251	292	^1LLCT
	(H−3)–(L+1) (9.1%)
S9	(H−5)–L (61.4%)	0.1603	4.273	290	^1MLCT/^1LLCT
	(H−1)–(L+1) (20.3%)
S10	(H−6)–L (96.9%)	0.0003	4.319	287	^1MLCT/^1LLCT

---

The results of the electronic transition energies of other systems (2–5) are presented in the ESI.†

The emission spectrum of the considered complexes has been determined at the optimized geometries of the lowest triplet excited state (T₁), using TD-DFT method. In Table 7, the phosphorescence energetic values resulting from T₁ → S₀ electronic transition are presented. As shown, the transitions are located in a range of 480–623 nm, corresponding to the green-red region of visible light. For those systems that the experimental emission spectrum has been reported in the literature (1–3),^23,28 the theoretical values of T₁ emission have been compared. The T₁ → S₀ transition wavelength values in 1–3 are 503, 483, and 623 nm, respectively; and the corresponding experimental λ_max of emitting bands has been reposted as 505, 477, and 534 nm (in dichloromethane at the room temperature). This indicates that the theoretical results are in good agreement with experiments, reflecting that the selected theoretical model is significantly reliable for describing the photophysical nature of these systems.

Table 7 The phosphorescence properties of complexes 1–5 calculated by TD-DFT/B3-LYP method

Complex	T1-pr^a (eV)	λ (nm)	f	Assignment	λexp (nm)
a pr stands to phosphorescence emission.The experimental emission wavelengths corresponding to the phosphorescence transitions in CH2Cl2 of titled complexes have been adopted from ref. 23 and 28.
1	2.47	503	0.218	^3MLCT/^3ILCT	λmax = 505 nm
2	2.57	483	0.206	^3MLCT/^3ILCT	λmax = 477 nm
3	1.99	623	0.746	^3LLCT	λmax = 534 nm
4	2.40	516	0.342	^3MLCT/^3ILCT
5	2.25	550	0.539	^3MLCT/^3ILCT

---

Moreover, considering the emitting properties of the selected systems, it could be concluded that our considered complexes are good candidates to be used in OLEDs, for emitting the green-red visible light.

In Table 8, the results related to phosphorescence quantum yield, containing radiative and nonradiative decay rates (k_r, k_nr) as well as the spin–orbit coupling elements (ISC) are presented. Certainly, the transition metal center in the selected systems plays an important role in mixing the emissive singlet (S₁) with the lowest triplet (T₁) states and hence producing large values for SOC coupling elements.⁶ The SOC effects can be understood from ΔE_S1–T1, singlet–triplet splitting energy values; the lower ΔE_S1–T1, the higher the ISC rate. Table 8 shows that the ΔE_S1–T1 is roughly 0.50 eV in all of the titled complexes. Consequently, the calculated phosphorescence quantum yield, Φ, has been determined to be greater than 98%, which indicating that the phosphorescence nature in the selected systems is quite promising, which is consistent with the results of Shahsavari et al.^23,24

Table 8 The phosphorescence quantum yield and traditional decay rates in the considered complexes 1–5 determined at the TD-DFT level of theory

Complex	SOC (cm^−1)	T1 (eV)	S1 (eV)	ΔES1–T1 (eV)	kr ×10^6 (s^−)	knr ×10^3 (s^−)	Φ (%)
1	184	2.67	3.14	0.47	22.4	0.93	99
2	827	2.71	3.23	0.52	47.4	0.73	99
3	65	2.27	2.29	0.02	29.5	2.49	97
4	656	2.65	3.17	0.52	20.0	1.06	98
5	835	2.67	3.16	0.49	26.1	1.44	98

---

Thus, overall, the selected Pt(II) systems show promising physical properties for being proposed to be used in OLED devices.

4. Conclusions

In this study, the photophysical and optoelectronic properties of five Pt(II) complexes have been investigated. Indeed, a great number of studies have previously dealt with their synthesis and characterization. These complexes are similar in terms of having a bidentate ppy ligand, and they are different from each other insofar as the other two coordinates for Pt(II) center are concerned. The results could be summarized as follows:

(i) From a computational point of view, and with consideration of the geometry and electronic structure parameters, it becomes evident that our computational method is significantly reliable for investigation of the photophysics of Pt(II) complexes.

(ii) The calculations reveal a planar structure for the ground and T₁ optimized geometry of the selected systems for their ppy + Pt region. In addition, the physical characters dealing with the possibility of intersystem-crossing (ISC) occurring, indicates high phosphorescence efficiency of all of the considered systems. Thus, the systems suggested in this study are promising candidates to be used in OLED devices.

(iii) Based on the emission character determined at the T₁ optimized geometries, it has been predicted that the suggested systems are capable of emitting the radiation in the long wavelength region (from green to red).

It is recommended to focus the future studies on investigating the emitting wavelengths of each system proposed in this study by probing electron donating or withdrawing substitution effects of the ligands, which result in tuneability of the emission range of each considered system, individually.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The support of the Research Council of the University of Isfahan is kindly appreciated. We also acknowledge extended discussions and valuable comments received from Professor S. Masoud Nabavizadeh (Shiraz University).

References

1. Y. Suzuri, T. Oshiyama, H. Ito, K. Hiyama and H. Kita, Sci. Technol. Adv. Mater., 2014, 15, 054202–054215.
2. R. Srivastava, Mol. Phys., 2015, 113, 1451–1464.
3. R. Srivastava, L. Joshi and B. Kotamarthi, Comput. Theor. Chem., 2014, 1035, 51–59.
4. R. Srivastava and L. R. Joshi, Phys. Chem. Chem. Phys., 2014, 16, 17284–17294.
5. G. Velmurugan, B. K. Ramamoorthi and P. Venuvanalingam, Phys. Chem. Chem. Phys., 2014, 16, 21157–21171.
6. G. Velmurugan and P. Venuvanalingam, Dalton Trans., 2015, 44, 8529–8542.
7. M. Velusamy, C.-H. Chen, Y. S. Wen, J. T. Lin, C.-C. Lin, C.-H. Lai and P.-T. Chou, Organometallics, 2010, 29, 3912–3921.
8. G. Li, G. Shen, X. Fang, Y.-F. Yang, F. Zhan, J. Zheng, W. Lou, Q. Zhang and Y. She, Inorg. Chem., 2020, 59, 18109–18121.
9. A. Haque, L. Xu, R. A. Al-Balushi, M. K. Al-Suti, R. Ilmi, Z. Guo, M. S. Khan, W.-Y. Wong and P. R. Raithby, Chem. Soc. Rev., 2019, 48, 5547–5563.
10. W. Li, J. Wang, X. Yan, H. Zhang and W. Shen, Appl. Organomet. Chem., 2017, 32, e3929.
11. R. Omidyan, M. Abbasi and G. Azimi, Int. J. Quantum Chem., 2019, 119, e25793–e25805.
12. W. Shen, W. Zhang and C. Zhu, Phys. Chem. Chem. Phys., 2017, 19, 23532–23540.
13. Y. Wu, S.-X. Wu, H.-B. Li, Y. Geng and Z.-M. Su, Dalton Trans., 2011, 40, 4480–4488.
14. L. Wang, Y. Wu, G.-G. Shan, Y. Geng, J.-Z. Zhang, D.-M. Wang, G.-C. Yang and Z.-M. Su, J. Mat. Chem. C, 2014, 2, 2859–2868.
15. S. Huo, J. Carroll and D. A. K. Vezzu, Asian J. Org. Chem., 2015, 4, 1210–1245.
16. S.-Y. Chang, Y.-M. Cheng, Y. Chi, Y.-C. Lin, C.-M. Jiang, G.-H. Lee and P.-T. Chou, Dalton Trans., 2008, 6901–6911.
17. T.-T. Feng, F.-Q. Bai, L.-M. Xie, Y. Tang and H.-X. Zhang, RSC Adv., 2016, 6, 11648–11656.
18. G. S.-M. Tong and C.-M. Che, Chem.–Eur. J., 2009, 15, 7225–7237.
19. X.-Q. Zhang, Y.-M. Xie, Y. Zheng, F. Liang, B. Wang, J. Fan and L.-S. Liao, Org. Electron., 2016, 32, 120–125.
20. H.-W. Fan, F.-Q. Bai, Z.-X. Zhang, Y. Wang, Z.-X. Qu, R.-L. Zhong and H.-X. Zhang, RSC Adv., 2017, 7, 17368–17376.
21. M. D. Aseman, S. M. Nabavizadeh, H. R. Shahsavari and M. Rashidi, RSC Adv., 2015, 5, 22692–22702.
22. M. G. Haghighi, M. Rashidi, S. M. Nabavizadeh, S. Jamali and R. J. Puddephatt, Dalton Trans., 2010, 39, 11396–11402.
23. H. R. Shahsavari, R. Babadi Aghakhanpour, M. Babaghasabha, M. Golbon Haghighi, S. M. Nabavizadeh and B. Notash, New J. Chem., 2017, 41, 3798–3810.
24. M. Jamshidi, M. Babaghasabha, H. R. Shahsavari and S. M. Nabavizadeh, Dalton Trans., 2017, 46, 15919–15927.
25. M. Niazi, H. R. Shahsavari, M. G. Haghighi, M. R. Halvagar, S. Hatami and B. Notash, RSC Adv., 2016, 6, 76463–76472.
26. M. G. Haghighi, S. M. Nabavizadeh, M. Rashidi and M. Kubicki, Dalton Trans., 2013, 42, 13369–13380.
27. S. R. Barzegar-Kiadehi, M. Golbon Haghighi, M. Jamshidi and B. Notash, Inorg. Chem., 2018, 57, 5060–5073.
28. M. Jamshidi, S. M. Nabavizadeh, H. R. Shahsavari and M. Rashidi, RSC Adv., 2015, 5, 57581–57591.
29. S. Paziresh, R. Babadi Aghakhanpour, S. Fuertes, V. Sicilia, F. Niroom Hosseini and S. M. Nabavizadeh, Dalton Trans., 2019, 48, 5713–5724.
30. A. Nahaei, S. M. Nabavizadeh, F. N. Hosseini, S. J. Hoseini and M. M. Abu-Omar, New J. Chem., 2019, 43, 8005–8014.
31. M. Samandar Sangari, M. Golbon Haghighi, S. M. Nabavizadeh, A. Pfitzner and M. Rashidi, New J. Chem., 2018, 42, 8661–8671.
32. M. S. Sangari, M. G. Haghighi, S. M. Nabavizadeh, M. Kubicki and M. Rashidi, New J. Chem., 2017, 41, 13293–13302.
33. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
34. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023.
35. D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105–134111.
36. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
37. F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2014, 4, 91–100.
38. F. Weinhold and C. R. Landis, Chem. Educ. Res. Pract., 2001, 2, 91–104.
39. C. Melzer, Characterization of Organic Semiconductors and Optoelectronic Elements, Ph.D. thesis, University of Groningen, The Netherlands, 2014.
40. A. F. Rausch, H. Homeier, P. I. Djurovich, M. E. Thompson and H. Yersin, Proc. SPIE, 2007, 6655, 66550F1-16.
41. H. Yersin, Highly efficient OLEDs with phosphorescent materials, John Wiley & Sons, 2008.
42. R. A. Marcus, J. Chem. Phys., 1956, 24, 979–989.
43. R. A. Marcus, Ann. Rev. Phys. Chem., 1964, 15, 155–196.
44. R. A. Marcus, Rev. Modern Phys., 1993, 65, 599–610.
45. L.-L. Shi, Y. Geng, H.-Z. Gao, Z.-M. Su and Z.-J. Wu, Dalton Trans., 2010, 39, 7733–7740.
46. S.-J. Yeh, M.-F. Wu, C.-T. Chen, Y.-H. Song, Y. Chi, M.-H. Ho, S.-F. Hsu and C. H. Chen, Adv. Mater., 2005, 17, 285–289.
47. Y. Tao, C. Yang and J. Qin, Chem. Soc. Rev., 2011, 40, 2943–2970.
48. R. Srivastava and L. R. Joshi, Phys. Chem. Chem. Phys., 2014, 16, 17284–17294.
49. L. Zhang, L. Tian, M. Li, R. He and W. Shen, Dalton Trans., 2014, 43, 6500–6512.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra06880j

---