Open Access Article
Open Access ArticleKinetic model for the dehydration of xylose to furfural from a boronate diester precursor†
Luca Ricciardia,
Willem Verboom *a,
Jean-Paul Lange
*a,
Jean-Paul Lange *bc and
Jurriaan Huskens
*bc and
Jurriaan Huskens *a
*a
aMolecular Nanofabrication Group, Department for Molecules & Materials, MESA+ Institute, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands. E-mail: w.verboom@utwente.nl; j.huskens@utwente.nl
bSustainable Process Technology Group, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands
cShell Global Solutions International B.V., Grasweg 31, 1031 HW Amsterdam, The Netherlands. E-mail: jean-paul.lange@shell.com
First published on 7th November 2022
Abstract
A comprehensive kinetic model describes the dehydration of xylose starting from the boronate diester-protected xylose (PBA2X). The model incorporates (de)esterification of PBA2X, partitioning, and xylose dehydration, and aims to evaluate the effects of the solvent system on these steps. The model explores the effect of the water contents in monophasic solvent systems, and that of ionic strength and mixing in biphasic aqueous–organic systems. At low water content, hydrolysis of PBA2X is the rate-limiting step, while xylose dehydration is fast. Conversely, in a monophasic three-solvent system, where the water content is higher, complete hydrolysis of the diester is achieved quickly. Under biphasic conditions, xylose dehydration is fast at high ionic strengths, but the slower partitioning/hydrolysis of PBA2X results in an overall slower furfural production. Furthermore, the observed different but high, constant xylose-to-furfural selectivities observed experimentally are tentatively ascribed to a higher order of parallel side-product formation.
Introduction
Furfural is a promising bio-based platform molecule that presents applications in the fuel and chemical industries and forms a rich source of derivatives.1 Industrial furfural production relies largely on batch-wise, acid-catalyzed dehydration of xylose contained in the biomass while it degrades the rest of the biomass.1,2 Emerging approaches spare the biomass by gently extracting the xylose and dehydrating it in a subsequent step.1–4 Dehydration of xylose in water typically delivers furfural with a yield of about 45 mol%, while dehydration in biphasic medium reaches yields of 65 mol%.1,3 Several approaches to further improve the selectivity of xylose dehydration to furfural have been described in the literature, e.g., monophasic aqueous–organic systems with polar organic solvents, such as DMSO or dioxane, or, alternatively, biphasic solvent systems at increased ionic strengths, by adding inorganic salts.5–13 But the improved selectivity comes with significant process challenges and costs, e.g., recovering the xylose from the diluted aqueous hydrolysate to transfer it to the monophasic organic medium or recovering the salt to allow treating or recycling of the aqueous phase in the case of biphasic operation.13,14Important for the optimization of the production of furfural is an understanding of the kinetics of xylose dehydration and the underlying mechanism.15,16 Several intermediate steps in the dehydration process have been hypothesized, such as the formation of partial dehydration products, the isomerization to xylulose, and ring opening and closing.15,17–28 The need to understand the mechanism of sugar dehydration motivates the development of kinetic models that are valid at various reaction conditions.15–28 For example, by kinetic modeling and experimental evidence, Ershova et al. were able to rule out xylulose as a relevant intermediate, relegating it along a parallel reaction pathway.17
Kinetic modeling has been used to compare the effects of different reaction conditions. Heating methods, for example traditional and microwave heating, have been compared.24–27 Kinetic models have also been used to study the effects of different types and concentrations of acid catalysts.18,20,21 In other cases, such models focus specifically on the degradation of furfural, in the presence and absence of sugars, offering insight into the formation of soluble side-products and humins.27,29–31 In most cases these models focus on fully aqueous environments, or exclusively on aqueous–organic biphasic environments.18–21,26,28 There are some instances in which the kinetics of the xylose dehydration in aqueous–organic monophasic systems (e.g., water–DMSO mixtures) has been modeled,23,27,28,31 however, with no particular attention to the solvent effect on the kinetics.28,30
Recently, we reported two efficient methods to convert diluted aqueous xylose to furfural with high selectivity.13,14,32 They are both based on liquid–liquid extraction of xylose, mediated by phenylboronic acid (PBA).33 Specifically, this extraction can be followed by hydrolysis of the resulting phenylboronate diester (PBA2X) and subsequent dehydration of the liberated xylose to furfural under monophasic or biphasic aqueous–organic conditions, the latter proceeding best in the presence of inorganic salts.14,32
The aim of the current work is to develop a kinetic model that describes these novel approaches, more specifically the hydrolysis of the xylose boronate diester to xylose and its subsequent dehydration to furfural, while considering the presence of mono or biphasic media as well as salt. The model can shed light on the differences between monophasic and biphasic operations and the role of salts and phase partitioning.
Results and discussion
Modelling approach to describe the kinetics of xylose dehydration
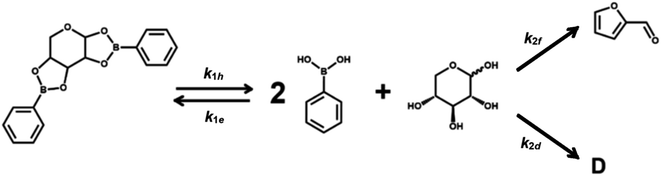
Scheme 1 describes the dehydration of xylose from PBA2X in two consecutive steps, regardless of the characteristics of the solvent system. The first step is the equilibrium of hydrolysis and formation (esterification) of PBA2X, while the second step is the (irreversible) dehydration of free xylose to furfural, with the possible (parallel) formation of by-products.1–3 Sequential degradation of the formed furfural into other side products, like humins, appeared to be marginal under the present conditions and only occurs at high conversions, if at all.1,14,33 Hence, it has not been incorporated in Scheme 1.Under monophasic conditions, where all species are well solubilized in the medium, the first step is defined by the two kinetic rate constants k1h and k1e, which describe the hydrolysis and the boronate ester formation of PBA2X, respectively. In this boronate (de)esterification equilibrium, we ignore the possible presence of intermediates, such as a putative monoester discussed elsewhere.33 The second reaction step, i.e., the dehydration of free xylose, is defined by the kinetic rate constant k2. So, the xylose dehydration from PBA2X can be modeled as presented in Scheme 1, with each step of the process related to a rate constant. In this model, the furfural concentration is not expressed explicitly, only the overall conversion of the xylose. Notice that Scheme 1 suggests a constant ratio between furfural and a degradation product D, which implies a ‘flat’ profile for the xylose-to-furfural selectivity with increasing conversion to >90 mol% (Fig. S1 and S2†), which is consistent with the observations discussed later.
To describe the kinetics of this system, we define the (apparent) equilibrium constant Kc (eqn (1)), which is based on the measurable concentrations, and the previously defined rate constants, k1e and k1h.
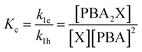 | (1) |
The definition of concentration is trivial for monophasic systems but not for biphasic ones. Under biphasic conditions, the concentration of PBA2X is taken to be in the organic phase (and assumed negligible in the water phase), while the concentration of xylose is taken in the water phase (and is absent in the organic phase), as proven experimentally.33 PBA resides in both phases and therefore the total amount of PBA divided by the total volume, i.e., the volume-weighed concentration average over the two phases, is taken as the overall PBA concentration. The diester is not observed in the aqueous phase probably because of its low solubility in water. In the biphasic case, we hold the rate constants k1h and k1e to describe the combined equilibria of partitioning and (de)esterification.
A simulation of the evolution of the concentrations of the various species (Scheme 1) over time can be built in the following manner. Assumed or fitted values for the three rate constants (k1h, k1e, and k2) can be used to predict the evolution of the concentration of free xylose with time (eqn (2)).
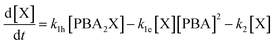 | (2) |
The first term of the equation describes the hydrolysis of PBA2X, with the role of water being embedded in k1h, the second the diester formation, and the third the xylose dehydration reaction. Similarly, eqn (3) describes the evolution of the concentration of PBA2X with time.
 | (3) |
PBA2X is always observed experimentally when both xylose and PBA are used, both in case using PBA2X as a starting material as well as when starting from free xylose and PBA.
Through eqn (2) and (3), the evolution of the concentrations of these two species can be evaluated in the desired time window, using the known initial concentrations of PBA2X and xylose. The concentration of PBA can then be calculated at any point of time from its mass balance, knowing the total amounts of PBA in the system and that of the PBA2X diester in the total volume.
The calculated overall xylose conversion, Xcalc, is obtained from eqn (4), taking into account the sugar in both its diester and free forms. The initial concentrations are indicated with the suffix “0”.
 | (4) |
Such simulations were used (see below) to fit the experimental data of xylose dehydration by varying three fit parameters, i.e., k1h, Kc, and k2 (k1e is calculated from Kck1h, eqn (1)). Specifically, Kc was chosen as a fit parameter over k1e as the former is descriptive of the properties of the medium (e.g., water, water–sulfolane–aromatic solvents, water–sulfolane or toluene–water). As will be shown, this model is able to handle different combinations of initial concentrations of free xylose, PBA2X and PBA using the same values of these three fit parameters, k1h, Kc, and k2. The fitting of the parameters k1h, Kc, and k2 was operated in the same way both at biphasic and monophasic conditions. Part of the data on the dehydration of xylose used in this study (see below), starting from PBA2X and from free xylose in various solvent systems, were taken from our previous work.14,32 Additional experimental work has been conducted both under biphasic conditions at high ionic strengths and different mixing conditions, and under aqueous–organic monophasic conditions, starting from PBA2X and from free xylose.
From the eqn (1)–(4) given above, all species concentrations can be calculated at any point in time, using the starting conditions of a given experimental run. Since the conversion takes hours, 0.01 h is taken as the time interval between time points in our simulations. The model was used to fit the experimental conversion data by least-squares minimization, performed in Excel. The model is implemented in Excel, and all equations are solved numerically in an iterative way. For example, the calculation of the xylose concentration in the aqueous phase is evaluated, from time 0, over a time window (0–4 h) divided into intervals of 0.01 h (Δt), with the concentration of xylose at time t + 1 being related to the concentration at time t of xylose, PBA and PBA2X, following eqn (5).
| [X]t+1 = [X]t + (k1h[PBA2X]t − k1e[X]t[PBA]t2 − k2[X]t)Δt | (5) |
The changes in the concentration of PBA2X are calculated in a similar manner. The fitting of the data is also performed in Excel. An initial value is given to all the model parameters to be fitted, namely Kc, k2 and k1h (k1e is derived from Kc and k1h and not fitted independently). Conversion values at each time for which an experimental value is available, are obtained from the simulation and compared to the experimental ones. A standard least-squares minimization routine is used to minimize the sum of errors over all conversion time points by varying the model parameters. A cumulative error is used, when applicable, to fit multiple experimental series simultaneously with one set of parameters.
The three fit parameters k1h, Kc, and k2 were optimized independently or kept the same across a set of data series depending on the relation between the experimental cases. For example, all data series for water–toluene biphasic systems at the same ionic strength were fitted altogether with the same values of k1h, Kc, and k2, regardless of the starting reactant (i.e., free xylose, free xylose and PBA, PBA2X). For studying effects of stirring speed, only k1h was varied to describe changes in mass transport, while Kc and k2 were kept the same over the different runs.
The data were fitted using a single lag time, found to be about 0.1 h as determined for cases in the absence of PBA, irrespective of starting feed and medium. This simplification is based on the expectation that the lag time is a consequence of the temperature ramp-up process only, as discussed elsewhere.32 The observed extension of the lag time due to the hydrolysis of PBA2X is simulated explicitly.
Xylose dehydration kinetics at monophasic conditions
The modeling of monophasic aqueous–organic solvent systems is conceptually the most straightforward. To study effects of the water content and polar solvent, experiments were performed on three, mainly organic, monophasic systems, i.e., dioxane–water mixtures (40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 20
1 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v ratio) and a 40
1 v/v ratio) and a 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
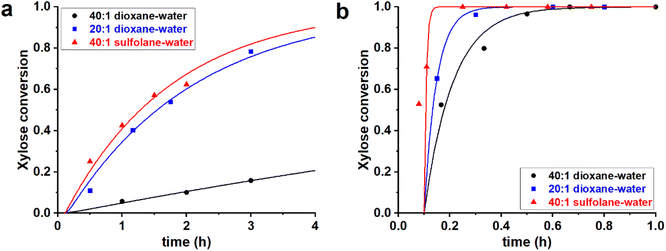
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v sulfolane–water mixture. In all cases H2SO4 was added to reach a [H2SO4] = 0.1 M. These three solvent mixtures were used to perform the reaction of xylose dehydration, starting both from PBA2X and from free xylose (in absence of PBA), yielding a total of six cases. The experimental and fitted data are shown in Fig. 1 (data points and fitted lines), while Table 1 gives the sets of optimized fit parameters. Cases performed in the same solvent mixture but from different starting situations (PBA2X or free xylose) were fitted with the same set of model parameters.
1 v/v sulfolane–water mixture. In all cases H2SO4 was added to reach a [H2SO4] = 0.1 M. These three solvent mixtures were used to perform the reaction of xylose dehydration, starting both from PBA2X and from free xylose (in absence of PBA), yielding a total of six cases. The experimental and fitted data are shown in Fig. 1 (data points and fitted lines), while Table 1 gives the sets of optimized fit parameters. Cases performed in the same solvent mixture but from different starting situations (PBA2X or free xylose) were fitted with the same set of model parameters.
| Starting material | Solvent system | k1h (h−1) | k1e (h−1 M−2) | Kc (M−2) | k2 (h−1) |
|---|---|---|---|---|---|
| PBA2X | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dioxane–water 1 dioxane–water |
0.49 | (0) | (0) | 19 |
| Free xylose | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dioxane–water 1 dioxane–water |
n.a. | n.a. | n.a. | 19 |
| PBA2X | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dioxane–water 1 dioxane–water |
0.06 | (0) | (0) | 8.6 |
| Free xylose | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dioxane–water 1 dioxane–water |
n.a. | n.a. | n.a. | 8.6 |
| PBA2X | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 sulfolane–water 1 sulfolane–water |
0.59 | (0) | (0) | 71 |
| Free xylose | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 sulfolane–water 1 sulfolane–water |
n.a. | n.a. | n.a. | 71 |
All data series fitted well with a single lag time of 0.1 h. In the case of free xylose in sulfolane, the somewhat poorer fit is the result of the fact that the reaction in sulfolane is too fast, leading to significant conversion during the temperature ramp-up and too few data points that can be assessed with sufficient accuracy. In all cases, the back-esterification could be completely ignored, meaning that any value of Kc > 0 M−2 (k1e > 0 h−1 M−2) did not lead to an improvement of the fit. This is indicated in Table 1 as “(0)”. The effect of starting from PBA2X compared to free xylose is seen as a slower conversion in the former case, observed both in the experimental data and in the fitted curves (Fig. 1). This is attributed to the necessary hydrolysis of the PBA2X diester, which has an effect on the equilibrium concentration of free xylose and on the rate of its formation. As the model shows (Fig. 2a), the concentration of free xylose remains very low under these conditions.
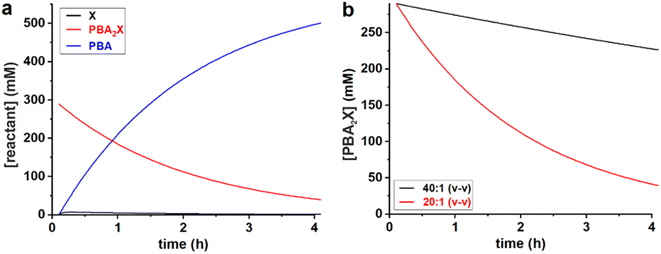 | ||
Fig. 2 Model curves for the concentrations of (a) PBA, free xylose and PBA2X in the 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dioxane system, and of (b) PBA2X in the 40 1 dioxane system, and of (b) PBA2X in the 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 20 1 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dioxane–water systems. 1 dioxane–water systems. | ||
The effect of the water contents is clearly seen by comparing the 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 40
1 and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dioxane–water cases (Table 1, Fig. 2b): more water leads to a faster ester hydrolysis and a faster xylose dehydration. It should be noticed that a doubling of water concentration results in a nearly 10-fold acceleration of the hydrolysis. This disproportionate acceleration could be in part explained by a high order in water for the ester hydrolysis, which would be consistent with the need for two molecules of water to hydrolyze one boronate group. When comparing the 40
1 dioxane–water cases (Table 1, Fig. 2b): more water leads to a faster ester hydrolysis and a faster xylose dehydration. It should be noticed that a doubling of water concentration results in a nearly 10-fold acceleration of the hydrolysis. This disproportionate acceleration could be in part explained by a high order in water for the ester hydrolysis, which would be consistent with the need for two molecules of water to hydrolyze one boronate group. When comparing the 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dioxane–water and 40
1 dioxane–water and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 sulfolane–water cases, the latter is an order of magnitude faster, both in ester hydrolysis and in xylose conversion. This is attributed to the higher polarity of sulfolane compared to dioxane.
1 sulfolane–water cases, the latter is an order of magnitude faster, both in ester hydrolysis and in xylose conversion. This is attributed to the higher polarity of sulfolane compared to dioxane.
PBA-containing, three-solvent mixtures of water with polar aprotic organic and aromatic solvents (e.g., toluene–sulfolane–water, pH = 1) transition from biphasic at room temperature to monophasic at reaction conditions.14 Three different starting conditions (PBA2X, free xylose in the presence of PBA, and free xylose in the absence of PBA) and two different solvent systems (toluene–sulfolane–water and methylnaphthalene (MN)–sulfolane–water, in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio) yield in total six cases; their experimental data have been reported elsewhere.14 All the cases were fitted independently. The experimental and fitted data are shown in Fig. 3, while Table 2 gives the sets of optimized fit parameters.
1 volume ratio) yield in total six cases; their experimental data have been reported elsewhere.14 All the cases were fitted independently. The experimental and fitted data are shown in Fig. 3, while Table 2 gives the sets of optimized fit parameters.
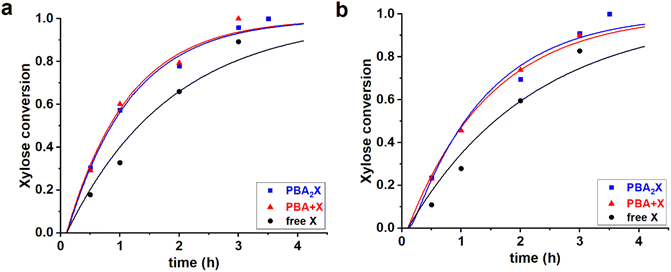 | ||
Fig. 3 Experimental data points (markers) and model curves (lines) for the xylose conversion for the reaction of dehydration of 94 mM of PBA2X (blue), free xylose in presence of 194 mM PBA (red), and free xylose (black), performed at 180 °C in (a) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v/v of toluene–sulfolane–water (pH = 1) and (b) 1 1 v/v/v of toluene–sulfolane–water (pH = 1) and (b) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v/v of MN–sulfolane–water (pH = 1) three-solvent systems. The raw data for toluene–sulfolane–water (a) have been reported before.14 1 v/v/v of MN–sulfolane–water (pH = 1) three-solvent systems. The raw data for toluene–sulfolane–water (a) have been reported before.14 | ||
| Starting material | Aromatic solvent | k1h (h−1) | k1e (h−1 M−2) | Kc (M−2) | k2 (h−1) |
|---|---|---|---|---|---|
| PBA2X | Toluene | 110 | (0) | (0) | 0.92 |
| PBA + xylose | Toluene | 110 | (0) | (0) | 0.95 |
| Xylose | Toluene | n.a. | n.a. | n.a. | 0.57 |
| PBA2X | MN | 15 | (0) | (0) | 0.77 |
| PBA + xylose | MN | 15 | (0) | (0) | 0.70 |
| Xylose | MN | n.a. | n.a. | n.a. | 0.47 |
All data series fitted well with a single lag time of 0.1 h. In all cases, the back-esterification could be completely ignored again, meaning that any value of Kc > 0 M−2 (k1e > 0 h−1 M−2) did not lead to an improvement of the fit. This is indicated in Table 2 as “(0)”. This is a confirmation that, in the case of PBA2X, the process of formation of PBA2X from free xylose is virtually non-existent, because it is outcompeted by the xylose dehydration.14 Conversely, hydrolysis of the diester, which results in the release of xylose, is a fast process as witnessed by the high k1h value. This is supported by the fact that the two cases in the presence of PBA are practically superimposable (Fig. 3). Notably, even though fitted independently, the cases starting from PBA2X and from free xylose in presence of PBA, gave the same value of k1h, and also the xylose conversion steps are comparable, indicating that the two solvent systems are very comparable in their ester hydrolysis and xylose conversion. In the absence of PBA, the reaction is slower, seen in the model fit as a lower value of k2. This can be rationalized considering that, in the absence of PBA, the system does not transition to monophasic at the reaction temperature.14 The modeling of biphasic systems is discussed separately below. It should also be noticed that the switch from toluene to MN decelerated both the diester hydrolysis and xylose dehydration reactions.
When comparing the water-lean, polar organic–aqueous systems (Table 1) to the water-richer, three-solvent systems (Table 2) discussed above, we note that the ester hydrolysis is more than two orders of magnitude faster for the water-rich system, while the xylose dehydration is 1–2 orders slower. More specifically, the water-lean systems appeared to be rate-limited by the ester hydrolysis step with k1h/k2 ratio < 0.05, whereas the water-rich systems were rate-limited by the dehydration step with k1h/k2 ratio > 20. The faster ester hydrolysis is attributed to the much higher water contents in the three-solvent system and is in line with the difference observed for the different dioxane–water mixtures discussed above. The slower dehydration reaction is likely due to the higher water concentration as well. Additional model curves predict a clear difference between the active concentration of xylose in the two systems; the concentration stays close to 0 mM throughout the whole reaction time in the organic–aqueous monophasic system (Fig. S3†), while it peaks right away in the three-solvent systems (Fig. S4†).
Xylose dehydration kinetics at biphasic conditions
Moving from monophasic to biphasic conditions, modeling the kinetics allows us to study additional effects of the partitioning of reagents and products over the two phases. We here study the effects of a biphasic system on the xylose dehydration for different starting conditions, when varying the nature of the organic phase, the ionic strength of the water phase and the stirring of both phases, as reported in part elsewhere32 and in part from new experiments. Specifically, we compare the dehydration of PBA2X and free xylose, with and without PBA, in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene–water biphasic system, both at 0.1 M and 3.1 M ionic strength (without and with added salt, i.e., Na2SO4, respectively), yielding in total six cases. In all cases H2SO4 was added to reach a [H2SO4] = 0.1 M. Subsequently, the 1
1 toluene–water biphasic system, both at 0.1 M and 3.1 M ionic strength (without and with added salt, i.e., Na2SO4, respectively), yielding in total six cases. In all cases H2SO4 was added to reach a [H2SO4] = 0.1 M. Subsequently, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene–water biphasic system is compared with a 1
1 toluene–water biphasic system is compared with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 MN–water biphasic system, both at 3.1 M ionic strength and using PBA2X as a starting material. For both systems, three different stirring speeds were used, i.e., no stirring, regular and heavy stirring,32 to explore the importance of interfacial area and mass transfer on the rate of hydrolysis, leading to a total of six cases. The experimental and fitted data are shown in Fig. 4 and 5, while Table 3 gives the sets of optimized fit parameters. Cases performed in the same solvent mixture but from different starting situations (PBA2X or free xylose) were fitted with the same set of model parameters.
1 MN–water biphasic system, both at 3.1 M ionic strength and using PBA2X as a starting material. For both systems, three different stirring speeds were used, i.e., no stirring, regular and heavy stirring,32 to explore the importance of interfacial area and mass transfer on the rate of hydrolysis, leading to a total of six cases. The experimental and fitted data are shown in Fig. 4 and 5, while Table 3 gives the sets of optimized fit parameters. Cases performed in the same solvent mixture but from different starting situations (PBA2X or free xylose) were fitted with the same set of model parameters.
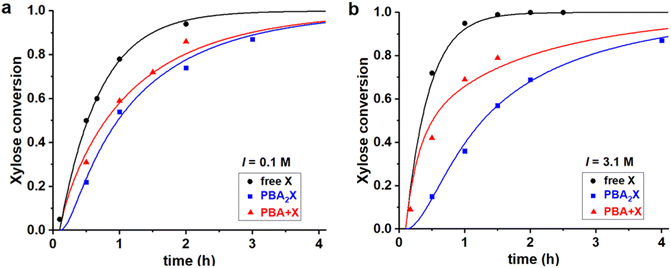 | ||
Fig. 4 Experimental data points (markers) and model curves (lines) for the xylose conversion, performed at 200 °C, at pH = 1, for a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene–water biphasic system, starting from 320 mM of various starting materials, (a) at I = 0.1 M and (b) at I = 3.1 M. The raw data have been reported before.32 1 toluene–water biphasic system, starting from 320 mM of various starting materials, (a) at I = 0.1 M and (b) at I = 3.1 M. The raw data have been reported before.32 | ||
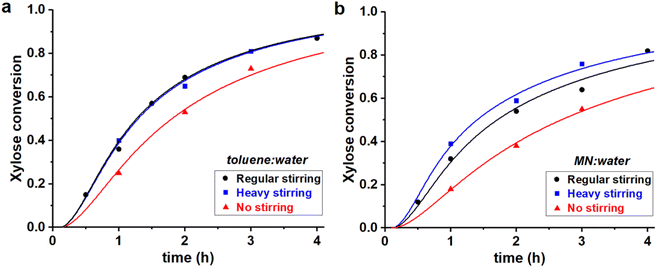 | ||
Fig. 5 Experimental data points (markers) and model curves (lines) for the xylose conversion, performed at 200 °C, at pH = 1, at I = 3.1 M, starting from 320 mM of PBA2X, at different stirring conditions, in (a) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene–water, (b) 1 1 toluene–water, (b) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 MN–water. The raw data for toluene (a) have been reported before.32 1 MN–water. The raw data for toluene (a) have been reported before.32 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene–water (pH = 1), biphasic system at different ionic strengths (I) and for the xylose dehydration reaction performed at 200 °C at 3.1 M ionic strength in a 1
1 toluene–water (pH = 1), biphasic system at different ionic strengths (I) and for the xylose dehydration reaction performed at 200 °C at 3.1 M ionic strength in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 organic–aqueous biphasic system composed of water (pH = 1) and either toluene or MN, at various stirring conditions
1 organic–aqueous biphasic system composed of water (pH = 1) and either toluene or MN, at various stirring conditions
| I (M) | Organic solvent | Stirring | k1h (h−1) | k1e (h−1 M−2) | Kc (M−2) | k2 (h−1) |
|---|---|---|---|---|---|---|
| 0.1 | Toluene | Regular | 4.2 | 56 | 13 | 1.6 |
| 3.1 | Toluene | Regular | 1.0 | 36 | 35 | 2.8 |
| 3.1 | Toluene | No | 0.56 | 19 | 35 | 2.8 |
| 3.1 | Toluene | Heavy | 1.0 | 35 | 35 | 2.8 |
| 3.1 | MN | Regular | 0.73 | 61 | 84 | 2.8 |
| 3.1 | MN | No | 0.35 | 29 | 84 | 2.8 |
| 3.1 | MN | Heavy | 1.1 | 94 | 84 | 2.8 |
All three cases, both in Fig. 4a and b, are fitted with a single set of parameters (shown in the first two lines in Table 3). Apparently, only changing the model input regarding the concentrations of the starting materials is sufficient to explain the differences in performance, which leads to good fits of the experimental data in all cases. Notably, a pronounced induction period observed upon starting from the boronate diester in the organic phase (Fig. 4, blue curves) is reproduced well by the model, despite that a single lag time of 0.1 h was used in all cases. Hence, the model confirms that the apparent, slower reaction at high salt when starting from the diester in the organic phase, can be attributed purely to the inhibited phase transfer and hydrolysis of the ester in water.32 The fits also confirm earlier reports that the rate constant for xylose dehydration in water (k2) is enhanced by increasing the ionic strength.8–10 High ionic strengths also result in an increased Kc (by a factor 2.6), as expected for a classical desalting effect.8–10 Kinetically, the salt effect is even stronger, as seen in particular in k1h (4.0 times lower at 3.1 M when compared to 0.1 M ionic strength), which represents the combined partitioning plus ester hydrolysis, and its reverse rate constant k1e is lowered as well (by a factor 1.5).
Differently than the monophasic cases, at biphasic conditions k1e is always significant, indicating that the back-esterification of xylose to PBA2X is relevant. In fact, k1e largely exceeds k2. At full hydrolysis that is characterized by a PBA concentration of 0.6 M, the pseudo-1st order rate constant for esterification k1e*[PBA]2 also exceeds the dehydration rate constant by 10-fold, indicating that the esterification of free xylose outcompetes its dehydration to furfural. It should be recalled that the opposite behavior was observed for the monophasic operation discussed above. Additionally, moving from the toluene–water to the MN–water solvent system affects the partitioning of the diester and the fitting parameters Kc, k1h and k1e. However, at the same ionic strength in water, the rate constant k2 is kept unvaried, as the xylose dehydration takes place in the aqueous phase and should be independent of the organic phase. Furthermore, the fit parameter Kc, which is an (apparent) equilibrium constant, is kept constant for all cases in which the solvent system is the same.
After the optimization of the parameter sets, the model simulations of all species concentrations over time can be viewed. It is interesting to follow the differences in the trends of the concentration of free xylose in water at different initial conditions (Fig. 6). The case with PBA2X as the starting material is compared to the one with free xylose (in water) with a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of PBA (in toluene) (Fig. 6a). When starting from PBA2X, the xylose concentration initially increases and, after reaching a maximum at around 0.5 h, starts to decrease, as more and more xylose is being converted. In contrast, when starting from free xylose in water, the concentration of xylose in water drops steadily. After about 0.5 h, the two curves become strongly comparable because the ester partitioning and hydrolysis/esterification have equilibrated and are following the pace of conversion, although the delay (of approx. 0.15 h) in the case starting from the diester is still apparent. Additional model curves show that both in the case of MN and toluene no stirring results in a lower, more distributed profile for the xylose concentration, while heavy stirring causes a higher peak of free xylose in the early stages of the reaction (Fig. S5†).
1 molar ratio of PBA (in toluene) (Fig. 6a). When starting from PBA2X, the xylose concentration initially increases and, after reaching a maximum at around 0.5 h, starts to decrease, as more and more xylose is being converted. In contrast, when starting from free xylose in water, the concentration of xylose in water drops steadily. After about 0.5 h, the two curves become strongly comparable because the ester partitioning and hydrolysis/esterification have equilibrated and are following the pace of conversion, although the delay (of approx. 0.15 h) in the case starting from the diester is still apparent. Additional model curves show that both in the case of MN and toluene no stirring results in a lower, more distributed profile for the xylose concentration, while heavy stirring causes a higher peak of free xylose in the early stages of the reaction (Fig. S5†).
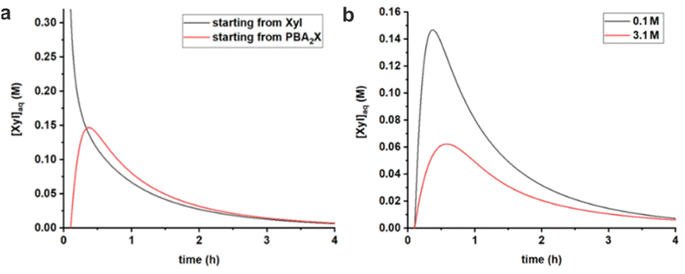 | ||
| Fig. 6 Comparison of simulated free xylose concentrations in water versus time, using rate constants given in Table 3, (a) starting from free sugar in water and PBA in toluene, or with PBA2X in toluene, both at 0.1 M ionic strength, and (b) starting with PBA2X in toluene at 0.1 M or at 3.1 M ionic strength. | ||
Comparing the cases with PBA2X as a starting material, but at different ionic strengths (Fig. 6b), shows that, at any given time, the total amount of free xylose present in the aqueous phase is considerably lower at high salt concentration, as a result of the more favorable partitioning of the diester into the organic phase as explained above. As explained above, this results in a slower apparent conversion at high salt, caused by the fact that the xylose concentration is lowered by approx. a factor 2.5 (at the maximum), while the reaction rate constant is enhanced by only a factor 1.7.
Table 3 shows that Kc increases when moving from toluene to MN, while keeping the ionic strength constant. This agrees with previous data on the extraction process and can be rationalized by a stronger interaction between MN and the diester and, more importantly, the lower solubility of water in MN compared to toluene.32 This depresses the hydrolysis rate of the ester and, consequently, the apparent xylose conversion is slower in MN (Fig. 5), even though the xylose dehydration rate constant is the same.
The stirring speed has a pronounced effect on the rate constants of hydrolysis/formation of the diester for both solvents (Fig. 5, Table 3). Overall, an increased stirring speed increases both rate constants k1h and k1e, indicating that the phase transfer is limiting the overall rate of hydrolysis. Switching from no stirring to regular stirring resulted in an about 2-fold increase of k1h (and also k1e since Kc was kept constant) for both solvents. For toluene there was no effect of increasing the stirring speed further. In contrast, for MN, the highest stirring speed increased the rate constants further. These effects are also observed from the free xylose concentrations obtained from the model simulations (Fig. 7).
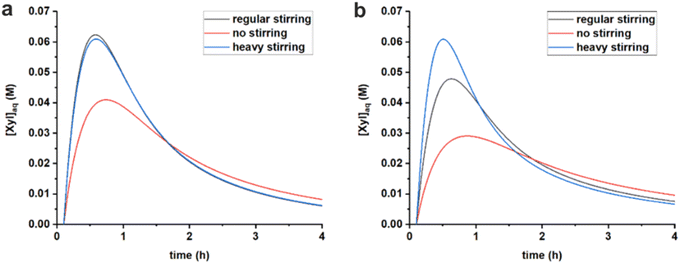 | ||
Fig. 7 Comparison of simulated free xylose concentrations in water starting from 320 mM PBA2X in toluene, at 3.1 M ionic strength, applying different stirring speeds and using the rate constants of Table 3, (a) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene–water system and (b) in a 1 1 toluene–water system and (b) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 MN–water system. 1 MN–water system. | ||
Tentatively, k1h is assumed to reach a maximum, of approx. 1 h−1, which is not further increased by better mixing. The difference between MN and toluene in reaching optimal mixing can potentially be explained by the difference in surface tension of the organic phase. The approx. 30% higher surface tension of MN (38.6 dyne cm−1 vs. 28.4 dyne cm−1 for toluene)34 could credibly require heavier agitation to properly disperse the organic and aqueous phases.
Selectivity of the xylose dehydration
So far, the kinetic model has focused on describing the balance between the hydrolysis of PBA2X and the subsequent dehydration of the liberated xylose, and the impact that the reaction medium exercises on this balance. However, the model has not yet addressed the changes in selectivity observed for the various conditions. Expanding the model to address the selectivity toward furfural is therefore highly relevant.Limiting side reactions is an important issue to boost selectivity further.1 Understanding the kinetics of the formation of side products will help finding conditions to minimize them. Commonly observed experimentally, the xylose-to-furfural selectivity does not start at 100 mol% when conversion commences, and there can be a large part of the reaction time in which the selectivity appears constant, as is also observed in the experiments described here.11,17,26,35–37 As shown in Fig. S1 and S2,† the selectivity profiles are flat over large time and conversion windows, from 5 to approx. 95 mol% conversion. All series together (Fig. 8, data points) show approximately linear trends with slightly varying slopes. Intriguingly, the furfural selectivity is seen to vary between approx. 60 and 90 mol% for the various cases. The results presented here, therefore, all seem to indicate parallel reactions for xylose conversion to furfural and to degradation products (see Fig. S6a, c and e† for k1/k2 = 5). In contrast, these results do not support the selectivity–conversion profiles that are typical for consecutive reactions of xylose conversion to furfural and subsequent furfural degradation that are typically reported for operation in water:1,33 they show a selectivity that is 100 mol% at <10 mol% conversion and dropping with increasing conversion (see Fig. S6b and f† for the same k1/k2 = 5).
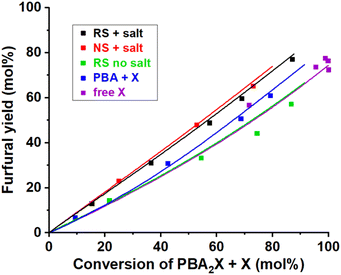 | ||
| Fig. 8 Furfural yield vs. overall xylose conversion in biphasic toluene–water medium at 200 °C under various conditions. The reference case run with PBA2X in 3.1 M saline medium and regular stirring (RS + salt), while single variations included operation in absence of salt (RS no salt), no stirring (NS + salt), starting from free xylose (free X) or from xylose + 2PBA (PBA + X). The points represent the experimental data, while the lines represent the model with the parameters shown in Table 4. | ||
Scheme 1 shows that the model assumes a concomitant production of furfural and by-products, all encompassed in the constant k2. With the aim to better understand the selectivity differences observed in biphasic systems, e.g., with different stirring methods, salinity or starting reagents, k2 can be dissected into k2f, to represent the contribution by the production of furfural, and k2d, to represent the formation of xylose degradation products.
The model based on Scheme 1 and Fig. S6a† can be used to describe the observed selectivity shifts occurring for different reaction conditions (Fig. S1 and S2†). In this scenario, k2f is defined as k2f = Savgk2, where Savg is the average selectivity over the conversion window. Hence, k2d can be obtained by subtracting k2f from k2 (additional information in the ESI†). The resulting deconvolution (detailed in Table S1†) indeed allows to fit the yield profiles reported in Fig. S1 and S2† with reasonable quality. However, it does not provide any insight into the chemical basis for such selectivity shifts between 60 and 90 mol%. For instance, it can fit the increased furfural selectivity achieved by increasing the ionic strength of the aqueous phase, by avoiding stirring of the medium or by switching from free xylose to PBA2X as feed. The selectivity increase is achieved by increasing the k2f/k2d ratio from 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 10
1 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, but this does not provide a rationale for the changing ratio.
1, but this does not provide a rationale for the changing ratio.
Interestingly, the conditions that favor selective furfural production also appear to disfavor the buildup of free xylose in the aqueous phase through slow PBA2X hydrolysis, as discussed earlier. Hence, these conditions could credibly disfavor degradation reactions that are higher order in xylose, e.g., by involving the condensation of several xylose molecules with each other (see Fig. S6c†). To investigate this hypothesis, we have adapted our model by describing the xylose conversion with two parallel reactions, one to furfural (k2f) that is first order in xylose and the other to degradation products (k2d) that is arbitrarily set to be second order in xylose (eqn (6)).
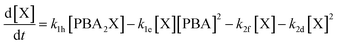 | (6) |
Moreover, in fitting the datasets, we have fixed the k2f/k2d ratio, i.e., we have fixed the intrinsic selectivity, in an attempt to describe all selectivity changes by changes in the xylose concentration profile only. We maintained the same logic as applied earlier by keeping Kc constant for the same solvent systems (i.e., toluene–water 0.1 M, or toluene–water 3.1 M, irrespective of stirring) and keeping k2f and k2d constant for the same aqueous phase (i.e., 0.1 and 3.1 M, irrespective of stirring). In this scenario, both the conversion of xylose and the production of furfural are modeled. The concentration of furfural [F] is followed using eqn (7). The furfural mol% produced are also used in the fit of the data to the model, specifically based on eqn (8).
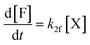 | (7) |
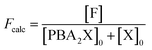 | (8) |
As already mentioned, the case of heavy stirring in toluene is problematic as the model overestimates furfural production (Fig. S7†). For this reason, these data were not considered in the fit, which resulted in a better overall fit of the other cases and comparable trends between biphasic operation in toluene and MN (Fig. S8†). The resulting kinetic data are summarized in Table 4.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene–water (pH = 1), biphasic system at different ionic strengths (I) and for the xylose dehydration reaction performed at 200 °C at 3.1 M ionic strength in a 1
1 toluene–water (pH = 1), biphasic system at different ionic strengths (I) and for the xylose dehydration reaction performed at 200 °C at 3.1 M ionic strength in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 organic–aqueous biphasic system composed of water (pH = 1) and either toluene or MN, at various stirring conditionsa
1 organic–aqueous biphasic system composed of water (pH = 1) and either toluene or MN, at various stirring conditionsa
| Stirring | I (M) | Solvent | Source | k1h (h−1) | k1e (h−1 M−2) | k2f (h−1) | k2d (h−1 M−1) | Kc (M−2) |
|---|---|---|---|---|---|---|---|---|
| a This fitting considers a parallel degradation of xylose that is 2nd order in xylose, and uses a (fitted) constant k2f/k2d = 0.42 over all the cases. | ||||||||
| Regular | 0.1 | Toluene | X (no PBA) | — | — | 0.50 | 1.2 | — |
| Regular | 0.1 | Toluene | X (PBA) | 27 | 0 | 0.50 | 1.2 | 0 |
| Regular | 0.1 | Toluene | PBA2X | 27 | 0 | 0.50 | 1.2 | 0 |
| Regular | 3.1 | Toluene | X (no PBA) | — | — | 2.1 | 4.9 | — |
| Regular | 3.1 | Toluene | X (PBA) | 1.2 | 9.0 | 2.1 | 4.9 | 7.8 |
| No | 3.1 | Toluene | PBA2X | 0.62 | 4.8 | 2.1 | 4.9 | 7.8 |
| Regular | 3.1 | Toluene | PBA2X | 1.1 | 9.0 | 2.1 | 4.9 | 7.8 |
| Heavy | 3.1 | Toluene | PBA2X | 1.2 | 9.1 | 2.1 | 4.9 | 7.8 |
| No | 3.1 | MN | PBA2X | 0.33 | 6.8 | 2.1 | 4.9 | 21 |
| Regular | 3.1 | MN | PBA2X | 1.0 | 21 | 2.1 | 4.9 | 21 |
| Heavy | 3.1 | MN | PBA2X | 1.1 | 22 | 2.1 | 4.9 | 21 |
This model reproduces all selectivity shifts observed experimentally without having to tune the k2f/k2d ratio (Fig. 8, data and model lines). It reproduces the benefit of high salinity, by decelerating the PBA2X hydrolysis by 20-fold and accelerating the xylose conversion to furfural and degradation products by 4-fold (Table 4). It reproduces the benefit of starting from PBA2X rather than free xylose or xylose + PBA by allowing slow xylose release by PBA2X hydrolysis (Table 4). Finally, it explains the slight increase in selectivity in absence of stirring by calculating a 50% slower PBA2X hydrolysis (Table 4), arguably due to lower interfacial area between toluene and saline aqueous phase and concomitantly slower mass transfer. The quality of the model is further illustrated by the parity plots illustrated in Fig. S9.†
It is also worth noticing that such reaction scheme shows a slight increase in selectivity upon increasing conversion, e.g., from 82 to 87 mol% for k1/k2 = 5 (Fig. S6e†). Such trend could also be detected in our experimental selectivity profiles of Fig. S1 and S2† (e.g., in Fig. S2a, d and e), though within experimental error.
The analysis reported here shows the possibility to account for selectivity changes through changes in xylose concentration profiles only. However, it does not pretend to demonstrate that this is the only cause, and that there would be no possible contribution from changes in k2f/k2d ratios. For instance, change in salinity could credibly affect the k2f/k2d ratio by affecting the solvation of transition states. In fact, other assumptions can be added to the relation between k2f and k2d. In fitting, either k2d can be kept constant for all cases, assuming that the degradation is not influenced by the ionic strength, or k2f and k2d can be fitted independently. These two scenarios appeared to fit the data equally well, with adjusted R2 of >0.99 (Fig. S10 and Table S2†), and the resulting k and Kc values are reported in Tables S3 and S4.† Moreover, there are experimental observations that do not fit the analysis. Specifically, the model fails to reproduce the lower selectivity observed when switching from toluene–water to MN–water, which are obvious outliers in the parity plot for selectivity (Fig. S11†). For this reason, those points were excluded from the analysis of Fig. 8.
It should be mentioned here that the selectivity profile of aqueous reaction is typically described by a combination of parallel condensation of xylose with itself and consecutive degradation of furfural with unconverted xylose. This scheme describes a selectivity of approx. 50 mol% at low conversion, which is dictated by the parallel reactions, and it drops monotonously with increasing conversion due to the consecutive degradation of furfural. Such profile does not fit the flat selectivity profile observed here between 5 and 95 mol% conversion for monophasic organic and biphasic systems.
Finally, while fitting the model to the data does not require consecutive furfural degradation for conversions up to 95%, it does not fully exclude the possibility of minor consecutive degradation of furfural with itself at full conversion. Fig. S1c and S2c† indeed suggest a minor drop in selectivity (from approx. 75 to approx. 70 mol%) between 1.5 h and 2.5 h, when the xylose is fully converted. Yet, such consecutive degradation remains insignificant for all other conditions applied in this study.
Conclusions
A kinetic model has been developed to describe the xylose dehydration at various reaction conditions, implementing the possibility of starting the reaction from PBA2X. This model encompasses all the steps from PBA2X hydrolysis to xylose dehydration. The fitting of the experimental data provided various sets of rate constants, which allow to isolate the effects of changing the solvent system, the stirring rate, etc., on each reaction step, deepening the understanding of the observed xylose conversion and xylose-to-furfural selectivity.Overall, the results described in this work show important aspects of the process. Firstly, xylose dehydration to furfural is very fast in water-lean organic media but much slower in water-rich media and in the aqueous phase of biphasic media. It is nevertheless accelerated by high salinity in the latter case. Secondly, the hydrolysis of the xylose boronate diester is a key reaction step in the process. It is fast and not limiting for water-rich monophasic systems (sulfolane–toluene–water) but becomes rate-limiting for water-lean monophasic systems and for biphasic systems. In the latter case it is even aggravated by high salinity or insufficient stirring. Thirdly, the effect of salinity and stirring on the selectivity plateau can be largely explained indirectly by the effect they have on PBA2X hydrolysis and, thereby, the effective xylose profile in the aqueous phase. This assumes that the xylose degradation is higher (e.g., 2nd) order in xylose than the desired furfural formation.
Additionally, this model allows to obtain curves that describe the evolution of the concentrations of the relevant species in solution (i.e., PBA2X, PBA and free xylose), which are, at times, impossible to gather experimentally. These model curves can further support hypotheses on the mechanism of dehydration and on the rate-limiting step, which varies from case to case. Applying the model to various cases resulted in an understanding of its limitations, which opens the possible application of such a kinetic model to other, more general, cases, not necessarily limited to the processes of biomass valorization.
Experimental section
Chemicals
D-(+)-Xylose (>99%), D2O (99.9% atom D), toluene-d8 (99% atom D), 3-(trimethylsilyl)propionic-2,2,3,3-d4 acid sodium salt (TMSP, 98% atom D), 1-methylnaphthalene (98%), sodium sulfate (99%), sulfolane (99%) were purchased from Sigma-Aldrich, while phenylboronic acid (PBA, 99%), dioxane (99%) and tetramethylsilane (TMS) were obtained from Alfa Aesar.Methods and equipment
All chemicals were used without further purification. PBA2X was obtained by extraction of xylose from water using PBA in toluene in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PBA
1 PBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xylose ratio.33 1H-NMR spectra were recorded at a 400 MHz Bruker spectrometer in a 1
xylose ratio.33 1H-NMR spectra were recorded at a 400 MHz Bruker spectrometer in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 H2O/D2O mixture with TMSP as the internal standard or in a 1
1 H2O/D2O mixture with TMSP as the internal standard or in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 organic solvent/toluene-d8 with TMS as the internal standard. In all cases the reactions were performed using a heating mantle and hard-glass reaction vessels.
1 organic solvent/toluene-d8 with TMS as the internal standard. In all cases the reactions were performed using a heating mantle and hard-glass reaction vessels.
Xylose conversion to furfural
A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v biphasic system (each solvent 2 mL) of 1-methylnaphthalene and water (pH = 1 from added H2SO4), containing an overall concentration of xylose of 160 mM (either 320 mM in its free form in water or 320 mM as PBA diester in the organic phase), and an ionic strength of 3.1 M was heated at 200 °C for reacting times varying between 0.1 and 4 h. In the case of the experiments performed with free xylose as the starting material, PBA was also added to the mixture, in a 2
1 v/v biphasic system (each solvent 2 mL) of 1-methylnaphthalene and water (pH = 1 from added H2SO4), containing an overall concentration of xylose of 160 mM (either 320 mM in its free form in water or 320 mM as PBA diester in the organic phase), and an ionic strength of 3.1 M was heated at 200 °C for reacting times varying between 0.1 and 4 h. In the case of the experiments performed with free xylose as the starting material, PBA was also added to the mixture, in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio to xylose. Stirring was either avoided or applied at 1000 rpm, either with a stirring rod of 6 mm or with an oval stirring bar of 1.6 cm. The latter fits the vessel but it is position diagonally on its bottom so, when the magnetic rotation starts, its rotation ensures turbulent mixing. In the case of the experiment at fully aqueous–organic monophasic conditions, a 20
1 molar ratio to xylose. Stirring was either avoided or applied at 1000 rpm, either with a stirring rod of 6 mm or with an oval stirring bar of 1.6 cm. The latter fits the vessel but it is position diagonally on its bottom so, when the magnetic rotation starts, its rotation ensures turbulent mixing. In the case of the experiment at fully aqueous–organic monophasic conditions, a 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 40
1 or 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v/monophasic systems (total volume of 6 mL) of either dioxane or sulfolane and water, with a total [H+] = 0.1 M (by addition of H2SO4), containing an overall concentration of 290 mM of xylose (either in its free form or as a PBA diester) was heated at 200 °C for reacting times varying between 0.1 and 4 h. Stirring was performed with a stirring bar of 6 mm at 1000 rpm. Prior the analysis with 1H-NMR spectroscopy, all the reactions were stopped by manually removing the reaction vessel from the heating bath and cooling to room temperature.
1 v/v/monophasic systems (total volume of 6 mL) of either dioxane or sulfolane and water, with a total [H+] = 0.1 M (by addition of H2SO4), containing an overall concentration of 290 mM of xylose (either in its free form or as a PBA diester) was heated at 200 °C for reacting times varying between 0.1 and 4 h. Stirring was performed with a stirring bar of 6 mm at 1000 rpm. Prior the analysis with 1H-NMR spectroscopy, all the reactions were stopped by manually removing the reaction vessel from the heating bath and cooling to room temperature.
Author contributions
J. H. conceived the project. J. H, W. V., J. L. and L. R. defined the approach and refined as the project progressed. L. R. conducted all the practical experimental work and the analysis of the raw data. J. H. provided the concept for the kinetic model. Further data analysis, manuscript preparation and subsequent editing/improvement of the text was performed by all authors.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
Financial support from Shell Global Solutions International B.V. is gratefully acknowledged.References
- J.-P. Lange, E. van der Heide, J. van Buijtenen and R. Price, ChemSusChem, 2012, 5, 150–166 CrossRef CAS PubMed.
- R. Mariscal, P. Maireles-Torres, M. Ojeda, I. Sádaba and M. López Granadosa, Energy Environ. Sci., 2016, 9, 1144–1189 RSC.
- J. E. Romo, N. V. Bollar, C. J. Zimmermann and S. G. Wettstein, ChemCatChem, 2018, 10, 4805–4816 CrossRef PubMed.
- L. Ricciardi, W. Verboom, J.-P. Lange and J. Huskens, ChemSusChem, 2020, 13, 3589–3593 CrossRef CAS PubMed.
- M. Peters, M. F. Eckstein, G. Hartjen, A. C. Spiess, W. Leitner and L. Greiner, Ind. Eng. Chem. Res., 2007, 46, 7073–7078 CrossRef CAS.
- C. B. T. L. Lee and T. Y. Wu, Renewable Sustainable Energy Rev., 2021, 137, 110172 CrossRef CAS.
- Y. Zhao, K. Lu, H. Xu, L. Zhu and S. Wang, Renewable Sustainable Energy Rev., 2021, 139, 110706 CrossRef CAS.
- L. Shuai and J. Luterbacher, ChemSusChem, 2016, 9, 133–155 CrossRef CAS PubMed.
- M. A. Mellmer, C. Sanpitakseree, B. Demir, P. Bai, K. Ma, M. Neurock and J. A. Dumesic, Nat. Catal., 2018, 1, 199–207 CrossRef CAS.
- F. Gao, R. Bai, F. Ferlin, L. Vaccaro, M. Li and Y. Gu, Green Chem., 2020, 22, 6240–6257 RSC.
- K. R. Enslow and A. T. Bell, ChemCatChem, 2015, 7, 479–489 CrossRef CAS.
- D. Montané, J. Salvadó, C. Torras and X. Farriol, Biomass Bioenergy, 2002, 22, 295–304 CrossRef.
- L. Ricciardi, W. Verboom, J.-P. Lange and J. Huskens, Sustainable Energy Fuels, 2022, 6, 11–28 RSC.
- L. Ricciardi, W. Verboom, J.-P. Lange and J. Huskens, Green Chem., 2021, 23, 8079–8088 RSC.
- B. Danon, G. Marcotullio and W. de Jong, Green Chem., 2014, 16, 39–54 RSC.
- B. Girisuta, L. P. B. M. Janssen and H. J. Heeres, Green Chem., 2006, 8, 701–709 RSC.
- O. Ershova, K. Nieminen and H. Sixta, ChemCatChem, 2017, 9, 3031–3040 CrossRef CAS.
- O. Ershova, J. Kanervo, S. Hellsten and H. Sixta, RSC Adv., 2015, 5, 66727–66737 RSC.
- K. Lamminpää, J. Ahola and J. Tanskanen, Ind. Eng. Chem. Res., 2012, 51, 6297–6303 CrossRef.
- R. O'Neill, M. N. Ahmad, L. Vanoye and F. Aiouache, Ind. Eng. Chem. Res., 2009, 48, 4300–4306 CrossRef.
- G. Marcotullio and W. de Jong, Green Chem., 2010, 12, 1739–1746 RSC.
- V. Krzelj, J. Ferreira Liberal, M. Papaioannou, J. van der Schaaf and M. F. Neira d'Angelo, Ind. Eng. Chem. Res., 2020, 59, 11991–12003 CrossRef CAS.
- Q. Jing and X. Lü, Chin. J. Chem. Eng., 2007, 15, 666–669 CrossRef CAS.
- C. Sener, A. H. Motagamwala, D. Martin Alonso and J. A. Dumesic, ChemSusChem, 2018, 11, 2321–2331 CrossRef CAS PubMed.
- L. Ricciardi, W. Verboom, J.-P. Lange and J. Huskens, ACS Sustainable Chem. Eng., 2019, 7, 14273–14279 CrossRef CAS.
- C. Xiouras, N. Radacsi, G. Sturm and G. D. Stefanidis, ChemSusChem, 2016, 9, 2159–2166 CrossRef CAS PubMed.
- R. Weingarten, J. Cho, C. Conner Jr. and G. W. Huber, Green Chem., 2010, 12, 1423–1429 RSC.
- M. Sajid, M. R. Dilshad, M. S. U. Rehman, D. Liu and X. Zhao, Molecules, 2021, 26, 2208 CrossRef CAS PubMed.
- H. Li, A. Deng, J. Ren, C. Liu, W. Wang, F. Peng and R. Sun, Catal. Today, 2014, 234, 251–256 CrossRef CAS.
- K. Lamminpää, J. Ahola and J. Tanskanen, RSC Adv., 2014, 4, 60243–60248 RSC.
- B. Danon, L. van der Aa and W. de Jong, Carbohydr. Res., 2013, 375, 145–152 CrossRef CAS PubMed.
- L. Ricciardi, W. Verboom, J.-P. Lange and J. Huskens, ACS Sustainable Chem. Eng., 2022, 10, 3595–3603 CrossRef CAS.
- L. Ricciardi, W. Verboom, J.-P. Lange and J. Huskens, ACS Sustainable Chem. Eng., 2021, 9, 6632–6638 CrossRef CAS.
- http://https://www.surface-tension.de.
- I. Agirrezabal-Telleria, I. Gandarias and P. L. Arias, Bioresour. Technol., 2013, 143, 258–264 CrossRef CAS PubMed.
- Z. Mor, S. Assouline, J. Tanny, I. M. Lensky and N. G. Lensky, Water Resour. Res., 2018, 54, 1460–1475 CrossRef CAS.
- R. Weingarten, J. Cho, W. C. Conner Jr and G. W. Huber, Green Chem., 2010, 12, 1423–1429 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra06898b |
| This journal is © The Royal Society of Chemistry 2022 |