Extracting kinetic information in catalysis: an automated tool for the exploration of small data†
Pedro S. F.
Mendes‡
 *,
Sébastien
Siradze‡
,
Laura
Pirro
*,
Sébastien
Siradze‡
,
Laura
Pirro
 and
Joris W.
Thybaut
and
Joris W.
Thybaut
 *
*
Laboratory for Chemical Technology, Department of Materials, Textiles and Chemical Engineering, Ghent University, Technologiepark 125, 9052 Ghent, Belgium. E-mail: Pedro.Mendes@UGent.be; Joris.Thybaut@UGent.be
First published on 6th October 2021
Abstract
For numerous reactions in catalysis, the lack of (big) data in kinetics is compensated for by the availability of numerous small, scattered datasets as typically found in the literature. To exploit the potential of such peculiar, small data, incorporation of fundamental knowledge into data-driven approaches is essential. In this work, a novel tool was developed to automatically extract kinetically relevant information from small datasets of steady-state kinetic data for heterogeneously catalysed reactions. The developed tool, based on the principles of qualitative trend analysis, was tailored to the needs of catalysis and enriched with chemical knowledge, balancing thereby the limited amount of data and ensuring that meaningful information is extracted. A detailed account of the development steps discloses how the chemical knowledge was incorporated, such that this approach can inspire new tools and applications. As demonstrated for a hydrodeoxygenation case study, such a tool is the first step into automatic construction of kinetic models, which will ultimately lead to a more rational design of novel catalysts.
1 Introduction
Data is the cornerstone of catalysis: to understand the catalytic action, multiple types of techniques and hence data need to be combined.1,2 As of today, this is still done mostly by experienced researchers, often in a manual and qualitative way. Whereas the role of the researcher is key for the interpretation and generation of new knowledge, software can better integrate data and extract information, typically based on models of statistical or physical nature. Catalysis informatics is a novel research field which aims at putting this computer-aided data exploitation to practice. Informatics tools are created to systematically extract information or knowledge from (catalytic) data.1,3Thanks to open science policies, scientific data is becoming openly available for any researcher to reuse, enabling joint worldwide efforts for, among others, catalyst development. Although several challenges still need to be overcome for useful data sharing to be a reality in chemical engineering and catalysis,4 considerable volumes of additional data are expected to become available in the next few years. In heterogeneous catalysis, the potential of simultaneous exploration of new and historical data for each and every reaction is tremendous, as those have typically been analyzed individually up to now. To do so efficiently, this will require automation in the processing, integration and extraction of information from data, as aimed at by catalysis informatics.1
Performance data plays a central role in catalysis as it is needed to measure key indicators, such as activity and selectivity, which are then used to establish structure–performance relationships. Even more importantly, when obtained under controlled conditions to ensure the absence of other phenomena such as mass and heat transfer limitations, deactivation, etc.,5,6 it directly reflects the action of the catalyst on the reaction kinetics. This subcategory of performance data, also called “kinetic catalytic data”,4 can thus lead to unique insights into the catalyst action and the reaction mechanism.2,7–9 To achieve such insights, a key step is the extraction of kinetic information from such data. As of today, this relies mostly on simple data visualization tools and the researcher's prior knowledge, leading to long data analysis and potentially incomplete information extraction.4 In other words, there is no automated methodology that can be applied to ensure that all the underlying information in an experimental dataset is extracted and the most relevant features are correctly identified.
Extracting information from data can be done via data science. Such techniques, and more specifically machine learning techniques, typically require high volumes of well-balanced data, i.e. big data.10 Conversely, despite the expected increase thanks to data sharing, kinetic catalytic data will remain (much) more limited in size than typical big data.4 To compensate for the small volumes of data, knowledge on elementary kinetics and catalysis can be incorporated into data science techniques.4,11 Such an integrated approach is commonly defined as a ‘grey-box’ one, halfway between the purely data-driven black-box approaches11,12 and the purely microkinetic white-box ones.13–15
The aim of this work is to develop a grey-box methodology, and the corresponding automated tool, to retrieve information from a set of catalytic experimental data. To do so, knowledge on the reaction kinetics is merged with a suitable data analysis technique into a unified algorithm. Firstly, the following two methodological aspects will be discussed: (i) which technique is best adapted to extract information from kinetic catalytic data and (ii) how to incorporate knowledge into it. Afterwards, the development of the algorithm is described as well as performance verification tests against data with relevant kinetic trends. The algorithm is then implemented in a more comprehensive piece of software, which starts from a raw dataset and extracts information considering all parts of the data. Finally, a case study is considered to test the performance of the developed tool. The tool is made available for any researcher to use and further modify for their specific application (see Data availability statement).
2 Automating kinetic information extraction
2.1 Input data: kinetic catalytic datasets and meaningful variables
The analysis of the experimental kinetic catalytic data aims at retrieving the latent information on the reaction and the catalyst, including hints at the reaction mechanism. Steady-state data is a common type of data which gives direct information on the evolution of catalyst metrics such as activity, selectivity towards a product, etc. as a function of the operating conditions or catalyst properties, e.g., temperature, pressure, number of active sites, etc. The sought information is hence situated in the trends between the dependent and the independent variables in steady-state experimentation.The first step towards comprehensive information extraction is to ensure that all relevant variable combinations are analysed. In intrinsic kinetic catalytic data, the number of independent variables is limited, as no phenomena other than the reaction kinetics play on the observations.4 For a given catalyst, the independent variables that determine the reaction rate are the temperature, the total pressure, and the reacting fluid inlet composition. Considering ideal isothermal and isobaric reactors, the space–time defined in terms of the limiting reactant is the only additional independent variable to take into account and which is typically employed to adjust the conversion.
In kinetic data analysis, the key dependent variables analyzed are typically the conversion of the limiting reactant and the selectivity towards the various, i.e. main and side, products. Nevertheless, the analysis of the variation of these dependent variables as a function of the independent ones might not be straightforward because commonly more than one independent variables are varying throughout the dataset. Multivariate statistics could be used to identify the most influential independent variables, but it requires a significant amount of data. Conversely, it is good practice, as part of a larger experimental plan (e.g. via DoE), to also design a few experiments in which all independent variables but one are kept constant. This means that a careful selection of sub-datasets allows for a two-variable analysis of kinetic data, i.e. a dependent one as a function of a single independent one (see section 3.3 for more details). An important advantage of such sub-datasets is that, being bidimensional, the researcher is able to directly visualize the extracted trends. On the other hand, this means that the number of data points at stake is even smaller. The methodology to be developed should hence be able to extract kinetic information from very small kinetic sub-datasets. At the limit, a trend in a single independent variable data can be determined based on a few points, in the range of five to ten data points. In the same manner as for manual interpretation, a trend drawn on a low number of points can likely be erroneous if the uncertainty in the data is relatively high. Hence, one must ensure that the error level is reasonable enough to extract meaningful trends or apply it to a sufficiently large number of datasets on the same reaction, such that a statistic interpretation of the most likely trend can be carried out.
2.2 Output information: kinetic features
For every kinetically meaningful pair of independent and dependent variables, the trends in the data should be extracted. This is illustrated in Fig. 1via two potential curves that describe the evolution of selectivity with conversion. The green dotted curve leads to a better quantitative description of the data (e.g. least-squares) than the blue dashed curve, but the latter describes the trend between selectivity and conversion better than the former. The relevant kinetic information is then in the features of a such a qualitative curve.16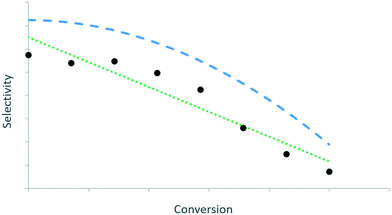 | ||
| Fig. 1 Two curves representing the same dataset: curve 1 (green dotted line) has the best quantitative description, but curve 2 (blue dashed line) reflects better the qualitative progression of the data. Based on Fig. 7 in ref. 16. | ||
More specifically, the main feature is the shape(s) of the curve (in this case, a concave negative trend). This can be categorized using so-called primitives,16,17 as exemplified in Fig. 2a. Primitives characterize the increase or decrease in the independent variable and the concavity or convexity in a given interval of a curve. If more than one primitive is present, the relevant features are then the sequence of the primitives and the extremes of the intervals corresponding to every primitive, as shown in Fig. 2b.
 | ||
| Fig. 2 Top: considered primitives, with the signs in brackets referring to the signs of the first and second derivative, respectively.16 Bottom: example of lists representing the shape of a curve. The trend of the curve can be represented by the primitive A, followed by the primitive D. | ||
2.3 Feature extraction algorithm
No such technique is available to extract kinetic features from small, steady-state performance data. In the following part of this section, the state of the art of the current techniques for (smooth) curve generation and feature recognition are briefly discussed separately. Then, the incorporation of knowledge on such techniques is outlined.
The QTA method is used in many applications, including chemical process control.23 The automatic observation of trends facilitates the supervision of processes and the detection of faults.24 The generation of data in these processes is often fast and the data can be approximated as continuous. In a similar way, fluctuations in experimental time series in dynamic kinetic experiments can be approximated by QTA.18–20 Even though large data sets (in the order of dozens of points) are still required for QTA, they are much smaller than the big data ones typically required for machine learning approaches. Owing also to its simple nature, QTA allows for the integration of chemical knowledge into the algorithms in such a way that the extracted features are not only mathematically significant but also chemically meaningful. Qualitative trend analysis was hence chosen as the preferred method for automated feature extraction of reaction kinetics data.
Within QTA, various mathematical approaches can be taken to generate smooth curves through experimental data. The two main possibilities are all-purpose functions, which are expected to fit basically any trend, and tailored functions,25 which are better suited for a specific trend but will not account for other ones. On the one hand, the use of tailored functions requires that a function is found for every possible trend, while there is a substantial number of different trends possible in catalysis. On the other hand, all-purpose functions make use of a larger number of degrees of freedom to fit any trend, potentially leading to trends in the curves that exceed the actual variability in data (i.e. overfitting) instead of representing chemical phenomena. A balanced approach is hence required. This is further discussed in the next section and its implementation is described extensively in section 3.
Once a chemically intuitive curve has been generated through the data, the kinetic features can be extracted from it in the form of primitives (see section 2.2). In QTA, there are methods available to efficiently assign primitives to curves.26 Hence, a state-of-the-art algorithm was selected and only minor adaptations are expected to be needed (see section 3.3.2).
In fact, this is done intuitively by researchers when interpreting data manually. A researcher would draw a curve through the data based on chemical intuition, limiting its shape (or sequence of primitives) to common ones in chemical kinetics. To translate this into an algorithm, knowledge incorporation means generating only chemically intuitive curves, which do not overfit the experimental data and/or give rise to unrealistic trends. In particular, in single independent variable catalytic datasets, e.g. on selectivity or conversion (see also section 2.1), smooth trends are expected.§ Based on this, it is possible to exclude overcomplex functions. Nevertheless, numerous trends are possible in catalytic data. Hence, simple, all-purpose functions (e.g. low-degree polynomials) are preferred by default, but whenever these would overfit simple kinetic trends, tailored functions to that trend should replace it (e.g. logarithmic functions). The selection of functions for curve generation is further discussed and implemented in sections 3.3.1, 3.3.3 and 3.3.4.
In the primitive recognition step, the curve features are recognized and can thus be used to further incorporate knowledge. Firstly, the adequacy of the function to the trend to be recognized can be verified. Functions that are known to poorly describe the combination of primitives at stake can be excluded (e.g. second-degree polynomials for straight lines). Secondly, overcomplex patterns can be prevented by excluding combinations of primitives that are kinetically unrealistic (as discussed in the previous paragraph). Curve generation and feature recognition were hence combined, as the identified features of a certain curve make it possible to assess whether the curve generated in the first step is chemically reasonable or not. This is implemented in section 3.3.2.
3 Methodology and tool development
3.1 Overview and practical implementation
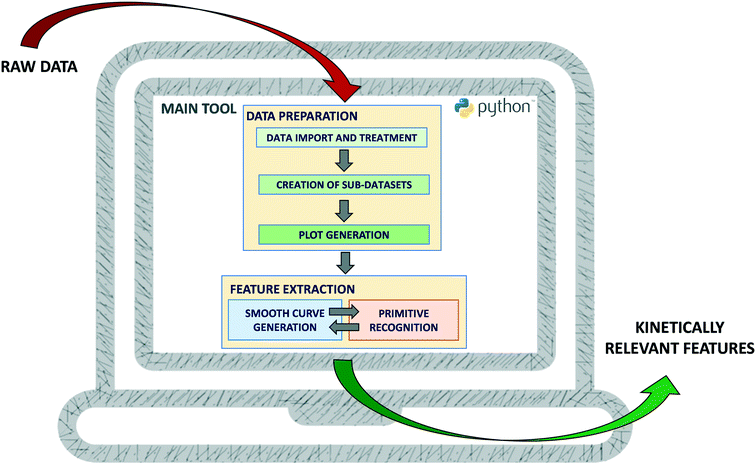
The translation of the principles described in section 2 into a software tool is discussed in this section. The tool was developed in Python using the web application Jupyter Notebook27 and is available for open use (under CC BY-NC 4.0 license) at GitHub (see Data availability statement for the hyperlink). Its structure is depicted in Fig. 3. Upstream of the feature extraction, a series of data handling operations needs to be performed (implementation described in section 3.2), namely the data should first be imported and treated to get meaningful variables. Then, the relevant single independent variable sub-datasets should be searched, created and visualized. To extract the features of the generated plots, a smooth curve is first generated and its primitives are then recognized (implementation described in section 3.3). An iterative procedure aiming at selecting the most suitable curve is executed and the results are finally visualised. At every step of development, the tool was tested with data mimicking catalytic kinetics and was compared to the original Python algorithms. These tests are discussed throughout section 3.3. Complementary tests on specific parts of the tool are also mentioned and can be found in the ESI.† Similarly to any other data-based tool, excessive noise will compromise the meaningfulness of the results (“garbage in, garbage out”), so one should carefully check the data quality before applying the tool.3.2 Data preparation
To notify the user of major anomalies in the data, a mass balance check is performed on the dataset to start with (see the ESI,† section A, for details). In the next step, the meaningful dependent and independent variables, described in section 2.1, are calculated based on the imported dataset (see also the ESI† for details). The only relevant assumption here is that, by default, the selectivities are calculated on a carbon basis. To decrease the impact of noise, data points with similar x-values are averaged out (see again the ESI† section A for details).
The tool automatically searches for data points which satisfy the conditions just mentioned above. Scatter plots corresponding to all sub-datasets are then generated for (optional) visual inspection by the researcher. The same plots are later used to present both the curve representing the data and the corresponding features.
3.3 Feature extraction
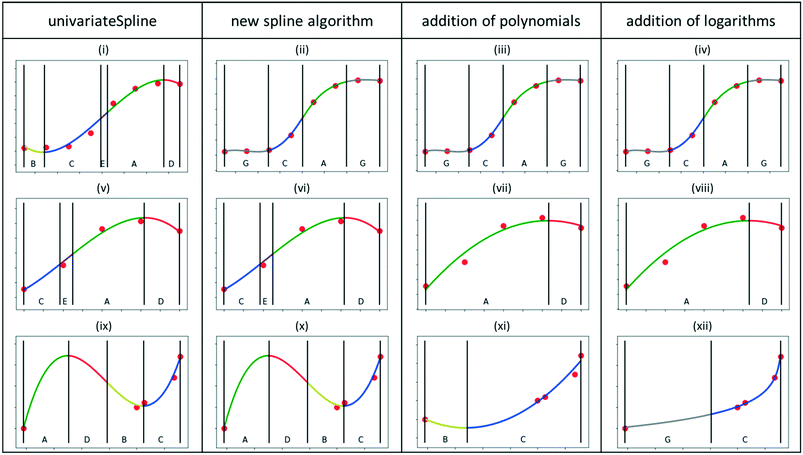
The key parts of the feature extraction methodology are described in what follows. For every section, the reasoning behind the approach is explained and then the implementation in Python is described. Representative results of the developed algorithms are summarized in Fig. 4 for three significant datasets, reproducing potential kinetic data trends, namely, conversion as a function of space–time, conversion as function partial pressure, and selectivity of a secondary product as a function of conversion, respectively. The first column corresponds to the results obtained with the standard UnivariateSpline algorithm (graphs i, v and ix), while the following correspond to the new algorithms in sections 3.3.1, 3.3.3 and 3.3.4. The results are discussed throughout these sections.Approach. It is first necessary to determine which all-purpose functions can generate chemically intuitive curves through experimental data. Polynomials are frequently used,25 but can result in pronounced oscillatory behaviour when the degree of the polynomial increases.30 Low-degree polynomials, however, often do not have enough degrees of freedom to describe a wide range of trends. Instead of increasing the degree of the polynomial to raise the number of degrees of freedom, piecewise polynomials, also known as splines, can allow for the flexibility needed with a reduced oscillatory behaviour. Hence, splines are a common choice for qualitative trend analysis,24,31,32 including for time series kinetic data.20,33,34
In each interval of the spline, a polynomial is fitted, ensuring continuity in the knots of the spline, which are the extremes of the intervals. To make sure that the spline is as smooth as possible, the first k − 1 derivatives are often chosen to be continuous in the knots as well, with k being the degree of the spline. To limit the oscillatory behaviour, the degree of the splines is typically set to three, as cubic splines present the ideal compromise between sufficient degrees of freedom while remaining smooth.35 To determine the number of knots, the weighted residual parameter (i.e. a measure of the quality of the fitting) is used as a threshold. This is the so-called smoothing factor. A high smoothing factor results in a low number of degrees of freedom but also results in a stiff spline, while a low smoothing factor leads to a better fit which is also more susceptible to oscillatory behaviour.
To automate the generation of splines for experimental datasets, it is necessary to automatically determine an appropriate smoothing factor for the spline. A value around the number of data points m is typically recommended.36 However, after some preliminary tests with the sub-dataset size of interest (ca. 5–10 data points, see section 2.1), it was found that this value was often too high for small datasets, leading to overfitting and, consequently, oscillatory behaviour (see Fig. 4i, v and ix and the ESI† section B).
A methodology is thus needed to determine the optimal smoothing factor for a given dataset. The goal is to find chemically realistic trends, and thus corresponding functions should not be overly complex (see section 2.3.3). To do so, the maximal number of knots nmax is limited depending on the amount of data. Within that constraint, various smoothing factors are screened and the spline with the best fitting to data (i.e. lowest smoothing factor) is selected. A series of tests (see the ESI† section C for results) led to the conclusion that seven knots typically suffice to describe trends which occur in catalytic data. The maximum number of knots was therefore set to seven. When the number of data points m is lower than nine, the maximum number of knots equals m − 2, as this is the maximum allowed number of knots due to the limited degrees of freedom. Still, this can lead to excessive oscillatory behaviour for very small data sets (see Fig. S2†).
Implementation. To implement spline fitting in Python, the class UnivariateSpline, which is part of the SciPy module, was used.37 It is an object class which fits a one-dimensional spline to a dataset defined by the arrays x and y and is based on an algorithm by Dierckx.38 To generate the spline, the UnivariateSpline algorithm starts with two knots at the extremes of the experimental data interval.39 Knots are added in the middle of the intervals with the highest weighted residual, until the total weighted residual is lower than or equal to the smoothing factor. The formula used to calculate the weighted residual is given in eqn (1). The weights of the residual wi are ideally equal to the inverse of the standard deviations of yi, but if no information is available on the standard deviations, they are set equal to 1, assuming hence a similar experimental error throughout the dataset.
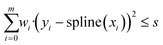 | (1) |
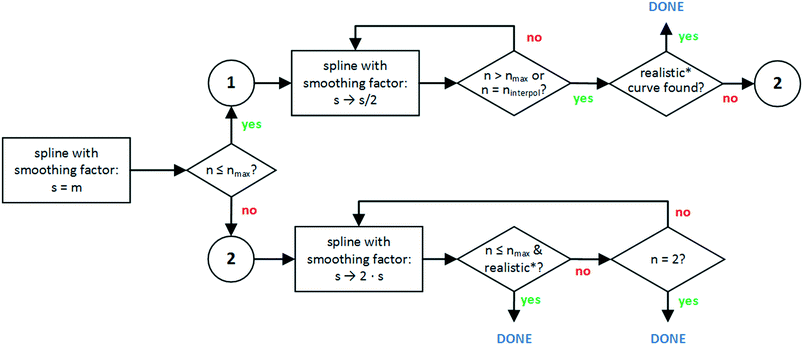 | ||
| Fig. 5 Flowchart of developed smooth curve generation algorithm. The generation of a spline with a given smoothing factor (rectangles) is iteratively carried out via the UnivariateSpline algorithm and it is not represented specifically in this scheme. *Check Fig. 6 for the meaning of ‘realistic’. | ||
Results. Starting from the default spline algorithm (UnivariateSpline), it can be clearly observed how for both the first and the third dataset (Fig. 4i and ix), the spline functions are overfitting the data, introducing oscillatory behaviour that is not expected in typical kinetic sub-datasets. For the second dataset (graph v), the standard algorithm is capable of reproducing the trends but some superfluous primitives (such as primitive E, linking C and A) are identified.
The second column of Fig. 4 reports the results obtained after having implemented the smooth curve generation via spline algorithm. For the first dataset, it can be appreciated how the limitations imposed in the splines generation lead to a more chemically realistic trend in the first dataset (graph ii). In other words, such an approach allows one to reproduce a smooth S-shaped curve, as can be seen in Fig. 4(ii), for which the UnivariateSpline had an oscillatory behaviour at both the low and high ends, Fig. 4(i). In both the second (graph vi) and third datasets (graph x), overfitting still persists, resulting in superfluous primitives and the oscillatory behaviour, respectively. Simpler curve functions must be therefore considered, as anticipated in section 2.4. Practically, the spline with the default smoothing factor is returned and another curve needs to be generated in a later algorithm.
Approach. As described in section 2 (see also Fig. 2), the kinetic information is determined via primitive recognition. The first step of primitive recognition is the discretization of the curve into a number of points in the range of interest of the independent variable.26 At these points, the first and second derivatives of the curve are calculated, and based on the signs of these values, one of the primitives is assigned. The derivative is either positive, negative or it can be considered zero if its absolute value is below a selected threshold (see Fig. 2a). If more than one primitive is present, the transition value(s) between different primitives should also be determined (see Fig. 2b). To ensure that primitives are correctly assigned, as well as the transition value between them, the number of discretization points (i.e. in which primitives are calculated) should be much larger than the number of knots in the splines.
Such information on the primitives can also be used to determine whether a curve can be kinetically realistic or not via the primitives extracted, as hinted at in section 2.4. For the datasets at stake, smooth trends are expected and overly complex trends can hence be simply excluded. By screening all possible primitives, three categories of unrealistic shapes were defined (see Fig. 6). The three categories consist of curves with more than two high-degree polynomials, curves with more than one high-degree primitive of the same type and curves with combinations of primitives A and B or primitives C and D. The first one could still be considered possible for very specific cases (of secondary products in selectivity vs. conversion plots). However, if incorporated in the tool, it would likely lead to false positives, e.g. it might be proposed by the tool as a potential trend for conversion as a function of space–time plots, while simpler trends are expected in such cases. Commonly, only a relatively small conversion range is analyzed, which means that only a small part of the theoretically possible trend will be captured in the data. As this risk of false positives is deemed higher than the prevalence of such trends in selectivity vs. conversion plots, it was preferred to consider it unrealistic.
Implementation. The UnivariateSpline class contains a method that computes the derivatives for the relevant function. It was still necessary to determine the number of equidistant points to be considered. After performing tests with fictional datasets, it was found that a hundred equidistant points suffice to extract the features (see the ESI,† section D, for results), as the trends in catalytic datasets at stake are relatively monotonous (see the previous section as well).
To extract linear primitives from the data, the values for the first and second derivatives must be considered zero below a chosen threshold value. However, the values for the derivatives depend on the units of the data and the considered ranges of x-values and y-values, so both derivatives were normalized (see the ESI,† section E). The first and second derivatives are considered to be zero if their absolute value is lower than the constants a and b, respectively. The constants a and b are threshold values, which determine how fast the code will consider a trend to be linear. In other words, lower values lead to a stricter definition of linearity and hence a decreased detection of linear trends. A value of 0.5 was chosen for both a and b, as it was found to lead to intuitive results using fictional, but relevant, datasets (see the ESI,† section E). Sometimes, a primitive G can appear between the primitives A and D or the primitives B and C, but this is a maximum or a minimum and not really a linear section. For this reason, the primitives G are removed in these cases and the boundary between the other two primitives is placed in the middle of the removed primitive.
Approach. In cases of low variability of the dependent variable and/or low number of data points, splines can be superfluous. For this reason, polynomials are also considered as a simplified alternative for the splines. In addition, polynomials are easy to differentiate which is of great use for primitive recognition (see the preceding section). A methodology was developed to replace the splines with polynomials when the use of a spline leads to overfitting and a polynomial might be more representative of the kinetic trend. As the goal is to only simplify if the polynomial is at least as good at describing the trend as the spline, a fitting criterion must be used. The multiple correlation coefficient R is a very simple way to measure the goodness of fit and does not take the number of parameters of the curve into account (see the ESI†, section F, for the definition). In this case, this is suitable, because the curve is only meant to represent the features of the data and the mathematical equation behind the curve does not need to have a physical meaning.
Implementation. The algorithm is shown schematically in Fig. 7 and consists of three steps, corresponding to the simplification to a cubic polynomial, a quadratic polynomial or parabola and a linear polynomial or straight line. The algorithm starts by comparing the spline to a cubic polynomial (step 1 in the figure). The simplification is enforced if the shape of the spline is considered unrealistic. Otherwise, the multiple correlation coefficients R of both curves are compared and the spline is kept if the difference is large. The difference between the two R-values is considered large if the ratio of the R-value of the cubic polynomial and the R-value of the spline exceeds 0.998. This value was chosen after doing tests with fictional and real datasets and evaluating which value led to the most intuitive results visually (see the ESI†, section F, for results).
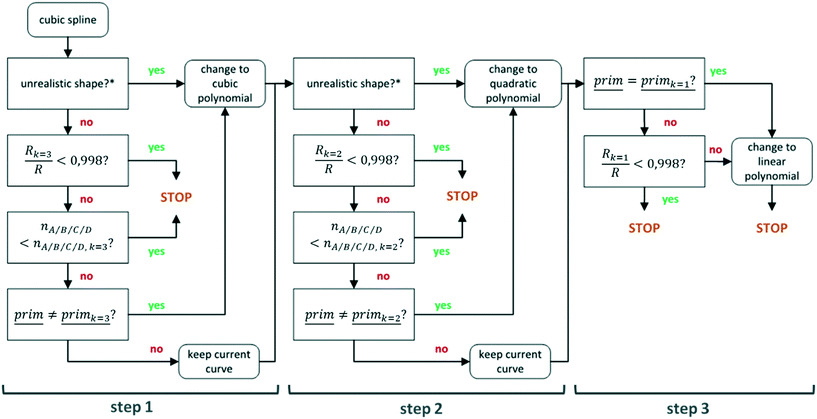 | ||
| Fig. 7 Flowchart of the smooth curve simplification algorithm. *Check Fig. 6. | ||
In some cases, the curve is not simplified to a cubic polynomial, even if the difference in R-value is small. This happens when the cubic polynomial is represented by more high-degree primitives (A–D) than the spline. Such a situation can arise when the low degrees of freedom of the polynomial are not sufficient to describe the trends in the data. It is then preferred to keep the curve which was able to capture the trends in the data with less oscillation than the polynomial (this corresponds to the STOP outcome in step 1 of Fig. 7). Another situation in which the curve is not simplified is when the two curves are described by the exact same primitives. The more complex curve is then kept as it has a better fit and more accurately represents the trends in the data using primitives (also leading to the STOP in step 1 of the figure).
In step 2 of the algorithm, the curve selected by step 1 is compared to a quadratic polynomial in an entirely analogous manner, also leading to two potential STOP situations where the curve is not simplified. The curve is finally compared to a linear polynomial in step 3, which is simpler than the two previous steps. The curve is automatically simplified to a linear polynomial if it is described by a linear primitive (the final STOP on the right of step 3 of Fig. 7). Otherwise, the R-values of the curves are once again compared and the curve is simplified only if the difference is small (STOP scenario on the left in step 3 of the figure).
Results. The results obtained with such a simplification strategy to low-degree polynomials are displayed in the third column of Fig. 4. The trends for the first and second dataset (graphs iii and vii) are now adequately captured thanks to the employment of polynomials instead of splines, without any visible overfitting. Concerning the third dataset (graph xi), the oscillatory behaviour is significantly reduced, but a superfluous minimum is still recognized. The latter is characteristic of second-order polynomials and hence another tailored function is needed.
Approach. As just observed, for a low number of points, it is possible that a polynomial indicates a minimum or a maximum when it is not explicitly present in the data (as in the third dataset in Fig. 4). From a kinetic point of view, trends such as logarithmic and exponential ones are also to be expected (e.g. first-order rate equations yield exponential functions for conversion when integrated for a plug-flow reactor40). For this reason, it is important to consider exponential and logarithmic types of patterns as well.
Implementation. The equation representing the generated curve does not necessarily need to have a physical meaning, as it is only used to extract the features. Only logarithmic curves are therefore considered, as the y-values do not need to be transformed to perform a linear regression in this case. As a matter of fact, the logarithmic function is able to mathematically describe the primitives A–D in Fig. 2, further confirming that it suffices to consider only logarithmic functions.
To adapt the logarithmic function to the datasets, a constant for translation of x-values needed to be added (see the ESI,† section G). It is consequently impossible to estimate all coefficients in the equations using linear regression. There are multiple methods possible for non-linear fitting, but they either require initial guesses or would be too complicated to incorporate in a simple tool.41 As a result, an approximative, but effective, method was derived to estimate the extra parameter in the equation (see the ESI,† section G, for the derivation), automatically fitting a logarithmic function to a dataset without having to input initial guesses for the coefficients. Furthermore, the curve is primarily generated to extract features, so exact values are not the main goal, as long as the correct features are extracted.
Results. The results obtained after the addition of the logarithmic functions to the algorithm are displayed in the fourth column of Fig. 4. The curve on the third dataset (graph xii) was successfully replaced by a logarithmic one, leading to the removal of the superfluous minimum and resulting in a chemically feasible, smooth trend.
3.4 Lessons learnt from kinetic knowledge incorporation
The developed algorithm is able to extract chemically feasible, smooth trends for all three datasets, even from a low (<10) number of data points, without compromising the performance for a higher number of data points. This was possible thanks to the synergetic use of low-degree splines and base functions. As numerous trends are possible in catalytic data, splines were the starting point. For simpler trends, polynomials gave rise to a smoother trend, while the addition of logarithmic functions was crucial to be able to capture ‘activated’ events such as the ones present in chemical reactions. This is a further peculiarity of kinetic datasets, which requires going beyond the state of the art of curve fitting to create a tool suitable for the specific purpose of catalytic kinetics.Moreover, in the primitive recognition step, where the curve features are recognized, further knowledge was incorporated by excluding combinations of primitives that are kinetically unrealistic and would otherwise lead to overcomplex trends. More importantly, the curve generation and feature recognition steps were iteratively combined, as the identified features of a certain curve made it possible to assess whether the curve generated in the first step was chemically reasonable or not.
4 Case study: hydrodeoxygenation of phenol
This case study aims at testing the applicability of the tool for typical literature data, thus a dataset not acquired in-house was looked for. On the one hand, the selection of a suitable dataset was based on the need to identify a typical dataset resulting from laboratory-scale, steady-state kinetic experimentation, with few datapoints and, on the other hand, to focus on a reaction which would be of interest to the broad catalysis community. The focus was put in the field of biomass valorisation where reaction pathways are often complex due to the high reactivity of the oxygenated species involved.42,43 The selected case study comprises a dataset on phenol hydrodeoxygenation, a catalysed reaction, resulting from research by Barrios et al.44 Multiple reaction pathways have indeed been proposed for this reaction up to now, with the catalyst having a particularly relevant role.45–47 This dataset was acquired to assess which reaction pathway was dominant for phenol hydrodeoxygenation over Pd catalysts supported on a SiO2 or a Nb2O5 support.In practice, the phenol hydrodeoxygenation dataset44 consists of the conversion and the product yields as a function of the space–time for both catalysts. The data were extracted from the figures in the articles graphically, making use of the open software WebPlotDigitizer, as the numerical data was not provided in the article. Based on the extracted conversion and yield data, the selectivities towards the products were calculated. To prevent further error propagation from one product data to another, the selectivities were not normalized and might not always sum up to 100%. The relevant sub-datasets plots were constructed, i.e. the phenol conversion as a function of the space–time and the product selectivities as a function of the conversion, the same as if a raw dataset was supplied to the tool. The results of the feature extraction of the generated plots are shown in Fig. 8.
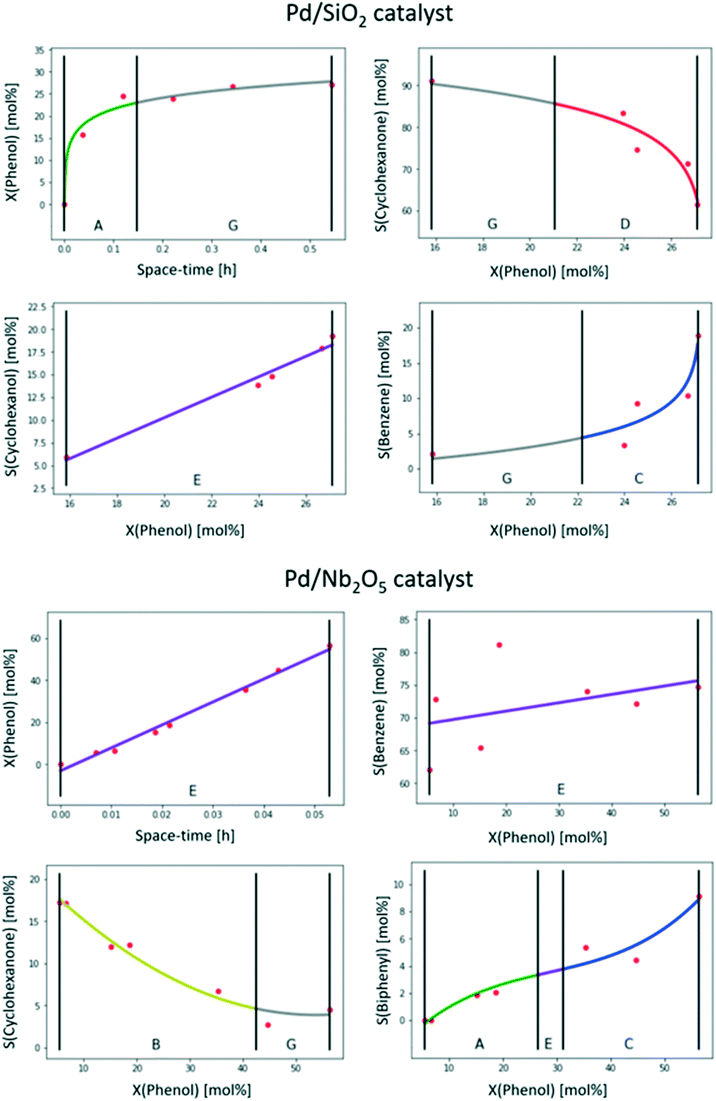 | ||
| Fig. 8 Results of feature extraction for the phenol conversion and product conversion over a Pd/SiO2 and a Pd/Nb2O5 catalyst. Operating conditions: 1 atm, 573 K, H2-to-phenol molar ratio of 60.44 | ||
Focusing on the Pd/SiO2 catalyst first, it can be immediately observed that the trends which were automatically generated by the tool for this catalyst seem to correspond to what a researcher would generally consider chemically intuitive and this is the most relevant and successful outcome for the purpose of the tool. For this catalyst, according to the extracted features, phenol conversion increased steeply with space–time (primitive A) till it reached a plateau at ca. 25% (primitive G). This might be an indication that equilibrium between phenol and one of the (primary) products has been reached. Alternatively, such a plateau in conversion for increasing space–times might also indicate catalyst deactivation. The selectivity towards cyclohexanone is high (around 90%) at low conversions (primitive G) and starts to decrease rapidly at higher conversions (primitive D). This indicates that cyclohexanone is a primary product, i.e. formed directly from phenol. The selectivity towards cyclohexanol, on the other hand, increases approximately linearly as a function of the conversion (primitive E). Both the linear increase and its slope point to a null selectivity when the conversion tends to zero, indicating that cyclohexanol is most likely a secondary product. For the third product, benzene, the selectivity increases rapidly at high conversions (primitive C), but it is only observed in small amounts at low conversions. There, the slope is also small (primitive G), indicating that this might be a tertiary product. In other words, only at higher conversions, when the concentration of the secondary product is sufficient, will the tertiary product be formed significantly. Nevertheless, to determine unequivocally the rank of benzene, data closer to null conversion would be needed.
In the case of the Pd/Nb2O5 catalyst, whereas the conversion and selectivity towards cyclohexanone trends are also in line with what a researcher would commonly draw, the other two are less consensual. Hence, these will be first discussed from the point of view of feature recognition before inferring kinetic knowledge. Firstly, on the selectivity towards benzene, the variability in the data is striking. This can be attributed to the original data (Fig. 6B in ref. 44), but it was less visible there as it was represented in the form of yield rather than selectivity. Due to the excessive variability (i.e. noise) in the data, the proposed trend is a straight line (primitive E), i.e. the simplest curve. This is most probably the same conclusion a researcher would have reached, focusing on the average trend and value range rather than a point-by-point trend. Concerning the selectivity towards biphenyl, the extracted trend (primitives A, E and C) is quite rare in catalytic data owing to the inflexion point (primitive E). Yet being considered possible, it is not part of the overly complex trends automatically excluded by the tool (see section 3.3.2) and so it is still proposed. It is still doubtful whether a researcher would have opted for a similar trend or proposed a straight line also in this case. However, the most important result is that the monotonously increasing trend is also well captured by the tool in this case.
Concerning the chemical meaning of the recognized trends, the conversion of phenol increases approximately linearly as a function of the space–time (primitive E). This means that equilibrium is not reached in the considered range of values for the space–time for this catalyst, and equilibrium conversion between phenol and the primary product(s) is higher than 60%. As cyclohexanone is present in much lower quantities than in the case of Pd/SiO2, it is indeed possible that equilibrium was attained in that case and not over Pd/Nb2O5. The selectivity towards benzene as a function of the conversion is represented by a linear trend (primitive E), as discussed above. Overall, the selectivity is high and the slope is rather moderate, which means that benzene is a primary product and will remain the main product, even at low conversion. The selectivity towards cyclohexanone, on the other hand, is significant at low conversions (ca. 20% at 16% conversion) and decreases rapidly (primitive B), apparently stabilizing at higher conversions (primitive G). Hence, cyclohexanone is a primary product as well. Concerning diphenyl, it is not observed at low conversions, but its selectivity increases at higher conversion (primitives A, E and C), making it a secondary product.
The knowledge generated about the product rankings makes it possible to propose a reaction pathway. Fig. 9 depicts the reaction pathways which can be constructed based on the product ranking deduced from the results of the feature extraction tool. For Pd/SiO2, every product had a different ranking, making the construction of the reaction pathway quite straightforward: phenol forms cyclohexanone, which is further hydrogenated to cyclohexanol which via dehydration and dehydrogenation forms benzene (Fig. 9). This scheme differs importantly from the one in the original study, as no direct pathway from phenol to cyclohexanol is expected from the analysis here, while it was proposed in the original one.44 In addition, benzene was not included in the original reaction scheme. For Pd/Nb2O5, two primary products (benzene and cyclohexanone) and one (biphenyl) secondary product are recognized. The decrease in cyclohexanone indicates that the biphenyl is most likely formed from cyclohexanone. Hence, the following reaction pathway can be proposed: phenol gives raise to both benzene and cyclohexanone, the former being further converted to biphenyl (Fig. 9). In the original study, only benzene was included in the reaction scheme as a primary product.44 Therefore, the scheme inferred here complements the original one, giving a more comprehensive view on the reaction pathways.
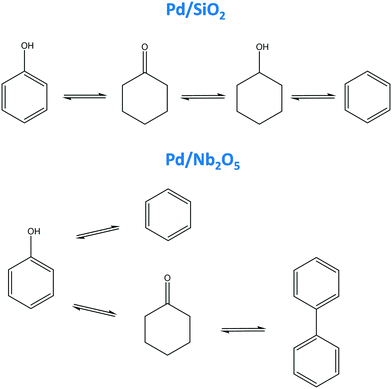 | ||
| Fig. 9 Reaction pathway for hydrodeoxygenation of phenol on a Pd/SiO2 and a Pd/Ni2O5 catalyst proposed based on features extracted by the developed tool. | ||
In short, via the automatically generated kinetic information (via trend lines through the relevant data and extracting primitives), a researcher could gain useful chemical knowledge about a reaction system which is a priori unknown. In other words, the information obtained from the tool, which does not take the structure of the actual molecules into account, allows for a gain in general knowledge about the reaction network for any system, independent of its chemistry. Obviously, the tool will not ensure that the reaction network is chemically feasible per se, but it will provide the basis for the researcher to do so, eventually in combination with other tools, e.g. for thermodynamic calculations. This can be particularly helpful when several datasets are at stake, allowing, for instance, to group datasets based on similar observations and statistically analysing their frequency (e.g. leading to the most likely reaction network from a large number of datasets on the same reaction).
The next logical step towards the automation of kinetic model generation is to automatically propose reaction pathways, such that the conclusions discussed above can be obtained as direct output from the tool. To do so, the product ranking recognition should be automated, but the results herein also highlight the challenges there. In particular, when the product has a low but non-zero selectivity at low conversion and moderate slope (such as the case of benzene over Pd/SiO2), the determination of the product ranking is not straightforward. To circumvent the lack of data at lower conversions, recurring to the Delplot technique is the obvious solution,29 but it implies a trustworthy extrapolation method to null conversion, independent of the reaction kinetics and type of reactor. Furthermore, there are also some relevant limitations intrinsic to this technique.29,48 Most importantly, the method is only rate law independent for the identification of primary products.29 In a nutshell, while the (partial) automation of product ranking recognition would be beneficial, the largest step is given by the current tool: the automation of extraction of relevant kinetic information which researchers can turn into chemical knowledge.
5 Conclusion
A tool for automated kinetic information extraction from catalytic data was developed, allowing the recognition of physically relevant patterns even in small sets of steady-state data. This was possible thanks to the incorporation of chemical knowledge, compensating for the small size of the data. In particular, the combination of simple all-purpose functions (low-degree splines) with complementary tailored functions (polynomials and logarithms) resulted in curves which were a good description of the trends in data without overfitting. The usage of primitive recognition to still exclude superfluous trends ensured that unrealistically complex trends were not attributed. The decisional parameters of each one of the developed algorithms was first fine-tuned and tested on a number of chemically relevant curves and then the full tool was applied to a literature dataset for the hydrodeoxygenation of phenol as a case study. In the latter, the kinetic information extracted by the tool could be used to generate new knowledge on the reaction scheme.The methodology developed in this work is a first step towards the automatic analysis of catalytic kinetic data. Being able to extract information from small datasets, the tool can be virtually applied to any dataset. A very relevant application is, therefore, the combination and cross-checking of multiple studies, quantifying and summarizing the latent information in data, e.g. on the same reaction. Furthermore, this work shows how (chemical) knowledge can be incorporated into data science methods, providing further inspiration for the development of tools tailored to small data by means of knowledge.
Data availability
The feature extraction tool developed in this work is made available at https://github.com/ssiradze/feature_extraction under a Creative Commons Attribution-NonCommercial 4.0 license (CC BY-NC 4.0). The extracted dataset from ref. 44 is available at the GitHub repository as well together with another dataset on raw data which allows one to test the full tool.Author contributions
According to CRediT, Contributor Roles Taxonomy, http://credit.niso.org/. P. S. F. Mendes: conceptualization; methodology; writing – original draft. S. Siradze: methodology; investigation; writing – original draft; data curation. L. Pirro: methodology; writing – review and editing; visualization. J. W. Thybaut: supervision; writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. S. F. Mendes acknowledges the financial support of the Special Research Fund of Ghent University for his post-doctoral assistant research mandate (BOF/PDO/2018/001901).References
- A. J. Medford, M. R. Kunz, S. M. Ewing, T. Borders and R. Fushimi, ACS Catal., 2018, 8, 7403–7429 CrossRef CAS.
- M. F. Reyniers and G. B. Marin, Annu. Rev. Chem. Biomol. Eng., 2014, 5, 563–594 CrossRef CAS.
- K. Takahashi, L. Takahashi, I. Miyazato, J. Fujima, Y. Tanaka, T. Uno, H. Satoh, K. Ohno, M. Nishida, K. Hirai, J. Ohyama, T. N. Nguyen, S. Nishimura and T. Taniike, ChemCatChem, 2019, 11, 1146–1152 CrossRef CAS.
- P. S. F. Mendes, S. Siradze, L. Pirro and J. W. Thybaut, ChemCatChem, 2021, 13, 836–850 CrossRef CAS.
- P. B. Weisz and C. D. Prater, in Advances in Catalysis, ed. W. G. Frankenburg, V. I. Komarewsky and E. K. Rideal, Academic Press, New York, 1954, vol. 6, pp. 143–196 Search PubMed.
- F. Kapteijn and J. A. Moulijn, in Handbook of Heterogeneous Catalysis, ed. G. Ertl, H. Knozinger, F. Schüth and J. Weitkamp, Wiley-VCH, Weinheim, 2008, pp. 2019–2045 Search PubMed.
- K. H. Yang and O. A. Hougen, Chem. Eng. Prog., 1950, 46, 146 CAS.
- M. A. Vannice, Kinetics of Catalytic Reactions, Springer, New York, 2005 Search PubMed.
- D. Constales, G. S. Yablonsky, D. R. D'hooge, J. W. Thybaut and G. B. Marin, Advanced Data Analysis & Modelling in Chemical Engineering, Elsevier, Amsterdam, 2017 Search PubMed.
- B. Krawczyk, Prog. Artif. Intell., 2016, 5, 221–232 CrossRef.
- V. Venkatasubramanian, AIChE J., 2019, 65, 466–478 CrossRef CAS.
- H. J. L. Van Can, H. A. B. Te Braake, S. Dubbelman, C. Hellinga, K. C. A. M. Luyben and J. J. Heijnen, AIChE J., 1998, 44, 1071–1089 CrossRef CAS.
- J. A. Dumesic, D. F. Rudd, L. M. Aparicio, J. E. Rekoske and A. A. Trevino, The Microkinetics of Heterogeneous Catalysis, American Chemical Society, Washington, 1993 Search PubMed.
- J. W. Thybaut and G. B. Marin, J. Catal., 2013, 308, 352–362 CrossRef CAS.
- A. Obradović, J. W. Thybaut and G. B. Marin, Chem. Eng. Technol., 2016, 39, 1996–2010 CrossRef.
- S. Katare, J. M. Caruthers, W. N. Delgass and V. Venkatasubramanian, Ind. Eng. Chem. Res., 2004, 43, 3484–3512 CrossRef CAS.
- M. E. Janusz and V. Venkatasubramanian, Eng. Appl. Artif. Intell., 1991, 4, 329–339 CrossRef.
- D. Schaich and R. King, Comput. Chem. Eng., 1999, 23, S415–S418 CrossRef.
- D. Schaich, R. Becker and R. King, IFAC Proceedings Volumes, 2000, 33, 421–426 CrossRef.
- D. Schaich, R. Becker and R. King, Control Eng. Pract., 2001, 9, 1373–1381 CrossRef.
- J. M. Caruthers, J. A. Lauterbach, K. T. Thomson, V. Venkatasubramanian, C. M. Snively, A. Bhan, S. Katare and G. Oskarsdottir, J. Catal., 2003, 216, 98–109 CrossRef CAS.
- L. Himanen, A. Geurts, A. S. Foster and P. Rinke, Adv. Sci., 2019, 6, 1900808 CrossRef.
- B. Zhou, H. Ye, H. Zhang and M. Li, AIChE J., 2017, 63, 3374–3383 CrossRef CAS.
- K. Villez, C. Rosén, F. Anctil, C. Duchesne and P. A. Vanrolleghem, Comput. Chem. Eng., 2013, 48, 187–199 CrossRef CAS.
- M. R. Maurya, R. Rengaswamy and V. Venkatasubramanian, Eng. Appl. Artif. Intell., 2007, 20, 133–146 CrossRef.
- B. Zhou and H. Ye, J. Process Control, 2016, 37, 21–33 CrossRef CAS.
- K. Wang, L. Wang, Q. Yuan, S. Luo, J. Yao, S. Yuan, C. Zheng and J. Brandt, J. Mol. Graphics Modell., 2001, 19, 427–433 CrossRef CAS.
- E. J. Molga and K. R. Westerterp, in Ullmann's Encyclopedia of Industrial Chemistry, 2013, pp. 1–99, DOI:10.1002/14356007.b04_005.pub2.
- N. A. Bhore, M. T. Klein and K. B. Bischoff, Ind. Eng. Chem. Res., 1990, 29, 313–316 CrossRef CAS.
- G. Dahlquist and Å. Björck, Numerical Methods in Scientific Computing, Society for Industrial and Applied Mathematics, Philadelphia, 2008, vol. I, ISBN: 978-0-89871-644-3 Search PubMed.
- H. Vedam, V. Venkatasubramanian and M. Bhalodia, Comput. Chem. Eng., 1998, 22, S827–S830 CrossRef CAS.
- K. Villez, V. Venkatasubramanian and R. Rengaswamy, Comput. Chem. Eng., 2013, 58, 116–134 CrossRef CAS.
- J. Madár, J. Abonyi, H. Roubos and F. Szeifert, Ind. Eng. Chem. Res., 2003, 42, 4043–4049 CrossRef.
- A. Mašić, S. Srinivasan, J. Billeter, D. Bonvin and K. Villez, IFAC-PapersOnLine, 2016, 49, 1145–1150 CrossRef.
- C. de Boor, A Practical Guide to Spline, 1978 Search PubMed.
- C. H. Reinsch, Numer. Math., 1967, 10, 177–183 CrossRef.
- Scipy module, https://www.scipy.org/, (accessed 20/12/2020).
- P. Dierckx, Curve and Surface Fitting with Splines, Oxford University Press, Oxford, 1993 Search PubMed.
- P. Dierckx, FITPACK, http://www.netlib.org/dierckx/, (accessed August 18, 2019).
- O. Levenspiel, Chemical Reaction Engineering, John Wiley & Sons, Ltd, New York, 3rd edn, 1999 Search PubMed.
- C. F. Goldsmith and R. H. West, J. Phys. Chem. C, 2017, 121, 9970–9981 CrossRef CAS.
- W. Jin, L. Pastor-Pérez, D. Shen, A. Sepúlveda-Escribano, S. Gu and T. Ramirez Reina, ChemCatChem, 2019, 11, 924–960 CrossRef CAS.
- M. Saidi, F. Samimi, D. Karimipourfard, T. Nimmanwudipong, B. C. Gates and M. R. Rahimpour, Energy Environ. Sci., 2014, 7, 103–129 RSC.
- A. M. Barrios, C. A. Teles, P. M. de Souza, R. C. Rabelo-Neto, G. Jacobs, B. H. Davis, L. E. P. Borges and F. B. Noronha, Catal. Today, 2018, 302, 115–124 CrossRef CAS.
- H. Wan, R. V. Chaudhari and B. Subramaniam, Top. Catal., 2012, 55, 129–139 CrossRef CAS.
- Q. Tan, G. Wang, L. Nie, A. Dinse, C. Buda, J. Shabaker and D. E. Resasco, ACS Catal., 2015, 5, 6271–6283 CrossRef CAS.
- L. Nie, P. M. de Souza, F. B. Noronha, W. An, T. Sooknoi and D. E. Resasco, J. Mol. Catal. A: Chem., 2014, 388–389, 47–55 CrossRef CAS.
- M. T. Klein, Z. Hou and C. Bennett, Energy Fuels, 2012, 26, 52–54 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1re00215e |
| ‡ These authors contributed equally. |
| § Even if various phenomena are simultaneously playing, a change in the independent variable will modify the balance between those phenomena but not drastically switch from one to the other. Therefore, smooth rather than “on–off” trends are expected in kinetic catalytic data. |
| This journal is © The Royal Society of Chemistry 2022 |