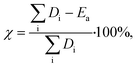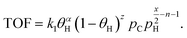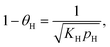Polyolefin plastic waste hydroconversion to fuels, lubricants, and waxes: a comparative study†
Pavel A.
Kots‡
a,
Brandon C.
Vance‡
ab and
Dionisios G.
Vlachos
 *ab
*ab
aCenter for Plastic Innovation, University of Delaware, 221 Academy St., Newark, DE 19716, USA. E-mail: vlachos@udel.edu
bDepartment of Chemical and Biomolecular Engineering, University of Delaware, 150 Academy St., Newark, DE 19716, USA
First published on 1st December 2021
Abstract
Hydroconversion technologies have surged to the forefront of deconstructing plastic waste. Recent studies have been performed over several catalysts with varying conditions and plastics that make comparisons difficult. We compile and compare data from the literature by introducing various metrics and perform a simple energy analysis. We draw mechanistic similarities to and differences from the past literature on small alkane hydroconversion and leverage the former to propose standard approaches to tune product selectivity. We exemplify the plastics materials gap and the challenges it creates. Finally, we discuss the current limitations and suggest future work.
Plastic waste (PW) represents an enormous threat due to its rapid accumulation in landfills with extensive leakage into the ecosystem.1,2 Mechanical recycling is unsuitable to handle packaging materials, which are a major component of PW. A prime solution to this ongoing challenge relies on the development of PW chemical recycling and upcycling.3 Polyolefins (PO), such as polyethylene (PE) and polypropylene (PP), represent more than half of all PW3,4 and their recycling rates are the lowest. Thus, significant attention has been directed towards discovering PO conversion catalysts to transform the PW to fuel and lubricant range hydrocarbons.
Recent review articles have compiled nicely the latest advancements in PW upcycling.5–7 Yet, an assessment of various catalysts and technologies is lacking due to significant differences in catalysts loadings, reaction conditions, and feedstocks among these studies. It is important to provide the growing PW community with comparative studies and metrics and emphasize key gaps in the PO upcycling to more efficiently direct and accelerate catalyst development. The lessons learned from the rich history of biomass and small alkane catalysis can be instrumental in this regard.
Traditional catalytic reaction engineering was focused primarily on C–C bond cracking of crude oil fractions and more recently on making new C–C bonds of building blocks of shale gas or biomass toward a higher molecular weight product. The extensive C–C bond breaking required to recycle or upcycle PO is a complicated task6 and functionalization of the products or the feedstock may also be necessary. Future chemistry for a circular economy should partially break existing C–C bonds,8 remake and rearrange them or noninvasively add and remove functionalities, like new C–O or C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds. The biomass upcycling is an excellent example where multiple bond activations take place, including deconstruction of biopolymers to building blocks or platform molecules and selectively remaking bonds to value-added products, such as fuels, lubricants, detergents, etc.
O bonds. The biomass upcycling is an excellent example where multiple bond activations take place, including deconstruction of biopolymers to building blocks or platform molecules and selectively remaking bonds to value-added products, such as fuels, lubricants, detergents, etc.
In this comparative paper, we analyze catalytic processes from recent papers for product distribution, selectivity, productivity, and energy use and identify knowledge gaps and comparison metrics. We propose metrics and standardization procedures to accelerate learnings. We perform a simple energy analysis of various processes that indirectly provides valuable insights into CO2 emissions. We draw mechanistic analogies to and differences from the rich small alkane chemistry and propose future directions to understand the mechanisms better. Unlike small molecule activation and biomass platform molecules, where the feedstock is molecularly known exactly, and more like the biopolymers of biomass, we exemplify the plastics materials gap and the challenges it creates in developing technologies for actual plastic waste.
1. Overview of catalytic processes for plastic deconstruction
Heterogeneous catalysis offers three distinct pathways for C–C bond breaking in PO at relatively mild reaction conditions. First, hydrocracking9 typically involves bifunctional metal/acid catalysts. It is an effective strategy to produce gasoline-range hydrocarbons from LDPE (low-density PE), HDPE (high-density PE), and PP at 225–275 °C over Pt/WO3/ZrO2 physically mixed with different solid acids. Second, monofunctional (metal) Ru- and Pt-catalysed hydrogenolysis makes heavier products, including diesel and lubricants. Metathesis coupled with dehydrogenation in excess of a low molecular weight co-reactant has also been reported.10,11 All three routes are fundamentally distinct, which makes direct comparisons nontrivial. We refer to hydrocracking and hydrogenolysis collectively as hydroconversion. Several catalyst options were proposed for hydroconversion in the past (Table 1).12–15 Among these catalytic technologies, metathesis is the least developed and is not discussed further.| Hydrocracking | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Year | Journal | Ref. | Catalyst | Polymer | M W (kDa) | Polymer to catalyst ratio | Temperature (°C) | Pressure (bar) | Time (h) | Yield liquid (%) | Gas yield (%) |
| 1996 | Energy & Fuels | Ref. 12 | 0.5Pt/1.5SO4/ZrO2 | HDPE | 250 | 5 | 375 | 83 | 0.42 | 68 | 35 |
| 0.5Pt/7WO3/ZrO2 | PP | 250 | 5 | 325 | 83 | 0.33 | 72 | 29 | |||
| 0.5Pt/1.5SO4/ZrO2 | PP | 250 | 5 | 325 | 83 | 0.33 | 77 | 23 | |||
| 1997 | Energy & Fuels | Ref. 13 | NiMo/SiO2–Al2O3 | HDPE | 125 | 1.5 | 375 | 69 | 1 | 38 | 61 |
| 2011 | Applied Catalysis B | Ref. 14 | Ni/BETA | LDPE | 416 | 30 | 310 | 20 | 0.75 | 88 | 13 |
| Ni/Al-SBA-15 | 0.75 | 88 | 12 | ||||||||
| Ni/Al-MCM-41 | 0.75 | 89 | 10 | ||||||||
| 2019 | Industrial and Engineering Chemistry | Ref. 15 | 1Pt/BEA | LDPE | 150 | 10 | 330 | 20 | 0.25 | 61 | 39 |
| 0.5 | 43 | 57 | |||||||||
| 1 | 44 | 56 | |||||||||
| 2021 | Science Advances | Ref. 9 | 0.5Pt/15WO3/ZrO2 + HY | LDPE | 76 | 10 | 250 | 30 | 2 | 70 | 30 |
| 0.5Pt/15WO3/ZrO2 + BEA | 250 | 2 | 41 | 34 | |||||||
| 0.5Pt/15WO3/ZrO2 + HY | 275 | 1 | 62 | 19 | |||||||
| 2021 | Applied Catalysis B | Ref. 16 | 0.5Pt/15WO3/ZrO2 | LDPE | 76 | 10 | 250 | 30 | 12 | 100 | 12 |
| Hydrogenolysis | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Year | Journal | Ref. | Catalyst | Polymer | M W (kDa) | Polymer to catalyst ratio | Temperature (°C) | Pressure (bar) | Time (h) | Yield liquid (%) | Gas yield (%) |
| 2019 | ACS Central Science | Ref. 17 | 18.8Pt/SrTiO3 | PE | 22.15 | 5 | 300 | 12 | 24 | 99 | N/A |
| 2020 | Science | Ref. 18 | 1.5Pt/γ-Al2O3 | PE | 3.5 | 0.59 | 280 | 1 | 24 | 70 | 9 |
| LDPE | 94.5 | 69 | 6 | ||||||||
| 2020 | Nature Catalysis | Ref. 19 | 1.7mSiO2/0.35Pt/SiO2 | HDPE | 26.5 | 88 | 300 | 14 | 24 | 42 | 42 |
| 2.4mSiO2/0.27Pt/SiO2 | HDPE | 27.5 | 67 | 300 | 14 | 24 | 60 | 38 | |||
| 3.4mSiO2/0.33Pt/SiO2 | HDPE | 28.5 | 83 | 300 | 14 | 24 | 72 | 26 | |||
| 2021 | JACS Au | Ref. 20 | 5Ru/C | PE | 4 | 25 | 200 | 22 | 16 | 54 | 35 |
| LDPE | 76 | 28 | 225 | 22 | 16 | 44 | 27 | ||||
| 2021 | Applied Catalysis B | Ref. 21 | 5Ru/CeO2 | PE | 4 | 34 | 240 | 35 | 8 | 90 | 10 |
| LDPE | 64 | 10 | 87 | 13 | |||||||
| 50 | 24 | 87 | 13 | ||||||||
| 35 | 18 | 88 | 13 | ||||||||
| 2021 | ACS Sustainable Chemistry & Engineering | Ref. 22 | 5Ru/C | PP | 340 | 14 | 250 | 40 | 14 | 36 | 64 |
| 16 | 25 | 73 | |||||||||
| 2021 | ACS Catalysis | Ref. 23 | 5Ru/TiO2 | PP | 250 | 20 | 250 | 30 | 16 | 65.6 | 28.2 |
| 5Ru/C | 8 | 0 | 100 | ||||||||
| 5Ru/CeO2 | 16 | 6.8 | 97.8 | ||||||||
| 2021 | Cell Reports Physical Science | Ref. 24 | 5Ru/FAU | LDPE | 76 | 17 | 300 | 50 | 3 | 0 | 99 |
| PP | 12 | 3 | 0 | 99 | |||||||
| 2021 | JACS Au | Ref. 25 | 5Ru/15WO3/ZrO2 | LDPE | 76 | 40 | 250 | 30 | 2 | 52 | 23 |
| 5Ru/ZrO2 | LDPE | 76 | 60 | 13 | |||||||
| 5Ru/25WO3/ZrO2 | LDPE | 76 | 53 | 8 | |||||||
Pyrolysis is a popular technology for converting solids. It employs high temperatures and is typically unselective and non-catalytic (a catalyst could also be invoked in the pyrolysis unit or downstream). Pyrolysis operates at higher reaction temperatures compared to hydroconversion. Under these conditions, thermal C–C bond cleavage in PO will cause their breakdown into liquid and gas products. A significant advantage of pyrolysis is its agnostic nature to the feedstock. While not the focus of this paper, we compare recent pyrolysis work to the hydroconversion catalytic technologies to provide context.
2. Metrics and benchmarking catalysis
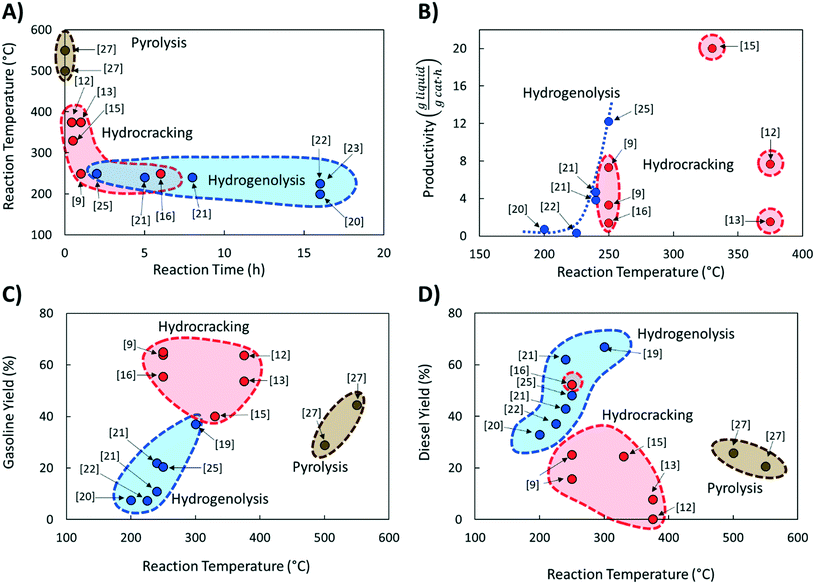
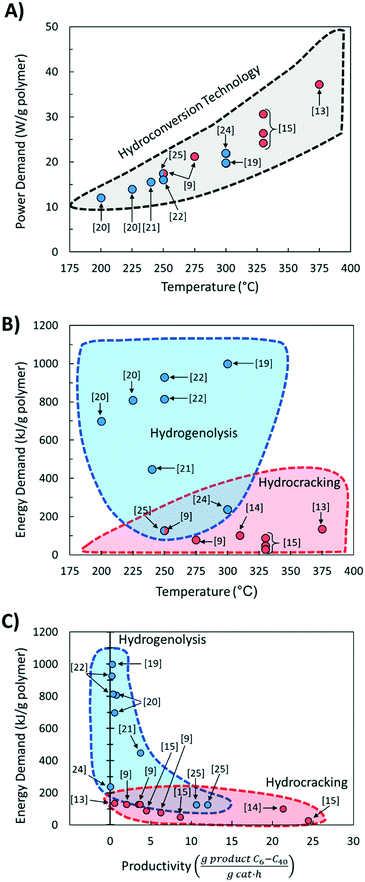
Comparing literature results is challenging because studies utilize different active phases, supports, and feedstocks (LDPE, HDPE, PP; different molecular weight; etc.). Yet, comparative studies are essential to advance the field. The significance of benchmarking in catalysis is frequently pointed out.26 Here we discuss several benchmarking aspects and make recommendations for future work.We compared the reaction temperatures and reaction times from several recent publications (see Table 1 for details and Fig. 1A). Compared to fast pyrolysis in a fluidized bed reactor,27 hydrocracking and hydrogenolysis operate at lower reaction temperatures and longer reaction times (Fig. 1). The lower temperatures lead to substantial energy savings discussed in the following section. Hydrogenolysis operates at lower temperatures at the expense of longer reaction times compared to hydrocracking. Nonetheless, these processes can overlap at moderate reaction conditions. The trade-off between reaction time and temperature (Fig. 1A) is expected. However, the reaction time varies significantly (by order of magnitude) depending on the catalyst, indicating the catalyst choice is vital for the CAPEX. Ru-Based hydrogenolysis catalysts, especially on TiO2,23 are very active at low temperatures. Similarly, among hydrocracking catalysts, metal/metal oxide catalysts physically mixed with zeolites operate at significantly lower temperatures than metals in zeolites and mesoporous materials, mixed metal oxides alone, or NiMo on SiO2–Al2O3.
These comparisons are rather simplistic as they do not distinguish the feedstock. Table 1 exposes large variations in molecular weight and plastics among studies. Unlike small molecule activation, the variation of the feedstock increases the complexity and makes comparisons harder. We return to this point below.
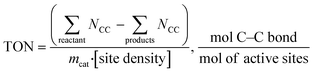
Catalyst activity should be benchmarked in turnover frequency (TOF) or turnover number (TON), which is the “numbers of turns of a catalytic cycle, equivalent to site-normalized catalytic productivities26”. For PE and PP hydroconversion, when it is almost impossible to deduce simple reaction steps, we propose to evaluate the number of broken C–C bonds:
Obviously, TON is insufficient to describe catalyst performance. C–C bonds can be broken internally (i.e., in the middle of the PE backbone17,25), in the terminal position leading to excessive methane formation,23 or on side chains leading to demethylation reported recently for PP hydrogenolysis over Ru/C.23 Whenever possible, experimental TON values should be accompanied by information about the C–C bond scission location.
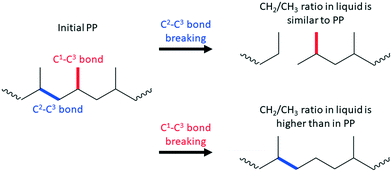
For example, terminal C–C bond cleavage in PE will produce light gases (mainly methane), while internal bond breaking will lead to liquids. Thus, differentiation is relatively simple. PP is more complicated, and liquid products should be characterized using NMR and/or GC. Similar to PE, terminal C1–C3 bond breaking will lead to methane formation. Internal C2–C3 bond cleavage will lead to a simple mixture of short PP oligomers (Scheme 1). In this case, liquid products will have a polypropylene-like structure with a CH2/CH3 molar ratio close to unity.
C1–C3 bond breaking is will remove CH3 groups in the middle of the chain of PP (Scheme 1). This demethylation process will alter the structure of the liquid products and generate undesired methane. Accurate estimation of demethylation reactions will enable researchers to differentiate and calculate TON values for specific C–C bond cleavage types. Newly formed C2–C2 bonds in demethylated products can participate in secondary cracking reactions, making calculations more complicated.
Catalyst productivity should also be normalized to the total catalyst mass, not only the active component. This is important for industrial applications when the total catalyst consumption per ton of product and the productivity per m3 of the reactor must meet strict limits.28 For instance, the catalyst consumption per ton of liquid products from PO should be in the range of ∼0.1–1 kg per ton, leading to an ideal polymer to catalyst mass ratio of 100–1000 in one reaction run. Published studies operate primarily with plastic to polymer ratios in the range of 0.5–30 (Table 1). More active catalysts are clearly needed.
Fig. 1B shows catalyst productivities compiled from recent papers. Those works did not aim at process optimization and productivity enhancement. Fig. 1B compares the amount of liquid produced per time and the amount of hydrocracking or hydrogenolysis catalyst. This metric accounts for the ratio of plastics to the catalyst and the reaction time that vary widely among studies (Table 1). Furthermore, the selectivity to light gases over liquids varies among catalysts. The data shows that at very low temperatures (200–250 °C), both hydrogenolysis and hydrocracking offer similar productivity. Hydrogenolysis exposes an upper limit at ∼250 °C above which extensive methane forms, leading to lower liquid yields (a volcano type of behavior). At high temperatures, hydrocracking performance is increased due predominantly to the shortening of the reaction time.9,15
PO conversion products can be grouped into gasoline (C5–C12) and diesel (C9–C22) based on the product alkane carbon number (Fig. 1C and D). Interestingly, hydrocracking is the most selective route to gasoline in the 250–375 °C temperature range. Hydrogenolysis shows a nearly linear increase of gasoline yield with increasing reaction temperature while being less selective overall. In contrast, hydrogenolysis is superior to hydrocracking for diesel production. Only one recent report16 shows an appreciable yield, comparable to hydrogenolysis, of light diesel-range alkanes over a Pt/WO3/ZrO2 catalyst under mild reaction conditions without a strong-solid acid. Overall, hydrocracking leverages the acid functionality to crack faster and produce lighter products. Lubricants and waxes are less commonly reported as main products.9,15,16
It is hard to compare the yields of different products since they change during the reaction and limited such time-dependent data has been published as batch experiments are time consuming. Selectivity–conversion curves are often used to compare catalysts, and this would be a good metric for future reports. Fig. 2 shows conversion–selectivity data for various catalysts tested for LDPE hydroconversion at 250 °C with the same LDPE substrate (MW ∼ 76 kDa) by varying the reaction time from 0.5 to 16 h. Light C1–C4 gas, gasoline, and diesel carbon numbers overlap so that the sum can be higher than 100% or lower due to heavy waxes/lubricants with carbon numbers larger than gasoline and diesel. Hydrocracking over Pt/WO3/ZrO2 + HY (Fig. 2A) produces more gasoline than diesel. As the conversion increases, the gasoline selectivity grows from 60 to ca. 75% due to secondary hydrocracking of intermediate C8–C17 hydrocarbons over zeolite acid sites. Without a zeolite (i.e., over Pt/WO3/ZrO2; Fig. 2B), the gasoline selectivity is nearly independent of the conversion and decreases slightly from 74 to 64%. This catalyst is more selective towards C8–C12 alkanes primarily due to the absence of confinement in the micropores and the milder acidity of the mixed-metal oxide support. The constant product selectivity over a wide range of conversions indicates that chemistry happens primarily on the macromolecule rather than the liquid products. The macromolecules selectively adhere to the catalyst surface and products are generated from the direct cleavage of the chain. This adhesive mechanism segregates the products into the melt bulk, preventing sequential cracking reactions. The difference between Pt to Ru on otherwise identical WO3/ZrO2 support (Fig. 2B and C) underscores the importance of the metal on product selectivity. Ru forms heavier products than Pt. For the Ru/WO3/ZrO2 catalysts (Fig. 2B and C), light gases are seen early on, but the selectivity to liquids improves significantly with increasing conversion. This behavior is due to the gradual deconstruction of LDPE to heavy products that remain in the solid state upon quenching, while methane is cleaved directly from the polymer chain. The selectivity to gasoline and diesel ranged products increases only when the solid product's molecular weight distribution begins to fall into this hydrocarbon range. Since conversion is calculated based on the total solid yield, it misses transformations within the solid, leading to high apparent selectivity to methane. We propose to compare the selectivity to light gases at longer times when conversion is sufficiently high to minimize this issue.
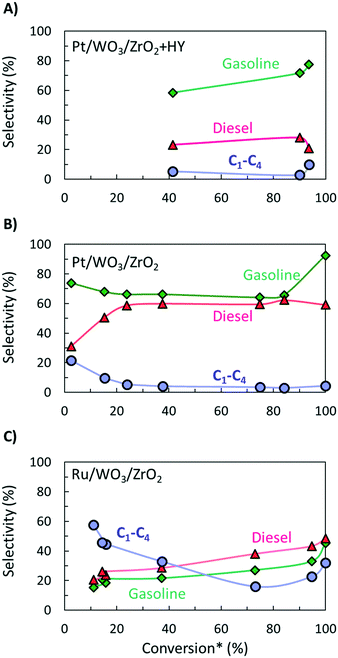 | ||
| Fig. 2 Selectivity to diesel, gasoline, and light gas hydrocarbons as function of apparent LDPE conversion for A) hydrocracking using a physical mixture of Pt/WO3/ZrO2 and HY;9 B) hydrogenolysis over a pure Pt/WO3/ZrO2 (ref. 16) and C) over Ru/WO3/ZrO2.25 * – conversion was calculated based on total yield of liquid products. | ||
3. Energy analysis
Energy use is a valuable metric of chemical processes. These estimations have become even more important due to a shift from traditional performance metrics to sustainability metrics, CO2 emissions, and climate impact.29 Moreover, such comparisons can provide valuable insights into the limitations of the technologies and guide the next generation of engineered processes. Despite these benefits, energy analyses for the hydroconversion of polyolefins are lacking. Meanwhile, in recent years, there has been an explicit preference for low-temperature catalytic processes as more environmentally friendly.We conducted energy balance calculations using data extracted from literature9,13–15,19–22,24,25 for the hydrocracking and hydrogenolysis of PE and PP. These calculations utilize eqn (1). Here, ΔEreactants represents the energy needed to bring the reactants (i.e., PE or PP and H2) from the standard state (25 °C, 1 bar) to reaction conditions, ΔErxn represents the energy of reaction to produce a product distribution at reaction conditions, and ΔElosses is an estimate of the energy lost to the surrounds over the total reaction time, assuming all reactions were ran in a cylindrical, non-insulated 50 mL batch reactor with a radius of 9 cm and a height of 10 cm. The ESI† provides details on the calculation of the energy.
| ΔEdemand = ΔEreactants + ΔErxn + ΔElosses | (1) |
These calculations could include the energy demand for downstream processes (i.e., separations) to produce commercial products. However, we refrain from doing this to maintain a fairer comparison as the dominant product fractions differ between hydrocracking and hydrogenolysis (Fig. 2). Downstream analysis should be reserved for comparing processes within the same hydroconversion technology.
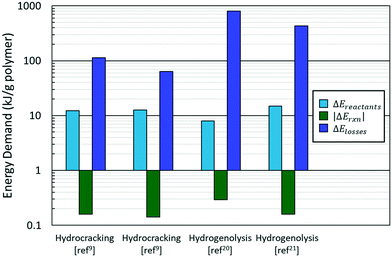
The typical breakdown in eqn (1) is shown in Fig. 3. Most of the energy in the PO hydroconversion is spent bringing the reactants (polymer and hydrogen) to reaction conditions and heat losses to the surroundings. These contributions dominate the energy of the reaction in eqn (1) by two orders of magnitude. This is because hydroconversion reactions are slightly exothermic (∼−50 kJ mol−1 product) and subsequently do not contribute significantly to the energy makeup. As reactors are scaled up, the heat loss declines. The primary energy consumption is to heat the plastic and hydrogen to reaction conditions (i.e., heating the polymer and hydrogen, melting the polymer, heating the melt, and compressing the hydrogen). The energy of fusion of the plastic is ca. 3% of the energy of heating and compressing the reactants; thus, the phase change energy can be left out for rough estimates. Furthermore, the identity of the plastic (PP vs. PE) negligibly affects the value of ΔEreactants but significantly alters the hydroconversion products, particularly for hydrogenolysis.20,22,23
Fig. 4A shows the calculated power demand normalized by polymer mass for PO hydrocracking and hydrogenolysis as a function of reaction temperature. There is an apparent increase in the power with increasing reaction temperature for both hydrocracking and hydrogenolysis. Moreover, the power for all hydroconversion processes vs. temperature exhibits a generalizable trend, regardless of variations in the H2 pressure and/or reaction times. This is consistent with the aforementioned trend toward lower temperature processes,30 and again, more active catalysts are desired to reduce the temperature and the processing time.
The total energy demand vs. temperature (Fig. 4B) does not show a clear correlation between variables. There is a large (an order of magnitude) variation in energy demand among studies. Furthermore, it becomes evident that lower reaction temperatures are not necessarily less energy-intensive than higher temperatures because mild processes require longer times to convert the polymer completely (Fig. 4B). Fig. 4B shows clustering of the hydrocracking and hydrogenolysis data, with hydrocracking requiring less energy to deconstruct both PP and PE compared to hydrogenolysis. Reactions that require longer times suffer higher losses to the surroundings, thereby increasing the energy demand. Interestingly, hydrocracking at mildly high temperatures (∼330 °C, ref. 15) has the lowest energy demand due to the shorter reaction times because reaction rates grow rapidly with temperature. This finding highlights that high-temperature processes can be beneficial for low-energy PO deconstruction as long as the selectivity can be controlled.
The energy demand as a function of liquid (C6–C40) productivity (Fig. 4C) clarifies the segregation between hydrocracking and hydrogenolysis seen in Fig. 4B. In Fig. 4C, all hydroconversion processes fall onto a monotonically decaying curve, but there is again clustering, with hydrocracking having, in general, better productivities (i.e., higher deconstruction rates) compared to hydrogenolysis. The differences in productivity are associated with differences in chemistry and its impact on the relative rates of deconstruction. In hydrogenolysis, mild C–C bond cracking occurs via metal-bound carbonaceous species, while C–C bond cleavage is mediated by fast carbocation chemistry in hydrocracking. The differences in the mediated reactive species make hydrocracking faster, therefore reducing the overall time needed for polyolefin deconstruction and the subsequent energy demand and improve productivity by limiting the generation of undesirable light gases (i.e., methane). The attainable range of carbon numbers differs between processes, as hydrocracking is restricted to branched C4–C∼16 products9,15,16 while hydrogenolysis produces heavier normal alkanes (C10+).20,21,25
This analysis alludes to future directions for hydrogenolysis and hydrocracking. For hydrocracking, one should engineer catalysts operating at mild temperatures while maintaining high rates and expanding the range of hydrocarbon products. As for hydrogenolysis, future work should enhance the deconstruction rates under the prevalent reaction temperatures and pressures while limiting light gas (C1–C5) production. For instance, our recent report25 shows that hydrogenolysis over a Ru/WO3/ZrO2 catalyst can breach the current productivity limit to enter the hydrocracking area in Fig. 4C.
4. Mechanistic knowledge transfer and plastic surrogates
It is well known that the surface of heterogeneous catalysts responds to and is significantly altered by the reaction environment.31 Only in rare instances32 information on active sites and intermediates can be transferred from low- to high-pressures. The connection of ultra-high vacuum and reactor conditions has been a long-standing hope of the scientific community. Still, decades of research have demonstrated that this happens only on certain occasions. A similar mechanistic gap exists in linking model small alkane conversion over metal or metal/acid catalysts to melted polymers under high hydrogen pressure. We elaborate on this point next.5. Hydrogenolysis
5.1. The nature of catalyst-reactant interactions
Hydrogenolysis catalysts should facilitate the breaking of C–C bonds in alkanes/polyolefins and the H–H bond in H2 with the subsequent formation of two new terminal C–H bonds in the products. The degree of compensation (χ) allows to estimate the efficiency of this bond redistribution:33where
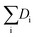 is a sum of all broken bond energies and Ea is the activation energy for hydrogenolysis. For most catalysts, χ equals 85–90%.34 Using standard bond energies,35 we can estimate the hydrogenolysis activation energy over good catalysts to be 80–120 kJ mol−1. This estimation quite accurately predicts the minimum Ea,36 while for poor catalysts, it can be much larger than 120 kJ mol−1.
is a sum of all broken bond energies and Ea is the activation energy for hydrogenolysis. For most catalysts, χ equals 85–90%.34 Using standard bond energies,35 we can estimate the hydrogenolysis activation energy over good catalysts to be 80–120 kJ mol−1. This estimation quite accurately predicts the minimum Ea,36 while for poor catalysts, it can be much larger than 120 kJ mol−1.
Several attempts were made to estimate the optimal catalyst–alkane interaction energy and maximize the reaction rate.33 Following ref. 33, we can consider the formation of the surface complex according to Scheme 2. This hypothetical scheme reflects that forming carbon–metal bonds weakens the C–C bond in an alkane.37 If the surface complex contains two metal atoms, then we can estimate the activation energy required in the first step in Scheme 2 using bond energies:
| E1 = 2DM–H + 2DM–C − DC–C − DH–H. |
| E2 = 2DC–H − 2DM–C − 2DM–C. |
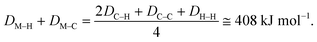 | (2) |
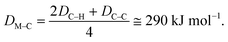 | (3) |
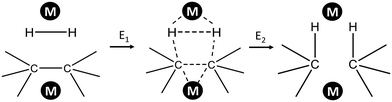 | ||
| Scheme 2 Formation of adsorbed complex during alkane hydrogenolysis though interaction with two metal sites. | ||
For Pt-catalyzed hydrogenolysis of neopentane,41 the authors show using DFT that Pt 5d electrons are primarily responsible for Pt binding to the alkyl radical, while the Pt 6sp electrons are involved in the Pt–H bond. Different supports for Pt clusters can significantly alter the electron densities on those orbitals. Thus, metal–support interactions can effectively change DPt–H and DPt–C on the left side of eqn (2) or (3). This change in bond energies induced by metal–support interactions can reduce the Pt activity.
Sinfelt compared the hydrogenolysis activity of different metals as a function of their d-band filling.42 He observed an activity maximum at a certain level, roughly estimated from the position of the metal in the periodic table. We can speculate that DM–C is influenced by the relative number of d-electrons, similar to Pt. So, the dependence on the d-character of the metal may also reflect the optimal DM–C values.
Another interesting consequence of eqn (3) is a different optimal DM–C for the hydrogenolysis of various bonds in the PO chain. For example, using the data from ref. 43, we can estimate that DM–C should be different for C2–C2 internal bond breaking in PE or for C3–C1 bonds in PP. Obviously, multiple adsorbed complexes can exist on the surface at the same time leading to a much more complicated reaction network. Yet, these simple principles are powerful for a basic analysis and design.
5.2. Small alkane hydrogenolysis kinetics
Detailed studies on alkanes hydrogenolysis for various substrates were reported by Flaherty et al.44–46 Here we aim only to highlight select concepts and lessons accumulated in the vast hydrogenolysis literature over the years. Hydrogenolysis involves C–H bond breaking by dissociative adsorption:| CnH2n+2 + zS ↔ CnHx + (2n + 2 − x)Hads. |
| CnHx → CaHb + Cn–aHx–b. |
| TOF = kθCθαH, | (4) |
The C–H bond breaking equilibration is based on the fast H/D exchange rates between alkanes and D2 under hydrogenolysis conditions and multiple observations of highly stable dehydrogenated species.39 Surface science studies show that small alkanes dissociation to CnHx and H2 on metal surfaces is orders of magnitude faster than hydrogenolysis. After connecting the dehydrogenation equilibrium with the rate in eqn (4), the TOF dependence on θH is:41
leading to eqn (5):
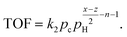 | (5) |
Several authors41,48 reported that the Langmuirian isotherm is inadequate to describe the θHvs. pH dependence, and the Temkin isotherm: θH ∼ α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(pH) is more suitable for non-ideal surfaces. This approach leads to an interesting nonlinear dependence of the apparent reaction orders and activation energy on hydrogen coverage with a sharp maximum.49
log(pH) is more suitable for non-ideal surfaces. This approach leads to an interesting nonlinear dependence of the apparent reaction orders and activation energy on hydrogen coverage with a sharp maximum.49
An essential limitation of eqn (5) is that the surface coverage of CnHx is calculated assuming dehydrogenation equilibrium. Leclercq et al.50 derived eqn (6) in better agreement with experimental data at moderate hydrogen pressures:
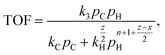 | (6) |
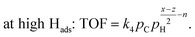 | (7) |
| at low Hads: r = k5pH. | (8) |
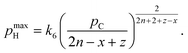 | (9) |
The pool of dehydrogenated surface compounds can isomerize to each other. Additionally, all surface species can participate in C–C bond breaking with different selectivity and rates. Furthermore, these key intermediates change with the metal catalyst. For instance, Hibbitts et al.37 showed that [CH2–CH3] has the lowest C–C bond breaking activation energy in ethane hydrogenolysis over Cu, whereas on Ir and Ru [CH–CH2] is the most reactive intermediate. Dumesic54,55 and Vlachos56 showed that microkinetic modeling parametrized with DFT calculations could capture the most reactive CnHx species. Microkinetic modeling also considers the hydrogen and alkyl coverage effects, which are hard to account for using simpler approaches41 that lead to various approximate rate expressions. While microkinetic models are feasible for small hydrocarbons, they are a formidable task for polymers.
Finally, the hydrogenolysis rate often has a negative order dependence on the hydrogen pressure, but for some hydrocarbons, a maximum is seen. Simplistically, the reaction order is related to the structure of the CnHx intermediate corrected to the number of surface sites. Deviation from the Langmuirian isotherm usually leads to a substantial variation of the apparent activation energy with temperature due to coverage effects.
5.3. Mechanistic comparison of PO and small alkane hydrogenolysis
There are intriguing similarities of PO hydrogenolysis to and differences from small alkanes. Ru and Pt-based catalysts were studied for PE20,21,25 and PP22,23 hydrogenolysis in the melt phase at 200–300 °C at H2 pressure above 10 bar. Ru particles on carbon, TiO2, and CeO2 show superior activity to other metals, resembling the catalyst activity trend of ethane hydrogenolysis.42In small alkane hydrogenolysis, the hydrogen reaction order is essential, and so is for macromolecules. For lighter normal C2–C10 alkanes, the hydrogen reaction order is usually negative (approx. −3 (ref. 44–46)). As discussed above, this implies an equilibrated alkane dehydrogenation and competitive substitution of CnHx with Hads over surface sites at high pH.
In PE conversion over Ru/WO3/ZrO2 catalysts, the liquid yields grow when pH increases from 25 to 130 bar.25 A similar effect occurs on Ru/C upon a pressure increase from 15 to 25 bar.20 This indicates that the hydrogen order in PE hydrogenolysis is positive, corresponding to eqn (6) or (8). The stronger binding of the polymer leads to depletion of Hads species, making the response different from the lighter alkanes. A high hydrogen pressure should rather promote the C–C breaking in accordance with eqn (4). This effect is not specific to polymers, and was previously observed for cycloalkanes at pH below 20 bar.46 The strong binding of polymers to metal surfaces changes the extent of secondary reactions. The methane production can strongly be modulated with pH, due to the strong binding of the polymer with CnHx intermediates undergoing secondary hydrogenolysis to methane. This sequence is depicted as steps 4 and 5 in Scheme 3. Similar observations were previously made for n-C6 and i-C6 hydrogenolysis over Ru/Al2O3.57 High hydrogen coverages hydrogenate the CnHx reaction intermediates followed by desorption of the hydrocarbons, reducing their time on the surface after the primary C–C bond breaking (step 3 in Scheme 3). At low hydrogen coverages, CnHx residues stay longer and crack further, leading to light alkanes (steps 4 and 5). This pressure dependence and learnings from small hydrocarbons provide a knob for methane suppression in PO hydrogenolysis. Specifically, catalysts with a stronger H bonding or an H reservoir and higher pressures improve the selectivity to liquids. For instance, polytungstate domains on the Ru/WO3/ZrO2 surface serve as reservoirs for hydrogen due to the partial WOx reduction. These reduced WOx species lead to higher liquid yields similar to using higher hydrogen pressures.26
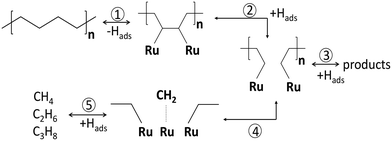 | ||
| Scheme 3 Reaction network of PE hydrogenolysis over Ru/WO3/ZrO2 catalyst.24 1) dehydrogenation; 2) C–C bond breaking; 3) hydrogenation with products desorption; 4) secondary hydrogenolysis; 5) formation of light gas products. | ||
Van der Waals interactions will increase with each additional CH2 group leading to stronger polymer binding compared to small alkanes. On the other hand, chemisorption on the catalyst surface, multisite binding and other factors can significantly impact the energetics of adsorbed intermediates.
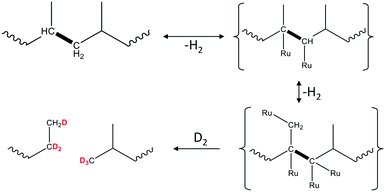
An important deviation from the classic hydrogenolysis is the hypothesis of quasi-equilibrated dehydrogenation steps. It may be true for polymers in certain instances. Recent results23 show that PP hydrogenolysis over Ru/TiO2 in D2 leads to the formation of evenly deuterated liquid products. At the same time, the solid residues only have significant deuteration in [CH2] groups, but not in [CH3]. This indirectly indicates that the rates of [CH3] group dehydrogenation are almost comparable to the rates of C–C bond hydrogenolysis. One possible explanation invokes the multisite binding of PP during surface dehydrogenation (Scheme 4). To sufficiently reduce the strength of C–C bonds, multiple Ru–C contacts should form not only in nearest C atoms, but also at the CH3 group. Formation of this intermediate can be challenging. After slow dehydrogenation, the internal C–C bond breaking can have a similar or even higher intrinsic rate.
To recap, we postulate that PO hydrogenolysis has several distinct features:
• PO chemisorption is stronger than hydrogen leading to a positive apparent reaction order with respect to pH
• Due to stronger macromolecule binding, secondary reactions are more influential for selectivity, compared to small alkanes.
• Dehydrogenation and C–C bond breaking rates can be comparable. The formation of multiple constrained Ru–C bonds is necessary for C–C bond breaking.
6. Hydrocracking
6.1. Hydrocracking of model alkanes
The literature on hydrocracking of model alkanes is vast; here, we describe some key aspects related to PO hydrocracking (Fig. 5).58–63 Hydrocracking requires bifunctional catalysts with metallic and acidic sites. Metallic sites dehydrogenate paraffin species to olefins. These olefins then diffuse to Brønsted acid sites that catalyze skeletal isomerization and β-scission (i.e., C–C cracking) reactions via well-established carbenium ion chemistry.59–61,64 Finally, the metallic sites hydrogenate the olefins produced from the acid-catalyzed reactions to final alkanes. The entire cycle keeps repeating itself.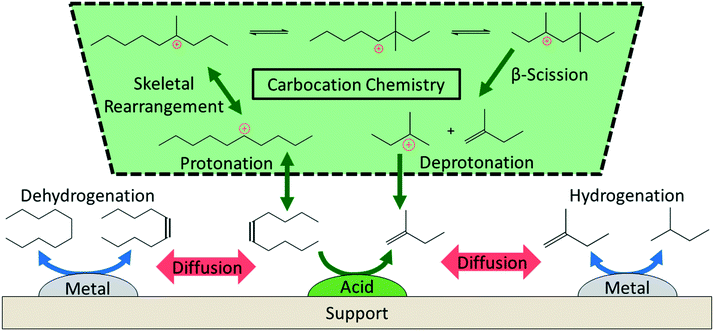 | ||
| Fig. 5 Overview of the reaction mechanism for the hydrocracking of small alkanes over a metal–acid bifunctional catalyst. | ||
Key reaction parameters60,65–68 in model alkanes (i.e., temperature, H2 pressure, alkane chain length, etc.) and catalyst descriptors62,69–75 (i.e., metal–acid balance, intimacy between sites, site accessibility, etc.) have been identified. The concept of ideal and nonideal hydrocracking is typically utilized to describe the effects of these variables.60,63 The ideal hydrocracking is characterized by 1) symmetric product distribution centered around half of the feedstock carbon number; 2) high selectivities to isomerized products; 3) acid-catalyzed reactions being rate-limiting; and 4) a reaction mechanism that converts the alkane feedstock sequentially to monobranched isomers, then dibranched isomers, and finally cracked products. Conversely, nonideal hydrocracking is characterized by 1) a highly left-skewed product distribution typically with large fractions of C3 and C4 alkanes; 2) low selectivity to isomerized products; 3) metal-catalyzed reactions being rate-limiting; and 4) a reaction mechanism that produces isomerized feedstock species and cracked species simultaneously.
Interestingly, the effect of system variables on the hydrocracking performance is captured well with the ideal/non-ideal hydrocracking regimes. For example, Thybaut et al.65 showed that high reaction temperatures, low reaction pressures, and high molar hydrogen-to-hydrocarbon ratios pushed n-dodecane hydrocracking to the nonideal regime. Their detailed kinetic analysis showed these parameters alter the reaction network in different ways. Specifically, higher reaction temperatures primarily increase the relative rates of acid-catalyzed and metal-catalyzed reactions. In contrast, low total pressures have a thermodynamic effect, impacting the concentration of the reactive intermediates (alkenes and therefore carbocations). Despite mechanistic differences, altering these parameters ultimately enhances the β-scission rates to lighter alkanes with less branching.
6.2. Applying concepts from alkane hydrocracking to PO
The model alkane literature provides an excellent foundation for designing PO hydrocracking catalysts. However, it is unclear if the relationships in model alkanes are valid for PO feedstocks. Our recent work,16 investigating the metal–acid balance (i.e., the metal-to-acid site molar ratio) and its role in LDPE hydrocracking, highlights many parallels between the model alkane and PO, such as the shift from type-B to type-A β-scission as the metal–acid balance increases. Additionally, we discovered crucial phenomena in LDPE hydrocracking absent from model alkane systems, such as the adhesive-like polymer adsorption to the catalytic surface, which significantly alters the hydrocracking dynamics.Subsequently, we need to understand the nature of polymer adsorption in reactive environments through comparative studies to probe key reaction parameters, identify catalyst descriptors, and bridge the gap between model alkanes and POs. Polymer diffusion is an essential topic in PO hydrocracking as several authors58,72–75 have highlighted the importance of mass transfer between the catalytic sites in the hydrocracking of alkanes. For example, Oenema et al.72 demonstrated the intimacy (i.e., distance) between solid acid and Pt sites supported on different zeolites directly impacts the cracking and isomerization selectivities of n-C7 hydroisomerization. The authors reported optimal isomerization selectivities with site intimacies in the nanoscale range for large pore zeolites; closest intimacies suffer from cracking reactions, whereas microscale separation reduces the activity and isomer selectivity due to the heptene concentration gradients. We believe mass transfer effects are likely compounded in the PO hydrocracking due to the complex polymer physics and are further influenced by the polymer structure. For example, in LDPE hydrocracking over Pt/USY, severe overcracking to C3–C6 alkanes has been observed.9,15 This catalytic behavior is likely due to the confinement of polymer chains in the zeolite pores, which restrict chain removal and result in excessive cracking. Thus, confinement effects and the diffusion r of polymers are an important area for further studies to further bridge the gap between PO and model alkanes.
It is crucial to note that the concept of (non)ideality has limited applicability in characterizing PO hydrocracking because of the distinct differences in the product distributions and the reaction mechanisms compared to alkane hydrocracking. Analysis of the symmetry/skewness is employed to determine (non)ideality.63 In PO hydrocracking, the product distributions across all products (gases, liquids, and solids) are asymmetric, i.e., PO hydrocracking processes are highly nonideal. Our work on LDPE hydrocracking16 demonstrates this feature as the entire carbon number distribution continues to be highly left-shifted over the range of metal–acid balances because the extractable (C1–C35) products are produced directly from β-scission of the polymer chain. In contrast, changes to the polymer residues are gradual due to their inherent size.
Small alkane hydrocracking follows sequential or concerted networks for ideal and non-ideal systems, respectively, to isomerized and cracked products.61,69,71 However, isomerization and cracking reactions appear decoupled in PO hydrocracking due to the adhesive adsorption of the polymer to the catalytic surface and the ability to incorporate significant branching in polymer chains that hinders β-scission in the interior.16 Subsequently, the characteristics of (non)ideal hydrocracking in small alkanes are ill-defined for POs. The terminology should be forgone or revised as more knowledge accumulates.
7. The plastics materials gap
A challenge in comparing the performance of catalysts owes to the wild variation of the properties and suppliers of virgin polymer materials employed in laboratory studies. The average molecular weight, the density, the degree of crystallinity, and possible impurities even in simple PE, significantly affect the rate of deconstruction and product distribution, rendering comparisons across studies nearly impossible. Fundamental experimental studies and models that can account for these material effects on reaction performance will be essential to close the feedstock materials gap and understand how catalysts interact with and deconstruct polymers. Meanwhile, we propose to use the same virgin materials among laboratories from the same vendors to standardize studies and facilitate benchmarking. For model polyolefins, we suggest Sigma-Aldrich HDPE (427985) for polyethylene substrates and Sigma-Aldrich isotactic-PP (427888) for polyethylene. It is also crucial to thoroughly characterize any polymer feedstock used for reactions. 13C NMR can be used to deduce branching density, GPC or MALDI to estimate molecular weight distributions, and GC-MS analysis to assess the type and concentration of additives and stabilizers.Furthermore, we propose studies to regularly characterize the polymer residues using gel-permeation chromatography (GPC), differential scanning calorimetry (DSC), and 1H and 13C nuclear magnetic resonance (NMR) to report changes in the neat polymer.
The complex nature of plastic waste, especially of packaging materials, has been extensively highlighted recently.6,76 Packaging materials contribute to ca. 40% of all waste and contain a substantial amount of PE or PP, but also other functionalized polymers and inorganic additives constitute several percent of the total material.
The effect of additives on catalyst performance has never been studied systematically in the open literature. Nonetheless, existing literature indicates the severity of additives.77 For example, a small fraction (14%) of EVA (ethylene vinyl acetate) leads to a significant decrease of Al-MCM-41 activity in the LDPE cracking at 420 °C.77 Interestingly, the inhibiting effect was not connected with the release of acetic acid. High-temperature decarboxylation of EVA produces polyene chains, which readily polymerize and cross-link into extended coke species. It was proposed that the microporous environment of ZSM-5 prevents extensive coking, leading to stable cracking performance. These phenomena can significantly change the entire research strategy for optimal catalysts and need to be considered.
8. Conclusions
Low-temperature hydroconversion processes have come to the forefront of catalytic research for the deconstruction of polyolefin (PO) plastic waste to fuels, lubricants, and waxes. Despite the progress, several unconventional challenges prevent direct comparison of results between laboratories and the rapid acceleration of catalyst and process development. Some of them include the varying and complex feedstock (composition, density, structure, etc.), impurities and additives, the different nature of polymer adsorption on the catalyst surfaces, the larger diffusion limitations, the presence of a melt phase or a solvent, analytical challenges, etc.In this comparative review, we highlighted fundamental insights into the hydrogenolysis and hydrocracking of model alkanes as a framework to engineer better catalysts and processes. We compared the results from small alkanes and PO feedstocks to identify major hurdles that currently hinder catalyst design. For hydrogenolysis, the key takeaways are:
• Polyolefins binding over metal active sites is stronger than small alkanes. This leads on one hand to a positive reaction order for hydrogen, and on the other, to strongly bonded intermediates that participate in secondary fragmentation leading to excessive quantities of light hydrocarbons.
• The classical concept of equilibrated dehydrogenation steps preceding the C–C bond breaking seems invalid for some polymers compared to small alkanes.
• Computational screening of metal–polymer surface complexes in search of optimal interaction strength can help to further catalyst development.
• Tuning of the metal electronic structure and its d-band closer to the optimum may allow selective targeting of different C–C bonds (C1–C2vs. C2–C2vs. C2–C3, etc.) in polyolefins.
For hydrocracking processes, key takeaways are:
• The impact of key reaction parameters and bifunctional catalyst descriptors need to be understood.
• The key differences of small alkanes and PO hydrocracking need to be delineated.
• The role of mass transfer and its effects on hydrocracking performance needs to be revealed.
Additionally, we analysed the energy consumption of the existing PO hydrocracking and hydrogenolysis technologies to draw a fairer comparison between these processes and provide broad guidance. Based on this analysis, future hydroconversion should:
• Engineer hydrocracking catalysts capable of maintaining high deconstruction rates at mild temperatures.
• Expand the feasible product distribution of PO hydrocracking to larger hydrocarbons.
• Enhance the hydrogenolysis deconstruction rates under the prevalent reaction temperatures and pressures while limiting light gas formation.
Finally, we have proposed fundamental studies, benchmarking, and standardization guidelines such as:
• Investigate the role of the polymer attributes (i.e., average molecular weight, density, degree of crystallinity) in PO deconstruction.
• Examine the impact of additives on catalyst performance and develop mitigation strategies.
• Standardize the virgin materials (same vendors, molecular weight, etc.) among laboratories.
• Characterize the polymer residues using GPC, DSC, and NMR techniques.
• Report turnover numbers and location of broken C–C bonds.
We believe these endeavours are necessary for the progress of plastic waste deconstruction technologies and will significantly contribute to addressing the global threat of plastic waste.
Author contributions
Manuscript has been written by equal contribution of all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The University of Delaware Center for Plastics Innovation is supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences under Award Number DE-SC0021166. Any opinions, findings, conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect those of the DOE. B. C. V. acknowledges a Graduate Research Fellowship through the National Science Foundation under Grant Number 1940700.Notes and references
- L. Lebreton and A. Andrady, Palgrave Commun., 2019, 5, 1–11 CrossRef
.
- J. J. Klemeš, Y. Van Fan and P. Jiang, Energy Sources, Part A, 2021, 43, 1549–1565 CrossRef
.
- R. Geyer, J. R. Jambeck and K. L. Law, Sci. Adv., 2017, 3, e1700782 CrossRef PubMed
.
-
P. F. Britt, G. W. Coates and K. I. Winey, in Basic Energy Sciences Roundtable, 2019, pp. 1–56 Search PubMed
.
- A. J. Martín, C. Mondelli, S. D. Jaydev and J. Pérez-Ramírez, Chem, 2021, 7, 1487–1533 Search PubMed
.
- L. D. Ellis, N. A. Rorrer, K. P. Sullivan, M. Otto, J. E. McGeehan, Y. Román-Leshkov, N. Wierckx and G. T. Beckham, Nat. Catal., 2021, 4, 539–556 CrossRef CAS
.
- X. Chen, Y. Wang and L. Zhang, ChemSusChem, 2021, 14, 4137–4151 CrossRef CAS PubMed
.
- J. Garcia-Martinez, Angew. Chem., Int. Ed., 2021, 60, 4956–4960 CrossRef CAS PubMed
.
- S. Liu, P. A. Kots, B. C. Vance, A. Danielson and D. G. Vlachos, Sci. Adv., 2021, 7, eabf8283 CrossRef CAS PubMed
.
- L. D. Ellis, S. V. Orski, G. A. Kenlaw, A. G. Norman, K. L. Beers, Y. Román-Leshkov and G. T. Beckham, ACS Sustainable Chem. Eng., 2021, 9, 623–628 CrossRef CAS
.
- C. Y. Chen, D. J. O'Rear and P. Leung, Top. Catal., 2012, 55, 1344–1361 CrossRef CAS
.
- K. R. Venkatesh, J. Hu, W. Wang, G. D. Holder, J. W. Tierney and I. Wender, Energy Fuels, 1996, 10, 1163–1170 CrossRef CAS
.
- W. Ding, J. Liang and L. L. Anderson, Energy Fuels, 1997, 11, 1219–1223 CrossRef CAS
.
- J. M. Escola, J. Aguado, D. P. Serrano, A. García, A. Peral, L. Briones, R. Calvo and E. Fernandez, Appl. Catal., B, 2011, 106, 405–415 CrossRef CAS
.
- A. Bin Jumah, V. Anbumuthu, A. A. Tedstone and A. A. Garforth, Ind. Eng. Chem. Res., 2019, 58, 20601–20609 CrossRef CAS
.
- B. C. Vance, P. A. Kots, C. Wang, Z. R. Hinton, C. M. Quinn, T. H. Epps, L. T. J. Korley and D. G. Vlachos, Appl. Catal., B, 2021, 299, 120483 CrossRef CAS
.
- G. Celik, R. M. Kennedy, R. A. Hackler, M. Ferrandon, A. Tennakoon, S. Patnaik, A. M. Lapointe, S. C. Ammal, A. Heyden, F. A. Perras, M. Pruski, S. L. Scott, K. R. Poeppelmeier, A. D. Sadow and M. Delferro, ACS Cent. Sci., 2019, 5, 1795–1803 CrossRef CAS PubMed
.
- F. Zhang, M. Zeng, R. D. Yappert, J. Sun, Y. H. Lee, A. M. LaPointe, B. Peters, M. M. Abu-Omar and S. L. Scott, Science, 2020, 370, 437–441 CrossRef CAS PubMed
.
- A. Tennakoon, X. Wu, A. L. Paterson, S. Patnaik, Y. Pei, A. M. LaPointe, S. C. Ammal, R. A. Hackler, A. Heyden, I. I. Slowing, G. W. Coates, M. Delferro, B. Peters, W. Huang, A. D. Sadow and F. A. Perras, Nat. Catal., 2020, 893–901 CrossRef CAS
.
- J. E. Rorrer, G. T. Beckham and Y. Román-Leshkov, JACS Au, 2021, 1, 8–12 CrossRef CAS PubMed
.
- Y. Nakaji, M. Tamura, S. Miyaoka, S. Kumagai, M. Tanji, Y. Nakagawa, T. Yoshioka and K. Tomishige, Appl. Catal., B, 2021, 285, 119805 CrossRef CAS
.
- J. E. Rorrer, C. Troyano-Valls, G. T. Beckham and Y. Román-Leshkov, ACS Sustainable Chem. Eng., 2021, 9, 11661–11666 CrossRef CAS
.
- P. A. Kots, S. Liu, B. C. Vance, C. Wang, J. D. Sheehan and D. G. Vlachos, ACS Catal., 2021, 11, 8104–8115 CrossRef CAS
.
- W. T. Lee, F. D. Bobbink, A. P. van Muyden, K. H. Lin, C. Corminboeuf, R. R. Zamani and P. J. Dyson, Cell Rep. Phys. Sci., 2021, 2, 100332 CrossRef CAS
.
- C. Wang, T. Xie, P. A. Kots, B. C. Vance, K. Yu, P. Kumar, J. Fu, S. Liu, G. Tsilomelekis, E. A. Stach, W. Zheng and D. G. Vlachos, JACS Au, 2021, 1, 1422–1434 CrossRef CAS PubMed
.
- T. Bligaard, R. M. Bullock, C. T. Campbell, J. G. Chen, B. C. Gates, R. J. Gorte, C. W. Jones, W. D. Jones, J. R. Kitchin and S. L. Scott, ACS Catal., 2016, 6, 2590–2602 CrossRef CAS
.
- D. Zhao, X. Wang, J. B. Miller and G. W. Huber, ChemSusChem, 2020, 13, 1764–1774 CrossRef CAS PubMed
.
- J. P. Lange, Nat. Catal., 2021, 4, 186–192 CrossRef CAS
.
- J. B. Zimmerman, P. T. Anastas, H. C. Erythropel and W. Leitner, Science, 2020, 367, 397–400 CrossRef CAS PubMed
.
-
P. T. Anastas and J. C. Warner, Green Chemistry Theory and Practice, Oxford University Press, Cary, North Carolina, 1998 Search PubMed
.
- J. J. Velasco-Vélez, V. Pfeifer, M. Hävecker, R. Wang, A. Centeno, A. Zurutuza, G. Algara-Siller, E. Stotz, K. Skorupska, D. Teschner, P. Kube, P. Braeuninger-Weimer, S. Hofmann, R. Schlögl and A. Knop-Gericke, Rev. Sci. Instrum., 2016, 87, 053121 CrossRef PubMed
.
- R. Imbihl, R. J. Behm and R. Schlögl, Phys. Chem. Chem. Phys., 2007, 9, 3459–3459 RSC
.
- G. I. Levi and A. A. Balandin, Bull. Acad. Sci. USSR, Div. Chem. Sci., 1958, 7, 1447–1449 CrossRef
.
-
G. K. Boreskov, Heterogeneous catalysis, Nova Science Publishers, 2003 Search PubMed
.
-
Y. R. Luo, Compr. Handb. Chem. Bond Energies, 2007, pp. 1–1656 Search PubMed
.
- G. C. Bond and J. C. Slaa, J. Mol. Catal. A: Chem., 1995, 101, 243–253 CrossRef CAS
.
- A. Almithn and D. Hibbitts, J. Phys. Chem. C, 2019, 123, 5421–5432 CrossRef CAS
.
- F. Zaera and S. Tjandra, J. Am. Chem. Soc., 1996, 118, 12738–12746 CrossRef CAS
.
- J. H. Sinfelt, Catal. Lett., 1991, 9, 159–171 CrossRef CAS
.
- H. Zimmer, P. Tétényi and Z. Paál, J. Chem. Soc., Faraday Trans. 1, 1982, 78, 3573–3586 RSC
.
- D. C. Koningsberger, M. K. Oudenhuijzen, J. De Graaf, J. A. Van Bokhoven and D. E. Ramaker, J. Catal., 2003, 216, 178–191 CrossRef CAS
.
- J. H. Sinfelt, Adv. Catal., 1973, 23, 91–119 CAS
.
- M. Boudart, AIChE J., 1972, 18, 465–478 CrossRef CAS
.
- D. D. Hibbitts, D. W. Flaherty and E. Iglesia, J. Phys. Chem. C, 2016, 120, 8125–8138 CrossRef CAS
.
- D. D. Hibbitts, D. W. Flaherty and E. Iglesia, ACS Catal., 2016, 6, 469–482 CrossRef CAS
.
- D. W. Flaherty, D. D. Hibbitts and E. Iglesia, J. Am. Chem. Soc., 2014, 136, 9664–9676 CrossRef CAS PubMed
.
- D. W. Flaherty and E. Iglesia, J. Am. Chem. Soc., 2013, 135, 18586–18599 CrossRef CAS PubMed
.
- G. A. Martin, J. Catal., 1979, 60, 345–355 CrossRef CAS
.
- G. A. Martin, R. Dutartre, S. Yuan, C. Márquez-Alvarez and C. Mirodatos, J. Catal., 1998, 177, 105–112 CrossRef CAS
.
- G. Leclercq, L. Leclercq and R. Maurel, Bull. Soc. Chim. Belg., 1979, 88, 599–620 CrossRef CAS
.
- G. C. Bond, J. Calhoun and A. D. Hooper, J. Chem. Soc., Faraday Trans., 1996, 92, 5117–5128 RSC
.
- D. W. Flaherty, A. Uzun and E. Iglesia, J. Phys. Chem. C, 2015, 119, 2597–2613 CrossRef CAS
.
- G. C. Bond, Appl. Catal., A, 1997, 149, 3–25 CrossRef CAS
.
- S. G. Podkolzin, R. Alcala, J. J. De Pablo and J. A. Dumesic, J. Phys. Chem. B, 2002, 106, 9604–9612 CrossRef CAS
.
- R. D. Cortright, R. M. Watwe and J. A. Dumesic, J. Mol. Catal. A: Chem., 2000, 163, 91–103 CrossRef CAS
.
- M. Salciccioli, Y. Chen and D. G. Vlachos, Ind. Eng. Chem. Res., 2010, 50, 28–40 CrossRef
.
- B. Coq, A. Bittar and F. Figueras, Appl. Catal., 1990, 59, 103–121 CrossRef CAS
.
- P. B. Weisz, Adv. Catal., 1962, 13, 137–190 CAS
.
- H. L. Coonradt and W. E. Garwood, Ind. Eng. Chem., 1964, 56, 69–69 CrossRef
.
- J. Weitkamp, Prepr. - Am. Chem. Soc., Div. Pet. Chem., 1975, 20, 489–507 Search PubMed
.
- J. A. Martens, P. A. Jacobs and J. Weitkamp, Appl. Catal., 1986, 20, 239–281 CrossRef CAS
.
- T. L. M. Maesen, S. Calero, M. Schenk and B. Smit, J. Catal., 2004, 221, 241–251 CrossRef CAS
.
- J. Weitkamp, ChemCatChem, 2012, 4, 292–306 CrossRef CAS
.
- L. A. Wall, S. L. Madorsky, D. W. Brown, S. Straus and R. Simha, J. Am. Chem. Soc., 1954, 76, 3430–3437 CrossRef CAS
.
- J. W. Thybaut, C. S. Laxmi Narasimhan, J. F. Denayer, G. V. Baron, P. A. Jacobs, J. A. Martens and G. B. Marin, Ind. Eng. Chem. Res., 2005, 44, 5159–5169 CrossRef CAS
.
- H. F. Schulz and J. H. Weitkamp, Ind. Eng. Chem. Prod. Res. Dev., 1972, 11, 46–53 CrossRef CAS
.
- M. Steijns and G. F. Froment, Ind. Eng. Chem. Prod. Res. Dev., 1981, 20, 660–668 CrossRef CAS
.
- V. Calemma, S. Peratello and C. Perego, Appl. Catal., A, 2000, 190, 207–218 CrossRef CAS
.
- G. E. Glannetto, G. R. Perot and M. R. Guisnet, Ind. Eng. Chem. Prod. Res. Dev., 1986, 25, 481–490 CrossRef
.
- T. F. Degnan and C. R. Kennedy, AIChE J., 1993, 39, 607–614 CrossRef CAS
.
- F. Alvarez, F. R. Ribeiro, G. Perot, C. Thomazeau and M. Guisnet, J. Catal., 1996, 162, 179–189 CrossRef CAS
.
- J. Oenema, J. Harmel, R. Pérez Vélez, M. J. Meijerink, W. Eijsvogel, A. Poursaeidesfahani, T. J. H. Vlugt, J. Zečević and K. P. De Jong, ACS Catal., 2020, 10, 14245–14257 CrossRef CAS PubMed
.
- J. Zecevic, G. Vanbutsele, K. P. De Jong and J. A. Martens, Nature, 2015, 528, 245–254 CrossRef CAS PubMed
.
- G. Noh, S. I. Zones and E. Iglesia, J. Phys. Chem. C, 2018, 122, 25475–25497 CrossRef CAS
.
- J. Sun, C. Mu, Y. Li, Y. Zhao, S. Wang and X. Ma, AIChE J., 2021, e17330 CAS
.
- K. Kaiser, M. Schmid and M. Schlummer, Recycling, 2018, 3, 1 CrossRef
.
- D. P. Serrano, J. Aguado, J. M. Escola, J. M. Rodríguez, L. Morselli and R. Orsi, J. Anal. Appl. Pyrolysis, 2003, 68–69, 481–494 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1re00447f |
| ‡ Equal contribution. |
| This journal is © The Royal Society of Chemistry 2022 |