Non-metal boron atoms on a CuB₁₂ monolayer as efficient catalytic sites for urea production

Abstract

An electrocatalytic C–N coupling reaction to convert CO₂ and N₂ into urea under mild conditions has been proposed to be a promising alternative experimentally, but the development of highly stable, low-cost and high-performance non-metal catalytic sites remains rare and challenging. Herein, a global-minimum CuB₁₂ monolayer with superior stability has been identified based on first-principles computations, and the most significant finding is that the CuB₁₂ monolayer possesses the best catalytic activity among the reported urea catalysts thermodynamically and kinetically. All possible reaction pathways to form urea (NH₂CONH₂) starting from the CO₂ molecule and N₂ molecule, including the CO₂ pathway, OCOH pathway, CO pathway, NCON pathway and mixed pathway, as well as the kinetic energy barriers of six possible C–N coupling reactions are systematically investigated. Non-metal B atoms at the midpoint of the edges of the squares act as excellent catalytic sites with a limiting potential of urea production of 0.23 V through the CO₂ pathway and OCOH pathway and the lowest kinetic energy barrier of C–N bond formation (0.54 eV) through the reaction *CO + *NHNH → *NHCONH. Therefore, this study not only identifies the first non-metal B catalytic sites for urea formation, but also perfects the reaction mechanism to convert CO₂ and N₂ into urea, which could provide great guiding significance to explore other high-performance urea catalysts.

---

Introduction

Electrocatalytic technology is considered to be the most promising strategy to replace energy-inefficient traditional industrial processes and achieve environmentally friendly approaches under ambient conditions.^1–5 In the last 20 years, electrocatalytic technology has been widely applied in various fields, including electrocatalytic CO₂ reduction reactions (CO₂RR) to alleviate the greenhouse effect,^6–8 electrocatalytic N₂ reduction reactions (NRR) to reduce energy consumption in the Haber–Bosch process,^9–11 electrocatalytic oxygen reduction and evolution reactions (ORR/OER) to promote the industrial applications of metal–air batteries,^12–14 and electrocatalytic hydrogen evolution reaction (HER) to obtain nonpolluting and zero emission energy resources.^15–17 In particular, the exploration of superior electrocatalysts for a lower-barrier C–C coupling reaction and highly effective activation of inert N≡N triple bonds has always been of great concern and has made great progress until now. The faradaic efficiency has increased to 79 ± 2% for the electrosynthesis of the C2 product on boron-doped copper catalysts through tuning the ratio of Cu^δ+ to Cu⁰ active sites.¹⁸ A high faradaic efficiency of 15.4 ± 1% toward the C3 product (n-propanol) has also been achieved on a double sulfur vacancy-rich CuS catalyst at −1.05 V versus the reversible hydrogen electrode, and the partial current density reaches up to 9.9 mA cm⁻² at −0.85 V in flow cells, which is the best reported electrochemical CO₂ reduction toward n-propanol.¹⁹ A faradaic efficiency of 56.55% and an NH₃ yield rate of 7.48 μg h⁻¹ mg⁻¹ starting from the N₂ molecule have been realized on a single-atom dispersed Fe–N–C catalyst under ambient conditions.²⁰

Inspired by the C–C coupling reaction and the activation of the N≡N triple bond, electrocatalytic C–N bond formation to convert CO₂ molecules and N₂ molecules into urea (NH₂CONH₂) under ambient conditions has been proposed to be a promising alternative to harsh industrial processes.²¹ Urea is regarded as one of the most important nitrogen fertilizers with a high nitrogen content (46%),²² while its industrial synthesis requires very large energy consumption under harsh reaction conditions (350–550 °C and 150–350 bar) and emits a massive amount of the green-house gas CO₂.^23–26 Therefore, the exploration of high-performance catalysts for urea production is a significant challenge and has attracted tremendous attention since 2020. In 2020, Chen et al. have successfully realized electrochemical urea synthesis with a formation rate of 3.36 mmol g⁻¹ h⁻¹ and a faradaic efficiency of 8.92% at −0.4 V versus the reversible hydrogen electrode via PdCu alloy nanoparticles on TiO₂ nanosheets.²¹ In 2021, Yuan et al. have achieved a higher urea formation rate and faradaic efficiency at the same applied potential via Mott–Schottky Bi–BiVO₄ heterostructures (5.91 mmol g⁻¹ h⁻¹ and 12.55%) and BiFeO₃/BiVO₄ heterojunctions (4.94 mmol g⁻¹ h⁻¹ and 17.18%), respectively.^27,28 Meanwhile, Meng et al. reported that the urea faradaic efficiency increased to 23.26% at −0.79 V versus the reversible hydrogen electrode on oxygen vacancy-rich ZnO porous nanosheets by using CO₂ and nitrite contaminants as precursors.²⁹ Recently, Zhu et al. have proposed three MBene (Mo₂B₂, Ti₂B₂ and Cr₂B₂) two-dimensional (2D) materials as excellent electrocatalysts for urea formation with limiting potentials ranging from −0.49 eV to −0.65 eV by means of DFT methods.³⁰ It is noted that urea is formed all on the metal sites in previous reports. The non-metal B atom possesses both empty and occupied p orbitals, which results in unique advantages to efficiently adsorb and activate the inert N₂ molecule by accepting the lone-pair electrons of N₂ and donating electrons to the anti-bonding orbitals of N₂ to weaken the N≡N triple bond.^31–33 Moreover, the electron-deficient B atom can also adsorb and activate the inert CO₂ by providing electrons to CO₂ and breaking the inherent π bond.^34–36 Therefore, the non-metal boron atom possesses unique advantages to efficiently adsorb and activate the CO₂ molecule and N₂ molecule, simultaneously, which is a prerequisite to synthesize urea by the C–N coupling reaction. Further considering the B atom's intrinsic merits of low cost, environmental friendliness and long durability,^37–39 the development of non-metal B catalytic sites for urea production possesses great scientific significance.

In this work, the entirely planar CuB₁₂ monolayer with superior stability has been identified to be a global-minimum configuration. Most importantly, the non-metal B atoms at the midpoint of the edge of the square are confirmed to be excellent catalytic sites on the CuB₁₂ monolayer with a limiting potential of urea production of 0.23 V through the CO₂ pathway and OCOH pathway and the lowest kinetic energy barrier of C–N bond formation (0.54 eV) through the reaction *CO + *NHNH → *NHCONH, which presents the best catalytic activity thermodynamically and kinetically among the reported urea catalysts. Furthermore, the competitive CH₃OH and CH₄ products can be significantly suppressed. In addition, all possible reaction pathways starting from the CO₂ molecule and N₂ molecule for urea production, including the CO₂ pathway, OCOH pathway, CO pathway, NCON pathway and mixed pathway, are plotted and investigated in detail.

Results and discussion

Structure, stability and electronic properties of the CuB₁₂ monolayer

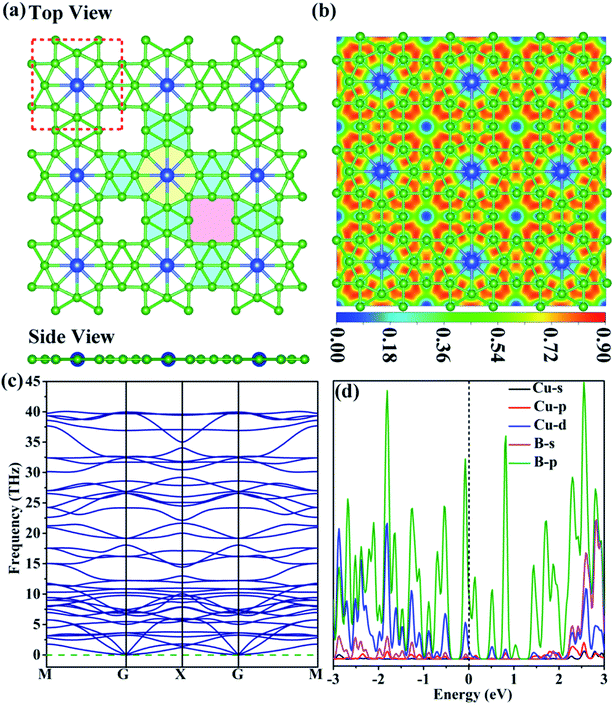
The entirely planar CuB₁₂ monolayer with the space group of P4/MMM is obtained and confirmed to be the global-minimum structure after a comprehensive search combined with first-principles calculation. The unit cell of the CuB₁₂ monolayer consists of one Cu atom and twelve B atoms in a square shape with the optimized lattice parameters of 6.18 Å (Fig. 1a and Table S2†). In the CuB₁₂ monolayer, the B₈-unit (blue-green colored parts in Fig. 1a) is formed by eight B atoms via multi-center multi-electron bonds, which is consistent with that in the predicted α-FeB₆ monolayer and is regarded as a subunit.⁴⁰ The entire planar periodic framework can be considered to be an extended framework of the B₈-unit along a and b directions by sharing the vertex. Meanwhile, two different eight-membered rings are constructed, including a round eight-membered ring with one embedded Cu atom (yellow colored part in Fig. 1a) and a square eight-membered ring with no anchored metal atom (pink colored part in Fig. 1a). Hence, each Cu atom binds with eight adjacent B atoms to form a planar hyper-coordinate moiety with 2.13 and 2.22 Å Cu–B bond lengths, and the Cu atom donates electrons to the adjacent B atoms to stabilize the electron-deficient boron framework. This CuB₁₂ monolayer develops planar hyper-coordinate 2D materials.^41–44 The computed electron transfer from the Cu atom to the boron framework is 0.46|e| based on the Bader charge,⁴⁵ which is also further supported by its electron location function (ELF) map⁴⁶ in the (001) direction (Fig. 1b). Moreover, the localized electron density over 0.75 among B atoms and uniform electron density around 0.50 in the whole ELF map suggest that strong bonding among B atoms exists and the delocalized electrons are distributed in the whole monolayer framework, which guarantees the superior stability of the CuB₁₂ monolayer. Remarkably, the square eight-membered ring can still exist in a steady state without any metal atom, which can be attributed to the multi-center multi-electron bonds with an ultrahigh electron density of 0.90 in the square eight-membered ring. The Bader charge analysis indicates that each B atom at the midpoint of the edges of the squares possesses +0.30|e|, which is expected to be potential catalytic sites.

Fig. 1 (a) Top and side views of the optimized global-minimum structure of the CuB₁₂ monolayer. The red dashed lines represent its primitive cell. The parts colored in blue-green, yellow and pink indicate the B₈-unit, the eight-membered ring with one embedded Cu atom and the empty eight-membered ring. (b) Electron location function (ELF) map sliced in the (001) direction of the CuB₁₂ monolayer. (c) Phonon dispersion of the CuB₁₂ monolayer. (d) Projected densities of states (PDOSs) of the CuB₁₂ monolayer using the PBE functional. The Fermi level is set to zero.

To evaluate the relative stability of the predicted CuB₁₂ monolayer, its thermodynamic, kinetic, thermal and mechanical stabilities are all examined. The cohesive energy of the CuB₁₂ monolayer is first computed to inspect the thermodynamic stability and to evaluate the binding strength of the connected framework, which is defined as E_coh = (E_Cu + 12E_B − E_CuB12)/13, in which E_Cu, E_B and E_CuB12 are the energies of a single Cu atom, a single B atom, and the CuB₁₂ monolayer, respectively. The calculated cohesive energy of the CuB₁₂ monolayer (5.71 eV per atom) is comparable to those of the predicted α-FeB₆ monolayer with the same B₈-unit (5.79 eV per atom),⁴⁰ the predicted ScB₁₂ monolayer with the same stoichiometry (5.94 eV per atom),⁴⁷ the predicted Ni₂B₅ monolayer (5.82 eV per atom),⁴⁸ and the experimentally available borophenes (5.90 eV per atom for triangular-borophene,⁴⁹ 5.95 eV per atom for β₁₂-borophene,⁵⁰ and 5.96 eV per atom for χ₃-borophene⁵⁰). Such cohesive energy indicates that the CuB₁₂ monolayer has a strongly bonded network and excellent thermodynamic stability. The kinetic stability of the CuB₁₂ monolayer is then confirmed by its phonon spectrum with no imaginary phonon modes (Fig. 1c). Its highest frequency of 1334 cm⁻¹ (40 THz) is comparable to those of the α-FeB₆ monolayer (1316 cm⁻¹),⁴⁰ ScB₁₂ monolayer (1290 cm⁻¹),⁴⁷ and AlB₆ nanosheet (1150 cm⁻¹).⁵¹ The phonon densities of states (PDOSs) of the CuB₁₂ monolayer presents the highest frequency corresponding to the B–B interactions, indicating robust B–B bonds in the B₈-unit (Fig. S1†). These data suggest the good kinetic stability of the CuB₁₂ monolayer. The outstanding thermal stability of the CuB₁₂ monolayer is also confirmed by AIMD simulations, because the CuB₁₂ monolayer can well maintain its original configuration with the B₈-unit up to 1200 K at the end of 10 ps MD simulation (Fig. S2†). Moreover, an explicit solvent environment is also evaluated to verify the stability of the CuB₁₂ monolayer under aqueous conditions. 112 H₂O molecules are present on the 3 × 3 supercell surface, which corresponds to the number of H₂O in 6 layers of pristine ice. The integral structure of the CuB₁₂ monolayer at 300 K at the end of 5 ps AIMD simulations can be well kept under aqueous conditions (Fig. S3†), suggesting its stability in the explicit solvent environment. The mechanical stability of the CuB₁₂ monolayer is examined by using computed elastic constants (C₁₁ = 194.93 N m⁻¹, C₂₂ = 215.99 N m⁻¹, C₁₂ = C₂₁ = 46.59 N m⁻¹ and C₄₄ = 19.87 N m⁻¹). These data meet the Born criteria: C₁₁C₂₂ – C₁₂² > 0 and C₆₆ > 0,⁵² indicating that the CuB₁₂ monolayer possesses good mechanical stability. Finally, the interlayer strengths in the complete overlap stacking (AA) and the crossing overlap stacking (AB) bilayers are both examined (Fig. S4†). The computed interlayer energies suggest that the AB bilayer is more favorable in energy with a relatively higher interaction energy of 38.4 meV per atom and a relatively shorter interlayer distance of 3.19 Å, which is weaker than the corresponding value of the graphene bilayer (141 meV per atom at a distance of 3.08 Å).⁵³ The reason for the AB bilayers possessing a stronger interaction energy is that the electron repulsion between the upper-layer Cu atom and the vacant site of the eight-membered ring in the sub-layer is weaker than that in the AA bilayers with the electrostatic repulsion between two Cu atoms in the upper layer and the sub-layer. In addition, the ELF plot also indicates that there is no obvious electron location between the layers. As mentioned above, the CuB₁₂ monolayer satisfies all stable conditions to be a promising 2D material, which provides a prerequisite for the wide utilization of a catalyst.

It is known that the activity of the catalyst is essentially governed by its electronic properties. Hence, the projected density of states (PDOS) of the CuB₁₂ monolayer is computed to preliminarily evaluate its potentiality as a catalyst for urea production. It is clear that the CuB₁₂ monolayer is intrinsically metallic due to no gap at the Fermi level using the PBE functional (Fig. 1d). The conducting nature is mainly originated from the p orbitals of B atoms due to the highest contribution near the Fermi level. Moreover, the co-existence of the occupied and unoccupied p-orbitals near the Fermi level can regulate the moderate “acceptation-donation” interaction between catalytic sites and reaction intermediates.^54,55 The outstanding electronic conductivity and the moderate “acceptation-donation” interaction are both beneficial for its application as an electrocatalyst.

Reaction mechanism of electrocatalytic urea production

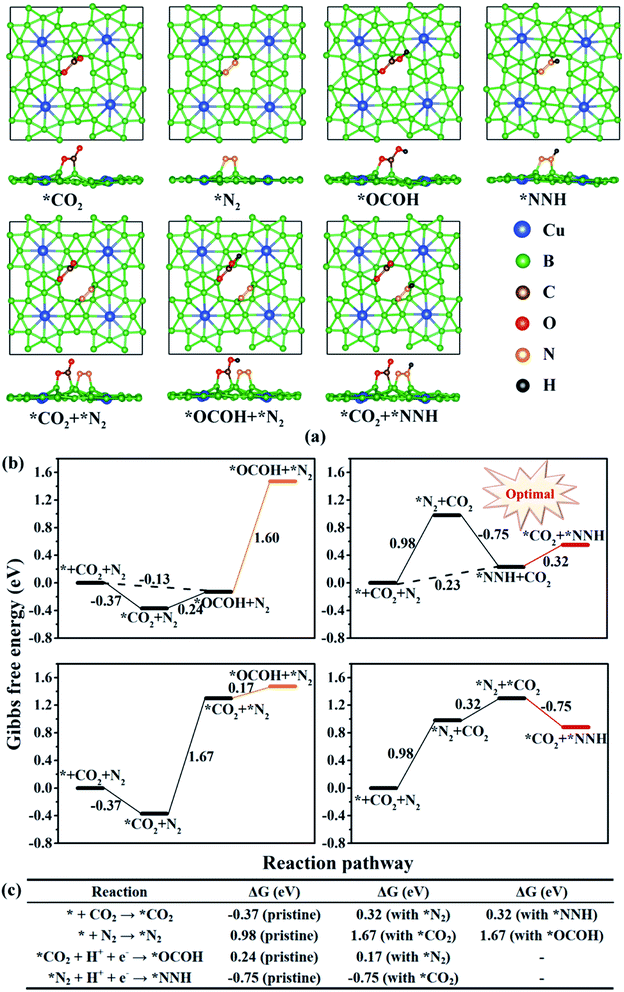
The reaction mechanism for electrochemical urea production starting from CO₂ and N₂ has been proposed in 2020, in which six consecutive protonation and reduction processes are involved.²¹ In the proposed reaction pathway, the adsorption of the *OCOH intermediate and the subsequent reduction to *CO are the first two protonation pathways, and they are also significant to further react for urea production. Subsequently, the C–N coupling reaction of *CO and *N₂ to form a *NCON intermediate is a kinetically determining factor in synthesizing urea. The *NCON intermediate is continuously hydrogenated to *NCONH, *NHCONH/*NCONH₂, *NHCONH₂, and *NH₂CONH₂, and then urea is finally released. This reaction pathway is named the NCON pathway in our work (marked in purple in Fig. 2a). However, is the NCON pathway the only reaction pathway for urea formation? To better explain the issue and complement the reaction mechanism of urea production, we review previous reports about C–N bonding formation and urea formation. Two valuable pieces of evidence are noticed: (1) the reduction of adsorbed *N₂ to *NNH with accessible Gibbs free energy change values (ΔG <0.75 eV) on most catalyst surfaces;^27,28,30 (2) the C–N bonding formation originated from *CO and *NH₂ on Te-doped Pd nanocrystals.⁵⁶ These results imply that it is also possible to form a C–N bond through *CO and *N₂H_x intermediates. Therefore, we propose another three potential reaction pathways for electrochemical urea production. According to the CO₂ reduction step, they are named the CO₂ pathway marked in red, the OCOH pathway marked in blue and the CO pathway marked in orange, respectively (Fig. 2a). The potential reaction intermediates on the CuB₁₂ monolayer in the aforementioned four reaction pathways are all optimized (side view in Fig. 2b and top view in S5†). Their detailed information, including total energy, zero-potential correction energy and entropy contribution energy, is also given in Table S3.†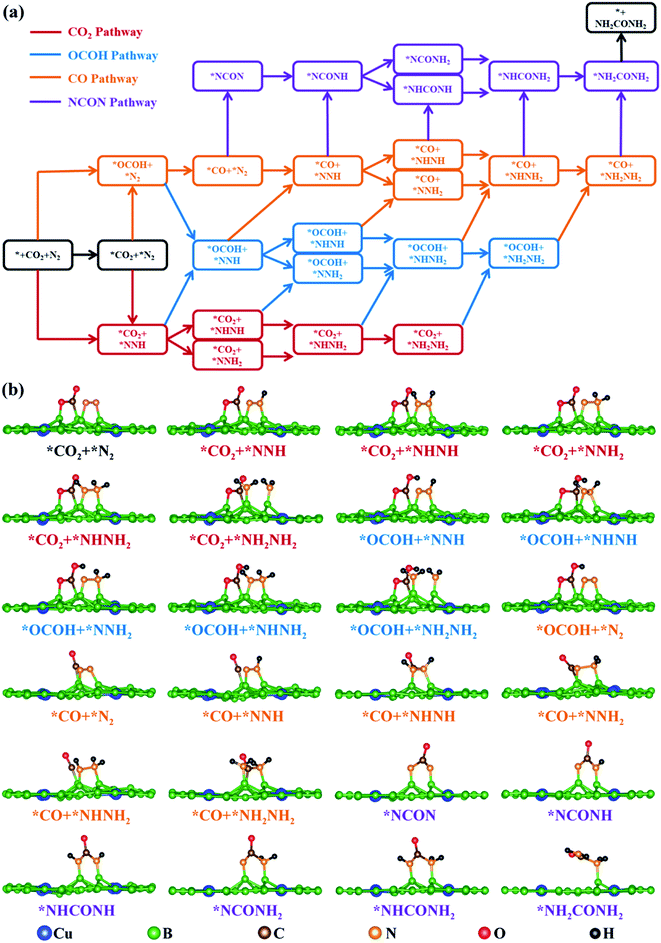

Fig. 2 (a) Schematic depiction of all possible mechanisms for urea production. (b) Side view of all optimized possible reaction intermediates for urea production on the CuB₁₂ monolayer.

In these four reaction pathways, the effective adsorption of *CO₂ and *N₂ on the catalyst surface is a prerequisite for electrochemical urea production. Moreover, *CO₂ and the first hydrogenated *NNH, or the first hydrogenated *OCOH and *N₂ as initial reactants are also feasible for urea production, because the inert CO₂ molecule and N₂ molecule can be directly activated and reduced to *OCOH and *NNH by the surface *H. In the CO₂ pathway, the first four proton-coupled electron transfer steps convert the N₂ molecule to a *NH₂NH₂ intermediate, and the following two proton-coupled electron transfer steps reduce *CO₂ to a *CO intermediate. The coupling reaction between the *CO intermediate and *NH₂NH₂ intermediate promotes the C–N bonding formation and the *NH₂CONH₂ product formation. In the OCOH pathway, the adsorbed *CO₂ is preferentially hydrogenated to a *OCOH intermediate. The formed *OCOH intermediate remains until the inert N≡N triple bond is completely broken and converted into a *NH₂NH₂ intermediate. After that, the *OCOH intermediate is further reduced to a *CO intermediate and simultaneously one H₂O molecule is released. In the CO pathway, the hydrogenation process of the N₂ molecule has just begun after the adsorbed *CO₂ is continuously reduced to a *CO intermediate. Specifically, the C–N coupling reaction can occur in any elementary reaction in this CO pathway, including *CO + *N₂ → *NCON, *CO + *NNH → *NCONH, *CO + *NNH₂ → *NCONH₂, *CO + *NHNH → *NHCONH, *CO + *NHNH₂ → *NHCONH₂, and *CO + *NH₂NH₂ → *NH₂CONH₂. Moreover, many mixed pathways can be feasible in Fig. 2a, such as * + CO₂ + N₂ → *NNH + CO₂ → *CO₂ + *NNH → *CO₂ + *NHNH → *OCOH + *NHNH → *CO + *NHNH → *NHCONH → *NHCONH₂ → *NH₂CONH₂ → * + NH₂CONH₂, * + CO₂ + N₂ → *NNH + CO₂ → *CO₂ + *NNH → *OCOH + *NNH → *OCOH + *NNH₂ → *CO + *NNH₂ → *NCONH₂ → *NHCONH₂ → *NH₂CONH₂ → * + NH₂CONH₂, * + CO₂ + N₂ → *NNH + CO₂ → *CO₂ + *NNH → *CO₂ + *NHNH → *OCOH + *NHNH → *OCOH + *NHNH₂ → *CO + *NHNH₂→ *NHCONH₂ → *NH₂CONH₂ → * + NH₂CONH₂ and so on. The schematic depiction presents greater possibilities and more reaction pathways for C–N bonding formation and urea production.

Catalytic activity of the CuB₁₂ monolayer toward urea production

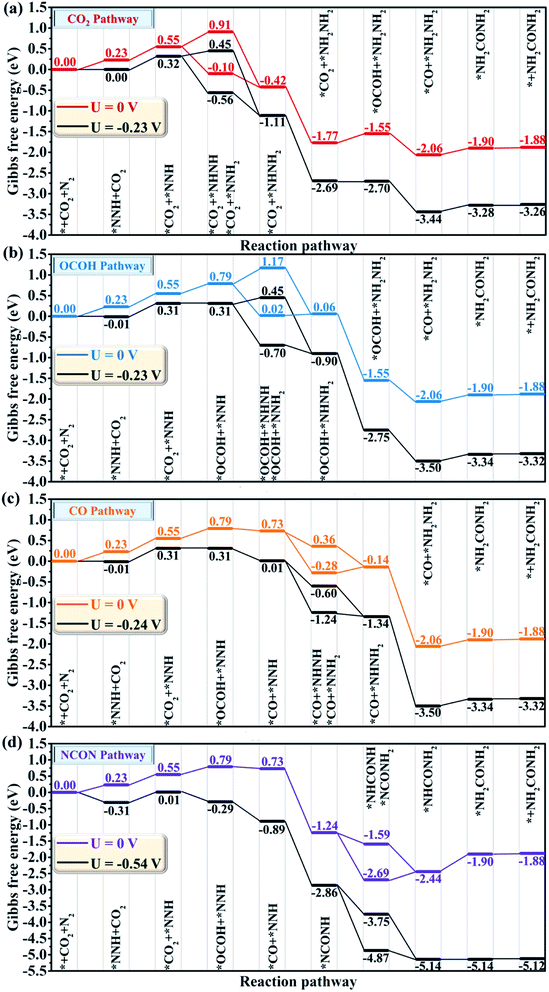
After complementing the reaction mechanism for electrochemical urea production starting from CO₂ and N₂, the catalytic activity and the optimal reaction process are further evaluated on the CuB₁₂ monolayer. The optimal catalytic sites and the initial adsorption configurations of *CO₂ and *N₂ are first screened according to the ΔG values. Herein, thirteen possible configurations of the CO₂ molecule and N₂ molecule adsorbed on the CuB₁₂ monolayer are considered (Fig. S6 and S7†). The computed ΔG values indicate that CO₂ and N₂ are favorably adsorbed on the midpoint-B atoms of squares (Fig. 3a, *CO₂ and *N₂). The adsorption of *CO₂ is exothermic with a downhill energy of −0.37 eV, while the adsorption of *N₂ is endothermic with an uphill energy of 0.98 eV (Fig. 3b). Nevertheless, the C–O and N–N bond lengths are both still elongated compared to the free CO₂ and N₂ molecules (from 1.17 Å to 1.22 Å and 1.38 Å for the C–O bond and from 1.16 Å to 1.24 Å for the N–N bond), and the linear structure of the free CO₂ molecule is greatly bent with the O–C–O angle being 121.09°. It is noted that some catalysts possessing very weak interaction with CO₂ and N₂ can still covert them to the corresponding CO, CH₄ and NH₃, which can be interpreted by the effective adsorption of the first hydrogenated *OCOH and *NNH intermediates.^21,57–64 Therefore, *OCOH and *NNH are also considered to be the initial C-based reactant and N-based reactant (Fig. 3a, *OCOH and *NNH). Interestingly, the computed ΔG values are both small, that is −0.13 eV and 0.23 eV for the reaction * + CO₂ + H⁺ + e⁻ → *OCOH and * + N₂ + H⁺ + e⁻ → *NNH, respectively (Fig. 3b). As a result, four possible reaction pathways are proposed to form the first hydrogenated intermediate for urea production (Fig. 3b), including * + CO₂ + N₂ + H⁺ + e⁻ → *OCOH + N₂ → *OCOH + *N₂, * + CO₂ + N₂ + H⁺ + e⁻ → *NNH + CO₂ → *CO₂ + *NNH, * + CO₂ + N₂ → *CO₂ + N₂ → *CO₂ + *N₂ + H⁺ + e⁻ → *OCOH + *N₂, and * + CO₂ + N₂ → *N₂ + CO₂ → *CO₂ + *N₂ + H⁺ + e⁻ → *CO₂ + *NNH. Among them, the * + CO₂ + N₂ + H⁺ + e⁻ → *NNH + *CO₂ + *NNH reaction is regarded as the optimal reaction pathway with the lowest ΔG value of 0.23 eV, and the *CO₂ + *NNH intermediate is regarded as the optimal initial reactant for urea production. Moreover, the ΔG value is the same or slightly lower compared with the elementary reaction *CO₂ + H⁺ + e⁻ → *OCOH and *N₂ + H⁺ + e⁻ → *NNH when another N₂ molecule or CO₂ molecule emerged in the adjacent catalytic sites (Fig. 3c). Hence, it can be deduced that the adsorbed *N₂ or *CO₂ can facilitate the hydrogenation process of the adjacent sites, which is consistent with previous reports.^21,27,28 However, the adsorption of the CO₂ molecule and N₂ molecule is more difficult when the adjacent catalytic site is occupied by another molecule or intermediate, and the adsorption free energy increases by ∼0.60 eV (Fig. 3c). It is speculated that the delocalized electrons and the multi-center multi-electron bonds are destroyed somewhat in the squares after the first molecule or intermediate is adsorbed, which results in an increased ΔG value for the following adsorption process. Importantly, the concentration, the ratio and the cycling period/interval of reactants CO₂ and N₂ must be optimized to maximize the production of urea and to suppress the competitive side reaction as mentioned for the PdCu alloy nanoparticles on TiO₂ nanosheets.²¹

Fig. 3 (a) Top and side views of the optimal geometric structures for *CO₂, *N₂, *OCOH, *NNH, *CO₂ + *N₂, *OCOH + *N₂ and *CO₂ + *NNH on the CuB₁₂ monolayer. (b) Gibbs free energy diagrams for the first hydrogenation process of CO₂ and N₂ reduced to a *OCOH + *N₂ intermediate and *CO₂ + *NNH intermediate. (c) Calculated Gibbs free energy change values (ΔG, eV) for the four elementary reactions on the pristine CuB₁₂ monolayer and the CuB₁₂ monolayer with other adsorption intermediates.

The whole reaction process for urea production beginning with the first hydrogenation intermediate of *CO₂ + *NNH through the CO₂ pathway, the OCOH pathway, the CO pathway, the NCON pathway and the mixed pathway on the CuB₁₂ monolayer is systematically investigated and analyzed (Fig. 4 and S8†). In the CO₂ and OCOH pathways, the first hydrogenation process (* + N₂ + H⁺ + e⁻ → *NNH) is its potential determining step for urea production. The corresponding ΔG value for this step is 0.23 eV, which decreases to the lowest value among all previous reports (0.78 eV for the PdCu surface,²¹ 0.48 eV for Mott–Schottky Bi–BiVO₄ heterostructures,²⁷ 0.54 eV for BiFeO₃/BiVO₄ heterojunctions,²⁸ 0.49 eV for Mo₂B₂,³⁰ 0.65 eV for Ti₂B₂,³⁰ and 0.52 eV for Cr₂B₂ (ref. 30)). In the CO pathway, the *OCOH + *NNH intermediate formation from the *CO₂ + *NNH intermediate is its potential determining step, and the computed ΔG value is 0.24 eV. In the aforementioned three pathways, the formation of urea is very straightforward after the formation of the first hydrogenation intermediate for carbon-based (*OCOH) and nitrogen-based (*NNH) reactants. In the NCON and mixed pathways, the potential determining step is the final hydrogenation step from *NHCONH₂ to *NH₂CONH₂ with a positive ΔG value of 0.54 eV. Therefore, the maximum limiting potential for different reaction pathways on the CuB₁₂ monolayer is only 0.54 V, indicating superior electrocatalytic activity toward urea formation. Moreover, the formed urea molecule on the CuB₁₂ monolayer can be easily released due to the negligible desorption free energy value (0.02 eV).

Fig. 4 Gibbs free energy diagrams for urea production through (a) the CO₂ pathway, (b) the OCOH pathway, (c) the CO pathway, and (d) the NCON pathway on the CuB₁₂ monolayer at different applied potentials.

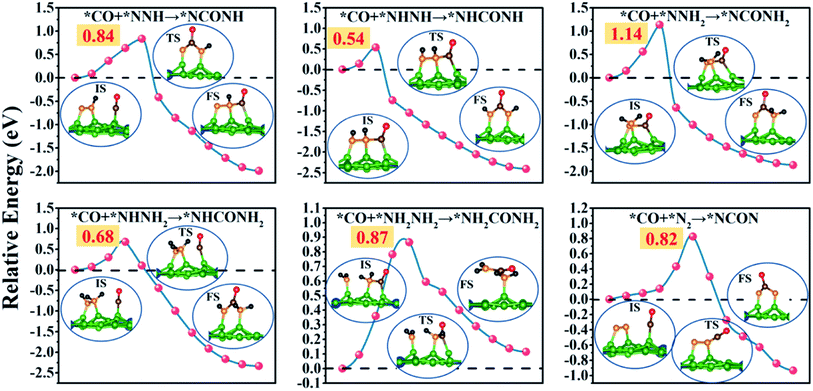
Remarkably, the C–N coupling reactions through the simultaneously adsorbed *CO and various *N₂H_y intermediates (*NNH, *NHNH, *NNH₂, *NHNH₂, and *NH₂NH₂) are all thermodynamically exothermic, expect for *CO + NH₂NH₂ → *NH₂CONH₂ with a slightly positive ΔG value of 0.11 eV. In particular, the C–N coupling products *NCONH, *NHCONH, *NCONH₂, and *NHCONH₂ are lower by ∼2.0 eV in energy than the corresponding C–N coupling reactants *CO + *NNH, *CO + *NHNH, *CO + *NNH₂, and *CO + *NHNH₂. Thermodynamic evaluation demonstrates that the C–N bond formation is feasible through various pathways. Their kinetic energy barriers are also investigated to further evaluate the feasibility of forming the urea molecule (Fig. 5). The computed kinetic energy barrier is 0.84 eV for *NCONH, 0.54 eV for *NHCONH, 1.14 eV for *NCONH₂, 0.68 eV for *NHCONH₂ and 0.87 eV for *NH₂CONH₂, respectively. Among them, the lowest kinetic energy barrier is 0.54 eV for the reaction *CO + NHNH → *NHCONH, which is also lower compared with those in previous reports (0.79 eV for the PdCu surface,²¹ 0.58 eV for Mo₂B₂,³⁰ 0.81 eV for Ti₂B₂,³⁰ and 0.71 eV for Cr₂B₂ (ref. 30)), indicating that the C–N bond coupling on the CuB₁₂ monolayer is kinetically feasible. Moreover, the computed kinetic energy barriers for *CO and *N₂H_y are comparable to or even lower than that of the direct coupling reaction between *CO and *N₂ (the reaction *CO + NNH₂ → *NCONH₂ with a 1.14 eV kinetic energy barrier is excepted), which indicates that the formation of *NCON species from *CO and *N₂ is not the sole reaction pathway for urea production. Therefore, it is of significance to complement the reaction mechanism and investigate the optimal formation pathway among all the potential schemes for urea production.

Fig. 5 Kinetic energy barrier for C–N bond formation through six different pathways. The optimized structures in the initial (IS), transition (TS) and final states (FS) along the C–N bond formation pathway are shown in insets.

Catalytic selectivity of the CuB₁₂ monolayer toward urea production

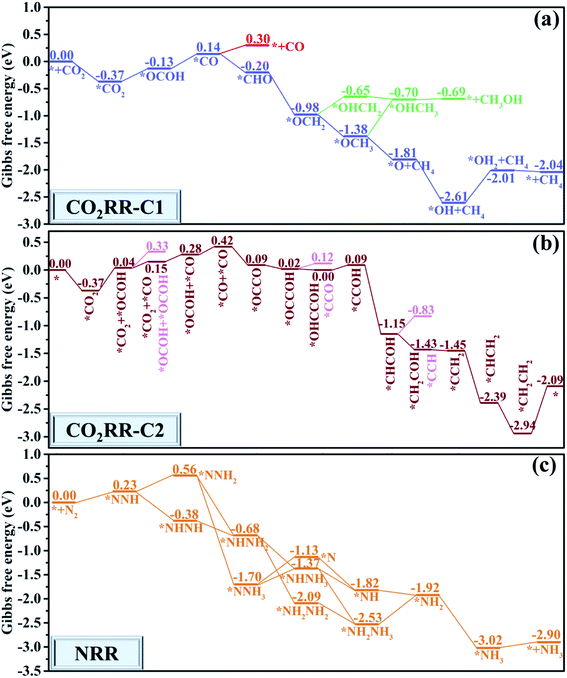
Besides the outstanding stability and activity, the catalytic selectivity toward urea formation is another intrinsic characteristic that influences the faradaic efficiency. The computed ΔG value for the H atom adsorbed on three different types of B atoms (from −0.27 eV to 0.14 eV in Fig. S9†) is comparable to that for the first hydrogenation step (−0.13 eV for * + CO₂ + H⁺ + e⁻ → *OCOH and 0.23 eV * + N₂ + H⁺ + e⁻ → *NNH). The HER can be efficiently suppressed experimentally by adjusting the electrolyte pH under neutral conditions. It is thus possible to maximize the urea production with real experimental adjustments and suppress the influence of the HER through applied potentials.^61,65 Meanwhile, the adsorbed *H can serve as a proton source to interact with other reaction intermediates via the Langmuir–Hinshelwood mechanism.^30,66,67

The catalytic selectivity toward urea production compared to the competitive CO₂RR to the C1 product is assessed. As shown in Fig. 6a and S10,† three possible reduction products (CO, CH₃OH and CH₄) are considered in the CO₂RR side reaction. Their desorption free energies are 0.16 eV for CO, 0.01 eV for CH₃OH, and −0.03 eV for CH₄, respectively, indicating that these possible reduction products can be easily released. Moreover, another possible intermediate *OCHO for the first hydrogenation step is not considered due to the larger kinetic energy barrier starting from the adsorbed *CO₂. For the 2e⁻ reduction product CO, the first hydrogenation process (*CO₂ + H⁺ + e⁻ → *OCOH) is its potential determining step with a ΔG value of 0.23 eV. The formed CO molecule can further react with the *N₂H_y intermediates via the Eley–Rideal mechanism, which is also beneficial for urea formation.^30,66,67 For the 6e⁻ reduction product CH₃OH, the reaction *OCH₂ + H⁺ + e⁻ → *OHCH₂ is the potential determining step with a ΔG value of 0.33 eV. Remarkably, the *OCH₂ intermediate is attacked by a proton-electron (H⁺/e⁻) pair to form the *OCH₃ intermediate with a negative ΔG value of −0.40 eV, or to form the *OHCH₂ intermediate with a positive ΔG value of 0.33 eV. To further assess the product distribution of CH₃OH and CH₄, the Boltzmann distribution formula exp[−(ΔG)/(k_BT)] is employed based on the Gibbs free energy difference.⁶⁸ The computed CH₃OH : CH₄ molar ratio is 1 : 2.19 × 10¹² at ambient temperature, indicating a strong selectivity toward the CH₄ product on the CuB₁₂ monolayer. Therefore, the 6e⁻ reduction product CH₃OH is not the major competitive product. For the 8e⁻ reduction product CH₄, the reaction *O + H⁺ + e⁻ → *OH is its potential determining step with a ΔG value of 0.60 eV, which is larger than the maximum ΔG value (0.54 eV) for urea production. These data suggest that the formation of CH₄ can be greatly suppressed on the CuB₁₂ monolayer. Moreover, the further reduction of *CO should be prohibited on the CuB₁₂ monolayer, which can improve the selectivity toward urea production. To better confirm the excellent catalytic selectivity toward urea production, the energy barriers of CO desorption and its further reduction to a *CHO intermediate are also computed (Fig. S11–S14†). It is obvious that *CO is preferred to be released due to a relatively lower kinetic energy barrier (0.84 eV) than that for the further reduction to a *CHO intermediate (1.76 eV). Therefore, the CO molecule is kinetically the final reduction product, which is also favorable to synthesize urea.

Fig. 6 Gibbs free energy diagrams for (a) the CO₂ reduction reaction to C1 products (CO₂RR-C1), (b) the CO₂ reduction reaction to C2 products (CO₂RR-C2) and (c) the N₂ reduction reaction (NRR) on the CuB₁₂ monolayer.

The catalytic selectivity toward urea production compared to the competitive CO₂RR to the C2 product is also assessed, in which the whole reaction pathways and the corresponding intermediates are investigated (Fig. 6b and S15†). As shown in Fig. 6b, the adsorption and hydrogenation of the second CO₂ molecule to generate the *CO₂ + *OCOH intermediate is uphill by 0.41 eV in the Gibbs free energy diagram, which is the potential limiting step to form the C2 product. The formed *CO₂ + *OCOH intermediate is preferred to be hydrogenated to the *CO₂ + *CO intermediate through releasing one water molecule rather than the *OCOH + *OCOH intermediate due to the relatively lower ΔG value (0.11 eV for *CO₂ + *CO and 0.29 eV for *OCOH + *OCOH). Afterward, the *CO₂ + *CO intermediate can be continuously attacked by two H⁺/e⁻ pairs to generate the *OCOH + *CO intermediate and *CO + *CO intermediate with a positive ΔG value of 0.13 eV and 0.14 eV, respectively. The C–C coupling reaction of the *CO + *CO intermediate to obtain the *OCCO intermediate is an exothermic process with a downhill energy of 0.33 eV. Two O atoms of the *OCCO intermediate are attacked by another two H⁺/e⁻ pairs to form the *OCCOH intermediate and *OHCCOH intermediate with a negative ΔG value. The next hydrogenation step of the *OHCCOH intermediate can generate the *CCOH intermediate followed by the generation of one H₂O molecule, and the computed ΔG value for this step is 0.09 eV. Subsequently, the *CCOH intermediate can be continuously reduced to *CHCOH, *CHCOH, *CH₂COH, *CCH₂, *CHCH₂ and *CH₂CH₂ intermediates by five H⁺/e⁻ pairs with no energy demand. Finally, a free CH₂CH₂ molecule can be generated after overcoming a thermodynamic barrier of 0.85 eV. According to the above discussion, two CO₂ molecules can be finally converted to CH₂CH₂ on the CuB₁₂ monolayer. The corresponding potential limiting step is the first hydrogenation step (*CO₂ + CO₂ + H⁺ + e⁻ → *CO₂ + *OCOH) with a maximum ΔG value of 0.41 eV, which is still higher than the optimal ΔG value of the reaction * + N₂ + H⁺ + e⁻ → *NNH (0.23 eV) to produce urea. Encouragingly, the competitive reaction of CO₂ reduction to CH₂CH₂ can be greatly suppressed on the CuB₁₂ monolayer.

The selectivity of the CuB₁₂ monolayer toward urea production compared with the NRR competitive reaction is also evaluated, where all possible reaction mechanisms and intermediates are considered (Fig. 6c and S16†). The optimal reaction pathway for NH₃ formation is N₂ → *NNH → *NHNH → *NHNH₂ → *NHNH₃ → *NH → *NH₂ → *NH₃ → NH₃. During this procedure, the generation of the first hydrogenation intermediate *NNH possesses a maximum ΔG value of 0.23 eV. Unfortunately, the potential determining step and the limiting potential for the byproduct NH₃ and the targeted urea are both identical. From another point of view, the NH₃ product is exactly the right reactant to synthesize urea in industrial processes, so it can probably promote the urea formation by other approaches.

Conclusions

In summary, the entirely planar CuB₁₂ monolayer with superior stability is identified to be a global-minimum configuration after a comprehensive search combined with first-principles calculation. The B atoms at the midpoint of the edges of the squares are firstly confirmed to be distinguished non-metal catalytic sites, which provide an electrocatalyst to convert the CO₂ molecule and N₂ molecule into urea. On the CuB₁₂ monolayer, all possible reaction pathways starting from the CO₂ molecule and N₂ molecule for urea production, including the CO₂ pathway, OCOH pathway, CO pathway, NCON pathway and feasible mixed pathways, are systematically investigated, which enrich the recognition of urea formation. Most importantly, the limiting potential of urea production through the CO₂ pathway and OCOH pathway is 0.23 V, which is much lower than the values of reported urea catalysts. The minimal kinetic energy barrier is 0.54 eV through *CO and *NHNH coupling reactions among six possible C–N coupling reactions accompanied by the hydrogenation of N₂, which is 0.28 eV lower than that through *CO and *N₂ coupling reactions. Furthermore, the competitive CH₃OH and CH₄ products can be suppressed in the urea formation process. This study will stimulate more experimentalist and theorist efforts to apply the perfected urea formation pathways and C–N formation pathways to explore other high-performance urea catalysts.

Methods

Global-minimum structure prediction

The global-minimum structure prediction of the CuB₁₂ monolayer was performed by the particle-swarm optimization (PSO) method within the evolutionary scheme as implemented in the CALYPSO code,⁶⁹ which can efficiently search for ground or metastable structures just depending on the input chemical compositions. Both planar and puckered structures are considered during its structure search. The population size and the number of generations are set to be 50 and 30, respectively. Unit cells containing 1 and 2 formula units (f.u.) are considered.

DFT computations

All first principles calculations were performed by spin-polarized density functional theory (DFT)⁷⁰via the Vienna ab initio simulation package (VASP).⁷¹ The ion-electron interactions were expressed by the projector augmented wave (PAW) pseudopotential.⁷² The electronic exchange-correlation effects were described with the generalized gradient approximation of the Perdew–Burke–Ernzerhof (PBE) functional with the generalized gradient approximation (GGA).⁷³ The solvation effects were simulated using the linearized implicit Poisson–Boltzmann solvation model as implemented in the VASP (VASP-sol), where the dielectric constant for water was considered to be 80.^74,75 Grimme's semiempirical DFT-D3 approach was chosen for the van der Waals (vdW) interaction between reaction intermediates and the CuB₁₂ monolayer.^76,77 A vacuum distance of 20 Å along the z direction was used to minimize interaction between periodic images, and a 2 × 2 supercell was employed to investigate the catalytic activity of the CuB₁₂ monolayer. The lane-wave cutoff energy was set to be 500 eV in all computations, and the Monkhorst–Pack k-point mesh resolution in reciprocal space was set to be 2π × 0.025 Å⁻¹ for all structures. The structures were optimized with an energy convergence of 10⁻⁵ eV and a force convergence of 10⁻² eV Å⁻¹ for each atom, respectively.

Stability evaluation

The phonon dispersion spectra were computed using the finite displacement method with the PHONOPY program.⁷⁸ The ab initio molecular dynamics (AIMD) simulations were performed in the NVT ensemble with a time step of 1.0 fs for 10 ps with a 3 × 3 supercell. Different temperatures (T = 300 K, 600 K, 900 K, 1200 K, 1500 K) were controlled using the Nosé–Hoover method.⁷⁹

Free energy computations

The Gibbs free energy diagram of each elementary step in the electrochemical synthesis of urea was obtained by using the computational hydrogen electrode (CHE) model proposed by Nørskov et al.^80,81 The transition states and kinetic barriers for the C–N coupling reaction were identified by the climbing-image nudged elastic band (CI-NEB) method.⁸² The computational details of global-minimum structure prediction and Gibbs free energy can be found in the ESI.†

Data availability

All the data supporting this article have been included in the main text and the ESI.†

Author contributions

M. Z. designed the research, and C. Y. Z., C. X. W. and M. W. demonstrated the initial idea and collected all the data. C. Y. Z. wrote the paper. M. Z., Y. G. and Z. M. S revised the paper and all authors commented on it.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge financial support from the National Natural Science Foundation of China (21673036 and 21771035), the Education Department of Jilin Prov. China (JJKH20211284KJ) and the Fundamental Research Funds for the Central Universities (2412018ZD006). Most computations were carried out on TianHe-2 at the LvLiang Cloud Computing Center of China. We acknowledge the support of the computational resources from the Institute of Theoretical Chemistry, Jilin University.

References

1. Z. Seh, J. Kibsgaard, C. Dickens, I. Chorkendorff, J. Nørskov and T. Jaramillo, Science, 2017, 355, eaad4998.
2. H. Jin, C. Guo, X. Liu, J. Liu, A. Vasileff, Y. Jiao, Y. Zheng and S. Qiao, Chem. Rev., 2018, 118, 6337–6408.
3. Z. Li, S. Ji, Y. Liu, X. Cao, S. Tian, Y. Chen, Z. Niu and Y. Li, Chem. Rev., 2020, 120, 623–682.
4. H. Zhuo, X. Zhang, J. Liang, Q. Yu, H. Xiao and J. Li, Chem. Rev., 2020, 120, 12315–12341.
5. Z. Zeng, L. Gan, H. Yang, X. Su, J. Gao, W. Liu, H. Matsumoto, J. Gong, J. Zhang, W. Cai, Z. Zhang, Y. Yan, B. Liu and P. Chen, Nat. Commun., 2021, 12, 4088.
6. L. Wang, W. Chen, D. Zhang, Y. Du, R. Amal, S. Qiao, J. Wu and Z. Yin, Chem. Soc. Rev., 2019, 48, 5310–5349.
7. X. Qiu, H. Zhu, J. Huang, P. Liao and X. Chen, J. Am. Chem. Soc., 2021, 143, 7242–7246.
8. C. Morales-Guio, E. Cave, S. Nitopi, J. Feaster, L. Wang, K. Kuhl, A. Jackson, N. Johnson, D. Abram, T. Hatsukade, C. Hahn and T. Jaramillo, Nat. Catal., 2018, 1, 764–771.
9. J. Choi, B. Suryanto, D. Wang, H. Du, R. Hodgetts, F. Ferrero Vallana, D. MacFarlane and A. Simonov, Nat. Commun., 2020, 11, 5546.
10. B. Suryanto, K. Matuszek, J. Choi, R. Hodgetts, H. Du, J. Bakker, C. Kang, P. Cherepanov, A. Simonov and D. MacFarlane, Science, 2021, 372, 1187–1191.
11. Y. Gu, B. Xi, W. Tian, H. Zhang, Q. Fu and S. Xiong, Adv. Mater., 2021, 33, 2100429.
12. D. Yu, Y. Ma, F. Hu, C. Lin, L. Li, H. Chen, X. Han and S. Peng, Adv. Energy Mater., 2021, 11, 2101242.
13. B. Hu, A. Huang, X. Zhang, Z. Chen, R. Tu, W. Zhu, Z. Zhuang, C. Chen, Q. Peng and Y. Li, Nano Res., 2021, 13, 1–7.
14. M. Tong, F. Sun, Y. Xie, Y. Wang, Y. Yang, C. Tian, L. Wang and H. Fu, Angew. Chem., Int. Ed., 2021, 60, 14005–14012.
15. K. Zhou, Z. Wang, C. Han, X. Ke, C. Wang, Y. Jin, Q. Zhang, J. Liu, H. Wang and H. Yan, Nat. Commun., 2021, 12, 3783.
16. Y. Wu, X. Li, Y. Wei, Z. Fu, W. Wei, X. Wu, Q. Zhu and Q. Xu, Adv. Mater., 2021, 33, 2006965.
17. Y. Wei, R. A. Soomro, X. Xie and B. Xu, J. Energy Chem., 2021, 55, 244–255.
18. Y. Zhou, F. Che, M. Liu, C. Zou, Z. Liang, P. De Luna, H. Yuan, J. Li, Z. Wang, H. Xie, H. Li, P. Chen, E. Bladt, R. Quintero-Bermudez, T. Sham, S. Bals, J. Hofkens, D. Sinton, G. Chen and E. Sargent, Nat. Chem., 2018, 10, 974–980.
19. C. Peng, G. Luo, J. Zhang, M. Chen, Z. Wang, T. Sham, L. Zhang, Y. Li and G. Zheng, Nat. Commun., 2021, 12, 1580.
20. M. Wang, S. Liu, T. Qian, J. Liu, J. Zhou, H. Ji, J. Xiong, J. Zhong and C. Yan, Nat. Commun., 2019, 10, 341.
21. C. Chen, X. Zhu, X. Wen, Y. Zhou, L. Zhou, H. Li, L. Tao, Q. Li, S. Du, T. Liu, D. Yan, C. Xie, Y. Zou, Y. Wang, R. Chen, J. Huo, Y. Li, J. Cheng, H. Su, X. Zhao, W. Cheng, Q. Liu, H. Lin, J. Luo, J. Chen, M. Dong, K. Cheng, C. Li and S. Wang, Nat. Chem., 2020, 12, 717–724.
22. B. Comer, P. Fuentes, C. Dimkpa, Y. Liu, C. Fernandez, P. Arora, M. Realff, U. Singh, M. Hatzell and A. Medford, Joule, 2019, 3, 1578–1605.
23. F. Barzagli, F. Mani and M. Peruzzini, Green Chem., 2011, 13, 1267–1274.
24. M. Kitano, Y. Inoue, Y. Yamazaki, F. Hayashi, S. Kanbara, S. Matsuishi, T. Yokoyama, S. Kim, M. Hara and H. Hosono, Nat. Chem., 2012, 4, 934–940.
25. M. Kitano, S. Kanbara, Y. Inoue, N. Kuganathan, P. Sushko, T. Yokoyama, M. Hara and H. Hosono, Nat. Commun., 2015, 6, 6731.
26. D. Kayan and F. Köleli, Appl. Catal., B, 2016, 181, 88–93.
27. M. Yuan, J. Chen, Y. Bai, Z. Liu, J. Zhang, T. Zhao, Q. Wang, S. Li, H. He and G. Zhang, Angew. Chem., Int. Ed., 2021, 60, 10910–10918.
28. M. Yuan, J. Chen, Y. Bai, Z. Liu, J. Zhang, T. Zhao, Q. Shi, S. Li, X. Wang and G. Zhang, Chem. Sci., 2021, 12, 6048–6058.
29. N. Meng, Y. Huang, Y. Liu, Y. Yu and B. Zhang, Cell Rep. Phys. Sci., 2021, 2, 100378.
30. X. Zhu, X. Zhou, Y. Jing and Y. Li, Nat. Commun., 2021, 12, 4080.
31. C. Ling, X. Niu, Q. Li, A. Du and J. Wang, J. Am. Chem. Soc., 2018, 140, 14161–14168.
32. X. Zhang, T. Wu, H. Wang, R. Zhao, H. Chen, T. Wang, P. Wei, Y. Luo, Y. Zhang and X. Sun, ACS Catal., 2019, 9, 4609–4615.
33. X. Lv, W. Wei, F. Li, B. Huang and Y. Dai, Nano Lett., 2019, 19, 6391–6399.
34. T. He, K. Reuter and A. Du, J. Mater. Chem. A, 2020, 8, 599–606.
35. G. Qin, Q. Cui, A. Du and Q. Sun, ChemCatChem, 2020, 12, 1483–1490.
36. Z. Feng, Y. Tang, Y. Ma, Y. Li, Y. Dai, H. Ding, G. Su and X. Dai, Appl. Surf. Sci., 2021, 538, 148145.
37. G. Welch, R. Juan, J. Masuda and D. Stephan, Science, 2006, 314, 1124–1126.
38. L. Dai, Y. Xue, L. Qu, H. Choi and J. Baek, Chem. Rev., 2015, 115, 4823–4892.
39. Y. Xu, M. Kraft and R. Xu, Chem. Soc. Rev., 2016, 45, 3039–3052.
40. H. Zhang, Y. Li, J. Hou, K. Tu and Z. Chen, J. Am. Chem. Soc., 2016, 138, 5644–5651.
41. R. Islas, T. Heine, K. Ito, P. v. R. Schleyer and G. Merino, J. Am. Chem. Soc., 2007, 129, 14767–14774.
42. L. Yang, E. Ganz, Z. Chen, Z. Wang and P. v. R. Schleyer, Angew. Chem., Int. Ed., 2015, 54, 9468–9501.
43. Y. Wang, Y. Li and Z. Chen, Acc. Chem. Res., 2020, 53, 887–895.
44. T. Heine and G. Merino, Angew. Chem., Int. Ed., 2012, 51, 4275–4276.
45. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
46. A. Savin, R. Nesper, S. Wengert and T. Fässler, Angew. Chem., Int. Ed., 1997, 36, 1808–1832.
47. C. Zhu, H. Chen, C. Wang, M. Zhang, Y. Geng, Q. Li and Z. Su, J. Phys. Chem. C, 2020, 124, 23221–23229.
48. C. Zhu, C. Wang, M. Zhang, H. Chen, Y. Geng and Z. Su, ACS Appl. Mater. Interfaces, 2021, 13, 3845–3855.
49. A. Mannix, X. Zhou, B. Kiraly, J. Wood, D. Alducin, B. Myers, X. Liu, B. Fisher, U. Santiago, J. Guest, M. Yacaman, A. Ponce, A. Oganov, M. Hersam and N. Guisinger, Science, 2015, 350, 1513–1516.
50. B. Feng, J. Zhang, Q. Zhong, W. Li, S. Li, H. Li, P. Cheng, S. Meng, L. Chen and K. Wu, Nat. Chem., 2016, 8, 563–568.
51. B. Song, Y. Zhou, H. Yang, J. Liao, L. Yang, X. Yang and E. Ganz, J. Am. Chem. Soc., 2019, 141, 3630–3640.
52. M. Born and K. Huang, Dynamical theory of crystal lattices; Clarendon press, 1954.
53. R. W. G. Wyckoff, Crystal Structures, Interscience Publishers, New York, 2nd edn, 1963, vol. 1, p. 7.
54. X. Guo, J. Gu, S. Lin, S. Zhang, Z. Chen and S. Huang, J. Am. Chem. Soc., 2020, 142, 5709–5721.
55. C. Zhu, C. Wen, C. Wang, M. Zhang, Y. Geng and Z. Su, J. Mater. Chem. A, 2021, 9, 10855–10868.
56. Y. Feng, H. Yang, Y. Zhang, X. Huang, L. Li, T. Cheng and Q. Shao, Nano Lett., 2020, 20, 8282–8289.
57. X. Zheng, Y. Ji, J. Tang, J. Wang, B. Liu, H. Steinrück, K. Lim, Y. Li, M. Toney, K. Chan and Y. Cui, Nat. Catal., 2019, 2, 55–61.
58. M. Shi, D. Bao, B. Wulan, Y. Li, Y. Zhang, J. Yan and Q. Jiang, Adv. Mater., 2017, 29, 1606550.
59. D. Bao, Q. Zhang, F. Meng, H. Zhong, M. Shi, Y. Zhang, J. Yan, Q. Jiang and X. Zhang, Adv. Mater., 2017, 29, 1604799.
60. S. Li, D. Bao, M. Shi, B. Wulan, J. Yan and Q. Jiang, Adv. Mater., 2017, 29, 170000.
61. J. Wang, L. Yu, L. Hu, G. Chen, H. Xin and X. Feng, Nat. Commun., 2018, 9, 1795.
62. M. Shi, D. Bao, S. Li, B. Wulan, J. Yan and Q. Jiang, Adv. Energy Mater., 2018, 8, 1800124.
63. C. Ling, Y. Zhang, Q. Li, X. Bai, L. Shi and J. Wang, J. Am. Chem. Soc., 2019, 141, 18264–18270.
64. J. Montoya, C. Tsai, A. Vojvodic and J. Nørskov, ChemSusChem, 2015, 8, 2180–2186.
65. L. Hu, A. Khaniya, J. Wang, G. Chen, W. Kaden and X. Feng, ACS Catal., 2018, 8, 9312–9319.
66. T. Cheng, H. Xiao and W. Goddard, J. Am. Chem. Soc., 2016, 138, 13802–13805.
67. E. Skúlason, T. Bligaard, S. Gudmundsdóttir, F. Studt, J. Rossmeisl, F. Abild-Pedersen, T. Vegge, H. Jónsson and J. Nørskov, Phys. Chem. Chem. Phys., 2012, 14, 1235–1245.
68. Y. Tian, C. Zhu, L. Yan, J. Zhao and Z. Su, J. Mater. Chem. A, 2019, 7, 15341–15346.
69. Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070.
70. D. Singh and J. Ashkenazi, Phys. Rev. B, 1992, 46, 11570.
71. B. Barbiellini, M. Puska, T. Korhonen, A. Harju, T. Torsti and R. Nieminen, Phys. Rev. B, 1996, 53, 16201.
72. G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758.
73. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
74. M. Fishman, H. Zhuang, K. Mathew, W. Dirschka and R. Hennig, Phys. Rev. B, 2013, 87, 245402.
75. K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. Arias and R. Hennig, J. Chem. Phys., 2014, 140, 084106.
76. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
77. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
78. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
79. G. Martyna, M. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643.
80. J. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
81. J. Rossmeisl and A. Logadottir, J. Chem. Phys., 2005, 319, 178–184.
82. G. Mills and H. Jónsson, Phys. Rev. Lett., 1994, 72, 1124.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc04845g

---