Open Access Article
Open Access ArticleStereoelectronic and dynamical effects dictate nitrogen inversion during valence isomerism in benzene imine†
Nilangshu
Mandal
 ,
Ankita
Das
,
Chandralekha
Hajra
and
Ayan
Datta
,
Ankita
Das
,
Chandralekha
Hajra
and
Ayan
Datta
 *
*
School of Chemical Sciences, Indian Association for the Cultivation of Science, 2A and 2B Raja S. C. Mullick Road, Jadavpur, Kolkata, 700032, West Bengal, India. E-mail: spad@iacs.res.in; Tel: +91-33-24734971
First published on 14th December 2021
Abstract
Benzene imine (1) ⇌ 1H-azepine (2) isomerization occurs through sequential valence and endo–exo isomerism. Quantum chemical and quasiclassical trajectory (QCT) simulations reveal the coupled reaction pathway – ring-expansion followed by N-inversion to the most stable isomer, exo-1H-azepine (Exo-2). Direct-dynamics produce a mixture of endo- and exo-1H-azepine stereoisomers and govern the endo-1H-azepine (Endo-2) ⇌ exo-1H-azepine (Exo-2) ratio. Exo-2 is computationally identified as the most stable product while Endo-2 is fleetingly stable with a survival time (ST) ∼50 fs. N-Methyl substitution exclusively results in an exo-1-methyl-1H-azepine isomer. F-substitution at the N-site increases the barrier for N-inversion and alters the preference by stabilizing Endo-2. Interestingly, the exo-1-fluoro-1H-azepine (minor product) is formed through bifurcation via non-statistical dynamics. A highly concaved Arrhenius plot for 1a → 2a highlights the influence of heavy-atom tunneling on valence isomerism, particularly at low temperatures. Heavy-atom tunneling also results in a normal N–H(D) secondary KIE above 100 K even though the increase in hybridization from sp2 to sp3 at nitrogen should cause an inverse KIE classically.
Introduction
The equilibrium between bicyclo[4.1.0]hepta-2,4-diene and cyclo-hepta-1,3,5-triene has been a subject of active interest.1 Ring-expansion is also known for oxygen (benzene-oxide ⇌ oxepin), nitrogen (benzene imine ⇌ 1H-azepine), sulfur (benzene sulfide ⇌ thiepine), and phosphorus (benzene phosphane ⇌ 1H-phosphepine).2,3 All of them undergo disrotatory electrocyclic rearrangement to form the ring-opened product.4 However, stereoelectronic induction can influence the reaction mechanism and conformations of strained molecules (see Scheme 1a).5,6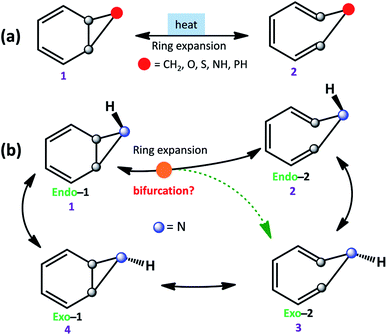 | ||
| Scheme 1 (a) Ring expansion reactions in substituted bicyclo[4.1.0]hepta-2,4-dienes. (b) Schematic possible reaction pathways for benzene imine (1). | ||
For example, 1H-azepine with 8π-electrons exists in a boat conformation as expected from its anti-aromatic Hückel electron count.7 Based on DFT calculations, Dardonville et al. estimated an anti-aromatic destabilization of 10.8 kcal mol−1 for 1H-azepine by computing its protonation energies.8 Ragyanszki and co-workers studied the oxidation of the anti-aromatic N-methyl-1H-azepine to the non-aromatic N-oxide of azepine.9 1H-Azepine, and its derivatives are also known to undergo rapid dimerization via (6 + 4)π exo-cycloaddition.10
Further, ring expansion of benzene imine into 1H-azepine (1 → 2) can in-principle also be accompanied by an inversion at the N-center (see Scheme 1b). Since the NMR spectra of 1H-azepine remain invariant in the range −90 °C to + 130 °C, Paquette et al. suggested that the inversion barrier should be less than 5.7 kcal mol−1.11 Additionally, they could not gather any signature for the existence of benzene imine in this temperature range. Therefore, Exo-2 is expected to be the thermodynamically most stable product. However, the mechanism is still unknown and a possible reaction pathway can be either stepwise (1 → 2 → 3) or coupled (1 → 2, 3) for the formation of 1H-azepine analogs.
In Scheme 2, we have used different substitutions at the N-site to examine the stereoelectronic effects on the valence isomerization of Endo-1. Obtaining a detailed reaction mechanism and understanding the effect of the stereoelectronic influence on the potential energy surface for the Endo-1 → Endo-2/Exo-2 isomerizations require further time-resolved mechanistic investigation using quasi-classical MD simulations.12–14 Additionally, the dynamics at sub-cryogenic temperatures would be dictated by quantum mechanical tunneling (QMT) instead of over-the-barrier crossing at ambient temperatures.15–27 In this context recently, Sander and co-workers have reported unequivocal signatures of heavy-atom tunneling for the benzene oxide – oxepin equilibrium at 3 K.28 The present article investigates post-transition state bifurcation reaction pathways for benzene imine ⇌ 1H-azepine. MD simulations were performed from the rate-limiting transition states to decipher the non-statistical effects on the stereoselectivity (Endo-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Exo-2) during the valence isomerism.29 Heavy-atom tunneling is shown to be the major pathway for ring expansion, particularly at low temperatures.
Exo-2) during the valence isomerism.29 Heavy-atom tunneling is shown to be the major pathway for ring expansion, particularly at low temperatures.
Computational details
Geometry optimization was performed at the M06-2X/6-31+G(d,p) level of theory with the Gaussian 16 (ver A.03) suite of programs (see the ESI, Page S2† for calibration and benchmarking).30,31 Reaction energies and activation barriers were investigated for Endo-1 → Exo-1, Endo-2, Exo-2, and their analogs (R = –F, and –CH3). The reactant, product, and transition-state were confirmed by intrinsic reaction coordinate (IRC) and harmonic frequency calculations.32 In addition, for computation of the reaction rates at low temperatures, the transition states (TS) were located using canonical variational transition-state theory (CVT) along the reaction path s where free-energy maximizes at the same level as used for geometry minimization.33 Tunneling corrections were incorporated within the rate coefficient calculations using the small-curvature tunneling (SCT) approximation.34 These were implemented within Gaussrate 17-B by interfacing with Gaussian 16 and Polyrate 17-C.35,36 Quantized reactant state tunneling (QRST) calculations were performed to determine the reaction rates accurately at sub-cryogenic temperatures.37Further, the ambient temperature behavior of Endo-1 for R = –H, –F, and –CH3 was studied using quasiclassical direct-dynamics simulations in the gas phase at 298.15 K. Reaction trajectories were simulated from rate-limiting sampled TS(1 → 2) structures using the Singleton's Progdyn code interfaced with Gaussian 16 (see the ESI for TS-sampling details, Fig. S4†).38–41 The reaction trajectories were simulated to the forward and backward directions until either one of the products or the reactants is formed. The classical equations of motion were integrated with a velocity-Verlet algorithm.42 The energies and derivatives were calculated on the fly with the M06-2X/6-31+G(d,p) level. The time step for integration is 1 fs. Thresholds for bond formations, trajectory terminations, and in-house code for trajectory characterization are shown on Page S8 and S50.†
Results and discussion
Benzene imine (Endo-1) can isomerize to exo-1H-azepine (Exo-2) either by ring expansion followed by N-inversion or vice versa. Both the plausible pathways are presented in Fig. 1.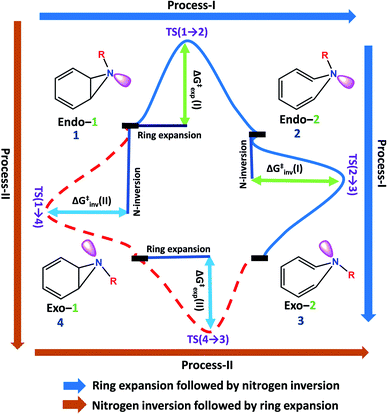 | ||
| Fig. 1 Two plausible mechanistic pathways for the formation of exo-1H-azepine, Exo-2 from benzene imine, Endo-1. | ||
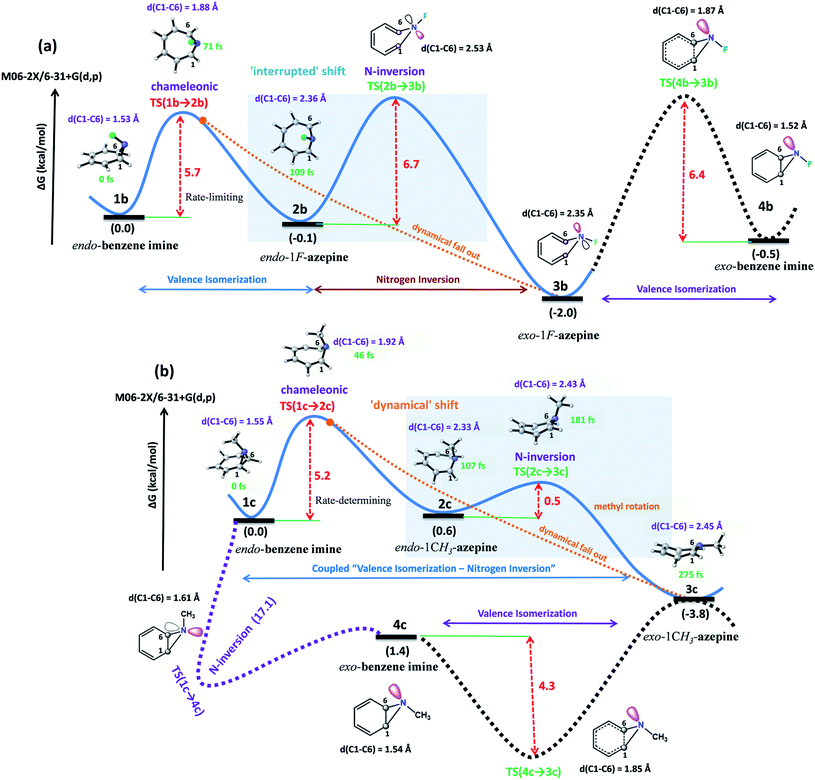
Each involves two steps and crossing two barriers, namely 1 → 2 → 3 or 1 → 4 → 3 with ΔG‡1→2 followed by ΔG‡2→3 or ΔG‡1→4 followed by ΔG‡4→3 respectively. The kinetic preference of either depends on the relative magnitudes of these barriers. Table 1 lists them for the various substituents on the nitrogen head. The exo-1H-azepine Exo-2 is the most stable isomer irrespective of the substituent. Therefore, the benzene imine ⇌ 1H-azepine equilibrium will shift towards the 1H-azepine side. This result is in agreement with previous experiments.11
| 1a (R = H) | 1b (R = F) | 1c (R = CH3) | |
|---|---|---|---|
| 1 (Endo-1) | 0.0 | 0.0 | 0.0 |
| ΔG‡1→2 | 4.4 | 5.7 | 5.2 |
| 2 (Endo-2) | 0.3 | −0.1 | 0.6 |
| ΔG‡2→3 | 1.4 | 6.7 | 0.5 |
| 3 (Exo-2) | −2.7 | −2.0 | −3.8 |
| ΔG‡1→4 | 18.0 | — | 17.1 |
| 4 (Exo-1) | 3.7 | −0.5 | 1.4 |
| ΔG‡4→3 | 5.5 | 6.4 | 4.3 |
In terms of the preference for either 1 → 2 → 3 or 1 → 4 → 3 (see Fig. 1), ring expansion followed by the inversion pathway (a process-I) is more favorable than inversion followed by expansion (process-II). For example, in 1a, ΔG‡1→2 = 4.4 kcal mol−1 and ΔG‡2→3 = 1.4 kcal mol−1 while ΔG‡1→4 = 18.0 kcal mol−1 and ΔG‡4→3 = 5.5 kcal mol−1.
The high inversion barrier for Endo-1 → Exo-1 (ΔG‡1→4 (inversion) = 18.0 and 17.1 kcal mol−1 for 1a and 1c respectively) arises due to the ring-strain in the three-membered aza-ring, which aggravates in the transition-state due to the planarity of the N-site. In contrast, the stereoelectronic modulation using R = –F leads to the cleavage of the bridging bond (rate-limiting step) of the 1b and disfavors the planarity of N–F with the cyclopropane ring in TS(1 → 4) for the 1 → 4 → 3 reaction pathway and therefore, its TS could not be located (process-II).43
Following the kinetically favorable 1 → 2 → 3 pathway (coupled valence isomerism along the C–C bond and endo–exo isomerism via N-inversion) 1a, 1b, and 1c show remarkable variation in their relative ΔG‡1→2 (expansion) and ΔG‡2→3 (inversion). For 1a the free-energy of activation for ring expansion is three times more than that for inversion, while for 1b, both the barriers are comparable. For 1c, the activation barrier for N-inversion is the smallest, ΔG‡2c→3c = 0.5 kcal mol−1. Ironically, 1b and 1c are isoelectronic, yet their significant differences in the N-inversion barriers make them ideal candidates to compare the product distributions between endo- and exo-1H-azepine conformational isomers viz.2b/3b and 2c/3c and contrast with the parent benzene imine ⇌ 1H-azepine, 2a/3a. See ESI Fig. S1–S3† for schematic potential energy surfaces for 1a, 1b, and 1c.
Valence isomerism in endo-benzene imine is an example of a dynamically rich system where rapid C–C bond dissociation assists N–H inversion. The rate-limiting C1–C6 bond activation facilitates both the ring expansion and N-inversion (see Fig. 2). The quasiclassical direct-MD simulations reveal a chameleonic transition state TS(1a → 2a) and the non-statistical effects on the product count (Endo-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Exo-2).44–48
Exo-2).44–48
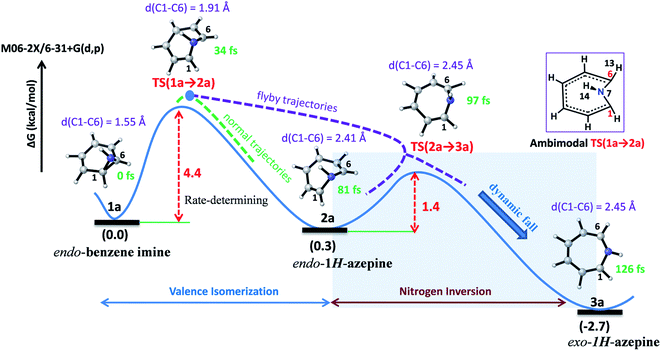 | ||
| Fig. 2 Representative reaction pathways for the valence isomerization assisted nitrogen inversion of 1a. | ||
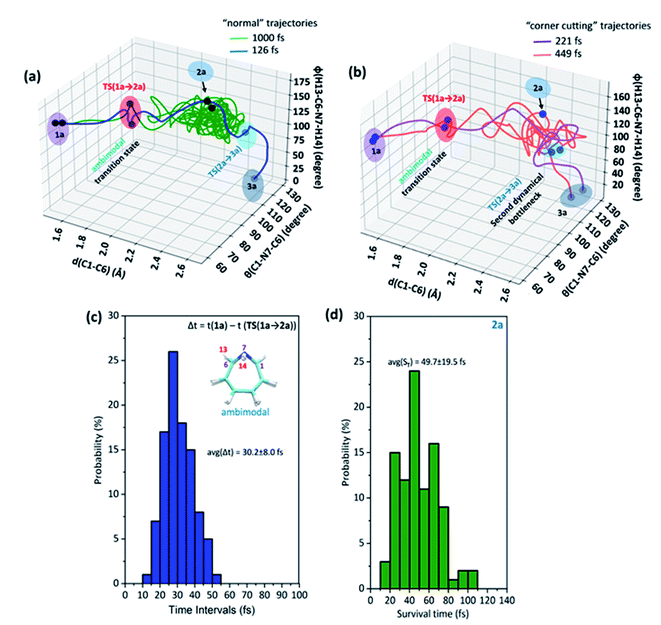
Fig. 2 depicts a typical trajectory and the time-resolved formation of azepine isomers (2a and 3a). A total of 142 reaction trajectories were propagated from rate-limiting TS(1a → 2a) (see ESI Fig. S4† for details). The reaction trajectories passing through the TS(1a → 2a) zone can be characterized as “normal” trajectories if they follow the IRC-pathway (1 → 2 → 3) or “flyby” trajectories when they skip the minimum energy pathway (bypassing the 2a-zone) and directly traverse to TS(2a → 3a), finally forming 3a.
Out of the 142 reaction trajectories, 108 (76%) “normal” reaction trajectories led to exo-1H-azepine (3a) while 20 (14%) “flyby” reaction trajectories afford the TS(2a → 3a) and finally fall to the exo-1H-azepine (3a) zone. Only 6 (4%) trajectories are found in the simulation that produces endo-1H-azepine (2a) up to 1 ps. The remaining 8 (6%) re-cross to either the reactant (1a) or product (3a) zones. This indicates a post-transition state bifurcation reaction where dynamical effects govern the stereoselectivity. The selectivity (2a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3a) for the 1a → 2a, 3a ring-opening reaction is ∼1
3a) for the 1a → 2a, 3a ring-opening reaction is ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21.
21.
Further, Fig. 3(a) represents two “normal” reaction trajectory propagations and time-resolved variation of the critical structural parameters (d, θ, and ϕ) during valence isomerization (benzene imine → 1H-azepine). The green-colored trajectory defines the reaction path that affords endo-1H-azepine (2a) which is found stable up to 1 ps during MD simulation. In contrast, the blue trajectory follows the ultrafast decay along the steepest descent path and eventually falls towards the exo-1H-azepine (3a) product zone.
These flyby reaction trajectories were found highly concerted and follow shorter dynamical routes to reach the 3a-product zone in the potential energy surface. In Fig. 3(b) a typical “flyby” trajectory (violet line) shows its transit from TS(1a → 2a) to TS(2a → 3a) and falls into the 3a-product basin without forming Endo-2 (2a). On the other hand, the orange line first approaches the TS(2a → 3a) zone, takes a short trip at the 2a-zone, and finally populates the exo-1H-azepine, Exo-2 (3a) basin.49
Further, the lower thermodynamic stability of endo-1H-azepine (ΔG (2a and 3a) = 3.0 kcal mol−1) and small activation barrier (ΔG‡ = 1.4 kcal mol−1) for the N–H inversion populates the 3a product basin. From Fig. 3(c), we can estimate that the average time (Δt) required to reach the rate-limiting transition state TS(1a → 2a) is 30.2 ± 8.0 fs. We have also calculated the survival time (ST) using the cut-offs: 2a appears when d(C1–C6) > 2.19 Å, θ(C1–N7–C6) > 98° and ϕ(H13–C6–N7–H14) > 135° whereas 2a disappears when d(C1–C6) > 2.38 Å, θ(C1–N7–C6) > 98° and ϕ(H13–C6–N7–H14) > 104°. The survival time (ST) vs. probability plot indicates that the average survival time (ST) of 2a is 49.7 ± 19.5 fs (see Fig. 3(d)). Therefore, the signature of the endo-1H-azepine (2a) formation can be traced using spectroscopic techniques.50,51
Additionally, the electronic and dynamical effect control on stereoselectivity was investigated by introducing R = –F and –CH3 at the inversion center. In Fig. 4(a), the relative free energy surface dictates an “interrupted” shift.52 The valence isomerism mediated inversion is decoupled at endo-1F-azepine (2b). In general, we can apply such a potential energy surface manipulation strategy either by stabilizing Endo-2 or destabilizing the N-inversion barrier for these coupled reactions. Interestingly, the stronger electron-withdrawing substitutions not only increase the Endo-2 → Exo-2 inversion barrier but also disfavors the transition state of direct Endo-1 → Exo-1 isomerization. In the case of –F substitution, the 1b → 2b → 3b → 4b pathway connects 1b ⇌ 4b. In contrast, TS(1c → 4c) connects 1c ⇌ 4c (Endo-1 → Exo-1) with a significantly higher activation energy barrier (Ea = 17.1 kcal mol−1). However, such isolobal –CH3 stereoelectronic induction accelerates the formation of exo-1CH3-azepine (3c) (see, Fig. 4(b)). In this case, 2c → 3c isomerization has such a small barrier which makes it a highly coupled pathway (1c → 3c), a “dynamical” shift.48
In Fig. 4(a) and (b), snapshots of typical trajectories are shown. The reaction trajectories are simulated from these rate-limiting transition states, TS(1b → 2b) and TS(1c → 2c) respectively. In the case of –F substitution, a typical trajectory affords 2b (Endo-2) within 109 fs and is stable in the simulation. However, the representative reaction trajectory forms 3c (Exo-2) within 275 fs.
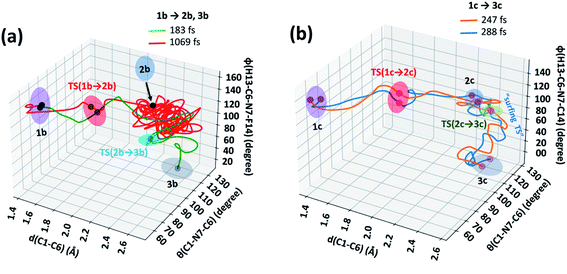
The 3D plots depict the typical trajectories simulated from rate-limiting TSs, TS(1b → 2b) and TS(1c → 2c) respectively (see Fig. 5). In Fig. 5(a), two typical reaction trajectories are depicted. The red “normal” reaction trajectory elucidates the formation of 2bvia the steepest descent path (IRC-pathway), whereas the green flyby route shows the dynamical pathway (non-statistical) that can afford exo-product 3b formation for the valence isomerism in 1b. On the other hand, the orange and blue lines show fast conversion into the N-methyl substituted exo-1H-azepine (3c) (see Fig. 5(b)).
Further, we performed 156 reaction trajectorie simulations from the TS(1b → 2b) at the M06-2X/6-31+G(d,p) level of theory (see ESI Fig. S4 and S5† for details). In this case, out of 132 (85%) product forming reaction trajectories, 87 (56%) afford endo-1F-azepine, 2b. Interestingly, 45 (29%) reaction trajectories follow the dynamical (non-statistical pathways) routes to reach the exo-product (3b) zone. Therefore, the R = –F stereoelectronic modulation manipulates the stereoselectivity of the valence isomerism in 1b. The stereoselectivity (2b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3b) of the reaction is 2
3b) of the reaction is 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
In addition, a total of 145 reaction trajectories are propagated from the TS(1c → 2c) at the same level of theory (see ESI Fig. S4 and S5† for details). Out of 141 (97%) productive trajectories, 104 (72%) follow the IRC path. Interestingly, out of 37 (25%) “corner cutting” reaction trajectories, 36 directly traverse through the N–CH3 inversion TS(2c → 3c) and further dynamically fall out to the 3c-zone, whereas only 1 “flyby” reaction trajectory leads to 2c-product viaTS(2c → 3c). We found that exo-1-methyl-1H-azepine 3c was the exclusive product (Endo-2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Exo-2= 1
Exo-2= 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140).
140).
On the other hand, out of 104 “normal” reaction trajectories, 32 were dynamically stepwise. The 32 stepwise trajectories “surf” the TS(2c → 3c) dividing the surface before leaving the TS zone. The average surfing time at the TS(2c → 3c) zone is 20.2 ± 7.4 fs (see the ESI, Fig. S5†). This is due to the conformational penalty which the methyl group needs to incur along the path 1c → TS(2c → 3c) while passing through the TS(2c → 3c) dividing the potential landscape. Quasielastic neutron scattering experiments are well-suited to recognize methyl-rotations in dynamically rich systems.53
Further, quantum mechanical tunneling (QMT) effects are investigated and they significantly dictate the benzene imine ⇌ 1H-azepine dynamics. Considering that ΔG‡1→2 (expansion) is the rate-limiting step along the preferred 1 → 2 → 3 pathway, ring isomerization of endo-benzene imine (Endo-1) to endo-1H-azepine (Endo-2) essentially would involve motion of the two bridged carbons (C1 and C6 in Scheme 2). A qualitative estimation of the width of the barrier (w) is obtained by the difference in d(C1–C6) between the benzene imine and azepine. For 1a → 2a, w is only 0.75 Å which along with a small ΔG‡1a→2a = 4.4 kcal mol−1 makes a strong case for heavy-atom tunneling.54,55
Since ring expansion is endergonic along 1a → 2a, the reaction rates are obtained by performing SCT dynamical calculations along the reverse (exergonic) direction followed by scaling them by microscopic reversibility.56 At 300 K, kCVT+SCT (1a → 2a) = 1.84 × 108 s−1 while kCVT (1a → 2a) = 1.75 × 108 s−1, acceleration by only 5% due to tunneling. However, at the liquid N2 temperature, kCVT+SCT (1a → 2a) and kCVT (1a → 2a) are 1.51 × 10−1 s−1 and 3.64 × 10−2 s−1, respectively, a gain of 75% by tunneling. The Arrhenius plot of the reaction rate shows strong curvature at low temperatures in Fig. 6(a). At 40 K, kCVT+SCT (1a → 2a) = 3.12 × 10−5 s−1 which is nine-orders more than the pure classical over-the-barrier transit. Such large enhancements in reaction rates at sub-cryogenic temperatures make ring-opening a highly QMT driven process.
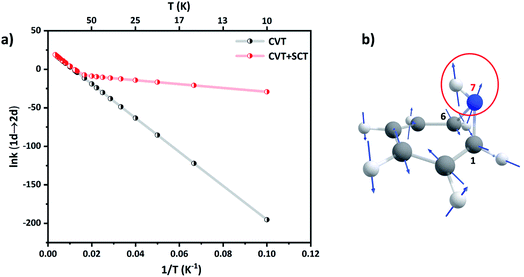 | ||
| Fig. 6 (a) Arrhenius plot of the CVT and CVT + SCT rates (in s−1) for 1a → 2a. (b) Displacement vectors for the normal mode of TS(1a → 2a). The directional motion of the N7–H bond is encircled. | ||
Ring expansion along the C1–C6 bond also remotely affects the N–H bond at the bridgehead. The C1–N7–C6 bond angle increases from θ(C1–N7–C6) = 63.9° in 1a to θ(C1–N7–C6) = 82.4° in TS(1a → 2a). Natural Bond Orbital (NBO)57 calculations at the M06-2X/6-31+G(d,p) level (see the ESI, Table ST5†) show that the hybridization at the N-center changes from sp2 to sp3. This should classically result in an inverse secondary KIE.58 Indeed, secondary H/D isotope effects at CVT are inverse at all temperatures. For example, kCVT (1a → 2a)/kCVT (1d → 2d) = 0.96, 0.89 and 0.32 at T = 300 K, 100 K and 10 K respectively. However, the normal mode for ring-expansion also shows motion along the N–H(D) bond in the translation vector for the TS, see Fig. 6(b). Therefore, because the H-atom is lighter than D, tunneling assists 1a → 2a preferentially over 1d → 2d. This makes the secondary KIE positive at high temperatures and reduces the extent of inverse secondary KIE with kCVT+SCT (1a → 2a)/kCVT+SCT (1d → 2d) = 1.08, 1.03, and 0.42 at T = 300 K, 100 K, and 10 K respectively.
Conclusion
Post-transition-state dynamics and quantum mechanical tunneling play an important role in the benzene imine ⇌ 1H-azepine equilibrium. This isomerism belongs to a peculiar class of pericyclic reactions where ring expansion dictates stereoselectivity. The C–C bond cleavage and N-inversion dynamics guide the rich diversity of endo-/exo-product outcomes. The dynamics can be selectively controlled by the electronic nature of the substituents on the N-end. While a strong electron-withdrawing group like –F decouples the ring-expansion and inversion pathways, for the –H/–CH3 groups they are strongly entangled to result in the final ring-expanded form with N-inversion. At sub-cryogenic temperatures when the reaction is driven by quantum mechanical tunneling, heavy-atom tunneling governs the reaction due to the small width of the barrier for ring expansion. Such coupled valence isomerism and N-inversion are also anticipated for other norcaradienes wherein the stereoelectronic effects of the substituents are critical.Data availability
The datasets supporting this article have been uploaded as part of the ESI.†Author contributions
NM performed the research, Ankita ran QMT calculations; CH did dynamics setup; AD planned the project.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
NM thanks CSIR for SRF. AD and CH thank DST Inspire and IACS for the research fellowship. AD thanks TRC-DST and SERB grant no. DIA/2018/000013 and CRG/2020/000301 for partial funding.References
- T. L. Gilchrist and R. C. Storr, Organic Reactions and Orbital Symmetry, Cambridge University Press, Cambridge, 2nd edn, 1979 Search PubMed.
- E. Vogel and H. Gunther, Benzene Oxide – Oxepin Valence Tautomerism, Angew. Chem., Int. Ed. Engl., 1967, 6, 385–401 CrossRef CAS.
- L. A. Paquette, Valence Isomerism in Selected Heterocyclic Systems, Angew. Chem., Int. Ed. Engl., 1971, 10, 11–20 CrossRef CAS.
- H. Jansen, J. C. Slootweg and K. Lammertsma, Valence Isomerism of Cyclohepta-1,3,5-triene and its Heteroelement Analogues, Beilstein J. Org. Chem., 2011, 7, 1713–1721 CrossRef CAS PubMed.
- I. V. Alabugin, Stereoelectronic Effects: A Bridge Between Structure and Reactivity, John Wiley & Sons, Ltd, Chichester, UK, 2016 Search PubMed.
- D. H. Ess, S. E. Wheeler, R. G. Lafe, L. Xu, N. Çelebi-Ölçüm and K. N. Houk, Bifurcations on Potential Energy Surfaces of Organic Reactions, Angew. Chem., Int. Ed., 2008, 47, 7592–7601 CrossRef CAS PubMed.
- L. A. Paquette, D. E. Kuhla, J. H. Barrett and R. J. Haluska, Unsaturated Heterocyclic Systems. LII. A General Synthetic Entry to Derivates of 1H-Azepine, J. Org. Chem., 1969, 34, 2866–2878 CrossRef CAS.
- C. Dardonville, M. L. Jimeno, I. Alkorta and J. Elguero, Homoheteroaromaticity: The Case Study of Azepine and Dibenzazepine, Org. Biomol. Chem., 2004, 2, 1587–1591 RSC.
- R. Fournier, A. R. Green, A. Greenberg, E. Lee-Ruff, J. F. Liebman and A. Ragyanszki, Predicted Reversal in N-Methylazepine/N-Methyl-7-azanorcaradiene Equilibrium Upon Formation of their N-Oxides, Molecules, 2020, 25, 4767 CrossRef CAS PubMed.
- L. A. Paquette, D. E. Kuhla and J. H. Barrett, Unsaturated Heterocyclic Systems. LIII. Thermochemical Reactions of 1H-Azepine Derivatives. II. Aromatization and Sigmatropic Migrations Involving Nitrogen, J. Org. Chem., 1969, 34, 2879–2884 CrossRef CAS.
- L. A. Paquette, J. H. Barrett and D. E. Kuhla, Thermochemical Reactions of 1H-Azepine Derivatives. I. Dimerization, J. Am. Chem. Soc., 1969, 91, 3616–3624 CrossRef CAS.
- K. Black, P. Liu, L. Xu, C. Doubleday and K. N. Houk, Dynamics, Transition States, and Timing pf Bond Formation in Diels–Alder Reactions, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 12860–12865 CrossRef CAS PubMed.
- J. Rehbein and B. K. Carpenter, Do we fully understand what controls chemical selectivity?, Phys. Chem. Chem. Phys., 2011, 13, 20906–20922 RSC.
- J. M. Burns, Computational evidence for a reaction pathway bifurcation in Sasaki-type (4 + 3)-cycloadditions, Org. Biomol. Chem., 2018, 16, 1828–1836 RSC.
- N. Mandal, A. K. Pal, P. Gain, A. Zohaib and A. Datta, Transition-State-like Planar Structures for Amine Inversion along Ultralong C–C Bonds in Diamino-o-carborane and Diamino-o-dodecahedron, J. Am. Chem. Soc., 2020, 142(11), 5331–5337 CrossRef CAS PubMed.
- C. Castro and W. L. Karney, Heavy-Atom Tunneling in Organic Reactions, Angew. Chem., Int. Ed., 2020, 59, 8355–8366 CrossRef CAS PubMed.
- S. K. Sarkar, E. Solel, S. Kozuch and M. Abe, Heavy-Atom Tunneling Processes during Denitrogenation of 2,3-Diazabicyclo[2.2.1]hept-2-ene and Ring Closure of Cyclopentane-1,3-diyl Diradical. Stereoselectivity in Tunneling and Matrix Effect, J. Org. Chem., 2020, 85(14), 8881–8892 CrossRef CAS PubMed.
- P. R. Schreiner, Quantum Mechanical Tunneling is Essential to Understand Chemical Reactivity, Trends Chem., 2020, 2, 980–989 CrossRef CAS.
- X. Zhang, D. A. Hrovat and W. T. Borden, Calculations Predict That Carbon Tunneling Allows the Degenerate Cope Rearrangement of Semibullvalene to Occur Rapidly at Cryogenic Temperatures, Org. Lett., 2010, 12, 2798–2801 CrossRef CAS PubMed.
- D. Gerbig, D. Ley and P. R. Schreiner, Light- and Heavy-Atom Tunneling in Rearrangement Reactions of Cyclopropylcarbenes, Org. Lett., 2011, 13(13), 3526–3529 CrossRef CAS PubMed.
- C. Doubleday, R. Armas, D. Walker, C. V. Cosgriff and E. M. Greer, Heavy-Atom Tunneling Calculations in Thirteen Organic Reactions: Tunneling Contributions are Substantial, and Bell’s Formula Closely Approximates Multidimensional Tunneling at ≥250K, Angew. Chem., Int. Ed., 2017, 129, 13279–13282 CrossRef.
- B. K. Carpenter, Heavy-atom tunneling as the dominant pathway in a solution-phase reaction? Bond shift in antiaromatic annulenes, J. Am. Chem. Soc., 1983, 105(6), 1700–1701 CrossRef CAS.
- M. Ertelt, D. A. Hrovat, W. T. Borden and W. Sander, Heavy-Atom Tunneling in the Ring Opening of a Strained Cyclopropene at Very Low Temperates, Chem.–Eur. J., 2014, 20(16), 4713–4720 CrossRef CAS PubMed.
- I. Sedgi and S. Kozuch, Heavy atom tunnelling on XeF6 pseudorotation, Phys. Chem. Chem. Phys., 2020, 22, 17725–17730 RSC.
- C. M. Nunes, I. R. Eckhardt, R. Fausto and P. R. Schreiner, Competitive Nitrogen versus Carbon Tunneling, J. Am. Chem. Soc., 2019, 141(36), 14340–14348 CrossRef CAS PubMed.
- C. M. Nunes, I. Reva, S. Kozuch, R. J. McMohan and R. Fausto, Photochemistry of 2-Formylphenylnitrene: A Doorway to Heavy-Atom Tunneling of a Benzazinine to a Cyclic Ketenimine, J. Am. Chem. Soc., 2017, 139(48), 17649–17659 CrossRef CAS PubMed.
- S. Karmakar and A. Datta, Heavy-atom tunneling in organic transformations, J. Chem. Sci., 2020, 132, 1–22 CrossRef.
- T. Schleif, M. P. Merini and W. Sander, The Mystery of the Benzene-Oxide/Oxepin Equilibrium – Heavy-Atom Tunneling Reversed by Solvent Interactions, Angew. Chem., Int. Ed., 2020, 59, 20318–20322 CrossRef CAS PubMed.
- X. Ma and W. L. Hase, Perspective: chemical dynamics simulations of non-statistical reaction dynamics, Philos. Trans. R. Soc., A, 2017, 375, 20160204 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- Y. Zhao and D. G. Truhlar, The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-class Functionals and 12 other Functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- K. Fukui, The Path of Chemical Reactions – The IRC Approach, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- D. G. Truhlar and B. C. Garrett, Variational Transition State Theory, Annu. Rev. Phys. Chem., 1984, 35, 159–189 CrossRef CAS.
- A. Fernandez-Ramos, B. A. Ellingson, B. C. Garrett and D. G. Truhlar, Variational Transition State Theory with Multidimensional Tunneling, Reviews in Computational Chemistry, ed. K. B. Lipkowitz and T. R. Cundari, Wiley-VCH, Hoboken, NJ, 2007, vol. 23, pp. 125–232 Search PubMed.
- J. Zheng, J. L. Bao, R. Meana-Pañeda, S. Zhang, B. J. Lynch, J. C. Corchado, Y.-Y. Chuang, P. L. Fast, W.-P. Hu, Y.-P. Liu, G. C. Lynch, K. A. Nguyen, C. F. Jackels, A. Fernandez Ramos, B. A. Ellingson, V. S. Melissas, J. Villà, I. Rossi, E. L. Coitiño, J. Pu, T. V. Albu, A. Ratkiewicz, R. Steckler, B. C. Garrett, A. D. Isaacson and D. G. Truhlar, Polyrate 17-C Search PubMed.
- J. Zheng, J. L. Bao, S. Zhang, J. C. Corchado, R. Meana-Pañeda, Y.-Y. Chuang, E. L. Coitiño, B. A. Ellingson and D. G. Truhlar, Gaussrate 2017-B Search PubMed.
- A. González-Lafont, J. Villà, J. M. Lluch, J. Bertrán, R. Steckler and D. G. Truhlar, Variational Transition State Theory and Tunneling Calculations with Reorientation of the Generalized Transition States for Methyl Cation Transfer, J. Phys. Chem. A, 1998, 102, 3420–3428 CrossRef.
- B. R. Ussing, C. Hang and D. A. Singleton, Dynamic Effects on the Periselectivity, Rate, Isotope Effects, and Mechanism of Cycloadditions of Ketenes with Cyclopentadiene, J. Am. Chem. Soc., 2006, 128, 7594 CrossRef CAS PubMed.
- Y. Oyola and D. A. Singleton, Dynamics and the Failure of Transition State Theory in Alkene Hydroboration, J. Am. Chem. Soc., 2009, 131(9), 3130–3131 CrossRef CAS PubMed.
- A. Patel, Z. Chen, Z. Yang, O. Gutiérrez, H. Liu, K. N. Houk and D. A. Singleton, Dynamically complex [6 + 4] and [4 + 2] cycloadditions in the biosynthesis of spinosyn A, J. Am. Chem. Soc., 2016, 138(11), 3631–3634 CrossRef CAS PubMed.
- S. R. Hare, A. Li and D. J. Tantillo, Post-transition state bifurcations induce dynamical detours in Pummerer-like reactions, Chem. Sci., 2018, 9, 8937–8945 RSC.
- L. Verlet, Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard–Jones Molecules, Phys. Rev., 1967, 159, 98–103 CrossRef CAS.
- C. C. Levin, A Qualitative Molecular Orbital Picture of Electronegativity Effects on XH3 Inversion Barriers, J. Am. Chem. Soc., 1975, 97(20), 5649–5655 CrossRef CAS.
- R. V. López, O. N. Faza and C. S. López, Dynamic Effects Responsible for High Selectivity in a [3,3] Sigmatropic Rearrangement Featuring a Bis-pericyclic Transition State, J. Org. Chem., 2017, 82(9), 4758–4765 CrossRef PubMed.
- N. Mandal and A. Datta, Origin of Gold(i)-Catalyzed Intramolecular Diels–Alder Reaction: Evolution of Trappable Intermediates via Asynchronous Transition States, J. Org. Chem., 2018, 83(18), 11167–11177 CrossRef CAS PubMed.
- J. B. Thomas, J. R. Waas, M. Harmata and D. A. Singleton, Control Elements in Dynamically Determined Selectivity on Bifurcating Surface, J. Am. Chem. Soc., 2008, 130(44), 14544–14555 CrossRef CAS PubMed.
- S. Le and J. M. Goodman, Rapid Route-Finding for Bifurcating Organic Reactions, J. Am. Chem. Soc., 2020, 142(20), 9210–9219 CrossRef PubMed.
- Y. Liu, S. Holm, J. Meisner, Y. Jia, Q. Wu, T. J. Woods, T. J. Martinez and J. S. Moore, Flyby reaction trajectories: Chemical dynamics under extrinsic force, Science, 2021, 373(6551), 208–212 CrossRef CAS PubMed.
- N. Mandal and A. Datta, Dynamical Effects along the Bifurcation Pathway Control Semibullvalene Formation in Deazetization Reactions, J. Phys. Chem. B, 2018, 122(3), 1239–1244 CrossRef CAS PubMed.
- A. H. Zewail, Femtochemistry: atomic-scale dynamics of the chemical bond, J. Phys. Chem. A, 2002, 104(24), 5660–5694 CrossRef.
- S. Pedersen, J. L. Herek and A. H. Zewail, The validity of the “diradical” hypothesis: direct femtosecond studies of the transition state structures, Science, 1994, 266(5189), 1359 CrossRef CAS PubMed.
- D. V. Vidhani, M. E. Krafft and I. V. Alabugin, Gold(i)-Catalyzed Allenyl Cope Rearrangement: Evolution from Asynchronicity to Trappable Intermediates Assisted by Stereoelectronic Switching, J. Am. Chem. Soc., 2016, 138(8), 2769–2779 CrossRef CAS PubMed.
- C. Smuda, G. Gemmecker and T. Unruh, Quasielastic and inelastic neutron scattering study of methyl group rotation in solid and liquid pentafluoroanisole and pentafluorotoluene, J. Chem. Phys., 2018, 128(19), 194502 CrossRef PubMed.
- S. Kozuch, Heavy atom tunneling in the automerization of pentalene and other antiaromatic systems, RSC Adv., 2014, 4, 21650–21656 RSC.
- A. Nandi, A. Sucher and S. Kozuch, Ping-Pong Tunneling Reactions: Can Fluorine Jump at Absolute Zero?, Chem.–Eur. J., 2018, 24(61), 16348–16355 CrossRef CAS PubMed.
- S. Karmakar and A. Datta, Role of Heavy Atom Tunneling in Myers–Saito Cyclization of Cyclic Enyne-Cumulene Systems, J. Phys. Chem. B, 2016, 120, 945–950 CrossRef CAS PubMed.
- NBO, F. Weinhold and C. R. Landis, Valency and Bonding: A Natural Bond Orbital Donor–Acceptor Perspective, Cambridge Univ. Press, Cambridge, 2005 Search PubMed.
- E. V. Anslyn and D. A. Dougherty, Modern Physical Organic Chemistry, University Science Books, Sausalito, CA, 2006 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Schematic potential energy surfaces, QCT inputs, details of MD simulations, QMT inputs, CVT and CVT + SCT rates for valence isomerism, NBO analyses, Cartesian coordinates, energies, and harmonic frequencies and Awk Code. See DOI: 10.1039/d1sc04855d |
| This journal is © The Royal Society of Chemistry 2022 |