Open Access Article
Open Access ArticleCan a Wanzlick-like equilibrium exist between dicoordinate borylenes and diborenes?†
Felipe
Fantuzzi
 *abcd,
Yinchun
Jiao
*abcd,
Yinchun
Jiao
 e,
Rian D.
Dewhurst
e,
Rian D.
Dewhurst
 bc,
Frank
Weinhold
bc,
Frank
Weinhold
 f,
Holger
Braunschweig
f,
Holger
Braunschweig
 bc and
Bernd
Engels
bc and
Bernd
Engels
 *a
*a
aInstitute for Physical and Theoretical Chemistry, Julius-Maximilians-Universität Würzburg, Emil-Fischer-Str. 42, 97074 Würzburg, Germany. E-mail: bernd.engels@uni-wuerzburg.de
bInstitute for Inorganic Chemistry, Julius-Maximilians-Universität Würzburg, Am Hubland, 97074 Würzburg, Germany
cInstitute for Sustainable Chemistry & Catalysis with Boron, Julius-Maximilians-Universität Würzburg, Am Hubland, 97074 Würzburg, Germany
dSchool of Physical Sciences, Ingram Building, University of Kent, Park Wood Road, Canterbury CT2 7NH, UK. E-mail: f.fantuzzi@kent.ac.uk
eKey Laboratory of Theoretical Organic Chemistry and Functional Molecules, Hunan University of Science and Technology, Xiangtan 411201, China
fTheoretical Chemistry Institute and Department of Chemistry, University of Wisconsin–Madison, Madison, WI 53706, USA
First published on 4th March 2022
Abstract
Boron chemistry has experienced tremendous progress in the last few decades, resulting in the isolation of a variety of compounds with remarkable electronic structures and properties. Some examples are the singly Lewis-base-stabilised borylenes, wherein boron has a formal oxidation state of +I, and their dimers featuring a boron–boron double bond, namely diborenes. However, no evidence of a Wanzlick-type equilibrium between borylenes and diborenes, which would open a valuable route to the latter compounds, has been found. In this work, we combine DFT, coupled-cluster, multireference methods, and natural bond orbital/natural resonance theory analyses to investigate the electronic, structural, and kinetic factors controlling the reactivity of the transient CAAC-stabilised cyanoborylene, which spontaneously cyclotetramerises into a butterfly-type, twelve-membered (BCN)4 ring, and the reasons why its dimerisation through the boron atoms is hampered. The computations are also extended to the NHC-stabilised borylene counterparts. We reveal that the borylene ground state multiplicity dictates the preference for self-stabilising cyclooligomerisation over boron–boron dimerisation. Our comparison between NHC- vs. CAAC-stabilised borylenes provides a convincing rationale for why the reduction of the former always gives diborenes while a range of other products is found for the latter. Our findings provide a theoretical background for the rational design of base-stabilised borylenes, which could pave the way for novel synthetic routes to diborenes or alternatively non-dimerising systems for small-molecule activation.
Introduction
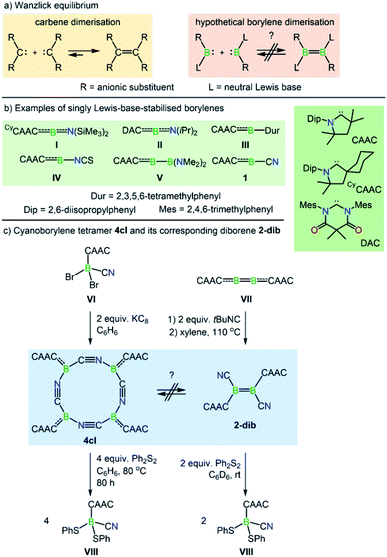
The Wanzlick equilibrium is a fundamental process whereby two diaminocarbenes, [(R2N)2C:], are in equilibrium with their C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonded dimers, i.e. [(R2N)2C
C bonded dimers, i.e. [(R2N)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(NR2)2] (Scheme 1a).1 While the Wanzlick equilibrium has only been confirmed to occur with a few specific carbenes, the process is of fundamental and historical interest in persistent carbene chemistry,2 and has even been observed in higher homologues of carbenes3 and a dialumene.4
C(NR2)2] (Scheme 1a).1 While the Wanzlick equilibrium has only been confirmed to occur with a few specific carbenes, the process is of fundamental and historical interest in persistent carbene chemistry,2 and has even been observed in higher homologues of carbenes3 and a dialumene.4
Dicoordinate borylenes of the form [LRB:] (L = Lewis base), isolobal and isoelectronic analogues of carbenes [R2C:], are very rare species. Contrary to their naked borylene analogues [RB:], which exhibit singlet ground states regardless of the R groups,5 [LRB:] species can have either singlet or triplet ground states.6 Two examples of dicoordinate borylenes have been isolated by employing π-accepting carbene ligands, the groups of Stephan and Bertrand using a cyclic (alkyl)(amino)carbene (CAAC) (I, Scheme 1b),7 and that of Hudnall using a diamidocarbene (II).8 Beyond isolated examples of dicoordinate borylenes, transient examples (III–V, Scheme 1b) have been inferred as intermediates in an intramolecular C–C insertion reaction,9 transition-metal-like ligand exchange reactions at boron,10 borylene-mediated dinitrogen fixation and dimerisation,11 and others.12 These species can also be generated from the more common doubly base-stabilised [L1L2RB:] precursors13 either by photolytic10a or thermal10b ligand extrusion processes. However, despite the fact that dicoordinate borylenes [LRB:] and their diborene14 cousins [LRB![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BRL] have now been both isolated and inferred from reactivity, no evidence for a bora-Wanzlick equilibrium has been presented. It is also important to note that the reduction of base-stabilised dihaloorganyl boranes [LBRX2] most often leads to the diborene [LRB
BRL] have now been both isolated and inferred from reactivity, no evidence for a bora-Wanzlick equilibrium has been presented. It is also important to note that the reduction of base-stabilised dihaloorganyl boranes [LBRX2] most often leads to the diborene [LRB![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BRL] when the L unit is a poor π-acceptor, but in contrast, boryl radicals,15 borylenes, or intramolecular C–C/C–H activation products16 are formed when the L unit is a strong π-acceptor. The elucidation of the underlying reasons is one of the topics of the present work.
BRL] when the L unit is a poor π-acceptor, but in contrast, boryl radicals,15 borylenes, or intramolecular C–C/C–H activation products16 are formed when the L unit is a strong π-acceptor. The elucidation of the underlying reasons is one of the topics of the present work.
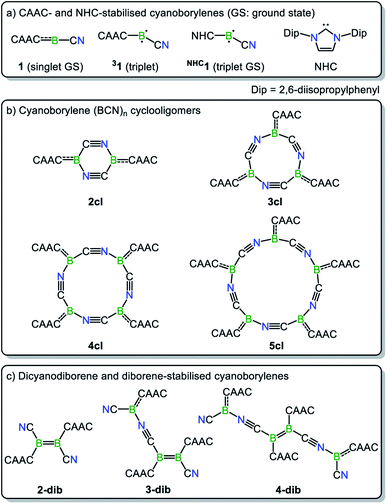
Along these lines, a particularly intriguing case is the singly base-stabilised cyanoborylene [(CAAC)(NC)B:] (1, Scheme 1b), which is not known as an isolated species but is present as a constituent fragment in its isolable cyclotetramer (4cl, Scheme 1c) and as its B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B-bonded dimer diborene species (2-dib, Scheme 1c).17 Although the borylene cyclotetramer acts as a synthetic equivalent of the cyanoborylene [(CAAC)(NC)B:], and both 4cl and 2-dib react with diphenyldisulfide (Ph2S2) to afford the CAAC-stabilised borane [(CAAC)B(CN)(SPh)2], no interconversion between the two isomers has been observed.
B-bonded dimer diborene species (2-dib, Scheme 1c).17 Although the borylene cyclotetramer acts as a synthetic equivalent of the cyanoborylene [(CAAC)(NC)B:], and both 4cl and 2-dib react with diphenyldisulfide (Ph2S2) to afford the CAAC-stabilised borane [(CAAC)B(CN)(SPh)2], no interconversion between the two isomers has been observed.
The close relationship between 4cl and 2-dib prompted us to take a closer look into the formation and reactivity of the two species. Considering our experimental findings,17 a number of questions arise: (i) why does 1 only form 4cl, but neither 2-dib nor any smaller (or larger) cyclooligomer? (ii) What is the mechanism of formation of 4cl from 1? (iii) Why do 4cl and 2-dib form the same product when treated with Ph2S2? (iv) Is it possible to form diborene-based oligomers from the reaction of diborenes and borylenes? And, finally, (v) is it possible to tune the cyanoborylene to induce its Wanzlick-like dimerisation through the boron atoms, instead of cyclotetramerisation? To shed some light on these important questions, in this work we performed a thorough computational investigation of the electronic, structural, and reactivity properties of monomeric and oligomeric forms of the CAAC-stabilised cyanoborylene 1 (see Scheme 2) by combining density functional theory (DFT), high-level multireference calculations and natural bond orbital (NBO)18 analysis. By replacing the CAAC with a classical N-heterocyclic carbene (NHC1, see Scheme 2) we also investigate the differences in the electronic structures of the corresponding compounds when a weaker π-accepting and more sterically demanding carbene ligand is used. With this, we will investigate the reasons for the general observation that NHC-stabilised borylenes tend to form diborenes, a trend that is not observed for the CAAC counterparts.14e
The nomenclature adopted in our paper is explained in Schemes 1 and 2. The CAAC-stabilised cyanoborylene is abbreviated as 1, while its corresponding diborene is abbreviated as 2-dib. Cyclic compounds in which the boron atoms are bridged by CN units are abbreviated as ncl, in which n denotes the number of units and cl indicates that a closed ring is formed. The corresponding open structures are given as nop. The prototypical systems formed by the interaction of 1 with 2-dib are labelled 3-dib and 4-dib.
Computational details
First, we benchmarked distinct density functionals against the domain-based local pair natural orbital coupled-cluster theory, DLPNO-CCSD(T),19 for selected closed-shell species and against the multireference N-electron valence state second-order perturbation theory (NEVPT2)20 approach for open-shell intermediates. The structural properties predicted by the functionals were benchmarked by a comparison with the available X-ray crystal structures. The analysis of the structural data (see Section S1 of the ESI†) indicated that B3LYP21-D3(BJ)22 with Alrich's double-zeta def2-SVP23 basis set showed the best compromise between accuracy and computational cost, and therefore this combination was used to compute geometries and hessians. Our analysis also showed that ωB97XD24/def2-TZVP is more suitable for the relative energies of the closed-shell species, which prompted us to perform additional single-point energy computations at this level for all optimised geometries. All structures were characterised as either minimum energy structures or transition states by the analysis of the vibrational frequencies obtained from the hessian calculations. In order to assess the connectivity between the obtained transition states and the corresponding minimum energy structures, we performed further geometry optimisations along the imaginary mode and additional intrinsic reaction coordinate (IRC)25 calculations. Free energies were obtained from single-point calculations on the optimised structures at the ωB97XD/def2-TZVP level. Solvation effects were considered using the solvation model for density (SMD)26 with benzene (ε = 2.2706) as the solvent. A concentration correction of ΔG0→* = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(24.46) = 1.89 kcal mol−1 (T = 298.15 K) was added to the free energies of all calculated species to change the 1 atm gas-phase values (ΔG0) to the condensed phase standard state concentration of 1 M (ΔG*). This leads to a proper description of associative/dissociative steps.27 For selected cases, we also performed calculations for triplet and open-shell singlet states. These were done using the unrestricted, broken-symmetry DFT approach, as well as with high-level multireference calculations based on the complete active space self-consistent field (CASSCF)28 and NEVPT2 (ref. 20) methods. For these calculations the def2-SVP basis sets was employed. Both approaches, which have been satisfactorily used to describe main-group biradicals and biradicaloids,29 were used herein to estimate vertical and adiabatic singlet–triplet (S–T) gaps. The biradical character index y0 was obtained for the open-shell singlet species using the Yamaguchi formula.30 Finally, the bonding situation of 1 and the ncl species was investigated with the natural bond orbital (NBO)18 and natural resonance theory (NRT) methods.31 All DFT calculations were performed with Gaussian 16, Revision C.01.32 Multireference calculations were done with Orca 4.1.1,33 and NBO/NRT calculations were carried out with the NBO 7 program.34 Images of three-dimensional structures were obtained with CYLview,35 while molecular orbitals and spin densities were plotted with GaussView 6.0.16.
ln(24.46) = 1.89 kcal mol−1 (T = 298.15 K) was added to the free energies of all calculated species to change the 1 atm gas-phase values (ΔG0) to the condensed phase standard state concentration of 1 M (ΔG*). This leads to a proper description of associative/dissociative steps.27 For selected cases, we also performed calculations for triplet and open-shell singlet states. These were done using the unrestricted, broken-symmetry DFT approach, as well as with high-level multireference calculations based on the complete active space self-consistent field (CASSCF)28 and NEVPT2 (ref. 20) methods. For these calculations the def2-SVP basis sets was employed. Both approaches, which have been satisfactorily used to describe main-group biradicals and biradicaloids,29 were used herein to estimate vertical and adiabatic singlet–triplet (S–T) gaps. The biradical character index y0 was obtained for the open-shell singlet species using the Yamaguchi formula.30 Finally, the bonding situation of 1 and the ncl species was investigated with the natural bond orbital (NBO)18 and natural resonance theory (NRT) methods.31 All DFT calculations were performed with Gaussian 16, Revision C.01.32 Multireference calculations were done with Orca 4.1.1,33 and NBO/NRT calculations were carried out with the NBO 7 program.34 Images of three-dimensional structures were obtained with CYLview,35 while molecular orbitals and spin densities were plotted with GaussView 6.0.16.
Results and discussion
Kinetics and thermodynamics of cyclotetramerisation
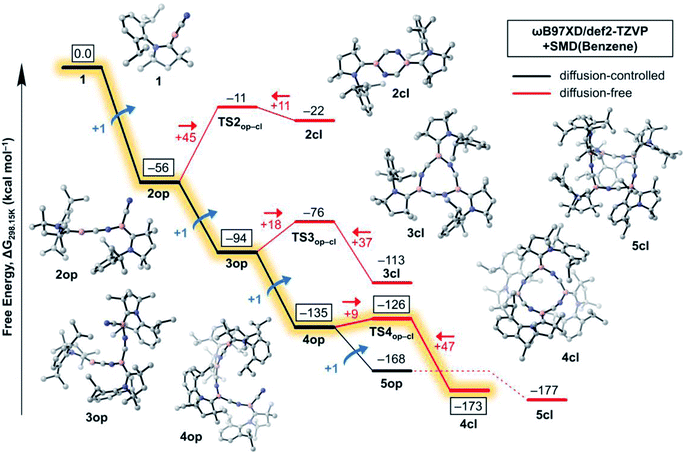
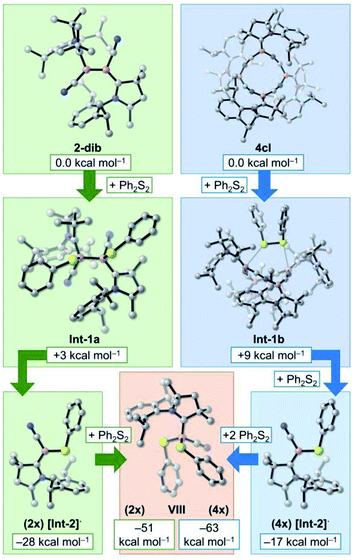
In this section, we investigate the mechanism of formation of cyanoborylene macrocycles ncl from the self-stabilising cyclooligomerisation of 1, aiming at understanding the preference of 4cl over similar structures. For that purpose, we compute the various possible products of the addition reactions. These structures are given in Scheme 2, and their computed free energies in benzene medium are summarised in Fig. 1–3. In Fig. 1, the addition reactions, which depend on the diffusion-controlled interaction of isolated species, are shown in black, while the intramolecular, diffusion-independent cyclisation reactions are shown in red. The most plausible reaction pathway is highlighted in yellow.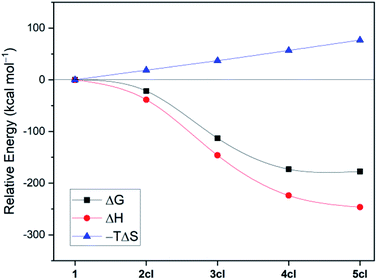 | ||
| Fig. 2 Disentanglement of the free energies (ωB97XD/def2-TZVP + SMD(benzene)//B3LYP-D3(BJ)/def2-SVP) of cyclooligomerisation of 1 to 2cl, 3cl, 4cl, and 5cl. | ||
The starting species 1, which is formed from the reduction of the stable precursor VI (see Scheme 1), possesses a singlet ground state with a linear CAACC–B–CN arrangement. The lowest triplet state (vertical S–T gap = +14.9 kcal mol−1; adiabatic S–T gap = +5.7 kcal mol−1 at the NEVPT2/def2-SVP level) shows a bent structure. The dimerisation of 1 can proceed via (i) attachment through the boron atoms, forming the diborene 2-dib, or (ii) donation from the CN group into the empty p orbital of boron. Reaction through the latter channel will form the open dimer 2op (see Fig. 1), whose cyclisation leads to the corresponding ring structure 2cl (see Scheme 2). The formation of 2op from 1 possesses no reaction barrier (see Fig. S3†), and is strongly exergonic (ΔG = −56 kcal mol−1). The cyclisation leading to the planar 2cl ring is endergonic by +34 kcal mol−1 (ΔG = −22 kcal mol−1), and possesses a high energy barrier of +45 kcal mol−1, as TS2op–cl is located at ΔG = −11 kcal mol−1. The six-membered ring 2cl is characterised as having a triplet ground state, with a nearby open-shell singlet biradical, whose y0 is calculated as 0.998 at the CASSCF(6,6)/def2-SVP level of theory (see Fig. S9†), and whose adiabatic S–T gap is merely −0.2 kcal mol−1 at the NEVPT2/def2-SVP level. The endergonic character of the cyclisation of 2op into the open-shell singlet 2cl is mainly a result of the high ring strain of the latter species, as will be discussed later in more detail.
In contrast to the endergonic cyclisation of 2op, addition of a third monomeric species 1 leading to 3op is again very exergonic by −38 kcal mol−1, with 3op being more stable than three non-interacting molecules of 1 by ΔG = −94 kcal mol−1. Geometry scans following the B–N bond stretch mode (see Fig. S4†) indicate that the formation of 3op from 2op is virtually barrierless. Indeed, this was expected as the nop structures have a bent, terminal B–C–N unit that has the correct orientation to allow the electrophilic attack of the electron-deficient, two-coordinate boron atom of 1 at their terminal CN groups. Subsequent cyclisation to 3cl is slightly exergonic by −19 kcal mol−1, as 3cl is located at ΔG = −113 kcal mol−1 with respect to 1. However, an energy barrier of +18 kcal mol−1, less than half of that of 2op to 2cl, has to be surmounted, with TS3op–cl lying at ΔG = −76 kcal mol−1. The free energy variations with respect to the cyclisation of 2op result from smaller ring strain effects at play in 3cl. In contrast, the (virtually) barrierless formation of 4op from 3op is exergonic by −41 kcal mol−1, indicating that such a transformation is preferred both from a kinetic and thermodynamic perspective, explaining the absence of 3cl in the experiments.
The structure of 4cl differs dramatically from those of the smaller cyanoborylene cyclooligomers. The system is composed of a butterfly-shaped, C2-symmetric twelve-membered ring, whose strain effects are significantly reduced due to loss of planarity. As a consequence, the cyclisation barrier of 4op to 4cl is only +9 kcal mol−1 and is so exergonic (−38 kcal mol−1) that 4cl is even lower in energy than 5op (ΔG = −173 kcal mol−1vs. −168 kcal mol−1 with respect to 1). Even with the formation of 5op being expected to be barrierless due to the reasons discussed above, this pentameric structure will not be formed because its formation is diffusion-controlled, which is kinetically hampered with respect to the diffusion-free, nearly barrierless cyclisation of 4op. Hence, the butterfly-shaped 4cl species represents a trap for further oligomerisation, because the formation of 5op starting from 4cl has a barrier of about +47 kcal mol−1. This barrier is related to the necessary ring-opening step from 4cl back to 4op. In addition, this reaction is slightly endergonic. The cyclopentameric 5cl species is more stable than 4cl, but the free energy difference is merely 4 kcal mol−1, indicating the absence of a thermodynamic driving force for ring expansion. Therefore, these results provide strong evidence for the thermodynamic and kinetic preference of 4cl over its chemically-related analogues, and successfully predict the outcome of the oligomerisation cascade reactions leading to 4cl from the fleeting CAAC-stabilised cyanoborylene monomer.
Fig. 2 disentangles the enthalpic and entropic contributions to the free energies of formation of the cycles 2cl, 3cl, 4cl, and 5cl. The ring expansion is both exothermic and exergonic up to 4cl. As expected, formation of 5cl from 4cl is still exothermic, but the entropy contribution (which increases linearly from 2cl to 5cl and is particularly destabilising in the latter) flattens the free energy curve. These results reinforce the findings of Fig. 1, revealing that enthalpic and entropic factors contribute to the preferred formation of 4cl over its analogous cyclooligomers.
While Fig. 1 explains why 4cl – and not smaller or larger cyanoborylene cyclooligomers – are formed, the question of why two monomers 1 do not form 2-dib remains open. Additionally the question of why 2-dib – obtained from the diboryne precursor VII (ref. 36) – does not form 4clvia its fragmentation to 1 also arises. These questions are answered in Fig. 3. The formation of 2-dib from two monomers 1 is as exergonic as the formation of 2op (see Fig. 1), but for this dimerisation reaction, we predict a reaction barrier of +11 kcal mol−1. Since the formation of 2op is computed to be barrierless, 1 will only react to 2op, as this intermediate is kinetically preferred. The difference between the kinetic profile of these dimerisation reactions arises because the formation of 2-dib requires the distortion of two linear CAACC–B–CN units, while for forming 2op one unit remains linear. The strong exergonicity of the formation of 2-dib from 1 also explains why the former does not fragment into two monomeric units of 1, which would be necessary for the interconversion of 2-dib to the tetramer 4cl.
The energetic profile of the computed oligomerisation steps strongly suggests that the addition of 1 to 2-dib should also be exergonic. Indeed, our computations predict that the formation of 3-dib from 2-dib is strongly exergonic (ΔG = −36 kcal mol−1). Species 3-dib can be rationalised as a diborene-stabilised borylene, and, if synthetically achieved, would be the first of its kind. Conversely, the attachment of another borylene to 3-dib, leading to the diborene-bridged bisborylene 4-dib, is slightly endergonic and significantly less stable than the formation of two isolated dicyanodiborenes 2-dib (4-dib: ΔG = −102 kcal mol−1; (2×) 2-dib: ΔG = −134 kcal mol−1). We predict that 3-dib, a closed-shell singlet molecule with a vertical S–T gap of ca. 10 kcal mol−1 as predicted by DFT calculations, could be formed by a controlled reaction where small amounts of the cyanoborylene 1 are generated in the presence of an excess of 2-dib. This would avoid the self-stabilising cyclotetramerisation of 1 to form 4cl, which is the preferred reaction pathway.
Bonding situation in (BCN)n cyclooligomers
In order to derive salient information about the bonding situation of the (BCN)n cyclooligomers, we performed further calculations based on the NBO/NRT approach. Due to size limitations, these calculations were done for model systems where the methyl and Dip groups of the CAAC ligands are replaced by hydrogen atoms. The NRT bond orders of the CAACC–B bond and the intraannular B–C, C–N and N–B bonds are shown in Table 1. The values of the most relevant NBO second-order perturbation energies, E(2), associated with the natural resonance structure of largest weight, are shown in Table 2. For the ncl species (n = 3–5), these values correspond to mean energies 〈E(2)〉 of the n individual donor–acceptor interactions. The corresponding values of the monomeric cyanoborylene 1 are also shown for comparison.| CAACC–B | B–C | C–N | N–B | |
|---|---|---|---|---|
| 1 | 1.67 | 1.34 | 2.62 | — |
| 2cl | 1.38 | 1.25 | 2.41 | 1.18 |
| 3cl | 1.49 | 1.18 | 2.67 | 1.13 |
| 4cl | 1.58 | 1.17 | 2.73 | 1.06 |
| 5cl | 1.59 | 1.18 | 2.75 | 1.06 |
| CAACC–B(π) → C–N(π*) | CAACC–B(π) → N–C(π*) | CAACN(lp) → CAACC–B(π*) | |
|---|---|---|---|
| 1 | 24.5 | — | 35.3 |
| 2cl | 18.9 | 11.1 | 30.3 |
| 3cl | 28.5 | 15.0 | 32.7 |
| 4cl | 30.6 | 16.5 | 34.2 |
| 5cl | 29.4 | 17.1 | 33.1 |
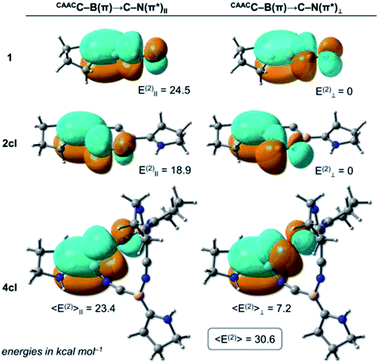
The NRT bond order of CAACC–B in 1 is 1.68 (see Table 1), indicating a strong backdonation from the boron atom to the CAAC ligand. From the NBO point of view, this interaction is stabilised mainly by a donor–acceptor contribution involving the CAACN(lp) donor orbital and the antibonding CAACC–B(π*) acceptor (see Table 2), where the E(2) value is 35.3 kcal mol−1. Analogously, two donor–acceptor pairs of the CAACC–B(π) → C–N(π*) type are found, depending on the orbitals' relative orientation. The first pair is formed between the CAACC–B(π) and the C–N(π*) orbital (quasi-) parallel to it (labelled CAACC–B(π) → C–N(π*)‖), while the second involves the CAACC–B(π) and the (quasi-) perpendicular C–N(π*) orbital (CAACC–B(π) → C–N(π*)⊥ term). The sum of these two contributions correspond to the CAACC–B(π) → C–N(π*) values in Table 1 while the individual CAACC–B(π) → C–N(π*)‖ and CAACC–B(π) → C–N(π*)⊥ pairs for 1, 2cl, and 4cl are shown in Fig. 4. In the case of 1, the value of CAACC–B(π) → C–N(π*)⊥ is negligible, with only the parallelly oriented pair contributing to the 24.5 kcal mol−1 of the CAACC–B(π) → C–N(π*) interaction. The C–N bond order of 1 is 2.62.
Formation of the cyclodimer 2cl, whose six-membered (BCN)2 ring is fully planar, hampers the CAACC–B(π) → C–N(π*) and CAACN(lp) → CAACC–B(π*) interactions by ca. 5 kcal mol−1 each. This is followed by a bond order decrease of the CAACC–B and the C–N bonds, respectively, to 1.38 and 2.41. Indeed, the NRT and NBO values experience the largest variation in going from 1 to 2cl, in comparison to those of the subsequent expansions. This is explained by the significant change in the CAACC–B–C–N bonding motif, particularly the BCN bond angle, which is 180° in 1 but is compressed to 129° in 2cl. Such a dramatic structural modification significantly distorts the B–C–N moiety from a perfectly linear arrangement, which leads to a highly strained ring, and reduces the overlap between the CAACC–B(π) and C–N(π*) orbital pairs, producing a smaller E(2) contribution. The destabilising nature of the bent B–C–N moiety is also reflected in the electronic structure of 2cl, whose lowest singlet state has a biradical character, with its corresponding closed-shell singlet lying 6.2 kcal mol−1 above at the DFT level. It is important to note that for the cyclic structures each CAACC–B(π) donor can interact with a second set of antibonding C–N(π*) acceptors through the B–N–C moiety. These interactions follow similar trends to those through the B–C–N motif, but with smaller energy values.
Inspection of Tables 1 and 2 reveals that the NRT and E(2) values change systematically as the ring size is increased to 4cl, and then do not vary considerably from 4cl to 5cl. For example, the CAACC–B bond order of 3cl (1.49) is larger than that of 2cl (1.38), but smaller than those of 4cl (1.58) and 5cl (1.59), which are virtually identical. Similar trends are observed for the other bonding descriptors. Indeed, 4cl is the first non-planar (BCN)n ring, with the adopted butterfly structure significantly decreasing strain effects, and also allowing more interactions due to reduction of symmetry. These findings indicate that 4cl already possesses the most relevant electronic and structural features contributing to the stabilisation of these (BCN)n rings, and that further ring expansion does not provide any additional benefit to the system. This is in total agreement with the computational findings based on the thermochemical analysis, which indicate that the thermodynamic driving force for ring expansion is significant only up to 4cl.
One last point should be noticed in the NBO/NRT values of Tables 1 and 2. The C–N bond orders of 4cl and 5cl are significantly larger than that of 1, with these cyclic systems also featuring larger CAACC–B(π) → C–N(π*) E(2) values. The increase of these donor–acceptor contributions comes from the interplay of the CAACC–B(π) → C–N(π*)II and CAACC–B(π) → C–N(π*)⊥ terms as the (BCN)n rings become non-planar. Due to an orientation mismatch between the (quasi-)parallel CAACC–B(π) and C–N(π*) orbitals, the CAACC–B(π) → C–N(π*)IIE(2) values are slightly decreased to 23.4 and 23.7 kcal mol−1. On the other hand, the CAACC–B(π) → C–N(π*)⊥ term, which features the (quasi-)perpendicular orbital orientation and is negligible in 1 since these orbitals are perfectly orthogonal, contributes to 7.2 and 5.7 kcal mol−1 in 4cl and 5cl, respectively. The increase of E(2) due to the (quasi-)perpendicular pair overcompensates the E(2) decrease due to the (quasi-)parallel pair, making the CAACC–B(π) → C–N(π*) donor–acceptor contribution more important for the non-planar (BCN)n rings. Therefore, we can conclude that donor–acceptor contributions of the CAACC–B(π) → C–N(π*) type are also at play in the further stabilisation of the non-planar (BCN)n rings in comparison to their planar analogues.
Thermochemistry of the reaction with Ph2S2
At this point, it is very clear that the formation of the 4cl butterfly cyclotetramer from the cyanoborylene 1 is both thermodynamically and kinetically preferred over the formation of diborene 2-dib, and that the interconversion of 2-dib and 4cl is hampered due to the high B–B dissociation energy of 2-dib. However, experimental results have shown that these two species have very similar reactivity patterns. In this section, we focus on the reaction of 2-dib and 4cl with Ph2S2 (see Scheme 1) to shed some light on their reactivity patterns. In both cases, compound VIII is formed. The relative free energies of the mentioned species – together with those of plausible intermediate candidates – are shown in Fig. 5.Addition of Ph2S2 across the B–B bond of 2-dib leads to Int-1, where the S–S σ and the B–B π bonds are broken, and two B–S σ bonds are formed. This transformation is slightly endergonic by +3 kcal mol−1. Contrary to 2-dib, the B–B dissociation of Int-1, which leads to two [Int-2]· radicals, is exergonic by −28 kcal mol−1. Moreover, reaction with a second Ph2S2 compound to form the product VIII is also exergonic, with the product located −51 kcal mol−1 below 2-dib. A strong thermodynamic driving force is, therefore, obtained for the chemical transformation of 2-dib to VIII.
In turn, addition of Ph2S2 to 4cl leads to Int-1b, which is merely +9 kcal mol−1 uphill. Surprisingly, even with 4cl being very thermodynamically stable, its dissociation into four [Int-2]· radicals after insertion of two equivalents of Ph2S2 is exergonic. As in the case of 2-dib, the formation of VIII from 4cl is remarkably favourable. Although the current computations do not unveil the whole mechanistic pathway, they suggest that 4cl and 2-dib can have the same reaction outcome even though they are not interconvertible, in accordance with the experimental findings.17c
NHC-stabilised cyanoborylenes
While CAAC-stabilized borylenes lead to quite different products, their NHC counterparts tend to form diborenes.14e To determine the reasons for this, in this section we investigate the effects that distinct types of carbenes confer on the electronic and structural properties of Lewis-base-stabilised cyanoborylene species. For this purpose, the main electrostructural features of the ground states and low-lying states of 1 and NHC1, the latter obtained by replacing the CAAC ligand with the classic imidazolylidene NHC with Dip substituents at the nitrogen atoms, are shown in Fig. 6. The propensity of CAACs to form stable radical and biradical main-group species is now well established, while their NHC analogues more often lead to closed-shell singlet species.29a,i However, in the cyanoborylene molecule, this tendency is inverted, as revealed by DFT and, particularly, high-level NEVPT2/CASSCF calculations (Fig. 6). The ground state of the CAAC-stabilised cyanoborylene 1 is a closed-shell singlet system (S0) featuring a linear CAACC–B–CN motif. The vertical excitation to the lowest triplet state (T1) is +14.9 kcal mol−1. Geometry optimisation at the T1 potential energy surface leads to a structure having a bent CAACC–B–CN moiety oriented parallel to the CAAC ligand, and which lies +5.7 kcal mol−1 above that of the S0 state of 1. In contrast, the most stable closed-shell singlet (S1) structure of NHC1 features a bent NHCC–B–CN motif perpendicularly oriented with respect to the NHC plane. The vertical singlet–triplet gap at the NEVPT2 level reveals that the triplet state (T0) is lower in energy than the singlet with this structure by −4.4 kcal mol−1. Geometry optimisation of the T0 state of NHC1 leads to a structure where the bent NHCC–B–CN motif is parallelly oriented with respect to the NHC ring, in a similar manner to that of the T1 structure of 1. The optimised T0 state lies −13.5 kcal mol−1 below the optimised S1 state. Finally, a constrained optimisation of the closed-shell singlet NHC1, where the NHCC–B–C and B–C–N angles are fixed to 180°, therefore producing a linear NHCC–B–C–N motif, leads to S1′, which lies +1.2 kcal mol−1 above S1 and +14.7 kcal mol−1 above T0.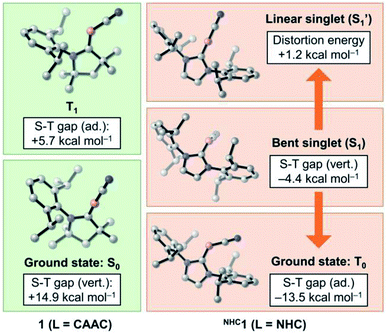 | ||
| Fig. 6 Energetic and structural features of the ground state and low-lying states of 1 and NHC1. Energies are at the NEVPT2/CASSCF(2,2)/def2-SVP level of theory. | ||
In order to shed some light on the destabilising nature of the linear NHCC–B–CN arrangement in the NHC-stabilised cyanoborylene NHC1, Fig. 7 presents the frontier MOs of the closed-shell systems 1 (L = CAAC) and the S1 and S1′ states of NHC1. The HOMO of 1 (−4.81 eV) is composed of a CAACC–B π bonding contribution, which originates from the backdonation of the borylene lone pair to the π acceptor CAACC atom. This orbital also features two nodal planes: one in the CAACN–CAACC bonding region, and another in the vicinity of the C–N bond. In turn, the LUMO of 1 (−2.46 eV) is also located in the vicinity of the CAACC–B–CN unit, but is orthogonally aligned with respect to the HOMO. This orbital also features antibonding character at the C–N bond, and antibonding σ contributions at the carbene backbone. The HOMO–LUMO (H–L) gap of the S0 state of 1 is calculated to be 2.34 eV. The replacement of the CAAC ligand by an NHC does not significantly affect either the shape or the orbital energies of the corresponding LUMO orbitals. However, important changes are observed in the HOMOs of the S1′ and S1 states of NHC1. Both orbitals are characterised by the presence of two nodal planes in the carbene ring. By comparing NHC1 (S1′) and 1 (S0), it is possible to see that the extension of the B → NHCC backdonation is reduced drastically. This is a direct consequence of the differences in π acidity of the CAAC and NHC ligands. Because of the lower π acidity of the NHC, the HOMO energy of NHC1 (S1′) is lifted by around 0.8 eV, consequently decreasing the H–L gap to 1.63 eV. The linear NHCC–B–CN configuration forces the boron atom to retain its sp hybridisation, which is destabilised due to the smaller backdonation effect. In turn, geometry relaxation of the closed-shell NHC1 (S1) system leads to a bent NHCC–B–CN moiety perpendicularly aligned with respect to the NHC. This allows the boron atom to change its hybridisation mode to sp2, with a pure lone pair localised at the boron centre. Compared to NHC1 (S1′), the HOMO of NHC1 (S1) is stabilised by ca. 0.2 eV, while the LUMO is lifted to −2.20 eV, leading to a H–L gap value of 1.99 eV. The variations in the H–L gaps are consistent with the energetic features depicted in Fig. 6. They reveal that the smaller π accepting nature of the classical NHC in comparison to that of CAAC, as a consequence of the extra π-donating and σ-withdrawing amino group, is responsible for the destabilisation of the closed-shell NHC analogue of 1.
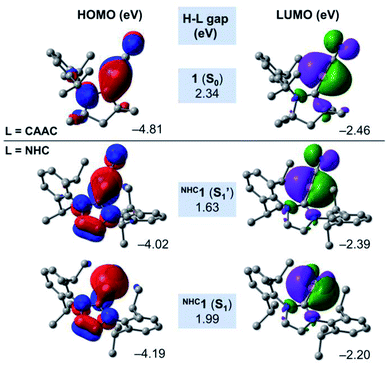 | ||
| Fig. 7 Canonical Kohn–Sham frontier orbitals and H–L gaps of 1 (S0), NHC1 (S1) and NHC1 (S1′) at the B3LYP-D3(BJ)/def2-SVP level of theory. | ||
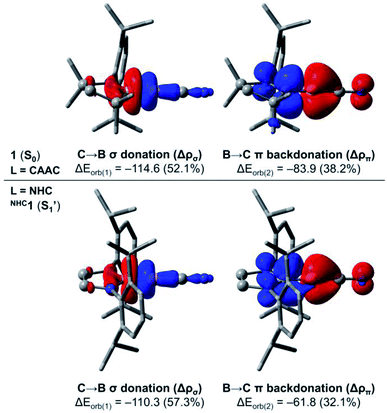
In order to investigate in more detail the origin of the preferred bent C–B–CN geometry of NHC1 in contrast to the linear arrangement of 1 (L = CAAC), we performed further computations based on the energy decomposition analysis coupled with natural orbitals for chemical valence (EDA-NOCV).37 These calculations were done for 1 and the corresponding linear singlet (S1′) of NHC1 considering the singlet fragments BCN + L = CAAC, NHC at the PBE0 (ref. 38)-D3(BJ)/TZ2P level of theory using the ADF 2019 (ref. 39) program package. It is important to mention that the BCN fragment must be computed in its electronically excited configuration, so that the p(π) lone pair at boron is doubly occupied.13b In the EDA-NOCV approach, the interaction energy ΔEint between the fragments is decomposed into distinct contributions, namely Pauli repulsion (ΔEpauli), dispersion (ΔEdisp), electrostatic (ΔEelstat) and orbital interaction (ΔEorb) energies. The latter term can be further decomposed into pairwise, donor–acceptor NOCV contributions. The main deformation densities associated with the EDA-NOCV description of 1 and NHC1 (S1′) are shown in Fig. 8. All energy terms from the EDA-NOCV decomposition of the aforementioned systems are shown in Table S11† in the ESI.
For 1, the ΔEint term is computed to be −242.3 kcal mol−1. The Pauli repulsion destabilises this interaction by +142.7 kcal mol−1, which is counterbalanced by the stabilising contributions of the remaining energy terms. While dispersion effects contribute to merely −4.4 kcal mol−1, the ΔEelstat and ΔEorb represent 41.7% (−160.7 kcal mol−1) and 57.1% (−219.9 kcal mol−1) of the stabilising contributions, respectively. A further inspection of the ΔEorb terms reveals that the two major contributions sum to roughly 90% of the total orbital interaction. These contributions are related to C → B σ donation (−114.6 kcal mol−1) and B → C π backdonation (−83.9 kcal mol−1). On the other hand, the EDA-NOCV description of NHC1 (S1′) indicates that the ΔEint term is −211.5 kcal mol−1, which is 30.8 kcal mol−1 less negative than that of 1. Inspection of the energy terms that compose ΔEint reveals that this difference is mainly attributed to ΔEorb, whose stabilising contributions in NHC1 (S1′) are smaller by 27.6 kcal mol−1. The analysis of the NOCV pairs clearly indicates that the decrease in the B → C π backdonation is the effect responsible for the less stabilising interaction between the NHC and the linear BCN fragment. In other words, the EDA-NOCV results confirm that the π-acidity of the ligand dictates the preferred linear structure of the CAAC-stabilised borylene, as the B → NHC π backdonation is significantly less effective.
The findings discussed above seem to be of great importance to the chemistry of the borylenes. They strongly suggest that the HOMO–LUMO gap, and consequently the ground state multiplicity, is more dependent on the Lewis base, rather than the R substituent. In that sense, NHC-stabilised borylenes would prefer to form triplet compounds, while their CAAC analogues would form closed-shell singlet species. This preference would lead to distinct reactivity patterns, and could explain the general observation that NHC-stabilised borylenes tend to form diborenes, formally the dimerisation product of triplet borylenes, while those with CAAC donors do not dimerise through the boron atom and show small molecule activation behavior.14e To further test this hypothesis, we computed the CAAC- and NHC-stabilised parent borylenes [LHB:] (see Fig. S5 and 6†). Indeed, the structural and electronic properties of [LHB:] are strikingly similar to those of the corresponding cyano compounds 1 and NHC1. While (CAAC)BH presents a linear CAACC–B–H bonding motif and a closed-shell singlet ground state, with an S–T gap of +11.0 kcal mol−1 at the NEVPT2 level, (NHC)BH has a bent NHCC–B–H structure with a triplet ground state (S–T gap of −12.0 kcal mol−1). Further calculations to test the generality of these findings to other Lewis-base-stabilised borylenes are in progress.
Lastly, we have analysed the formation of the dicyanodiborene compound stabilised by two NHC ligands, NHC2-dib, from the dimerisation of two cyanoborylenes NHC1. As discussed above, the monomeric structure has a bent NHCC–B–CN motif, with a ground-state triplet multiplicity. Thus, it already has the appropriate electrostructural features to allow dimerisation through the boron atoms. Geometry scans along the B–B bond stretching mode reveal that, indeed, this dimerisation is barrierless (see Fig. S7†). In contrast, the NHC version of the cyclotetrameric structure, herein labelled as NHC4cl, is sterically crowded (see Fig. S8†). As a consequence, while the free energy of 4cl is −39 kcal mol−1 relative to that of two 2-dib species, the free energy of NHC4cl is +45 kcal mol−1 relative to that of two isolated NHC2-dib systems. These results strongly suggest that the formation of the diborene NHC2-dib from fleeting triplet borylenes is feasible, albeit less likely to happen than with singlet borylenes. These findings could pave the way for new synthetic methods for the formation of boron–boron multiply bonded systems, or alternatively non-dimerising systems for small-molecule activation, which will be explored in subsequent studies.
Conclusions
In summary, we apply DFT, natural bond orbital, natural resonance theory, and high-level multireference calculations to investigate the electronic, structural, bonding, and kinetic factors driving the spontaneous cyclotetramerisation of a CAAC-stabilised boron(I) species, and the reasons why its interconversion into a boron–boron doubly bonded compound through a Wanzlick-type equilibrium is hampered. In addition, we investigate why the NHC counterparts tend to dimerise, which is not the case for CAAC-stabilised boron(I) species. The cyanoborylene species 1, which features a linear CAACC–B–CN motif, strong B → CAACC backdonation, and a closed-shell singlet multiplicity, preferably undergoes a barrierless dimerisation leading to a bis(borylene) compound through formation of a boron–nitrogen bond. Indeed, the diffusion-controlled, cascade oligomerisation of 1 following this route is not hampered by kinetic barriers, and the formation of the final reaction product is driven by diffusion-free cycloisomerisation steps. While high energy barriers are obtained for the cyclisation to six- and nine-membered (BCN)n rings from their corresponding open-chain isomers due to electronic and structural factors, the formation of the butterfly-type, cyclotetrameric twelve-membered ring 4cl is both virtually barrierless and highly exergonic. In contrast, dimerisation of 1 through the boron atoms has a free-energy barrier of +11 kcal mol−1, while the dissociation of the diborene 2-dib to its monomeric units is uphill by +78 kcal mol−1. Besides correctly predicting the reactivity of 1, and hinting towards a synthetic route for elusive diborene-stabilised borylenes, our results provide thermodynamic and kinetic reasoning for the non-interconvertibility of 4cl and 2-dib and the lack of a Wanzlick-type equilibrium between 1 and 2-dib. We also use computations to explore the reactivity of 4cl and 2-dib with Ph2S2, indicating that in both cases their deconstruction to a tetracoordinate boron(III) species is thermodynamically favourable. Finally, the replacement of the CAAC ligand to a classic NHC in the singly Lewis-base-stabilised species 1 leads to a triplet borylene featuring an NHCC–B–CN motif, whose electronic and structural properties allow its dimerisation through the boron atom. Additional computations for the corresponding [LHB:] parent borylenes indicate that the preference of CAACs for closed-shell singlet compounds, and those of conventional NHCs for triplet compounds, might be a general trend in borylene chemistry. Further studies aimed at investigating the generality of these findings, and at developing new synthetic avenues to boron–boron multiply bonded systems based on this approach, are underway in our laboratories.Data availability
All relevant data is presented in the paper and ESI. The Cartesian coordinates of all computed structures are provided as part of the ESI.†Author contributions
F. F. and B. E. designed the computations which were performed by F. F. and Y. J. F. F., B. E. and R. D. wrote the original draft. H. B., F. W. and B. E. acquisited fundings and contributed methodologies. All authors contributed to the interpretation of the computed data and the writing and editing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project was funded by the European Research Council (ERC) under the European Union Horizon 2020 Research and Innovation Program (grant agreement no. 669054) and the Deutsche Forschungsgemeinschaft (DFG), e.g. in the framework of the GRK2112. F. F. thanks the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) and the Alexander von Humboldt (AvH) Foundation for a Capes-Humboldt postdoctoral fellowship.Notes and references
-
(a) H.-W. Wanzlick and H.-J. Kleiner, Angew. Chem., 1961, 73, 493 CrossRef CAS
; (b) H. W. Wanzlick, Angew. Chem., Int. Ed. Engl., 1962, 1, 75–80 CrossRef
; (c) H.-W. Wanzlick, F. Esser and H.-J. Kleiner, Chem. Ber., 1963, 96, 1208–1212 CrossRef CAS
; (d) F. E. Hahn, L. Wittenbecher, D. Le Van and R. Fröhlich, Angew. Chem., Int. Ed., 2000, 39, 541–544 ( Angew. Chem. , 2000 , 112 , 551–554 ) CrossRef CAS
; (e) V. P. W. Böhm and W. A. Herrmann, Angew. Chem., Int. Ed., 2000, 39, 4036–4038 ( Angew. Chem. , 2000 , 112 , 4200–4202 ) CrossRef
.
-
(a) D. Bourissou, O. Guerret, F. P. Gabbaï and G. Bertrand, Chem. Rev., 2000, 100, 39–92 CrossRef CAS PubMed
; (b) T. Dröge and F. Glorius, Angew. Chem., Int. Ed., 2010, 49, 6940–6952 ( Angew. Chem. , 2010 , 122 , 7094–7107 ) CrossRef PubMed
; (c) M. N. Hopkinson, C. Richter, M. Schedler and F. Glorius, Nature, 2014, 510, 485–496 CrossRef CAS
.
- S. Tsutsui, K. Sakamoto and M. Kira, J. Am. Chem. Soc., 1998, 120, 9955–9956 CrossRef CAS
.
- R. Falconer, K. Byrne, G. Nichol, T. Krämer and M. Cowley, 2021, ChemRxiv, This content is a preprint and has not been peer-reviewed.
-
(a) M. Krasowska and H. F. Bettinger, J. Am. Chem. Soc., 2012, 134, 17094–17103 CrossRef CAS PubMed
; (b) F. Fantuzzi, T. M. Cardozo and M. A. C. Nascimento, J. Phys. Chem. A, 2015, 119, 5335–5343 CrossRef CAS PubMed
; (c) M. Krasowska, M. Edelmann and H. F. Bettinger, J. Phys. Chem. A, 2016, 120, 6332–6341 CrossRef CAS PubMed
.
- D. Lu, Y. He and C. Wu, Phys. Chem. Chem. Phys., 2019, 21, 23533–23540 RSC
.
- F. Dahcheh, D. Martin, D. W. Stephan and G. Bertrand, Angew. Chem., Int. Ed., 2014, 53, 13159–13163 (
Angew. Chem.
, 2014
, 126
, 13375–13379
) CrossRef CAS PubMed
.
- A. D. Ledet and T. W. Hudnall, Dalton Trans., 2016, 45, 9820–9826 RSC
.
- H. Braunschweig, R. D. Dewhurst, F. Hupp, M. Nutz, K. Radacki, C. W. Tate, A. Vargas and Q. Ye, Nature, 2015, 522, 327–330 CrossRef CAS PubMed
.
-
(a) H. Braunschweig, I. Krummenacher, M.-A. Légaré, A. Matler, K. Radacki and Q. Ye, J. Am. Chem. Soc., 2017, 139, 1802–1805 CrossRef CAS PubMed
; (b) C. Pranckevicius, M. Weber, I. Krummenacher, A. K. Phukan and H. Braunschweig, Chem. Sci., 2020, 11, 11055–11059 RSC
.
-
(a) M.-A. Légaré, G. Bélanger-Chabot, R. D. Dewhurst, E. Welz, I. Krummenacher, B. Engels and H. Braunschweig, Science, 2018, 359, 896–900 CrossRef PubMed
; (b) M.-A. Légaré, M. Rang, G. Bélanger-Chabot, J. I. Schweizer, I. Krummenacher, R. Bertermann, M. Arrowsmith, M. C. Holthausen and H. Braunschweig, Science, 2019, 363, 1329–1332 CrossRef PubMed
; (c) M.-A. Légaré, G. Bélanger-Chabot, M. Rang, R. D. Dewhurst, I. Krummenacher, R. Bertermann and H. Braunschweig, Nat. Chem., 2020, 12, 1076–1080 CrossRef PubMed
.
- S. Hagspiel, M. Arrowsmith, F. Fantuzzi, A. Vargas, A. Rempel, A. Hermann, T. Brückner and H. Braunschweig, Angew. Chem., Int. Ed., 2021, 60, 6446–6450 (
Angew. Chem.
, 2021
, 133
, 6519–6524
) CrossRef CAS PubMed
.
-
(a) R. Kinjo, B. Donnadieu, M. A. Celik, G. Frenking and G. Bertrand, Science, 2011, 333, 610–613 CrossRef CAS PubMed
; (b) M. A. Celik, R. Sure, S. Klein, R. Kinjo, G. Bertrand and G. Frenking, Chem.–Eur. J., 2012, 18, 5676–5692 CrossRef CAS PubMed
; (c) D. A. Ruiz, M. Melaimi and G. Bertrand, Chem. Commun., 2014, 50, 7837–7839 RSC
; (d) L. Kong, Y. Li, R. Ganguly, D. Vidovic and R. Kinjo, Angew. Chem., Int. Ed., 2014, 53, 9280–9283 ( Angew. Chem. , 2014 , 126 , 9434–9437 ) CrossRef CAS PubMed
; (e) H. Wang, J. Zhang, Z. Lin and Z. Xie, Chem. Commun., 2015, 51, 16817–16820 RSC
; (f) L. Kong, W. Lu, L. Yongxin, R. Ganguly and R. Kinjo, Inorg. Chem., 2017, 56, 5586–5593 CrossRef CAS PubMed
; (g) M. Arrowsmith, J. I. Schweizer, M. Heinz, M. Härterich, I. Krummenacher, M. C. Holthausen and H. Braunschweig, Chem. Sci., 2019, 10, 5095–5103 RSC
; (h) U. Schmidt, F. Fantuzzi, M. Arrowsmith, A. Hermann, D. Prieschl, A. Rempel, B. Engels and H. Braunschweig, Chem. Commun., 2020, 56, 14809–14812 RSC
.
-
(a) Y. Wang, B. Quillian, P. Wei, C. S. Wannere, Y. Xie, R. B. King, H. F. Schaefer, P. v. R. Schleyer and G. H. Robinson, J. Am. Chem. Soc., 2007, 129, 12412–12413 CrossRef CAS PubMed
; (b) Y. Wang, B. Quillian, P. Wei, Y. Xie, C. S. Wannere, R. B. King, H. F. Schaefer, P. v. R. Schleyer and G. H. Robinson, J. Am. Chem. Soc., 2008, 130, 3298–3299 CrossRef CAS PubMed
; (c) H. Braunschweig and R. D. Dewhurst, Angew. Chem., Int. Ed., 2013, 52, 3574–3583 ( Angew. Chem. , 2013 , 125 , 3658–3667 ) CrossRef CAS PubMed
; (d) M. Arrowsmith, H. Braunschweig and T. E. Stennett, Angew. Chem., Int. Ed., 2017, 56, 96–115 ( Angew. Chem. , 2017 , 129 , 100–120 ) CrossRef CAS PubMed
; (e) M.-A. Légaré, C. Pranckevicius and H. Braunschweig, Chem. Rev., 2019, 119, 8231–8261 CrossRef PubMed
.
-
(a) Y. Su and R. Kinjo, Coord. Chem. Rev., 2017, 352, 346–378 CrossRef CAS
; (b) S. Kundu, S. Sinhababu, V. Chandrasekhar and H. W. Roesky, Chem. Sci., 2019, 10, 4727–4741 RSC
; (c) S. Hagspiel, M. Arrowsmith, F. Fantuzzi, A. Hermann, V. Paprocki, R. Drescher, I. Krummenacher and H. Braunschweig, Chem. Sci., 2020, 11, 551–555 RSC
.
- L. Wu, R. D. Dewhurst, H. Braunschweig and Z. Lin, Organometallics, 2021, 40, 766–775 CrossRef CAS
.
-
(a) J. Böhnke, H. Braunschweig, T. Dellermann, W. C. Ewing, T. Kramer, I. Krummenacher and A. Vargas, Angew. Chem., Int. Ed., 2015, 54, 4469–4473 (
Angew. Chem.
, 2015
, 127
, 4551–4555
) CrossRef PubMed
; (b) M. Arrowsmith, D. Auerhammer, R. Bertermann, H. Braunschweig, G. Bringmann, M. A. Celik, R. D. Dewhurst, M. Finze, M. Grüne, M. Hailmann, T. Hertle and I. Krummenacher, Angew. Chem., Int. Ed., 2016, 55, 14464–14468 ( Angew. Chem. , 2016 , 128 , 14680–14684 ) CrossRef CAS PubMed
; (c) D. Auerhammer, M. Arrowsmith, R. D. Dewhurst, T. Kupfer, J. Böhnke and H. Braunschweig, Chem. Sci., 2018, 9, 2252–2260 RSC
.
- F. Weinhold, C. R. Landis and E. D. Glendening, Int. Rev. Phys. Chem., 2016, 35, 399–440 Search PubMed
.
-
(a) C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed
; (b) C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed
; (c) C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109 CrossRef PubMed
; (d) M. Saitow, U. Becker, C. Riplinger, E. F. Valeev and F. Neese, J. Chem. Phys., 2017, 146, 164105 CrossRef PubMed
; (e) Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, J. Chem. Phys., 2018, 148, 011101 CrossRef PubMed
.
-
(a) C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS
; (b) C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS
; (c) C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS
.
-
(a) S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS
; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed
; (c) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
; (d) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS
.
-
(a) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
; (b) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC
.
- K. Ishida, K. Morokuma and A. Komornicki, J. Chem. Phys., 1977, 66, 2153–2156 CrossRef CAS
.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed
.
-
(a) C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2005, 1, 1133–1152 CrossRef CAS PubMed
; (b) M. Sparta, C. Riplinger and F. Neese, J. Chem. Theory Comput., 2014, 10, 1099–1108 CrossRef CAS PubMed
; (c) F. Fantuzzi, M. A. C. Nascimento, B. Ginovska, R. M. Bullock and S. Raugei, Dalton Trans., 2021, 50, 840–849 RSC
.
-
B. O. Roos, in Advances in Chemical Physics: Ab Initio Methods in Quantum Chemistry Part 2, Volume 69, ed. K. P. Lawley, John Wiley & Sons, 1987, pp. 399–445 Search PubMed
.
-
(a) E. Welz, J. Böhnke, R. D. Dewhurst, H. Braunschweig and B. Engels, J. Am. Chem. Soc., 2018, 140, 12580–12591 CrossRef CAS PubMed
; (b) S. K. Mellerup, Y. Cui, F. Fantuzzi, P. Schmid, J. T. Goettel, G. Bélanger-Chabot, M. Arrowsmith, I. Krummenacher, Q. Ye, V. Engel, B. Engels and H. Braunschweig, J. Am. Chem. Soc., 2019, 141, 16954–16960 CrossRef CAS PubMed
; (c) T. Thiess, G. Bélanger-Chabot, F. Fantuzzi, M. Michel, M. Ernst, B. Engels and H. Braunschweig, Angew. Chem., Int. Ed., 2020, 59, 15480–15486 ( Angew. Chem. , 2020 , 132 , 15608–15614 ) CrossRef CAS
; (d) C. Saalfrank, F. Fantuzzi, T. Kupfer, B. Ritschel, K. Hammond, I. Krummenacher, R. Bertermann, R. Wirthensohn, M. Finze, P. Schmid, V. Engel, B. Engels and H. Braunschweig, Angew. Chem., Int. Ed., 2020, 59, 19338–19343 ( Angew. Chem. , 2020 , 132 , 19502–19507 ) CrossRef CAS PubMed
; (e) T. Ullrich, P. Pinter, J. Messelberger, P. Haines, R. Kaur, M. M. Hansmann, D. Munz and D. M. Guldi, Angew. Chem., Int. Ed., 2020, 59, 7906–7914 ( Angew. Chem. , 2020 , 132 , 7980–7988 ) CrossRef CAS PubMed
; (f) M. Pinheiro, F. B. C. Machado, F. Plasser, A. J. A. Aquino and H. Lischka, J. Mater. Chem. C, 2020, 8, 7793–7804 RSC
; (g) M. Rang, F. Fantuzzi, M. Arrowsmith, I. Krummenacher, E. Beck, R. Witte, A. Matler, A. Rempel, T. Bischof, K. Radacki, B. Engels and H. Braunschweig, Angew. Chem., Int. Ed., 2021, 60, 2963–2968 ( Angew. Chem. , 2021 , 133 , 3000–3005 ) CrossRef CAS PubMed
; (h) D. K. Roy, T. Tröster, F. Fantuzzi, R. D. Dewhurst, C. Lenczyk, K. Radacki, C. Pranckevicius, B. Engels and H. Braunschweig, Angew. Chem., Int. Ed., 2021, 60, 3812–3819 ( Angew. Chem. , 2021 , 133 , 3856–3863 ) CrossRef CAS PubMed
; (i) P. Schmid, F. Fantuzzi, J. Klopf, N. B. Schröder, R. D. Dewhurst, H. Braunschweig, V. Engel and B. Engels, Chem.–Eur. J., 2021, 27, 5160–5170 CrossRef CAS PubMed
; (j) M. K. Sharma, F. Ebeler, T. Glodde, B. Neumann, H.-G. Stammler and R. S. Ghadwal, J. Am. Chem. Soc., 2021, 143, 121–125 CrossRef CAS PubMed
; (k) M. K. Sharma, D. Rottschäfer, T. Glodde, B. Neumann, H. Stammler and R. S. Ghadwal, Angew. Chem., Int. Ed., 2021, 60, 6414–6418 ( Angew. Chem. , 2021 , 133 , 6485–6489 ) CrossRef CAS PubMed
; (l) M. Gerlach, F. Fantuzzi, L. Wohlfart, K. Kopp, B. Engels, J. Bozek, C. Nicolas, D. Mayer, M. Gühr, F. Holzmeier and I. Fischer, J. Chem. Phys., 2021, 154, 114302 CrossRef CAS PubMed
; (m) A. Maiti, F. Zhang, I. Krummenacher, M. Bhattacharyya, S. Mehta, M. Moos, C. Lambert, B. Engels, A. Mondal, H. Braunschweig, P. Ravat and A. Jana, J. Am. Chem. Soc., 2021, 143, 3687–3692 CrossRef CAS PubMed
; (n) T. Brückner, F. Fantuzzi, T. E. Stennett, I. Krummenacher, R. D. Dewhurst, B. Engels and H. Braunschweig, Angew. Chem., Int. Ed., 2021, 60, 13661–13665 ( Angew. Chem. , 2021 , 133 , 13774–13779 ) CrossRef PubMed
; (o) M. Härterich, B. Ritschel, M. Arrowsmith, J. Böhnke, I. Krummenacher, A. K. Phukan and H. Braunschweig, J. Am. Chem. Soc., 2021, 143(43), 18339–18345 CrossRef
.
-
(a) K. Yamaguchi, Chem. Phys. Lett., 1975, 33, 330–335 CrossRef CAS
; (b) S. Yamanaka, M. Okumura, M. Nakano and K. Yamaguchi, J. Mol. Struct., 1994, 310, 205–218 Search PubMed
; (c) M. Nakano, Top. Curr. Chem., 2017, 375, 47 CrossRef PubMed
.
-
(a) E. D. Glendening and F. Weinhold, J. Comput. Chem., 1998, 19, 593–609 CrossRef CAS
; (b) E. D. Glendening and F. Weinhold, J. Comput. Chem., 1998, 19, 610–627 CrossRef CAS
; (c) E. D. Glendening, J. K. Badenhoop and F. Weinhold, J. Comput. Chem., 1998, 19, 628–646 CrossRef CAS
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS
.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40, 2234–2241 CrossRef CAS PubMed
.
-
C. Y. Legault, CYLview, version 1.0.561b. Université de Sherbrooke, Sherbrooke, QC, Canada, 2009, http://www.cylview.org Search PubMed
.
- J. Böhnke, H. Braunschweig, W. C. Ewing, C. Hörl, T. Kramer, I. Krummenacher, J. Mies and A. Vargas, Angew. Chem., Int. Ed., 2014, 53, 9082–9085 (
Angew. Chem.
, 2014
, 126
, 9228–9231
) CrossRef PubMed
.
- M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975 CrossRef CAS PubMed
.
-
(a) M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS
; (b) C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS
.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc05988b |
| This journal is © The Royal Society of Chemistry 2022 |