Open Access Article
Open Access ArticleAnatomy and formation mechanisms of early amyloid-β oligomers with lateral branching: graph network analysis on large-scale simulations†
Miao
Yuan
,
Xuan
Tang
and
Wei
Han
 *
*
State Key Laboratory of Chemical Oncogenomics, Guangdong Provincial Key Laboratory of Chemical Genomics, School of Chemical Biology and Biotechnology, Peking University Shenzhen Graduate School, Shenzhen, 518055, China. E-mail: hanw@pkusz.edu.cn
First published on 8th February 2022
Abstract
Oligomeric amyloid-β aggregates (AβOs) effectively trigger Alzheimer's disease-related toxicity, generating great interest in understanding their structures and formation mechanisms. However, AβOs are heterogeneous and transient, making their structure and formation difficult to study. Here, we performed graph network analysis of tens of microsecond massive simulations of early amyloid-β (Aβ) aggregations at near-atomic resolution to characterize AβO structures with sizes up to 20-mers. We found that AβOs exhibit highly curvilinear, irregular shapes with occasional lateral branches, consistent with recent cryo-electron tomography experiments. We also found that Aβ40 oligomers were more likely to develop branches than Aβ42 oligomers, explaining an experimental observation that only Aβ40 was trapped in network-like aggregates and exhibited slower fibrillization kinetics. Moreover, AβO architecture dissection revealed that their curvilinear appearance is related to the local packing geometries of neighboring peptides and that Aβ40's greater branching ability originates from specific C-terminal interactions at branching interfaces. Finally, we demonstrate that whether Aβ oligomerization causes oligomers to elongate or to branch depends on the sizes and shapes of colliding aggregates. Collectively, this study provides bottom-up structural information for understanding early Aβ aggregation and AβO toxicity.
Introduction
The onset and development of Alzheimer's disease is widely believed to be linked with abnormal aggregation of amyloid-β peptides (Aβ).1 Aggregation of this peptide eventually leads to the formation of amyloid plaques in patients' brains and can also yield other intermediate aggregates, such as Aβ oligomers (AβOs). Evidence suggests that AβOs have key roles in Aβ's neurotoxicity, which has shifted biomedical research focus from amyloid plaques to AβOs.2,3 Aβs are comprised of various dynamically interconverting species differing in size, structure, biophysical properties, and toxicity,4,5 with certain types of AβOs, such as those with high molecular weight (HMW) (typically MW > 50 kDa), being particularly toxic.5–8 Knowledge about their structures and assembly pathways is crucial for understanding Aβ oligomerization mechanisms, the molecular basis of AβO toxicity, and its interplay with other aggregation diseases,9 based on which aggregation inhibition strategies may be designed.10,11 There are two major Aβ alloforms that contain 40 and 42 amino acids, respectively. Aβ42, which has two more amino acids at the C-terminus, oligomerizes more easily and is more neurotoxic.12,13 Comparing how the two alloforms oligomerize would further our understanding of AβO pathology.Aβ oligomerization has been difficult to characterize due to AβO metastability and heterogeneity. Several spectroscopic and imaging techniques have been applied14 but provided only low-resolution structural information, such as secondary structure contents, overall morphologies and, in some cases, the time evolution of these properties with low8,15,16 to medium resolutions.17,18 Intermediate-size and HMW AβOs that rapidly formed during early aggregation stages were found to assume spherical or elongated, curvilinear shapes,19–24 as well as annular structures.13,25–27 Recently, three-dimensional imaging of elongated AβOs with high-resolution cryo-electron tomography (cryoET) revealed that the curvilinear aggregates were more irregular than previously thought and exhibited branched structures.28 Despite these structural insights, it remains largely unclear how Aβ peptides are spatially organized within AβOs, how they are packed against each other, and how these structural properties are realized through self-assembly. Addressing these questions is key to elucidating AβO assembly mechanisms.
Molecular dynamic (MD) simulations are useful for deciphering the details of self-assembled supramolecular structures that are experimentally inaccessible.14,29,30 Both atomic and coarse-grained (CG) simulations have been applied to study small AβOs ranging from dimers to hexamers.14,31 Recently, Zheng et al. employed a CG model and the umbrella sampling technique to determine the octamer formation free energy surface from which fibrillar assembly pathways were inferred.32
Computational investigation of larger assembly systems is significantly more challenging due to the rapidly growing number of degrees of freedom that need to be sampled and analyzed.33 Only a few computational studies have employed CG models or atomic models in implicit solvent to probe the formation of AβOs containing more than ten full-length Aβ chains. These studies revealed the importance of hydrophobic and charged interactions for early oligomerization of Aβ40 and Aβ42,34,35 and demonstrated that AβOs with extended shapes have greater ability to aggregate than compact ones.36,37 Large AβOs of up to ∼20 chains were occasionally observed, but a thorough examination of the structures and assembly pathways of large AβOs has not been possible, probably due to insufficient sampling (e.g., a simulation length of 2–5 μs for assembly of each alloform) and the small number of chains (typically 20–30 chains) included in simulations, which does not considerably outnumber large AβO size.14
In this study, we performed extensive simulations of Aβ40 and Aβ42 oligomerization. For each alloform, we followed the aggregation of 100 interacting chains using 30 μs MD simulations with an efficient model that simplifies solvent representation but retains peptides' atomic details.38,39 This model has proven to be reliable in predicting native structures of several small proteins,38,39 determining the structures and assembly pathways of Aβ dimers,40,41 and elucidating the mechanisms of Aβ fibril growth.42 Moreover, graph networks43 were adopted to represent an AβO assembly hierarchy. This representation abstracts essential topological characteristics of nano-structured assembly, quantitatively describes an assembly hierarchy, and enables advanced graph theory to recognize structural patterns. It has been applied to self-assembly systems such as colloidal clusters, DNA-bricks, and metallic glasses to elucidate their assembly mechanisms.44–50 Here, we further developed a network decomposition algorithm to facilitate the understanding of assembly hierarchy.
With these computational techniques, we investigated the anatomy of early AβOs with sizes up to ∼20-mers. We found that these AβOs displayed curvilinear, irregular shapes with occasional lateral branches, consistent with AβO morphologies reported by recent cryo-ET experiments.28 Aβ40 oligomers were more likely to develop branches than Aβ42 oligomers, which may explain the tendency of Aβ40, but not Aβ42, to be trapped in network-like aggregates, as reported previously,20,25 potentially explaining the slower fibrillization kinetics of Aβ40. Our graph network analysis further revealed the molecular basis of the observed AβO morphologies and the difference in branching propensities between Aβ40 and Aβ42 oligomers. Finally, we found that Aβ elongation and lateral branching are affected by the topologies and geometries of interacting aggregates. Taken together, our atomistic simulations provide bottom-up structural information for elucidating AβO structures and the difference in early Aβ aggregation of the two alloforms.
Results
Sampling a dynamic equilibrium of early metastable Aβ oligomers using ten-microsecond simulations
To investigate early-stage Aβ40 and Aβ42 oligomerization, we performed simulations starting with 100 randomly dispersed and oriented peptide chains. The chain conformations were taken from monomeric state conformational ensembles (see Methods). For each alloform, we conducted two independent 15 μs-long simulations to enhance sampling of AβOs with large sizes. As shown in Fig. S1 in the ESI,† the AβO size distribution (n) evolved quickly during the early stage (t < ∼2 μs) of simulations from predominantly monomeric states to larger oligomers. Similar oligomer size evolution has also been reported in previous CG and atomic simulations on a time scale of 0.5–1 μs.34,36 The size distributions continued to evolve and reached a steady state after t = 5 μs. At this stage, the largest Aβ40 and Aβ42 oligomers observed were 27-mers and 33-mers, respectively. Dynamic oligomerization events during t = 5–15 μs were further analyzed. These results are presented in detail in the last part of the Results section; however, it should be noted that AβO association and dissociation were frequently observed at steady state (Fig. S2†). The numbers of these association and dissociation events were roughly equal, indicating that the observed steady distribution in oligomer size is an outcome of dynamic equilibrium between oligomeric species rather than certain trapped oligomeric states.Conformational dynamics of Aβ during t = 5–15 μs were also examined. Aβ monomers exhibited a significant amount of turn structures (43–47%) but few helical (2–3%) or β-sheet (14–15%) structures, which agrees with previous CD measurements and atomic simulations.51,52 Nonetheless, the conformational ensemble of Aβ monomers covers dynamically interconverted conformations varying in secondary and tertiary structures (Fig. S3†), including both the ones lacking in any helical or sheet structures observed also in previous simulations,53 and the partially folded ones with their helical and sheet contents up to ∼15% and ∼35%, respectively, some of which, such as multi-stranded conformations54 or conformations with a partial helix around the central region,55 have been reported experimentally.
Similar Aβ peptide secondary structural contents were also observed in oligomeric states, and there was no significant increase in β-sheet content with oligomer size (Table S1†). Thus, our observations most likely corresponded to disordered intermediates at the very early stage of the aggregation process preceding any slow conformational conversion needed for fibril pathways.56 The presence of such oligomeric intermediates has also been observed in recent microsecond atomistic simulations of Aβ oligomerization with implicit solvent36,37 and supported by experimental evidence for both small and large AβOs.57,58 Nonetheless, we did occasionally observed slow conformational change of Aβ's tertiary structures in oligomers based on our tertiary structural state analysis described in the ESI (Fig. S4†).59 In this analysis, we identified for Aβ40 and Aβ42 several major tertiary structural states, each of which is substantially different from the other in tertiary contact pattern. Based on how soon Aβ peptides in oligomers evolved from its current tertiary structural state into a different one in the simulations, we employed a two-state Poisson process model (see the ESI†)60,61 to estimate the timescale of global reconfiguration of these peptides. The reconfiguration timescales for Aβ40 and Aβ42 were calculated to be ∼66 ms and ∼39 ms, respectively. This result suggested that the observed oligomers rearranged their structures very slowly and may even be off the pathways. It has been shown that high Aβ concentrations retard fibrilization due to the rapid formation of off-pathway oligomers exhibiting high conversion barriers.62 This finding is corroborated with our result given that Aβ concentration in our simulations was rather high (3.9 mM). Regardless of whether these oligomers are on or off the pathways, their conversion timescales are far too long for our simulations.
Both Aβ40 and Aβ42 form flexible elongated oligomers with branches, but Aβ42 oligomers appear more extended and less branched
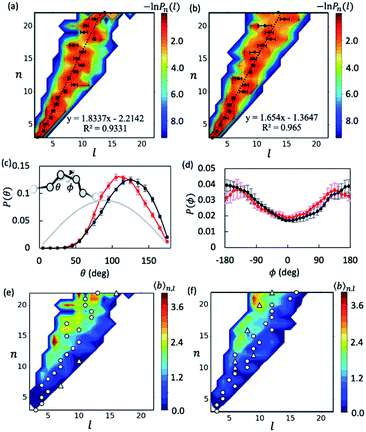
With the data collected from t = 5–15 μs of the simulations, we first examined the overall shapes of AβOs using topological networks. In these networks, nodes and edges indicate monomeric building blocks and their physical contacts, respectively.44,45,47,48,63 This representation allows us to quantitatively describe the global topological features of supramolecular structures. For instance, the longest dimension of a topological network can be measured with the network diameter, defined as the length (l) of the longest shortest path traversing the network. Fig. 1a and b show the diameter distributions Pn(l) with respect to oligomer size n. A wide oligomer diameter distribution was observed, especially for AβOs with large sizes, indicating that AβOs can assume distinct topologies varying in diameter. However, the average diameter![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) of oligomeric topologies grew linearly with n, suggesting that AβOs in general grow linearly and that there is an elongated backbone going across the entire oligomer.
of oligomeric topologies grew linearly with n, suggesting that AβOs in general grow linearly and that there is an elongated backbone going across the entire oligomer.
We then analyzed AβO backbone structures. An AβO backbone is thought to be comprised of the monomers present on the longest shortest path, as well as those in direct contact with the path (see Methods). If monomers have a spherical shape, the elongated structure formed by the monomers on the path should accommodate exactly one monomer in its cross-section. When additional monomers are attached laterally to the elongated structure without increasing its length l, the cross-section of the structure would on average accommodate more monomers. Thus, if there are m monomers included in the backbone, the m/l ratio corresponds to the average number of monomers that can be accommodated in the cross-section of the backbone, thereby providing an estimate of its thickness. As shown in Fig. S5a,† this ratio was calculated to be ∼1.3 for both Aβ40 and Aβ42 oligomers and remained largely constant with oligomer size. The average AβO thickness h was estimated according to h ≈ 2Rgm/l, where Rg = ∼1.0 nm is the average radius of gyration of an Aβ chain packed in oligomers. Our calculation indicated that AβOs are ∼2.6 nm in thickness, which roughly agrees with the diameter value (∼2.7 nm) reported in a recent cryo-ET study of large Aβ42 oligomers.28
We also examined AβO backbone geometries through conformational analysis of the longest shortest paths. These paths can be simplified as a string of beads with each bead representing the center of mass of each monomer. The AβO backbone conformations are thus defined by all three-bead angles θ and four-bead dihedral angles ϕ along the longest shortest paths. As shown in Fig. 1c, both Aβ40 and Aβ42 oligomers avoided a sharp θ angle (<60°) in their backbone parts, probably due to the exclusion of self-volume. The dihedral angle ϕ distributions (Fig. 1d) were flat with a 60%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40% ratio of anti-conformations (|ϕ| > 90°) to syn-conformations (|ϕ| < 90°). Thus, the AβO backbone conformations observed here largely resemble those of a freely rotating chain that has a large rotational isomerism and high conformational flexibility. This may explain why AβOs have been reported to be highly curvilinear and irregular.28 Despite the flexibility of both types of AβOs, we found that Aβ42 oligomers were more extended than Aβ40 oligomers, as indicated by a larger Flory's characteristic ratio C∞ of Aβ42 oligomers (3.01 ± 0.21 versus 1.95 ± 0.23) (see the ESI and Fig. S5b†). For a freely rotating chain, its characteristic ratio can be related to the local angle θ by C∞ = (1 − cos
40% ratio of anti-conformations (|ϕ| > 90°) to syn-conformations (|ϕ| < 90°). Thus, the AβO backbone conformations observed here largely resemble those of a freely rotating chain that has a large rotational isomerism and high conformational flexibility. This may explain why AβOs have been reported to be highly curvilinear and irregular.28 Despite the flexibility of both types of AβOs, we found that Aβ42 oligomers were more extended than Aβ40 oligomers, as indicated by a larger Flory's characteristic ratio C∞ of Aβ42 oligomers (3.01 ± 0.21 versus 1.95 ± 0.23) (see the ESI and Fig. S5b†). For a freely rotating chain, its characteristic ratio can be related to the local angle θ by C∞ = (1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/(1 + cos
θ)/(1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). Based on this relationship, we predicted that the C∞ of Aβ42 oligomers is indeed larger than that of Aβ40 (3.00 versus 2.28), since on average Aβ42 oligomers have a wider θ angle (∼120° versus ∼113°). This prediction is largely in accord with our C∞ calculation.
θ). Based on this relationship, we predicted that the C∞ of Aβ42 oligomers is indeed larger than that of Aβ40 (3.00 versus 2.28), since on average Aβ42 oligomers have a wider θ angle (∼120° versus ∼113°). This prediction is largely in accord with our C∞ calculation.
Inspecting representative oligomeric structures revealed further AβO branching structure, especially in AβOs with large size (n > ∼10) (Fig. 2). Intriguingly, branched morphologies of large AβOs have recently been reported in several studies using advanced imaging techniques such as high-resolution AFM, solution TEM, and cryo-ET.20,25,28 We evaluated the degree of branching in AβOs by counting the number of branches (b) present in these oligomers. This quantity was calculated by finding disconnected components after the entire backbone part was removed from the topological networks.
Fig. 1e and f show plots of the average number of branches ![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) (n, l) present in AβOs as a function of oligomer size n and backbone length l. As expected, AβOs with larger size and shorter backbones are more likely to have branches. With a given oligomer size and a given backbone length, Aβ40 oligomers contain more branches than Aβ42 oligomers on average (Fig. 1e and f). This difference in branch structure is further exemplified by comparing representative Aβ40 and Aβ42 oligomer structures with select n and l values (Fig. 2a and cversus2b and d). On average, there are 0.6 ± 0.1 and 0.4 ± 0.1 branches in mid-sized AβOs (n = 11–15) formed by Aβ40 and Aβ42, respectively. In larger AβOs (n = 16–22), Aβ40 oligomers developed twice as many branches as Aβ42 oligomers (1.4 ± 0.1 versus 0.7 ± 0.2 branches). Thus, our results suggest that Aβ40 has a greater tendency to form branched structures than Aβ42 when assembled into large oligomers.
(n, l) present in AβOs as a function of oligomer size n and backbone length l. As expected, AβOs with larger size and shorter backbones are more likely to have branches. With a given oligomer size and a given backbone length, Aβ40 oligomers contain more branches than Aβ42 oligomers on average (Fig. 1e and f). This difference in branch structure is further exemplified by comparing representative Aβ40 and Aβ42 oligomer structures with select n and l values (Fig. 2a and cversus2b and d). On average, there are 0.6 ± 0.1 and 0.4 ± 0.1 branches in mid-sized AβOs (n = 11–15) formed by Aβ40 and Aβ42, respectively. In larger AβOs (n = 16–22), Aβ40 oligomers developed twice as many branches as Aβ42 oligomers (1.4 ± 0.1 versus 0.7 ± 0.2 branches). Thus, our results suggest that Aβ40 has a greater tendency to form branched structures than Aβ42 when assembled into large oligomers.
Observed Aβ oligomer mass distributions and cross collision-section areas agree with previous experimental results
To assess the relevance of our AβO observations to those reported experimentally, we first calculated the mass distribution of AβOs that have been extensively characterized in experiments. Nevertheless, our simulations were conducted at 3.9 mM, a concentration much higher than normal experimental condition for characterizing the AβO mass distribution. Following Kindt et al.,64,65 the oligomer particle densities ρn derived from the simulations were used to parameterize a model of non-interacting aggregates with which one can obtain the AβO partition functions q0n (Fig. S6a†) and thereby determine their mass distributions at any given peptide concentration. We paid attention to the oligomer mass distribution at two particular concentrations, a lower one at 30 μM and a higher one at 200 μM. At both concentrations, the mass distribution of AβO has been probed experimentally.57,66 At 30 μM, Aβ40 and Aβ42 monomers, dimers, and trimers were predicted to be the major species, and their probabilities were close to what has been reported at the same concentration in ion-mobility mass-spectroscopy (IM-MS) experiments (Table 1).57 At 200 μM, oligomers up to 15-mer were predicted to exist for both alloforms with a nonnegligible probability (>0.01), which agrees with another IM-MS experiment conducted at the same peptide concentration.66 At the two concentrations, Aβ42 11-mers to 15-mers were two to four times more probable than those of Aβ40, also in accord with previous experimental observation.67 For AβOs of even larger sizes (n ≥ 15), there was a linear correlation between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) q0(n) and n (Fig. S6b†), indicating the existence of a critical oligomer concentration (COC) for early metastable AβOs.24
q0(n) and n (Fig. S6b†), indicating the existence of a critical oligomer concentration (COC) for early metastable AβOs.24
| n | Aβ40 | Aβ42 | ||||
|---|---|---|---|---|---|---|
| 30 μMa | 200 μM | Exptb | 30 μM | 200 μM | Exptb | |
| a Monomer concentration at which the mass distributions were calculated. b Obtained from the IM-MS experiment carried out at 30 μM peptide concentration.57 | ||||||
| 1 | 0.71 | 0.11 | ∼0.61 | 0.60 | 8.2 × 10−2 | ∼0.59 |
| 2 | 0.25 | 0.29 | ∼0.19 | 0.36 | 0.37 | ∼0.22 |
| 3 | 3.4 × 10−2 | 0.30 | ∼0.11 | 2.9 × 10−2 | 0.22 | ∼0.11 |
| 4 | 1.9 × 10−3 | 0.13 | ∼4.0 × 10−2 | 1.9 × 10−3 | 0.11 | ∼4.2 × 10−2 |
| 5–10 | 1.3 × 10−4 | 0.17 | — | 1.7 × 10−4 | 0.14 | — |
| 11–15 | 6.9 × 10−11 | 1.1 × 10−2 | — | 2.2 × 10−10 | 6.3 × 10−2 | — |
| >15 | 5.8 × 10−14 | 5.4 × 10−4 | — | 2.4 × 10−14 | 1.2 × 10−2 | — |
Of note, the COCs of Aβ40 and Aβ42 were predicted based on our statistical mechanical model to be about 500 μM and 300 μM, respectively. We also calculated the COC using reported average monomer density from previous large scale simulations (cf.Fig. 1 in ref. 34 and Fig. 3a in ref. 36). Our COCs are comparable to the ones (COC40 = ∼370 μM, COC42 = ∼210 μM) derived based on the study of Urbanc et al.34 using CG models but larger than those (COC40 = ∼54 μM, COC42 = ∼46 μM) based on the study of Barz et al.36 using atomistic peptide models in implicit solvent. Several experimental studies using different characterization techniques reported 18–50 μM COCs for Aβ40.68–70 Hence, the COC of Aβ40 can be reproduced with the atomic simulations in implicit solvent but appeared somewhat overestimated in the simulations by Urbanc et al. and by us. The critical concentration of some prefibrillar aggregates of Aβ42 was determined in a more recent study to be 90 nM,71 significantly lower than the COC measured for Aβ40 or derived based on any of the above simulations. As such, these Aβ42 aggregates were highly stable. The thermodynamic stability of protein aggregates is governed by their structures. It has been suggested24 that for aggregation-prone proteins including Aβ, β sheet-rich aggregates such as fibrils assembled through strong intermolecular hydrogen bonding (HB) are normally more stable and have a lower critical concentration than early aggregates induced by amphiphilic character of polypeptide chains.72 As the stability of the Aβ42 prefibrillar aggregates probed in that study even rivals that of Aβ40/42 fibrillar aggregates whose critical concentrations are 100–200 nM,73,74 these aggregates may already develop a considerable β-sheet character, stabilized largely by intermolecular HBs. Conversely, the Aβ oligomers observed here, which have not undergone conformational conversion yet, exhibit low β-sheet contents (14–15%), and their incorporation of each new monomer brings about only ∼2.5 additional interchain HBs. This structural difference between the aggregates probed in the experiment study and our simulations may explain the large difference between the measured and simulated critical concentrations of Aβ42.
We also examined the collision cross-section (CCS) values of low order oligomers, a quantity related to the overall AβO shapes that has been carefully characterized in IM-MS experiments.57,66,67 As described in Methods, the oligomer structures taken from solution simulations were relaxed in gas phase and their protonation states were properly adjusted to be consistent with experimental conditions reported by Bernstein et al.67 The average CCS values agreed reasonably well with the experimental data, with a better agreement observed for Aβ40 than for Aβ42 (Table S2†). Compared to the data reported by Berstein et al., our Aβ42 tetramer CCS value was underestimated by ∼200 Å2, but agreed better with the CCS value reported more recently by Zhang et al. (2100 Å2versus 2172 Å2).75 Despite the deviation from these experimental data, our calculations revealed that the CCS values of Aβ42 dimers to hexamers are always greater than those of Aβ40, suggesting that low order Aβ42 oligomers tend to be more “open” than those of Aβ40. This trend is consistent with our characteristic ratio calculations, as well as previous experiments and atomistic simulations.36,67
Early Aβ oligomer internal topological networks consist of a mixture of line and small cyclic fragments organized in favor of elongated morphologies
Having validated our observations of AβOs, we proceeded to analyze molecular arrangements within the oligomers. In the graph network representation framework each network represents a possible arrangement of monomers within an oligomer. The molecular arrangement pattern could be identified from the most representative networks. Using a network clustering algorithm that considers particle labelling degeneracy (see Methods),44,45,63 we examined the nonisomorphic arrangements of AβOs sampled in our simulations (Fig. S7†).There are two theoretically possible trimer arrangements, a linear arrangement and a triangular one, and we observed both with similar chance (Fig. S7†). We also sampled all six and 18 possible arrangements of monomers in tetramers and pentamers, respectively, but only three tetrameric arrangements and five pentameric arrangements were populated with a combined probability >0.9, indicating that only certain types of molecular arrangements are preferred in these oligomers. For larger AβOs, the number of preferred arrangements grows exponentially with oligomer size, but these arrangements account for only a small fraction (e.g., 5–6 × 10−2 for n = 6 and 2–4 × 10−6 for n = 10) of all those theoretically allowed (Fig. S8†),44 indicating that large oligomers formed by Aβ40 and Aβ42 can only access a tiny fraction of the theoretical topological space.
Despite their topological heterogeneity, our inspection of representative topological networks indicated that AβOs exhibit topological networks that appear to be made of structural elements including line segments and triangles (Fig. S7†). The triangular rings are either separated in the networks or share common nodes or edges. Bigger rings containing more than three nodes were also observed, but their probability of occurrence decays fast as ring size grows (Fig. S9†).
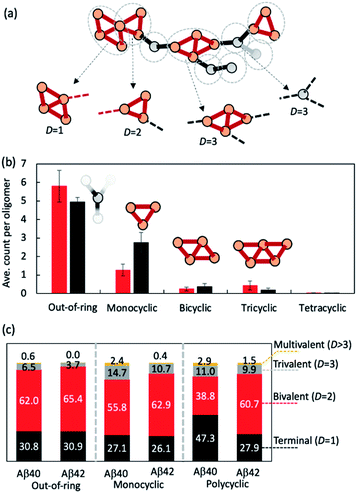
We then investigated how the line segments and triangle rings are organized to form elongated oligomeric morphologies. To this end, we developed an algorithm that decomposes the topological networks into basic building fragments. This algorithm is described in the Methods and illustrated in Fig. 3a. It identifies three building fragment types, namely nodes that do not belong to any ring structures (thus termed ‘out-of-ring nodes’), monocyclic fragments that do not share any edge with other rings, and fused polycyclic fragments whose cyclic members have common edges with one another.
Fig. 3b shows the average count of each type of building fragment present in large Aβ40 or Aβ42 oligomers (n > 10). For both alloforms, the out-of-ring nodes are the most frequently observed fragment types (with 5–6 such nodes per oligomer). The chance of observing a monocyclic fragment is 1/3–1/2 of that of out-of-ring nodes. The probability of observing fused polycyclic fragments is further reduced. There is a noticeable difference in fragment compositions of Aβ40 and Aβ42 oligomers. There are ∼20% more out-of-ring nodes in Aβ40 oligomers than in Aβ42 oligomers, but Aβ42 oligomers harbor twice as many monocyclic fragments as Aβ40 oligomers. This suggests that although both Aβ40 and Aβ42 can form oligomers with similar elongated shapes, the underlying pattern of molecular arrangement is not the same.
Because topological features of supramolecular assemblies are linked closely with the coordination behaviors of underlying building blocks,46,47,49 we examined the coordination properties of the building fragments identified above. A key coordination property is the coordination number D, defined here as the number of linkages between a fragment and the remaining part of the network (see Methods). Building fragments with a single linkage (D = 1) form network termini. Those with a bivalent coordination (D = 2) can only elongate the networks and, therefore, are necessary for elongated topology formation. Fragments with a trivalent coordination (D = 3) will cause the network to bifurcate, and those with higher coordination numbers (D > 3) could form even more complex network structures. Therefore, an elongated network must be composed predominantly of monovalent and bivalent fragments.
Fig. 3c compares the coordination propensities of the three building fragment types. In general, all three types are most likely coordinated with two neighbours and have a rather low chance (<∼15%) of being coordinated with more than two. Out-of-ring nodes are less likely to interact with more than two neighbours compared with the other two types. The prevalence of bivalent fragments in the AβO topological networks explains why AβOs normally prefer elongated topologies. Of note, Aβ40 always has a greater tendency to form fragments with large coordination umbers (D ≥ 3) compared with Aβ42 (Fig. 3c), which corroborates our finding that Aβ40 oligomers are more likely to branch than Aβ42 oligomers.
Greater Aβ40 oligomer branching propensity is attributed to the ability of Aβ40 to form strong C-terminal hydrophobic interactions at branching interfaces
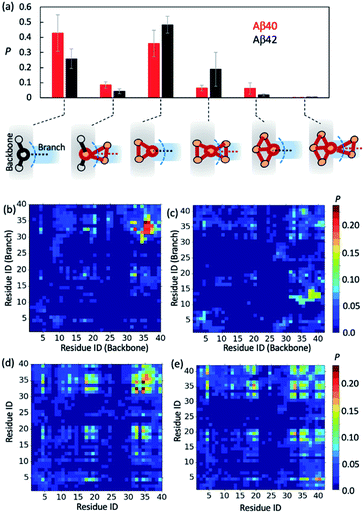
To further gain insights into AβO branching propensity, we focused our analysis on where these oligomers branched. Because a branch is an extension in different directions from an oligomer backbone part, the nature of branch and backbone interfaces is key to understanding AβO branching propensity. We thus analyzed branching interfaces in the topological networks. Our results showed that these interfaces were formed mainly through interactions between a single node from the branch and an out-of-ring node from the topological network backbone or a backbone node that belongs only to a single ring (Fig. 4a). The former type of interface is more favored by Aβ40 oligomers (∼40%) and the latter one is more favored by Aβ42 oligomers (∼50%). In addition, about 20% of branching interfaces in Aβ42 oligomers consist of a backbone node and two branch nodes in a triangular arrangement.To understand why Aβ40 oligomers exhibit a greater branching propensity, we analyzed the inter-chain residual contacts formed at branching interfaces. The resulting contact probability maps (Fig. 4b and c) showed that at Aβ40 oligomer branching points, the backbone peptide mainly used its L34–G37 region to contact the I31–L34 region of its neighbor. The probabilities of these contacts were mostly >0.2. In contrast, interfaces at Aβ42 oligomer branching points were formed between the G37–V40 and V12–H14 regions of the peptides from the backbone and the branch, respectively, with a lower probability (0.1–0.15). This result suggests that the greater tendency of Aβ40 oligomers to branch is likely attributed to the ability of Aβ40 to form stronger C-terminal hydrophobic interactions at branching interfaces.
Regardless of their locations in oligomers, both Aβ40 and Aβ42 can form extensive contacts with their neighbors (Fig. 4d and e), mainly using their central region L17–F21 and C-terminal region I31–V39/I41. Previous nuclear magnetic resonance (NMR) studies as well as simulations also revealed that the similar regions of both Aβ alloforms participated in the initial docking of monomers to early Aβ aggregates.41,76–78 A different docking region, namely F19–N27, was recently reported by Brender et al.,79 but it was found to recognize fibrils that are structurally different from AβOs observed here. In addition, for both alloforms, the aromatic residues such as F4, F19 and F20 were involved heavily in hydrophobic interactions but direct intermolecular contacts between aromatic residues were infrequent (with an average chance of <0.15, Fig. S10†), suggesting that the aromatic π–π interactions might not be crucial to early oligomer formation, as opposed to their reported role in fibril formation.80 Overall, the average intermolecular contact patterns of Aβ40 and Aβ42 are markedly different from the ones observed at branching interfaces. On average Aβ42 can form more interchain residual contacts than Aβ40 (24.8 contacts versus 23.2 contacts), largely due to additional interactions associated with V40–A42 of Aβ42 (Fig. S10†). This is opposite to the observed tendencies of the two alloforms to form interchain interactions at branching interfaces but in line with the general notion that Aβ42 has a greater ability to form intermolecular interactions due to its enhanced hydrophobicity by I41 and A42. Taken together, the above results indicate that the difference in branching contact patterns between Aβ40 and Aβ42 cannot be explained based only on their average contact propensity.
As a polypeptide segment involved too much with intramolecular contacts can be hindered from intermolecular contacts, we thus examined intramolecular tertiary contacts in Aβ40 and Aβ42 to seek clues to the different contact propensity at branching interfaces between the two alloforms. In particular, the tertiary contacts involving the C-terminal region of Aβ were carefully analyzed since Aβ40, but not Aβ42, can use this region to form extensive hydrophobic interactions at branching interfaces. As shown in Fig. S11a and b,† Aβ42 is more likely to form a C-terminal reversed loop than Aβ40. This loop is centered at V36–G37 and promoted by intramolecular interactions involving V39–I41, a structural feature of Aβ42 monomers reported previously in NMR and MD studies.81 At branching interfaces, Aβ42 was observed to lose more intramolecular contacts in its C-terminal region than Aβ40 (−2.3 versus −0.9 residual contacts) when it needs to use this region to form substantial intermolecular contacts (≥5.0 residual contacts) (Fig. S11c and d†). In other words, Aβ42 needs to disrupt its C-terminal tertiary structure to a greater extent to form C-terminal intermolecular interactions at branching interfaces. Therefore, the stronger tendency of Aβ40 to form interchain C-terminal interactions at branching interfaces is a special coordination property of Aβ40, probably due to its lesser tendency to form loop or turn structures at its C-terminus.
Oligomer elongation and branching are affected by their size and shape
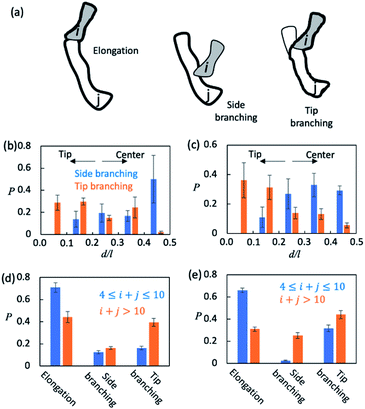
Finally, we sought to understand how AβOs elongated themselves or developed branches. We first monitored the association events that took place during the simulation period t ∈ [5 μs, 15 μs] (see Method). There were ∼2.5 × 104 total association events each for Aβ40 and Aβ42, during most of which the resulting initial binding complexes quickly dissociated within ∼1–2 ns and failed to generate metastable AβOs. Only a fraction (∼0.04) of the events led to the formation of firmly bound complexes. The initial binding was stabilized mainly by electrostatic interactions (0.9–1.0 salt bridges) involving Aβ's N-terminal regions and, to a lesser extent, by non-specific hydrophobic interactions (0.3–0.4 contacts). In most cases (>0.97), there was only a single Aβ from each colliding aggregate that participated in the binding interfaces. Hence, the ring structures in topological networks did not arise from the association events but instead were formed through the internal structural rearrangement of AβOs.We then monitored the change in the backbone length (l) and the number of branches (b) in topological networks after each association event (see the ESI†). An increase in l indicates elongation of oligomers and an increase in b indicates the formation of new side branches (Fig. 5a). Intriguingly, we also observed events in which both l and b increased. These events involved the attachment of a monomer/oligomer to a site near a second oligomer's backbone tips, unlike the side branching events in which the attachment point was close to the center of the second oligomer's backbone (Fig. 5b and c). As these events effectively caused the newly formed oligomers to bifurcate at its tip, they were henceforth termed tip branching.
We counted the elongation and side/tip branching occurrence frequencies. As shown in Fig. 5d and e, AβOs with relatively small sizes (4 ≤ n ≤ 10) were mainly formed via elongation at a chance of 60–70%. On the other hand, larger AβOs (n > 10) were formed more often via side or tip branching. This observation is expected since AβOs exhibit a linear topology that can only elongate at its tips, but new branches can be developed from any other AβO part. In addition, tip branching is the preferred branching mode for both Aβ40 and Aβ42 oligomers, especially when their sizes are large (n > 10). We attributed this preference for tip branching mode to the curvilinear shapes of AβOs whose center parts are likely less accessible, a disadvantage to side branching. Moreover, the ratios of tip branching events to side branching events were ∼2.5 and ∼1.8 for Aβ40 and Aβ42 oligomers, respectively, indicating that side branching is even less favored by Aβ40 oligomers. This finding is consistent with our characteristic ratio calculation which showed that Aβ40 oligomer shapes are more curvilinear and compact (Fig. S5b†). Taken together, our results suggest that both AβO elongation and branching can be affected by oligomeric topologies and geometries.
Discussion
In summary, we used computer simulations to reveal the anatomy of early Aβ oligomer (AβO) aggregates. These AβOs had curvilinear morphologies, consistent with experimental reports.28 Of particular interest is our observation that AβOs could occasionally develop branched structures, with larger sized oligomers (e.g., n > 15) having a greater branching tendency. There have been several reports of oligomer branching for both Aβ40 and Aβ42 using imaging techniques such as AFM82 and, more recently, liquid-state TEM,20 as well as high-resolution cryo-ET.28 Especially considering their curvilinear, irregular appearance and assembly thickness, the oligomeric species observed here most likely represent one type of early AβO that was reported in the cryo-ET study.28 Although previous atomistic and CG simulations of systems containing 20–30 full-length Aβ chains permitted for the observation of large oligomers (n ≈ 20) with linear topologies,34,36 our simulations of 100 chain-containing systems allowed us to observe AβO branching. Lateral branching was also observed in recent studies of shorter peptide fragment (2–7 amino acids) self-assembly through simulations of hundreds of interacting peptides.83–85 These studies, together with ours, highlight the need to include enough peptide chains in self-assembly simulations to observe events like oligomer branching, which takes place on a longer length scale than small oligomer formation.86,87We have elucidated how Aβ coordination properties dictate topological and geometric features of resulting AβOs. We found that in AβOs, Aβ peptides with low coordination numbers tend to form AβO's linear parts while those with high coordination numbers tend to form cyclic (mostly triangular ring) or fused polycyclic fragments, which on their own can be deemed as building blocks that were predominantly bivalent. AβOs, being composed of primarily bivalent building blocks, thereby prefer elongated topologies. The adjacent Aβ peptides along the elongated AβO backbones exhibited no clear preference for any rotational isomeric arrangement, indicating that the AβOs are expected to behave like a freely rotating chain that is characterized by its floppy appearance, consistent with what was observed experimentally. We also found that the more extended Aβ42 oligomer shapes (compared to Aβ40 oligomers), which has been reported experimentally and computationally,36,67 could largely be attributed to a larger bond angle formed by every three consecutive monomers along the Aβ42 oligomer backbone.
Of particular interest is our finding that Aβ40 oligomers are more likely to branch than Aβ42 oligomers. The growth of branches from linear aggregates is one of the important ways of cross-linking linear aggregates, which leads to the formation of fibrous network structures required for gelation.86,87 Although the formation of gels by Aβ has never been reported, both AFM and liquid-state TEM experiments have confirmed that Aβ40, but not Aβ42, could form network-like early aggregates.20,25 These findings corroborate our observation that Aβ40 oligomers have greater branching propensity. The network-like aggregates appeared kinetically stable20,25 and may be off the fibril pathway,56,88 which could explain in part why Aβ40 fibrilization kinetics are slower than Aβ42.12 Furthermore, we ascribe the greater branching ability of Aβ40 peptides to the formation of strong hydrophobic interactions between the C-terminal parts of the peptides at branching interfaces (Fig. 4b). Conversely, Aβ42 does not exhibit such strong interchain interactions at these interfaces (Fig. 4c) even though in oligomeric states, on average, Aβ42 can form stronger interactions with its neighbors than Aβ40 (Fig. 4d and e). It seems that C-terminal turn structure formation in Aβ42, but not in Aβ40 (Fig. S11†), prevented strong contacts formed between the C-terminal parts of the peptides at early stage, a consequence of competition between intramolecular and intermolecular interactions. These findings raise the possibility of redirecting early assembly processes either away from or toward the formation of branched or network-like aggregates by targeting those specific C-terminal interactions that are essential for oligomer branching. This prediction awaits further experimental and computational assessment.
Materials and methods
Model setup and simulation details
The PACE force field (version 1.4, https://github.com/hanlab-pkusz/hanlab/tree/master/PACE%20for%20GROMACS) was used for all simulations.39 It couples a united-atom peptide model with explicit coarse-grained solvent. The details of PACE and its parameterization can be found in ref. 38 and 39 PACE, as used here, has proven to be accurate in reproducing experimental observations of Aβ aggregation, including Aβ monomer 3J-coupling constants,42 Aβ42 dimer rupture force and distance patterns,40 Aβ17–42 fibril growth thermodynamics and kinetics,42 and the affinity of Aβ40 fibrils for peptides.89,90 For both Aβ40 and Aβ42, 100 peptide chains were randomly dispersed and orientated in a 35 × 35 × 35 nm3 box containing CG water particles and neutralized and buffered with a 0.15 M NaCl solution. Initial chain conformations were randomly taken from 700 ns replica of Aβ40/42 monomer exchange molecular dynamic (REMD) simulations. Of note, for each alloform, two independent self-assembly simulations were performed, each starting with a distinct set of conformations randomly selected from the pool of disordered or partially folded ones (Fig. S3†). As shown in Fig. S12,† for both alloforms, the two simulations yielded vary similar results, all consistent with the main findings of the present study including the linear growth of AβOs with their size, a more extended shape of large AβO42, and a greater branching propensity of large AβO40, indicating that our findings are independent of initial monomer conformations used.There were 24 replicas at temperatures of 310–450 K in each REMD simulation. Exchange was attempted every 2 ps and accepted with a probability ∼30%. All simulation systems were first energy minimized for 5000 steps, followed by 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps of pre-equilibrium simulations with heavy atoms being restrained before production runs. Self-assembly simulations were conducted at 1 atm and 310 K. Simulation timestep was set to 4.5 fs, a typical value used in PACE simulations.38,39 GROMACS software (version 5) was used to conduct the simulations mentioned above.
000 steps of pre-equilibrium simulations with heavy atoms being restrained before production runs. Self-assembly simulations were conducted at 1 atm and 310 K. Simulation timestep was set to 4.5 fs, a typical value used in PACE simulations.38,39 GROMACS software (version 5) was used to conduct the simulations mentioned above.
To calculate the CCS values of a given oligomeric structure, we first estimated the pKa values of all titratable groups with PROPKA.91,92 Those groups with the highest pKa were protonated such that the oligomer charge states were adjusted to those reported experimentally.67 The structure was energy-minimized in gas phase with PACE for 5000 steps each, and its CCS value was calculated using the trajectory method93,94 implemented in the IMPACT software.95
Graph network analysis of topological networks
The topology of an oligomer of size n can be described by a graph G(V, E), where V are nodes, each representing one monomer, and E are edges of connecting nodes. Two nodes are connected by an edge if not less than 10 pairs of atoms from the corresponding monomers are closer to each other than 0.45 nm. The longest shortest path of G was detected by first identifying the shortest paths between any pair of nodes via the breadth-first search and then choosing the longest one. All ring substructures in G were identified through a depth-first search excluding those containing shortcuts, followed by the removal of redundancies using a bookkeeping list.To decompose a topological graph G, we first constructed an auxiliary graph G′ whose nodes denote rings found in G and connectivity indicates whether rings share edges. Each disconnected component of G′ corresponds to a monocyclic or polycyclic fragment. Any ring fragment sharing at least one edge with the longest shortest path was considered to belong to the backbone part of an oligomer. The coordination number of a building fragment was the summation of the coordination numbers of all its nodes. Of note, a direct coordination with another ring fragment is only counted as a single coordination (red dashed lines in Fig. 2a) as ring structures are closed.
The similarity between two topological networks GA and GB was measured with a score Q expressed as follows
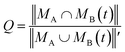 | (1) |
Mass distribution calculation
Considering a system of N peptide chains in a volume V that can form various clusters, there will be different partitions of the system into clusters, each of which must satisfy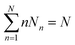 , where Nn is the count of clusters of size n. Assuming that the system is ideal, the total partition function of the system can be written as64
, where Nn is the count of clusters of size n. Assuming that the system is ideal, the total partition function of the system can be written as64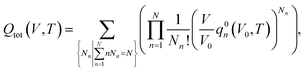 | (2) |
Now let ρn be the equilibrium density of n-mers in unit ρ0. For a system with infinite peptide chains, 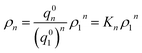 , where Kn is the equilibrium constant of the formation of n-mers. Thus, the mass percentage of n-mers can be expressed as a function of monomer concentration ρ1, i.e.,
, where Kn is the equilibrium constant of the formation of n-mers. Thus, the mass percentage of n-mers can be expressed as a function of monomer concentration ρ1, i.e.,
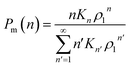 | (3) |
Of note, the estimation of Kn with q0n is not reliable for large n due to insufficient sampling. Instead, they were extrapolated according to an apparent linear relationship between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) q0n and n for n ≥ 20 (Fig. S6b†).
q0n and n for n ≥ 20 (Fig. S6b†).
Detection of association and dissociation events
The association events and dissociation events that took place between t and t + dt were identified with an algorithm illustrated in Fig. S13.† We first determined the oligomerization status of the systems at two time points based on peptide chain contact status. Two unbound peptide chains were thought to form a contact if they have no less than 10 pairs of atoms within 0.45 nm and, thereafter, they remain in contact unless the minimum atomic distance between them is beyond 0.45 nm. This approach avoids considering oligomer reorganization as dissociation.96 We constructed a graph whose nodes represent oligomers from either frame t or frame t + dt, and two nodes from different frames can be connected if they share the same peptide chains. Each node from frame t with more than one linkage indicates a dissociation event and each node from t + dt with more than one linkage indicates an association event. Starting from an association event, we constructed an event tree of four subsequent association/dissociation events. If at any point of the event tree the dissociated oligomers were identical to one of the original two, the original association event was thought to be nonreactive.Author contributions
M. Y. performed the computational experiments. M. Y., X. T. and W. H. analyzed the data. W. H. designed and supervised the research. M. Y. and W. H. wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank financial supports from the National Science Foundation of China (grant no. 21977011) and the Shenzhen Fundamental Research Program (grant no. GXWD20201231165807007-20200827170132001).Notes and references
- J. Hardy and D. J. Selkoe, Science, 2002, 297, 353–356 CrossRef CAS PubMed.
- E. Y. Hayden and D. B. Teplow, Alzheimer's Res. Ther., 2013, 5, 60 CrossRef PubMed.
- D. J. Selkoe and J. Hardy, EMBO Mol. Med., 2016, 8, 595–608 CrossRef CAS PubMed.
- I. Benilova, E. Karran and B. De Strooper, Nat. Neurosci., 2012, 15, 349–357 CrossRef CAS PubMed.
- E. N. Cline, M. A. Bicca, K. L. Viola and W. L. Klein, J. Alzheimer's Dis., 2018, 64, S567–s610 CAS.
- P. T. Velasco, M. C. Heffern, A. Sebollela, I. A. Popova, P. N. Lacor, K. B. Lee, X. Sun, B. N. Tiano, K. L. Viola, A. L. Eckermann, T. J. Meade and W. L. Klein, ACS Chem. Neurosci., 2012, 3, 972–981 CrossRef CAS PubMed.
- P. Liu, M. N. Reed, L. A. Kotilinek, M. K. Grant, C. L. Forster, W. Qiang, S. L. Shapiro, J. H. Reichl, A. C. Chiang, J. L. Jankowsky, C. M. Wilmot, J. P. Cleary, K. R. Zahs and K. H. Ashe, Cell Rep., 2015, 11, 1760–1771 CrossRef CAS PubMed.
- T. Watanabe-Nakayama, K. Ono, M. Itami, R. Takahashi, D. B. Teplow and M. Yamada, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5835–5840 CrossRef CAS PubMed.
- M. I. Ivanova, Y. Lin, Y. H. Lee, J. Zheng and A. Ramamoorthy, Biophys. Chem., 2021, 269, 106507 CrossRef CAS PubMed.
- S. Sharma, P. Modi, G. Sharma and S. Deep, Biophys. Chem., 2021, 278, 106665 CrossRef CAS PubMed.
- G. J. Morgan, Biophys. Chem., 2022, 281, 106711 CrossRef CAS PubMed.
- R. Jakob-Roetne and H. Jacobsen, Angew. Chem., Int. Ed., 2009, 48, 3030–3059 CrossRef CAS PubMed.
- D. C. Bode, M. D. Baker and J. H. Viles, J. Biol. Chem., 2017, 292, 1404–1413 CrossRef CAS PubMed.
- P. H. Nguyen, A. Ramamoorthy, B. R. Sahoo, J. Zheng, P. Faller, J. E. Straub, L. Dominguez, J. E. Shea, N. V. Dokholyan, A. De Simone, B. Ma, R. Nussinov, S. Najafi, S. T. Ngo, A. Loquet, M. Chiricotto, P. Ganguly, J. McCarty, M. S. Li, C. Hall, Y. Wang, Y. Miller, S. Melchionna, B. Habenstein, S. Timr, J. Chen, B. Hnath, B. Strodel, R. Kayed, S. Lesné, G. Wei, F. Sterpone, A. J. Doig and P. Derreumaux, Chem. Rev., 2021, 121, 2545–2647 CrossRef CAS PubMed.
- L. Feng, H. Watanabe, P. Molino, G. G. Wallace, S. L. Phung, T. Uchihashi and M. J. Higgins, J. Mol. Biol., 2019, 431, 2687–2699 CrossRef CAS PubMed.
- S. Banerjee, Z. Sun, E. Y. Hayden, D. B. Teplow and Y. L. Lyubchenko, ACS Nano, 2017, 11, 12202–12209 CrossRef CAS PubMed.
- E. E. Cawood, T. K. Karamanos, A. J. Wilson and S. E. Radford, Biophys. Chem., 2021, 268, 106505 CrossRef CAS PubMed.
- B. R. Sahoo, S. J. Cox and A. Ramamoorthy, Chem. Commun., 2020, 56, 4627–4639 RSC.
- I. A. Mastrangelo, M. Ahmed, T. Sato, W. Liu, C. Wang, P. Hough and S. O. Smith, J. Mol. Biol., 2006, 358, 106–119 CrossRef CAS PubMed.
- K. Nakajima, T. Yamazaki, Y. Kimura, M. So, Y. Goto and H. Ogi, J. Phys. Chem. Lett., 2020, 11, 6176–6184 CrossRef CAS PubMed.
- B. A. Chromy, R. J. Nowak, M. P. Lambert, K. L. Viola, L. Chang, P. T. Velasco, B. W. Jones, S. J. Fernandez, P. N. Lacor, P. Horowitz, C. E. Finch, G. A. Krafft and W. L. Klein, Biochemistry, 2003, 42, 12749–12760 CrossRef CAS PubMed.
- M. P. Lambert, A. K. Barlow, B. A. Chromy, C. Edwards, R. Freed, M. Liosatos, T. E. Morgan, I. Rozovsky, B. Trommer, K. L. Viola, P. Wals, C. Zhang, C. E. Finch, G. A. Krafft and W. L. Klein, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 6448–6453 CrossRef CAS PubMed.
- D. M. Walsh, D. M. Hartley, Y. Kusumoto, Y. Fezoui, M. M. Condron, A. Lomakin, G. B. Benedek, D. J. Selkoe and D. B. Teplow, J. Biol. Chem., 1999, 274, 25945–25952 CrossRef CAS PubMed.
- F. Hasecke, T. Miti, C. Perez, J. Barton, D. Schölzel, L. Gremer, C. S. R. Grüning, G. Matthews, G. Meisl, T. P. J. Knowles, D. Willbold, P. Neudecker, H. Heise, G. Ullah, W. Hoyer and M. Muschol, Chem. Sci., 2018, 9, 5937–5948 RSC.
- N. J. Economou, M. J. Giammona, T. D. Do, X. Zheng, D. B. Teplow, S. K. Buratto and M. T. Bowers, J. Am. Chem. Soc., 2016, 138, 1772–1775 CrossRef CAS PubMed.
- W. Xi and U. H. E. Hansmann, Sci. Rep., 2017, 7, 6588 CrossRef PubMed.
- W. Xi, D. N. Dean, K. A. Stockmal, S. E. Morgan, U. H. E. Hansmann and V. Rangachari, J. Chem. Phys., 2019, 150, 075101 CrossRef PubMed.
- Y. Tian, R. Liang, A. Kumar, P. Szwedziak and J. H. Viles, Chem. Sci., 2021, 12, 6896–6907 RSC.
- L. Nagel-Steger, M. C. Owen and B. Strodel, ChemBioChem, 2016, 17, 657–676 CrossRef CAS PubMed.
- I. M. Ilie and A. Caflisch, Chem. Rev., 2019, 119, 6956–6993 CrossRef CAS PubMed.
- S. J. Bunce, Y. Wang, K. L. Stewart, A. E. Ashcroft, S. E. Radford, C. K. Hall and A. J. Wilson, Sci. Adv., 2019, 5, eaav8216 CrossRef PubMed.
- W. Zheng, M. Y. Tsai and P. G. Wolynes, J. Am. Chem. Soc., 2017, 139, 16666–16676 CrossRef CAS PubMed.
- B. Strodel, Curr. Opin. Struct. Biol., 2021, 67, 145–152 CrossRef CAS PubMed.
- B. Urbanc, M. Betnel, L. Cruz, G. Bitan and D. B. Teplow, J. Am. Chem. Soc., 2010, 132, 4266–4280 CrossRef CAS PubMed.
- S. Zhang, D. M. Fox and B. Urbanc, J. Phys. Chem. B, 2017, 121, 5523–5535 CrossRef CAS PubMed.
- B. Barz, Q. Liao and B. Strodel, J. Am. Chem. Soc., 2018, 140, 319–327 CrossRef CAS PubMed.
- B. Barz, O. O. Olubiyi and B. Strodel, Chem. Commun., 2014, 50, 5373–5375 RSC.
- W. Han and K. Schulten, J. Chem. Theory Comput., 2012, 8, 4413–4424 CrossRef CAS PubMed.
- W. Han and K. Schulten, J. Phys. Chem. B, 2013, 117, 13367–13377 CrossRef CAS PubMed.
- Y. Zhang, M. Hashemi, Z. Lv and Y. L. Lyubchenko, Nanoscale, 2016, 8, 18928–18937 RSC.
- Y. Cao, X. Jiang and W. Han, J. Chem. Theory Comput., 2017, 13, 5731–5744 CrossRef CAS PubMed.
- W. Han and K. Schulten, J. Am. Chem. Soc., 2014, 136, 12450–12460 CrossRef CAS PubMed.
- J. Zivkovic and B. Tadic, Nanoscale Syst.: Math. Model., Theory Appl., 2013, 2, 30–48 CAS.
- N. Arkus, V. N. Manoharan and M. P. Brenner, SIAM J. Discrete Math., 2011, 25, 1860–1901 CrossRef.
- N. Arkus, V. N. Manoharan and M. P. Brenner, Phys. Rev. Lett., 2009, 103, 118303 CrossRef PubMed.
- S. Hormoz and M. P. Brenner, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 5193–5198 CrossRef CAS PubMed.
- Z. Zeravcic, V. N. Manoharan and M. P. Brenner, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15918–15923 CrossRef CAS PubMed.
- W. M. Jacobs, A. Reinhardt and D. Frenkel, J. Chem. Phys., 2015, 142, 021101 CrossRef PubMed.
- W. M. Jacobs, A. Reinhardt and D. Frenkel, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 6313–6318 CrossRef CAS PubMed.
- A. Hirata, L. J. Kang, T. Fujita, B. Klumov, K. Matsue, M. Kotani, A. R. Yavari and M. W. Chen, Science, 2013, 341, 376–379 CrossRef CAS PubMed.
- M. D. Kirkitadze, M. M. Condron and D. B. Teplow, J. Mol. Biol., 2001, 312, 1103–1119 CrossRef CAS PubMed.
- P. Das, B. Murray and G. Belfort, Biophys. J., 2015, 108, 738–747 CrossRef CAS PubMed.
- P. H. Nguyen and P. Derreumaux, Biophys. Chem., 2020, 264, 106421 CrossRef CAS PubMed.
- K. A. Ball, A. H. Phillips, D. E. Wemmer and T. Head-Gordon, Biophys. J., 2013, 104, 2714–2724 CrossRef CAS PubMed.
- S. Vivekanandan, J. R. Brender, S. Y. Lee and A. Ramamoorthy, Biochem. Biophys. Res. Commun., 2011, 411, 312–316 CrossRef CAS PubMed.
- Y. Lin, B. R. Sahoo, D. Ozawa, M. Kinoshita, J. Kang, M. H. Lim, M. Okumura, Y. H. Huh, E. Moon, J. H. Jang, H. J. Lee, K. Y. Ryu, S. Ham, H. S. Won, K. S. Ryu, T. Sugiki, J. K. Bang, H. S. Hoe, T. Fujiwara, A. Ramamoorthy and Y. H. Lee, ACS Nano, 2019, 13, 8766–8783 CrossRef CAS PubMed.
- R. Pujol-Pina, S. Vilaprinyó-Pascual, R. Mazzucato, A. Arcella, M. Vilaseca, M. Orozco and N. Carulla, Sci. Rep., 2015, 5, 14809 CrossRef CAS PubMed.
- S. A. Kotler, J. R. Brender, S. Vivekanandan, Y. Suzuki, K. Yamamoto, M. Monette, J. Krishnamoorthy, P. Walsh, M. Cauble, M. M. Holl, E. N. Marsh and A. Ramamoorthy, Sci. Rep., 2015, 5, 11811 CrossRef PubMed.
- F. Meng, M. M. J. Bellaiche, J. Y. Kim, G. H. Zerze, R. B. Best and H. S. Chung, Biophys. J., 2018, 114, 870–884 CrossRef CAS PubMed.
- V. A. Voelz, G. R. Bowman, K. Beauchamp and V. S. Pande, J. Am. Chem. Soc., 2010, 132, 1526–1528 CrossRef CAS PubMed.
- H. Yu, W. Han, W. Ma and K. Schulten, J. Chem. Phys., 2015, 143, 243142 CrossRef PubMed.
- M. Nick, Y. Wu, N. W. Schmidt, S. B. Prusiner, J. Stöhr and W. F. DeGrado, Biopolymers, 2018, 109, e23096 CrossRef PubMed.
- R. S. Hoy, J. Harwayne-Gidansky and C. S. O'Hern, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 051403 CrossRef PubMed.
- J. T. Kindt, J. Chem. Theory Comput., 2013, 9, 147–152 CrossRef CAS PubMed.
- L. A. Patel and J. T. Kindt, J. Chem. Theory Comput., 2017, 13, 1023–1033 CrossRef CAS PubMed.
- M. Kłoniecki, A. Jabłonowska, J. Poznański, J. Langridge, C. Hughes, I. Campuzano, K. Giles and M. Dadlez, J. Mol. Biol., 2011, 407, 110–124 CrossRef PubMed.
- S. L. Bernstein, N. F. Dupuis, N. D. Lazo, T. Wyttenbach, M. M. Condron, G. Bitan, D. B. Teplow, J. E. Shea, B. T. Ruotolo, C. V. Robinson and M. T. Bowers, Nat. Chem., 2009, 1, 326–331 CrossRef CAS PubMed.
- L. O. Tjernberg, A. Pramanik, S. Björling, P. Thyberg, J. Thyberg, C. Nordstedt, K. D. Berndt, L. Terenius and R. Rigler, Chem. Biol., 1999, 6, 53–62 CrossRef CAS PubMed.
- W. Yong, A. Lomakin, M. D. Kirkitadze, D. B. Teplow, S. H. Chen and G. B. Benedek, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 150–154 CrossRef CAS PubMed.
- R. Sabaté and J. Estelrich, J. Phys. Chem. B, 2005, 109, 11027–11032 CrossRef PubMed.
- M. Novo, S. Freire and W. Al-Soufi, Sci. Rep., 2018, 8, 1783 CrossRef PubMed.
- B. Soreghan, J. Kosmoski and C. Glabe, J. Biol. Chem., 1994, 269, 28551–28554 CrossRef CAS.
- K. Brännström, A. Öhman, L. Nilsson, M. Pihl, L. Sandblad and A. Olofsson, J. Am. Chem. Soc., 2014, 136, 10956–10964 CrossRef PubMed.
- E. Hellstrand, B. Boland, D. M. Walsh and S. Linse, ACS Chem. Neurosci., 2010, 1, 13–18 CrossRef CAS PubMed.
- X. Zheng, D. Liu, R. Roychaudhuri, D. B. Teplow and M. T. Bowers, ACS Chem. Neurosci., 2015, 6, 1732–1740 CrossRef CAS PubMed.
- N. L. Fawzi, J. Ying, R. Ghirlando, D. A. Torchia and G. M. Clore, Nature, 2011, 480, 268–272 CrossRef CAS PubMed.
- N. L. Fawzi, J. Ying, D. A. Torchia and G. M. Clore, J. Am. Chem. Soc., 2010, 132, 9948–9951 CrossRef CAS PubMed.
- P. H. Nguyen, M. S. Li, G. Stock, J. E. Straub and D. Thirumalai, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 111–116 CrossRef CAS PubMed.
- J. R. Brender, A. Ghosh, S. A. Kotler, J. Krishnamoorthy, S. Bera, V. Morris, T. B. Sil, K. Garai, B. Reif, A. Bhunia and A. Ramamoorthy, Chem. Commun., 2019, 55, 4483–4486 RSC.
- E. Gazit, FASEB J., 2002, 16, 77–83 CrossRef CAS PubMed.
- N. G. Sgourakis, Y. Yan, S. A. McCallum, C. Wang and A. E. Garcia, J. Mol. Biol., 2007, 368, 1448–1457 CrossRef CAS PubMed.
- T. Kowalewski and D. M. Holtzman, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 3688–3693 CrossRef CAS PubMed.
- P. Chakraborty, Y. Tang, T. Yamamoto, Y. Yao, T. Guterman, S. Zilberzwige-Tal, N. Adadi, W. Ji, T. Dvir, A. Ramamoorthy, G. Wei and E. Gazit, Adv. Mater., 2020, 32, 1906043 CrossRef CAS PubMed.
- M. Chiricotto, S. Melchionna, P. Derreumaux and F. Sterpone, J. Phys. Chem. Lett., 2019, 10, 1594–1599 CrossRef CAS PubMed.
- P. Chakraborty, Y. Tang, T. Guterman, Z. A. Arnon, Y. Yao, G. Wei and E. Gazit, Angew. Chem., Int. Ed., 2020, 59, 23731–23739 CrossRef CAS PubMed.
- J.-L. Li and X.-Y. Liu, Adv. Funct. Mater., 2010, 20, 3196–3216 CrossRef CAS.
- E. R. Draper and D. J. Adams, Chem, 2017, 3, 390–410 CAS.
- M. So, D. Hall and Y. Goto, Curr. Opin. Struct. Biol., 2016, 36, 32–39 CrossRef CAS PubMed.
- X. Jiang, Y. Cao and W. Han, ACS Chem. Neurosci., 2018, 9, 935–944 CrossRef CAS PubMed.
- Y. Jiang, X. Jiang, X. Shi, F. Yang, Y. Cao, X. Qin, Z. Hou, M. Xie, N. Liu, Q. Fang, F. Yin, W. Han and Z. Li, iScience, 2019, 17, 87–100 CrossRef CAS PubMed.
- M. H. M. Olsson, C. R. Søndergaard, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 525–537 CrossRef CAS PubMed.
- C. R. Søndergaard, M. H. Olsson, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 2284–2295 CrossRef PubMed.
- M. F. Mesleh, J. M. Hunter, A. A. Shvartsburg, G. C. Schatz and M. F. Jarrold, J. Phys. Chem., 1996, 100, 16082–16086 CrossRef CAS.
- A. A. Shvartsburg and M. F. Jarrold, Chem. Phys. Lett., 1996, 261, 86–91 CrossRef CAS.
- E. G. Marklund, M. T. Degiacomi, C. V. Robinson, A. J. Baldwin and J. L. P. Benesch, Structure, 2015, 23, 791–799 CrossRef CAS PubMed.
- M. Carballo-Pacheco, A. E. Ismail and B. Strodel, J. Chem. Theory Comput., 2018, 14, 6063–6075 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc06337e |
| This journal is © The Royal Society of Chemistry 2022 |