Unprecedented mid-infrared nonlinear optical materials achieved by crystal structure engineering, a case study of (KX)P₂S₆ (X = Sb, Bi, Ba)

Abstract

Three acentric type-I phase-matchable infrared nonlinear optical materials KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆, showing excellent balance between the second harmonic generation coefficient, bandgap, and laser damage threshold, were synthesized via a high-temperature solid-state method. KSbP₂S₆ is isostructural to KBiP₂S₆, which both crystallize in the β-KSbP₂Se₆ structure type. K₂BaP₂S₆ was discovered for the first time, which crystallizes in a new structure type. KSbP₂S₆ and KBiP₂S₆ exhibit close structural similarity to the parent compound, centrosymmetric Ba₂P₂S₆. The [P₂S₆] motifs, isotypic to ethane, exist in Ba₂P₂S₆, KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆. The mixed cations, K/Sb pair, K/Bi pair, and K/Ba pair, play a dual-role of aligning the [P₂S₆] structure motifs, contributing to a high SHG coefficient, as well as enlarging the bandgap. KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆ are direct bandgap semiconductors with a bandgap of 2.9(1) eV, 2.3(1) eV and 4.1(1) eV, respectively. KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆ exhibit a high second harmonic response of 2.2× AgGaS₂, 1.8× AgGaS₂, and 2.1× AgGaS₂, respectively, coupled with a high laser damage threshold of 3× AgGaS₂, 3× AgGaS₂, and 8× AgGaS₂, respectively. The DFT calculations also confirm that the large SHG coefficient mainly originates from [P₂S₆] anionic motifs.

---

Introduction

Middle infrared lasers have various important applications such as instrumental spectroscopy,¹ optical sensing,² optical imaging,^3,4 and long-distance communications.⁵ One critical way to obtain middle infrared lasers is via the nonlinear harmonic process, where middle infrared nonlinear optical materials (MIR NLO) are the key components. Even after many years of intense research, state-of-the-art MIR NLO materials utilized to cover the spectrum range of 3–25 μm are still underdeveloped. The commercial materials such as ZnGeP₂, AgGaS₂, and AgGaSe₂ are impeded from use in the range of 3–25 μm due to their intrinsic efficiency loss originating from double photon absorption (ZnGeP₂), the low laser damage threshold (AgGaS₂), and non-phase matchable behavior (AgGaSe₂).^6–9 A state-of-the-art MIR NLO should balance a large second harmonic generation coefficient (d_ij > AgGaS₂), moderate birefringence Δn for phase matchability, a high laser damage threshold (LDT, many times > AgGaS₂), and a large bandgap for a good transmission range (>3.5 eV), which is almost impossible for many systems. Many studies, including experimental and theoretical studies, all proved the existence of a “3.5 eV wall” for middle IR NLO.^10–15 Now the major strategy to achieve a large bandgap is through the investigation of oxides, with good examples of Cs₄V₈O₂₂,¹⁶ La₃SnGa₅O₁₄,¹⁷ LiCd(IO₃)₃,¹⁸ Li₂MTeO₆ (M = Ti, Sn),¹⁹ and M₂LiVO₄ (M = Rb, Cs).²⁰ Compared with oxygen, which has intrinsic vibration modes within the infrared spectrum range, sulfides constituted from heavier sulfur atoms can have better performance.^21–24 For sulfide MIR NLO materials, they currently remain in a vacuum without a promising material to balance d_ij, Δn, and LDT with a bandgap breaking through the “3.5 eV wall”. A new research strategy is called for to break the “3.5 eV wall” with a good balance of d_ij, Δn, and LDT for MIR NLO.

Mixed cations with a combination of two chemically different atoms may increase the structural complexity of the target system, which has a higher chance of forming NCS structures, moderate birefringence for phase-matching behavior, and interactions between cations and anionic groups for better NLO properties.^21,25–30 Our research was firstly inspired by Ba₂P₂S₆, which contains [P₂S₆] ethane-like motifs and crystallizes in a centrosymmetric structure.³¹ The K⁺ cation was selected to replace Ba²⁺ cations due to their comparable ionic sizes: 152 pm and 149 pm, respectively.³² Trivalent cations containing stereochemically active lone pair electrons (SCALP) such as Sb and Bi were also incorporated into the system. Many previous studies have demonstrated that SCALP play an important role in enhancing NLO properties.^33–38 Herein, in this study, we verified that a new strategy of applying crystal structure engineering via mixed cations plays a dual-role in three emerging MIR NLO materials, KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆. The mixed cations, K/Sb, K/Bi and K/Ba, align the [P₂S₆] structure motifs, contributing to both a high SHG coefficient and enlarging the bandgap. The bandgap of K₂BaP₂S₆ is 4.1(1) eV, which sets a new record for superior MIR NLO sulfide materials. KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆ are all type-I phase-matchable materials with very large bandgaps (2.9(1) eV, 2.3(1) eV, and 4.1(1) eV, respectively), high SHG coefficients (2.2× AgGaS₂, 1.8× AgGaS₂, and 2.1× AgGaS_2, respectively) and large LDT (3× AgGaS₂, 3× AgGaS₂, and 8× AgGaS₂, respectively). The structural chemistry between KSbP₂S₆, KBiP₂S₆, K₂BaP₂S₆, and the parent centrosymmetric compound Ba₂P₂S₆ ³¹ is presented. The synthesis, crystal structure, electronic structure, linear and nonlinear optical properties, and DFT calculations of KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆ and the parent centrosymmetric compound Ba₂P₂S₆ are discussed.

Experimental

Synthesis

All starting materials were stored and used in an Ar-filled glove box. Starting materials were used as received without further handling: K metal (Alfa Aesar, 99.95%), P powder (Alfa Aesar, 99.5%), S powder (Alfa Aesar, 99.5%), Ba rod (Sigma-Aldrich 99.9%), Bi (Fisher, 99.99%), and Sb (Fisher, 99.5%). The P₂S₅ precursor was made via loading P and S at a molar ratio of 2 : 5 and heating them to 573 K in 10 hours and holding for 10 hours. Polycrystalline samples of K₂BaP₂S₆, KSbP₂S₆, and KBiP₂S₆ were grown by a two-step solid-state reaction. First step: stoichiometric amounts of reactants (K₂BaP₂S₆: K/Ba/P/S = 2 : 1 : 2 : 6, KSbP₂S₆: K/Sb/P/S = 1 : 1 : 2 : 6, KBiP₂S₆: K/Bi/P/S = 1 : 1 : 2 : 6) were loaded into silica quartz tubes and were flame-sealed under vacuum at 10⁻² torr and placed into a programmable furnace. The sealed silica tubes were heated to 398 K in 10 h, held for 10 h, heated to 923 K in 10 h, held for 144 h, and cooled to RT over 48 h. Second step: the quartz tubes from the first step were opened in a glovebox and the products were manually ground using a mortar and pestle. The finely mixed powders were then loaded into a new carbonized quartz tube. The ampoules were sealed and heated again using an identical temperature profile to the first step. After the second step, the homogeneous powders appearing in various colors (K₂BaP₂S₆: white transparent, KSbP₂S₆: yellow-green, KBiP₂S₆: red) were collected and checked by powder X-ray diffraction. The powder X-ray diffraction verified the single-phase nature of K₂BaP₂S₆, KSbP₂S₆, and KBiP₂S₆ (Fig. S1–S3†).

Single crystal X-ray diffraction

X-ray diffraction data were collected at 298(2) K for K₂BaP₂S₆ using a Bruker Kappa APEX II diffractometer with graphite monochromated Mo Kα radiation (λ = 0.71073 Å). Data reduction and integration, together with global unit cell refinements, were performed in the APEX2 software.³⁹ Multi-scan absorption corrections were employed.³⁹ The structures were solved by direct methods and refined by full matrix least-squares methods on F² using the SHELX package with anisotropic displacement parameters for all atoms.⁴⁰ In the last refinement cycles, the atomic positions for the three compounds were standardized using the program structure TIDY.^41,42 Details of the data collection and structure refinement are provided in Table 1. Atomic coordinates and selected bond distances are summarized in Tables S1 and S2.† During the structure refinement process, a residual peak separated from the K2 atom by 2.87(2) Å with an intensity of 5.22 e Å⁻³ was found in K₂BaP₂S₆. The final refinement ended up with a high wR₂ of 0.1458 ([I > 2σ(I)]) and G.O.F of 1.200. The twinning refinement and reproduced data collection with better crystal quality did not improve the refinement results. With defining the residual peak as K1 with adding constraints of occupancy of K1 + K2 = 100%, the final structure model ended up with a much lower wR₂ of 0.0807 ([I > 2σ_(I)]), wR₂ of 0.0874 (all data), and G.O.F of 1.071. When solely refining the occupancy of K2, a value of 97% was obtained. The occupancy of interstitial K1 is around 13% from single crystal refinement results. Since K₂BaP₂S₆ was revealed as a large bandgap semiconductor by theoretical simulation and experimental UV-vis results (vide infra), the charge-balanced formula (K⁺)₂(Ba²⁺)(P⁴⁺)₂(S²⁻)₆ can be established by assigning a formal charge of 1+ to the K atoms, 2+ to the Ba atoms, 4+ to the P atoms due to the presence of homoatomic interactions, and 2− to the S atoms. Hence, the actual occupancy of interstitial K1 would be much lower than 10% to keep the charge balanced nature of K₂BaP₂S₆. To simplify the discussion of K₂BaP₂S₆, the interstitial K1 was not included. The crystallographic data such as atomic coordinate parameters and selected interatomic distances of K1 atoms are listed in Tables S1 and S2,† respectively. Crystallographic data for K₂BaP₂S₆ have been deposited with the Cambridge Crystallographic Data Centre, CCDC, 12 Union Road, Cambridge CB21EZ, UK. Copies of the data can be obtained free of charge on quoting the depository number CCDC-2119928 (K₂BaP₂S₆).

Table 1 Selected crystal data and structure refinement parameters for K₂BaP₂S₆ at 173(2) K

Empirical formula	K2BaP2S6
a R 1 = ∑‖Fo| − |Fc‖/∑|Fo|; wR2 = [∑[w(Fo^2 − Fc^2)^2]/∑[w(Fo^2)^2]]^1/2, and w = 1/[σ^2Fo^2 + (A·P)^2 + B·P], P = (Fo^2 + 2Fc^2)/3; A and B are weight coefficients.
Formula weight	469.84 g mol^−1	Unit cell volume	1211.8(2) Å^3
Temperature	173(2) K	Z	4
Radiation, wavelength	Mo Kα, 0.71073 Å	Density (calc.)	2.575 g cm^−3
Crystal system	Orthorhombic	Absorption coefficient	5.203 mm^−1
Space group	Pna21 (no. 33)
Unit cell dimensions	a = 12.3592(13) Å	Final R indices^a [I > 2σ(I)]	R 1 = 0.0373
			wR2 = 0.0807
	b = 14.4324(14) Å	Final R indices^a [all data]	R 1 = 0.0561
			wR2 = 0.0874
	c = 6.7939(7) Å	G.O.F	1.071

---

Powder X-ray diffraction

Data were collected at room temperature using a Rigaku Mini Flex II diffractometer with Cu Kα radiation (λ = 1.5406 Å).

UV-vis measurements

Diffuse-reflectance spectra were recorded at room temperature using a PERSEE-T8DCS UV-vis spectrophotometer equipped with an integration sphere in the wavelength range of 230–850 nm. The reflectance data, R were recorded and converted to the Kubelka–Munk function, f(R) = (1 − R)²(2R)⁻¹. The Tauc plots, (KM × E)² and (KM × E)^1/2, were applied to estimate direct and indirect bandgaps, respectively.

Second harmonic measurements

Using the Kurtz and Perry method,⁴³ powder SHG responses of title compounds were investigated using a Q-switch laser (2.09 μm, 3 Hz, 50 ns) with different particle sizes, including 38.5–54, 54–88, 88–105, 105–150, and 150–200 μm. The detailed process of sample preparation would be: the as-synthesized sample and the as-synthesized reference AgGaS₂ sample were manually ground into particles within a glovebox first. The ground samples were sieved using standard brass sieves with various mesh sizes. The particles were sorted out and separated using standard brass sieves with various mesh sizes with the potential of a large range of particle size distribution. The LDTs of the title compounds were evaluated on powder samples (150–200 μm) with a pulsed YAG laser (1.06 μm, 10 ns, 10 Hz). The judgment criterion is as follows: with increasing laser energy, the color change of the powder sample is constantly observed using an optical microscope to determine the damage threshold. To adjust different laser beams, an optical concave lens is added to the laser path. The damaged spot is measured using the scale of the optical microscope.

Theoretical calculations

The density of states (DOS), partial density of states (PDOS), band structure, crystal orbital Hamilton population (COHP), and electron localization function (ELF) of Ba₂P₂S₆, KBiP₂S₆, and K₂BaP₂S₆ are calculated using the tight binding-linear muffin tin orbitals-atomic sphere approximation (TB-LMTO-ASA) program.^44,45 The Barth–Hedin exchange potential was employed for the LDA calculations.⁴⁵ The radial scalar-relativistic Dirac equation was solved to obtain the partial waves. The basis set used contained K (4s), Ba (6s, 5d, 4f), Bi (6s, 5d, 6p), P (3s, 3p) and S (3s, 3p) orbitals, and was employed for a self-consistent calculation, with downfolded functions of K (4p, 3d), Ba (5f, 6p), Bi (6d, 5f), P (3d) and S (3d). The density of states and band structures were calculated after converging the total energy on a dense k-mesh of Ba₂P₂S₆ (20 × 20 × 10 points with 1122 irreducible k-points), K₂BaP₂S₆ (12 × 12 × 24 points with 1176 irreducible k-points), and KBiP₂S₆ (16 × 16 × 8 points with 1056 irreducible k-points). The optical properties were calculated based on ab initio calculations implemented in the CASTEP package through density functional theory (DFT).⁴⁶ The generalized gradient approximation (GGA)⁴⁷ was adopted, and the Perdew–Burke–Ernzerhof (PBE)⁴⁸ function was chosen to calculate the exchange–correlation potential, with an energy cutoff of 650 eV. The numerical integration of the Brillouin zone was performed using Monkhorst–Pack k-point sampling. The k-point separation for each material was set as 0.04 Å⁻¹. The geometry optimizations were applied prior to property calculations. Norm-conserving pseudopotentials were employed.

Results and discussion

Crystal structure

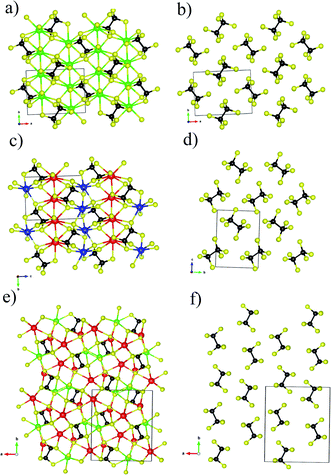
KSbP₂S₆ is isostructural to KBiP₂S₆, which crystallizes in the β-KSbP₂Se₆ structure type.⁴⁹ KSbP₂S₆ and KBiP₂S₆ form in the monoclinic space group P2₁ (no. 4), which were discovered by Manrique, V. et al. without investigating any properties.⁵⁰ K₂BaP₂S₆ crystallizes in the orthorhombic space group Pna2₁ (no. 33) with unit cell parameters of a = 12.018(1) Å, b = 23.762(2) Å, and c = 3.984(1) Å. The Wyckoff sequence of K₂BaP₂S₆ is a¹¹ with Pearson symbol oP44. Searching for isostructural compounds through the ICSD database did not return any results. Therefore, K₂BaP₂S₆ crystallizes in a new structure type. The selected crystal data and structure refinement parameters for K₂BaP₂S₆ are summarized in Table 1. The atomic coordinate parameters and selected interatomic distances are listed in Tables S1 and S2.†

To discuss the structural chemistry between KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆, a centrosymmetric compound Ba₂P₂S₆ ³¹ must be discussed for a few reasons: (1) the fundamental building units of Ba₂P₂S₆ are the [P₂S₆] motifs, which are the same fundamental building units in KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆; (2) there are close unit cell parameters between Ba₂P₂S₆, KSbP₂S₆, and KBiP₂S₆ with very comparable unit cell volumes as shown in Table S3;† (3) the chemical formula of Ba₂P₂S₆ can be presented by [Ba²⁺]₂[P₂S₆]⁴⁻, where the charge of cations would be 4+. The same charge requirements remain in KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆ with representation as [K⁺Sb³⁺][P₂S₆]⁴⁻, [K⁺Bi³⁺][P₂S₆]⁴⁻, and [K₂⁺Ba²⁺][P₂S₆]⁴⁻ respectively; (4) Ba₂P₂S₆ inspired our research interest in compounds containing [P₂S₆] motifs. Since KSbP₂S₆ is isostructural to KBiP₂S₆, only KBiP₂S₆ is selected for structural discussion. The structural comparisons between centrosymmetric Ba₂P₂S₆, KSbP₂S₆, and K₂BaP₂S₆ are summarized in Fig. 1 with emphasis on the [P₂S₆] motifs on the right.

Fig. 1 (a) Ball-stick structure model of Ba₂P₂S₆ viewed along the [001] axis, (b) the arrangement of [P₂S₆] motifs within Ba₂P₂S₆. (c) Ball-stick structure model of KBiP₂S₆ viewed along the [100] axis, (d) the arrangement of [P₂S₆] motifs within KBiP₂S₆. (e) Ball-stick structure model of K₂BaP₂S₆ viewed along the [001] axis, (f) the arrangement of [P₂S₆] motifs within K₂BaP₂S₆. K red color, Ba: green color, Bi: blue color, P: black color, S: yellow color.

Ba₂P₂S₆ crystallizes in the centrosymmetric P2₁/n (no. 14) space group with unit cell parameters of a = 6.7459(6) Å, b = 7.5871(6) Å, and c = 9.9983(9) Å, β = 91.204(3)°, which were redetermined in this work. The crystal structure of Ba₂P₂S₆ is shown in Fig. 1a and b. The three-dimensional (3D) framework of Ba₂P₂S₆ is constructed by isolated [P₂S₆] motifs interconnected by 2D [Ba₂S₆] slabs, where the center Ba atoms are surrounded by nine sulfur atoms. The Ba–S interactions within [BaS₉] polyhedra fall into the range of 3.217–3.567 Å. The theoretical simulation also verified the ionic bonding nature of Ba–S interactions (vide infra). The crystal structure of KBiP₂S₆ shows high similarity to Ba₂P₂S₆, as summarized in Table S3† and Fig. 1. KBiP₂S₆ crystallizes in the acentric P2₁ (no. 4) space group with unit cell parameters of a = 6.6200(6) Å, b = 7.4058(7) Å, and c = 9.9002(9) Å, β = 92.108(1) °.⁵⁰ The unit cell volume of Ba₂P₂S₆ and KBiP₂S₆ is 508.82 ų and 485.04 ų, respectively. The 3D framework of KBiP₂S₆ is formed by isolated [P₂S₆] motifs linked by alternatively arranged 2D [KS₅] slabs and 2D [BiS₅] slabs, which are shown in Fig. 1c. The 2D [KS₅] slabs are constructed by [KS₉] polyhedra interlinked via sharing vertices and edges. The K–S interactions within [KS₉] polyhedra are 3.191–3.592 Å, comparable to Ba–S interactions of 3.217–3.567 Å within Ba₂P₂S₆, which are revealed as dominantly ionic bonds (vide infra). The 2D [BiS₅] slabs are made by distorted [BiS₇] polyhedra with Bi–S interactions of 2.706–3.210 Å. The Bi–S interactions of 2.71 Å show strong polarized ionic bonding characteristics (vide infra).

K₂BaP₂S₆ exhibits a much more complex structure than Ba₂P₂S₆ and KBiP₂P₆. K₂BaP₂S₆ crystallizes in the orthorhombic space group Pna2₁ (no. 33) with unit cell parameters of a = 12.3592(13) Å, b = 14.4324(14) Å, and c = 6.7939(7) Å with unit cell volume of 1211.8(2) ų, about two times higher than those of Ba₂P₂S₆ (508.82 ų) and KBiP₂P₆ (485.04 ų). The 3D framework of K₂BaP₂S₆ can be viewed as isolated [P₂S₆] motifs connected by 2D [K₂BaS₆] slabs, where the K/Ba ratio is two. The 2D [K₂BaS₆] slabs are made of [KS₇] polyhedra, [KS₈] polyhedra, and [BaS₁₀] polyhedra. The K–S interactions in [KS₇] and [KS₈] fall into the range of 3.213(16)–3.679(5) Å, which is close to those of many potassium-sulfides such as K₂FeGe₃S₈ (3.131–3.762 Å),⁵¹ K₂CoGe₃S₈ (3.130–3.765 Å),⁵¹ KBiP₂S₆ (3.191–3.562 Å),⁵⁰ K₂MnP₂S₆ (3.226–3.600 Å),⁵² KSbP₂S₆ (3.206–3.592 Å).⁵⁰ The 3.220(5) Å K–S interactions are revealed by theoretical calculations as weak ionic bonds (vide infra). The Ba–S interactions in [BaS₁₀] polyhedra fall into the range of 3.226(3)–3.535(7) Å, which is close to those of many barium-sulfides such as Ba₆(Cu₂Mg)Ge₄S₁₆ (3.084–3.454 Å),⁵³ Ba₂P₂S₆ (3.217–3.567 Å),³¹ Ba₂AlSbS₅ (3.217–3.567 Å),⁵⁴ BaAg₂GeS₄ (3.251–3.306 Å),⁵⁵ BaCd₂As₂S₆ (3.248–3.374 Å),⁵⁶etc. The 3.24 Å ionic Ba–S interactions exhibit certain bond strengths as revealed by theoretical calculations (vide infra). The structural details of K₂BaP₂S₆ are shown in Fig. 1e and f. The [P₂S₆] motifs are the common features existing in Ba₂P₂S₆, KBiP₂P₆ and K₂BaP₂S₆. The [P₂S₆] motif is isotypic to ethane, constructed by a P–P dimer with three sulfur atoms surrounding each P atom. The interatomic P–P bonds for Ba₂P₂S₆, KBiP₂P₆ and K₂BaP₂S₆ are 2.205 Å, 2.219 Å, and 2.223(4) Å, respectively, which are typical for homoatomic P–P bond distances such as BaCu₅P₃ (2.263 Å),⁵⁷ La₂Ba₆Cu₁₆P₃₀ (2.071–2.428 Å),⁵⁸ BaCu₂P₄ (2.183 and 2.289 Å),⁵⁹ Ba₈Cu₁₆P₃₀ (2.159–2.299 Å),⁶⁰ La₇Zn₂P₁₁ (2.207(7) Å),⁶¹ Ba₂Cu₃P₄ (2.236 Å),⁶² La₄Zn₇P₁₀ (2.151(8) Å),⁶³etc. The P–S interatomic distances within Ba₂P₂S₆ are 2.016–2.025 Å, and are slightly expanded into a wider range of distances to 1.962–2.057 Å and 1.958(17)–2.066(15) Å for KBiP₂P₆ and K₂BaP₂S₆, respectively. Even though all [P₂S₆] motifs have identical geometry within Ba₂P₂S₆, KBiP₂P₆, and K₂BaP₂S₆, the slightly different interatomic distances coupled with various ∠S–P–S angles indicate that the degrees of distortion of the [P₂S₆] motifs are distinct. The strong covalent bonding nature of P–P interactions and P–S interactions together with complex interactions between cations and [P₂S₆] was uncovered by theoretical simulation (vide infra).

Another intriguing structural feature of Ba₂P₂S₆, KBiP₂P₆ and K₂BaP₂S₆ is the arrangement of [P₂S₆] motifs as shown in Fig. 1b, d and f. To discuss the alignment of [P₂S₆] motifs, we introduce the ∠P–P–P angles as a measure, where the three P atoms are coming from two neighbor [P₂S₆] motifs. The ∠P–P–P angles are summarized in Table 2. From Table 2, the ∠P–P–P angle significantly increases from Ba₂P₂S₆ to K₂BaP₂S₆ of 70.73(4)° and 89.4(3)° respectively. The ∠P–P–P angle in KBiP₂S₆ resides between Ba₂P₂S₆ and K₂BaP₂S₆ of 73.57(3)°. The ∠P–P–P angle is closer to 90°, which indicates that [P₂S₆] motifs are arranged more parallel to each other. As shown in Fig. 1f, the [P₂S₆] motifs within K₂BaP₂S₆ are arranged nearly parallel. The later studies demonstrate that the alignment of [P₂S₆] motifs is crucial for the optical properties of K₂BaP₂S₆ (vide infra).

Table 2 The comparison of ∠P–P–P angles between Ba₂P₂S₆, KBiP₂S₆, and K₂BaP₂S₆

	Ba2P2S6	KbiP2S6	K2BaP2S6
∠P–P–P/°	70.53(4)	73.57(3)	89.4(3)

---

Electronic structures

To elucidate the electronic structures of Ba₂P₂S₆, KBiP₂S₆, and K₂BaP₂S₆, the calculations of band structure and density of states (DOS) were employed. The band structures are summarized in Fig. S4–S11.† The density of states of Ba₂P₂S₆, KBiP₂S₆, and K₂BaP₂S₆ is shown in Fig. 2. To validate the accuracy of theoretical simulations, two different methods, TB-LMTO-ASA and VASP, were employed to study the electronic structures of Ba₂P₂S₆, KBiP₂S₆, and K₂BaP₂S₆ (Fig. 2 and S4–S14†), which exhibited comparable results.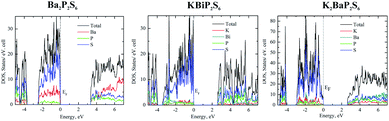

Fig. 2 Left: density of states of Ba₂P₂S₆, middle: density of states of KBiP₂S₆, right: density of states of K₂BaP₂S₆.

The charge-balanced formula (Ba²⁺)₂(P⁴⁺)₂(S²⁻)₆, (K¹⁺)(Bi³⁺)(P⁴⁺)₂(S²⁻)₆, and (K¹⁺)₂(Ba²⁺)(P⁴⁺)₂(S²⁻)₆ can be easily achieved via assigning a formal charge of 2+ to the Ba atoms, 1+ to the K atoms, 3+ to the Bi atoms, 4+ to the P atoms due to the presence of P–P homoatomic bonds, and 2− to the S atoms. The Bi³⁺ is confirmed by the presence of 6p² lone pair electrons elucidated by ELF calculations (vide infra) and bond valence sum calculations.^64–66 Bond valence sum calculations indicated that the BVS of K atoms, Ba atoms and Bi atoms is 1.1, 1.9, and 2.5, respectively, which suggests K atoms, Ba atoms and Bi atoms with oxidation states of +1, +2, and +3, respectively. The semiconductor nature of Ba₂P₂S₆, KBiP₂S₆, and K₂BaP₂S₆ was verified by DFT calculations and UV-vis measurements (Fig. S15–S19†). The band structure calculation indicated the direct semiconductor nature of Ba₂P₂S₆, KBiP₂S₆, and K₂BaP₂S₆ (Fig. S6, S7, S9 and S10†). As shown in Fig. 2 left, the calculated bandgap of Ba₂P₂S₆ is 3.3 eV, which is lower than the measured value of 4.3(1) eV (Fig. S15 and S16†). In Ba₂P₂S₆, the top of the valence band is dominantly contributed by S 3p orbitals and Ba 5s orbitals with some contributions from P 3p orbitals. The bottom of the conduction band is mainly contributed by S 3p orbitals and P 3p orbitals with certain contribution from Ba orbitals. The Ba orbitals significantly contribute a high energy interval of 5–7 eV as shown on the left of Fig. 2. We can anticipate that the Ba–S interactions are crucial for enlarging the bandgap of Ba₂P₂S₆ and the optical properties of Ba₂P₂S₆ are mainly controlled by Ba–S interactions and P–S interactions.

The direct bandgap of KBiP₂S₆ was predicated to be 2.6 eV, which is slightly higher than the measured value of 2.3(1) eV (Fig. S18†). The HSE calculated bandgap is 2.37 eV, which agrees very well with the measured value (Fig. S7†). KBiP₂S₆ exhibits a comparable electronic structure to Ba₂P₂S₆, which is shown in the middle of Fig. 2. The top of the valence band is mainly contributed by S 3p orbitals with almost equal contributions from K 4s orbitals, Bi 6p orbitals and P 3p orbitals. The bottom of the conduction band is dominantly contributed by Bi 6p orbitals and S 3p orbitals with significant contribution from P 3p orbitals. Interestingly, K 4s orbitals had a negligible contribution to the bottom of the conduction band. Compared with Ba₂P₂S₆, [BiS₇] polyhedra will be expected to significantly affect the optical properties of KBiP₂S₆, which was verified by DFT calculations (vide infra). The nonlinear optical process is mainly dominated by electrons transferring between these frontier orbitals. Within KBiP₂S₆, K–S interactions, Bi–S interactions and [P₂S₆] motifs all determine the optical properties of KBiP₂S₆. The stereochemically active lone pair electrons (SCALP) on Bi atoms are expected to significantly enhance the NLO properties of KBiP₂S₆, which is confirmed by experimental observations and DFT calculations (vide infra). Compared with the centrosymmetric Ba₂P₂S₆, the mixed cations of K/Bi play a dual-role of shifting the arrangement of [P₂S₆] to form a NCS structure and shrinking the bandgap.

The dual-role of mixed cations is even more obvious in K₂BaP₂S₆. The direct bandgap of K₂BaP₂S₆ was predicated to be 2.6 eV and 2.5 eV by the tight bonding method and HSE calculation respectively (Fig. S9 and S10†). The experimentally measured bandgap of K₂BaP₂S₆ is 4.1(1) eV, where the underestimation of the bandgap is normal for DFT calculations. The electronic structures of K₂BaP₂S₆ exhibit certain high similarity to Ba₂P₂S₆ and KBiP₂S₆. The top of the valence band is predominantly contributed by S 3p orbitals and small contents of contribution from K 4s orbitals and Ba 6s orbitals. The contribution from P 3p orbitals can be ignored at the top of the valence band. Inversely, the P 3p orbitals coupled with S 3p orbitals and Ba 6s orbitals dominantly contribute to the bottom of the conduction band, where K 4s orbitals have certain contributions. From the density of states, we can expect that [P₂S₆] motifs significantly shift the nonlinear optical properties of K₂BaP₂S₆, while mixed cations of K/Ba forming ionic K–S interactions and Ba–S interactions are responsible for the large bandgap of K₂BaP₂S₆. In addition to enlarging the bandgap of K₂BaP₂S₆, mixed cations of K/Ba also account for the nearly parallel alignment of [P₂S₆] motifs, which is crucial for its superior optical performance (vide infra).

Bonding picture studies

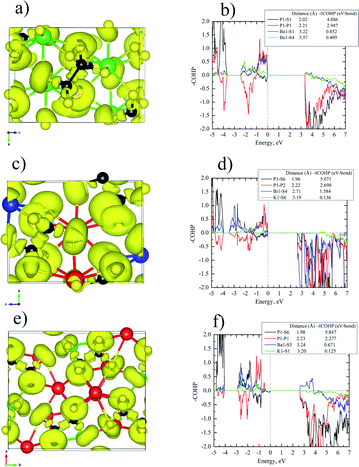
The bonding pictures of Ba₂P₂S₆ (Fig. 3a and b), KBiP₂S₆ (Fig. 3c and d), and K₂BaP₂S₆ (Fig. 3e and f) were understood with the aid of the electron localization function (ELF) coupled with crystal orbital Hamilton population (COHP) calculations. For Ba₂P₂S₆, there are no detectable attractors (ELF maxima isosurfaces) found between Ba–S interactions with attractors only surrounding S atoms, which suggests the dominant ionic character of Ba–S interactions. The Ba–S interactions exhibit certain strong bonding characteristics with –ICOHPs of 0.852 eV per bond and 0.409 eV per bond for 3.22 Å Ba–S interactions and 3.57 Å Ba–S interactions, respectively. An obvious attractor was located between P–P interactions with –ICOHPs of 2.947 eV per bond for 2.21 Å P–P interactions, which indicates the strong covalent bonding nature of P–P interactions. The strongest bonding character was found between P–S interactions. The –ICOHPs for 2.02 Å P–S interactions are 4.886 eV per bond. There were significant attractors located between P–S bonds with a small shift toward P atoms. All attractors surrounding S atoms show irregular spherical shapes, which indicates the polarized bonding nature of Ba–S interactions and P–S interactions. For KBiP₂S₆, K atoms play the role of cations with no attractors surrounding and existing between K–S interactions and low calculated –ICOHPs of 0.136 eV per bond for 3.19 Å K–S interactions, which demonstrates the weak ionic bonding nature of K–S interactions. The attractors capping the Bi atoms correspond to the 6s² electron lone pairs on Bi atoms, which verifies that the oxidation states of Bi should be +3. The COHP calculations indicate the strong bonding interactions for 2.71 Å Bi–S bonding with –ICOHPs of 1.584 eV per bond. For Bi–S interactions, the attractors are solely surrounding S atoms with irregular shapes, which suggests the strong polarized dominantly ionic bonding characters of Bi–S interactions. The electronic studies predict that [BiS₇] polyhedra will significantly contribute to NLO properties due to the presence of SCALP, which is confirmed by DFT calculations (vide infra). The P–P interactions and P–S interactions within KBiP₂S₆ exhibit comparable characters to Ba₂P₂S₆. There are attractors located in the middle of P–P interactions with –ICOHPs of 2.698 eV per bond for 2.22 Å P–P interactions. There are attractors detected between P–S interactions with –ICOHPs of 5.071 eV per bond for 1.96 Å P–S interactions. Hence, both P–P interactions and P–S interactions exhibit strong covalent bonding characteristics.

Fig. 3 (a, c and e) 3D isosurfaces of the electron localization function (ELF) for Ba₂P₂S₆ (a), KBiP₂S₆ (c), and K₂BaP₂S₆ (e) with η = 0.75, Ba: green color, K: red color, Bi: blue color, P: Black color, S: yellow color, (b, d and f): Crystal Orbital Hamilton Population (COHP) analyses of the selected interactions within Ba₂P₂S₆ (b), KBiP₂S₆ (d), and K₂BaP₂S₆ (f).

For K₂BaP₂S₆, there are no ELF maxima isosurfaces residing between K–S interactions and Ba–S interactions. The calculated –ICOHPs for 3.24 Å Ba–S interactions are 0.671 eV per bond, which indicates that 3.24 Å Ba–S has certain strong bonding characteristics. The 3.20 Å K–S interactions have much weaker ionic bonding nature with –ICOHPs of 0.125 eV per bond as shown in Fig. 3f. The electronegativity difference between K (0.8) and Ba (0.9) may account for this slight bonding picture difference. The strong covalent bonding nature of P–P interactions and P–S interactions was verified by the presence of attractors between them and high –ICOHPs values of 5.847 eV per bond and 2.277 eV per bond for 1.98 Å P–S bonds and 2.23 Å P–P bonds, respectively. Similar to Ba₂P₂S₆ and KBiP₂S₆, the K–S interactions and Ba–S interactions are also strongly polarized. When comparing Ba₂P₂S₆, KBiP₂S₆, and K₂BaP₂S₆ together, one very interesting observation is the decrease of bonding strengths in P–P interactions and the inverse trend of enhancement of bonding strengths in P–S interactions from Ba₂P₂S₆ to KBiP₂S₆, and finally to K₂BaP₂S₆. All our observations indicate the complex interactions happening between cations and anionic [P₂S₆] motifs.

Linear and nonlinear optical properties

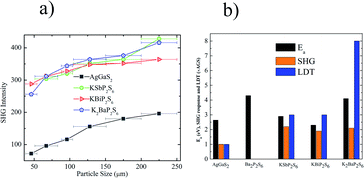
The linear and nonlinear optical properties of KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆ were measured and are reported in Fig. 4. From Fig. 4a, Ba₂P₂S₆, KBiP₂S₆, and K₂BaP₂S₆ exhibited type-I phase-matching behavior, where the SHG response increases with particle size increasing. The calculated birefringence of KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆ is shown in Fig. S12–S14.† The moderate birefringence of KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆ accounts for their phase-matching capability, which is crucial for practical applications. For samples of particle size 225 μm, the SHG response of KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆ is 2.2× AGS, 1.8× AGS and 2.1× AGS, respectively. The measured bandgap of KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆ is 2.9(1) eV, 2.3(1) eV and 4.1(1) eV respectively. The high bandgap of K₂BaP₂S₆ results in an extraordinarily high LDT of 8× AGS. KSbP₂S₆ and KBiP₂S₆ also possess excellent LDT of about 3× AGS for both samples. The type-I phase matching behavior, large bandgap, high SHG response, and high LDT make KSbP₂S₆, KBiP₂S₆, and especially K₂BaP₂S₆ ideal candidates for middle IR NLO applications.

Fig. 4 (a) SHG intensities of Ba₂P₂S₆, KBiP₂S₆, K₂BaP₂S₆, and AgGaS₂ were measured on variable particle size samples utilizing a 2.09 μm laser. (b) The comparison of the bandgap (Ea), SHG response (×AgGaS₂ based on 225 μm particle size samples) and LDT (×AgGaS₂) between Ba₂P₂S₆, KBiP₂S₆, K₂BaP₂S₆, and AgGaS₂.

DFT calculations

To better understand the origin of the superior NLO properties of KSbP₂S₆, KBiP₂S₆ and K₂BaP₂S₆, DFT calculations were carried out and are summarized in Table 3, Fig. 5 and S20–S22.† The calculations of KSbP₂S₆ are presented in Fig. S20.† As shown in Table 3, KSbP₂S₆ and KBiP₂S₆ were predicated to show a high SHG response, which agrees well with our experimental observations. The calculated χ²²² for KSbP₂S₆ is 67.267 pm V⁻¹ which is slightly higher than that of KBiP₂S₆ at χ²²² = 63.404 pm V⁻¹. The experimentally measured SHG response of KSbP₂S₆ is also slightly better than that of KBiP₂S₆. From Fig. 5a and b, the occupied virtual electrons (VE) states of KSbP₂S₆ and KBiP₂S₆ are mainly contributed by the [P₂S₆] motif and [XS₇] (X = Sb or Bi) polyhedra due to the presence of SCALP, which is verified by the analysis of unoccupied virtual electrons states and virtual holes (VH) (Fig. S20 and S21†). These observations agree well with our previous electronic structure analysis.

Table 3 Calculated second-order nonlinear susceptibility χ^abc for KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆

	KSbP2S6	KBiP2S6	K2BaP2S6
χ ^abc/pm V^−1	χ ^112 = 1.647	χ ^112 = 11.234	χ ^113 = 0.171
	χ ^123 = 16.114	χ ^123 = 1.890	χ ^333 = 0.678
	χ ^222 = 67.267	χ ^222 = 63.404	—
	χ ^233 = 16.691	χ ^233 = 0.4067	—

---

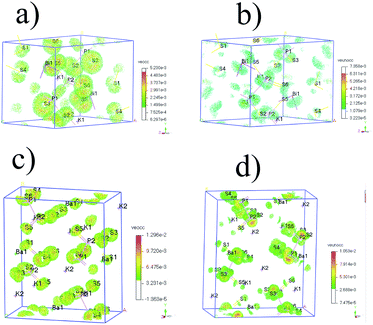Fig. 5 (a) SHG density of VE occupied (veocc) and (b) unoccupied (veunocc) states in KBiP₂S₆. (c) SHG density of VE occupied (veocc) and (d) unoccupied (veunocc) states in K₂BaP₂S₆.

For K₂BaP₂S₆, the analysis of occupied and unoccupied states of VE and VH concluded that the [P₂S₆] motif plays a critical role in determining the SHG response, which agrees well with our electronic structure study. The calculated χ³³³ of K₂BaP₂S₆ is only around 0.678 pm V⁻¹, which is much lower than that of KSbP₂S₆ and KBiP₂S₆. The experimentally measured SHG response of K₂BaP₂S₆ is comparable to that of KSbP₂S₆ and slightly better than that of KBiP₂S₆. This controversy can be explained by the alignment of [P₂S₆] motifs, as discussed in the crystal structure analysis. The nearly parallel alignment of [P₂S₆] motifs guarantees that the dipole moments originating from the [P₂S₆] motif do not cancel each other out during the nonlinear polarization process.^67,68 For KSbP₂S₆ and KBiP₂S₆, the “imperfect” alignment of [P₂S₆] motifs is compensated by the presence of SCALP, which also results in a superior SHG response. In summary, K₂BaP₂S₆ exhibits an excellent example of middle IR NLO materials with a good balance of a large bandgap (4.1(1) eV), high SHG coefficient (2.1× AGS), and large LDT (8× AGS) through a mixed cation routine. From centrosymmetric Ba₂P₂S₆ to acentric KSbP₂S₆ and KBiP₂S₆, then finally to K₂BaP₂S₆, our observations demonstrate the important dual-role of mixed cations: aligning structural motifs to form NCS structures and enlarging bandgaps. Our research provides a new direction for discovering novel middle IR NLO materials. To better evaluate the properties of (KX)P₂S₆ (X = Sb, Bi, Ba), obtaining high quality single crystals is essential. Our initial experiments of crystal growth of K₂BaP₂S₆ utilizing salt flux have resulted in mm-sized crystals, which are shown in Fig. S23.† Type-I phase-matching capability, good air stability, and high SHG and LDT all indicate that (KX)P₂S₆ compounds (X = Sb, Bi, Ba) are excellent infrared nonlinear optical materials. The next phase for this system would be crystal growth of (KX)P₂S₆ compounds (X = Sb, Bi, Ba) and systemically studying their physical properties such as LDT and thermal conductivity, which are ongoing.

Conclusions

Three acentric thiophosphates KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆ were synthesized via a high-temperature solid-state method. KSbP₂S₆ is isostructural to KbiP₂S₆, which crystallizes in the β-KSbP₂Se₆ structure type. K₂BaP₂S₆ was discovered for the first time and forms in a new structure type. KSbP₂S₆, KbiP₂S₆, and K₂BaP₂S₆ were predicted to be direct bandgap semiconductors. The measured bandgaps for KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆ are 2.9(1) eV, 2.3(1) eV and 4.1(1) eV respectively. KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆ were discovered as superior middle IR NLO materials with excellent balance between the bandgap, second harmonic generation coefficient, and laser damage threshold. The superior NLO properties of KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆ originate from the comprehensive interactions between mixed cations and [P₂S₆] motifs. The mixed cations play a dual-role of aligning [P₂S₆] motifs and enlarging the bandgap in KSbP₂S₆, KBiP₂S₆, and K₂BaP₂S₆, which is elucidated by a comprehensive study of crystal structure measurements, DFT calculations, and property tests. This study opens a new avenue for breaking the “3.5 eV wall” for middle IR NLO materials research.

Data availability

Crystallographic data for K₂BaP₂S₆ has been deposited at the CCDC under CCDC 2119928. The datasets supporting this article have been uploaded as part of the ESI,† DOI: 10.1039/d1sc06849k.

Author contributions

J. W. conceived the project, designed the experiments and supervised the study. V. V. and J. B. performed the experiments and analysed the data. K. W. performed the SHG test. B. Zhang performed SHG theoretical calculations. V. V., J. B., K. W., B. Zhang., and J. W. discussed the data and wrote the paper.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research is supported by start-up funds from Wichita State University. J. Wang thanks Arka Sarkar from Iowa State University for confirming the single crystal structure and Xiaocun Liu from Shandong University, China for help on the SEM test.

References

1. M. Yu, Y. Okawachi, A. G. Griffith, N. Picqué, M. Lipson and A. L. Gaeta, Nat. Commun., 2018, 9, 1869.
2. A. V. Muraviev, V. O. Smolski, Z. E. Loparo and K. L. Vodopyanov, Nat. Photonics, 2018, 12, 209.
3. J. S. Dam, P. Tidemand-Lichtenberg and C. Pedersen, Nat. Photonics, 2012, 6, 788.
4. D. Pestov, X. Wang, G. O. Ariunbold, R. K. Murawski, V. A. Sautenkov, A. Dogariu, A. V. Sokolov and M. O. Scully, Proc. Natl. Acad. Sci. U.S.A., 2008, 105, 422.
5. A. K. Majumdar and J. C. Ricklin, Free-Space Laser Communications: Principles and Advances, Springer Science & Business Media, New York, NY, 2010, vol. 2.
6. S.-F. Li, X.-M. Jiang, Y.-H. Fan, B.-W. Liu, H.-Y. Zeng and G.-C. Guo, Chem. Sci., 2018, 9, 5700.
7. A. Abudurusuli, J. Li and S. Pan, Dalton Trans., 2021, 50, 3155.
8. Z. Li, J. Yao and Y. Wu, Cryst. Growth Des., 2020, 20, 7550.
9. X. Chen and K. M. Ok, Chem.–Asian J., 2020, 15, 3709.
10. D. Mei, W. Cao, N. Wang, X. Jiang, J. Zhao, W. Wang, J. Dang, S. Zhang, Y. Wu, P. Rao and Z. Lin, Mater. Horiz., 2021, 8, 2330.
11. F. Liang, L. Kang, Z. Lin and Y. Wu, Cryst. Growth Des., 2017, 17, 2254.
12. I. Chung and M. G. Kanatzidis, Chem. Mater., 2014, 26, 849.
13. X. Cui, J. Xiao, Y. Wu, P. Du, R. Si, H. Yang, H. Tian, J. Li, W.-H. Zhang, D. Deng and X. Bao, Angew. Chem., Int. Ed. Engl., 2016, 55, 6708.
14. K. Wu, B. Zhang, Z. Yang and S. Pan, J. Am. Chem. Soc., 2017, 139, 14885.
15. L. Kang, M. Zhou, J. Yao, Z. Lin, Y. Wu and C. Chen, J. Am. Chem. Soc., 2015, 137, 13049.
16. C. Wu, X. Jiang, L. Lin, Y. Hu, T. Wu, Z. Lin, Z. Huang, M. G. Humphrey and C. Zhang, Angew. Chem., Int. Ed. Engl., 2021, 60, 22447.
17. H. Lan, F. Liang, X. Jiang, C. Zhang, H. Yu, Z. Lin, H. Zhang, J. Wang and Y. Wu, J. Am. Chem. Soc., 2018, 140, 4684.
18. Y.-J. Jia, Y.-G. Chen, Y. Guo, X.-F. Guan, C. Li, B. Li, M.-M. Liu and X.-M. Zhang, Angew. Chem., Int. Ed. Engl., 2019, 58, 17194.
19. X. Du, X. Guo, Z. Gao, F. Liu, F. Guo, S. Wang, H. Wang, Y. Sun and X. Tao, Angew. Chem. Weinheim Bergstr. Ger., 2021, 133, 23508.
20. G. Han, Y. Wang, X. Su, Z. Yang and S. Pan, Sci. Rep., 2017, 7, 1901.
21. B.-W. Liu, H.-Y. Zeng, X.-M. Jiang and G.-C. Guo, CCS Chem., 2020, 2, 964.
22. W. Zhou, W.-D. Yao, Q. Zhang, H. Xue and S.-P. Guo, Inorg. Chem., 2021, 60, 5198.
23. K. Wu, Y. Chu, Z. Yang and S. Pan, Chem. Sci., 2019, 10, 3963.
24. R.-A. Li, Z. Zhou, Y.-K. Lian, F. Jia, X. Jiang, M.-C. Tang, L.-M. Wu, J. Sun and L. Chen, Angew. Chem., Int. Ed. Engl., 2020, 59, 11861.
25. X. Luo, Z. Li, F. Liang, Y. Guo, Y. Wu, Z. Lin and J. Yao, Inorg. Chem., 2019, 58, 7118–7125.
26. Y.-N. Li, H. Xue and S.-P. Guo, Inorg. Chem., 2020, 59, 3546–3550.
27. H. Lin, W.-B. Wei, H. Chen, X.-T. Wu and Q.-L. Zhu, Coord. Chem. Rev., 2020, 406, 213150.
28. H. Huang, R. He, W. Yao, Z. Lin, C. Chen and Y. Zhang, J. Cryst. Growth, 2013, 380, 176–181.
29. Y. Wang, B. Zhang, Z. Yang and S. Pan, Angew. Chem., Int. Ed. Engl., 2018, 57, 2150–2154.
30. H. Huang, L. Liu, S. Jin, W. Yao, Y. Zhang and C. Chen, J. Am. Chem. Soc., 2013, 135, 18319–18322.
31. S. Jörgens, A. Mewis, R.-D. Hoffmann, R. Pöttgen and B. D. Mosel, Z. Anorg. Allg. Chem., 2003, 629, 429.
32. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
33. Q. Wei, C. He, K. Wang, X.-F. Duan, X.-T. An, J.-H. Li and G.-M. Wang, Eur. J. Chem., 2021, 27, 5880–5884.
34. M. Luo, F. Liang, X. Hao, D. Lin, B. Li, Z. Lin and N. Ye, Chem. Mater., 2020, 32, 2615–2620.
35. R. Yin, C. Hu, B.-H. Lei, S. Pan and Z. Yang, Phys. Chem. Chem. Phys., 2019, 21, 5142–5147.
36. H.-Y. Chang, S.-H. Kim, P. S. Halasyamani and K. M. Ok, J. Am. Chem. Soc., 2009, 131, 2426–2427.
37. W. Cai, Q. Jing and J. Zhang, New J. Chem., 2020, 44, 1228–1235.
38. M. Yan, H.-G. Xue and S.-P. Guo, Cryst. Growth Des., 2021, 21, 698–720.
39. Bruker APEX2, Bruker AXS Inc., Madison, WI, 2005.
40. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112.
41. E. Parthé and L. M. Gelato, Acta Crystallogr., Sect. A: Found. Crystallogr., 1984, 40, 169.
42. L. M. Gelato and E. Parthé, J. Appl. Crystallogr., 1987, 20, 139.
43. S. K. Kurtz and T. T. Perry, J. Appl. Phys., 1968, 39, 3798.
44. O. Jepsen, A. Burkhardt and O. K. Andersen, The Program TB-LMTO-ASA, Version 4.7, Max-Planck-Institut für Festkörperforschung, Stuttgart, Germany, 1999..
45. U. Barth and L. Hedin, J. Phys. C: Solid State Phys., 1972, 5, 1629.
46. B. G. Pfrommer, M. Côté, S. G. Louie and M. L. Cohen, J. Comput. Phys., 1997, 131, 233.
47. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
48. A. M. Rappe, K. M. Rabe, E. Kaxiras and J. D. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1227.
49. J. D Breshears and M. G. Kanatzidis, J. Am. Chem. Soc., 2000, 122, 7839.
50. V. Manrique, A. Galdámez, D. R. León, M. T. Garland and M. Jiménez, Z. Kristallogr. - New Cryst. Struct., 2003, 218, 163.
51. B. Ji, K. Pandey, C. P. Harmer, F. Wang, K. Wu, J. Hu and J. Wang, Inorg. Chem., 2021, 60, 10603.
52. F. Menzel, W. Brockner, W. Carrillo-Cabrera, H. G. Von Schnering and Z. Anorg, Allg. Chem., 1994, 620, 1081.
53. G. Cicirello, K. Wu and B. J. Wang, J. Solid State Chem., 2021, 296, 122017.
54. X. Wu, X. Gu, H. Pan, Y. Hu and K. Wu, Crystals, 2018, 8, 165.
55. L. Nian, K. Wu, G. He, Z. Yang and S. Pan, Inorg. Chem., 2018, 57, 3434.
56. Y. Guo, F. Liang, M. Zhou, Z. Lin, J. Yao and Y. Wu, J. Alloys Compd., 2018, 762, 143.
57. G. Cicirello, A. Swindle and J. Wang, J. Solid State Chem., 2021, 296, 122017.
58. J. Wang, Y. He, N. E. Mordvinova, O. I. Lebedev and K. Kovnir, Chem, 2018, 4, 1465.
59. J. Wang, J.-A. Dolyniuk, E. H. Krenkel, J. L. Niedziela, M. A. Tanatar, E. I. Timmons, T. Lanigan-Atkins, H. Zhou, Y. Cheng, A. J. Ramirez-Cuesta, D. L. Schlagel, U. S. Kaluarachchi, L.-L. Wang, S. L. Bud'ko, P. C. Canfield, R. Prozorov, O. Delaire and K. Kovnir, Chem. Mater., 2020, 32, 7932.
60. J. Dünner and A. Mewis, Z. Anorg. Allg. Chem., 1995, 621, 191.
61. J. Wang, P. Yox, J. Voyles and K. Kovnir, Cryst. Growth Des., 2018, 18, 4076.
62. I. Pilchowski and A. Mewis, Z. Anorg. Allg. Chem., 1990, 581, 173.
63. J. Wang, K. Lee and K. Kovnir, Inorg. Chem., 2017, 56, 783.
64. B. Ji, E. Guderjahn, K. Wu, T. H. Syed, W. Wei, B. Zhang and J. Wang, Phys. Chem. Chem. Phys., 2021, 23, 23696.
65. N. E. Brese and M. O'Keeffe, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 192.
66. N. A. Moroz, C. Bauer, L. Williams, A. Olvera, J. Casamento, A. A. Page, T. P. Bailey, A. Weiland, S. S. Stoyko, E. Kioupakis, C. Uher, J. A. Aitken and P. F. P. Poudeu, Inorg. Chem., 2018, 57, 7402.
67. Z. Li, Y. Liu, S. Zhang, W. Xing, W. Yin, Z. Lin, J. Yao and Y. Wu, Inorg. Chem., 2020, 59, 7614.
68. A. Abudurusuli, K. Wu, A. Tudi, Z. Yang and S. Pan, Chem. Commun., 2019, 55, 5143.

---

Footnote

† Electronic supplementary information (ESI) available: The crystallographic data, powder X-ray diffraction results, Tauc plots, DFT calculation, calculated birefringence, and the calculated SHG intensity map. CCDC 2119928. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1sc06849k

---