Open Access Article
Open Access ArticleThe importance of the compact disordered state in the fuzzy interactions between intrinsically disordered proteins†
Dan
Wang‡
a,
Shaowen
Wu‡
b,
Dongdong
Wang‡
c,
Xingyu
Song
a,
Maohua
Yang
a,
Wolun
Zhang
d,
Shaohui
Huang
ef,
Jingwei
Weng
*a,
Zhijun
Liu
*g and
Wenning
Wang
 *a
*a
aDepartment of Chemistry, Multiscale Research Institute of Complex Systems and Institute of Biomedical Sciences, Fudan University, Shanghai 200438, China. E-mail: jwweng@fudan.edu.cn; wnwang@fudan.edu.cn
bGuangdong Key Laboratory for Crop Germplasm Resources Preservation and Utilization, Agro-biological Gene Research Center, Guangdong Academy of Agricultural Sciences, Guangzhou 510640, Guangdong, China
cDP Technology, Beijing 100080, China
dLightEdge Technologies Limited, Zhongshan 528403, China
eInstitute of Biophysics, Chinese Academy of Sciences, Beijing 100101, China
fUniversity of Chinese Academy of Science, Beijing 101408, China
gNational Facility for Protein Science in Shanghai, Zhangjiang Lab, Shanghai Advanced Research Institute, Chinese Academy of Sciences, Shanghai 201210, China. E-mail: liuzhijun@sari.ac.cn
First published on 28th January 2022
Abstract
The intrinsically disordered C-terminal domain (CTD) of protein 4.1G is able to specifically bind a 26-residue intrinsically disordered region of NuMA, forming a dynamic fuzzy complex. As one of a few cases of extremely fuzzy interactions between two intrinsically disordered proteins/regions (IDPs/IDRs) without induced folding, the principle of the binding is unknown. Here, we combined experimental and computational methods to explore the detailed mechanism of the interaction between 4.1G-CTD and NuMA. MD simulations suggest that the kinetic hub states in the structure ensemble of 4.1G-CTD are favorable in the fuzzy complex. The feature of these hub states is that the binding ‘hot spot’ motifs βA and βB exhibit β strand propensities and are well packed to each other. The binding between 4.1G-CTD and NuMA is disrupted at low pH, which changes the intramolecular packing of 4.1G-CTD and weakens the packing between βA and βB motifs. Low pH conditions also lead to increased hydrodynamic radius and acceleration of backbone dynamics of 4.1G-CTD. All these results underscore the importance of tertiary structural arrangements and overall compactness of 4.1G-CTD in its binding to NuMA, i.e. the compact disordered state of 4.1G-CTD is crucial for binding. Different from the short linear motifs (SLiMs) that are often found to mediate IDP interactions, 4.1G-CTD functions as an intrinsically disordered domain (IDD), which is a functional and structural unit similar to conventional protein domains. This work sheds light on the molecular recognition mechanism of IDPs/IDRs and expands the conventional structure-function paradigm in protein biochemistry.
Introduction
Intrinsically disordered proteins or protein regions (IDPs/IDRs) are abundant in the eukaryotic proteome and play crucial roles in various cellular processes.1,2 IDPs/IDRs lack stably folded three-dimensional (3-D) structures under physiological conditions, thereby challenging the classical structure-function paradigm in protein biochemistry.2–8 The major functional role of IDPs/IDRs is mediating protein–protein interactions.6,7,9 Since the functional states of IDPs/IDRs are conformational ensembles,10 the potential functional advantage of IDP/IDRs is the ability to bind with multiple partners, perhaps in different conformations.11,12The molecular recognition process of IDPs/IDRs exhibits extreme diversity. Some IDPs/IDRs fold into stable structures upon binding, the so-called folding upon binding process.13,14 Yet more and more IDPs/IDRs have been found to form “fuzzy complexes”, in which the degree of disorder in the bound state may vary with the partner or cellular conditions.15–17 Fuzzy binding includes polymorphic bound structures, conditional folding and dynamic binding.18 The notion of fuzziness spans a broad spectrum of IDP/IDR-involved protein–protein interactions with dynamic and multivalent features, resulting in protein complex ensembles with heterogeneous conformation, promiscuous binding, stoichiometry and kinetics.9 While most of the reported fuzzy complexes are formed between one IDP/IDR and one structured protein/domain, extreme cases of fuzzy complexes between two IDPs/IDRs have recently been characterized.19–21 We previously reported the extremely fuzzy interaction between two disordered protein regions: the C-terminal domain of protein 4.1G (4.1G-CTD, aa 939–1005, Fig. 1a) and a 26-residue motif (aa 1800–1825, Fig. 1a) at the C-terminal region of nuclear mitotic apparatus (NuMA),19 which binds specifically and plays a major role in regulations of both symmetrical and asymmetrical cell divisions.19,22,23 4.1G-CTD and NuMA1800–1825 form a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex through dynamic multisite interactions without disorder-to-order transition.19 The molecular recognition mechanism in such an extreme fuzzy complex is, however, largely elusive. Unlike the extremely fuzzy complex formed between the disordered H1 and ProTα,20 in which the electrostatic attraction between two highly charged proteins is the dominant driving force, the binding between 4.1G-CTD and NuMA exhibits site specificity and hydrophobic interaction plays a major role.19 Different from the long-range electrostatic attraction, the short-ranged interactions such as hydrophobic effect, van der Waals interaction and hydrogen bonding require more specific pairings during the recognition process. Given the disordered nature of the two interacting partners, different conformations of the two IDRs have different capacities for binding, and even different stoichiometry of binding are possible. It is intriguing as to what conformations are favorable for binding and what the determinant factor of the binding affinity is. Here, through MD simulations and Markov state model (MSM) analysis, we have identified binding-relevant conformational states of 4.1G-CTD, which feature specific packing between two hydrophobic stretches that are molecular recognition ‘hot spots’. Then we have shown that the acidic pH condition would disrupt the binding between 4.1G-CTD and NuMA. At the same time, acidic pH condition was found to accelerate protein backbone dynamics and attenuate intra-molecular packing of 4.1G-CTD, suggesting that the tertiary structural attributes and stable local structural arrangement are crucial for molecular recognition in the fuzzy interaction between two IDRs.
1 complex through dynamic multisite interactions without disorder-to-order transition.19 The molecular recognition mechanism in such an extreme fuzzy complex is, however, largely elusive. Unlike the extremely fuzzy complex formed between the disordered H1 and ProTα,20 in which the electrostatic attraction between two highly charged proteins is the dominant driving force, the binding between 4.1G-CTD and NuMA exhibits site specificity and hydrophobic interaction plays a major role.19 Different from the long-range electrostatic attraction, the short-ranged interactions such as hydrophobic effect, van der Waals interaction and hydrogen bonding require more specific pairings during the recognition process. Given the disordered nature of the two interacting partners, different conformations of the two IDRs have different capacities for binding, and even different stoichiometry of binding are possible. It is intriguing as to what conformations are favorable for binding and what the determinant factor of the binding affinity is. Here, through MD simulations and Markov state model (MSM) analysis, we have identified binding-relevant conformational states of 4.1G-CTD, which feature specific packing between two hydrophobic stretches that are molecular recognition ‘hot spots’. Then we have shown that the acidic pH condition would disrupt the binding between 4.1G-CTD and NuMA. At the same time, acidic pH condition was found to accelerate protein backbone dynamics and attenuate intra-molecular packing of 4.1G-CTD, suggesting that the tertiary structural attributes and stable local structural arrangement are crucial for molecular recognition in the fuzzy interaction between two IDRs.
Results
The kinetic hub states are preferred in the 4.1G-CTD/NuMA complex
We have previously constructed the conformational ensemble of 4.1G-CTD based on replica exchange molecular dynamics (REMD) simulations.19 In order to obtain a more accurate equilibrium structural ensemble and the detailed conformational dynamics of 4.1G-CTD, we conducted large scale unbiased MD simulations (up to 185 μs) based on the previous REMD trajectories19 (see Methods for more details) and constructed a kinetic network model using Markov state model (MSM) analysis with the tICA (time-structure-based independent component analysis) algorithm (Fig. S1a and b†).24,25 NMR Cα chemical shifts were calculated using SHIFTX2 (ref. 26) based on the 1200-microstate MSM, yielding good agreement with the experimental results (Fig. S2a and b†). To gain more mechanistic insights into the kinetic behavior, the microstates were further lumped into 200 macrostates (Fig. S1c and d†). The mean first passage times (MFPTs) among the 200 macrostates were calculated. The time scales of the inter-state transitions among the most populated 50 states span a wide range from several microseconds to milliseconds (Fig. S2c†). The kinetic network of the first 50 states can be grouped into two sub-networks (Fig. 1b). In one of the sub-networks, state 1 with the second large population (10.6%) is a typical ‘hub state’, a concept proposed in studies of protein folding.27,28 The feature of hub state is that many states in the kinetic network can transit directly to the hub state with high rate, while transitions among the non-hub states are relatively slow and rare. Most of the states in this sub-network are directly connected to state 1. The hub state features of the 200 macrostates were quantitatively evaluated by calculating the respective ‘hub scores’.29 It turns out that state 1 has the highest hub score of 0.98 (Fig. S2d†). The second sub-network is composed of fewer states, though some are of high populations, including states 0, 2, 3, 5, 6, 7 (Fig. 1b). These states account for a significant portion (36.6%) of the total population, with relatively low hub scores around 0.2 (Fig. S2d†), and are roughly disconnected to state 1 in the kinetic network (Fig. 1b).The concept of hub state was first proposed in the protein folding study, where the folded structure of the protein is the kinetic hub that explains the two-state folding model.28 Here, 4.1G-CTD is an intrinsically disordered domain that lacks a unique well-folded structure. To investigate the role of the kinetic hub state in IDP's function, i.e. the interaction with NuMA, we examined the structural similarity between the 200 macrostates of free form 4.1G-CTD and those in the structural ensemble of 4.1G-CTD/NuMA complex (the structural ensemble of 4.1G-CTD/NuMA complex was taken from previous REMD simulations19). Since the free-form 4.1G-CTD and 4.1G-CTD/NuMA complex are both represented as structural ensembles, the harmonic ensemble similarity (HES) method30,31 was employed to evaluate the similarities. The correlation between HES and the state hub score is shown in Fig. 1c, revealing that two states (state 1 and 8, Fig. 1d) with the highest hub scores are most similar to the 4.1G-CTD structures in the complex (Fig. 1e). In another word, the high hub score states are preferred in the 4.1G-CTD/NuMA complex.
Inspection of the representative structures of state 1 and 8 reveals that both of them have two parallel β strands at the core of the CTD domain in addition to the stably folded αA helix, consisting of βA (955EKRIVIT961) and βB (988VTRVVV993) strands that are enriched with hydrophobic residues (Fig. 1d). In contrast to the stably folded αA helix, βA and βB strands are marginally stable and only appear in 1 and 8 among the ten most highly populated macrostates (Fig. S3†). Notably, the βB region (988VTRVVV993) encompasses a major NuMA binding motif on 4.1G-CTD and it has been previously showed that single mutation V988D or triple mutation V991,992,993D completely disrupted the interaction between 4.1G-CTD and NuMA.19 To examine the role of βA in the binding, we generated another triple mutation I958D/V959D/I960D to examine the role of βA in the binding. ITC measurements show that mutating these three hydrophobic residues significantly reduced NuMA binding affinity (Fig. S4,†KD = 333 ± 73 μM). Therefore, βA and βB are both NuMA binding ‘hot spots’ on 4.1G-CTD.
Lowering pH disrupts the interaction between 4.1G-CTD and NuMA
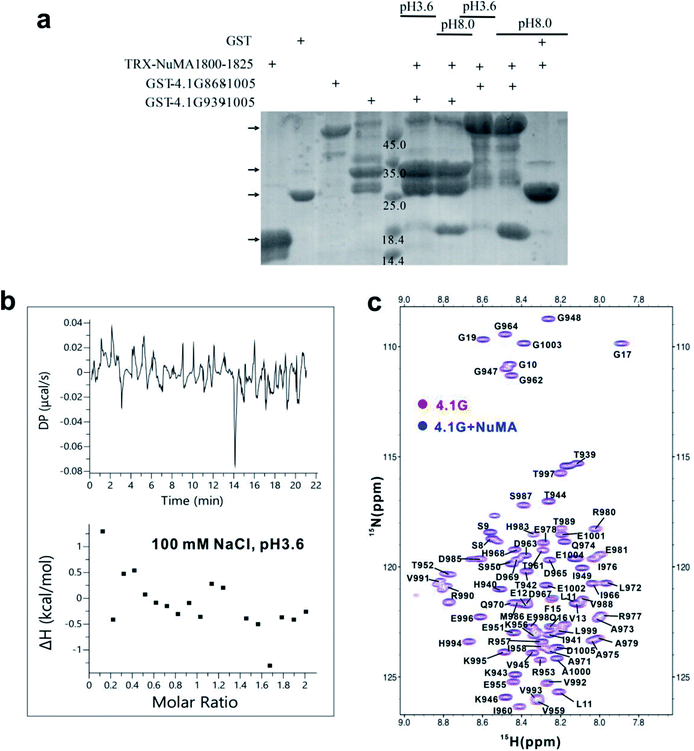
To verify the role of the hub-state conformations in the fuzzy interaction, we set out to find a condition that could disrupt the binding, and examine how the dysfunction condition changes the conformational ensemble of 4.1G-CTD. After a few tries, we found that acidic pH could disrupt the interaction. GST-pull down, isothermal titration calorimetry (ITC) and NMR 1H-15N HSQC spectra all indicate that 4.1G-CTD is not able to bind NuMA at pH 3.6 (Fig. 2 and S4a–d†). The 1H-15N HSQC spectrum of 4.1G-CTD at pH 3.6 displays limited amide proton chemical shift dispersion (Fig. 2c), indicating that 4.1G-CTD remains disordered. However, almost all resonance peaks experience significant chemical shift changes at pH 3.6 (Fig. S6a†). More resonances were observed at pH 3.6 with respect to the spectrum at neutral pH, leading to 84% backbone assignment (Fig. 2c, only 60% assignment was achieved at neutral pH). These results suggest that the conformational ensemble of 4.1G-CTD have been changed under acidic condition. To obtain better-resolved spectra, we carried out NMR measurements at 278 K under both pH conditions. The spectra qualities are higher at low temperature and more peak assignments were obtained (Fig. S6b and c,† 97.4% and 98.7% assignments were achieved for neutral and acidic pH conditions, respectively). By recording a series of HSQC spectra between 278 K and 298 K, some assignments at 278 K were transferred to the HSQC spectrum of 298 K and the assignment shown in Fig. 2c also achieves a level of 97.4%. We also characterized the binding between 4.1G-CTD and NuMA at 278 K, finding that the low temperature does not perturb the protein interaction (Fig. S7†). Therefore, we performed NMR experiments under 278 K in the following characterizations.Our previous work has shown that the binding between 4.1G-CTD and NuMA is multivalent and dynamic, including various non-covalent interactions, such as electrostatic interactions and hydrophobic interactions.19 At first glance, lowering the pH value directly affects the electrostatic interactions by changing the net charges of the two proteins. The protonation state prediction of 4.1G-CTD using H++32 indicates that the net charge number changes from −6 at neutral pH to +5 at pH 3.6, while that of NuMA changes from +7 to +8. Therefore, the like-charge repulsion between the two proteins seems to be a major factor that impairs the binding at acidic pH. To estimate the contribution of electrostatic interaction in 4.1G-CTD/NuMA binding, we compared the binding affinities at different ionic strengths. ITC measurements at neutral pH conditions showed that variation of ionic strength hardly changes the binding affinity (KD = 0.92–4.40 μM at 0–600 mM NaCl concentrations) (Fig. S8a–f†). We also carried out ITC measurements at acidic pH with different NaCl concentrations, and it turns out that 4.1G-CTD could not bind NuMA at various salt concentrations (Fig. 2b and S7g, h†). Therefore, ionic strength does not impact the interaction at both pH values. We have summarized the thermodynamics parameters of ITC measurements in Table S1.† The enthalpy changes are all favorable, and the entropy changes are negative, suggesting that the binding is enthalpy driven. The value of ΔH exhibits small variations with the change of salt concentrations. The value of −TΔS increases slightly with the increase of salt concentration. Therefore, the slight weakening of the binding with salt concentration increase is mainly an entropy effect. Overall, the inter-molecular electrostatic interaction induced by pH changes only has minor effects on the disruption of binding. The finding also strongly indicates that hydrophobic interactions have major contributions to 4.1G-CTD/NuMA binding, which are mainly between the βA and βB motifs on 4.1G-CTD and the 1814IINITM1819 motif on NuMA as has been shown previously.19 The loss of hydrophobic interactions could result from the pH-induced conformational changes.
The pH-induced secondary structure changes
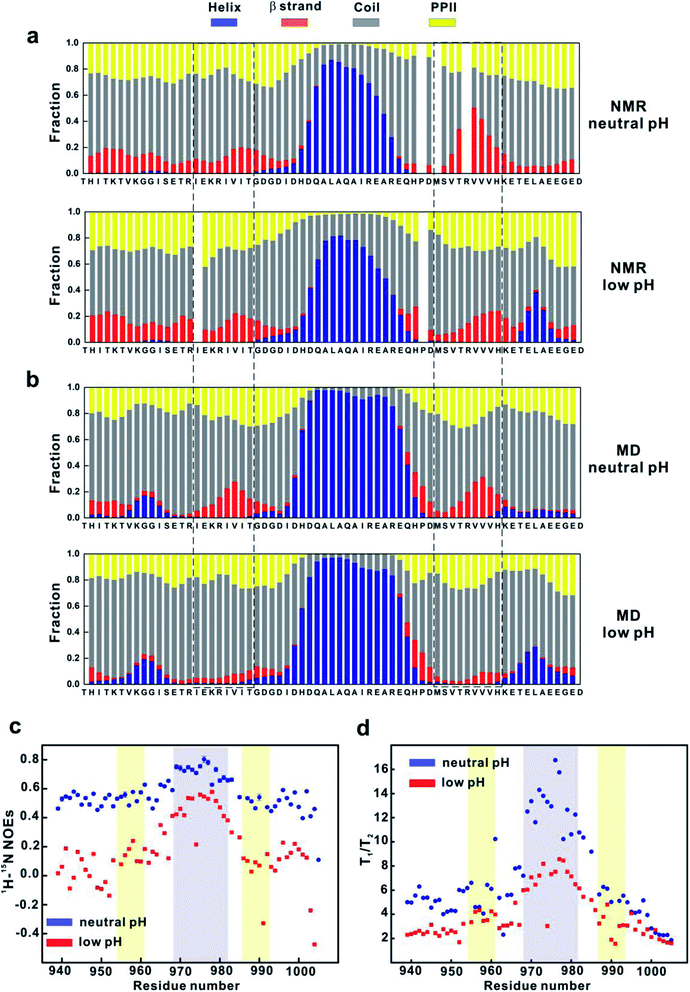
The MD simulation results suggest that conformational states with more stable βA and βB secondary structures (such as state 1 and 8 in MSM) could be important for binding. Therefore, we first examined whether acidic pH significantly changes the secondary structures of 4.1G-CTD. Calculation of the secondary structure propensities using the δ2D method33 based on NMR chemical shifts shows that αA helix remains stable at pH 3.6 (Fig. 3a). The most prominent change at pH 3.6 is that the most C-terminal end of CTD (aa 992–1005) has a much higher propensity of α-helix, while at neutral pH this region is mainly coil or PPII (Fig. 3a). The propensity of β strand within βB region is reduced upon lowering pH, while that of βA does not change (Fig. 3a). It is worth noting that the βA region has at most 20% fraction of β-strand element at both pH conditions.To obtain the atomic details of the structural ensemble and the secondary structure information of 4.1G-CTD at low pH, we performed 9.6 μs REMD simulations of 4.1G-CTD at pH 3.6 (see Methods for more details, Fig. S9, S10a and Table S2†). The calculated chemical shifts of Cα and the secondary chemical shifts (SCSs) of Cα are generally in good agreement with the NMR experiments (Fig. S10b and c†). The secondary structure fractions are also calculated using δ2D method.33 As shown in Fig. 3b, the secondary structure distributions and pH-induced changes based on MD simulation generally agree with those from NMR measurements, i.e. αA helix remains stable, C-terminal end (aa 992–1005) has a higher propensity of α-helix and the β strand propensity within βB region decreased at low pH (Fig. 3b). Different from the NMR results, lowering pH also results in an obvious reduction of the β strand propensity within the βA region in MD simulation (Fig. 3b). Therefore, both NMR and MD show evidence of β strand propensity reduction within the βB region under low pH, but only MD simulation show β-strand reduction at the βA region. On the other hand, MD simulations in our previous work demonstrated that NuMA binding does not change the propensities of βA and βB strands obviously, while NMR spectra did not show obvious chemical shift changes but line broadening upon NuMA binding.19 Altogether, we concluded that the reduction of β-strand content is only partially responsible for the loss of function of CTD under pH 3.6.
Lowering pH accelerates the backbone dynamics of 4.1G-CTD
Besides the changes of local secondary structures, we went on to explore the changes of the overall conformation and backbone dynamics of 4.1G-CTD under low pH. To explore the backbone dynamics of 4.1G-CTD, we carried out NMR spin relaxation experiments to measure the T1, T2 and 15N-1H nuclear Overhauser effects (NOEs) under both pH conditions. At neutral pH, the heteronuclear NOEs of 4.1G-CTD are all between 0.4 and 0.6 except the αA region, with values around 0.7–0.8 (Fig. 3c). The NOEs are particularly sensitive to fast local motions, with typical values for rigid fragments in structured proteins around 0.9 and those for highly flexible sites in the disordered regions being largely negative. Therefore, the NOE profile of 4.1G-CTD is consistent with the secondary structure analysis, where the αA helix is stably folded and the other regions are mainly disordered with transient secondary structures. Notably, the NOEs of all residues at pH 3.6 decreased obviously with respect to those under neutral pH (Fig. 3c), suggesting that the overall mobility of the protein increased. However, the αA region still exhibits relatively higher NOE values than other regions (Fig. 3c). The chemical shifts analysis indicates that the αA helix under pH 3.6 is as stable as that under neutral pH and the secondary structure propensity in other regions of CTD did not obviously decrease upon lowering pH. So the decreased NOE values suggest that the intra-molecular packing of CTD becomes weaker at low pH.In line with this, the spin relaxation times T1 and T2 show the similar trend. For structured proteins, the ratio of T1/T2 is proportional to the overall rotational correlation time of the tumbling motion of the molecule. For IDPs/IDRs, the concept of overall rotational correlation time is no longer applicable. However, as long as there are relatively stable structure motifs in the IDP, the concept of tumbling is applicable and the T1/T2 ratio allows distinguishing regions with significant secondary and tertiary structural propensities from the completely unstructured regions. In 4.1G-CTD, the αA region exhibits higher T1/T2 ratios (Fig. 3d), corresponding to longer rotational correlation time, than the rest parts of the protein. Under low pH, most of the T1 values decrease at the αA region and increase at other regions, while T2 increased for all residues (Fig. S11†). The resulting T1/T2 values for all residues are smaller than those at neutral pH except for a few sites (Fig. 3d). The αA region still exhibits higher T1/T2 values relative to other regions.
As a control, we also measured the T1, T2 and NOE values of 4.1G-CTD in the presence of NuMA (Fig. S12†). Since NuMA binding leads to line broadening, the experiments were carried out under an unsaturated concentration of NuMA, with a molar ratio of NuMA to 4.1G-CTD being 0.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The NOE values do not exhibit obvious changes while the T1/T2 values increase slightly for almost all residues upon NuMA binding (Fig. S12a and b†), indicating that the backbone dynamics is slowed down. The increases are more obvious at N-terminus, βA and βB regions (Fig. S12b†).
1. The NOE values do not exhibit obvious changes while the T1/T2 values increase slightly for almost all residues upon NuMA binding (Fig. S12a and b†), indicating that the backbone dynamics is slowed down. The increases are more obvious at N-terminus, βA and βB regions (Fig. S12b†).
Overall, the spin relaxation experiments demonstrate that at low pH the backbone dynamics of 4.1G-CTD is accelerated, a change that is most likely originated from the attenuated intra-molecular packing.
Lowering pH leads to increased dimension of 4.1G-CTD
The accelerated backbone dynamics revealed by the spin relaxation experiments suggests that 4.1G-CTD is less compact under pH 3.6. To address this, we measured the hydrodynamics radius RH of 4.1G-CTD by using fluorescence correlation spectroscopy (FCS). As expected, the hydrodynamics radius of 4.1G-CTD increased upon lowering pH (Fig. S13,†Table 1). The mean values of RH under pH 6.8 and pH 3.6 are 1.56 ± 0.22 and 2.02 ± 0.20 nm, respectively. Theoretical values of RH could be estimated according to different scale laws. As shown in Table 1, the theoretical RH of 4.1G-CTD at neutral pH is close to folded proteins. This is consistent with our previous prediction by calculating the charge/hydropathy (C/H) ratios (Fig. S4 in ref. 19). Therefore, 4.1G-CTD at neutral pH could be described as a compact disordered state, and lowering pH increases its RH to average value of IDPs (Table 1).| Model | R (Å) |
|---|---|
| a MG stands for molten globule. b Ref. 1, Tcherkasskaya O. et al., J. Proteome Res., 2003, 2, 37–42. c Ref. 2, March J. A. and Forman-Kay J. D., Biophys. J., 2010, 98, 2383–2390. | |
| R (native) = (0.75 ± 0.05)M(0.33± 0.02)b | 12.0–15.5–19.9 |
| R (MG)a = (0.90 ± 0.10)M(0.33±0.02)b | 13.7–18.6–24.8 |
| R (pre-MG)a = (0.60 ± 0.10)M(0.40±0.02)b | 16.4–23.6–33.0 |
| R (coiled) = (0.28 ± 0.10)M(0.49±0.01)b | 21.3–25.1–29.5 |
| R (8 M urea) = (0.22 ± 0.01) M(0.52±0.01)b | 22.6–26.0–29.8 |
| R (6 M GdnHCl) = (0.19 ± 0.01) M(0.54±0.01)b | 23.3–27.0–31.1 |
| R (folded) = 4.92N0.285c | 17.6 |
| R (denatured) = 2.33N0.549c | 27.0 |
| R (IDP) = 2.49N0.509c | 24.2 |
| R = (1.24Ppro + 0.904)(0.00759|Q| + 0.963)0.901 × 2.49N0.509c | 20.6 |
| R H (FCS) pH = 6.8 | 15.6 ± 2.2 |
| R H (FCS) pH = 3.6 | 20.2 ± 2.0 |
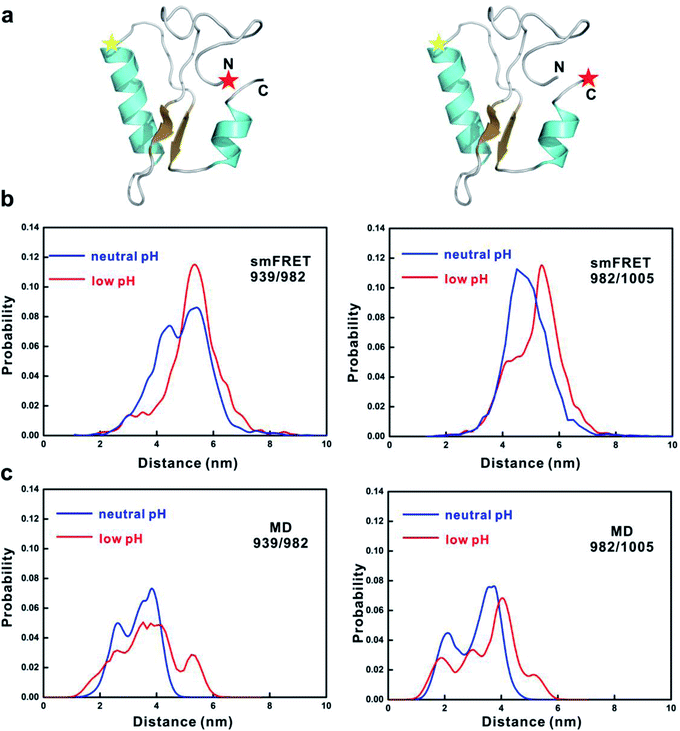
To further consolidate the dimensional change of 4.1G-CTD from neutral to low pH, we performed smFRET measurements at low pH and compared the results with those at neutral pH.19 Two pairs of fluorescence dye labeling sites for donor and acceptor (939/982 and 982/1005) were generated by mutating Thr939, Gln982 and Asp1005 to cysteine and labeled with Alex555 and Alex647, respectively (Fig. 4a). At low pH, the FRET efficiency distributions of both labeling systems shift toward the low values (Fig. S14†). In order to compare the results from smFRET measurements and MD simulations, we converted the FRET efficiency to inter-dye distance and used the available volume method34,35 to calculate the donor-acceptor distances of the MD snapshots. In both labeling systems, the distance distributions calculated from MD simulations shift to larger values, qualitatively in agreement with the smFRET results (Fig. 4b and c). Therefore, both FCS and smFRET measurements demonstrate that the conformation of 4.1G-CTD is less compact under low pH.
Details of pH-induced changes of intra-molecular interactions in 4.1G-CTD
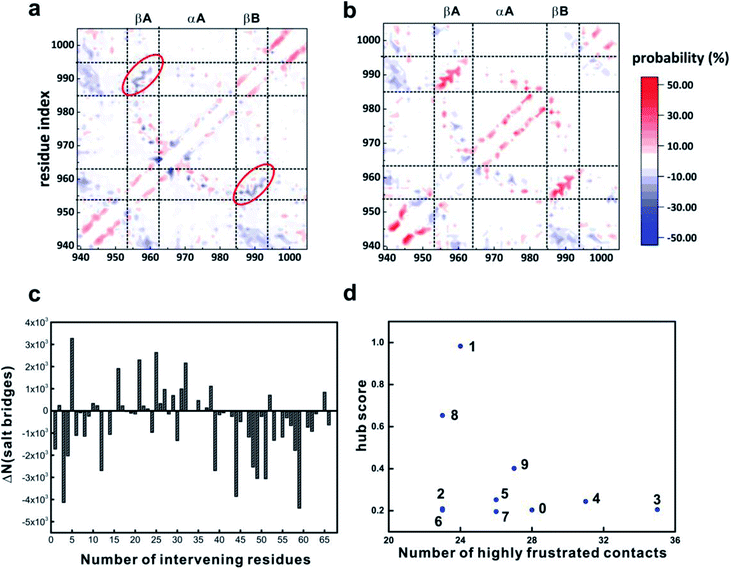
To exploit the atomic details of the conformational changes of 4.1G-CTD under low pH, the intra-molecular contacts were analyzed using the MD simulation results. Calculations based on the MD trajectories at two pH conditions demonstrate that the total number of intra-molecular contacts is only reduced by 1.11% at pH 3.6, though the contact maps reveal notable differences. The intra-molecular contact map at neutral pH shows that relatively stable long-range interactions occur between βA and βB (Fig. S15a,† highlighted with red ovals). This β-sheet motif also contacts αA helix with high probability (Fig. S15a,† highlighted with green ovals), forming a metastable βA–αA–βB motif that is prominent in state 1 and 8 of the MSM (Fig. 1c). The difference of contact probabilities of 4.1G-CTD at two pH conditions shows that the probability of long-range contacts between βA and βB decreased obviously at low pH, while some of the local contacts increased due to the higher helical propensity at low pH (Fig. 5a). Interestingly, the comparison of the contact maps of isolated 4.1G-CTD and 4.1G-CTD/NuMA complex (REMD simulation results obtained from our previous work) at neutral pH reveals that the probability of contacts between βA and βB increased upon NuMA-binding (Fig. 5b). These results suggest that the intra-molecular interactions between βA and βB are important for 4.1G-CTD/NuMA complex and the pH-induced functional loss could be largely ascribed to the weakened interaction between βA and βB.In line with the above analysis, detailed statistics show that the average number of hydrogen bonds related to βA and βB at low pH, neutral pH and 4.1G/NuMA complex system are 1.19, 2.00 and 3.36, respectively. On the other hand, the total number of salt bridges during the simulation at pH 3.6 exhibits a significant decrease (by 21.6%) with respect to neutral pH (Fig. S15d†). Interestingly, almost all salt-bridges with >35 intervening residues decrease significantly upon lowering pH (Fig. 5c). The loss of long-range electrostatic interactions may account for the expansion of the overall dimension of 4.1G-CTD. In conclusion, the acidic environment changes the protonation state of 4.1G-CTD and the decrease of intra-molecular electrostatic interactions attenuates the tertiary compaction of 4.1G-CTD and the specific packing between βA and βB, which is crucial for NuMA binding.
The potential role of NuMA in the pH-induced disruption of 4.1G-CTD/NuMA interaction
Since acidic pH could also change the property of NuMA, thus affecting the 4.1G-CTD/NuMA interaction. To examine this possibility, we generated a mutant D1824A of NuMA, and examined its binding affinity to 4.1G-CTD at both neutral and acidic pH conditions. The reasoning is: in the sequence of NuMA1800–1825 (Fig. 1a), D1824 is the only residue that may change protonation state at pH 3.6. If the pH-induced property change of D1824 could significantly change the ensemble of NuMA and is crucial for binding, the D1824A mutation may rescue the 4.1G/NuMA interaction at pH 3.6. The ITC measurements in Fig. S16† show that the binding property of D1824A is similar to that of wild type NuMA, i.e. being able to bind 4.1G-CTD at neutral pH and unable to bind at acidic pH. This indicates that D1824A mutation does not disturb 4.1G/NuMA binding at neutral pH and the protonation state change of D1824 at pH 3.6 is unlikely a cause for loss of interaction between 4.1G-CTD and NuMA.Discussion
In previous work, we have shown that the interaction between the intrinsically disordered 4.1G-CTD and NuMA1800–1825 is highly dynamic, without a persistent binding interface and large-scale disorder-to-order transition.19 On the other hand, multiple ‘hot spots’ have been identified, among which the hydrophobic interactions show major contributions to binding. Here, we have tried to explore the recognition mechanism underlying this fuzzy interaction. The major finding underscores the role of structural attributes in IDP interaction. Firstly, the local secondary structure propensity may play a role in binding. The βA and βB region encompass the major hydrophobic binding sites of the interaction, and both of them have transient β strand propensities. The characters of βA and βB seemingly comply with the concept of preformed structure elements,36 which are transient secondary structural elements in IDPs/IDRs. The concept of preformed structure element was proposed to explain the folding upon binding recognition process. Most preformed structure elements (if not all) experience disorder-to-order transitions, or become stably folded upon target binding. The case of βA and βB in 4.1G-CTD is different from the situation in folding upon binding interactions. Although MD simulation shows that the contact number between βA and βB increased upon NuMA binding (Fig. 5b), the β-strand populations of these two regions are very similar with those in free form 4.1G-CTD (Fig. S7 in ref. 19). In another word, the βA and βB motifs are target recognition ‘hot spots’ on 4.1G-CTD for NuMA binding and the interaction between 4.1G-CTD and NuMA slows down the backbone dynamics of 4.1G-CTD (Fig. S12b†) without inducing folding or large-scale transition to ordered structures in 4.1G-CTD. Therefore, the secondary structure propensity may not be a stringent requirement for binding, at least its role is different from that of the preformed structure element.Secondly, the tertiary structure could be more important for molecular recognition of 4.1G-CTD. It was shown that the acidic pH condition accelerates the backbone dynamics and results in conformational expansion of 4.1G-CTD. This suggests that the spatial organization of the key binding motifs, i.e. βA and βB stretches, is critical for molecular recognition. Although 4.1G-CTD is intrinsically disordered, the compaction of the domain helps to maintain a metastable/transient ‘binding interface’ for target recognition. Here, the feature of the ‘binding interface’ is likely the effective packing between βA and βB, as demonstrated in the MD simulations. These two hydrophobic stretches have major contributions to binding affinity, thereby holding βA and βB in close proximity may facilitate target recognition. The backbone dynamics is the other side of the coin, which is more restrained at neutral pH with respect to that at lower pH, and NuMA binding further slows down the backbone motions.
The case of 4.1G-CTD/NuMA reveals a new binding principle of the molecular recognition of IDPs. We have shown that the specificity is not only originated from the physicochemical complementarity of the ‘hot spot’ motifs on the two IDPs, but is also dependent on the compaction and tertiary conformational state of 4.1G-CTD. The advantage of the compact state in ligand-binding, however, is not modulating the accessibility of the target-binding ‘hot spots’. Comparison of the solvent accessible surface areas (SASAs) of the hydrophobic residues under both pH conditions shows that lowering pH does not lead to larger exposure of these residues (Fig. S17†). Therefore, the functional role of compaction is to spatially organize the recognition motifs. The structural attributes, in addition to the physicochemical properties of the recognition motifs, are crucial for binding affinity and specificity.
Protein–protein interactions of many IDP/IDRs are mediated via short sequence-embedded motifs called short linear motifs (SLiMs).37,38 SLiMs are typically 6–12 residues long and can often be recognized as patterns of conserved residues within a sparsely conserved sequence stretch.37 The SLiM is the central anchoring site for IDP interactions. In recent years, it has been realized that the interaction of IDP/IDRs could not be totally explained by the SLiM anchoring sites of binding, the flanking region and the entire context of the disordered chain need to be taken into account.39 As for 4.1G-CTD, the context should be considered as a domain. The notion of intrinsically disordered domain (IDD) was considered as a new kind of protein–protein interaction module of IDPs40 4.1G-CTD was originally identified as one of the two conserved domains in 4.1 proteins from vertebrates to invertebrates, while the other is known as FERM domain.41,42 According to the domain boundary defined by C. Scott et al., the C-terminal half of CTD, which corresponds to the fragment we used in this study (4.1G 939–1005), is more conserved than the N-terminal half (Fig. S18†).42 In line with this, our previous work found that the longer fragments including less conserved N-terminal half residues (4.1G 886–1005 and 4.1G 868–1005) do not show a significant increase of binding affinities.19 Moreover, the sequences of βA and βB do not exhibit a higher degree of conservation than the rest regions within 4.1G-CTD-939–1005.42 These evidences suggest that the highly conserved 4.1G-CTD-939–1005 is a functional and structural unit that was inherited during evolution. Although it lacks one unique 3-D structure, the tertiary structural attributes necessary for ligand binding are encoded in the sequence. In this respect, IDD like 4.1G-CTD is not very different from a conventional protein domain. It was previously believed that one major distinction between IDDs and short linear motifs (SLiM)37,38 is that SLiMs can only bind ordered partners but IDDs are able to bind ordered partners as well as other IDDs through mutual induced folding.40 The binding between 4.1G-CTD and NuMA represents a case of one SLiM (NuMA1800–1825) binds to one IDD without induced folding. We speculate that IDDs, like structured protein domains, are able to bind SLiMs or other IDDs and not necessarily through induced folding. The structure attributes encoded in the conserved sequence of IDDs are key determinants of binding affinity.
The role of hydrophobic packing is well known to be the main driving force for protein folding. Hydropathy is also correlated to the compaction of IDRs.43 However, for 4.1G-CTD the hydrophobic residues are not obviously more buried at neutral pH with respect to low pH (Fig. S17†), implying that the hydrophobic effect may not be the main determinant for protein dimension. On the other hand, charge interaction can also drive compaction. pH-induced expansion of 4.1G-CTD is most likely the effect of net charge changes, as indicated by the simulation results. Despite the different driving forces, the compaction of IDDs may have similar kinetic attributes as the folding of a structured domain, such as the hub state feature revealed by the MSM analysis of 4.1G-CTD. The native state in protein folding is often considered a kinetic hub, but that is not always the case.29 The hub score analyses have been mostly applied to structured proteins, except one previous simulation study of hIAPP peptide that found no kinetic hub exists in this intrinsically disordered peptide.44 Here, we found that 4.1G-CTD, a compact disordered domain, also has kinetic hub states and they are more favorable in the fuzzy complex than the non-hub states. This might be due to the compactness of 4.1G-CTD, which has a similar hydrodynamic radius with folded domains and molten globules. There is correlation between hub score and similarity to complex (Fig. 1c). On the other hand, relatively higher β-strand content is the most obvious structure feature of high hub score states (state 1 and state 8), but we could not say that these two factors are quantitatively related. The higher hub score does not necessarily correspond to higher β-strand content.
The kinetic hub feature may also be related to frustration.45 It was recently found that although binding induced folding results in well-defined structures in the bound state, there is often multiple qualitatively different folding pathways in the process, thereby leading to high frustration.46,47 On the other hand, in the processes of fuzzy interactions local frustrations are often minimized though not totally eliminated.46 Notably, the conformational states with high hub scores (states 1 and 8 in the MSM) also have the least frustrated contacts (Fig. 5d). This may partly explain the role of hub states in the molecular recognition of IDP. We realized that there remain many unanswered questions about the exact role of kinetic hub states in the IDP binding process. For example, to answer the question as to what is the relationship between the hub state and the low pH condition, we need much more simulations at low pH to analyze the kinetic behavior of 4.1G-CTD in its dysfunctional state. In addition, ligand binding may also change the kinetics of an IDP/IDR, and we also need to examine the kinetic hubs in the complex system. Moreover, it is not for sure if kinetic hubs are prevalent in IDPs. These will be the topics of our future study.
It is worth noting that pH change could also affect the property of NuMA, thus affecting its binding to 4.1G-CTD. We did not perform NMR characterization of NuMA because it suffers from severe aggregation at higher concentrations. The boundary of the NuMA fragment used here (1800–1825) is necessary and sufficient for binding to 4.1G-CTD. We have tried to prepare several longer fragments of NuMA, but the sample qualities are even worse. To make a detour, we generated a mutant D1824A of NuMA to explore the role of NuMA. It turns out that the D1824A mutation does not affect the interaction between 4.1G-CTD and NuMA. We know that this could not totally exclude the possibility that acidic pH-induced property change of NuMA contributes to the disruption of 4.1G/NuMA binding. In the future study, perturbation of the 4.1G-CTD conformational ensemble could be realized by generating point mutations on 4.1G without disturbing NuMA.
Methods
Protein expression and purification
Fragments of human 4.1G and NuMA were individually cloned into a modified version of pET32a vector or pGEX-4T-1 vector, with the resulting proteins containing a Trx tag or GST tag at the N-termini. For NMR experiments, 4.1G-CTD (939–1005) were cloned into a pET-M3C vector, with the resulting proteins containing a His6 tag at the N-termini. All of the mutations were created through a standard PCR-based mutagenesis method and confirmed by DNA sequencing. Recombinant proteins were expressed in E. coli BL21 (DE3) host cells at 16 °C and were purified by using Ni2+-NTA or GST-agarose affinity chromatography followed by size-exclusion chromatography. Uniformly 15N/13C-labeled 4.1G-CTD were prepared by growing the bacteria in an M9 minimal medium using 15NH4Cl as the sole nitrogen source or 15NH4Cl and 13C-labeled glucose as the sole nitrogen and carbon source, respectively. All protein samples for NMR backbone assignment experiments were in a PBS buffer of pH 6.8 or 3.6 (23 mM Na2HPO4, 27 mM NaH2PO4, 1 mM EDTA, and 1 mM 2-mercaptoethanol). The protein sample for NMR titration and spin relaxation experiments were in a PBS buffer of pH 7.1 or 3.6 (23 mM Na2HPO4, 27 mM NaH2PO4, 1 mM EDTA, and 1 mM 2-mercaptoethanol).GST pull-down assay
GST or GST-tagged fusion protein (8 μM for the final concentration) were first loaded to 40 μl GSH-Sepharose 4B slurry beads in a 500 μl assay buffer containing 50 mM Tris (pH 8.0 or 3.6), 100 mM NaCl, 1 mM 2-mercaptoethanol and 1 mM EDTA. The GST fusion protein-loaded beads were then mixed with potential binding partners (24 μM each for the final concentration), and the mixtures were incubated for 1 h at 4 °C. After four times washing, proteins captured by affinity beads were eluted by boiling, resolved by 15% SDS-PAGE, and detected by Coomassie blue staining.Isothermal titration calorimetry
ITC measurements were performed on an ITC200 Micro calorimeter (MicroCal) at 18 °C. All protein samples were dissolved in a buffer containing 50 mM Tris (pH 8.0 or pH 3.6), 100 mM NaCl, and 1 mM EDTA. The titrations were carried out by injecting 40 μl aliquots of the 4.1G fragments (0.5 mM) into NuMA fragments (0.05 mM) at time intervals of 2 min to ensure that the titration peak returned to the baseline. The titration data were analyzed using the program Origin7.0 and fitted with the one-site binding model.NMR experiments
NMR spectra were acquired at 298 K or 278 K on Bruker AVIII 600 and 900 MHz spectrometers. Backbone resonance assignments of 4.1G-CTD were achieved by standard heteronuclear correlation experiments, including HNCO, HNCACB, CACB(CO)NH using a ∼1 mM 15N/13C-labeled protein sample at 298 K, and ∼0.3 mM 15N/13C-labeled protein sample at 278 K. 15N relaxation experiments were carried out as described by Farrow et al.48 on a Bruker AVIII 600 MHz spectrometer using a 15N-labeled 4.1G-CTD sample at a protein concentration of 0.1 mM. With a 2 s recycle delay, T1 and T2 were measured with eight (2, 20, 40, 80, 160, 320, 640 and 1280 ms) and ten relaxation delays (0, 20, 40, 80, 100, 120, 160, 200, 300 and 400 ms), respectively. The spectra measuring 1H-15N NOEs were acquired with a 2 s relaxation delay, and followed by a 3 s period of proton saturation. In the absence of proton saturation, the spectra were recorded with a relaxation delay of 5 s. NMR data were processed and analyzed with NMRPipe49 and Sparky. The secondary structure propensity (SSP) scores were calculated using the Cα and Cβ chemical shifts with the method proposed by Marsh J. A. et al.50smFRET experiments and data process
The double cysteine mutants of 4.1G were generated and purified. The 4.1G mutant proteins were labeled with the donor (Alexa Fluor 555-maleimide, Thermo Fisher Scientific Inc., MA, U.S.), and acceptor (Alexa Fluor 647-maleimide, Thermo Fisher Scientific Inc., MA, U.S.) by following the vendor provided protocol. The unreacted dye was separated from the labeled protein by using size exclusion chromatography (SEC).We first cleaned the glass coverslip and drilled glass slide by sonicating them in water and ethanol three times respectively, then etched them in plasma cleaner (PDC-002, Harrick Plasma Inc., NY, U.S.) for 5 min to destroy the residual dusts further. Then, we stuck the coverslip on the bottom of the drilled glass slide to make a flow cell. We added about 100 μl 0.1 mg ml−1 poly-lysine-PEG-NTA (PLL(20)-g[3.5]-PEG(2)-NTA, SuSoS AG Inc., Switzerland) solution to the flow cell and incubated it for 20 min in order to put a layer of PEG on the coverslip surface and passivate it. After we washed the flow cell with buffer thoroughly, we added 0.1 M NiCl2 solution to introduce Ni2+ to the NTA. After 20 min incubation and complete wash, we added 1 nM labeled 4.1G solution to the flow cell in order to tether the protein down to the glass surface upon the binding between the His-tag of 4.1G and the NTA group on the PEG layer. To examine the non-specific binding of molecules to the glass, we performed control experiment without adding NiCl2 solution. We observed very few fluorescent spots on the coverslip that is less than 6% of the number of fluorescent spots in the presence of NiCl2. Such small portion of non-specific binding suggests that its effect is negligible.
The single molecule FRET images were taken by using a home-built wide-field fluorescence imaging system with an exposure time of 100 ms. In the titration experiment, one thousand-fold molar excess of NuMA was used. The single molecule FRET time trace was extracted from the image by using iSMS software51 and the statistical histogram of FRET was fitted to the sum of two Gaussian functions by using Matlab (Mathworks Inc., MA, U.S.) program. The detailed methods refer to our previous work.52
To make a direct comparison between smFRET and simulation, the FRET efficiency ET was converted to the donor–acceptor distance r according to:
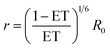 | (1) |
For Alexa555 and Alexa647, the effective Förster radius R0 was set to 51 Å. The MD simulation systems did not explicitly include the fluorophores since the large size of the dye molecules would significantly increase the computational costs. Therefore, we used the available volume (AV) method34,35 to calculate the inter-dye distance based on MD snapshots. This method uses a simple geometrical algorithm assuming that all dye positions are equally probable and there are no interactions between the dyes and the protein. The python script of AV method written by K. Walczewska-Szewc et al.35 was employed here to calculate the inter-dye distance. The distance distributions of smFRET measurement have a systematic deviation from those of the MD simulations (Fig. 4b and c). Such discrepancy could be caused by the errors from both experiment and simulation. From the simulation side, sampling could not be perfect although the enhanced sampling algorithm REMD method was employed. And since we did not explicitly include dye molecules in the simulation, AV method could also introduce errors. From the experimental side, errors include the uncertainty in FRET efficiency measurements, and the variations of effective Förster radius R0 due to anisotropic tumbling of the donor and acceptor fluorophores, or changes in the donor quantum yield. R0 is proportional to the sixth roots of the orientation factor κ2 and the donor quantum yield QD. The orientation factor κ2, which is assigned a value of 0.67 based on an assumption of perfect isotropic tumbling can in fact sample a wide range of values.
MD simulations of 4.1G-CTD at neutral pH
We conducted extensive conventional MD simulations of 4.1G-CTD based on previous REMD simulations. 109 initial conformations were obtained from our previous work19 and each was used to conduct 500 ns MD simulation. Specifically, we used the Gromos algorithm with a backbone RMSD cut-off of 0.3 nm to conduct the cluster analysis of the previous REMD trajectory. 109 clusters were obtained and the central structure of each cluster was chosen as the initial conformation. Then, we divided all these trajectories into 100 clusters using k-centers clustering algorithm. We randomly chose two or three conformations from each cluster and initiated the second round MD simulations from them. Finally, we obtained 370 trajectories, each lasting 500 ns and summing up to 185 μs of simulation time in total. All parameters of the seeding MD simulations were the same as in our previous work.19MSM construction of protein 4.1G at neutral pH
The MSMBuilder3.8 software53 was used to construct the Markov state model (MSM). The backbone dihedral angles φ and ψ were used as features and time-lagged independent component analysis (tICA)24,54 was used for dimensionality reduction. tICA is a variant of principal component analysis and it computes the time-lag correlation matrix, whose eigenvectors represent linear combinations of the most slowly decorrelating degrees of freedom in a system. The time-lag correlation matrices were calculated with a delta time of 130 ns and the phase space was projected onto the slowest 5 tICs. Then we clustered the reduced phase space into 1200 states using k-medoids algorithm. We constructed the count matrix Cij(τ) by counting the number of transitions from state i to state j after a lag time τ. From the count matrix, we used the maximum likelihood estimate to obtain the transition probability matrix, T. If the model is Markovian, the dynamics can be propagated to long time scale dynamics:| P(nΔt) = [T(Δt)nP(0)] | (2) |
The implied timescales, τk, are computed from the eigenvalues as follows:
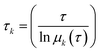 | (3) |
The MFPT from state i to state f, mif, is defined as the average time taken to reach state f for the first time given that the system was initially in state i. The MFPT between two states can be determined by solving the following linear system of equations:56
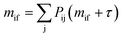 | (4) |
REMD simulation of protein 4.1G at low pH
The conformational ensemble of 4.1G939–1005 at pH 3.6 was explored using replica-exchange molecular dynamics (REMD)57–59 simulations. Four initial structures were used the same as our previous work19 which from the structural prediction programs I-TASSER60,61 and QUARK62 and were evenly distributed in 48 different replicas for REMD simulation. The protonation states at pH 3.6 were predicated by the server H++,32 and thus 11 titratable residues were protonated. GROMACS-4.6.5 software package was used to conduct the simulation with CHARMM force field63 and the TIP3P water model. Na+ and Cl− ions were added to neutralize uncompensated charges, and further conferred a salt concentration of 0.1 M. Steepest descent algorithm was used to minimize the energy of the system, and the added solvent was equilibrated with position restraints on the heavy atoms of the protein. The temperatures were maintained using the V-rescale method with a relaxation time of 0.1 ps. We used the Parrinello–Rahman barostat64 to keep the pressure at 1 bar with a time constant of 2 ps. The cutoff of electrostatic interactions and van der Waals interactions were both set to be 1.2 nm, and the particle mesh Ewald method65 was used to treat electrostatic interactions. All bonds were constrained by the LINCS algorithms.66 A total of 48 different temperatures ranging from 310–430 K were generated from the web server Temperature generator for REMD-simulations. The exchange time between two adjacent replicas was 2 ps and each replica lasted for 200 ns. The average acceptance ratio was 23%. To confirm the convergence of the simulation, we checked the backbone RMSD, probabilities of secondary structure contents, the ratio of hydrophilic/hydrophobic SASA of 4.1G939–1005 within two independent time intervals (60–130 and 130–200 ns), which are all very similar (Fig. S8†).The last 140 ns of trajectories at 310 K were used for analysis. All secondary structure analyses of the simulation trajectories were performed using the DSSP program. Chemical shift prediction based on REMD simulations was performed using the SHIFTX2 software. Secondary chemical shift Δδ, such as Δδ of Cα (ΔδCα), is defined as ΔδCα = δCαexp/simu − δCαrandom. When calculating the contact probability map, two residues within 0.3 nm were regarded as a contact, and the contacts between residue i and i + 1 as well as those between residue i and i + 2 were not counted because the probabilities of these contacts are always close to 1 no matter what the secondary structure is.
Data availability
The experimental and computational data have already been presented in the manuscript and ESI.†Author contributions
Wenning Wang, Zhijun Liu and Jingwei Weng designed and conceived the project. Dan Wang and Shaowen Wu performed the biochemical experiments. Dan Wang and Zhijun Liu performed NMR experiments and spectra analysis. Shaowen Wu performed smFRET experiments and data analysis. Wolun Zhang and Shaohui Huang performed the FCS experiments and data analysis. Jingwei Weng designed the computer simulation plan. Dongdong Wang, Jingwei Weng, Xingyu Song and Maohua Yang performed the MD simulation, MSM construction and data analysis. Wenning Wang, Jingwei Weng and Zhijun Liu prepared the manuscript. All authors contributed to data interpretation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Ministry of Science and Technology of the People's Republic of China (2016YFA0501702), National Natural Science Foundation of China (22073018, 21877017), Shanghai Municipal Science and Technology Major Project (No. 2018SHZDZX01) and Zhangjiang Lab for the financial support.References
- P. E. Wright and H. J. Dyson, Nat. Rev. Mol. Cell Biol., 2015, 16, 18–29 CrossRef CAS PubMed.
- R. van der Lee, M. Buljan, B. Lang, R. J. Weatheritt, G. W. Daughdrill, A. K. Dunker, M. Fuxreiter, J. Gough, J. Gsponer, D. T. Jones, P. M. Kim, R. W. Kriwacki, C. J. Oldfield, R. V. Pappu, P. Tompa, V. N. Uversky, P. E. Wright and M. M. Babu, Chem. Rev., 2014, 114, 6589–6631 CrossRef CAS PubMed.
- A. K. Dunker, J. D. Lawson, C. J. Brown, R. M. Williams, P. Romero, J. S. Oh, C. J. Oldfield, A. M. Campen, C. R. Ratliff, K. W. Hipps, J. Ausio, M. S. Nissen, R. Reeves, C. H. Kang, C. R. Kissinger, R. W. Bailey, M. D. Griswold, M. Chiu, E. C. Garner and Z. Obradovic, J. Mol. Graph. Model., 2001, 19, 26–59 CrossRef CAS PubMed.
- A. K. Dunker and J. Gough, Curr. Opin. Struct. Biol., 2011, 21, 379–381 CrossRef CAS PubMed.
- N. Rezaei-Ghaleh, M. Blackledge and M. Zweckstetter, Chembiochem, 2012, 13, 930–950 CrossRef CAS PubMed.
- P. Tompa, Curr. Opin. Struct. Biol., 2011, 21, 419–425 CrossRef CAS PubMed.
- H. J. Dyson and P. E. Wright, Nat. Rev. Mol. Cell Biol., 2005, 6, 197–208 CrossRef CAS PubMed.
- V. N. Uversky, Int. J. Biochem. Cell Biol., 2011, 43, 1090–1103 CrossRef CAS PubMed.
- J. Weng and W. Wang, Curr. Opin. Struct. Biol., 2020, 62, 9–13 CrossRef CAS PubMed.
- V. N. Uversky and A. K. Dunker, Biochim. Biophys. Acta, 2010, 1804, 1231–1264 CrossRef CAS PubMed.
- W. L. Hsu, C. J. Oldfield, B. Xue, J. Meng, F. Huang, P. Romero, V. N. Uversky and A. K. Dunker, Protein Sci., 2013, 22, 258–273 CrossRef CAS PubMed.
- V. N. Uversky, Front. Phys., 2019, 7, 10 CrossRef.
- H. J. Dyson and P. E. Wright, Curr. Opin. Struct. Biol., 2002, 12, 54–60 CrossRef CAS PubMed.
- P. E. Wright and H. J. Dyson, Curr. Opin. Struct. Biol., 2009, 19, 31–38 CrossRef CAS PubMed.
- P. Tompa and M. Fuxreiter, Trends Biochem. Sci., 2008, 33, 2–8 CrossRef CAS PubMed.
- M. Fuxreiter, Mol. Biosyst., 2012, 8, 168–177 RSC.
- R. Sharma, Z. Raduly, M. Miskei and M. Fuxreiter, FEBS Lett., 2015, 589, 2533–2542 CrossRef CAS PubMed.
- M. Fuxreiter, Int. J. Mol. Sci., 2020, 21, 8615 CrossRef CAS PubMed.
- S. Wu, D. Wang, J. Liu, Y. Feng, J. Weng, Y. Li, X. Gao, J. Liu and W. Wang, Angew. Chem., Int. Ed., 2017, 56, 7515–7519 CrossRef CAS PubMed.
- A. Borgia, M. B. Borgia, K. Bugge, V. M. Kissling, P. O. Heidarsson, C. B. Fernandes, A. Sottini, A. Soranno, K. J. Buholzer, D. Nettels, B. B. Kragelund, R. B. Best and B. Schuler, Nature, 2018, 555, 61–66 CrossRef CAS PubMed.
- W. Wang and D. Wang, Biomolecules, 2019, 9, 81 CrossRef CAS PubMed.
- T. Kiyomitsu and I. M. Cheeseman, Cell, 2013, 154, 391–402 CrossRef CAS PubMed.
- L. Seldin, N. D. Poulson, H. P. Foote and T. Lechler, Mol. Biol. Cell, 2013, 24, 3651–3662 CrossRef CAS PubMed.
- G. Perez-Hernandez, F. Paul, T. Giorgino, G. De Fabritiis and F. Noe, J. Chem. Phys., 2013, 139, 015102 CrossRef PubMed.
- C. R. Schwantes and V. S. Pande, J. Chem. Theory Comput., 2013, 9, 2000–2009 CrossRef CAS PubMed.
- B. Han, Y. Liu, S. W. Ginzinger and D. S. Wishart, J. Biomol. NMR, 2011, 50, 43–57 CrossRef CAS PubMed.
- F. Rao and A. Caflisch, J. Mol. Biol., 2004, 342, 299–306 CrossRef CAS PubMed.
- G. R. Bowman and V. S. Pande, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 10890–10895 CrossRef CAS PubMed.
- A. Dickson and C. L. Brooks 3rd, J. Chem. Theory Comput., 2012, 8, 3044–3052 CrossRef CAS PubMed.
- K. Lindorff-Larsen and J. Ferkinghoff-Borg, PLoS One, 2009, 4, e4203 CrossRef PubMed.
- M. Tiberti, E. Papaleo, T. Bengtsen, W. Boomsma and K. Lindorff-Larsen, PLoS Comput. Biol., 2015, 11, e1004415 CrossRef PubMed.
- R. Anandakrishnan, B. Aguilar and A. V. Onufriev, Nucleic Acids Res., 2012, 40, W537–W541 CrossRef CAS PubMed.
- C. Camilloni, A. De Simone, W. F. Vranken and M. Vendruscolo, Biochemistry, 2012, 51, 2224–2231 CrossRef CAS PubMed.
- S. Sindbert, S. Kalinin, H. Nguyen, A. Kienzler, L. Clima, W. Bannwarth, B. Appel, S. Muller and C. A. Seidel, J. Am. Chem. Soc., 2011, 133, 2463–2480 CrossRef CAS PubMed.
- K. Walczewska-Szewc and B. Corry, Phys. Chem. Chem. Phys., 2014, 16, 12317–12326 RSC.
- M. Fuxreiter, I. Simon, P. Friedrich and P. Tompa, J. Mol. Biol., 2004, 338, 1015–1026 CrossRef CAS PubMed.
- N. E. Davey, K. Van Roey, R. J. Weatheritt, G. Toedt, B. Uyar, B. Altenberg, A. Budd, F. Diella, H. Dinkel and T. J. Gibson, Mol. Biosyst., 2012, 8, 268–281 RSC.
- K. Van Roey, B. Uyar, R. J. Weatheritt, H. Dinkel, M. Seiler, A. Budd, T. J. Gibson and N. E. Davey, Chem. Rev., 2014, 114, 6733–6778 CrossRef CAS PubMed.
- K. Bugge, I. Brakti, C. B. Fernandes, J. E. Dreier, J. E. Lundsgaard, J. G. Olsen, K. Skriver and B. B. Kragelund, Front. Mol. Biosci., 2020, 7, 110 CrossRef CAS PubMed.
- P. Tompa, M. Fuxreiter, C. J. Oldfield, I. Simon, A. K. Dunker and V. N. Uversky, Bioessays, 2009, 31, 328–335 CrossRef CAS PubMed.
- A. J. Baines, H. C. Lu and P. M. Bennett, Biochim. Biophys. Acta, 2014, 1838, 605–619 CrossRef CAS PubMed.
- C. Scott, G. W. Phillips and A. J. Baines, Eur. J. Biochem., 2001, 268, 3709–3717 CrossRef CAS PubMed.
- A. S. Holehouse and R. V. Pappu, Annu. Rev. Biophys., 2018, 47, 19–39 CrossRef CAS PubMed.
- Q. Qiao, G. R. Bowman and X. Huang, J. Am. Chem. Soc., 2013, 135, 16092–16101 CrossRef CAS PubMed.
- H. Frauenfelder, S. G. Sligar and P. G. Wolynes, Science, 1991, 254, 1598–1603 CrossRef CAS PubMed.
- S. Gianni, M. I. Freiberger, P. Jemth, D. U. Ferreiro, P. G. Wolynes and M. Fuxreiter, Acc. Chem. Res., 2021, 54, 1251–1259 CrossRef CAS PubMed.
- M. I. Freiberger, P. G. Wolynes, D. U. Ferreiro and M. Fuxreiter, J. Phys. Chem. B, 2021, 125, 2513–2520 CrossRef CAS PubMed.
- N. A. Farrow, R. Muhandiram, A. U. Singer, S. M. Pascal, C. M. Kay, G. Gish, S. E. Shoelson, T. Pawson, J. D. Forman-Kay and L. E. Kay, Biochemistry, 1994, 33, 5984–6003 CrossRef CAS PubMed.
- F. Delaglio, S. Grzesiek, G. W. Vuister, G. Zhu, J. Pfeifer and A. Bax, J. Biomol. NMR, 1995, 6, 277–293 CrossRef CAS PubMed.
- J. A. Marsh, V. K. Singh, Z. Jia and J. D. Forman-Kay, Protein Sci., 2006, 15, 2795–2804 CrossRef CAS PubMed.
- S. Preus, S. L. Noer, L. L. Hildebrandt, D. Gudnason and V. Birkedal, Nat. Methods, 2015, 12, 593–594 CrossRef CAS PubMed.
- Y. Feng, L. Zhang, S. Wu, Z. Liu, X. Gao, X. Zhang, M. Liu, J. Liu, X. Huang and W. Wang, Angew. Chem., Int. Ed., 2016, 55, 13990–13994 CrossRef CAS PubMed.
- M. P. Harrigan, M. M. Sultan, C. X. Hernandez, B. E. Husic, P. Eastman, C. R. Schwantes, K. A. Beauchamp, R. T. McGibbon and V. S. Pande, Biophys. J., 2017, 112, 10–15 CrossRef CAS PubMed.
- L. Molgedey and H. G. Schuster, Phys. Rev. Lett., 1994, 72, 3634–3637 CrossRef PubMed.
- J. H. Prinz, H. Wu, M. Sarich, B. Keller, M. Senne, M. Held, J. D. Chodera, C. Schutte and F. Noe, J. Chem. Phys., 2011, 134, 174105 CrossRef PubMed.
- N. Singhal, C. D. Snow and V. S. Pande, J. Chem. Phys., 2004, 121, 415–425 CrossRef CAS PubMed.
- Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141–151 CrossRef CAS.
- U. H. E. Hansmann, Chem. Phys. Lett., 1997, 281, 140–150 CrossRef CAS.
- U. H. E. Hansmann and Y. Okamoto, J. Comput. Chem., 1993, 14, 1333–1338 CrossRef CAS.
- Y. Zhang, BMC Bioinf., 2008, 9, 40 CrossRef PubMed.
- A. Roy, A. Kucukural and Y. Zhang, Nat. Protoc., 2010, 5, 725–738 CrossRef CAS PubMed.
- D. Xu and Y. Zhang, Proteins, 2012, 80, 1715–1735 CrossRef CAS PubMed.
- P. Bjelkmar, P. Larsson, M. A. Cuendet, B. Hess and E. Lindahl, J. Chem. Theory Comput., 2010, 6, 459–466 CrossRef CAS PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc06825c |
| ‡ These authors contribute equally to the work. |
| This journal is © The Royal Society of Chemistry 2022 |