A small-molecule organic ferroelectric with piezoelectric voltage coefficient larger than that of lead zirconate titanate and polyvinylidene difluoride

Abstract

Piezoelectric materials that generate electricity when deforming are ideal for many implantable medical sensing devices. In modern piezoelectric materials, inorganic ceramics and polymers are two important branches, represented by lead zirconate titanate (PZT) and polyvinylidene difluoride (PVDF). However, PVDF is a nondegradable plastic with poor crystallinity and a large coercive field, and PZT suffers from high sintering temperature and toxic heavy element. Here, we successfully design a metal-free small-molecule ferroelectric, 3,3-difluorocyclobutanammonium hydrochloride ((3,3-DFCBA)Cl), which has high piezoelectric voltage coefficients g₃₃ (437.2 × 10⁻³ V m N⁻¹) and g₃₁ (586.2 × 10⁻³ V m N⁻¹), a large electrostriction coefficient Q₃₃ (about 4.29 m⁴ C⁻²) and low acoustic impedance z₀ (2.25 × 10⁶ kg s⁻¹ m⁻²), significantly outperforming PZT (g₃₃ = 34 × 10⁻³ V m N⁻¹ and z₀ = 2.54 × 10⁷ kg s⁻¹ m⁻²) and PVDF (g₃₃ = 286.7 × 10⁻³ V m N⁻¹, g₃₁ = 185.9 × 10⁻³ V m N⁻¹, Q₃₃ = 1.3 m⁴ C⁻², and z₀ = 3.69 × 10⁶ kg s⁻¹ m⁻²). Such a low acoustic impedance matches that of the body (1.38–1.99 × 10⁶ kg s⁻¹ m⁻²) reasonably well, making it attractive as next-generation biocompatible piezoelectric devices for health monitoring and “disposable” invasive medical ultrasound imaging.

---

Introduction

Existing piezoelectric devices, such as sensors, transducers, actuators, surface acoustic wave devices, frequency control devices, ultrasound imaging devices, and energy-harvesting devices, command a huge market value of multibillion dollars.^1–6 Each application generally requires different piezoelectric characteristics, i.e., corresponding to the different figures of merit (FOM).⁷ Of particular note is the piezoelectric voltage constant g, which serves as a useful FOM for characterizing the sensitivity of sensors by relating the applied stress and induced voltage (g_ij = d_ij/ε, where d is the piezoelectric strain coefficient and ε is the dielectric permittivity).^8,9 To obtain a high g is extremely challenging, as any increase in d often brings forth a greatly increased ε.^10,11 Upon measuring force, torque, strain, pressure, acceleration, and acoustic emission, piezoelectric sensors have established their pervasive influence in medicine, the military, and civilian and automobile industries with fascinating technologies from ultrasound imaging to underwater ultrasound, underwater acoustic sensors, smart sensor systems, and non-destructive testing.¹² It is expected that the application range of sensors will continue to further grow with emerging piezoelectric materials, improved performance, or tailored properties.

The key obstacles to realizing a desirable piezoelectric sensor material include a large g₃₃ for better detecting the generated signal above the background noise, a high Curie temperature (T_c) that is crucial towards extending the usage temperature range, and especially the adaptability to varying environmental conditions.¹³ Since the 1950s, inorganic ferroelectric ceramics represented by barium titanate (BTO) and lead zirconate titanate (PZT) have been the leading piezoelectric materials.^14–16 Nevertheless, their g₃₃ values are relatively limited (<40 × 10⁻³ V m N⁻¹), while the high acoustic impedance poses problems when operated in a hydrostatic environment and bodily tissues.¹⁷ If the difference in the acoustic impedance of the two media is large, most of the energy will not be transmitted and will be reflected. The obvious comparison is ferroelectric polymers like polyvinylidene difluoride (PVDF), which has been widely investigated as a sensor material because of the much higher g₃₃ coefficient up to 286.7 × 10⁻³ V m N⁻¹, as well as enhanced acoustic impedance matching with water or the human body.^18–22 As the representative and the most important organic ferroelectrics without toxic metals, their attractive advantages of solution-based low-temperature processing, low fabrication cost, biocompatibility, and integrability with silicon technology also show great promise for next-generation wearable and biomedical devices.²³ Notably, there are also inevitable challenges for PVDF. Although much effort has been made to reduce the large coercive field (∼0.5 MV cm⁻¹ for PVDF),^24,25 due to the nature of the polymer, switching polarization still needs to overcome the large energetic barrier. Moreover, the usage of PVDF will be further hindered by the poor crystallinity and nondegradable properties of plastic, and the degraded polar properties after being heated to about 353 K.²⁶

Actually, the family of organic ferroelectrics is not just limited to those well-known and extensively studied polymers, but includes small-molecule ferroelectric materials. In addition to most of the above attractive superiorities of organic ferroelectrics, these simple small-molecule candidates can also possess potentially easier, less expensive, and lower power processing than their polymeric counterparts.^27–31 More importantly, as compared to PVDF, they also give added large benefits like the ability to form a long-range crystalline order and the freedom of molecular design, offering a rich platform for engineering high-g₃₃ piezoelectric materials. A renewed surge of interest in the field of organic electronics has occurred in the past decade, and there is a strong impetus to explore replacement metal-free small-molecule materials with comparable piezoelectric or ferroelectric properties to those of commercial inorganic and polymeric species.^32–34 Herein, on the basis of the substitution strategy of hydrogen by F atoms in the prototype compound cyclobutanammonium hydrochloride ((CBA)Cl), we obtained a metal-free small-molecule ferroelectric, 3,3-difluorocyclobutanammonium hydrochloride ((3,3-DFCBA)Cl) (Scheme S1 and Table S1†).^35–37 The introduction of F atoms changes the hydrogen bonding network and results in a polar crystal structure. Its unprecedentedly high g₃₃ coefficient of 437.2 × 10⁻³ V m N⁻¹ of the (3,3-DFCBA)Cl thin film far outperforms that of the state-of-art ferroelectric ceramics and is two times larger than that of PVDF. Moreover, this purely organic component endows (3,3-DFCBA)Cl with a low acoustic impedance (2.25 × 10⁶ kg s⁻¹ m⁻²), comparable to that of PVDF (3.69 × 10⁶ kg s⁻¹ m⁻²) and an order of magnitude lower than that of inorganic ferroelectric ceramics (PZT, 2.54 × 10⁷ kg s⁻¹ m⁻²), which matches that of the body (1.38–1.99 × 10⁶ kg s⁻¹ m⁻²) reasonably well.¹⁸ This combination of outstanding piezoelectric properties and good biocompatibility suggests that (3,3-DFCBA)Cl may replace PVDF in some applications such as health monitoring and medical ultrasound imaging, with benefits in terms of easiness and environment-friendly processing.

Results and discussion

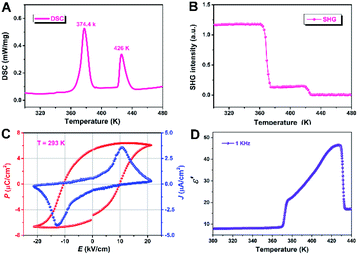
The solid–solid phase transition behavior of (3,3-DFCBA)Cl and (CBA)Cl was first determined by differential calorimetric scanning (DSC) measurement. The powder sample was placed in an aluminum crucible and tested under a nitrogen atmosphere with a rate of 20 K min⁻¹. As shown in Fig. 1, the DSC curve of (3,3-DFCBA)Cl shows two endothermic peaks at 374.4 K (T_c1) and 426 K (T_c2) in the heating run, while the prototype compound (CBA)Cl has only one endothermic peak at 318.6 K (T_c) in the heating run (Fig. S1†). It is worth noting that, compared with the prototype compound (CBA)Cl, the phase transition temperature (T_c) of the H/F substituted compound (3,3-DFCBA)Cl is significantly improved. This is due to the introduction of the F atom, which can raise the potential energy barrier of molecular tumbling motion, thereby increasing the T_c. Similar phenomena can be observed in (pyrrolidinium)MCl₃ (M = Mn²⁺ and Cd²⁺), and [benzylammonium]₂PbCl₄.^35–38

Fig. 1 Ferroelectric properties of (3,3-DFCBA)Cl. (A) DSC curve and (B) temperature-dependent SHG intensity of (3,3-DFCBA)Cl in the heating run, showing two phase transitions at 374.4 and 426 K, respectively. (C) P–E hysteresis loop of (3,3-DFCBA)Cl measured at 293 K by using the double-wave method. (D) The dependence of the real part ε′ of (3,3-DFCBA)Cl at 1 kHz for a polycrystalline sample in the heating run.

For ferroelectric materials, compounds must crystallize in the ten polar point groups (C₁, C₂, C_s, C_2v, C₄, C_4v, C₃, C_3v, C₆, and C_6v). Therefore, second harmonic generation measurements were performed on (3,3-DFCBA)Cl and (CBA)Cl to detect whether the compound has inversion symmetry. For convenience, the phase below T_c1 can be labeled as the low-temperature phase (LTP), the phase above T_c2 as the high-temperature phase (HTP), and the phase between T_c1 and T_c2 as the intermediate-temperature phase (ITP). As shown in Fig. 1B and S2,† (3,3-DFCBA)Cl and (CBA)Cl show a clear second harmonic generation (SHG) signal at room temperature, representing the SHG activity. It is worth noting that the SHG intensity of (3,3-DFCBA)Cl is stronger than that of (CBA)Cl, which can be attributed to the enhanced dipole moment of an organic cation after H/F substitution. For (3,3-DFCBA)Cl, the SHG intensity drops sharply from 1.2 to 0.14 around T_c1 and then drops to about 0 around T_c2. While for (CBA)Cl, the SHG intensity drops sharply from 0.78 to 0.41 around T_c1. The variable-temperature SHG measurements indicate that (3,3-DFCBA)Cl undergoes phase transitions from noncentrosymmetry to noncentrosymmetry and then to centrosymmetry, while (CBA)Cl undergoes a phase transition from noncentrosymmetry to noncentrosymmetry.

The polarization–electric field (P–E) hysteresis loops were measured to characterize the switchable polarization of (3,3-DFCBA)Cl by using the double-wave method. A typical ferroelectric J–E (current density–electric field) curve is shown in Fig. 1C with two opposite peaks at 293 K. According to the J–E curve, we obtained the P–E hysteresis loop by measuring the current. Under the influence of the applied voltage, the measured saturated polarization (P_s) value is about 6.4 μC cm⁻², which is close to the calculated value (6.9 μC cm⁻²) depending on the point charge model (Fig. S3†).

In the vicinity of T_c, dielectric permittivity as a function of temperature generally shows noticeable anomalies in ferroelectrics. As shown in Fig. 1D, the real part ε′ of the dielectric constant of the (3,3-DFCBA)Cl polycrystalline sample at 1 kHz maintains a very low value about 7.88 at 300 K and its value is almost constant in the temperature range of 300–370 K (LTP). Near T_c1, the ε′ shows a significant increase with a step type, entering into ITP, and then increasing gradually. When the temperature increases to T_c2, the ε′ exhibits a remarkable λ-shape dielectric response, and finally stabilizes in the HTP. Similarly, (CBA)Cl also shows obvious dielectric anomalies near the phase transition temperature, which is consistent with the DSC measurement (Fig. S4†). The real part ε′ of the dielectric constant for the (CBA)Cl polycrystalline sample is about 2.6 at 1 kHz and 1.9 at 1 MHz at 300 K, respectively. Specifically, the ε′ measured here is the relative dielectric constant ε_r.

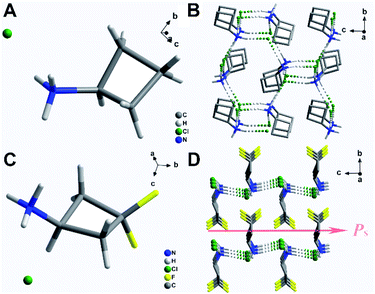
The crystal data for (3,3-DFCBA)Cl and (CBA)Cl are summarized in Table S2.† At 293 K, (CBA)Cl crystallizes in the orthorhombic chiral space group P2₁2₁2₁ with cell parameters of a = 7.8522(6) Å, b = 8.8201(6) Å, c = 8.9227(6) Å, and V = 617.96(8) ų, which means that it is impossible for (CBA)Cl to have ferroelectricity. Fortunately, when the F atom replaces the H atom in the para position of the CBA molecule, (3,3-DFCBA)Cl crystallizes in the orthorhombic polar space group Pmn2₁ with cell parameters of a = 6.0473(4) Å, b = 7.0878(5) Å, c = 7.6493(5) Å, and V = 327.87(4) ų, meaning the possibility of ferroelectricity. As shown in Fig. 2A and C, all the crystal structures of (CBA)Cl and (3,3-DFCBA)Cl consist of monoprotonated cations and Cl anions, all in an ordered state. In particular, the introduction of F atoms has subtly changed the molecular structure of CBA. As shown in Fig. S5 and Table S3,† the plane angle of the CBA molecule decreases from 32.6(2)° in CBA to 22.6(2)° in 3,3-DFCBA, and the N1–C1–C3 bond angle changes from 146.0(2)° to 139.5(2)°. The different molecular sizes and the degree of twist in the molecular structure between CBA and 3,3-DFCBA directly affect the hydrogen bonding interaction, and then change the packing mode of the crystal structure. In the (CBA)Cl and (3,3-DFCBA)Cl crystals, each H atom on the N atom forms N–H⋯Cl hydrogen bonding interaction with its adjacent Cl atoms with a donor–acceptor distance from 3.17(2) Å to 3.22(1) Å (Fig. S5 and Table S4†). As shown in Fig. 2B and S6C,† CBA cations arrange in an anti-parallel manner in the ac plane and form a three-dimensional network through hydrogen bonding interaction. However, (3,3-DFCBA)Cl forms a two-dimensional hydrogen bonding network in the ac plane (Fig. 2D and S6D†). Different from (CBA)Cl, 3,3-DFCBA cations align head-to-head in the ac plane and tilt towards the same direction along the c-axis, which should lead to a spontaneous polarization (P_s).

Fig. 2 Crystal structures of (CBA)Cl and (3,3-DFCBA)Cl. The structural unit of (CBA)Cl (A) and (3,3-DFCBA)Cl (C) at 293 K. Packing views of (CBA)Cl (B) and (3,3-DFCBA)Cl (D) along the a-axes at 293 K. Hydrogen atoms were omitted for clarity. The green dashed lines stand for the N–H⋯Cl hydrogen bonding interactions. The direction of spontaneous polarization of (3,3-DFCBA)Cl is shown with the red arrow.

In order to explore the ferroelectric phase transition of (3,3-DFCBA)Cl, we have tried to determine the crystal structure of the paraelectric phase. Unfortunately, the crystal of (3,3-DFCBA)Cl becomes nontransparent at 363 K before T_c1, resulting in poor X-ray diffraction. Thanks to the low phase transition temperature of the prototype compound (CBA)Cl (T_c = 318.6 K), we successfully obtained the HTP crystal structure of (CBA)Cl at 343 K. (CBA)Cl crystallized in the cubic chiral space group P2₁3 at 343 K. As shown in Fig. S7,† and the CBA cations are located in a special position of the three-fold rotation axes in the HTP, which are highly disordered compared to the ordered state in the LTP. Thus, it can be inferred that the phase transitions of (3,3-DFCBA)Cl are also caused by the ordered-disordered transition of cations. This kind of phase transition caused by ordered-disordered molecular motion is very common in the molecular-based ferroelectric system, such as 3-hydroxyquinucline hydrochloride.³⁹ To further determine the HTP of (3,3-DFCBA)Cl, variable-temperature powder X-ray diffraction (PXRD) measurements were carried out to provide some information about the phase transition behaviors (Fig. S8†). The pattern in the HTP of (3,3-DFCBA)Cl shows obvious changes in the number of diffraction peaks. The Pawley refinements indicate a few possible tetragonal systems with the point group 4/mmm for (3,3-DFCBA)Cl. This simulation result is consistent with the SHG measurement. According to the Aizu rule, the phase transition from the 4/mmm to mm2 point group in (3,3-DFCBA)Cl is definitely a ferroelectric one with the Aizu notion of 4/mmmFmm2, revealing a multiaxial ferroelectric characteristic.

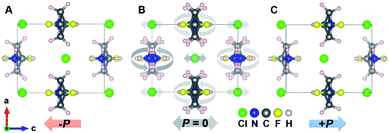
In order to gain deep insight into the ferroelectric polarization reversal, density functional theory (DFT) calculations were carried out to evaluate the origin of polarization.^40,41 According to the modern theory of polarization,^42,43 the necessity of constructing a polarization change path lies in selecting the polarization quantum properly to avoid a wrong estimation of the polarization value. A dynamic path between two ferroelectric states is constructed based on the crystal structure obtained from single crystal X-ray diffraction. Accordingly, the structure of the room temperature ferroelectric phase at 293 K is used as one ferroelectric configuration, while the other states are obtained from the matrix transformation of the coordinates considering both the rotation of the 3,3-DFCBA cations and displacement of anionic Cl⁻ (Fig. 3). In the dynamic path, the sense of 3,3-DFCBA cation rotation is defined as a pair of clockwise and counterclockwise rotations to keep the polarization along the c axis during the ferroelectric reversal (canceling each other perpendicular to the c-axis). The variation of polarization as a function of the dynamic path is shown in Fig. S9A,† from which the ferroelectric polarization with 7.62 μC cm⁻² along the c-axis can be extracted from two equivalent ferroelectric configurations (λ = ±1). During the ferroelectric switching process (−1 < λ < 1), the polarization value changes monotonously, and becomes zero at λ = 0, which indicates a reference phase with zero polarization. On the other hand, the energies of two ferroelectric states with an antiparallel polarization direction (λ = ±1) are symmetric (Fig. S9B†). The energy barrier for the polarization reversal reaches a maximum at theλ = 0 state. The variation of the energy path shows a typical ferroelectric double-well potential with two opposite polarization states located at two symmetric energy minimums, which provides direct proof for the appropriate polarization explanation.

Fig. 3 Structural evolution during the ferroelectric polarization inversion. Domain structure observed in the as-grown (3,3-DFCBA)Cl thin film. (A) Initial structure in one ferroelectric phase of (3,3-DFCBA)Cl with negative polarization direction. (B) Hypothetical structure with zero polarization. (C) Switched structure in another ferroelectric phase with positive polarization.

The ferroelectric properties of (3,3-DFCBA)Cl are further characterized by performing piezoresponse force microscopy (PFM) measurements in its thin-film samples. Fig. 4A–D shows the domain structure observed in the as-grown (3,3-DFCBA)Cl thin film, where the images are constructed by overlaying the lateral and vertical PFM phase and amplitude mappings on three-dimensional (3D) topography. No topographic features or crosstalk are observed in the PFM images. The same domain patterns can be clearly observed in the lateral (Fig. 4C) and vertical (Fig. 4D) PFM amplitude images. For PFM phase imaging which reflects the domain orientation, we observed that the adjacent domains have a phase contrast of 180° in the lateral PFM mode (Fig. 4A), while it is an almost unique color tone in the vertical PFM mode (Fig. 4B). Therefore, the polarization directions of adjacent domains are the same in the out-of-plane component, and different in the in-plane component, suggesting that domain walls should be non-180° ones. These findings indicate that (3,3-DFCBA)Cl is a multiaxial ferroelectric, where the non-180° domain wall is permitted.⁴⁴

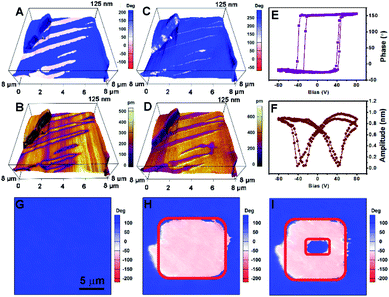Fig. 4 PFM of (3,3-DFCBA)Cl. Lateral PFM (A) phase and (B) amplitude mappings overlaid on 3D topography. Vertical PFM (C) phase and (D) amplitude mappings are overlaid on 3D topography. (E) PFM phase hysteretic loops and (F) butterfly-shaped amplitude loops for a selected point. Vertical phase images of a single domain region (G) in the initial state, (H) after electric writing over the red-box region with a voltage of +50 V and (I) back switching operation proceeded by applying an opposite voltage of −50 V over the smaller red-box region. The corresponding topography and amplitude images for (G)–(I) are shown in Fig. S10.†

PFM is also an efficient tool for probing and switching the local ferroelectric polarization at the nanoscale. We detected a DC bias-dependent PFM amplitude and phase response underneath the PFM tip. As shown in Fig. 4E and F, the typically butterfly-shaped amplitude curves and hysteretic phase curves demonstrate the switchable polarization in the (3,3-DFCBA)Cl thin film. Then, we selected a single-domain region for domain switching measurements (Fig. 4G). The red-box region in Fig. 4H was first poled with a voltage of +50 V, and followed with second electric writing with an opposite voltage of −50 V in the smaller red-box region in Fig. 4I. Finally, a box-in-box switched domain pattern was generated, providing robust evidence for the ferroelectricity of (3,3-DFCBA)Cl.

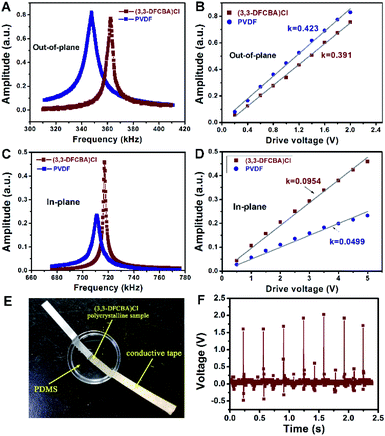
Next, the piezoelectricity of the (3,3-DFCBA)Cl thin film was investigated by using the PFM technique, a powerful method to probe electromechanical coupling at the nanoscale.^33,45 We first excited the thin film by using PFM tip across the resonant frequency in the vertical PFM mode at a voltage of 2 V and compared it to that of the PVDF film at the same drive voltage. We found that the resonance peak of the (3,3-DFCBA)Cl thin film was comparable with that of the PVDF thin film (Fig. 5A). The vertical PFM measures the z-axis vibration of the tip cantilever, which is proportional to the piezoelectric coefficient d₃₃ of the sample. To estimate the value of the piezoelectric coefficient, d₃₃, of the (3,3-DFCBA)Cl thin film in the out-of-plane component, such resonance measurements have been performed under a set of drive voltages. The peak values which have been corrected by quality factors were plotted against the drive voltages, as shown in Fig. 5B. Both lines show good linearity, indicating that the response comes from intrinsic piezoelectricity.⁴⁶ Their slopes represent the relative magnitude of d₃₃. Here, the PVDF thin film was set as the benchmark, whose d₃₃ is known as 33 pC N⁻¹.³⁴ We then estimated the d₃₃ of the (3,3-DFCBA)Cl thin film as 30.5 pC N⁻¹ according to the slope values, comparable to those of classical organic piezoelectrics (Table S5†).^47–53

Fig. 5 Piezoelectricity of (3,3-DFCBA)Cl. (A) Comparison of vertical PFM resonance peaks of the films of (3,3-DFCBA)Cl and PVDF. (B) Comparison of the effective vertical piezoelectric coefficient of the films of (3,3-DFCBA)Cl and PVDF. (C) Comparison of lateral PFM resonance peaks of the films of (3,3-DFCBA)Cl and PVDF. (D) Comparison of the effective lateral piezoelectric coefficient of the films of (3,3-DFCBA)Cl and PVDF. (E) The photograph for the device based on (3,3-DFCBA)Cl. (F) Output voltages of our device under a set of impacts.

Moreover, we observed that the (3,3-DFCBA)Cl thin film also has a strong in-plane piezoresponse when we aligned the PFM cantilever along the y-axis direction, as shown in Fig. S11.† In this case, the measured polarization is along the x component, and the cantilever motion is induced by the piezoelectric coefficient d₃₁.⁵⁴ Using the same approach, we extract the d₃₁ of the (3,3-DFCBA)Cl film from the comparison with that of PVDF, whose d₃₁ has been determined to be 21.4 pC N⁻¹.⁵⁵Fig. 5C shows the resonance peaks for both films in the lateral PFM mode under a voltage of 5 V, where a stronger resonance peak is observed in the (3,3-DFCBA)Cl film. Furthermore, we drove both films under a set of voltages up to 5 V, as shown in Fig. 5D. The slope of the (3,3-DFCBA)Cl film is 1.91 times larger than that of the PVDF film. Then, we estimated the d₃₁ of (3,3-DFCBA)Cl to be about 40.9 pC N⁻¹.

For practical application, the piezoelectric voltage coefficient (g_ij), as a key parameter for piezoelectric sensors, can be evaluated through piezoelectric effects and dielectric permittivity. The piezoelectric voltage coefficient g₃₃ can be obtained through the formula g₃₃ = d₃₃/ε₃₃, in which ε₃₃ can be derived from ε_r = ε₃₃/ε₀. Therefore, we calculated that the g₃₃ for our thin film is 437.2 × 10⁻³ V m N⁻¹, about two times larger than that of PVDF, 286.7 × 10⁻³ V m N⁻¹, and much higher than that of high-end PZT-based piezoelectric ceramics (about 20–40 × 10⁻³ V m N⁻¹) (Table S5†). With regard to the in-plane piezoelectric voltage coefficient, g₃₁ = d₃₁/ε₃₃, we calculated it to be about 586.2 × 10⁻³ V m N⁻¹. The large in-plane piezoelectric voltage coefficient makes the (3,3-DFCBA)Cl thin film have great merit for in-plane devices. Of particular note is the low acoustic impedance (z₀) of (3,3-DFCBA)Cl. The z₀ value of (3,3-DFCBA)Cl (2.25–3.26 × 10⁶ kg s⁻¹ m⁻²) is significantly lower than that of the conventional molecular ferroelectric triglycine sulfate (TGS, 9.74 × 10⁶ kg s⁻¹ m⁻²) and even that of the ferroelectric polymer PVDF (3.69 × 10⁶ kg s⁻¹ m⁻²) (Table S6†), an order of magnitude lower than that of inorganic ferroelectric ceramics (PZT, 2.54 × 10⁷ kg s⁻¹ m⁻²), which suggests good biocompatibility and efficient broadband operation of (3,3-DFCBA)Cl based electroacoustic and electromechanical transducers operating in tissue, water, or other low impedance material.

In addition to a large piezoelectric voltage coefficient (g₃₃), a large electrostriction coefficient (Q₃₃), which can make the materials have the characteristics of a fast response speed, temperature stability, and reducing aging effects, is also critical for good piezoelectrics. Based on the relation of Q₃₃ = g₃₃/2P_s, the electrostriction coefficient Q₃₃ of the (3,3-DFCBA)Cl thin film is calculated to be 4.29 m⁴ C⁻², which is much larger than that of PVDF (1.3 m⁴ C⁻²) (Fig. S12†), and two orders of magnitude larger than that of ceramic ferroelectrics.^5,20 Herein, an energy harvesting device was fabricated with an electrode-(3,3-DFCBA)Cl-electrode structure based on its pristine polycrystalline sample, which was made with a pressed-powder pellet (Fig. 5E). The generated piezoelectric voltages were recorded after repetitively impacting at a certain mechanical pressure, and measured by using an oscilloscope. As shown in Fig. 5F, the device exhibits an average voltage of about 1.7 V. The good performance of electromechanical energy conversion revealed that (3,3-DFCBA)Cl has great potential in the application of self-powered devices.

Conclusions

In summary, we report a metal-free small-molecule ferroelectric material (3,3-DFCBA)Cl with a remarkable piezoelectric and biocompatible performance, which is far beyond that of the commercialized polymer PVDF. (3,3-DFCBA)Cl is a fluorine-containing organic ferroelectric without toxic metals, whose solubility in water is very high, about 167 g/100 g. Such excellent properties, i.e. a large piezoelectric voltage coefficient g₃₃ (437.2 × 10⁻³ V m N⁻¹), in-plane piezoelectric voltage coefficient g₃₁ (586.2 × 10⁻³ V m N⁻¹), electrostriction coefficient Q₃₃ (4.29 m⁴ C⁻²), and low acoustic impedance (2.25–3.26 × 10⁶ kg s⁻¹ m⁻²), give metal-free small-molecule ferroelectric (3,3-DFCBA)Cl the possibility for application in medical piezoelectric sensor devices.

Experimental

Material synthesis and crystal growth

All the required chemical reagents were commercially purchased and used without any further purification for synthesis. The crystals of (3,3-DFCBA)Cl and (CBA)Cl were obtained through slow evaporation of a solution of ethanol/H2O (1 : 1). Thermal stability of (3,3-DFCBA)Cl and (CBA)Cl was measured by thermogravimetric analysis (Fig. S13†).

Thin-film preparation

The precursor solution of (3,3-DFCBA)Cl was prepared by dissolving 20 mg of the crystals in 500 μL ethanol. Then, 20 μL precursor solution was spread on a clean indium-doped tin oxide (ITO) glass substrate. The thin film was obtained after annealing at 300 K for 30 min.

X-ray diffraction characterization studies

Variable-temperature XRD patterns were measured using a Rigaku Saturn 724+ CCD diffractometer with Mo-Kα radiation (λ = 0.71073 Å). Data collection, cell refinement, and data reduction were performed using a Rigaku CrystalClear 1.3.5. The structures were solved by direct methods and refined by the full-matrix method based on F² using the SHELXTL software package. All non-hydrogen atoms were refined anisotropically and the positions of all the hydrogen atoms were generated geometrically. The CCDC 1978969–1978973 contains the supplementary crystallographic data for this paper.

DSC, SHG, and dielectric measurements

Differential scanning calorimetry (DSC) measurements were performed on a PerkinElmer Diamond DSC under a nitrogen atmosphere in aluminum crucibles with a heating or cooling rate of 20 K min⁻¹. For second harmonic generation (SHG) experiments, an unexpanded laser beam with low divergence (pulsed Nd:YAG at a wavelength of 1064 nm, 5 ns pulse duration, 1.6 MW peak power, and 10 Hz repetition rate) was used. The instrument model is Ins 1210058, INSTEC Instruments, while the laser is Vibrant 355 II, OPOTEK. The numerical values of the nonlinear optical coefficients for SHG have been determined by comparison with a KDP reference. For macroscopic dielectric property measurement, the samples were made with a pressed-powder pellet. Silver conductive paste deposited on the plate surfaces was used as the top and bottom electrodes. Complex dielectric permittivities were measured with a TH2828A impedance analyzer over a frequency of 1 kHz.

Ferroelectric property measurements and PFM characterization

The double-wave method was employed to examine the ferroelectric properties. A thin-film crystal capacitor was fabricated for the P–E hysteresis loop measurement. The ferroelectric hysteresis measurements were conducted with this capacitor architecture (GaIn/sample film/ITO) by the double wave method. The double-wave method was carried out on a home-built system consisting of a programmable waveform generator (Keysight, Model: 33500B), high voltage amplifier (Trek, model: 609E-6) and programmable low-current electrometer (Keithley, model: 6514). A conductive ITO was used as the bottom electrode. For the prepared thin film (about 2 μm thick), the top electrode was directly selected as liquid GaIn eutectic. Liquid GaIn eutectic presents an ellipsoid shape, and the area of residual traces after removal of the eutectic is taken as the contact area (0.21 mm²). The operation frequency is 50 Hz and the applied electric field is E = ±25 to ±28 kV cm⁻¹. The PFM measurement was carried out on a commercial piezoresponse force microscope (Oxford instrument, MFP-3D) with a high-voltage package and in situ heating stage. PFM is based on atomic force microscopy (AFM), with an AC drive voltage applied to the conductive tip. Conductive Pt/Ir-coated silicon probes (EFM, Nanoworld) were used for domain imaging and polarization switching studies, with a nominal spring constant of ∼2.8 nN nm⁻¹ and a free-air resonance frequency of ∼75 kHz. Since the amplitude of the low-frequency vertical PFM was within the noise level of the quadrant photodetector of the AFM, we performed the PFM experiments at contact resonance. The typical drive frequency was in the range of 320 to 380 kHz for out-of-plane PFM images and 660 to 780 kHz for in-plane PFM images, depending on the contact resonance frequency.

Calculation conditions

In order to investigate the microscopic ferroelectric polarization, we carried out density functional calculations based on the Berry phase method developed by Kingsmith and Vanderbilt.^49,50 The first-principles calculations were performed within the framework of density functional theory implemented in the Vienna ab initio Simulation Package (VASP).^51,52 The energy cut-off for the expansion of the wave functions was fixed at 550 eV and the exchange–correlation interactions were treated within the generalized gradient approximation of the Perdew–Burke–Ernzerhof type.⁵³ For the integrations over the k-space, we used a 4 × 4 × 3 k-point mesh. The experimental room temperature (293 K) crystal structure was used as the ground state for evaluating the ferroelectric polarization. The rotation of the 3,3-DFCBA cations and displacement of Cl⁻ are realized by matrix transformation of the coordinates using Microsoft Excel.

Data availability

The experimental data supporting this article have been uploaded as part of the ESI.†

Author contributions

Han-Yue Zhang devised and developed the project, performed the experiments, analysed the data, discussed the results and participated to the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The manuscript was improved by the insightful reviews by anonymous reviewers. This work was supported by the Ten Science and Technology Problem of Southeast University.

Notes and references

1. D. Damjanovic, Rep. Prog. Phys., 1998, 61, 1267.
2. K. Uchino, Piezoelectric actuators and ultrasonic motors, Springer Science & Business Media, 1996.
3. M. E. Lines and A. M. Glass, Principles and applications of ferroelectrics and related materials, Oxford University Press, 1977.
4. J. Scott, Science, 2007, 315, 954–959.
5. C. Qiu, B. Wang, N. Zhang, S. Zhang, J. Liu, D. Walker, Y. Wang, H. Tian, T. R. Shrout, Z. Xu, L.-Q. Chen and F. Li, Nature, 2020, 577, 350–354.
6. F. Li, M. J. Cabral, B. Xu, Z. Cheng, E. C. Dickey, J. M. LeBeau, J. Wang, J. Luo, S. Taylor, W. Hackenberger, L. Bellaiche, Z. Xu, L.-Q. Chen, T. R. Shrout and S. Zhang, Science, 2019, 364, 264–268.
7. S. Zhang and F. Li, J. Appl. Phys., 2012, 111, 031301.
8. K. Uchino, Ferroelectric devices, CRC Press, 2018.
9. S. J. Zhang, F. Li, X. N. Jiang, J. Kim, J. Luo and X. C. Geng, Prog. Mater. Sci., 2015, 68, 1.
10. S. Zhang and F. Yu, J. Am. Ceram. Soc., 2011, 94, 3153.
11. B. H. Liu, P. Li, B. Shen, J. W. Zhai, Y. Zhang, F. Li and X. Liu, J. Am. Ceram. Soc., 2018, 101, 265.
12. J. F. Tressler, S. Alkoy and R. E. Newnham, J. Electroceram., 1998, 2, 257.
13. S. Tadigadapa and K. Mateti, Meas. Sci. Technol., 2009, 20, 092001.
14. G. H. Haertling, J. Am. Ceram. Soc., 1999, 82, 797–818.
15. B. Jaffe, R. Roth and S. Marzullo, J. Appl. Phys., 1954, 25, 809.
16. J. Rodel, W. Jo, K. T. P. Seifert, E. M. Anton, T. Granzow and D. Damjanovic, J. Am. Ceram. Soc., 2009, 92, 1153.
17. J. Rodel, K. G. Webber, R. Dittmer, W. Jo, M. Kimura and D. Damjanovic, J. Eur. Ceram. Soc., 2015, 35, 1659.
18. H. Azhari, Basics of Biomedical Ultrasound for Engineers, IEEE Press, 2010.
19. M. Y. Li, H. J. Wondergem, M. J. Spijkman, K. Asadi, I. Katsouras, P. W. M. Blom and D. M. de Leeuw, Nat. Mater., 2013, 12, 433.
20. Y. Liu, H. Aziguli, B. Zhang, W. Xu, W. Lu, J. Bernholc and Q. Wang, Nature, 2018, 562, 96–100.
21. B. Neese, B. Chu, S.-G. Lu, Y. Wang, E. Furman and Q. M. Zhang, Science, 2008, 321, 821–823.
22. B. Chu, X. Zhou, K. Ren, B. Neese, M. Lin, Q. Wang, F. Bauer and Q. M. Zhang, Science, 2006, 313, 334–336.
23. K. S. Ramadan, D. Sameoto and S. Evoy, Smart Mater. Struct., 2014, 23, 033001.
24. S. Horiuchi and Y. Tokura, Nat. Mater., 2008, 7, 357–366.
25. M. A. Marcus, Ferroelectrics, 1982, 40, 29–41.
26. Q.-D. Ling, D.-J. Liaw, C. Zhu, D. S.-H. Chan, E.-T. Kang and K.-G. Neoh, Prog. Polym. Sci., 2008, 33, 917.
27. P.-P. Shi, Y.-Y. Tang, P.-F. Li, W.-Q. Liao, Z.-X. Wang, Q. Ye and R.-G. Xiong, Chem. Soc. Rev., 2016, 45, 3811.
28. Y.-Y. Tang, P.-F. Li, W.-Q. Liao, P.-P. Shi, Y.-M. You and R.-G. Xiong, J. Am. Chem. Soc., 2018, 140, 8051.
29. D. W. Fu, H. L. Cai, Y. Liu, Q. Ye, W. Zhang, Y. Zhang, X. Y. Chen, G. Giovannetti, M. Capone, J. Li and R. G. Xiong, Science, 2013, 339, 425–428.
30. J. Harada, T. Shimojo, H. Oyamaguchi, H. Hasegawa, Y. Takahashi, K. Satomi, Y. Suzuki, J. Kawamata and T. Inabe, Nat. Chem., 2016, 8, 946–952.
31. G. C. Xu, W. Zhang, X. M. Ma, Y. H. Chen, L. Zhang, H. L. Cai, Z. M. Wang, R. G. Xiong and S. Gao, J. Am. Chem. Soc., 2011, 133, 14948–14951.
32. D. W. Fu, W. Zhang, H. L. Cai, J. Z. Ge, Y. Zhang and R. G. Xiong, Adv. Mater., 2011, 23, 5658.
33. W.-Q. Liao, D. Zhao, Y.-Y. Tang, Y. Zhang, P.-F. Li, P.-P. Shi, X.-G. Chen, Y.-M. You and R.-G. Xiong, Science, 2019, 363, 1206.
34. Y.-M. You, W.-Q. Liao, D. Zhao, H.-Y. Ye, Y. Zhang, Q. Zhou, X. Niu, J. Wang, P.-F. Li and D.-W. Fu, Science, 2017, 357, 306–309.
35. Y. Ai, X.-G. Chen, P.-P. Shi, Y.-Y. Tang, P.-F. Li, W.-Q. Liao and R.-G. Xiong, J. Am. Chem. Soc., 2019, 141, 4474.
36. T.-T. Sha, Y.-A. Xiong, Q. Pan, X.-G. Chen, X.-J. Song, J. Yao, S.-R. Miao, Z.-Y. Jing, Z.-J. Feng, Y.-M. You and R.-G. Xiong, Adv. Mater., 2019, 31, e1901843.
37. P.-P. Shi, S.-Q. Lu, X.-J. Song, X.-G. Chen, W.-Q. Liao, P.-F. Li, Y.-Y. Tang and R.-G. Xiong, J. Am. Chem. Soc., 2019, 141, 18334.
38. W.-J. Xu, P.-F. Li, Y.-Y. Tang, W.-X. Zhang, R.-G. Xiong and X.-M. Chen, J. Am. Chem. Soc., 2017, 139, 6369–6375.
39. P. F. Li, Y. Y. Tang, Z. X. Wang, H. Y. Ye, Y. M. You and R. G. Xiong, Nat. Commun., 2016, 7, 13635.
40. D. Di Sante, A. Stroppa, P. Jain and S. Picozzi, J. Am. Chem. Soc., 2013, 135, 18126–18130.
41. A. Stroppa, P. Barone, P. Jain, J. M. Perez-Mato and S. Picozzi, Adv. Mater., 2013, 25, 2284–2290.
42. R. Resta and D. Vanderbilt, Theory of Polarization: A Modern Approach, in Physics of Ferroelectrics. Topics in Applied Physics, Springer, 2007.
43. N. A. Spaldin, J. Solid State Chem., 2012, 195, 2–10.
44. P.-P. Shi, S.-Q. Lu, X.-J. Song, X.-G. Chen, W.-Q. Liao, P.-F. Li, Y.-Y. Tang and R.-G. Xiong, J. Am. Chem. Soc., 2019, 141, 18334–18340.
45. Y. Zhang, Y. Liu, H. Y. Ye, D. W. Fu, W. Gao, H. Ma, Z. Liu, Y. Liu, W. Zhang, J. Li, G. L. Yuan and R. G. Xiong, Angew. Chem., Int. Ed., 2014, 53, 5064–5068.
46. Y. Liu, Y. Zhang, M.-J. Chow, Q. N. Chen and J. Li, Phys. Rev. Lett., 2012, 108, 078103.
47. T. Vijayakanth, D. J. Liptrot, E. Gazit, R. Boomishankar and C. R. Bowen, Adv. Funct. Mater., 2022, 2109492.
48. T. Vijayakanth, F. Ram, B. Praveenkumar, K. Shanmuganathan and R. Boomishankar, Chem. Mater., 2019, 31, 5964–5972.
49. V. Basavalingappa, S. Bera, B. Xue, J. O'Donnell, S. Guerin, P.-A. Cazade, H. Yuan, E. u. Haq, C. Silien, K. Tao, L. J. W. Shimon, S. A. M. Tofail, D. Thompson, S. Kolusheva, R. Yang, Y. Cao and E. Gazit, ACS Nano, 2020, 14, 7025–7037.
50. W. Ji, B. Xue, S. Bera, S. Guerin, Y. Liu, H. Yuan, Q. Li, C. Yuan, L. J. W. Shimon, Q. Ma, E. Kiely, S. A. M. Tofail, M. Si, X. Yan, Y. Cao, W. Wang, R. Yang, D. Thompson, J. Li and E. Gazit, ACS Nano, 2020, 14, 10704–10715.
51. S. Guerin, S. A. M. Tofail and D. Thompson, NPG Asia Mater., 2019, 11, 10.
52. S. Bera, S. Guerin, H. Yuan, J. O'Donnell, N. P. Reynolds, O. Maraba, W. Ji, L. J. W. Shimon, P.-A. Cazade, S. A. M. Tofail, D. Thompson, R. Yang and E. Gazit, Nat. Commun., 2021, 12, 2634.
53. T. Vijayakanth, A. K. Srivastava, F. Ram, P. Kulkarni, K. Shanmuganathan, B. Praveenkumar and R. Boomishankar, Angew. Chem., Int. Ed., 2018, 57, 9054–9058.
54. W. S. Su, Y. F. Chen, W. Y. Shin, H. Luo and W. H. Shih, Appl. Phys. Lett., 2007, 91, 112903.
55. R. G. Kepler and R. A. Anderson, Adv. Phys., 1992, 41, 1–57.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1978969–1978973. For ESI and crystallographic data in CIF or other electronic format see https://doi.org/10.1039/d1sc06909h

---